Exploring the Dynamics of Global Plate Motion Based on the Granger Causality Test

Abstract

The geodynamic mechanism is the research focus and core issue of plate motions and plate tectonics. Analyzing the time series of earthquakes may help us understand the relationship between two plate boundaries and further explore movement mechanisms. Therefore, this paper uses earthquake event data and the Granger causality test method to quantitatively analyze the interaction and energy transfer relationship of plate boundaries from the viewpoint of statistics. The paper aims to explore the relationship between the pull effect and the push effect of plate motion and to provide knowledge to explore seismic energy transfer relationships, and even to predict earthquakes: (1) The directions of the global plate motion field are opposite to the directions of Granger causality between plate boundaries of the Pacific, Nazca, African, Australian, Eurasian, and Philippine plates. (2) The slab-pull force (not limited to the subduction force of the ocean plates) provides a main driving force for plate motions in the Pacific plate, Nazca plate, African plate, Australian plate, Eurasian plate, and Philippine sea plate. (3) The causality relationship and optimal lag length of energy release between plate boundaries may provide another view to forecasting earthquakes.

1. Introduction

The Earth is a complex whole, and its interior is composed of multiple layers. The composition of the Earth’s interior, which is the structure of each sphere inside the Earth, can be inferred through the observation of seismic waves. This structure includes the crust, the upper mantle, the transition layer, the lower mantle, the D’’ layer, the outer core, and the inner core [1]. There are intricate interactions between the spherical layers, which can manifest in the form of crustal movements. Many forms of movement of the lithosphere composing the Earth’s surface can be found. There is not only the rotation of the Earth’s axis caused by the Earth’s rotation but also the relative motion within the lithosphere. With the development of geology and geophysics, the Earth’s surface can be divided into six major plates, including the Eurasian, African, Indian Ocean, Antarctica, Pacific, and America plates [2]. The second-generation model [3,4], the third-generation model [5], and the fourth-generation model [6] were successively proposed. These lithospheric plates vary in size, and the relative motion between them is too slow to notice by humans. However, as time goes by, the plates will develop intense movements when their relative motions exceed the critical state. Thus, various geological disasters such as earthquakes and volcanoes can be triggered and cause serious damage to the lives and property of humans. Therefore, understanding the movement law and geodynamic mechanism of these plates is a fascinating subject. It is of great significance to study the occurrences of earthquakes and eruptions of volcanoes mechanically, and to predict these events to minimize the loss of life and property, thus ensuring the sustainable development of human society.

During the last century, benefiting from the development of science and technology, increasingly advanced technologies have been applied to studying the patterns of plate movements. Paleomagnetism, a powerful tool for the quantitative study of plate kinematics and ancient geography, emerged in the 1960s [7,8]. Using high-quality paleomagnetic data, Zhang et al. quantitatively established the first geologically viable configuration and depicted the paleogeographic positions of the Nuna supercontinent [9]. Yang et al. took advantage of reliable Cretaceous paleomagnetic data obtained from the Lhasa terrane (a crust fragment formed on a tectonic plate and accreted or “sutured” to crust lying on another plate) to study the complex process and timing of the India-Asia plate collision, and found the collision time was Eocene [10]. Furthermore, the development of new space geodetic technologies, such as the global positioning system (GPS), very long baseline interferometry (VLBI), and satellite laser ranging (SLR), opened up new ways of monitoring and studying crustal movements and can measure the overall motion of Earth with millimeter-level precision. In addition, these new technologies and new tools have been applied to research on plate motions and crustal deformation, which provide the possibility of solving many basic problems in plate motion research and have fundamentally changed human monitoring and study of earth movements [11,12,13].

The geodynamic mechanism is the research focus and core issue of plate motions and plate tectonics, and it is also the greatest mystery in Earth science [14,15]. Since the discovery by humans of the phenomenon of plate motion, geologists have been exploring the dynamic mechanisms and sources of power, and various geodynamic hypotheses have been created, such as earth contraction [16], earth expansion [17], continental drift [18,19], seafloor spreading [20], plate tectonics [2,6,21], mantle convection [22,23], mantle plumes [24,25,26], and surge tectonics [27]. Some of these are in contradiction, some are not. Mantle convection is the most famous among many Earth dynamic hypotheses and the most recognized by Earth scientists. After years of research, this hypothesis has made great progress. The hypothesis includes the following: (1) the mid-ocean ridge is the outlet for the rise of mantle material, forming a new oceanic crust and promoting the expansion of the crust on both sides; (2) when mantle convection occurs inside the Earth, the solid lithosphere is driven to move; (3) the crust in the subduction zone sinks, carried by the cold, heavy, downward-moving mantle, inducing movement of the oceanic crust behind. Nevertheless, some problems have not been resolved by the hypothesis. Various aspects need to be improved and developed. For example, in global plate motion, the question is, which one is the dominant force, the pull effect existed at the subduction zone or the push effect existed at the mid-ocean ridge? Few articles have discussed this issue [28,29,30,31]. Forsyth’s study suggests that the forces acting on the downgoing slab control the velocity of the oceanic plates and are an order of magnitude stronger than any other force [32]; Parmentier found that the stress generated by a subduction zone can drive an entire plate to move in the horizontal direction through the hypothesis test [33]; and Stadler [34] believed that the strength of subducted slabs probably regulates the velocity of plate tectonics. In contrast, some people hold opposing views about this hypothesis [30,35]. Although many geophysicists have discussed this issue, there is no unified understanding and no definitive answer. Meanwhile, although some researchers found that the subduction force is the main force of plate motion, it is not known if this conclusion applies to all global plates, or only to a few plates.

The output of an earthquake is the most direct result of relative plate movement and results from the sudden release of energy in the Earth’s lithosphere. Thus, analyzing the series of earthquakes occurring at the border areas between plates may help us understanding the geodynamic mechanism and comprehend the relationship between the subduction and expansion effects. Therefore, based on plate motion and continental drift theory, this paper uses earthquake events data and the Granger causality test method to quantitatively analyze the interaction and energy transfer relationship between plate boundaries from the perspective of statistical physics. The objective of this paper is to explore the relationship between the pull effect and the push effect of plate motion, as well as the ductile mantle convection theory, to provide a new view for seismic energy transfer research and earthquake prediction.

2. Methods

The Granger causality test is mostly used to examine the causal relationships between two or more variables. If the accuracy of prediction of one time series can be improved by the incorporation of another time series, it can be said that the second series has a causal effect on the first one. In other words, according to Granger causality, a time series X can cause Y if the hysteresis value of X can help increase the accuracy of the prediction of Y. The idea of causal effect, which is the Granger causality, was first introduced by Wiener [36] and then formulated by Granger with linear regression models [37,38].

There are three main steps in processing the Granger causality test: estimating a bivariate linear model, determining the optimal lag length, and testing the significance of the lags in the exogenous variables [39]. Vector autoregression (VAR) is the most popular model used in the economic field to capture the interdependencies and causality relationship among multiple time series. VAR has a unique advantage where it treats each variable in the system as potentially endogenous and relates each to its past values and the past values of all other variables included in the model [40].

$$X_{\mathrm{t}}=\mathsf{\alpha }+{{\displaystyle \sum }}_{i=1}^m{\beta }_{\mathrm{i}}{X}_{\mathrm{t}-\mathrm{i}}+{{\displaystyle \sum }}_{j=1}^n{\gamma }_{\mathrm{j}}{Y}_{\mathrm{t}-\mathrm{j}}+u_{\mathrm{t}}$$

(1)

$$Y_{\mathrm{t}}=\mathsf{\alpha }+{{\displaystyle \sum }}_{i=1}^q{b}_{\mathrm{i}}{Y}_{\mathrm{t}-\mathrm{i}}+{{\displaystyle \sum }}_{j=1}^r{c}_{\mathrm{j}}{X}_{\mathrm{t}-\mathrm{j}}+v_{\mathrm{t}}$$

(2)

where u_t and v_t refer to random disturbances that may be correlated for various time series; t to the time period; i and j to the lag; and m, n, q, and r to the optimum lag length, which are determined by the Akaike information criterion.

Now, for the two equations there is one-way Granger causality running from Y to X if, in the first equation, not all γ_j are zero but, in the second equation, all c_i is zero; on the contrary, X Granger causes Y if, in the second equation, not all c_i is zero but, in the first equation, all γ_j are zero. In addition to these two cases, there is two-way Granger causality between X and Y if neither all γ_j nor all c_i is zero, and there is no Granger causality between X and Y if all γ_j and c_i is zero [41,42,43].

However, spurious and misleading results may be obtained if the variables are nonstationary [44,45]. Therefore, before performing the Granger causality test, a unit root test, which is used to test time-series stability, should be performed first using augmented Dickey–Fuller (ADF) and/or nonparametric Z(t_α) statistics [46]. If the test is not passed, depending on the time series, an initial or some higher difference of the time series needs to be made. The next step is to test the possibility of cointegration among the variables, which is used to rule out the possibility of a “spurious” correlation with the help of the Engle–Granger technique. However, the cointegration test indicates only whether there is a Granger causality between the variables. It should be emphasized that the direction of Granger causality can be obtained by constructing the VAR model.

3. Data Analysis and Results

3.1. Data Preparation

The International Seismological Center-Global Earthquake Model (ISC-GEM) provides a global earthquake catalog that has been widely used in a broad range of studies, such as tectonics, seismicity assessment, and determination of seismic hazard [47]. In addition to this catalog, there are several other international centers that provide earthquake record data, such as the National Earthquake Information Center (NEIC) and the International Data Center (IDC). Cheng [48] compared the numbers of events against magnitude based on the three catalogs and found that the numbers of events with magnitudes (a characterization of earthquake intensity) greater than five are similar. In other words, these databases from the three centers have the same recording capabilities for large earthquakes. Therefore, in this paper, a global database of earthquake records acquired from ISC was used, and the time period ranged from 1904 to 2014.

Before any scientific analysis of the earthquake catalog, an important procedure for most studies related to seismicity is to assess the consistency, quality, and homogeneity of the data. In the research, one specific aspect of quality control was addressed, which was determining the minimum magnitude of complete recording, M_c. This value was considered the lowest magnitude at which all of the earthquakes in a space-time volume were detected [49,50]. Here, the frequency-magnitude distribution (FMD) [51], which is one of the most popular methods to describe the relationship between the frequency and magnitude of an earthquake, was used to estimate M_c. The data were plotted as Log[N(>M)] against M and fitted with a linear function by the least-squares method (Figure 1). Based on the catalog earthquakes with magnitudes above 5.6, a general linear trend implied a power-law–frequency-size relationship between LogN and M. The result gives Log[N(>M)] = 15.66–2.69 M, with R² = 0.992. Therefore, M₀ = 5.6 was set as a threshold magnitude considering the completeness of the earthquake catalog, which included 24,650 large earthquakes from 1904 to 2014.

For demonstration purposes, the locations of earthquake events with magnitudes greater than 5.6 are shown in Figure 2. A global set of plate boundaries that contains 52 plates is presented by Bird in digital form [52]. However, the dataset is too meticulous to meet the needs of this study because it contains many small plates that do not have enough earthquake events. Thus, based on the dataset, new plate boundaries are formulated based on the USGS (http://volcanoes.usgs.gov/about/edu/dynamicplanet (accessed on 29 June 2018)) model, which contains 12 plates in total (Figure 2).

Plate boundaries are the border areas between two plates. There are 28 boundaries in this study (Figure 2). Because the purpose of this paper is to study the energy transfer relationship between plate border areas based on statistical physics methods, earthquakes are divided into 28 regions according to adjoining plate boundaries (

Table 1. Earthquakes and energy release at plate boundaries.

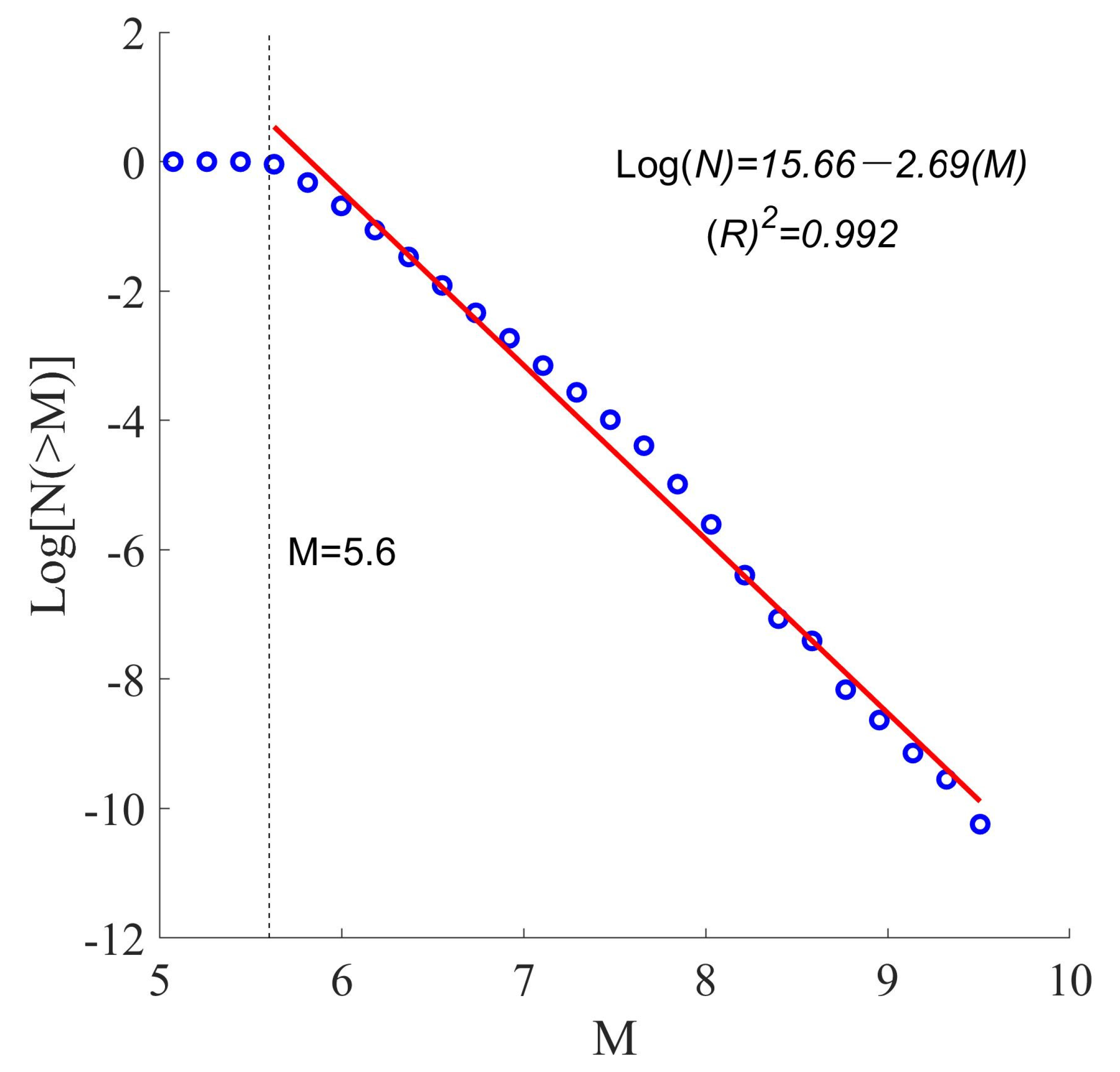
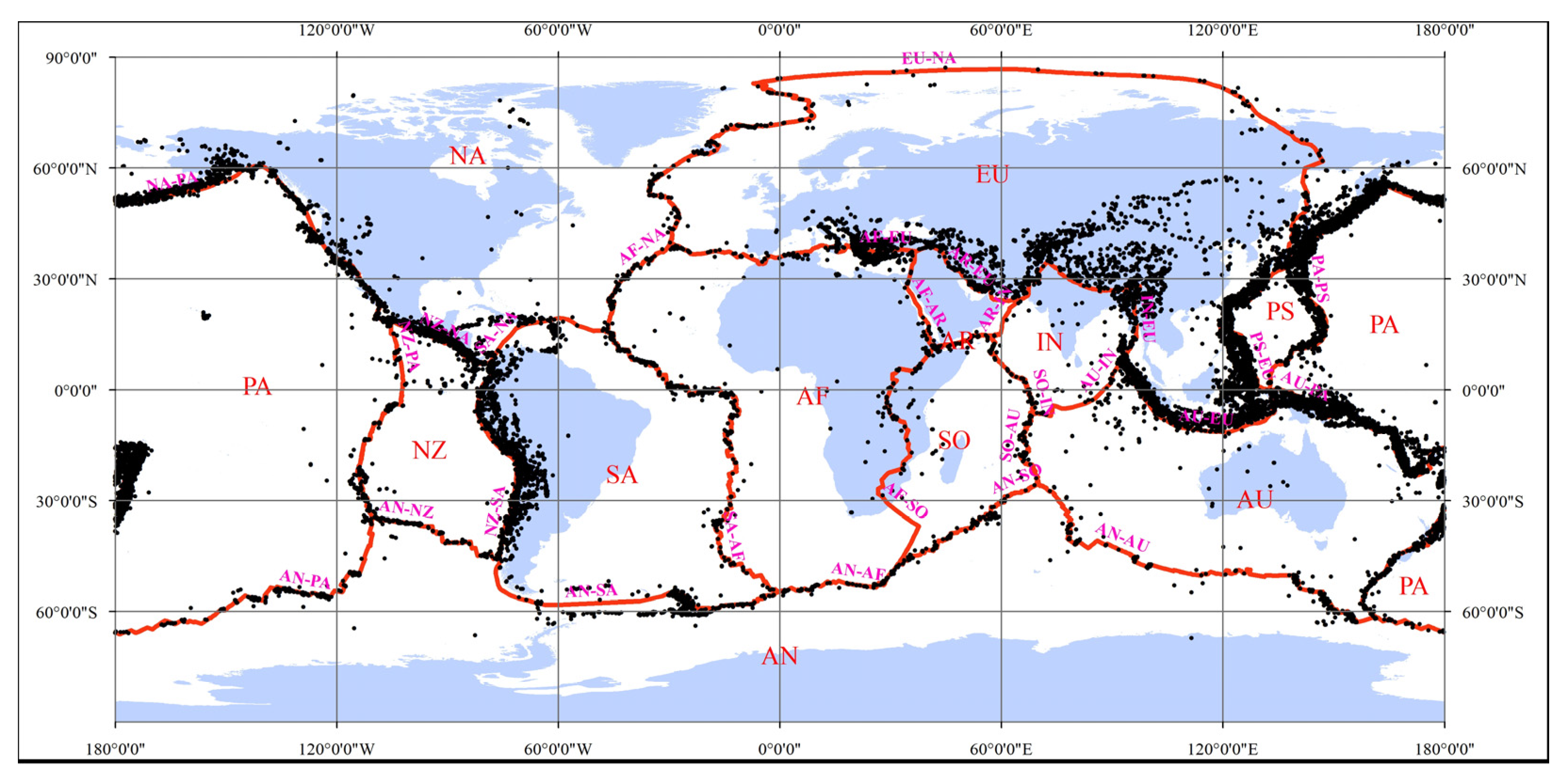
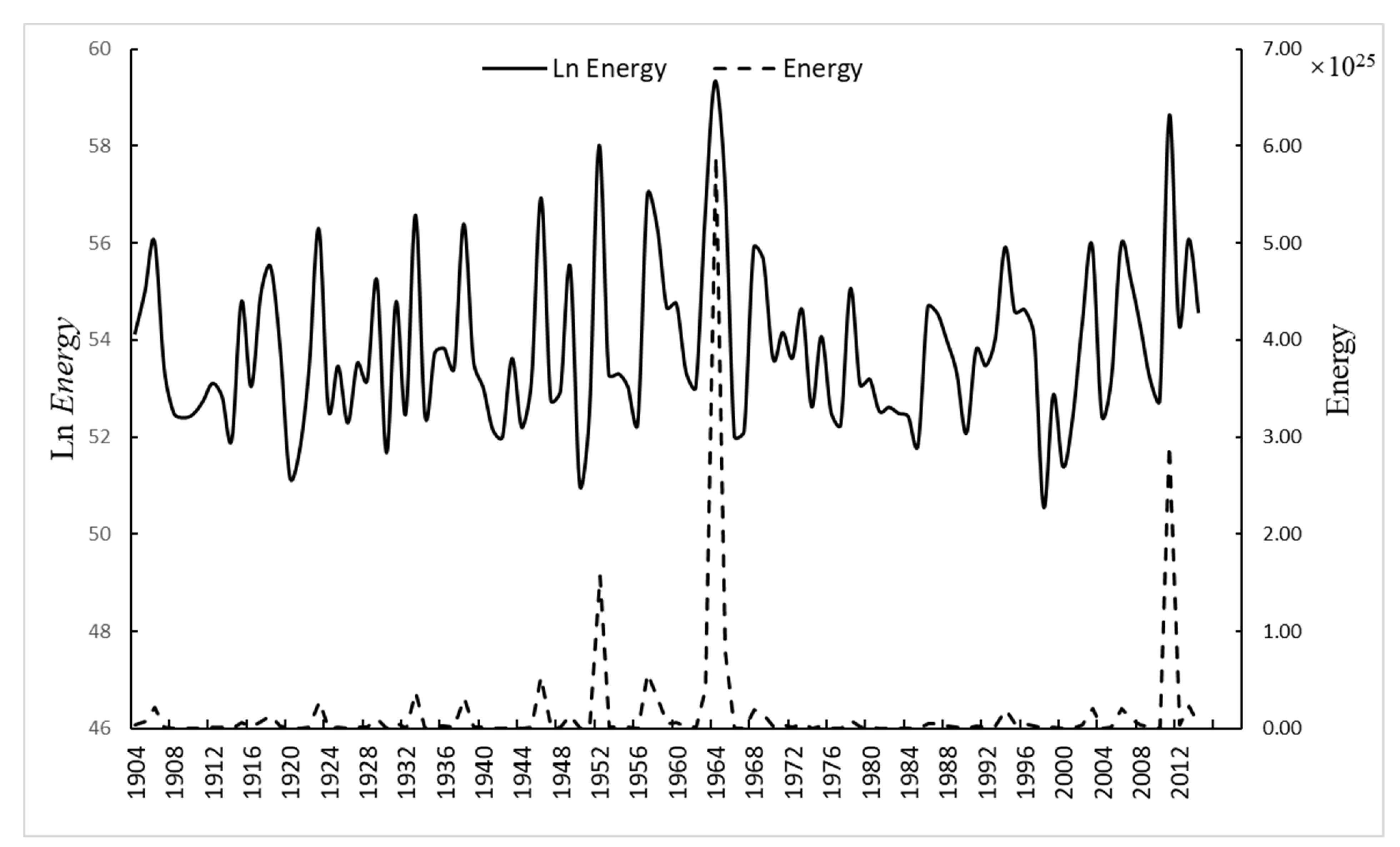
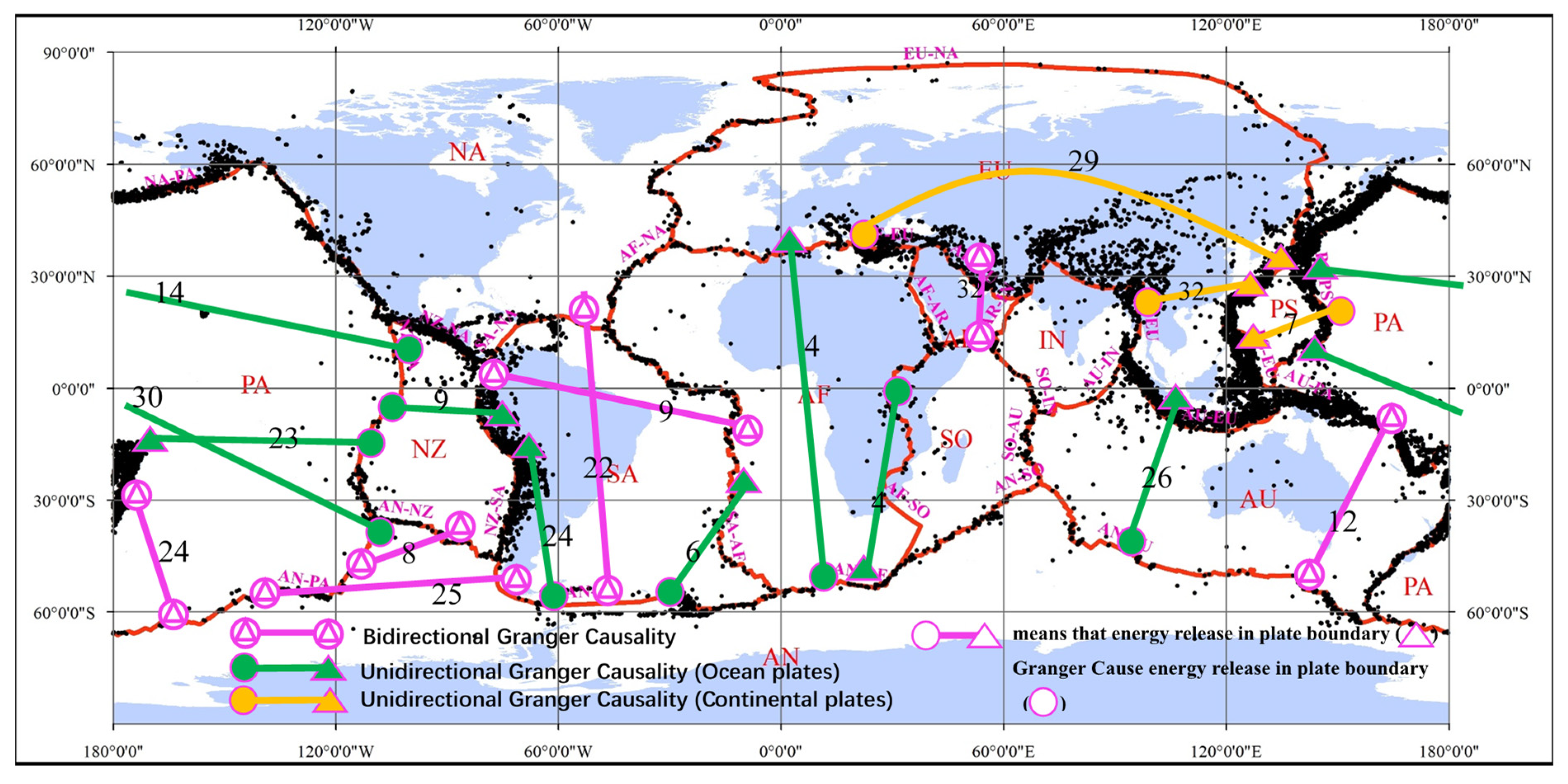
Boundary name

NA-PA

NZ-PA

AN-PA

AU-PA

NZ-NA

NZ-SA

AN-NZ

SA-NA

SA-AF

AN-SA

AF-NA

AF-EU

AF-AR

AF-SO

Earthquake Number

4479

283

275

6305

1017

1569

169

296

455

469

106

458

56

107

Energy release

1.75 × 1026

2.2 × 1023

1.71 × 1023

5.16 × 1025

1.07 × 1025

2.21 × 1026

1.51 × 1023

1.49 × 1024

8.18 × 1023

3.28 × 1024

5.79 × 1022

3.81 × 1024

8.32 × 1022

2.56 × 1023

Boundary name

AN-AF

AR-EU

AR-IN

SO-AR

SO-IN

SO-AU

AN-SO

IN-EU

AU-IN

AU-EU

AN-AU

PA-PS

PS-EU

EU-NA

Earthquake Number

84

387

7

57

65

84

121

1346

91

1507

355

681

2871

422

Energy release

7.24 × 1023

2.4 × 1024

9.09 × 1020

2.95 × 1022

1.82 × 1023

5.42 × 1022

3.89 × 1023

1.78 × 1025

2.39 × 1024

5.12 × 1025

1.23 × 1024

3.39 × 1024

2.87 × 1025

2.52 × 1024

). The earthquake energy release is related to the moment magnitude [53,54]. Therefore, the energy released by an earthquake with a moment magnitude (M_w, an evaluation method of earthquake magnitude) was calculated by the following equations. Due to the inconsistency and heterogeneity of earthquake occurrence, the energy release of an earthquake is processed into energy release at annual intervals. Following the above procedure, all energy release at plate boundaries was transformed into natural logs to help induce stationarity (Figure 3).

$$M_{\mathrm{w}}=0.67\times M_{\mathrm{x}}+2.07M_{\mathrm{s}}\le 6.1$$

(3)

$$M_{\mathrm{w}}=0.99\times M_{\mathrm{s}}+0.08M_{\mathrm{s}}\ge 6.2$$

(4)

$$\mathrm{Log}E=1.5\times M_{\mathrm{s}}+11.8$$

(5)

3.2. Stationarity Test of Energy Release

The following procedure employs the annual energy release after transformation into natural logs from 1904 to 2014 of 28 plate boundaries, as shown in Figure 3. The augmented Dickey–Fuller (ADF) test is the most frequently used unit root test to examine the stationarity of time series. It is an extension of the DF test, which is a parametric approach originally proposed by Dickey and Fuller [55,56]. Although the method is questioned by some studies, it is still one of the most widely used methods. In addition, Akiboade anticipated that many unit root test methods would support the same conclusion if a sufficient sample size was used. Therefore, ADF was used to test the stationarity of the energy release at all plate boundaries, and the results are presented in

Table 2. Unit root test using ADF for annual energy release at plate boundaries.

Boundary name

AF-AR

AF-EU

AF-NA

AF-SO

AN-AF

AN-AU

AN-NZ

AN-PA

AN-SA

AN-SO

AR-EU

AR-IN

AU-EU

AU-IN

ADF statistic

−10.52 ***

−12.393 ***

−8.244 ***

−10.45 ***

−11.275 ***

−7.871 ***

−11.24067 ***

−10.595 ***

−8.655 ***

−8.908 ***

−11.9 ***

−11.079 ***

−14.159 ***

−10.898 ***

Order of integration

0

0

0

0

0

0

0

0

0

0

0

0

0

0

Boundary name

AU-PA

EU-NA

IN-EU

NA-PA

NZ-NA

NZ-PA

NZ-SA

PA-PS

PS-EU

SA-AF

SA-NA

SO-AR

SO-AU

SO-IN

ADF statistic

−13.002 ***

−10.892 ***

−32.275 ***

−9.021 ***

−10.406 ***

−5.686 ***

−10.255 ***

−4.916 ***

−42.734 ***

−6.758 ***

−10.183 ***

−8.643 ***

−11.015 ***

−10.683 ***

Order of integration

0

0

0

0

0

0

0

0

0

0

0

0

0

0

*** denotes significance at 1%.

.

The null hypothesis that the time series contains a unit root can be rejected for all of the series at the 1% level. This result means that the annual energy release at all plate boundaries is I(0) in nature. The results of the stationarity test reported in Table 2 show that all variables are confirmed to be stationary at the 0.05 level.

3.3. Results of the Causality Test between Plate Boundaries

This paper has proven that energy releases at plate boundaries have an order of integration of zero. The next step was to investigate the possibility of cointegration among the energy releases at plate boundaries. For this, the Engle–Granger test was used. The results for cointegration are reported in

Table 3. Results of Granger causality between energy releases at plate boundaries.

Direction of Causality		Granger Test			Cointegration Test
From	To	F-Statistics	P	Lag Length	Statistics	P
NZ-PA	PA-PS	11.68343	0.6317	14	−6.609	0
PA-PS	NZ-PA	24.52843	0.0395	14
AN-PA	PA-PS	21.36072	0.8763	30	−4.647	0.001
PA-PS	AN-PA	69.31429	0.0001	30
NZ-PA	AU-PA	19.72928	0.6582	23	−4.96	0.001
AU-PA	NZ-PA	38.60992	0.0219	23
AN-PA	AU-PA	60.61951	0.0001	24	−7.365	0
AU-PA	AN-PA	46.5939	0.0038	24
NZ-PA	NZ-SA	8.091878	0.5249	9	−5.243	0
NZ-SA	NZ-PA	23.13383	0.0059	9
AN-SA	SA-NA	43.688	0.0039	22	−3.932	−0.012
SA-NA	AN-SA	49.71639	0.0006	22
AN-SA	NZ-SA	31.60144	0.1372	24	−4.044	0.009
NZ-SA	AN-SA	67.6177	0	24
NZ-SA	SA-AF	66.31497	0	9	−11.09	0
SA-AF	NZ-SA	125.734	0	9
AN-SA	SA-AF	3.560421	0.7359	6	−5.298	0
SA-AF	AN-SA	16.40422	0.0117	6
AN-AF	AF-SO	12.18294	0.0166	4	−8.485	0
AF-SO	AN-AF	2.911122	0.5728	4
AN-AF	AF-EU	6.970334	0.1375	4	−8.45	0
AF-EU	AN-AF	8.452415	0.0763	4
SO-AR	AR-EU	43.16792	0.0899	32	−8.652	0
AR-EU	SO-AR	45.15261	0.0615	32
PA-PS	PS-EU	8.290653	0.3077	7	−5.19	0
PS-EU	PA-PS	20.3014	0.005	7
AF-EU	PS-EU	29.18502	0.4555	29	−10.875	0
PS-EU	AF-EU	58.76574	0.0009	29
IN-EU	PS-EU	14.77975	0.996	32	−10.156	0
PS-EU	IN-EU	54.48406	0.0079	32
AN-PA	AN-NZ	15.00008	0.0591	8	−10.671	0
AN-NZ	AN-PA	19.33468	0.0132	8
AN-PA	AN-SA	112.5939	0	25	−5.414	0
AN-SA	AN-PA	109.1282	0	25
AN-AU	AU-EU	21.11864	0.7358	26	−2.564	0.26
AU-EU	AN-AU	97.2081	0	26
AN-AU	AU-PA	28.10634	0.0053	12	−2.492	0.29
AU-PA	AN-AU	45.1501	0	12

. The Engle–Granger test indicated that cointegration is present between the energy releases at most plate boundaries at the 1% significant value because the null hypothesis of no cointegration was rejected. This outcome indicated a long-term relationship. However, the Engle–Granger test indicated that the statistics between AN-AU and AU-EU, as well as AN-AU and AU-PA, were lower than the critical value at the 5% level. Therefore, there was no cointegration among the energy releases at these plate boundaries.

The existence of a cointegrating relationship among energy releases at plate boundaries suggests the presence of Granger causality, at least in one direction, but it does not suggest the direction of causality between plate boundaries. In other words, the existence of causality in either direction cannot be ruled out. The direction of Granger causality would be determined by a traditional F test through constructing a VAR model and its associated probability value. Based on the Akaike information criterion (AIC), the optimal lag length was chosen [57]. As shown in Table 3, the F-statistics and the associated probabilities permit us to reject the null hypothesis that there is non-causality between the two plate boundaries. Therefore, there is unidirectional Granger causality between two plate boundaries, such as from PA-PS to NZ-PA, from PA-PS to AN-PA, from AU-PA to NZ-PA, from NA-SA to NZ-PA, from NZ-SA to AN-SA, from SA-AF to AN-SA, from AN-AF to AF-SO, from AF-EU to AN-AF, from PS-EU to PA-PS, from PS-EU to AF-EU, from PS-EU to IN-EU, and from AU-EU to AN-AU. This list means that the energy releases at the former plate boundaries are the Granger causes of the energy releases at the latter. In addition to this result, there is bidirectional Granger causality between some pairs of plate boundaries, such as between AN-PA and AU-PA, between AN-SA and SA-NA, between NZ-SA and SA-AF, between SO-AR and AR-EU, between AN-PA and AN-NZ, between AN-PA and AN-SA, and between AN-AU and AU-PA. In addition, the results were highly significant. For demonstration and visualization, a map of Granger causality between energy releases at plate boundaries is reported (Figure 4).

4. Discussion

The geodynamic mechanism is the research focus and core issue of plate motions and plate tectonics. It is also the greatest mystery in Earth science, and the evidence of plate motion remains the focus of researchers’ studies. During the last century, an increasing number of advanced technologies have been applied to research patterns of plate motion. The global positioning system (GPS) has opened up new ways of monitoring and studying crustal movement, and many research papers concerning the global plate motion field have emerged [11,58,59,60]. General plate motion fields on a global scale can show the direction of plate movement, but they cannot describe the mechanism of plate motions. Due to the natural property of earthquakes, the Earth’s crust accumulates stress during the movement of plates, and crustal shaking occurs when the stress exceeds the critical point. Based on the earthquake catalog, the main purpose of this paper was to study the relationship and causality of energy release between two plate boundaries to further understand the movement mechanism from another point of view. By comparing the global plate motion field and Figure 4, an interesting point can be revealed: the directions of plate movement are opposite to the directions of Granger causality between plate boundaries. For example, the causality direction between a subduction zone and a mid-ocean ridge in one plate is mostly from the subduction zone to the mid-ocean ridge, which is opposite to the directions of plate motions, especially for the Australia, Nazca, and Pacific plates.

Mantle convection may be the most famous hypothesis, and it includes the following forces that existed in plate motion: the push force of mid-ocean ridge, the force that drive solid lithosphere to move, and the pull force that downward-moves the subduction zone; the crust in the subduction zone sinks, carried by the cold, heavy, downward-moving mantle, inducing movement of the oceanic crust behind. Nevertheless, this theory does not indicate which force, e.g., subduction effect or the expansion effect, is the dominant role in global plate motion. The causality direction of energy release at plate boundaries, estimated from the Granger test based on global earthquake records from 1904 to 2014, has shown that the energy released at a subduction zone Granger causes the energy release at a mid-ocean ridge in the Pacific, Nazca, African, Australian, Eurasian, and Philippine sea plates. Due to the earthquakes caused by crustal movement, the conclusion can be made that seismic energy is first released in the subduction zone and then released in the mid-ocean ridge, as well as that the speed of plate motion at the subduction zone is much higher than that at the mid-ocean ridge. It can be further inferred that the pull force is the main driving force of plate motion in the Pacific, Nazca, African, Australian, Eurasian, and Philippine plates regarding the global plate motion field. This interpretation is in agreement with the findings by Forsyth [32], who suggests that the forces acting on the downgoing slab control the velocity of the oceanic plates and are an order of magnitude stronger than any other force. In addition, the conclusion that subduction’s pull force provides the main driving force for plate motion has also been recognized in other studies [31,61]. However, some people hold opposing views about this process [35,62,63]; they think the subduction force may be overestimated and the force is similar in magnitude to the ridge-push force. The results obtained from the perspective of statistical physics in the current research are generally in agreement with previous studies, and further point out the plates where this conclusion applies [32,33,34]. However, the conclusion does not apply to certain plates, such as the SO and IN plates, which requires further study.

Mechanically, the faulting events occurring in mid-ocean ridges usually represent normal faulting due to separating plates, causing less differential stress tensional regimes. In contrast, in collision zones and subduction zones, high stress is generated due to the compressive regime, which usually causes thrust faulting.

In addition to revealing the relationship between a subduction zone and a mid-ocean ridge, this research also found a causality relationship between continental plate boundaries. Boundaries of the Eurasian plate also have causality relationships. Unidirectional Granger causality running from PS-EU to AF-EU and from PS-EU to IN-EU can be distinguished (yellow marks in Figure 4). At the same time, there is a causality relationship between the two boundaries of the Philippine sea plate running from PS-EU to PA-PS. This direction is also opposite to the global plate motion field. In other words, it is consistent with the previous conclusions that the slab pull force provides the main driving force for plate motion in the Eurasian plate and the Philippine sea plate.

Due to the great destructive power of earthquakes and large risks to personal safety, earthquake prediction is a very important job. Even though it has motivated an international effort and achieved certain results, our ability to forecast earthquakes remains weak. In the present paper, the causality relationship between energy release and earthquake events at plate boundaries provides another point of view to forecasting earthquakes. An earthquake can Granger cause an earthquake at another plate boundary after a certain period of time. In addition, the period, the optimal lag length, and the rupture size were estimated with the Granger causality test. Here, we do not directly analyze the geological characteristics of a region, such as fault geometry, geodetic strain rates, past earthquakes, and a slip rates, to forecast earthquakes. Instead, we consider the transfer relationship of energy between seismic fault zones. Although the validity of the conclusions of the study remains to be verified, it is a meaningful attempt to forecast earthquakes from the perspective of statistical physics.

By analyzing the earthquake catalog dataset, the paper studied the relationship and interaction between energy release and plate boundaries from the perspective of statistical physics. The analysis yields various results that can provide a new way to understand the geodynamic mechanism and seismic energy transfer relationship, and even earthquake prediction. However, there are certain limitations in this study that need to be considered in the future. (1) The use of statistical physics methods requires high-quality data. Although the completeness of the earthquake catalog has been evaluated using the Gutenberg–Richter law (states that earthquake magnitudes are distributed exponentially [51] as Log 10N(m) = a − bm, where N(m) is the number of earthquakes with magnitude larger or equal to m, b is a scaling parameter, and a is a constant), the study has been limited to some extent due to the short time range of earthquake record data. Therefore, it is still necessary to build earthquake datasets with longer observation times and higher precision. (2) Energy release at subduction zones and collision zones Granger causes energy release at mid-ocean ridges. Therefore, this method may provide a reference for earthquake prediction at mid-ocean ridges. However, how can earthquakes that occur in subduction zones and collision zones be predicted? (3) The study analyzes the interaction of plate boundaries from a macroscopic perspective; however, in small areas, the lack of earthquake data limits its application.

5. Conclusions

Earth is a complex system. There are intricate interactions between the spherical layers, which can manifest in the form of crustal movement. The geodynamic mechanism is the research focus and core issue of plate motions and plate tectonics. The earthquake is the most direct result of relative plate movement, causing serious damage to the lives and property of humans. Thus, analyzing the time series of earthquakes may help us understand the relationship and causality between two plate boundaries and further explore the movement mechanism. Therefore, based on plate motions and continental drift theory, this paper uses earthquake events data and the Granger causality test method to quantitatively analyze the interaction and energy transfer relationship of plate boundaries from the view of statistics. The objective of this paper is to explore the relationship between the pull effect and the push effect of plate motion and to provide knowledge to explore seismic energy transfer relationships, and even to predict earthquake: (1) The directions of the global plate motion Field are opposite to the directions of Granger causality between plate boundaries of the Pacific, Nazca, African, Australian, Eurasian and Philippine plates, but they do not conflict with each other. For example, the energy release at the subduction zone Granger causes the energy release at the mid-ocean ridge at the Pacific plate, which is opposite to the directions of plate movement. (2) The slab-pull force (not limited to subduction force of the ocean plates) provides the main driving force for plate motions in the Pacific plate, Nazca plate, African plate, Australian plate, Eurasian plate, and Philippine sea plate. (3) The causality relationship and optimal lag length of energy release between plate boundaries may provide another point of view for forecasting earthquakes.