Designing of the Tracks and Modeling of the Carrier Arrangement in Square Rotary Braiding Machine
Abstract
:1. Introduction
2. Track-Splicing Process
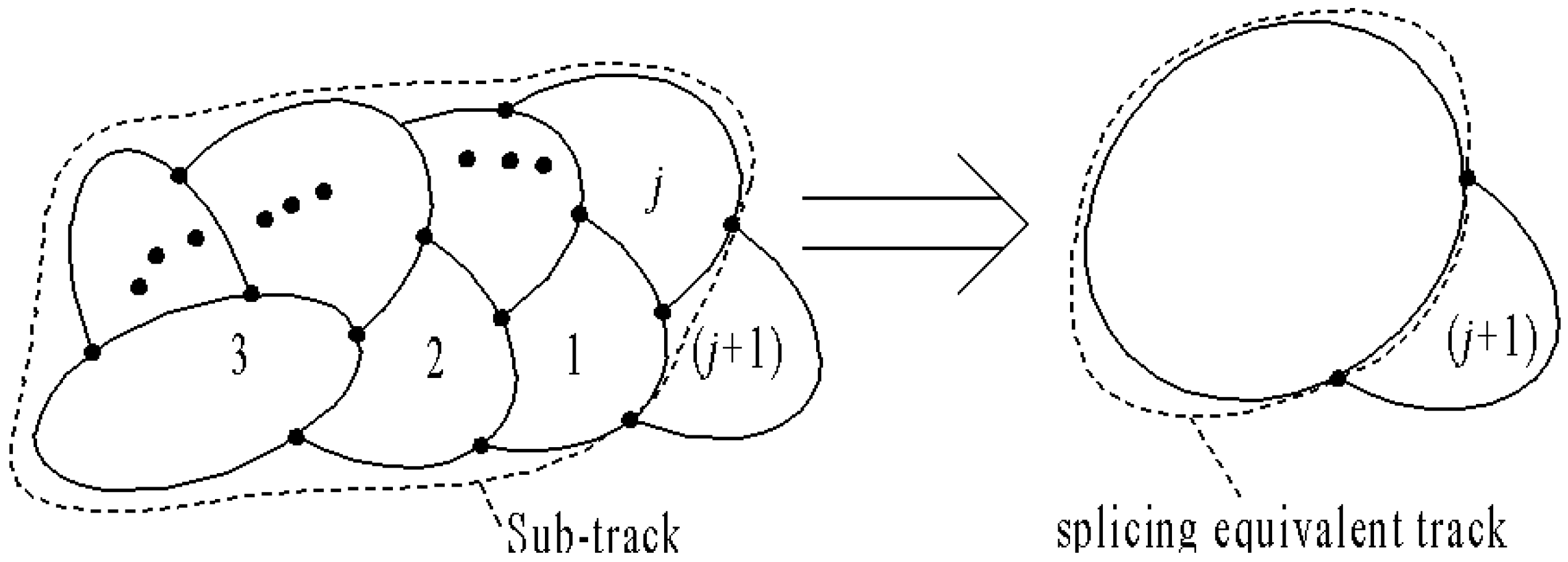
2.1. General Steps of Track Splicing
- (1)
- Determine the characteristics of the carrier arrangement in the 4 × 4 track (). This step can determine the existence of the carriers in the 4 × 4 track units, indicated by 1, 2, 3, ..., (j + 1) in Figure 2, in the arrangement period. The characteristics of the carrier arrangement represent the CAC set of carriers that do not collide with each other in the tracks, while the elements in only represent the existence of the carriers in the slots in an arrangement period of the carrier.
- (2)
- Determine the characteristic number of carrier arrangement for track units 1, 2. This step can determine the number of carriers at the slots in the track composed of the first two track units (1 and 2 in Figure 2), called dim. {M} and the dim. {M} is the number of elements in the CAC, that is, the dimension of the CAC. There is no collision constraint between the carriers, and it is independent of the track unit number.
- (3)
- Determine the carrier arrangement characteristics of the first sub-track, composed of the first and second track units.This step can determine the existence of the carriers in the first sub-track composed of the first track unit “1” and the second track unit “2”, as shown in Figure 2.
- (4)
- Determine the characteristic carrier arrangement number of the first jth sub-track, composed of j track units ranging from the first track unit “1” to the jth track unit (j):
- (5)
- Determine the carrier arrangement characteristics of the track spliced by the first (j + 1) track units, where the existence of the carriers in the track units—from the first unit “1” to the final one (j + 1) in Figure 2—in the arrangement period is obtained:
- (6)
- Determine the arrangement period (T) of the carriers in the spliced track unit. is the summation of the ith track unit, m is the number of track units, and is the number of track loops. indicates the number of carriers and the arrangement characteristics of the jth track unit (formed by the equivalent track units that are formed by the first j track units and the (j + 1)th track unit shown in Figure 2).
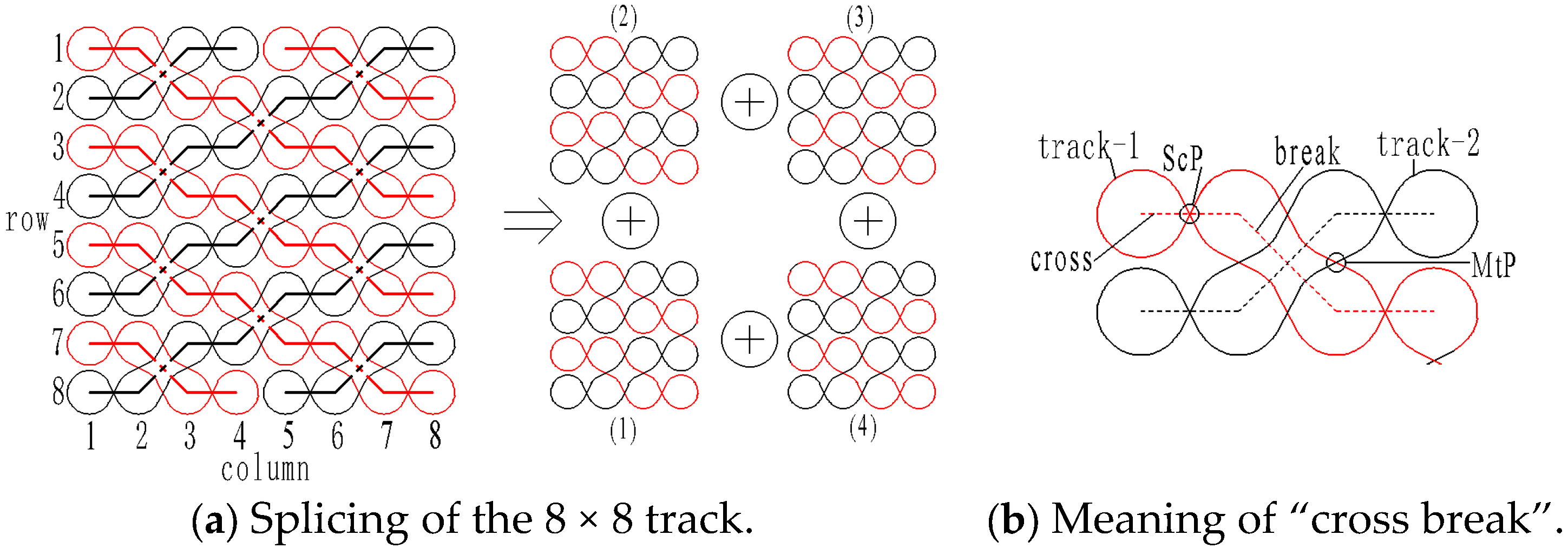
2.2. The Splicing Process of 8 × 8 484 Cross-Break Track
- (1)
- Determine the CAC of the first to fourth 4 × 4 track units:
- (2)
- Determine the CAC carrier arrangement number in the first sub-track, composed of track unit (1) and track unit (2):
- (3)
- Determine the CAC of track unit (1) and track unit (2):
- (4)
- Determine the CAC carrier arrangement number in the second sub-track, consisting of track units (1), (2), and (3):
- (5)
- Determine the CAC of track unit (1), track unit (2), and track unit (3):
- (6)
- Determine the CAC number in the third sub-track, which consists of track units (1), (2), (3), and (4):
- (7)
- Determine the arrangement period of the carrier in the 8 × 8 484 cross-break track:
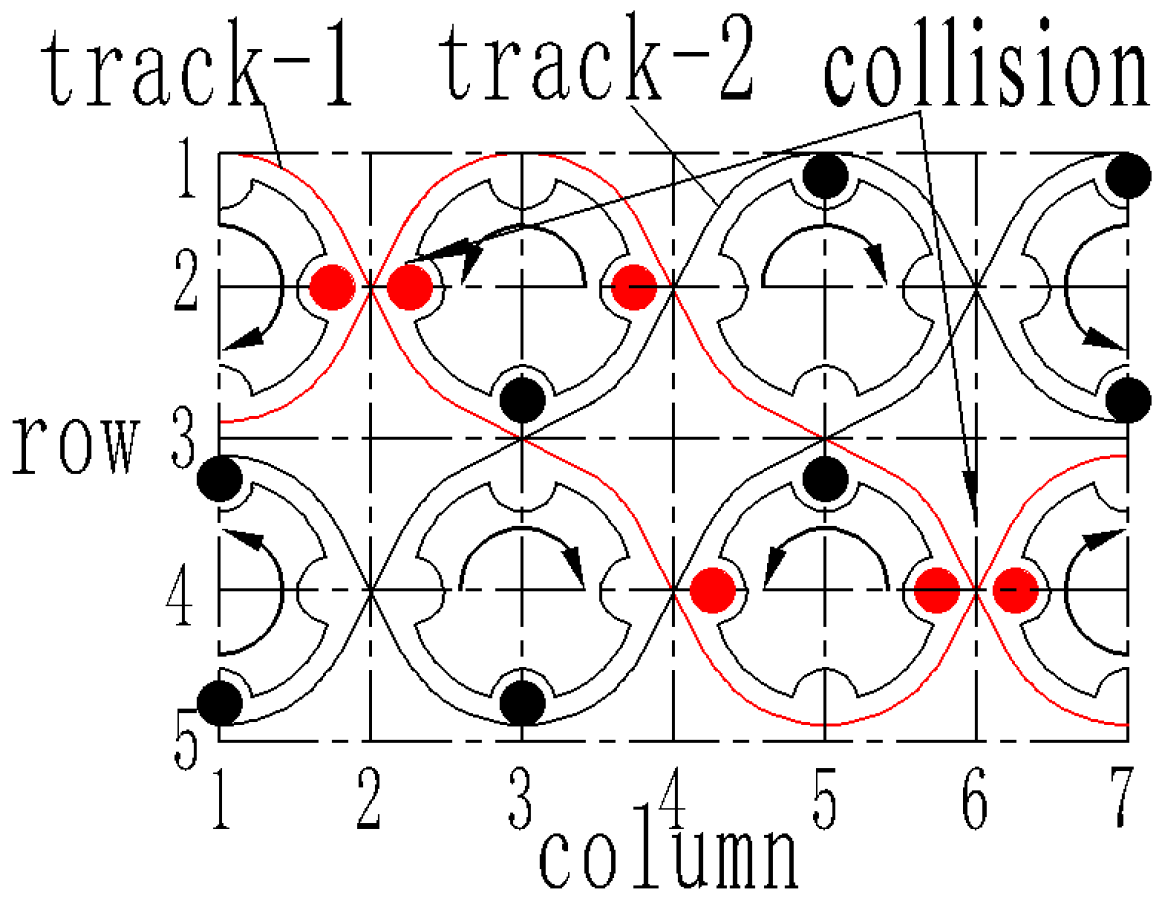
3. Analysis of the Carrier Arrangement
3.1. Modeling of the Carrier Position
3.2. Numerical Results and Analysis of the Carrier Arrangement in 3D Square Rotary Braiding Machine
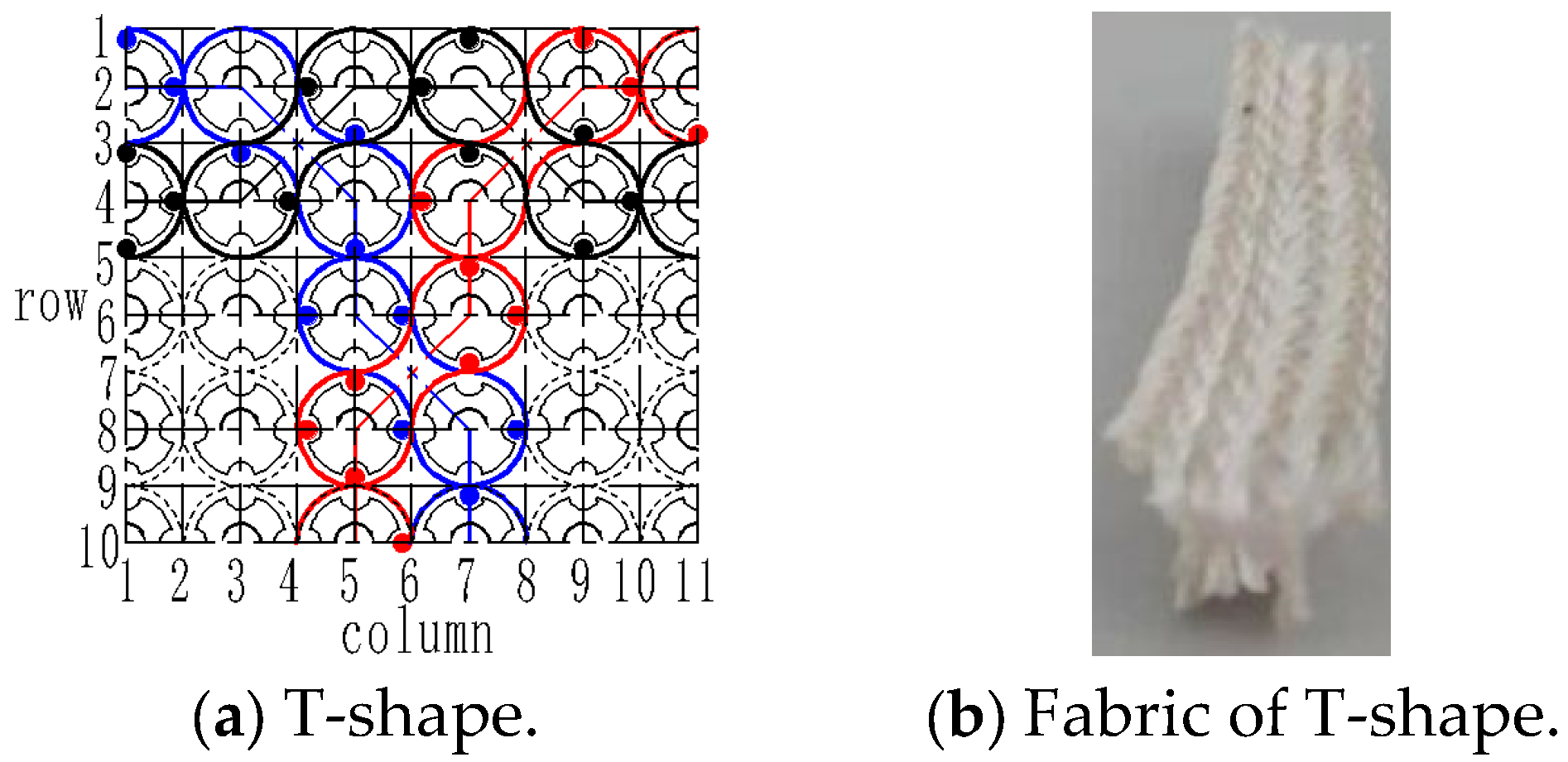
4. Carrier Arrangement of 3D Two-Shaped Cross-Sections
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stover, E.R.; Mark, W.C.; Marfowitz, I.; Mueller, W. Preparation of an Omniweave Reinforced Carbon-Carbon Cylinder as a Candidate for Evaluation in the Advanced Heat Shield Screening Program; AFML-TR-70-283; Wright-Patterson AFB: Fairborn, OH, USA, 1971. [Google Scholar]
- Mouritz, A.P.; Bannister, M.K.; Falzon, P.J.; Leong, K.H. Review of applications for advanced three-dimensional fibre textile composites. Compos. Part A Appl. Sci. Manuf. 1999, 30, 1445–1461. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, L.; Sun, Y.; Zhang, Y.; Qian, K. Multi-scale modeling of an integrated 3D braided composite with applications to helicopter arm. Appl. Compos. Mater. 2017, 24, 1233–1250. [Google Scholar] [CrossRef]
- Kelly, A. Concise Encyclopedia of Composite Materials; Elsevier Science Ltd.: Oxford, UK, 1994; pp. 50–128. [Google Scholar]
- Liu, G.; Zhang, P.; Wang, W. Study on braiding parameters of braiding nerve conduit. J. Donghua Univ. 2003, 29, 54–57. [Google Scholar]
- Kiyotani, T.; Teramachi, M.; Takimoto, Y.; Nakamura, T.; Shimizu, Y.; Endo, K. Nerve regeneration across a 25-mm gap bridged by a polyglycolic acid-collagen tube: A histological and electrophysiological evaluation of regenerated nerves. Brain Res. 1996, 740, 66–74. [Google Scholar] [CrossRef] [Green Version]
- Ueng, K.C.; Wen, S.P.; Lou, C.W.; Lin, J.H. Braiding structure stability and section treatment evaluations of braided coronary stents made of stainless steel and bio-absorbable polyvinyl alcohol via a braiding technique. Fibers Polym. 2015, 16, 675–684. [Google Scholar] [CrossRef]
- Yau, S.S.; Chou, T.W.; Ko, F.K. Flexural and axial compressive failures of three-dimensionally braided composite l-beams. Composites 1986, 17, 227–232. [Google Scholar] [CrossRef]
- Chen, L. Application of 3D textile technology in aerospace field. Aeronaut. Manuf. Technol. 2008, 4, 45–47. [Google Scholar]
- Kostar, T.D.; Chou, T.W. A methodology for Cartesian braiding of three-dimensional shapes and special structures. J. Mater. Sci. 2002, 37, 2811–2824. [Google Scholar] [CrossRef]
- Kostar, T.D. Analysis, Design, Fabrication, and Performance of Three-Dimensional Braided Composites. Ph.D. Thesis, Philosophy in Mechanical Engineering, Faculty of the University of Delaware, University of Delaware, Newark, DE, USA, 1998. [Google Scholar]
- Li, Y. Study on the Law of Three-Dimensional Rectangle Braiding. Ph.D. Thesis, Textile Engineering, Donghua University, Shanghai, China, 2005. [Google Scholar]
- Li, Y.; Chen, X.; Li, T. Arrangement of carriers on the track and column braiding bed. J. Donghua Univ. 2003, 6, 58–61. [Google Scholar]
- Bogdanovich, A.E. An overview of three-dimensional braiding technologies. In Advances in Braiding Technology; Woodhead Publishing: Duxford, UK, 2016; pp. 3–78. [Google Scholar]
- Mungalov, D.; Bogdanovich, A. Complex shape 3-D braided composite preforms: Structural shapes for marine and aerospace. Sampe J. 2004, 40, 7–21. [Google Scholar]
- Tolosana, N.; Lomov, S.; Stüve, J.; Miravete, A. Development of a simulation tool for 3D braiding architectures. In Proceedings of the AIP Conference Proceedings, Zaragoza, Spain, 18–20 April 2007; pp. 1005–1010. [Google Scholar]
- Tada, M.; Uozumi, T.; Nakai, A.; Hamada, H. Structure and machine braiding procedure of coupled square braids with various cross sections. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1485–1489. [Google Scholar] [CrossRef]
- Akiyama, Y.; Maekawa, Z.; Hamada, H.; Yokoyama, A.; Uratani, Y. Braid and Braiding Method. U.S. Patent 5,385,077, 31 January 1995. [Google Scholar]
- Kyosev, Y. Square and other types of form braiding. In Braiding Technology for Textiles: Principles, Design and Processes; Woodhead Publishing: Duxford, UK, 2014; pp. 283–311. [Google Scholar]
- Kyosev, Y. Process emulation based development of braided structures and machines. In Topology-Based Models of Tubular and Flat Braided Structures: Principles, Algorithms and Limitations; Springer: Cham, Switzerland, 2019; pp. 65–87. [Google Scholar]
- Kyosev, Y.; Hübner, M.; Cherif, C. Virtual development and numerical simulation of 3D braids for composites. In Proceedings of the TEXCOMP-13: 13th International Conference on Textile Composites, Milano, Italy, 17–19 September 2018; Volume 406, p. 012025. [Google Scholar]
- Kyosev, Y. Numerical modelling of 3D braiding machine with variable paths of the carriers. Appl. Compos. Mater. 2018, 25, 773–783. [Google Scholar] [CrossRef]
- Glessner, P.; Kyosev, Y. Carrier delay-based method for development of the tracks for the transitions between patterns on 3D braiding machines with continuous rotating horn gears. Text. Res. J. 2021, 00405175211026533. [Google Scholar]
- Guowei, S.; Zhihong, S.; Qihong, Z.; Zhenxi, W.; Bing, W.; Chang, X.; Tao, F.; Hua, L. Track design and realization of braiding for three-dimensional variably shaped cross-section preforms. J. Eng. Fibers Fabr. 2021, 16, 15589250211002510. [Google Scholar]

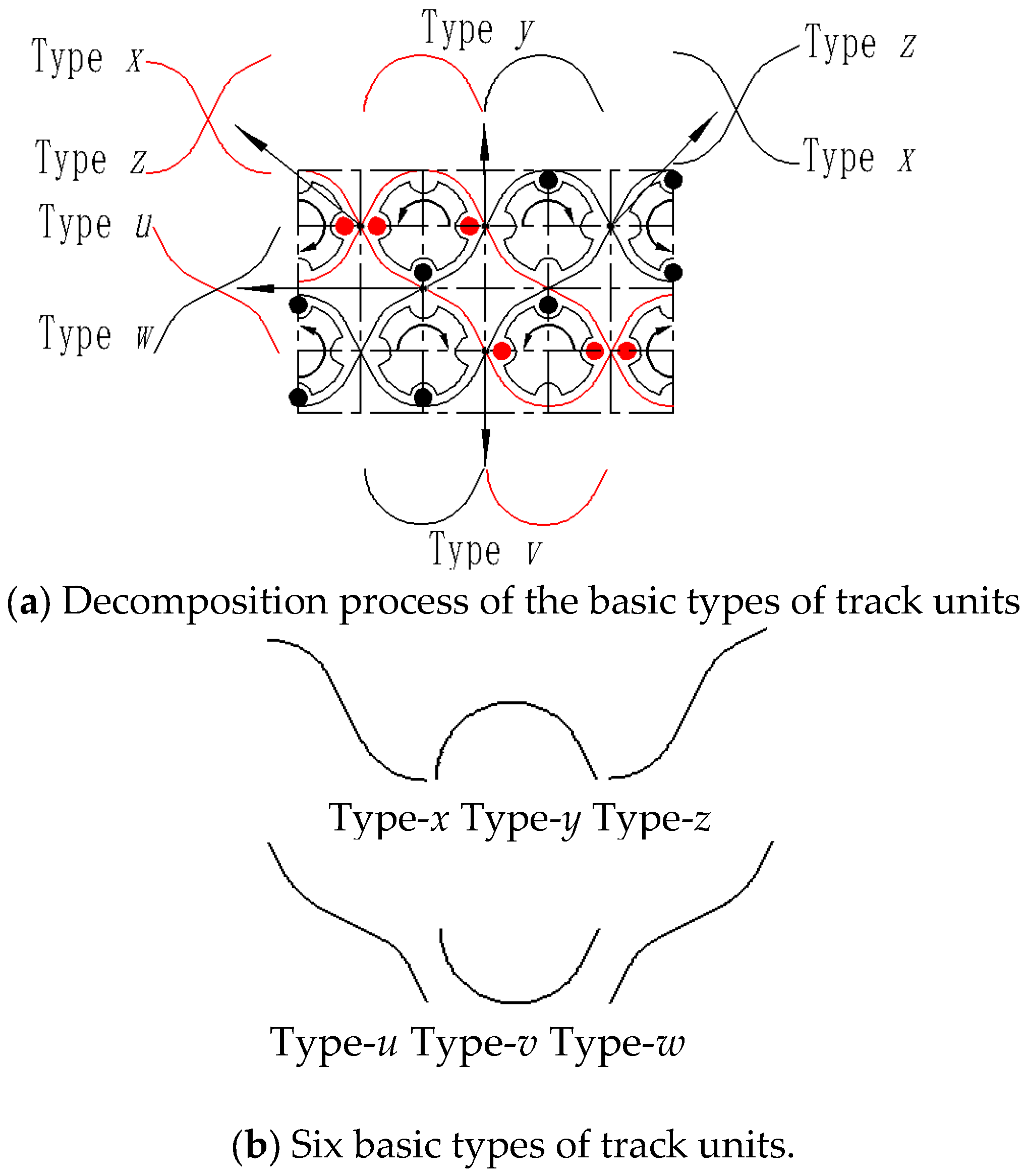



| Rotation | Type | |||||
|---|---|---|---|---|---|---|
| x | y | z | u | v | w | |
 |  |  | 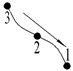 |  |  | |
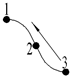 |  | 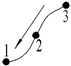 |  |  | 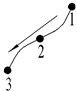 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, G.; Sun, Z.; Chen, G.; Zhou, Q.; Wang, Z.; Wang, B. Designing of the Tracks and Modeling of the Carrier Arrangement in Square Rotary Braiding Machine. Appl. Sci. 2021, 11, 7861. https://doi.org/10.3390/app11177861
Shao G, Sun Z, Chen G, Zhou Q, Wang Z, Wang B. Designing of the Tracks and Modeling of the Carrier Arrangement in Square Rotary Braiding Machine. Applied Sciences. 2021; 11(17):7861. https://doi.org/10.3390/app11177861
Chicago/Turabian StyleShao, Guowei, Zhihong Sun, Ge Chen, Qihong Zhou, Zhenxi Wang, and Bing Wang. 2021. "Designing of the Tracks and Modeling of the Carrier Arrangement in Square Rotary Braiding Machine" Applied Sciences 11, no. 17: 7861. https://doi.org/10.3390/app11177861






