Computational Investigation for Biomechanical Characteristics of Lumbar Spine with Various Porous Ti–6Al–4V Implant Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Characteristics of Spinal Implant
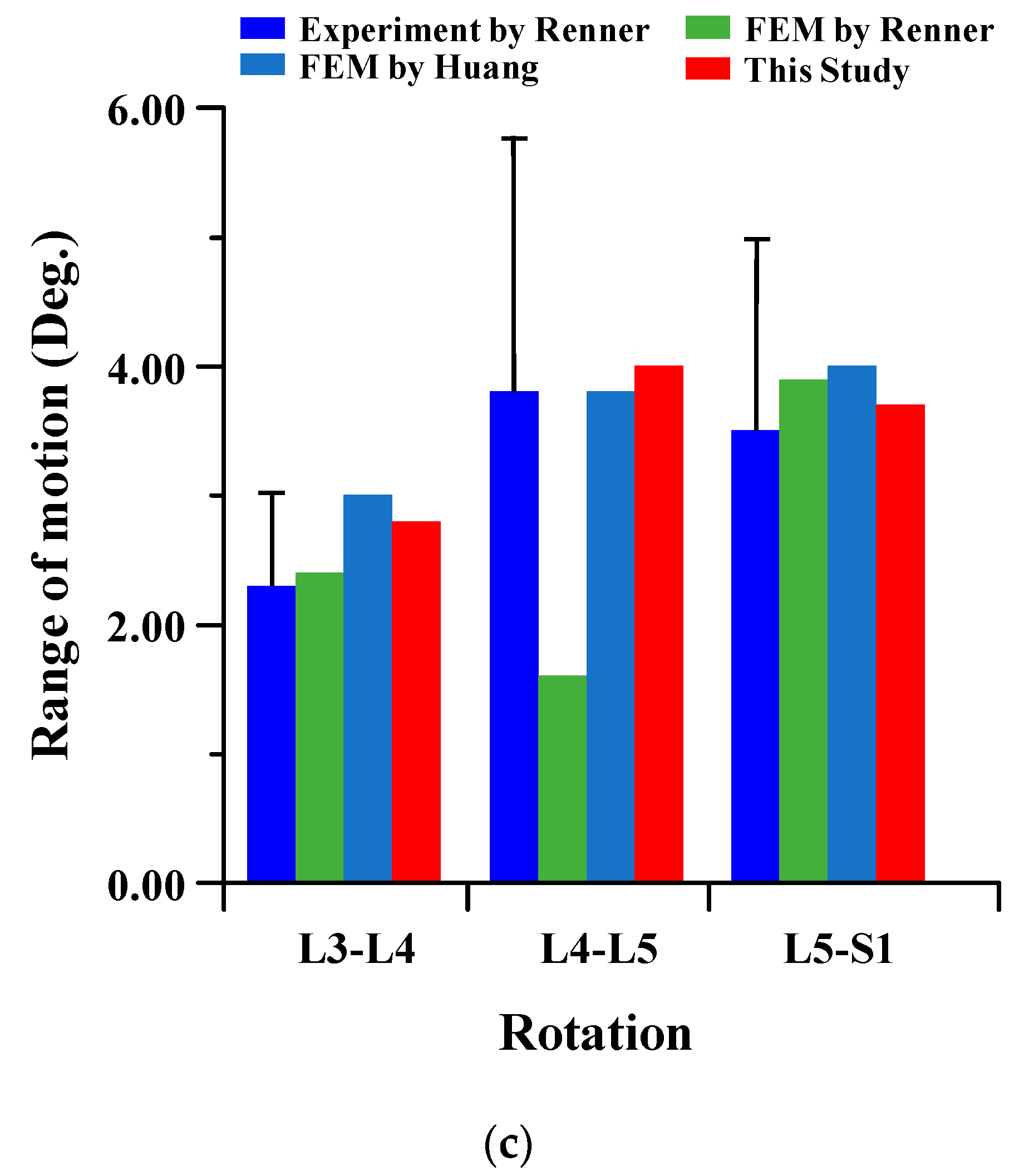
2.2. Finite Element Modeling and Validation
2.3. Scenarios of Spinal Rod for Finite Element Analysis
3. Results
3.1. Range of Motion
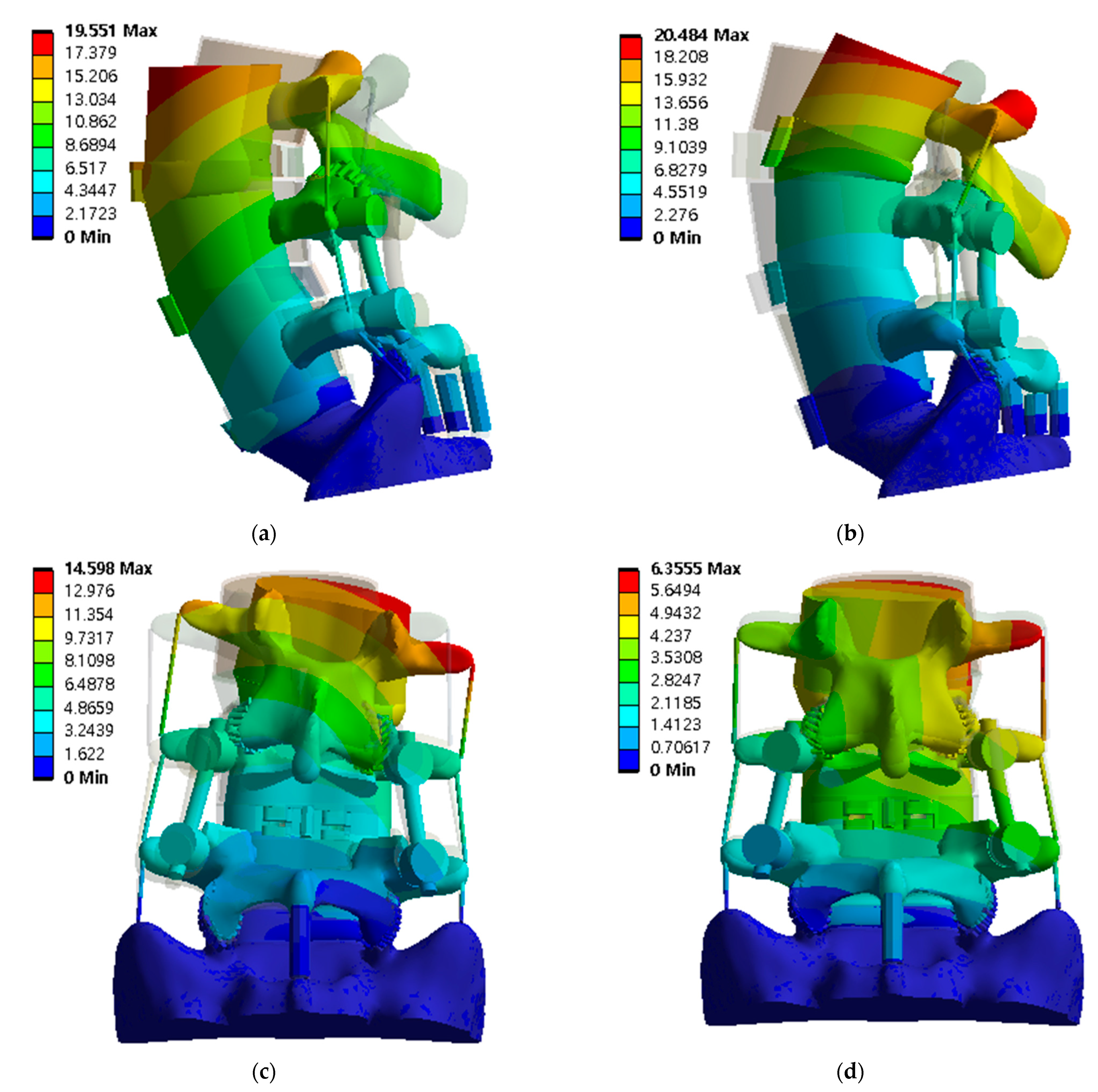
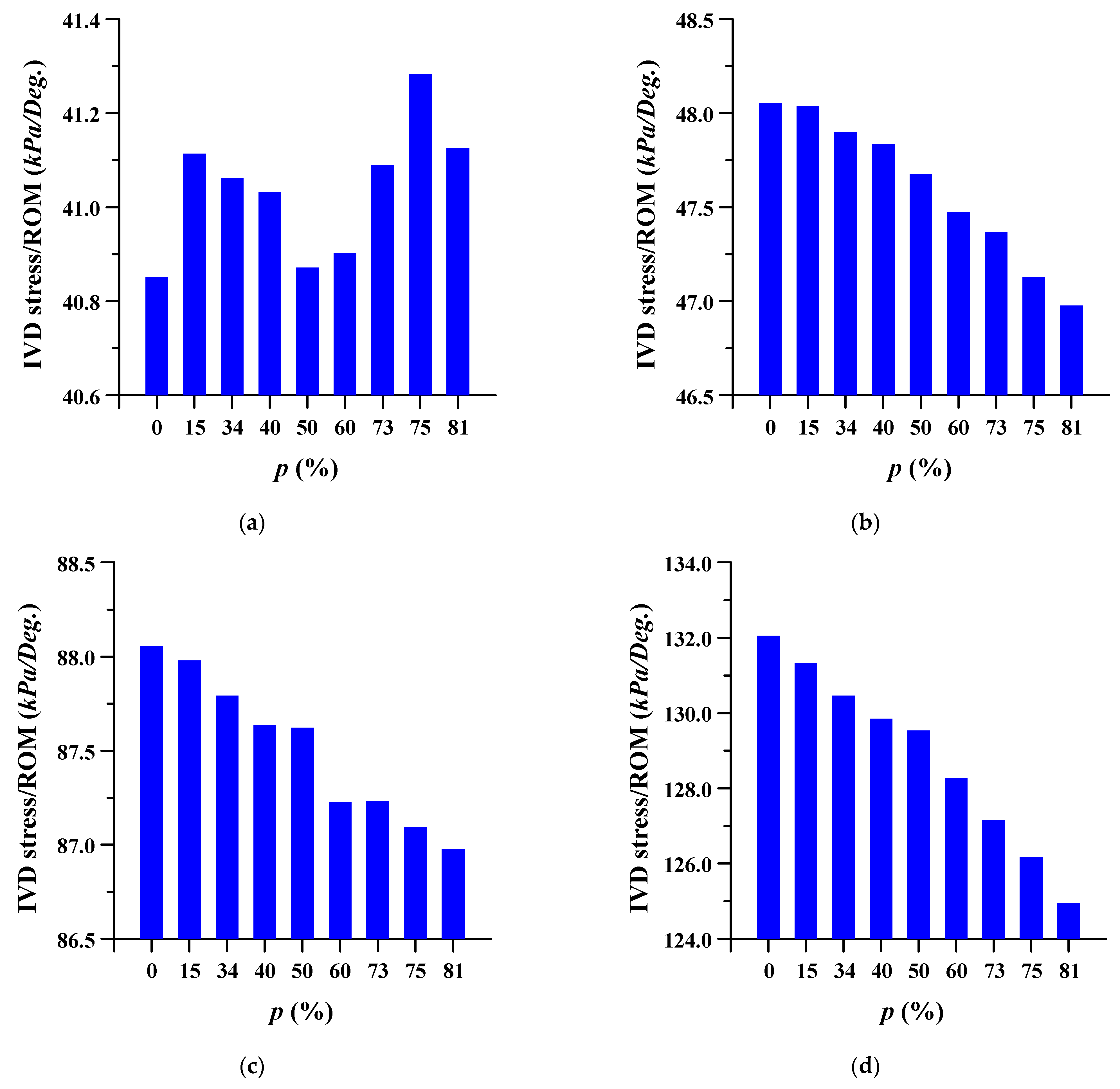
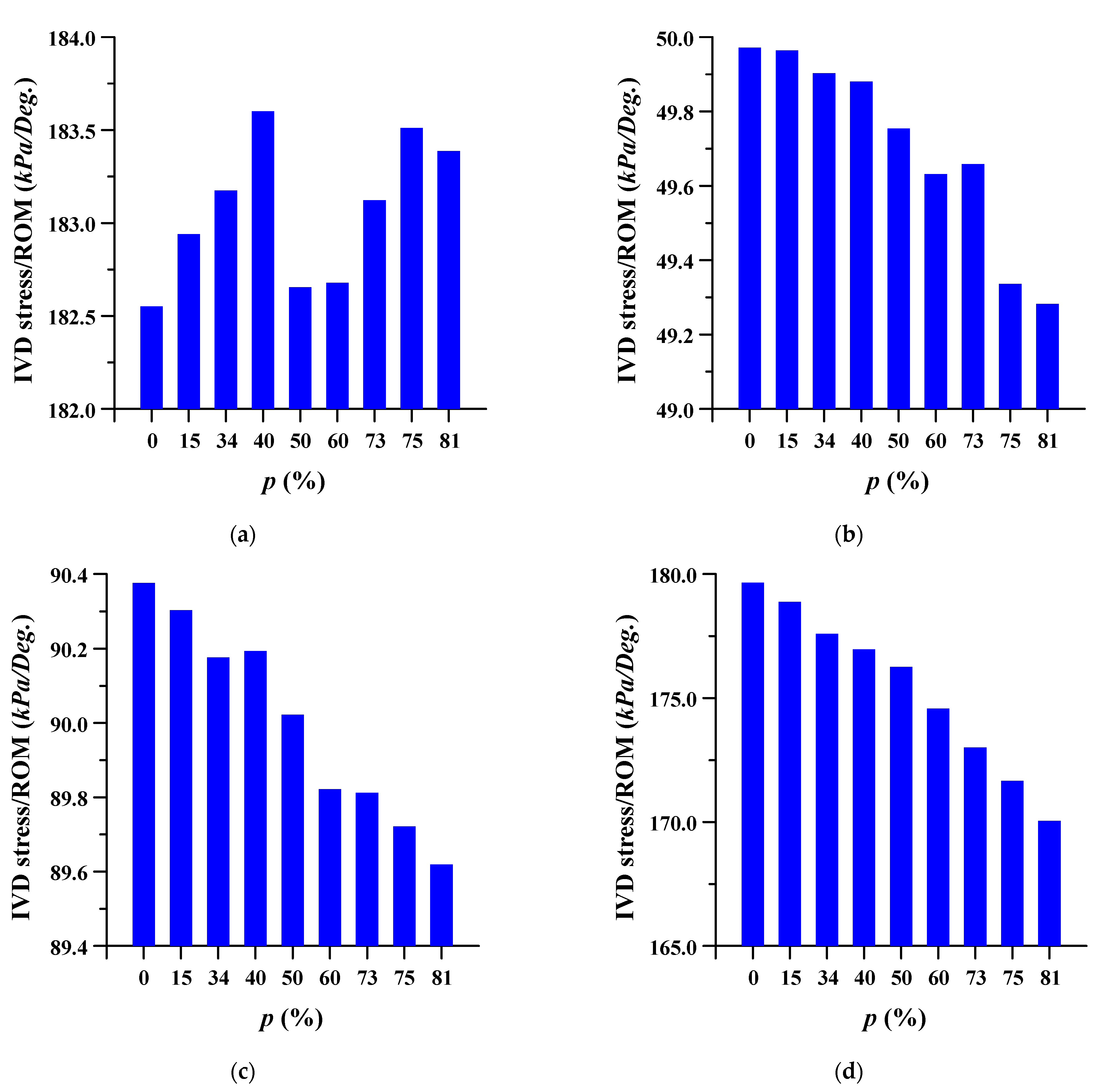
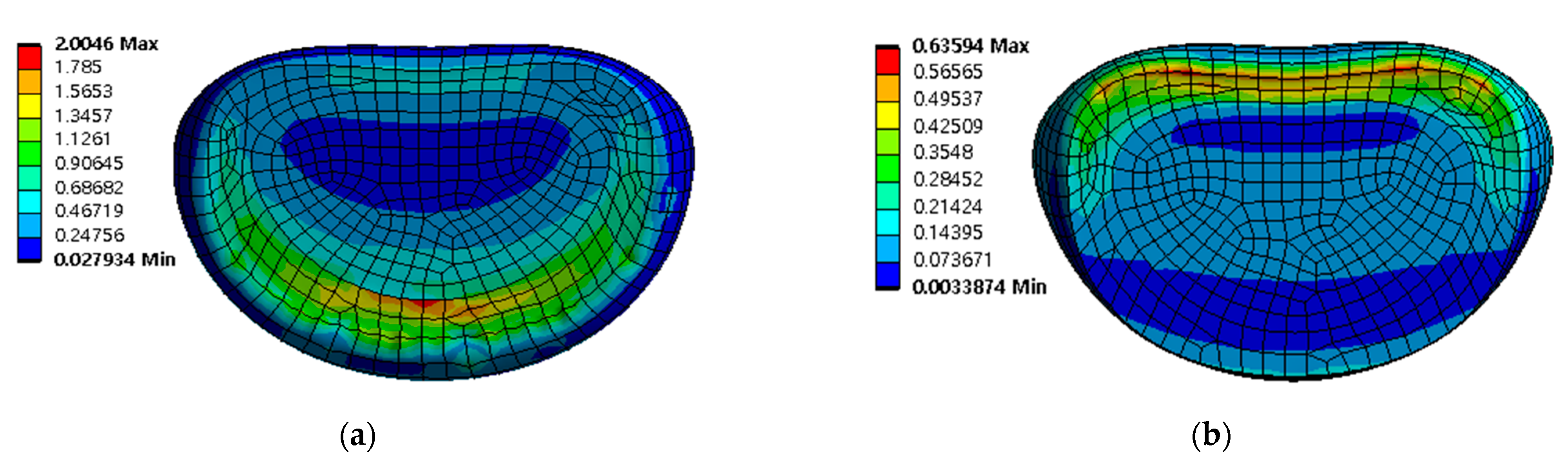
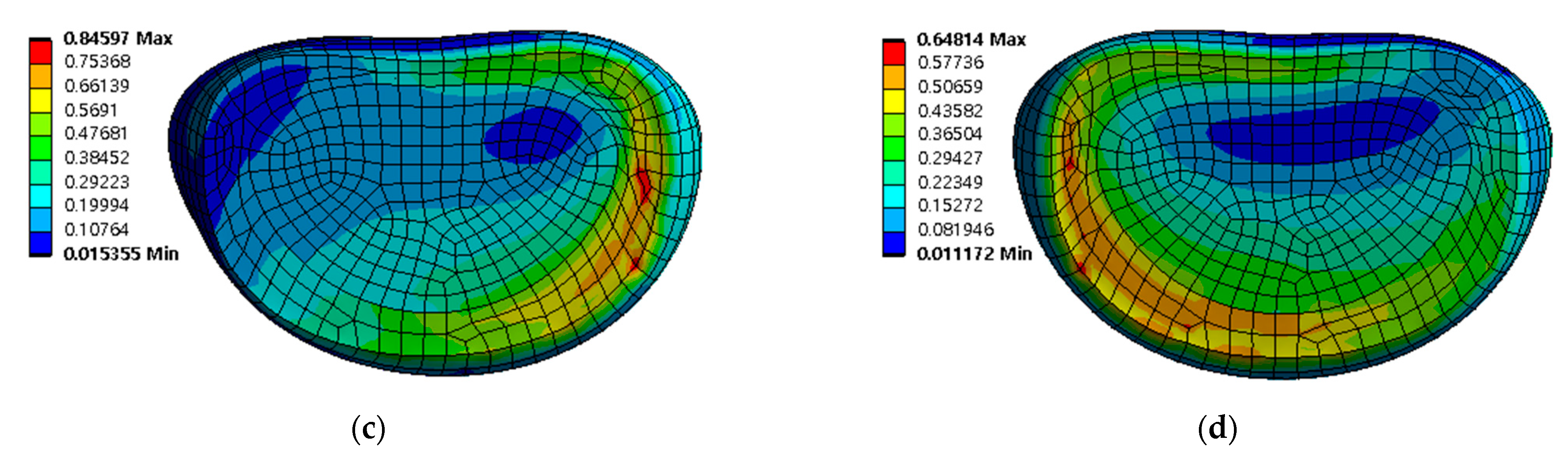
3.2. Equivalent Stress at Adjacent Intervertebral Disc
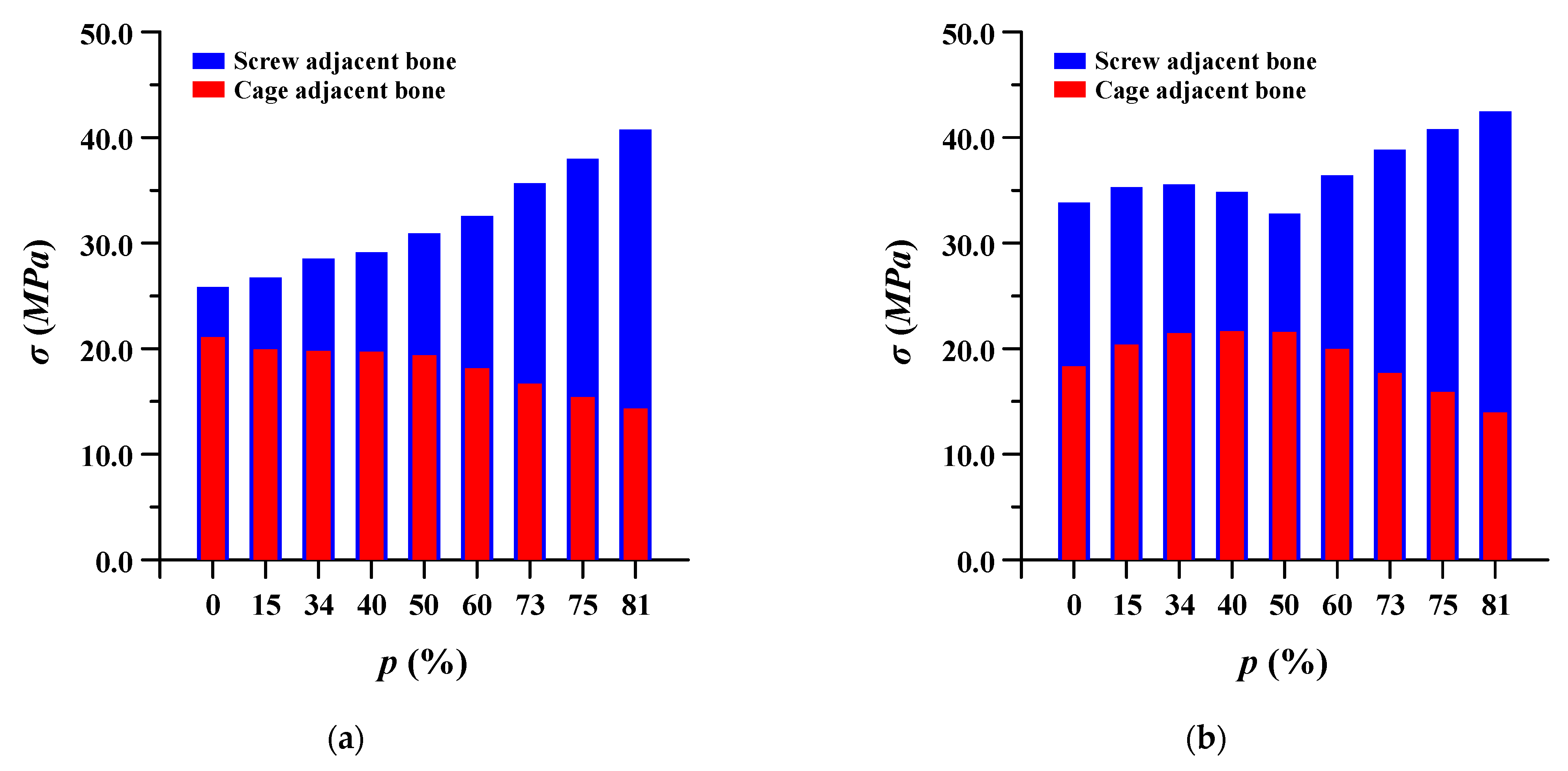
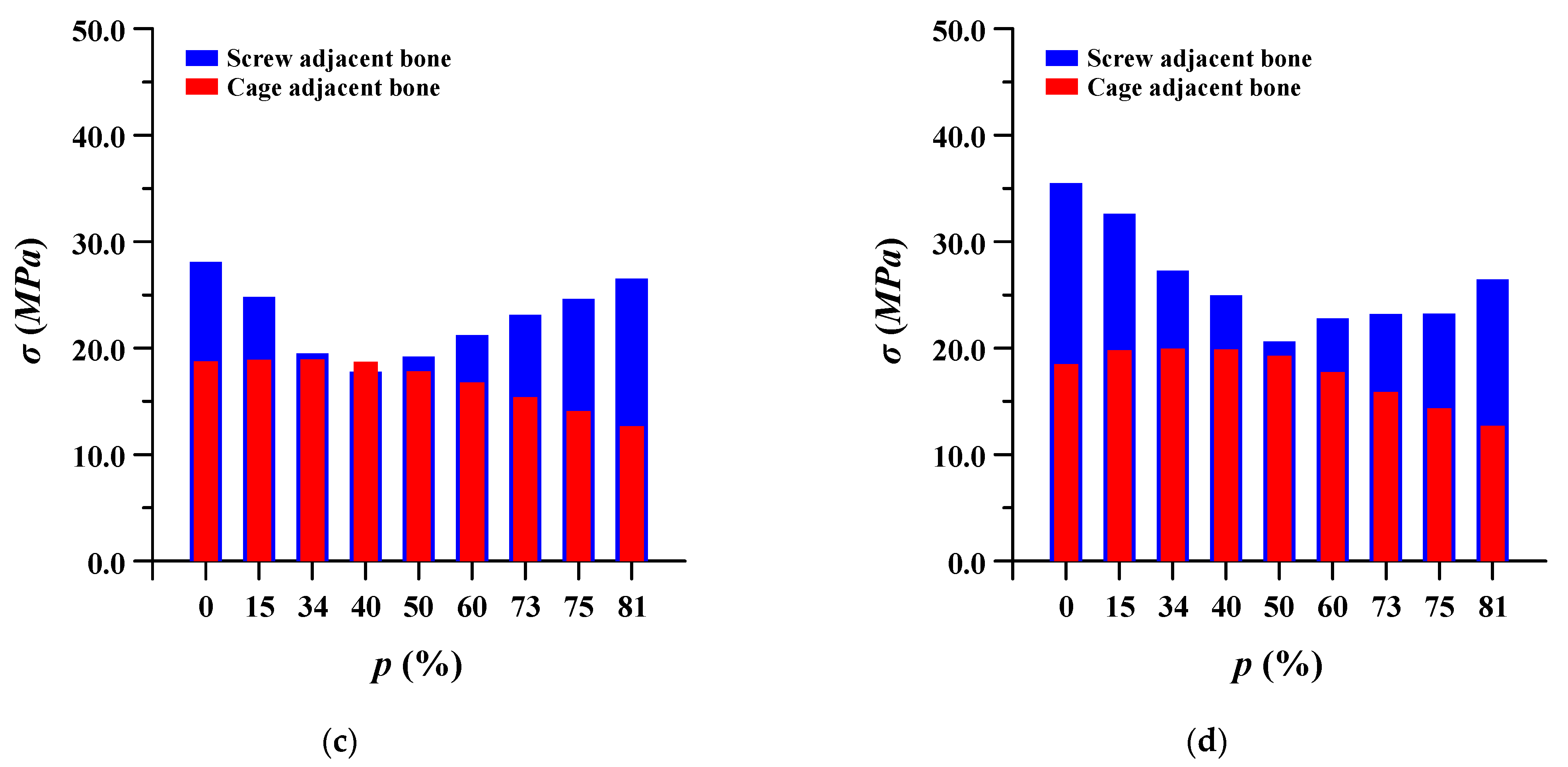
3.3. Equivalent Stress at Adjacent Bone of Pedicle Screws and Spinal Cages
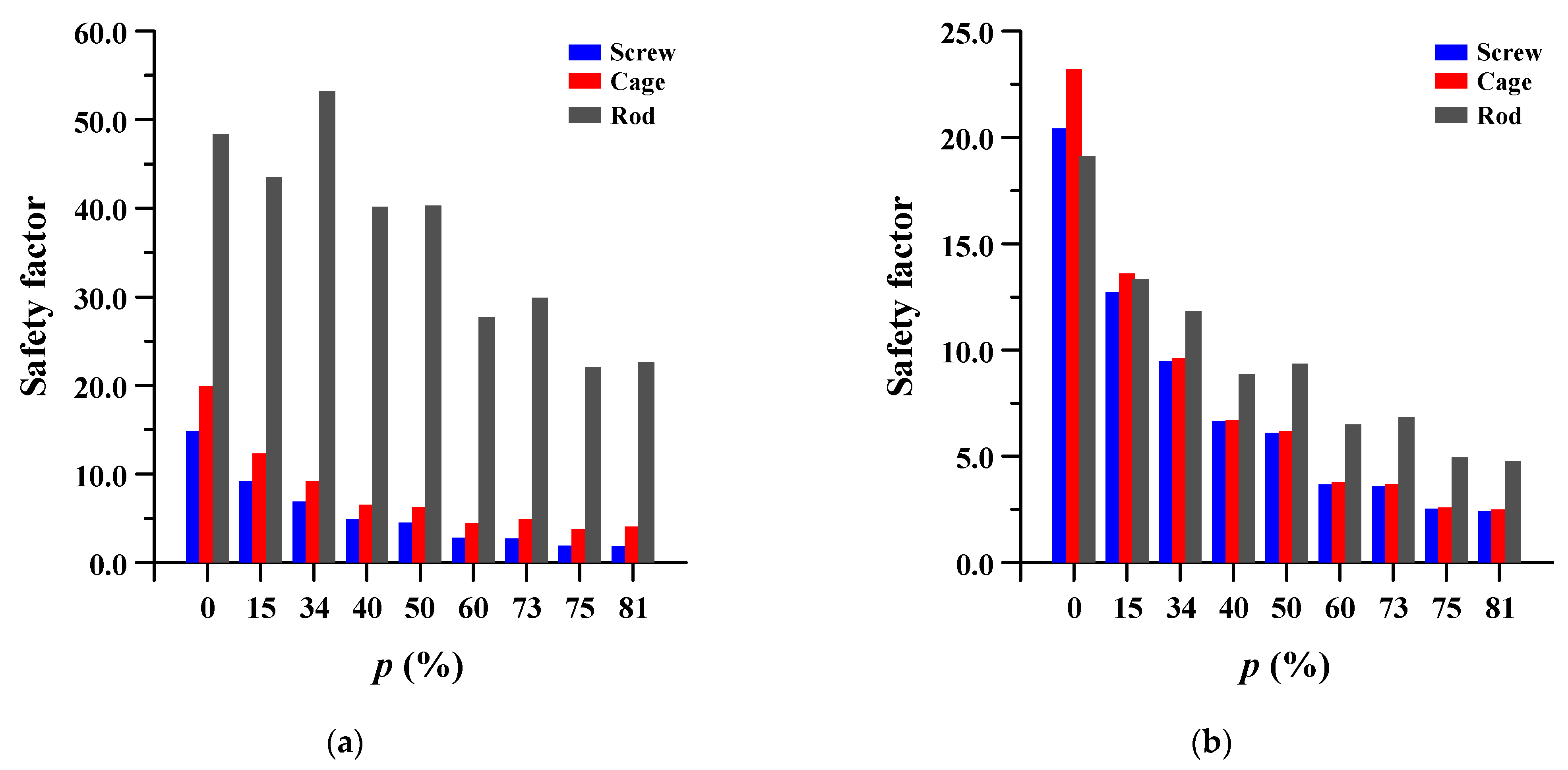
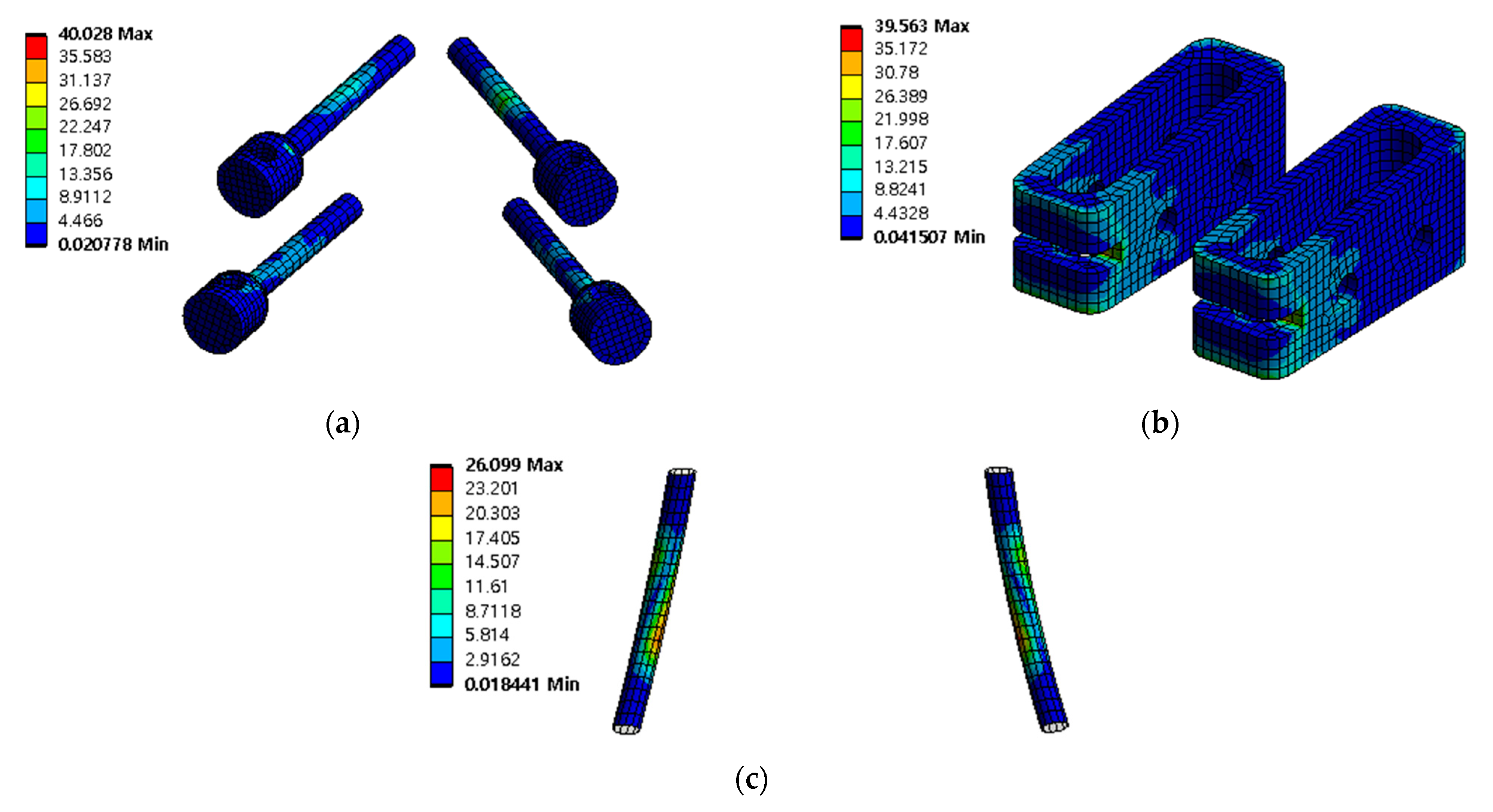
3.4. Safety Factor of Spinal Implants at Different Porosity
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Warburton, A.; Girdler, S.J.; Mikhail, C.M.; Ahn, A.; Cho, S.K. Biomaterials in spinal implants: A review. Neurospine 2020, 7, 101. [Google Scholar] [CrossRef] [PubMed]
- McAfee, P.; Khoo, L.T.; Pimenta, L.; Capuccino, A.; Coric, D.; Hes, R.; Conix, B.; Asgarzadie, F.; Hamzaoglu, A.; Mirofsky, Y.; et al. Treatment of lumbar spinal stenosis with a total posterior arthroplasty prosthesis: Implant description, surgical technique, and a prospective report on 29 patients. Neurosurg. Focus 2007, 22, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Abumi, K.; Panjabi, M.M.; Kramer, K.M.; Duranceau, J.; Oxland, T.; Crisco, J.J. Biomechanical evaluation of lumbar spinal stability after graded facetectomies. Spine 1990, 15, 1142–1147. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Jung, T.-G.; Park, E.-Y.; Kang, G.-W.; Kim, K.-A.; Lee, S.-J. Biomechanical efficacy of a combined interspinous fusion system with a lumbar interbody fusion cage. Int. J. Precis. Eng. Manuf. 2015, 16, 997–1001. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Dai, L.-Y.; Xu, H.-Z.; Chi, Y.-L. Biomechanical effect of the extent of vertebral body fracture on the thoracolumbar spine with pedicle screw fixation: An in vitro study. J. Clin. Neurosci. 2008, 15, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, Z.; Hua, W.; Wang, K.; Li, S.; Zhang, Y.; Ye, Z.; Shao, Z.; Wu, X.; Yang, C. Clinical outcome and surgical strategies for late post-traumatic kyphosis after failed thoracolumbar fracture operation: Case report and literature review. Medicine 2017, 96, e8770. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.K.; Lim, B.-Y.; Goh, T.S.; Son, S.M.; Kim, H.-S.; Lee, J.S.; Lee, C.-S. Effect of the screw type (S2-alar-iliac and iliac), screw length, and screw head angle on the risk of screw and adjacent bone failures after a spinopelvic fixation technique: A finite element analysis. PLoS ONE 2018, 13, e0201801. [Google Scholar] [CrossRef] [PubMed]
- Elias, W.J.; Simmons, N.E.; Kaptain, G.J.; Chadduck, J.B.; Whitehill, R. Complications of posterior lumbar interbody fusion when using a titanium threaded cage device. J. Neurosurg. Spine 2000, 93, 45–52. [Google Scholar] [CrossRef] [PubMed]
- Soroceanu, A.; Diebo, B.G.; Burton, D.; Smith, J.S.; Deviren, V.; Shaffrey, C.; Kim, H.J.; Mundis, G.; Ames, C.; Errico, T.; et al. Radiographical and implant-related complications in adult spinal deformity surgery. Spine 2015, 40, 1414–1421. [Google Scholar] [CrossRef] [PubMed]
- Dailey, S.K.; Crawford, A.H.; Asghar, F.S. Implant Failure Following Posterior Spinal Fusion—Caudal Migration of a Fractured Rod: Case Report. Spine Deform. 2015, 3, 380–385. [Google Scholar] [CrossRef] [PubMed]
- Torstrick, F.B.; Safranski, D.L.; Burkus, J.K.; Chappuis, J.L.; Lee, C.S.; Guldberg, R.E.; Gall, K.; Smith, K.E. Getting PEEK to stick to bone: The development of porous PEEK for interbody fusion devices. Tech. Orthop. 2017, 32, 158. [Google Scholar] [CrossRef]
- Poel, R.; Belosi, F.; Albertini, F.; Walser, M.; Gisep, A.; Lomax, A.J.; Weber, D.C. Assessing the advantages of CFR-PEEK over titanium spinal stabilization implants in proton therapy—a phantom study. Phys. Med. Biol. 2020, 65, 245031. [Google Scholar] [CrossRef]
- Li, C.S.; Vannabouathong, C.; Sprague, S.; Bhandari, M. The use of carbon-fiber-reinforced (CFR) PEEK material in orthopedic implants: A systematic review. Clin. Med. Insights Arthritis Musculoskelet. Disord. 2015, 8, CMAMD–S20354. [Google Scholar] [CrossRef]
- Boriani, S.; Tedesco, G.; Ming, L.; Ghermandi, R.; Amichetti, M.; Fossati, P.; Krengli, M.; Gasbarrini, A. Carbon-fiber-reinforced PEEK fixation system in the treatment of spine tumors: A preliminary report. Eur. Spine J. 2018, 27, 874–881. [Google Scholar] [CrossRef]
- Uri, O.; Folman, Y.; Laufer, G.; Behrbalk, E. A novel spine fixation system made entirely of carbon-fiber-reinforced PEEK composite: An in vitro mechanical evaluation. Adv. Orthop. 2020, 2020, 4796136. [Google Scholar] [CrossRef] [PubMed]
- Brockett, C.L.; Carbone, S.; Abdelgaied, A.; Fisher, J.; Jennings, L.M. Influence of contact pressure, cross-shear and counterface material on the wear of PEEK and CFR-PEEK for orthopaedic applications. J. Mech. Behav. Biomed. Mater. 2016, 63, 10–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cofano, F.; Di Perna, G.; Monticelli, M.; Marengo, N.; Ajello, M.; Mammi, M.; Vercelli, G.; Petrone, S.; Tartara, F.; Zenga, F.; et al. Carbon fiber reinforced vs titanium implants for fixation in spinal metastases: A comparative clinical study about safety and effectiveness of the new “carbon-strategy”. J. Clin. Neurosci. 2020, 75, 106–111. [Google Scholar] [CrossRef]
- Li, P.; Jiang, W.; Yan, J.; Hu, K.; Han, Z.; Wang, B.; Zhao, Y.; Cui, G.; Wang, Z.; Mao, K.; et al. A novel 3D printed cage with microporous structure and in vivo fusion function. J. Biomed. Mater. Res. Part A 2019, 107, 1386–1392. [Google Scholar] [CrossRef]
- Cao, X.; Duan, S.; Liang, J.; Wen, W.; Fang, D. Mechanical properties of an improved 3D-printed rhombic dodecahedron stainless steel lattice structure of variable cross section. Inter. J. Mech. Sci. 2018, 145, 53–63. [Google Scholar] [CrossRef]
- Sallica-Leva, E.; Jardini, A.L.; Fogagnolo, J.B. Microstructure and mechanical behawior of porous Ti–6Al–4V parts obtained by selective laser melting. J. Mech. Behav. Biomed. Mater. 2013, 26, 98–108. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Li, J.; Huang, T.; Kou, H.; Zhou, L. Compression fatigue behavior and failure mechanism of porous titanium for biomedical applications. J. Mech. Behav. Biomed. Mater. 2017, 65, 814–823. [Google Scholar] [CrossRef] [PubMed]
- Attar, H.; Calin, M.; Zhang, L.C.; Scudino, S.; Eckert, J. Manufacture by selective laser melting and mechanical behavior of commercially pure titanium. Mater. Sci. Eng. A 2014, 593, 170–177. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.; Chen, X.; Yi, C.; Chen, R.; Zhang, Z. Configuration Optimization Design of Ti6Al4V Lattice Structure Formed by SLM. Materials 2018, 11, 1856. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Li, Q.; Yin, S.; Chen, Z.; Jenkins, R.; Chen, C.; Wang, J.; Ma, W.; Bolot, R.; Lupoi, R.; et al. Mechanical and in vitro study of an isotropic Ti6Al4V lattice structure fabricated using selective laser melting. J. Alloys Compd. 2019, 782, 209–223. [Google Scholar] [CrossRef]
- Hedayati, R.; Ahmadia, S.M.; Lietaertc, K.; Pourana, B.; Lia, Y.; Weinansa, H.; Ranse, C.D.; Zadpoora, A.A. Isolated and modulated effects of topology and material type on the mechanical properties of additively manufactured porous biomaterials. J. Mech. Behav. Biomed. Mater. 2018, 79, 254–263. [Google Scholar] [CrossRef]
- Kang, I.; Choi, M.; Lee, D.; Noh, G. Effect of Passive Support of the Spinal Muscles on the Biomechanics of a Lumbar Finite Element Model. Appl. Sci. 2020, 10, 6278. [Google Scholar] [CrossRef]
- Wang, X.; Xu, S.; Zhou, S.; Xu, W.; Leary, M.; Choong, P.; Qian, M.; Brandt, M.; Xie, Y.M. Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants: A review. Biomaterials 2016, 83, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.; Heuer, F.; Simon, U.; Kettler, A.; Rohlmann, A.; Claes, L.; Wilke, H.-J. Application of a new calibration method for a three-dimensional finite element model of a human lumbar annulus fibrosus. Clin. Biomech. 2006, 21, 337–344. [Google Scholar] [CrossRef]
- Pitzen, T.; Geisler, F.; Matthis, D.; Müller-Storz, H.; Barbier, D.; Steudel, W.-I.; Feldges, A. A finite element model for predicting the biomechanical behaviour of the human lumbar spine. Control Eng. Pract. 2002, 10, 83–90. [Google Scholar] [CrossRef]
- Huynh, K.T.; Gao, Z.; Gibson, I.; Lu, W.F. Haptically integrated simulation of a finite element model of thoracolumbar spine combining offline biomechanical response analysis of intervertebral discs. Comput. Aided Des. 2010, 42, 1151–1166. [Google Scholar] [CrossRef]
- Goh, T.S.; Lim, B.-Y.; Lee, J.S.; Lee, C.-S. Identification of surgical plan for syndesmotic fixation procedure based on finite element method. Appl. Sci. 2020, 10, 4349. [Google Scholar] [CrossRef]
- Dreischarf, M.; Zander, T.; Bergmann, G.; Rohlmann, A. A non-optimized follower load path may cause considerable intervertebral rotations. J. Biomech. 2010, 43, 2625–2628. [Google Scholar] [CrossRef] [PubMed]
- Dreischarf, M.; Zander, T.; Shirazi-Adl, A.; Puttlitz, C.M.; Adam, C.J.; Chen, C.S.; Goel, V.K.; Kiapour, A.; Kim, Y.H.; Labus, K.M.; et al. Comparison of eight published static finite element models of the intact lumbar spine: Predictive power of models improves when combined together. J. Biomech. 2014, 47, 1757–1766. [Google Scholar] [CrossRef] [Green Version]
- Dooris, A.P.; Goel, V.K.; Grosland, N.M.; Gilbertson, L.G.; Wilder, D.G. Load-sharing between anterior and posterior elements in a lumbar motion segment implanted with an artificial disc. Spine 2001, 26, E122–E129. [Google Scholar] [CrossRef]
- Goel, V.K.; Monroe, B.T.; Gilbertson, L.G.; Brinckmann, P. Interlaminar shear stresses and laminae separation in a disc: Finite element analysis of the L3–L4 motion segment subjected to axial compressive loads. Spine 1995, 20, 689–698. [Google Scholar] [CrossRef] [PubMed]
- Falkowska, A.; Seweryn, A.; Skrodzki, M. Strength properties of a porous titanium alloy Ti6Al4V with diamond structure obtained by laser power bed fusion (LPBF). Materials 2020, 13, 5138. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.P.; Du, C.F.; Cheng, C.K.; Zhong, Z.C.; Chen, X.W.; Wu, G.; Li, Z.-C.; Ye, J.-D.; Lin, J.-H.; Wang, L.Z. Preserving posterior complex can prevent adjacent segment disease following posterior lumbar interbody fusion surgeries: A finite element analysis. PLoS ONE 2016, 11, e0166452. [Google Scholar] [CrossRef] [PubMed]
- Renner, S.M.; Natarajan, R.N.; Patwardhan, A.G.; Havey, R.M.; Voronov, L.I.; Guo, B.Y.; Andersson, G.B.; An, H.S. Novel model to analyze the effect of a large compressive follower pre-load on range of motions in a lumbar spine. J. Biomech. 2007, 40, 1326–1332. [Google Scholar] [CrossRef] [PubMed]
- Dowling, N.E. Mechanical Behavior of Materials, 4th ed.; Pearson: London, UK, 2015; pp. 118–615. [Google Scholar]
- ANSYS Inc. Introduction to Contacts—ANSYS Mechanical Structural Nonlinearities; ANSYS Inc.: Canonsburg, PA, USA, 2010. [Google Scholar]
- ANSYS. ANSYS Help Documentation. 2018. Available online: www.ansys.com (accessed on 5 June 2019).
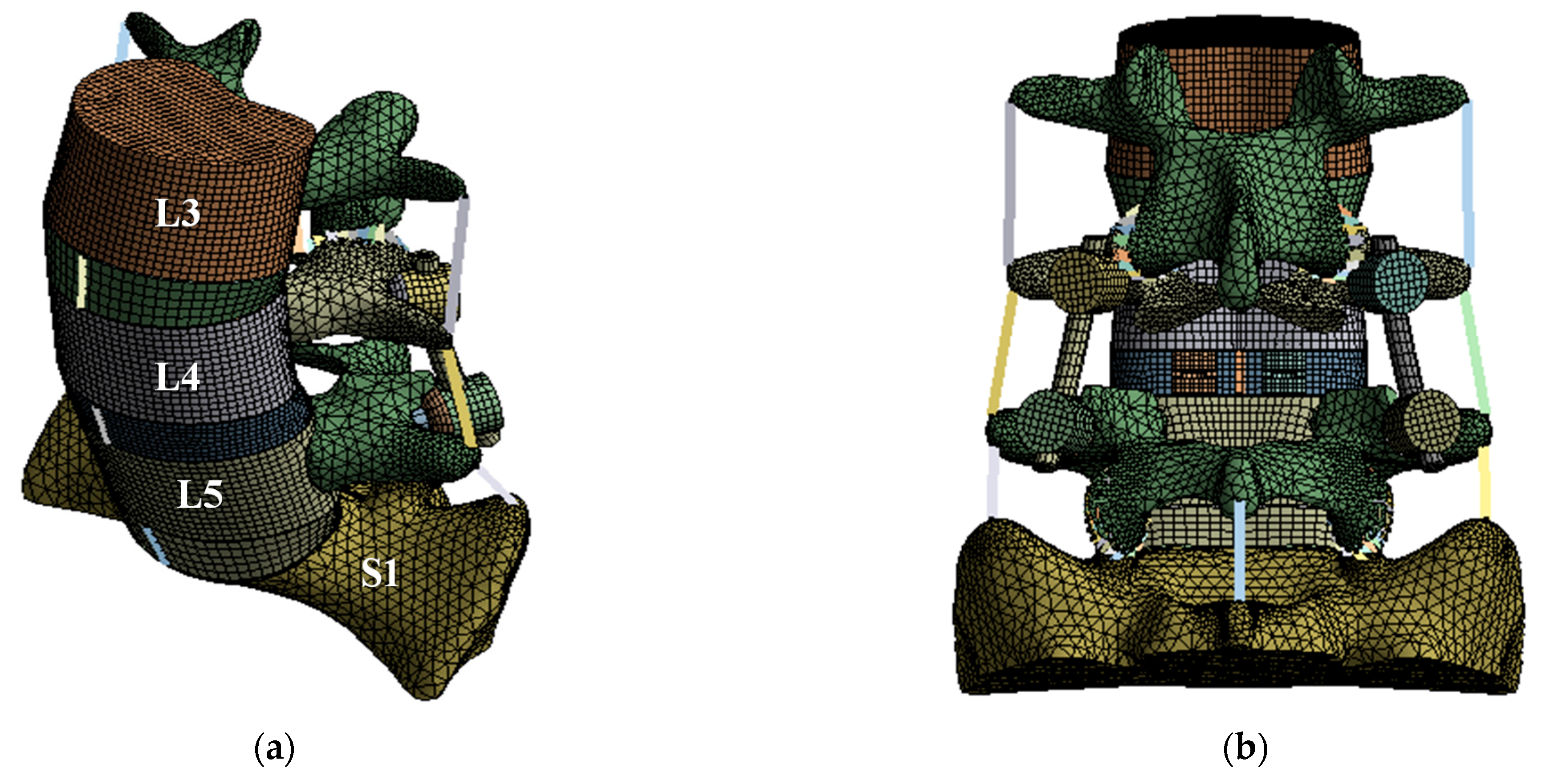
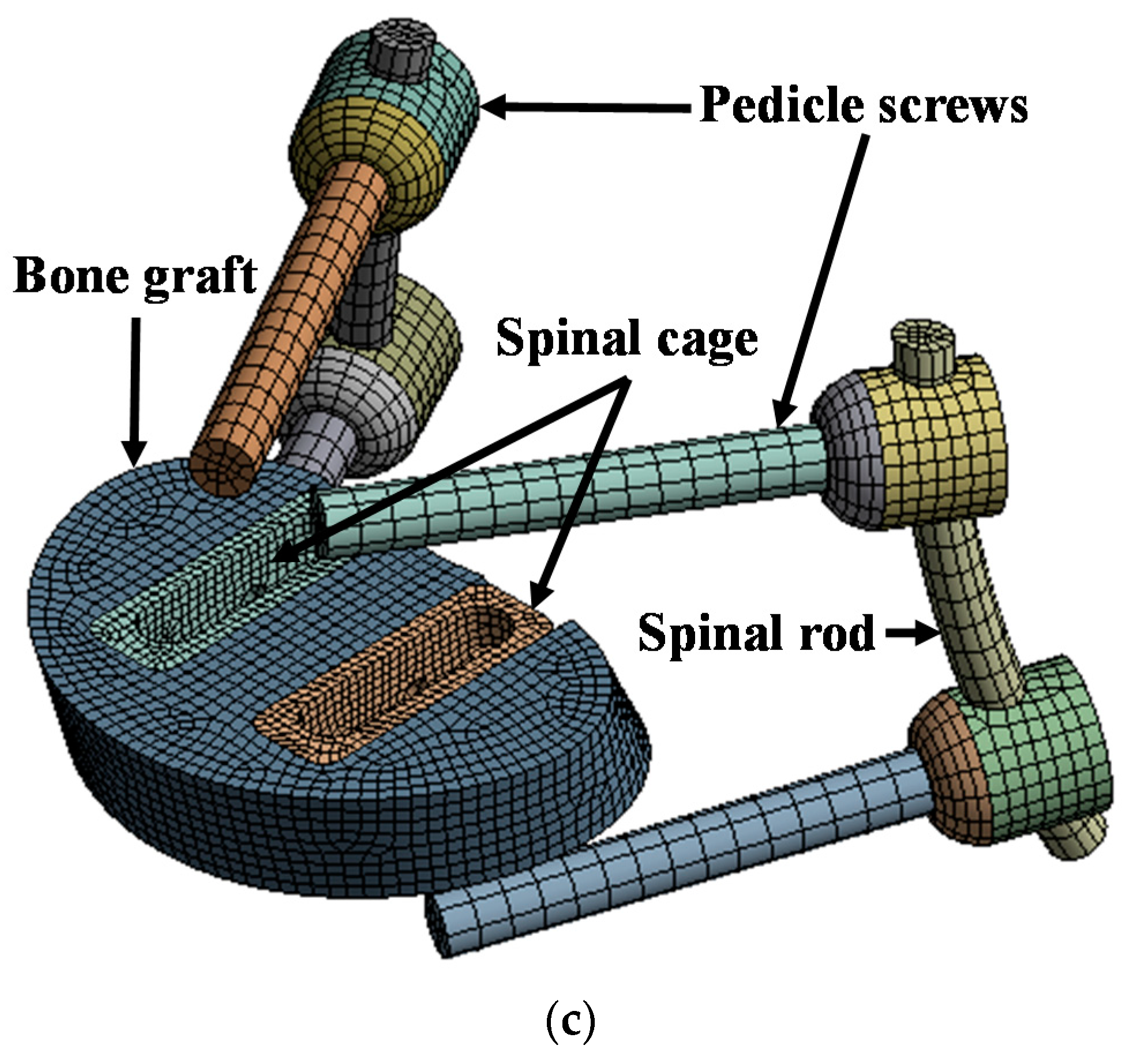
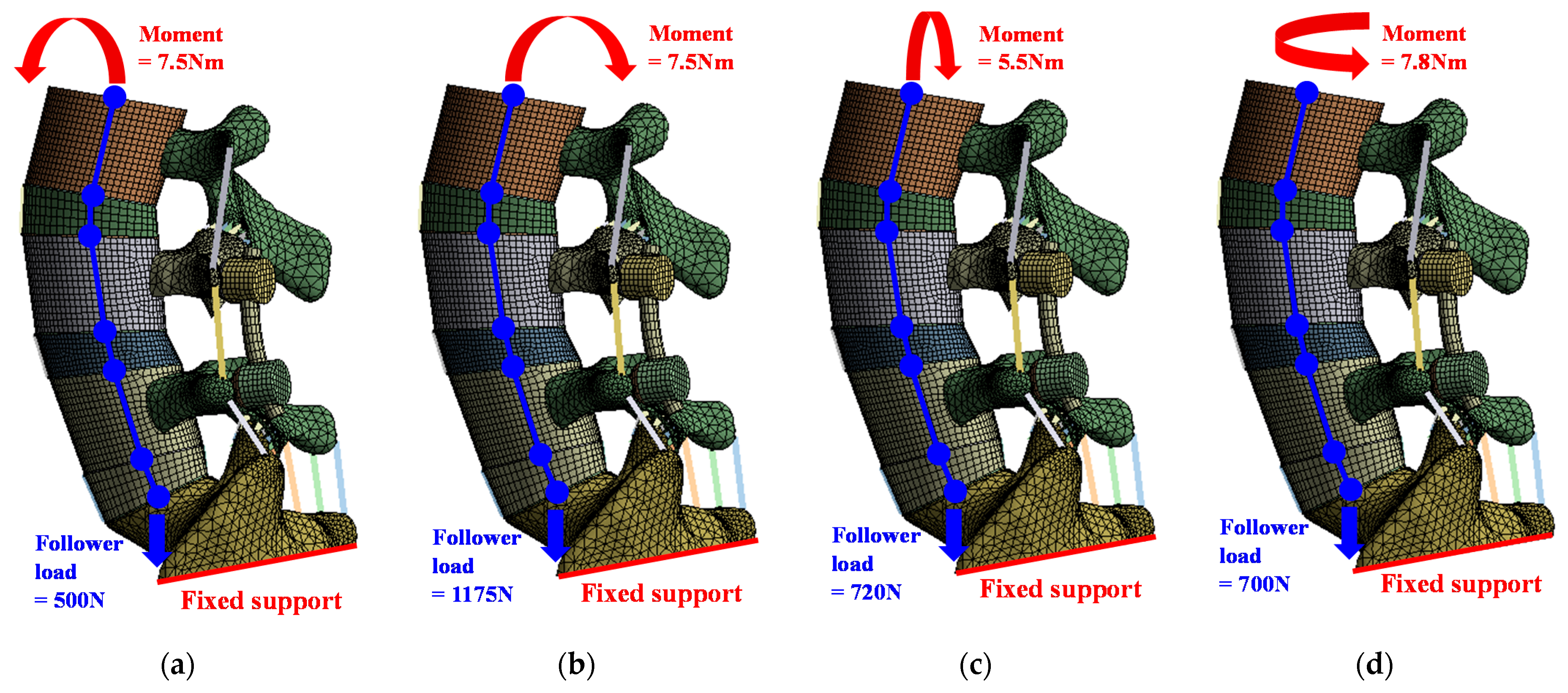
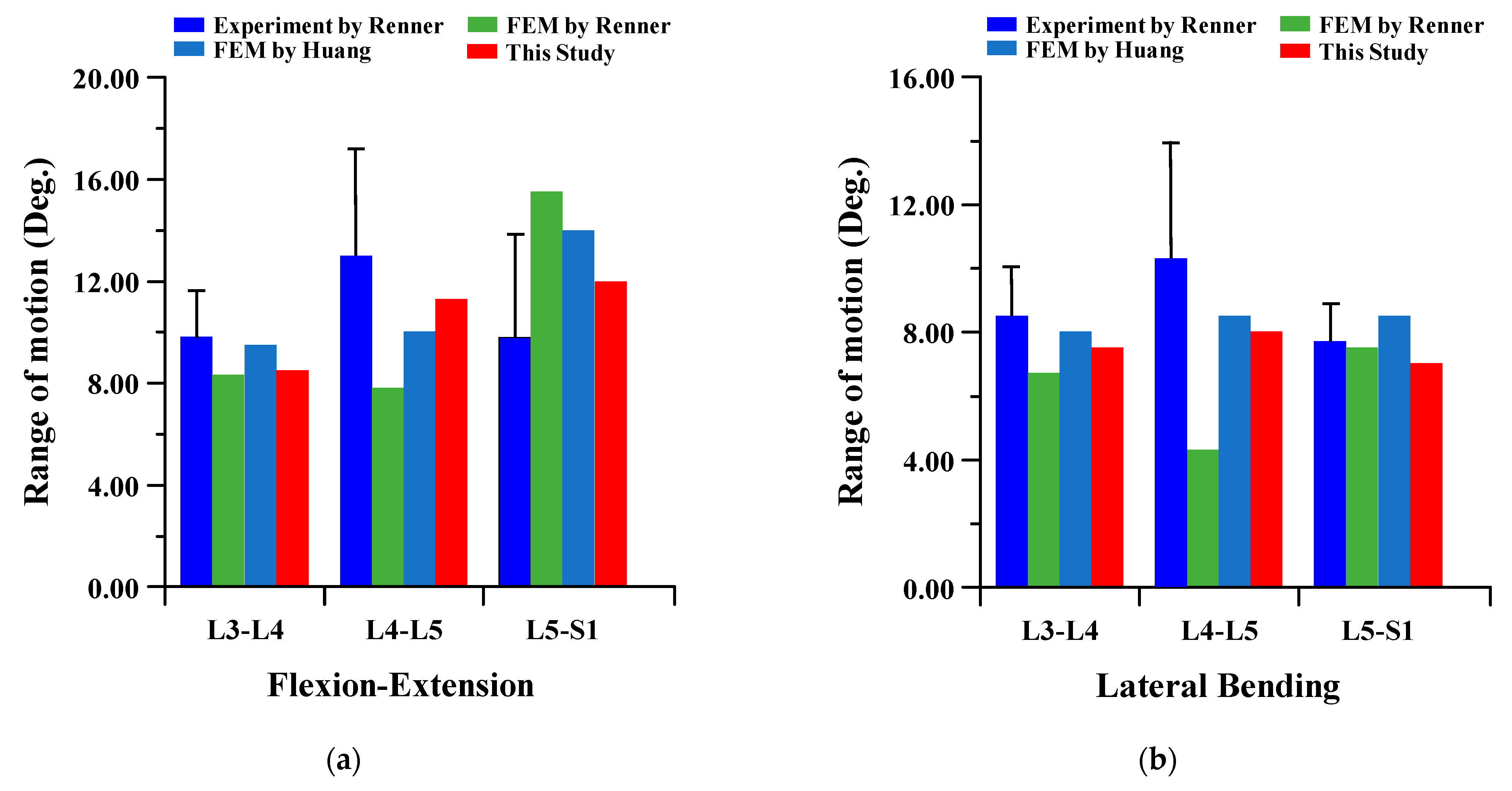



| Component | Elastic Modulus (MPa) | Poisson Ratio (ν) | Cross-Sectional Area (mm2) | Source | |
|---|---|---|---|---|---|
| Cortical bone | 14,000 | 0.3 | - | Wang et al., 2014 | |
| Trabecular bone | 100 | 0.2 | |||
| Posterior bone | 3500 | 0.25 | |||
| Sacrum | 5000 | 0.2 | |||
| Endplate | 10,000 | 0.25 | |||
| Annulus fibrosus | Mooney-Rivlin C1 = 0.18, C2 = 0.045 | ||||
| Nucleus pulposus | 1 | 0.499 | - | Dooris et al., 2001 | |
| Anterio longitudinal ligament | 7.8 | 0.3 | 63.7 | Goel et al., 1995 Range of motion | |
| Posterior longitudinal ligament | 10 | 20 | |||
| Ligamentum flavum | 15 | 40 | |||
| Intertransverse ligament | 10 | 3.6 | |||
| Interspinous ligament | 10 | 40 | |||
| Supraspinous ligament | 8 | 30 | |||
| Facet capsulary ligament | 32.9 | 80 | |||
| Spinal Implants (Pedicle screw, spinal cage, spinal rod) | 0% | 118,700 | 0.31 | - | Falkowska et al., 2020 |
| 34% | 41,800 | 0.31 | |||
| 50% | 20,400 | 0.32 | |||
| 73% | 7400 | 0.35 | |||
| 81% | 3700 | 0.42 | |||
| Bone graft | 50 | 0.2 | - | Hung et al., 2016 | |
| p (%) | n | H | E (GPa) | ν |
|---|---|---|---|---|
| 0 | 0.0605 | 1236.232 | 118.7 | 0.31 |
| 34 | 0.0815 | 559.114 | 41.8 | 0.31 |
| 50 | 0.0897 | 339.078 | 20.4 | 0.32 |
| 73 | 0.0963 | 169.512 | 7.4 | 0.35 |
| 81 | 0.1102 | 101.977 | 3.7 | 0.42 |
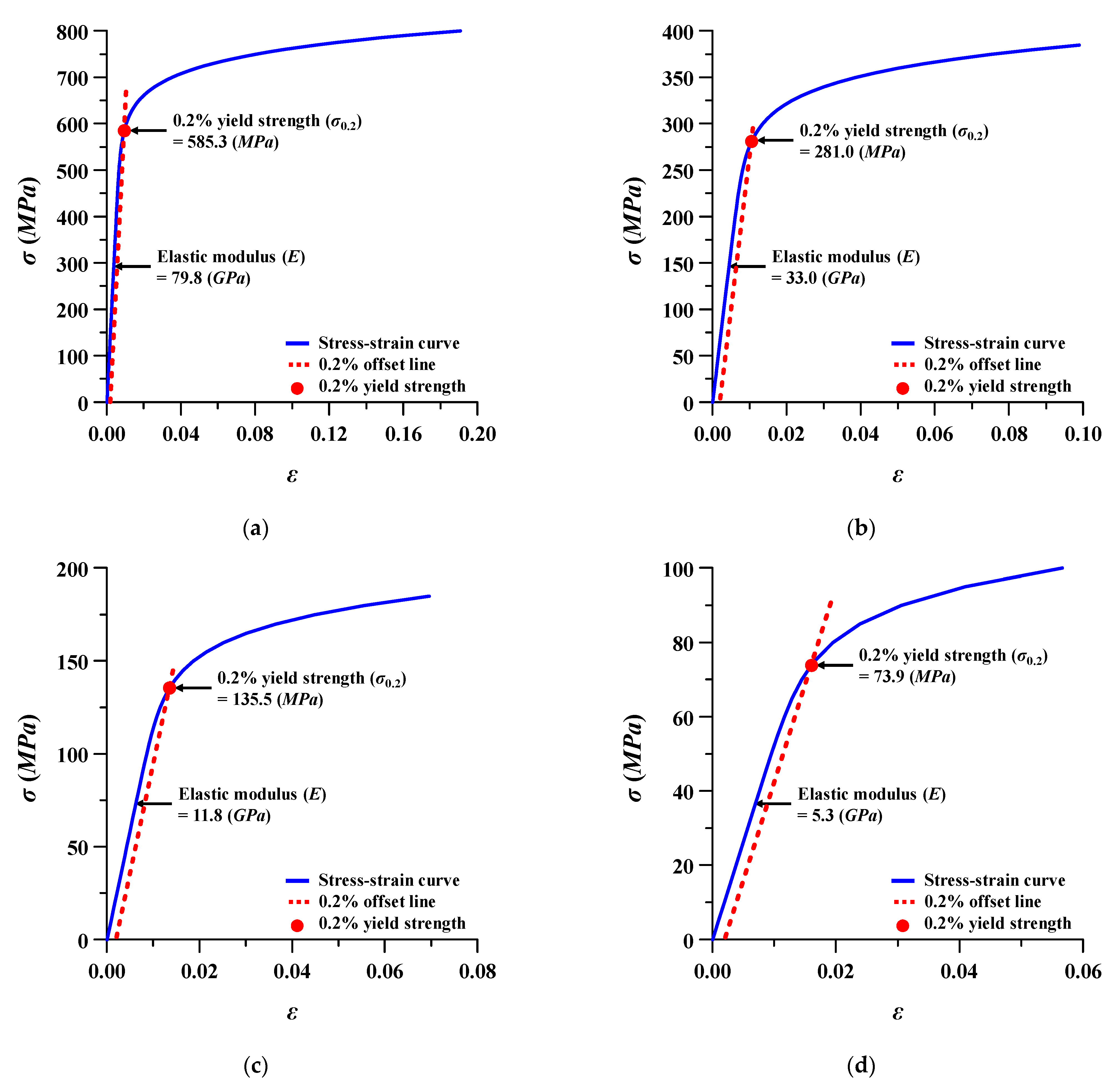
| Scenario | p (%) | E (GPa) | ν | σ0.2 (MPa) |
|---|---|---|---|---|
| 1 | 0 | 118.7 | 0.31 | 898.8 |
| 2 | 15 | 79.8 | 0.31 | 585.3 |
| 3 | 32 | 41.8 | 0.31 | 331.7 |
| 4 | 40 | 33.0 | 0.31 | 281.0 |
| 5 | 50 | 20.4 | 0.32 | 193.5 |
| 6 | 60 | 11.8 | 0.33 | 135.5 |
| #7 | 73 | 7.4 | 0.35 | 90.8 |
| #8 | 75 | 5.3 | 0.38 | 73.9 |
| #9 | 81 | 3.7 | 0.41 | 50.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.-H.; Park, J.-S.; Choi, B.-W.; Lee, J.S.; Lee, C.-S. Computational Investigation for Biomechanical Characteristics of Lumbar Spine with Various Porous Ti–6Al–4V Implant Systems. Appl. Sci. 2021, 11, 8023. https://doi.org/10.3390/app11178023
Song C-H, Park J-S, Choi B-W, Lee JS, Lee C-S. Computational Investigation for Biomechanical Characteristics of Lumbar Spine with Various Porous Ti–6Al–4V Implant Systems. Applied Sciences. 2021; 11(17):8023. https://doi.org/10.3390/app11178023
Chicago/Turabian StyleSong, Chan-Hee, Jun-Sung Park, Byung-Wan Choi, Jung Sub Lee, and Chi-Seung Lee. 2021. "Computational Investigation for Biomechanical Characteristics of Lumbar Spine with Various Porous Ti–6Al–4V Implant Systems" Applied Sciences 11, no. 17: 8023. https://doi.org/10.3390/app11178023
APA StyleSong, C.-H., Park, J.-S., Choi, B.-W., Lee, J. S., & Lee, C.-S. (2021). Computational Investigation for Biomechanical Characteristics of Lumbar Spine with Various Porous Ti–6Al–4V Implant Systems. Applied Sciences, 11(17), 8023. https://doi.org/10.3390/app11178023






