Design of Autonomous Mobile Robot for Cleaning in the Environment with Obstacles

Abstract

This paper describes the design and development of a cleaning robot, using adaptive manufacturing technology and its use with a control algorithm for which there is a stability proof. The authors’ goal was to fill the gap between theory and practical implementation based on available low-cost components. Adaptive manufacturing was chosen to cut down the cost of manufacturing the robot. Practical verification of the effectiveness of the control algorithm was achieved with the experiments. The robot comprises mainly three assemblies, a four-wheel-drive platform, a four-degrees-of-freedom robotic arm, and a vacuum system. The inlet pipe of the vacuum system was attached to the end effector of the robotic arm, which makes the robot more flexible to clean uneven areas, such as skirting on floors. The robot was equipped with a LIDAR sensor and web camera, giving the opportunity to develop more complex methods. A low-level proportional–integral–derivative (PID) speed controller was implemented, and a high-level controller that uses artificial potential functions to generate repulsive components, which avoids collision with obstacles. Robot operating system (ROS) was installed in the robot’s on-board system. With the help of the ROS node, the high-level controller generates control signals for the low-level controller.

1. Introduction

Researchers and many companies have introduced different types of cleaning robot designs over the last two decades [1,2,3,4,5]. A study was conducted on some of the vacuum robots available in the market about cleaning efficiency, which showed that the manual vacuum cleaner is still more efficient for cleaning than vacuum robots [6]. The coverage area issue of the vacuum robots was also mentioned in the same article. The area above the floor, such as skirting, is unreachable for the vacuum robots (iRobot, Xiaomi Mi Robot Vacuum, etc.) having a fixed inlet on the bottom side. A vacuum robot with a flexible vacuum inlet may increase the cleaning efficiency and coverage area problems. In 1997, an autonomous vacuum cleaner, “Koala”, was introduced [7], which has a two-degrees-of-freedom robotic arm, cleaning head on the second link of the arm.

The paper presents experimental verification of the method, which was developed by the second author and presented in paper [8], including a stability analysis. The results described here are a continuation of these studies. The authors’ goal was to fill the gap between theory and practical implementation based on available low-cost components. Adaptive manufacturing was used to cut down the cost of manufacturing the robot. Practical verification of the effectiveness of the algorithm is an undeniably important phase of the research process. Proper operation, even though the test was used on a relatively simple, inexpensive mobile platform equipped with units of low computing power, is an additional advantage of the method presented here. Although the algorithm was not tested on expensive laboratory hardware equipped with high-precision sensors and actuators, it proved to be effective. Figure 1 demonstrates the cleaning robot, where the inlet pipe of the vacuum system was attached to the end effector of the robotic arm. The robot is equipped with a LIDAR sensor and web camera, giving the opportunity to develop more complex methods. The touch screen on the robot helps to displays the information from the robot. A low-level proportional–integral–derivative (PID) speed controller is used to achieve the desired speeds. A high-level controller [8] helps the robot to follow a virtual robot path with avoiding obstacles.

Creating a virtual model of the robot opens another field where we can verify the algorithm and potential problems in the design of the robot [9]. The FPGA-based controller also shows high potentials for the robotic arm [10] and power-saving architecture for the motions [11].

Artificial potential fields were introduced by Khatib [12] in 1986. In this control algorithm, attraction (to the goal) and repulsion (from the obstacle) are negated gradients of the artificial potential functions (APF). Many articles have been published using the navigation function (NF) [12,13,14,15,16,17]. The control of multiple mobile robots based on the kinematic model [18,19] and dynamic model [20,21] have also been published.

A sliding mode control strategy with an artificial potential field was shown in [22]. An obstacle potential field function considers the robot’s size and obstacle size and accordingly changes the weight of the obstacle potential field function, which adaptively makes the robot escape from local minima [23].

Authors of [24] addressed the problem of tracking the control of multiple differentially driven mobile platforms (leader–follower approach is used). The algorithm is distinguished by its simplicity and ease of implementation. The components of the control have an obvious physical interpretation, which facilitates the tuning based on observations of the robot’s behavior. The linear velocity control depends on the linear velocity of the reference robot (virtual leader) and the position error along the axis perpendicular to the axle of the robot wheels. The angular velocity is a function of the angular velocity of the virtual leader, orientation error, and the position error along the axle of the robot wheels, transformed by a non-linear function and activated periodically by a square persistently exciting function. The stability proof is based on the decomposition of the error dynamics into position and orientation subsystems that are ISS (input to state stable). Simulations confirm the effective error reduction for stadium-circuit shape trajectories composed of two straight lines and two half circumferences. The collision avoidance was not taken into account.

Collision avoidance with other robots and static obstacles was added in [8]. The position errors were replaced by correction variables, which combine the position errors and the gradients of APFs surrounding obstacles. When robots are outside of collision avoidance regions of other robots/obstacles (APF takes the value zero) the analysis given in [24] is actual. For the other cases, stability analysis based on the Lyapunov-like function was presented. Numerical verification was performed on a formation of fifteen robots in the environment with five obstacles. The desired trajectory was composed of straight lines and arcs.

The trajectory tracking algorithm proposed in [8] was based on [24]. In its original form, the collision avoidance was not included. It was assumed that the initial positions of robots guarantee that no collisions would occur. The extension proposed in [24] removes this limitation. The method guarantees the stability of the closed-loop system and collisions avoidance. A tracking method with similar computational complexity was proposed in work [25]. It does not involve a persistent excitation block. The stability of the system was also proven. Another method that was considered is the VFO (vector field orientation) algorithm [26]. This approach uses a special vector field and an auxiliary orientation variable. Stability was also proven for it, but its implementation on a real robot is more complex. In [27], this approach was extended by collision avoidance capability. There is tracking and collision avoidance for the multiple robots, but it takes into account the robot’s dynamics (mass, inertia) and is very complex to implement [20].

Section 2 shows the mechanical design and electronics parts of the robot. The control algorithm is presented in Section 3. Section 4 describes the methodology, and the experiment results are presented in Section 5.

2. Mechanical Design and Electronics Parts

Solid Edge 2020 software was used as a modeling tool to design our robot. The software’s synchronous technology was one of the main features by which authors modified the parts and assembly at any time. The 3D-printing support of this software makes it more user-friendly. The cloud feature of the software was helpful for the authors to work in a team and shared the design. The following points were considered while designing the parts:

• Lightweight parts.
• Suitable for 3D printing.
• Strength of PLA material.
• Ease of assembly.

The designs were saved as STL files, which were later used in the 3D printer. The “Creality Ender 3” 3D printer was used to print the parts. PLA material was used, which had the property of showing minor printing failures without close enclosure of the printer. The printer was set up for 200 degrees Celsius for the nozzle temperature and 60 degrees Celsius for the heat bed. The robot consist of mainly three assemblies as follows:

• Robotic arm.
• Vacuum system.
• Mobile platform.

2.1. Robotic Arm

The robot was equipped with a four-degrees-of-freedom robotic arm. All the joints consisted of revolute joints. The total length of the fully enlarged robotic arm was 44.8 cm, and the width was 14.8 cm.

Table 1. Details of servo motors.

Joint Number	Servo Name	Quantity	Torque
Joint 1	Tower Pro SG-5010	1	6.5 kg × cm
Joint 2	Feetech FS5115M	2	15.5 kg × cm
Joint 3	Tower Pro SG-5010	1	6.5 kg × cm
Joint 4	Tower Pro SG-90-micro	1	1.8 kg × cm

shows the details of the servo motors used in the robotic arm. Ball bearings were used to support and transfer the weight of one part to another. ABEC 3 skateboard bearings were used, with an outer diameter of 22 mm, core diameter of 8 mm, and 7 mm width.

2.2. Vacuum System

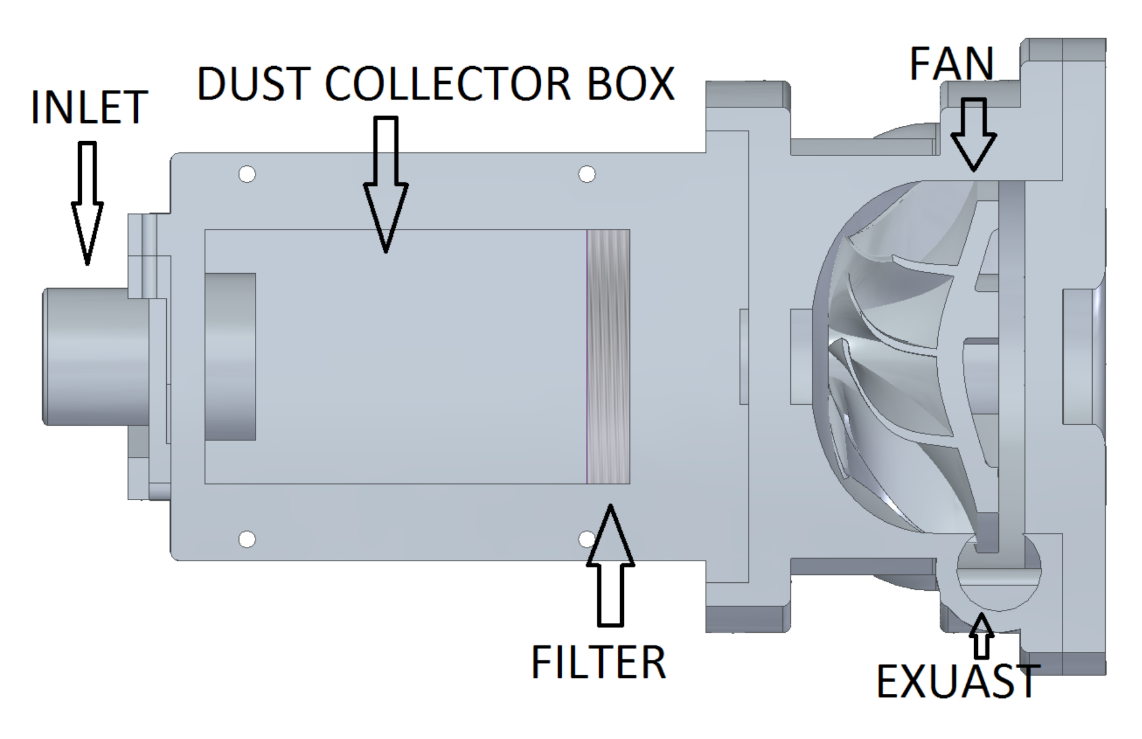
The vacuum system of the robot consists of 3D-printed parts, such as a fan, collector box, cover of the collector box, and fan chamber. Other parts include the filter, flexible pipe, and brushless motor. One end of the flexible tube is connected to the vacuum system and another end to the end-effector of the robotic arm. The collector box has a volume of 378 cubic cm (10 cm × 6 cm × 6.3 cm). Figure 2 shows the cut sectional view of the vacuum system. When the vacuum system starts vacuuming the floor, the air with the dust comes into the collector box, where the layer of vertical filter stops the dust, while allowing the air to pass through it.

Table 2. Details of electronics component for vacuum system.

S.No	Component Name	Specification
1	ESC, skywalker	Input- 2–4 s Lipo, continous current 50 A
2	Brushless motor, iFlight XING	2750 KV, max current 50.03 A
3	Lipo battery	11.1v, 50C, 5000 mAh

shows the electronics items used for the vacuum system.

2.3. Mobile Platform

The robot has a four-wheel-drive platform, which gives the robot more power to carry the weight of its robotic arm and vacuum system. DC geared motors with encoders are used in the mobile platform. A low-level PID speed controller is implemented in Arduino Mega. Each wheel has a diameter of 10 cm. The total length of the mobile platform is 23.9 cm, and the width is 24.9 cm with wheels. The lead battery is used to power the electronics of the mobile platform.

The upper body of the mobile platform is made up of three parts. These parts play a vital role in connecting the lower body part of the mobile platform with the vacuum system and robotic arm. The LIDAR holder provides the platform for the LIDAR sensor. The touch screen holder is also designed to hold a 7 inch touch screen connected to the top of the vacuum system. The height of the complete robot is 54.1 cm from the ground, a length of 54.1 cm when the robotic arm is fully enlarged, and 24.9 cm is the width of the platform with tires.

Table 3. Details of electronics part of mobile platform.

S.No	Component Name	Quantity	Specification
1	Motor Driver, L298N	2	Maximum current 2A
2	Arduino Mega	1	54 digital input/output pins
3	Arduino Uno	1	14 digital input/output pins
4	Raspberry Pi 4	1	2 GB RAM
5	Battery	1	6 V, 12 Ah
6	DC motor- Pololu 99:1 Metal	4	Integrated 48 CPR quadrature encoder
	gearmotor 25D×66L		4741.44 CPR, Torque-15 kg/cm
			14 digital input/output pins

shows the components of the electronics part of the mobile platform. The robot in total has two batteries. A 6 V DC battery is used to power the motor drivers and low-level controllers, such as Arduino UNO and Arduino Mega, while a Lipo battery is used to power the servo motors of the robotic arm, vacuum system, and Raspberry Pi computer. The robot has three controllers. Raspberry Pi acts as the master controller connected through the serial link to Arduino Mega, which serves as the first slave controller. The Arduino Mega is also connected with Arduino Uno, using serial communication. As a result, Arduino Uno serves as the second slave controller, which controls the direction and speed of one motor. The other three motors are controlled with Arduino Mega, due to the limitations of the external interrupt pins. The L298n motor drivers control the motors’ direction and speed. Each motor driver is capable of controlling two motors. Two wires from the microcontroller to the motor driver control the direction, and one wire controls the speed of the motor.

“Camera Tracer HD WEB008” is the digital camera used for the vision system. The device captures HD-quality images with a resolution of 1280 × 720 pixels. The lens has a wide-angle view of horizontal 100 degrees and can capture images with 30 frames per second. “Hokuyo urg-04lx-ug01” is used as the LIDAR sensor.

3. Control Algorithm

The control algorithm for the mobile platform was taken from the research paper [8]. The control algorithm was tested in the numerical simulation in the same research paper. To move one step further, the authors decided to test the algorithm with the proposed cleaning robot. With this control algorithm, the cleaning robot tried to follow a virtual robot path while avoiding the obstacles with artificial potential functions (APF). A repulsive field was generated to repel the robot from the obstacles.

The kinematics of the robot is given by the following formula:

$$\dot{q}=\left[\begin{array}{cc}cos\theta & 0\\ sin\theta & 0\\ 0& 1\end{array}\right]u$$

(1)

where vector $u={\left[\begin{array}{cc}v& \omega \end{array}\right]}^{\top }$ is the control vector with v denoting linear velocity control, and $\omega$ denotes the angular velocity control of the follower robot. Vector $q={\left[xy\theta \right]}^{\top }$ denotes the pose, and x, y, $\theta$ are the position coordinates and orientation of the robot with respect to a global, fixed coordinate frame.

The robot has to follow the virtual robot, which moves with the desired linear velocity and angular velocity ${\left[v_d{\omega }_d\right]}^T$ along the planned trajectory. The robot should achieve the same velocities as that of the virtual robot; ${\left[x_d{y}_d\right]}^T$ are the position coordinates of the virtual leader, which acts as a reference position of the real robot, and its orientation $\theta$ converges to the orientation of the virtual leader ${\theta }_d$.

The APF repels the robot from the obstacles as it rises to infinity near the obstacle’s borders, $r_j$ (j—number of the obstacles) and decreases to zero at some distance $R_j$, $R_j>r_j$.

Equations for APF are written as follows:

$$B_{aj}\left(l_j\right)=\left\{\begin{array}{ccc}0& \mathrm{for}& l_j<r_j\\ e^{\frac{l_j-r_j}{l_j-R_j}}& \mathrm{for}& r_j\le l_j<R_j\\ 0& \mathrm{for}& l_j\ge R_j\end{array}\right.,$$

(2)

which gives output $B_{aj}\left(l_j\right)\in \left.〈0,1\right)$, the distance between the robot and the j-th obstacle, which is defined as the Euclidean length $l_j=∥{\left[x_j{y}_j\right]}^{\top }-{\left[xy\right]}^{\top }∥$.

Scaling the function given by Equation (2) within the range $\left.〈0,\infty \right)$ can be given as follows:

$$V_{aj}\left(l_j\right)=\frac{B_{aj}\left(l_j\right)}{1-B_{aj}\left(l_j\right)},$$

(3)

which is used later to avoid collisions.

In further description terms, the ’collision area’ is used for location fulfilling conditions $l_j<r_j$. The range $r_j<l_j<R_j$ is called the ’collision avoidance area’.

The goal of the controller is to drive the robot along the desired trajectory along with avoiding obstacles, which result brings the following quantities to zero:

$$\begin{array}{cc}\hfill p_x& =x_d-x\hfill \\ \hfill p_y& =y_d-y\hfill \\ \hfill p_{\theta }& ={\theta }_d-\theta .\hfill \end{array}$$

(4)

Assumption 1.

$\forall \{i,j\},i\ne j,\left|\right|{\left[x_d{y}_d\right]}^T-{\left[x_j{y}_j\right]}^T\left|\right|>R_j$ where ${\left[x_j{y}_j\right]}^T$ is location of the center of the j-th obstacle.

Assumption 2.

If the robot gets into the avoidance region, its desired trajectory is temporarily frozen (${\dot{x}}_d=0$, ${\dot{y}}_d=0$). If the robot leaves the collision avoidance area, then its desired coordinates are immediately updated. As long as the robot remains in the avoidance region, its desired coordinates are periodically updated at certain discrete instants of time. The time period $t_u$ of this update process is large in comparison to the main control loop sample time.

Assumption 1 tells that the desired path of the virtual robot should be planned in such a way that in the steady state, the virtual robot should remain outside of the collision avoidance regions.

Assumption 2 means that the tracking process is temporarily suspended when the follower robot gets into collision regions because collision avoidance has a higher priority. Once the robot is outside of the collision detection region, it updates the reference to the new values. In addition, when the robot is in the collision avoidance region, its reference trajectory is periodically updated. It supports leaving the unstable equilibrium points (which occurs, for example, when one robot is located precisely between the other robots and its goal) if the reference trajectory is exciting enough. In rare cases, the robot may get stuck at a saddle point, but the set of such points is of measure zero and is not considered further.

The error with respect to the coordinate frame fixed to the robot can be calculated as follows:

$$\left[\begin{array}{c}{e}_x\\ e_y\\ e_{\theta }\end{array}\right]=\left[\begin{array}{ccc}cos\left(\theta \right)& sin\left(\theta \right)& 0\\ -sin\left(\theta \right)& cos\left(\theta \right)& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{p}_x\\ p_y\\ p_{\theta }\end{array}\right].$$

(5)

The error dynamics can be written with the above equations and non-holonomic constraint $\dot{y}cos\left(\theta \right)-\dot{x}sin\left(\theta \right)=0$ as follows:

$$\begin{array}{cc}\hfill {\dot{e}}_x& =e_y\omega -v+v_{d}cos{e}_{\theta }\hfill \\ \hfill {\dot{e}}_y& =-e_x\omega +v_{d}sin{e}_{\theta }\hfill \\ \hfill {\dot{e}}_{\theta }& ={\omega }_d-\omega ,\hfill \end{array}$$

(6)

where $v_d$ and ${\omega }_d$ are controls of the reference virtual robot.

The position error and collision avoidance terms can be used to calculate position correction variables as follows:

$$\begin{array}{cc}\hfill P_x& =p_x-\sum _{j=1}^M\frac{\partial V_{aj}}{\partial x}\hfill \\ \hfill P_y& =p_y-\sum _{j=1}^M\frac{\partial V_{aj}}{\partial y}.\hfill \end{array}$$

(7)

$V_{aj}$ depends on x and y according to Equation (3); M is a number of static obstacles in the task space. The robot avoids collisions with them. The correction variables can be transformed to the local coordinate frame fixed to the geometric center of the mobile platform:

$$\left[\begin{array}{c}{E}_x\\ E_y\\ e_{\theta }\end{array}\right]=\left[\begin{array}{ccc}cos\left(\theta \right)& sin\left(\theta \right)& 0\\ -sin\left(\theta \right)& cos\left(\theta \right)& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{P}_x\\ P_y\\ p_{\theta }\end{array}\right].$$

(8)

Equation (8) can be transformed to the following form [8]:

$$\begin{array}{cc}\hfill E_x& =p_{x}cos\left(\theta \right)+p_{y}sin\left(\theta \right)+\sum _{j=1}^M\frac{\partial V_{aj}}{\partial e_x}\hfill \\ \hfill E_y& =-p_{x}sin\left(\theta \right)+p_{y}cos\left(\theta \right)+\sum _{j=1}^M\frac{\partial V_{aj}}{\partial e_y}\hfill \\ \hfill e_{\theta }& =p_{\theta }\hfill \end{array}$$

(9)

where each derivative of the APF is transformed from the global coordinate frame to the local coordinate frame fixed to the robot. Finally, the correction variables expressed with respect to the local coordinate frame are as follows:

$$\begin{array}{cc}\hfill E_x& =e_x+\sum _{j=1}^M\frac{\partial V_{aj}}{\partial e_x}\hfill \\ \hfill E_y& =e_y+\sum _{j=1}^M\frac{\partial V_{aj}}{\partial e_y}.\hfill \end{array}$$

(10)

The trajectory tracking algorithm combined with collision avoidance is as follows:

$$\begin{array}{c}v=v_d+c_2{E}_x\\ \omega ={\omega }_d+h(t,E_y)+c_1{e}_{\theta }\end{array}$$

(11)

where $c_1$ and $c_2$ are the positive constant design parameters, while $h(t,E_y)$ depends on $E_y$ and continuously differentiable function. $h(t,E_y)$ plays a vital role in the persistent excitation of the virtual robots angular velocity.

Assumption 3.

If the value of the linear control signal is less than the considered threshold value $v_t$, i.e., $\left|v\right|<v_t$ ($v_t$—positive constant), it is replaced by a new scalar function $\tilde{v}=S\left(v\right)v_t$, where the following holds:

$$S\left(v\right)=\left\{\begin{array}{ccc}-1& \mathit{for}& v<0\\ 1& \mathit{for}& v\ge 0\end{array}\right..$$

(12)

Substituting (11) into (6), the error dynamics is given by the following equations:

$$\begin{array}{c}{\dot{e}}_x=e_y\omega -c_2{E}_x+v_d(\cos e_{\theta }-1)\\ {\dot{e}}_y=-e_x\omega +v_{d}sin{e}_{\theta }\\ {\dot{e}}_{\theta }=-h(t,E_y)-c_1{e}_{\theta }\end{array}.$$

(13)

Transforming (13) using (11) and taking into account Assumption 2 (when the robot gets into the collision avoidance area, velocities $v_d$ and ${\omega }_d$ are substituted as 0) error dynamics can be expressed in the following form:

$$\begin{array}{c}{\dot{e}}_x=h(t,E_y)e_y+c_1{e}_y{e}_{\theta }-c_2{E}_x\\ {\dot{e}}_y=-h(t,E_y)e_x-c_1{e}_{\theta }{e}_x\\ {\dot{e}}_{\theta }=-h(t,E_y)-c_1{e}_{\theta }\end{array}.$$

(14)

A stability analysis based on Lyapunov-like function was given in [8].

The control algorithm generates the linear and angular velocity for the real robot. The equations which convert these control velocities into wheel velocities are as follows:

$$\begin{array}{c}{v}_r=v+\left(\omega L\right)/2\\ v_l=v-\left(\omega L\right)/2\end{array}.$$

(15)

where $v_r$ is the robot right side velocities for both wheels, and $v_l$ is the robot left side velocities for both wheels. v and $\omega$ are the linear and angular velocities respectively. L is the distance between the left- and right-side wheels.

Now, the velocities for each wheels can be written using (15) as follows:

$$\begin{array}{c}{v}_{rf}=v_{rb}=v_r\\ v_{lf}=v_{lb}=v_l\end{array}.$$

(16)

where $v_{rf}$ represents the linear speed for the right-hand side front wheel, $v_{rb}$ represents the linear speed for the right-hand side back wheel, $v_{lf}$ represents the linear speed for the left-hand side front wheel, and $v_{lb}$ represents the linear speed for the left-hand side back wheel.

Wheel velocities are desired signals of the motor’s PID controllers.

4. Methodology

Two experiments were performed to verify the high-level controller explained in Section 3. A standard PC was used with the Linux system (Ubuntu 20.04) and the robot operating system (ROS) Noetic to collect data and implement the high-level controller. For the cleaning robot, Ubuntu LTS 20.04 with ROS Noetic was installed in the Raspberry Pi. The kinematic equations of the unicycle-like robot, low-level PID controller, odometry equations were installed in Arduino Mega (slave controller of Raspberry Pi). The PC and the cleaning robot were connected under the same Wi-Fi router to establish the ROS master and slave connectivity. The control algorithm in the graphical form is represented in Figure 3. The Figure 4 shows the real-time data exchange between the PC and the robot during the experiments. The high-level control algorithm was implemented in a ROS node written in Python language on the PC. In real-time, the odometry data coming from the robot were directly injected into the control algorithm to calculate the control signals for the robot. The calculated control signals were sent to the robot by the PC. The generated data were also saved by the PC as text files during the experiments. After completing the experiments, the authors used MATLAB software to plot the graphs from the text (txt) files. The control method was not very computationally complex, as it had 52 addition and subtraction operators, 54 multiplication operators, 19 sines, cosine, and hyperbolic tangent functions, and one exponential function. The computational complexity analysis was conducted for one obstacle.

5. Experiment Results

Experiments 1 and 2 were both performed in the indoor areas with even flooring. A long corridor was selected for Experiment 1, while the authors chose a rectangular area for Experiment 2. The scenarios presented in the experiments (motion along the line and circle that can be divided into arcs) were not accidental. These two types of motion can be used as components of a complex movement that a cleaning platform can carry out.

5.1. Experiment 1

In this experiment, one obstacle was placed at (2, 1) coordinates, the virtual robot starts from (0, 0) coordinates, and the real robot (cleaning robot) was placed at (1, 0) coordinates. Other settings included the following: $c_1$ was 2, and $c_2$ was 0.5, obstacle radius r was 0.23 m, tu was 0.5 s, and R was 0.7 m. The total experiment was performed for 140 s. The linear velocity for the virtual robot was 0.15 m/s, whereas the angular velocity was 0 rad/s. Persistent excitation was $h(t,E_y)=\varphi \left(t\right)tanh\left(E_y\right)$ where $\varphi \left(t\right)$ was a non-smooth pulse function of amplitude 0.5, 4 s period with the pulse width of 80 percent. Figure 5 shows the experimental results of this experiment. The scale of Figure 5a is 2 m for 1 unit of the x-axis and 0.5 m for 1 unit of the y-axis. Due to the scale, the circular obstacle looks elliptical. Figure 5a shows the paths of both the robots in the XY plot. The green color indicates the path of the virtual robot, which started from (0, 0) coordinates and traveled into a straight path. The robot starts from (0, 1), avoids the obstacle in its way, and converges to the desired trajectory in 45 s. Figure 5b shows the error in the x-coordinates as a function of time. As time passes, the controller helps the robot to achieve near-zero error in the x-axis. Figure 5c shows the error in the y-coordinates as a function of time, which also shows that error in the y-axis converges near zero, due to the controller. The error graph starts with 1 m in the negative direction, due to the initial setup of the robot concerning the virtual robot. The robot orientation error also tries to converge to zero, as shown in Figure 5d. The real-time control signal generated by the controller (linear velocity and angular velocity) for the robot can be shown in Figure 5e,f. However, in these plots, some high linear velocities and angular velocities are generated. In that case, the robot only moves to its top speeds. Freeze signals for the robot can be seen in Figure 5g, where zero means no freeze signal is generated and one unit shows that the robot is frozen. These are generated by the controller when the robot is in the potential field near the obstacle.

5.2. Experiment 2

In this experiment, two obstacles were placed at (−1, 1.5) and (1.2, 0.75) coordinates, the virtual robot started from (0, 0) coordinates, and the real robot (cleaning robot) was placed at (−2, 1) coordinates. $c_1$ was 2, and $c_2$ was 2, obstacle radius r was 0.23 m, tu was 0.4 s, and R was 0.7 m. The total experiment was performed for 120 s. The linear velocity for the virtual robot was 0.15 m/s, whereas the angular velocity was −0.15 rad/s. The persistent excitation was $h(t,E_y)=\varphi \left(t\right)tanh\left(E_y\right)$ where $\varphi \left(t\right)$ was a non-smooth pulse function of amplitude 0.5, 4 s period with the pulse width of 80 percent. Figure 6 shows the experimental results of this experiment. The scale of Figure 6a is 0.5 m for 1 unit of the x-axis and 1 m for 1 unit of the y-axis. Due to the scale, obstacles are not in a complete circular shape. Figure 6a shows the paths of both the robots in the XY plot. The green color indicates the path of the virtual robot, which starts from (0, 0) coordinates and moves in a circle in the anti-clockwise direction. The robot starts from (0, 1), avoids the two obstacles in its way, and converges to the desired trajectory at the end. Figure 6b shows the error in the x-coordinates as a function of time. As time passes, the controller helps the robot to achieve near-zero error in the x-axis. Figure 6c shows the error in the y-coordinates as a function of time, which also shows that error in the y-axis converges near zero, due to the controller. The robot orientation error also tries to converge to zero, as shown in Figure 6d. The real-time control signal generated by the controller (linear velocity and angular velocity) for the robot can be shown in Figure 6e,f. However, in these plots, some high linear velocities and angular velocities are generated. In that case, the real robot only moves to its top speeds. Freeze signals for the robot can be seen in Figure 6g, where zero means no freeze signal is generated and one unit shows that the robot is frozen. These are generated by the controller when the robot is in the potential field near the obstacle.

6. Conclusions

In this paper, experimental verification of the control algorithm was done on a cleaning robot. The robot was built with readily available electronics on the market and manufactured with additive manufacturing to cut down the cost. The design and the electronics of the robot were well explained in the paper. Experiments 1 and 2 were performed for 120 s. In Experiment 1, the robot errors were smaller than 1 percent after 52 s. In Experiment 2, the robot’s errors were smaller than 1 percent after 110 s. The initial conditions were chosen so that in the transient state, the robot had to avoid collisions with two obstacles. It worked well, as a collision did not occur, but this lengthened the transient state and thus the convergence time. The two experiment results show the effectiveness of the control algorithm. The robot avoided the obstacles and achieved the desired trajectory after some time. ROS gave a platform to implement the control algorithm on the standard PC and control the robot wirelessly. The proposed cleaning robot is already equipped with LIDAR and a web camera, which can create a map of an unknown environment and terrain, using the vision system to detect dust on the floor. Mecanum wheels can also be used to have more degrees of freedom for the mobile platform. The control of the robotic arm, vacuum system, vision system, and mobile platform can be synchronized to make a fully autonomous system for cleaning in an unknown environment.