Direct Evaluation of the Stress Intensity Factors for the Single and Multiple Crack Problems Using the P-Version Finite Element Method and Contour Integral Method
Abstract
:1. Introduction
2. P-Version Finite Element Method
2.1. Development of P-FEM
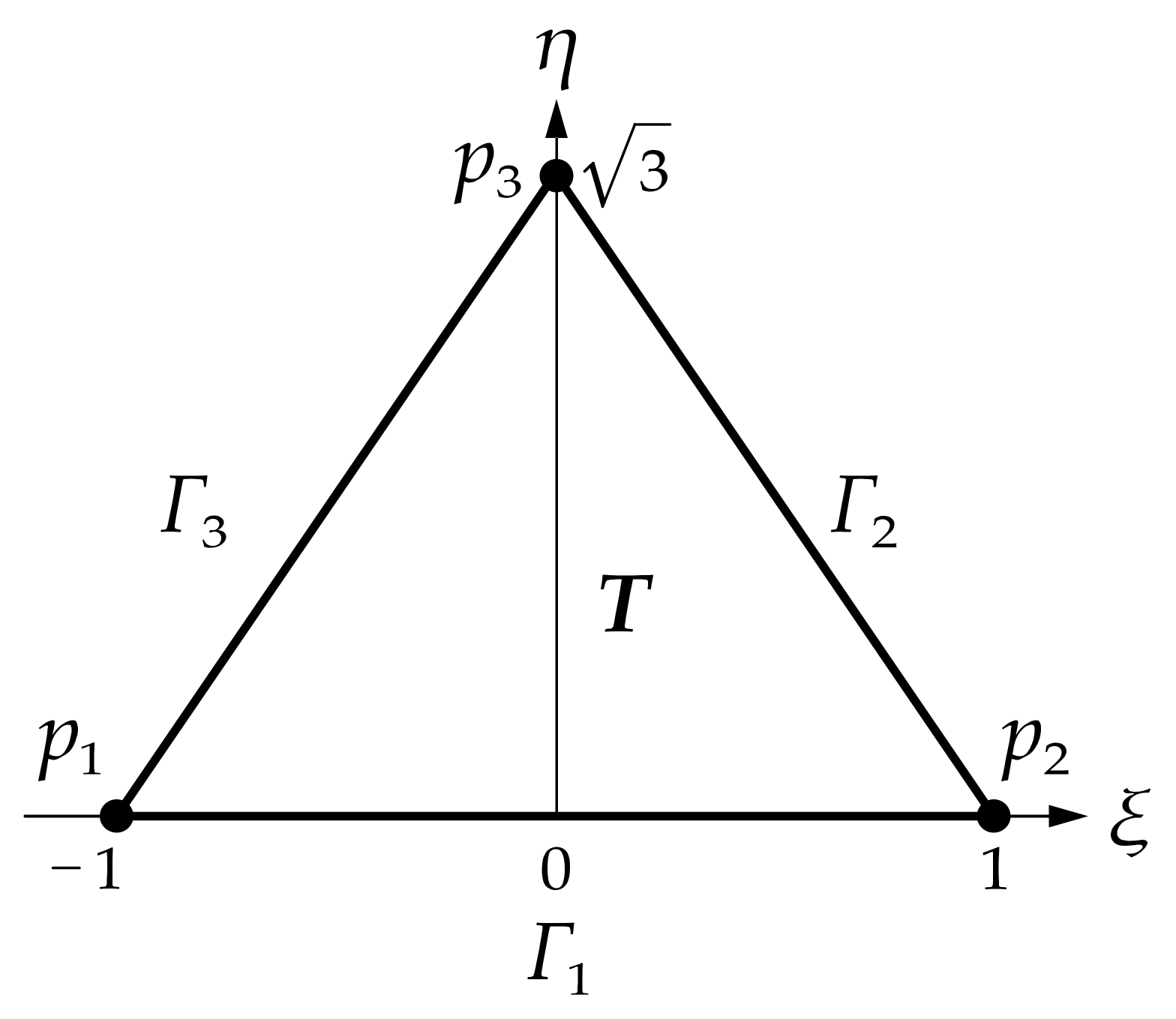
2.2. Shape Functions of the P-FEM
2.2.1. Nodal Modes Shape Functions for
2.2.2. Side Modes Shape Functions for
2.2.3. Internal Modes Shape Functions for
3. Contour Integral Method
4. Numerical Examples
4.1. A Central Straight Crack Plate
4.2. A Slanted Single-Edge Crack Plate
4.3. The Offset Double Edge Cracks Plate
4.4. A Branched Crack in an Infinite Plate
4.5. A Crucifix Crack in a Square Plate under Bi-Axial Tension
5. Conclusions
- The computation based on the P-FEM and CIM only needs a fewer number of meshes (less preprocessing), has a faster convergence rate, which can not only be used to analyze the single-crack problems, but also can be used to calculate the SIFs of multiple-crack problems. Furthermore, the present method can also be used to analyze three-dimensional fracture problems and simulate the crack growth path.
- The CIM is a super-convergent method based on the Betti’s theorem of reciprocal works. The SIFs are derived by using the displacements and stresses of higher accuracy on the integral path. Therefore, the CIM can obtain results of relatively higher precision.
- The P-FEM does not need fine meshes, has a faster convergence rate and higher accuracy. However, in the study of crack propagation behavior, it is inevitable to meet the problem of remeshing. On the other hand, the XFEM need not consider the internal geometry of structures and materials; it employs the partition of unity (PU) concept to simulate fracture and crack propagation. The XFEM uses the enrichment functions to reflect the local characteristics of the crack tip and avoids remeshing of meshes. The high-order extended finite element method (high-order XFEM), a combination of the P-FEM with XFEM, will probably have the advantages of both: avoiding remeshing as well as obtaining higher accuracy. The study of the high-order XFEM will be an interesting issue.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moës, N.; Dolbow, J.; Belytschko, T. A Finite Element Method for Crack Growth without Remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Liu, X.Y.; Xiao, Q.Z.; Karihaloo, B.L. XFEM for Direct Evaluation of Mixed Mode SIFs in Homogeneous and Bi-Materials. Int. J. Numer. Methods Eng. 2004, 59, 1103–1118. [Google Scholar] [CrossRef]
- Dong, Y.W.; Yu, T.T.; Ren, Q.W. Extended Finite Element Method for Direct Evaluation of Strength Intensity Factors. Chin. J. Comput. Mech. 2008, 25, 72–77. [Google Scholar]
- Shouyan, J.; Du Chengbin, G.C.; Xiaocui, C. Computation of Stress Intensity Factors for Interface Cracks between Two Dissimilar Materials Using Extended Finite Element Methods. Eng. Mech. 2015, 32, 22–27. [Google Scholar]
- Su, Y.; Wang, S.; Lu, L. SIFs of Interfacial Crack Using Generalized Extended Finite Element Method. J. Beijing Univ. Aeronaut. Astronaut. 2016, 42, 1162–1168. [Google Scholar] [CrossRef]
- Nianga, J.M.; Mejni, F.; Kanit, T.; Imad, A.; Li, J. Analysis of Crack Parameters under Mixed Mode Loading by Modified Exponential Matrix Method. Theor. Appl. Fract. Mech. 2019, 102, 30–45. [Google Scholar] [CrossRef]
- Liao, M.; Zhang, P. An Improved Approach for Computation of Stress Intensity Factors Using the Finite Element Method. Theor. Appl. Fract. Mech. 2019, 101, 185–190. [Google Scholar] [CrossRef]
- Chen, C.H.; Wang, C.L. Stress Intensity Factors and T-Stresses for Offset Double Edge-Cracked Plates under Mixed-Mode Loadings. Int. J. Fract. 2008, 152, 149–162. [Google Scholar] [CrossRef]
- Cui, X.; Li, H.; Cheng, G.; Tang, C.; Gao, X. Contour Integral Approaches for the Evaluation of Stress Intensity Factors Using Displacement Discontinuity Method. Eng. Anal. Bound. Elem. 2017, 82, 119–129. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, J.; Wu, L. Extraction of Stress Intensity Factors by Using the P-Version Finite Element Method and Contour Integral Method. Acta Mech. Solida Sin. 2020, 33, 836–850. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, R.; He, Y.; Yang, W. Direct Computation of 3-D Stress Intensity Factors of Straight and Curved Planar Cracks with the P-Version Finite Element Method and Contour Integral Method. Materials 2021, 14, 3949. [Google Scholar] [CrossRef]
- Gui, W.; Babuška, I. The h, p Andh-p Versions of the Finite Element Method in 1 Dimension. Numer. Math. 1986, 49, 613–657. [Google Scholar] [CrossRef]
- Babuška, I.; Suri, M. The Optimal Convergence Rate of the P-Version of the Finite Element Method. SIAM J. Numer. Anal. 1987, 24, 750–776. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, J. Stable and Compatible Polynomial Extensions in Three Dimensions and Applications to the p and H-p Finite Element Method. SIAM J. Numer. Anal. 2009, 47, 1195–1225. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiang, S. Research on 3D p-version hierarchical FEM for unsteady temperature field. Rock Soil Mech. 2009, 30, 487–491. [Google Scholar]
- Cheng, Y.; Yu, Z.; Wu, X.; Yuan, Y. Vibration Analysis of a Cracked Rotating Tapered Beam Using the P-Version Finite Element Method. Finite Elem. Anal. Des. 2011, 47, 825–834. [Google Scholar] [CrossRef]
- Stoykov, S.; Ribeiro, P. Vibration Analysis of Rotating 3D Beams by the P-Version Finite Element Method. Finite Elem. Anal. Des. 2013, 65, 76–88. [Google Scholar] [CrossRef]
- Kangsheng, Y.; Zhenwei, Y. A P-Type Superconvergent Recovery Method for FE Analysis of in-Plane Free Vibration of Planar Curved Beams. Eng. Mech. 2019, 36, 28–36. [Google Scholar]
- Farahmand, H.; Ahmadi, A.R.; Arabnejad, S. Thermal Buckling Analysis of Rectangular Microplates Using Higher Continuity P-Version Finite Element Method. Thin-Walled Struct. 2011, 49, 1584–1591. [Google Scholar] [CrossRef]
- Fei, W.; Chen, S. 3-D p-Version Elasto-Viscoplastic Adaptive FEM Model for Hydraulic Structures. J. Hydraul. Eng. 2003, 34, 86–92. [Google Scholar]
- Fei, W.; Chen, S. 3D Steady Seepage Analysis Using p Version Adaptive FEM. ROCK SOIL Mech.-WUHAN- 2004, 25, 211–215. [Google Scholar]
- Yosibash, Z. P-FEMs in Biomechanics: Bones and Arteries. Comput. Methods Appl. Mech. Eng. 2012, 249, 169–184. [Google Scholar] [CrossRef]
- Houmat, A. Three-Dimensional Free Vibration Analysis of Variable Stiffness Laminated Composite Rectangular Plates. Compos. Struct. 2018, 194, 398–412. [Google Scholar] [CrossRef]
- Wu, Y.; Xing, Y.; Liu, B. Hierarchical P-Version C1 Finite Elements on Quadrilateral and Triangular Domains with Curved Boundaries and Their Applications to Kirchhoff Plates. Int. J. Numer. Methods Eng. 2019, 119, 177–207. [Google Scholar] [CrossRef]
- Rahulkumar, P.; Saigal, S.; Yunus, S. Singular P-version finite elements for stress intensity factor computations. Int. J. Numer. Methods Eng. 1997, 40, 1091–1114. [Google Scholar] [CrossRef]
- Munaswamy, K.; Pullela, R. Computation of Stress Intensity Factors for through Cracks in Plates Using P-Version Finite Element Method. Commun. Numer. Methods Eng. 2008, 24, 1753–1780. [Google Scholar] [CrossRef]
- Yu, Z.; Chu, F. Identification of Crack in Functionally Graded Material Beams Using the P-Version of Finite Element Method. J. Sound Vib. 2009, 325, 69–84. [Google Scholar] [CrossRef]
- Wowk, D.; Gamble, K.; Underhill, R. Influence of P-Method Finite Element Parameters on Predictions of Crack Front Geometry. Finite Elem. Anal. Des. 2013, 73, 1–10. [Google Scholar] [CrossRef]
- Wowk, D.; Alousis, L.; Underhill, P.R. An Adaptive Remeshing Technique for Predicting the Growth of Irregular Crack Fronts Using P-Version Finite Element Analysis. Eng. Fract. Mech. 2019, 207, 36–47. [Google Scholar] [CrossRef]
- Szabó, B.; Babuška, I. Introduction to Finite Element Analysis: Formulation, Verification and Validation; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-1-119-99348-3. [Google Scholar]
- Pereira, J.P.; Duarte, C.A. The Contour Integral Method for Loaded Cracks. Commun. Numer. Methods Eng. 2006, 22, 421–432. [Google Scholar] [CrossRef]
- Leblanc, A.; Lavie, A. Solving Acoustic Nonlinear Eigenvalue Problems with a Contour Integral Method. Eng. Anal. Bound. Elem. 2013, 37, 162–166. [Google Scholar] [CrossRef]
- Garzon, J.; Duarte, C.A.; Pereira, J.P. Extraction of Stress Intensity Factors for the Simulation of 3-D Crack Growth with the Generalized Finite Element Method. Key Eng. Mater. 2013, 560, 1–36. [Google Scholar] [CrossRef]
- Feng, C.; Li, D.; Gao, S.; Daniel, K. Calculating the Reflected Radiation Error between Turbine Blades and Vanes Based on Double Contour Integral Method. Infrared Phys. Technol. 2016, 79, 171–182. [Google Scholar] [CrossRef]
- Szabo, B.A.; Babuška, I. Computation of the Amplitude of Stress Singular Terms for Cracks and Reentrant Corners. In Fracture Mechanics: Nineteenth Symposium; ASTM International: West Conshohocken, PA, USA, 1988; pp. 101–124. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.; Irwin, G. The Analysis of Cracks Handbook, 3rd ed.; ASME Press: New York, NY, USA, 2000; ISBN 978-0-7918-0153-6. [Google Scholar]
- Wu, J.; Wang, Y.; Cai, Y.; Ma, G. Direct Extraction of Stress Intensity Factors for Geometrically Elaborate Cracks Using a High-Order Numerical Manifold Method. Eng. Fract. Mech. 2020, 230, 106963. [Google Scholar] [CrossRef]
- Xiao, Q.Z.; Karihaloo, B.L.; Liu, X.Y. Direct Determination of SIF and Higher Order Terms of Mixed Mode Cracks by a Hybrid Crack Element. Int. J. Fract. 2004, 125, 207–225. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Hasebe, N. New Integration Scheme for the Branch Crack Problem. Eng. Fract. Mech. 1995, 52, 791–801. [Google Scholar] [CrossRef]
- Cai, Y.C.; Wu, J.; Atluri, S.N. A New Implementation of the Numerical Manifold Method (NMM) for the Modeling of Non-Collinear and Intersecting Cracks. Comput. Model. Eng. Sci. 2013, 92, 63–85. [Google Scholar]
- Cai, Y.C.; Wu, J. A Robust Algorithm for the Generation of Integration Cells in Numerical Manifold Method. Int. J. Impact Eng. 2016, 90, 165–176. [Google Scholar] [CrossRef]
- Cheung, Y.K.; Woo, C.W.; Wang, Y.H. A General Method for Multiple Crack Problems in a Finite Plate. Comput. Mech. 1992, 10, 335–343. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, D.; Sun, G.; Zheng, H. Modeling Complex Crack Problems Using the Three-Node Triangular Element Fitted to Numerical Manifold Method with Continuous Nodal Stress. Sci. China Technol. Sci. 2017, 60, 1537–1547. [Google Scholar] [CrossRef]









| p | DOF | Error of Energy Norm (%) | Relative Error (%) | ||
|---|---|---|---|---|---|
| 1 | 548 | 11.92 | 2.999 | 0.892 | −19.60 |
| 2 | 1602 | 3.28 | 3.535 | 1.051 | −5.23 |
| 3 | 2688 | 2.17 | 3.685 | 1.096 | −1.21 |
| 4 | 4278 | 1.45 | 3.724 | 1.107 | −0.16 |
| 5 | 6372 | 1.13 | 3.732 | 1.110 | 0.05 |
| 6 | 8970 | 0.94 | 3.733 | 1.110 | 0.08 |
| 7 | 12,072 | 0.81 | 3.733 | 1.110 | 0.08 |
| 8 | 15,678 | 0.71 | 3.733 | 1.110 | 0.08 |
| Analytical | NMM [37] | Present | ||||||
|---|---|---|---|---|---|---|---|---|
| a/W | Relative Error/(%) | Relative Error/(%) | ||||||
| 0.1 | 1.69 | 1.005 | — | — | — | 1.691 | 1.006 | 0.06% |
| 0.2 | 2.44 | 1.026 | 2.431 | 1.022 | −0.37% | 2.437 | 1.025 | −0.12% |
| 0.3 | 3.08 | 1.058 | — | — | — | 3.082 | 1.058 | 0.06% |
| 0.4 | 3.73 | 1.109 | 3.724 | 1.107 | −0.16% | 3.733 | 1.110 | 0.08% |
| 0.5 | 4.46 | 1.186 | — | — | — | 4.464 | 1.187 | 0.09% |
| 0.6 | 5.37 | 1.304 | 5.357 | 1.301 | −0.24% | 5.371 | 1.304 | 0.02% |
| 0.7 | 6.62 | 1.488 | — | — | — | 6.623 | 1.489 | 0.05% |
| SIFs | ||||
|---|---|---|---|---|
| Present | 4.7195 | 5.7810 | 2.2621 | |
| EMM [6] | r/a = 1/12 | 4.7290 | 5.7730 | 2.2613 |
| r/a = 1/6 | 4.7255 | 5.7737 | 2.2611 | |
| r/a = 1/3 | 4.7236 | 5.7745 | 2.2612 | |
| r/a = 1/2 | 4.7229 | 5.7752 | 2.2614 | |
| r/a = 2/3 | 4.7225 | 5.7758 | 2.2617 | |
| Abaqus solution [6] | 4.7183 | 5.7802 | 2.2615 | |
| FEOD [38] | 4.6883 | 5.7376 | 2.2400 | |
| BCM [38] | 4.1970 | 5.1776 | 2.0184 |
| p | DOF | Error of Energy Norm/(%) | Relative Error/(%) | Relative Error/(%) | ||
|---|---|---|---|---|---|---|
| 1 | 86 | 59.76 | 2.4576 | −47.9131 | 1.4320 | −36.6810 |
| 2 | 250 | 17.42 | 4.3832 | −7.1028 | 2.0667 | −8.6117 |
| 3 | 434 | 12.41 | 4.5766 | −3.0022 | 2.1598 | −4.4971 |
| 4 | 696 | 6.12 | 4.7010 | −0.3662 | 2.2496 | −0.5250 |
| 5 | 1036 | 3.87 | 4.7148 | −0.0733 | 2.2586 | −0.1278 |
| 6 | 1454 | 2.88 | 4.7171 | −0.0244 | 2.2614 | −0.0056 |
| 7 | 1950 | 2.24 | 4.7195 | 0.0244 | 2.2618 | 0.0148 |
| 8 | 2524 | 1.80 | 4.7195 | 0.0244 | 2.2621 | 0.0250 |
| c/L | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | |
|---|---|---|---|---|---|---|---|
| Present | 12.010 | 9.147 | 8.431 | 8.577 | 9.370 | 11.010 | |
| 4.791 | 3.649 | 3.363 | 3.422 | 3.738 | 4.392 | ||
| Liao et al. [7] | 11.884 | 9.099 | 8.387 | 8.525 | 9.302 | 10.914 | |
| 4.741 | 3.630 | 3.346 | 3.401 | 3.711 | 4.354 | ||
| Chen et al. [8] | 12.059 | 9.114 | 8.400 | 8.543 | 9.330 | 10.961 | |
| 4.811 | 3.636 | 3.351 | 3.408 | 3.722 | 4.373 | ||
| Present | −0.623 | −0.9405 | −1.362 | −1.885 | −2.618 | −3.818 | |
| −0.249 | −0.375 | −0.543 | −0.752 | −1.044 | −1.523 | ||
| Liao et al. [7] | −0.664 | −0.975 | −1.404 | −1.933 | −2.670 | −3.863 | |
| −0.265 | −0.389 | −0.560 | −0.771 | −1.065 | −1.541 | ||
| Chen et al. [8] | −0.567 | −0.983 | −1.411 | −1.945 | −2.695 | −3.910 | |
| −0.226 | −0.392 | −0.563 | −0.776 | −1.075 | −1.560 |
| c/L | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | |
|---|---|---|---|---|---|---|---|
| Present | 8.546 | 7.120 | 7.002 | 7.108 | 7.287 | 7.646 | |
| 3.409 | 2.840 | 2.793 | 2.836 | 2.907 | 3.050 | ||
| Liao et al. [7] | 8.372 | 7.096 | 6.981 | 7.086 | 7.264 | 7.620 | |
| 3.340 | 2.831 | 2.785 | 2.827 | 2.898 | 3.040 | ||
| Chen et al. [8] | 8.528 | 7.119 | 7.004 | 7.109 | 7.289 | 7.648 | |
| 3.402 | 2.840 | 2.794 | 2.836 | 2.908 | 3.051 | ||
| Present | −0.313 | −0.458 | −0.403 | −0.333 | −0.407 | −0.736 | |
| −0.125 | −0.183 | −0.161 | −0.133 | −0.162 | −0.294 | ||
| Liao et al. [7] | −0.318 | −0.456 | −0.401 | −0.333 | −0.406 | −0.732 | |
| −0.127 | −0.182 | −0.160 | −0.133 | −0.162 | −0.292 | ||
| Chen et al. [8] | −0.326 | −0.461 | −0.406 | −0.338 | −0.411 | −0.742 | |
| −0.130 | −0.184 | −0.162 | −0.135 | −0.164 | −0.296 |
| c/L | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | |
|---|---|---|---|---|---|---|---|
| Present | 7.494 | 6.968 | 7.046 | 7.083 | 7.102 | 7.168 | |
| 2.990 | 2.780 | 2.811 | 2.826 | 2.833 | 2.860 | ||
| Liao et al. [7] | 7.445 | 6.931 | 7.009 | 7.046 | 7.064 | 7.129 | |
| 2.970 | 2.765 | 2.796 | 2.811 | 2.818 | 2.844 | ||
| Chen et al. [8] | 7.490 | 6.971 | 7.049 | 7.086 | 7.104 | 7.171 | |
| 2.988 | 2.781 | 2.812 | 2.827 | 2.834 | 2.861 | ||
| Present | −0.397 | −0.338 | −0.120 | −0.030 | −0.042 | −0.153 | |
| −0.158 | −0.135 | −0.048 | −0.012 | −0.017 | −0.061 | ||
| Liao et al. [7] | −0.399 | −0.336 | −0.120 | −0.030 | −0.043 | −0.150 | |
| −0.159 | −0.134 | −0.048 | −0.012 | −0.017 | −0.060 | ||
| Chen et al. [8] | −0.326 | −0.461 | −0.406 | −0.338 | −0.411 | −0.742 | |
| −0.161 | −0.135 | −0.048 | −0.012 | −0.017 | −0.061 |
| p | DOF | Error of Energy Norm/(%) | Relative Error/(%) | Relative Error/(%) | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 328 | 38.730 | 5.471 | 2.182613 | −22.386 | −0.069 | −0.02753 | −42.292 |
| 2 | 940 | 14.790 | 6.832 | 2.725574 | −3.078 | −0.065 | −0.02593 | −45.500 |
| 3 | 1584 | 8.210 | 6.980 | 2.784617 | −0.979 | −0.110 | −0.04388 | −8.333 |
| 4 | 2512 | 4.430 | 7.032 | 2.805362 | −0.241 | −0.114 | −0.04548 | −5.000 |
| 5 | 3724 | 3.120 | 7.039 | 2.808155 | −0.142 | −0.119 | −0.04747 | −0.750 |
| 6 | 5220 | 2.350 | 7.043 | 2.80975 | −0.085 | −0.120 | −0.04787 | −0.333 |
| 7 | 7000 | 1.930 | 7.045 | 2.810548 | −0.057 | −0.120 | −0.04787 | 0.000 |
| 8 | 9064 | 1.620 | 7.046 | 2.810947 | −0.043 | −0.120 | −0.04787 | 0.083 |
| Reference Solutions [39] | Cai et al. [40] | Relative Error (%) | Cai et al. [41] | Relative Error (%) | Present | Relative Error (%) | |
|---|---|---|---|---|---|---|---|
| 1.040 | 1.029 | −1.058 | 1.029 | −1.058 | 1.042 | 0.192 | |
| 0.495 | 0.492 | −0.606 | 0.489 | −1.212 | 0.496 | 0.202 | |
| 0.503 | 0.501 | −0.398 | 0.501 | −0.398 | 0.504 | 0.199 |
| a | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 |
|---|---|---|---|---|---|---|
| Present | 0.8824 | 0.9084 | 0.9507 | 1.0190 | 1.1320 | 1.3170 |
| Ref [42] | 0.8800 | 0.9092 | 0.9537 | 1.0223 | 1.1300 | 1.2866 |
| Ref [43] | 0.8831 | 0.9246 | 0.9614 | 1.0040 | 1.1370 | 1.3247 |
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
|---|---|---|---|---|---|
| Present | 252 | 39 | 142 | 329 | 580 |
| Ref [37] | 4410 | — | — | — | — |
| Ref [6] | — | — | — | — | — |
| Ref [38] | — | 423 | — | — | — |
| Ref [7] | — | — | 2494 | — | — |
| Ref [8] | — | — | — | — | — |
| Ref [40] | — | — | — | 3678 nodes | — |
| Ref [41] | — | — | — | 2489 nodes | — |
| Ref [42] | — | — | — | — | 3600 collocation points |
| Ref [43] | — | — | — | — | 1858 physical patches |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yang, W.; Chen, J.; Xu, R. Direct Evaluation of the Stress Intensity Factors for the Single and Multiple Crack Problems Using the P-Version Finite Element Method and Contour Integral Method. Appl. Sci. 2021, 11, 8111. https://doi.org/10.3390/app11178111
Zhang J, Yang W, Chen J, Xu R. Direct Evaluation of the Stress Intensity Factors for the Single and Multiple Crack Problems Using the P-Version Finite Element Method and Contour Integral Method. Applied Sciences. 2021; 11(17):8111. https://doi.org/10.3390/app11178111
Chicago/Turabian StyleZhang, Jianming, Wensheng Yang, Jun Chen, and Rui Xu. 2021. "Direct Evaluation of the Stress Intensity Factors for the Single and Multiple Crack Problems Using the P-Version Finite Element Method and Contour Integral Method" Applied Sciences 11, no. 17: 8111. https://doi.org/10.3390/app11178111






