1. Introduction
In the hydraulic analysis of water distribution systems (WDSs), there have been several approaches throughout the decades for designing and representing the behavior of these systems more realistically, especially in case of abnormal operating conditions. Generally, the risk of an abnormal condition can define a measure with which a hazard or threat resulting either from probable events beyond our control or from the possible consequences of a decision may be assessed [
1,
2]. This abnormal condition can be generated frequently in WDSs fields such as pipe breakage, leakage, extreme demand e.g., fire flow, and for this reason, the realistic quantification of damage via efficient hydraulic analysis approaches is needed. There are two main approaches for hydraulic analysis such demand-driven analysis (DDA) and pressure-driven analysis (PDA) with different characteristics and levels of complexity. The conventional hydraulic analysis of WDSs corresponds to a demand-driven analysis, in which the energy equation is nonlinear. Because of this, some iterative method is needed to solve a set of hydraulic equations (nonlinear energy equation and linear mass balance equation). The history of the development of these iterative methods is long and wide; finally, it was Todini and Pilati [
3] who suggested the gradient method, an improved version of the Newton–Raphson approach that assumes and obtains unknown values of nodal head and pipe flows simultaneously. This approach does not need a balance of equations at the beginning of the method, which is a big improvement compared with previous methods, becoming the most prominent iterative method for simple formulation and computational benefits. The accurate results of this method under normal operation conditions (no leakage, pipe breaks, or unexpected fire demands) were enough reason to implement it in commercial hydraulic solvers, such as EPANET [
4] and KYPipe [
5]. However, these simulators, which are applied DDA as a hydraulic analysis approach, can be appropriately hydraulically analyzed only under abnormal system conditions, such as a sudden increase in demand flow due to a fire, the effect of a network condition during the system for damaged pipe reparation, rehabilitation, and replacement.
In reality, when there is a problem in the network, usually, the water pressure in each head might be less than the minimum required to satisfy the nodal demands. As a consequence, the simulation will give a negative or unacceptably low nodal pressure compared with the nodal pressure head in normal conditions [
6,
7,
8]. In other words, it is necessary to accurately predict the water supply and water pressure shortage area according to abnormal conditions through hydraulic analysis, approximating the behavior of the actual system, and through this, design and operation techniques should be performed in consideration of each abnormal situation. To overcome this negative pressure and other unrealistic results, a pressure-driven analysis (PDA) was developed to solve the unrealistic hydraulic analysis problem of DDA. PDA identifies the nodes where the pressure head can satisfy the current demand; otherwise, the nodal demand can be partially satisfied and becomes dependent on the available pressure head. Traditional hydraulic analysis of WDSs based on DDA considers the fixed demand that applies the whole of the nodal demand regardless of the normal and abnormal system condition. However, the paradigm of WDSs has changed from delivering the required amount of water to a stable water supply similar to normal conditions, even under abnormal system conditions. Therefore, the WDSs design is performed by considering the cost, system resilience, and robustness for a stable water supply and to prepare for uncertain future system conditions. Some studies have applied an evolutionary optimization approach for the optimal design of WDSs under various system failure scenarios (e.g., pipe failure, fire flow, and isolation of connections to all water sources) [
9,
10,
11,
12,
13]. These have used demand-driven hydraulic analysis for checking the hydraulic constraints (i.e., minimum nodal pressure and pipe flow) in the WDSs design process. In addition, the system resilience and robustness can be evaluated by applying the abnormal condition after an optimal design in the postprocess. The minimum cut-set method considers a pipe breakage situation to calculate system resilience under abnormal system conditions. Cimorelli et al. [
14] performed WDSs design using hydraulic resilience under system construction cost constraints, and it was derived by the correlation of resilience with postprocessing for pipe failure conditions. Jung and Kim [
15] considered two redundancy measures (i.e., topological and mechanical redundancies) and a system cost in the design of WDSs, proposed a multivariate linear reliability model, and derived Pareto optimal solutions. Recently, Choi and Kim [
16] developed an optimal design model using a system redundancy measure (i.e., topological, mechanical, and hydraulic redundancy) under abnormal conditions and identified the relationships between network configuration and each redundancy factor. These studies consisted of two steps: (1) deriving an optimal design by considering the construction cost or reliability and robustness and (2) applying to abnormal situations (e.g., leakage, pipe breakage, and fire situation) to evaluate system resilience in the post design process.
However, in the above studies, WDSs design was applied to DDA method as a hydraulic analysis approach, although PDA has high analysis reliability and realistic analysis even in abnormal situations. Because the system resilience and robustness indices in these works were estimated by considering hydraulic characteristics (e.g., the surplus head/energy and pressure deficit) and mechanical characteristics (e.g., alternative flow route, and meshedness) under the steady-state condition.
Therefore, in this study, the designs by the DDA-based design model and PDA-based design were compared, and their design characteristics were analyzed to identify the efficiency of the WDSs design under abnormal system conditions. For an efficient comparison, three water distribution systems were applied, which have different sizes and levels of complexity when abnormal operating conditions appear along with the systems. This study will help to select a reasonable hydraulic analysis technique for WDSs design through the application of the DDA and PDA techniques, which are actively used in hydraulic analysis techniques in WDSs design by considering abnormal situations; it can be used as a reference research in the WDSs design field in the future.
2. Methodology
The demand-driven analysis (DDA) assumes that the nodal demands will always be satisfied regardless of the nodal pressure head. The numerical model inside DDA is the gradient method, which considers a hydraulic network of
pipe with unknown flow rates,
nodes with unknown heads (internal nodes), and
nodes with known heads (e.g., tank levels). The hydraulics can be analyzed by solving the following system, which contains one nonlinear energy equation and one linear mass balance equation:
The first equation in Equation (1) corresponds to the nonlinear energy equation that defines the head loss in each pipe between two nodes. The second equation in Equation (1) is a linear equation that defines the mass balance in the system and ensures continuity in the system. The elements in Equation (1) are explained in a more detailed manner as follows:
= is a diagonal matrix of (
) defined as:
where
= discharge vector of [
],
= calibration parameters with relevant field data, and
= “connectivity matrix” associated with each node and dimension [
]. It can have only two nonzero elements in each
ith row defined as follows: −1 in the column corresponding to the initial node of pipe
i and 1 in the columon corresponding to the final node of pipe
i,
= matrix with dimensions [
] of an unknown piezometric head vector,
fixed piezometric head vector with dimensions [
] where
is the number of fixed head nodes, and
= matrix with dimensions [
] with −1 in the rows corresponding to pipelines connected to fixed head nodes.
The second equation in Equation (1) corresponds to the continuity equation for the nodes in the system:
where
= transpose matrix of
, and
= column vector of water demands in the nodes with a dimension of [
].
Expressing the equations in the matrix is presented as:
Because of the nonlinearity of the energy equation, an iterative approach is needed. The gradient method consists of a truncated Taylor series expansion, which computes both equations simultaneously as follows:
where N is a diagonal matrix (
) with dimensions [
] and
=
in case there are no pumps in the network.
is the energy imbalance in each pipe, and
is the discharge imbalance in each node given as:
The gradient method solves the system of equations presented in Equation (5), considering that each iteration is ruled by the following conditions:
Finally, the solution of the system of Equation (5) can be achieved by solving the following matrixes:
On the other hand, the pressure-driven analysis (PDA) is known for simulating more realistically the behavior of the system in case of abnormal operating conditions. For this approach, the assumptions are not focused on the water demand. Instead, the nodal pressure defines how much water can be supplied according to several conditions. These conditions or relationships are the nodal head–outflow relationship (HOR) and the leakage relationship [
17].
The nodal head–outflow relationship (HOR) is parabolic and continues the equation in which for nodal heads above the desirable head pressure (
), the required demand (
) can be withdrawn, and for nodal head pressure below the minimum head (
), no demand can be withdrawn. If the required demand is between the thresholds (
), a portion of the required demand can be withdrawn (
). Many researchers have studied this relationship, with the one presented by Wagner et al. [
18] having superior results. For every node
j in the network, the HOR is given as:
The leakage relationship in the pipes of the system given by Germanopoulos [
17] models the leakage of each pipe
ij, assigning the effects to its start and end nodes as follows:
where
,
, and
correspond to the leakage discharge head and ground level of node
i,
is the length of pipes connected to node
i, and
is a fixed coefficient from network characteristics obtained from [
19] the methodology. K is the pressure exponent that is determined by the FAVAD theory [
18]. The energy and mass balance equation for the pressure-driven analysis are both nonlinear and given in matrix form as follows:
where most of the terms can be derived from the demand-driven analysis.
is a diagonal matrix conformed by the scalar product of
.
is a column vector of pressure/head-driven nodal demands, and
is a column vector of nodal leakage flow rates. The systems that need to be solved for the pressure-driven analysis are presented as follows:
where
iter is the counter of the iterative solving method,
is a diagonal matrix whose elements are the derivatives of the head loss function with respect to
, and
is a diagonal matrix whose elements are the derivatives with respect to the network pressure of
.
3. Application and Results
This chapter shows the formulation of this model for considering real-world problems that can occur within WDSs through (1) the application of abnormal system conditions in WDSs and (2) the evaluation of the optimal design using DDA and PDA approaches. First of all, abnormal condition scenarios that might occur in the actual field are created and modeled using hydraulic simulators (i.e., EPANET [
4] and WaterGEMS [
20]), which are well-known hydraulic simulators for WDSs and applied various WDSs design and operation problems. WaterGEMS is a widely applied hydraulic modelling software for water distribution systems with advanced interoperability [
21,
22,
23]. Among many modules, WaterGEMS can be used to support the design process of new distribution systems, assess fire flow capacity, develop network flushing plans, identify water losses, manage and minimize energy use, and prioritize pipe renewal. The generated abnormal condition scenarios are applied on three WDSs and derive the difference depending on the hydraulic methods (i.e., DDA and PDA). Then based on the characteristic of hydraulic results, each WDSs performs optimal design using metaheuristic optimization algorithm, considering the least cost as an objective function and the threshold for nodal pressure as constraints.
3.1. Description of Applied Water Distribution Systems
As mentioned in the previous section, the three WDSs selected for the application of our model are shown in
Figure 1.
The two-loop network [
24] is a small-size network that allows us to verify the validity of our results. This network is represented in
Figure 1 and consists of 6 demand nodes, 1 reservoir, and 8 pipes. The Hanoi network [
25] is a famous system located in the city of Hanoi, Vietnam, and has been frequently used by researchers. It consists of 31 demand nodes, 1 single reservoir, and 34 pipes. The third water distribution system is a large-scale network called the Balerma network [
26]. It is located in Italy and consists of 443 demand nodes, 4 reservoirs, and 454 pipes.
3.2. Optimization Formulations
3.2.1. Genetic Algorithm
This study applied a genetic algorithm (GA) as an optimization technique [
27]. GA is inspired by the survival of the fittest in Darwin’s theories, which is a principle of natural selection and evolution processes, and it is known as a robust metaheuristic optimization approach capable of efficiently resulting in various engineering fields. Generally, GA has four kinds of main characteristics: representations, mutation, crossover, and selection. Each mechanism relates to improving the optimal solution, considering global search and local search.
In the first step, the optimization process using GA begins with the generation of the population at random. Each population has a chromosome, and it is composed of genes that reflect the decision variable for the problem. In the case of the standard GA, a gene assigns either 1 or 0. The next step is a calculation of the fitness value following the objective function. Each fitness is calculated using the binary string value, and the fitness value is considered to construct a mating pool for the generation of an offspring population. The mating pool is composed of an outstanding population-based on fitness value so that more can be selected, and this process can be applied to various selection operators (e.g., tournament and roulette wheel). Through the completion of the mating pool construction, the task of the reproduction process is continued to generate the offspring population. To generate two offspring populations, the two populations from the mating pool are selected at random, and the two populations are formed by the crossover operator to create two offspring solutions. In the offspring generated by the crossover, the mutation operator is applied to consider a global search, and it is a randomly selected individual from the mating pool. A more specific GA process is described in
Figure 2.
3.2.2. Objective Function and Design Constraints
As an objective function in the optimal design of WDSs, the pipe construction cost is used. The pipe construction cost is among the construction costs for WDSs, including most of the costs compared with other facilities’ costs (e.g., valve, joint, and affiliated facility installation costs). The pipe construction cost considers determining the most effective set of network configurations, containing the pipe diameter and layout, and satisfying hydraulic constraints. In this study, the pipe materials, installations (i.e., base installation, trenching, excavation, embedment, backfill, and compaction costs), and affiliated facilities (e.g., valves, fittings, and hydrants) are considered to calculate the pipe construction cost [
28]. The function of the pipe construction cost can be expressed as shown in Equation (13), and
Table 1 describes the parameters for calculating the pipe construction cost, considering the pipe materials, installations, and affiliated facilities. Moreover, the diameter of the pipes is used as the determinant variable of the optimal design of water distribution systems in this study. Therefore, the optimization is to perform the least-cost design within the range that satisfies the hydraulic constraints through the combination of various pipe diameters.
where
y is the unit pipe cost (
$/ft; 1 ft = 0.3048 m);
x is the pipe diameter in inches (1 in = 2.54 cm);
u is the indicator variable; and
a,
b,
c,
d,
e, and
f are component-specific parameter values estimated using regression analyses.
Table 1 shows the representative parameters.
For hydraulic constraints, this study uses the water threshold of pressure. If the pressure at each node does not meet the pressure constraint during the hydraulic analysis of the optimal design, it gives a penalty point by adding a large value to penalty constant
α. This penalty point has an impact on the value of the objective function so that it can not to be selected. If it comes approximately close to the hydraulic constraints, it cannot affect the selection of the optimal solution because of the small penalty point. In order to prevent such occurrence, a large penalty point can be generated by adding a large value to
β. The penalty function value determined here is added to the construction cost (CC) in Equation (13). Then, for the solution that satisfies the constraint, the CC is smaller than the solution that does not, and through this, effective optimization can proceed. The penalty function
P is shown in Equation (14).
where,
P is a penalty function,
hi is the pressure head at node
i (m),
hmin and
hmax are the minimum and maximum pressure heads (m), and
and
are the penalty constants.
3.3. Hydraulic Comparison of Abnormal System Conditions for WDSs
In this chapter, to derive the characteristic of hydraulic analysis approaches, DDA and PDA, two kinds of abnormal scenarios are generated. The scenarios consist of two cases: fire flow and pipe breakage conditions. The first scenario considers the possibility of a fire flow in one or mode nodes. Due to the unexpected high demand of water in these nodes, the system can considerably change in pressures and demand availability. The second scenario simulates an unexpected break in one or more pipes, depending on the size of the network. To implement these changes, the nodes and pipes are selected randomly, and DDA and PDA are applied to all the scenarios in order to derive the hydraulic conditions in the applied WDSs.
To apply Scenario 1 (fire flow condition) in WDSs, node 6 is selected to increase the demand, and Scenario 2 is simulated by a fire flow pipe breakage condition simultaneously with pipe 2 and node 6, as shown in
Figure 3. The results for Scenario 1 for the two-loop network are presented in
Table 2.
It is interesting to analyze the pressure results from the DDA method. In node 6, there is a negative pressure, which is considered unrealistic in the water distribution system. On the contrary, the PDA approach shows more realistic positive pressures in all the nodes. It is important to note that in other nodes where the demand has not been affected, the behavior of both approaches is considered consistent, confirming that both methodologies can be applied in a water distribution system for normal conditions.
Figure 4 represents the pressure in each node for both approaches, comparing the variable pressures.
A similar analysis was performed for Scenario 2, where pipe 2 and node 6 were both selected to simulate an abnormal condition.
Table 3 shows the results of DDA and PDA analyses. The difference between the two approaches is noticeable because the negative pressures are replaced with zero values in PDA due to the insufficient nodal pressure. Finally,
Figure 5 presents a comparison of nodal pressure results from Scenario 2. The incidence of pipe break can be easily identified because of the high number of nodes with negative pressure.
In the case of the Hanoi network, the fire flow was simulated by increasing the demand on node 31, while in the case of pipe break, pipes 24 and 33 were closed.
Figure 6 shows the layout of the network for both scenarios. Due to the high number of nodes for the Hanoi and Balerma networks, the tables of final nodal pressures are not presented in this paper; instead, a comparative graph is presented for both scenarios.
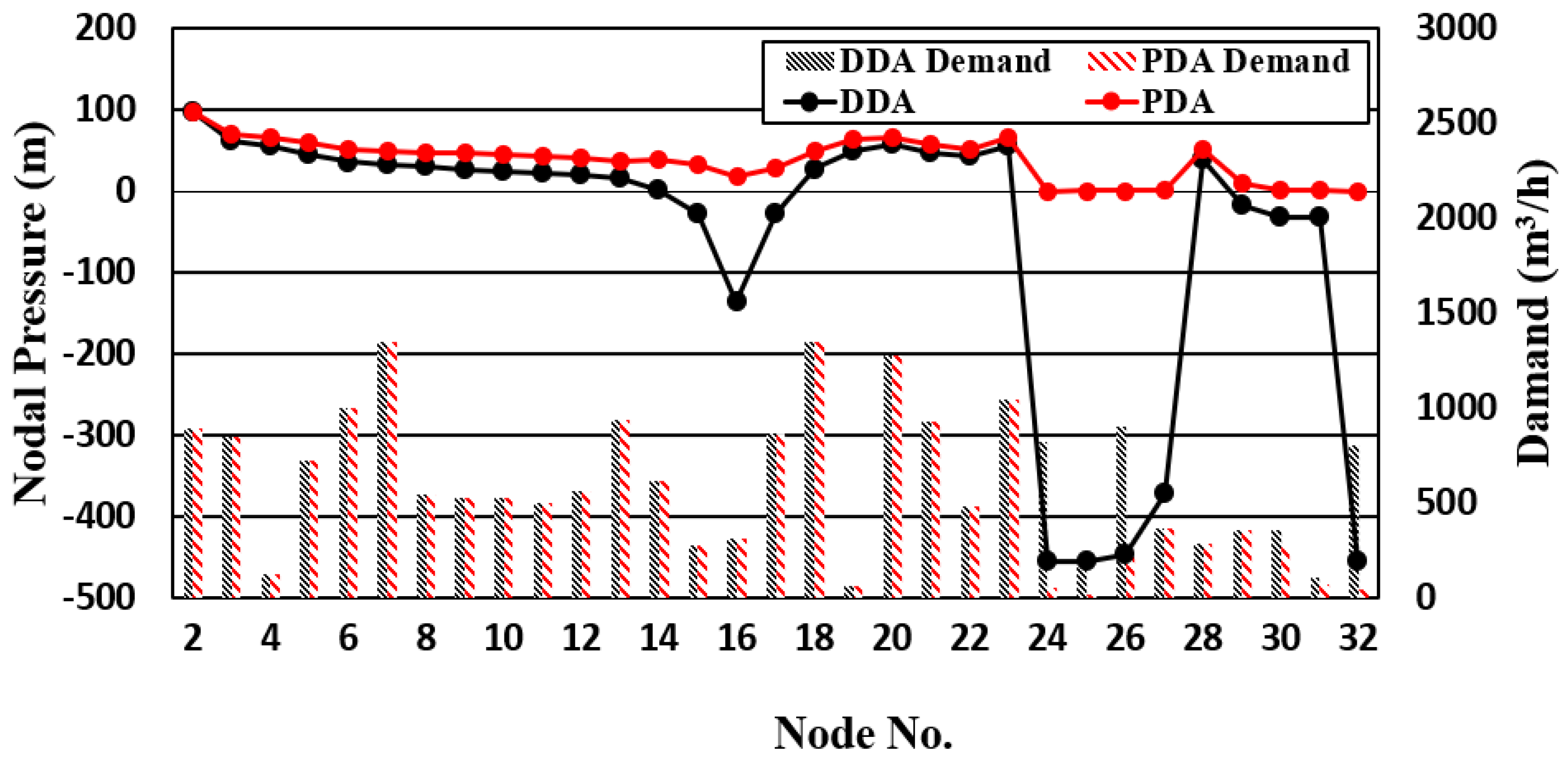
If an abnormal situation occurs as in Scenarios 1 and 2 (
Figure 6) in the Hanoi network with a total demand of 21,440 m
3/h, the difference in pressure and supply flow for each scenario is shown in
Figure 7 and
Figure 8, where the difference between the two approaches can be clearly appreciated.
In the case of Scenario 1, when node 31 increases the extreme demand for fire flow, the total supplied discharge using PDA is reduced to 97.4%, and in each nodal demand aspect, the demand in the vicinity of the fire area decreases significantly to 73.8–87.5%. For the pressure difference, the nodal pressure that is not directly affected by the fire area presents a maximum 34.2% pressure reduction. In the case of the fire area, the DDA analysis shows negative pressure, but the PDA analysis shows a positive pressure value through a realistic flow supply.
For the Balerma network, since this network is a large-scale network and has multiple reservoirs, the abnormal scenarios considered multiple fire flow situations that nodes 200 and 418 were chosen for Scenario 1, and a reservoir failure was simulated for Scenario 2. The scheme of the network is presented in
Figure 9, while the results of Scenarios 1 and 2 are presented in
Figure 10 and
Figure 11. Among the whole network hydraulic results, the pressure and demand of the partial nodes (nodes 390–420) were selected, which were significantly affected by applying abnormal system conditions.
For the multiple fire flow (Scenario 1), the reporting nodal pressure for PDA was decreased maximum of 76.6% (node 404), and the pressure of some nodes that are directly affected by the fire flow resulted in negative pressure in DDA. However, for the PDA hydraulic simulation, these nodes (nodes 411, 414, 416, and 418) were supplied zero flow to reflect realistic conditions, and for this reason, the nodal pressure was zero. In the case of Scenario 2, since a reservoir failure situation is a serious abnormal condition that even the Balerma network has four reservoirs, most of the selected nodes showed negative pressure for DDA. However, in the PDA condition, some nodes that showed negative pressure did not serve the water demand; therefore, the pressure values were zero.
3.4. Optimal Design Water Distribution Systems
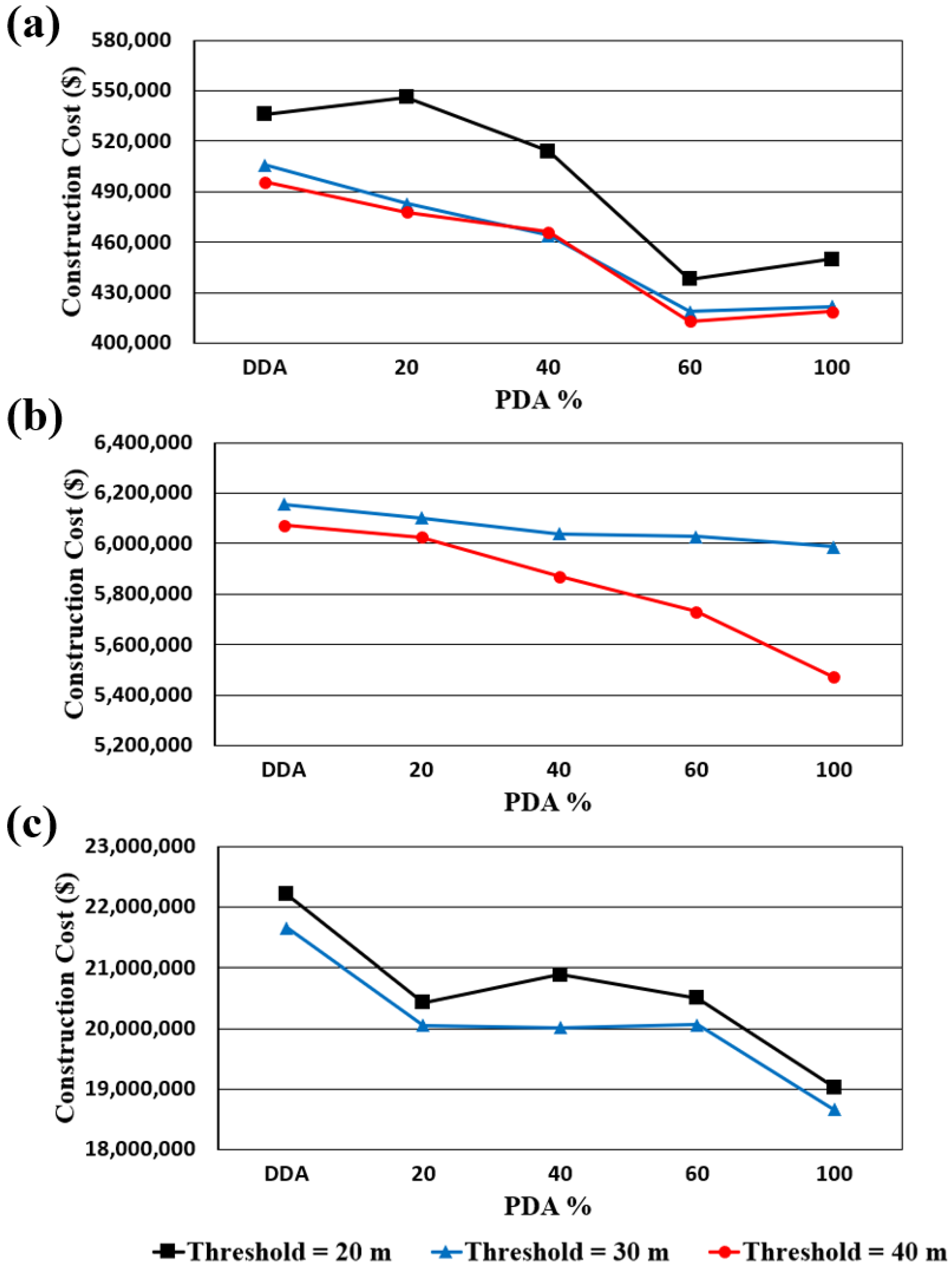
In the above hydraulic results, which applied abnormal system conditions (i.e., fire flow and pipe breakage), the relationship of pressure and acquired actual demand was analyzed under DDA and PDA. According to the results of the above analysis, this chapter performs the optimal design of WDSs by considering each hydraulic analysis approach and compares the results. Each optimal design of WDSs is performed using metaheuristic optimization algorithm by considering the least-cost as an objective function and the threshold for nodal pressure as constraints. In the optimal design using the PDA method, a different percentage of pressure-driven analysis is implemented to derive the characteristics (e.g., the construction cost of the design and supply flow rate) according to the degree of PDA. Moreover, to compare the construction costs of applying PDA and DDA, GA was applied to minimize the pipe construction cost for the three benchmark networks. The parameters of GA are used according to the sensitivity analysis. In the sensitivity analysis, the number of populations considers 10 to 50 interval 10. In addition, the crossover rate (0.7–0.99, interval 0.05) and the mutation rate (0.05–0.3, interval 0.05) are considered for generating parameter combinations. Among these parameter combinations, the best set of parameters is used for the comparison results. A minimum threshold that represents the minimum pressure in every node was assumed for both approaches. The two-loop network considered 20, 30, and 40 m as minimum thresholds; the Hanoi network applied 30 and 40 m; and the Balerma network assumed 20 and 30 m. Various percentages of pressure-driven analysis (PDA) were implemented (0%; DDA, 20%, 40%, 60%, and 100%) to visualize the change in the cost of designing the network. The design cost of the benchmark networks and the results of this analysis are presented in
Figure 12 and
Table 4.
According to the optimal design using different hydraulic analyses (DDA and PDA), the results presented a trend of the construction cost with various PDA% under the minimum threshold. In the case of the two-loop network, by increasing the percentage of the PDA in the hydraulic design of the network with interval 20% from 0% (DDA hydraulic analysis) to 100% (full PDA hydraulic analysis), the construction cost diminishes by about 6%–17% because of the quantity of the demand change with the actual demand based on the pressure-driven model. However, the two-loop design cost is a bit higher than 60% of PDA% in 100% PDA, which would be reflected by the network characteristics for the size and network configuration (consisting of a looping system and no branch). The main cause of this trend is the decrease in pipe diameter to satisfy the minimum threshold of each node, and the PDA percentage increases and the fixed demand decreases, resulting in the reduction of the construction cost. This is because an increase in the minimum threshold caused a decrease in the construction cost. Especially, in the case of the Hanoi network, since the network size is larger than the two-loop network, the increment of the minimum threshold and PDA percentage makes the rate of reduction in the construction cost enlarged. For the same reason, the design cost variance of the Balerma network is larger than that of the Hanoi network by up to 9%. Furthermore, when selecting a minimum threshold of 40 m and an analysis entirely using PDA, the minimum cost can be reached.
4. Conclusions and Future Studies
The hydraulic analysis of WDSs is categorized into two types of the demand-driven hydraulic analysis, which should be supplied by the fixed demand and the pressure-driven hydraulic analysis, which considers the head–outflow relationship for abnormal conditions. Previous studies have demonstrated that DDA is appropriate in normal conditions, and PDA presents realistic hydraulic results under abnormal system conditions.
Therefore, this study quantified the hydraulic results of DDA and PDA under various single/multiple abnormal situations applied to three WDSs that have different characteristics (e.g., network size and configuration), and according to the results of hydraulic analysis, the DDA-based design model and the PDA-based design model were compared, and their design characteristics were analyzed to identify the efficiency of an WDSs design under abnormal system conditions. To verify the characteristics of the two hydraulic analysis approaches, two scenarios combined with abnormal conditions (i.e., fire flow and pipe breakage situation) for single/multiple conditions were generated, and these scenarios were applied to three benchmark networks. In the system abnormal conditions of the benchmark networks, PDA showed practical quantification, such as identifying the nodes with the most variations in pressure and analyzing the critical pipes that have the greatest impact on the hydraulic results under abnormal situations (e.g., fire flow and pipe breakage). Identified critical nodes and pipes can be reinforced by the planning and management of WDSs.
Moreover, for a comparison of WDSs designs using the DDA-/PAD-based design model, GA was applied as an optimization technique to consider the minimum construction cost. To efficiently compare the optimal design, depending on the different minimum thresholds (20, 30, and 40 m), the percentage of PDA was considered (0%; DDA, 20%, 40%, 60%, and 100%). As a result of an optimal design with various PDA% values under the minimum threshold, increasing the percentage of PDA in the hydraulic design of the network, the construction cost decreased for the quantity of the demand change with the actual demand based on the pressure-driven model. Moreover, the design cost variance showed that a larger network is more different, and also the higher minimum threshold affected the lower design cost. Therefore, this study will help to select a reasonable hydraulic analysis technique for WDSs design through the application of the DDA and PDA techniques, which are actively used as hydraulic analysis techniques in WDSs design considering abnormal situations. It can be used as a reference research in the WDSs design field in the future. Additionally, a PDA model with uncertainty quantification can be used for reliability and resilience analyses of an actual WDN considering abnormal system conditions.
A future study may refer to the results of this study to consider the optimal design of WDSs. For this work, various kinds of objective functions (e.g., energy consumption, water quality, system resilience, robustness, and CO2 emission) should be considered in order to apply the multiobjective optimization approaches, and to validate this analysis extensively, it is necessary to apply the characteristics of various networks and the real-world network.