Disturbance Observer-Based Chattering-Attenuated Terminal Sliding Mode Control for Nonlinear Systems Subject to Matched and Mismatched Disturbances
Abstract
:1. Introduction
2. Problem Statement
3. Results
3.1. Nonlinear Disturbance Observer
3.2. Disturbance Observer-Based Terminal Sliding Mode Control
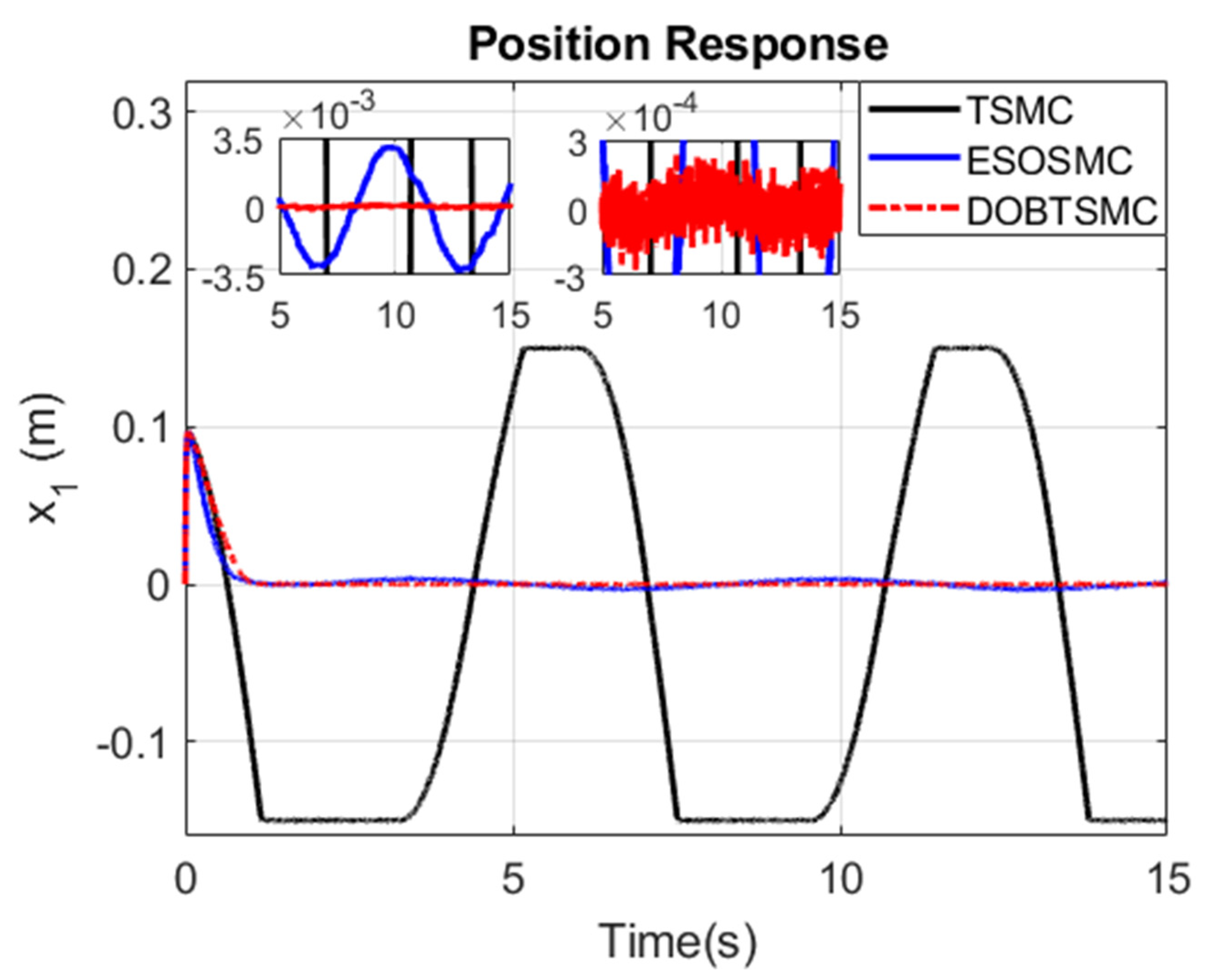
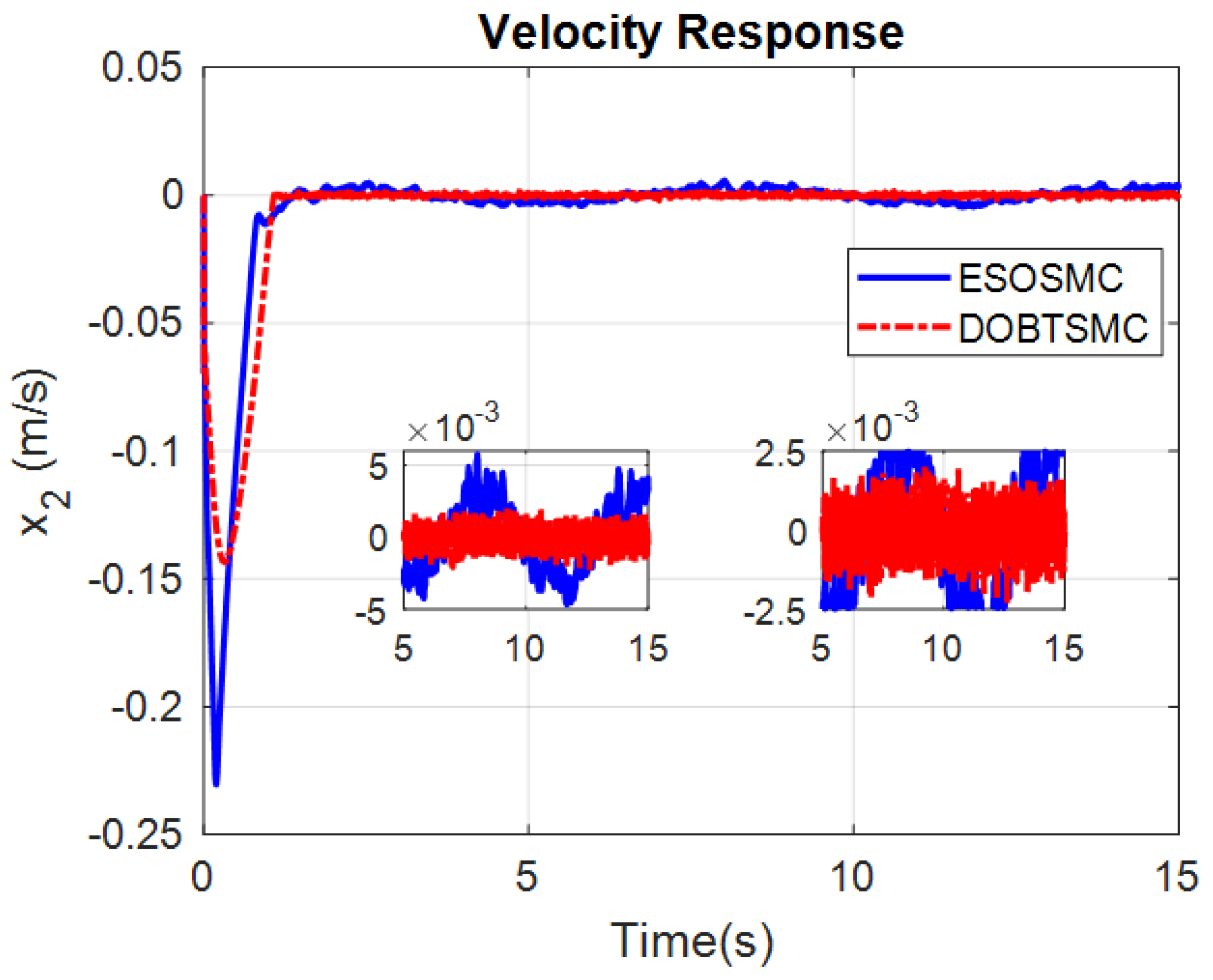
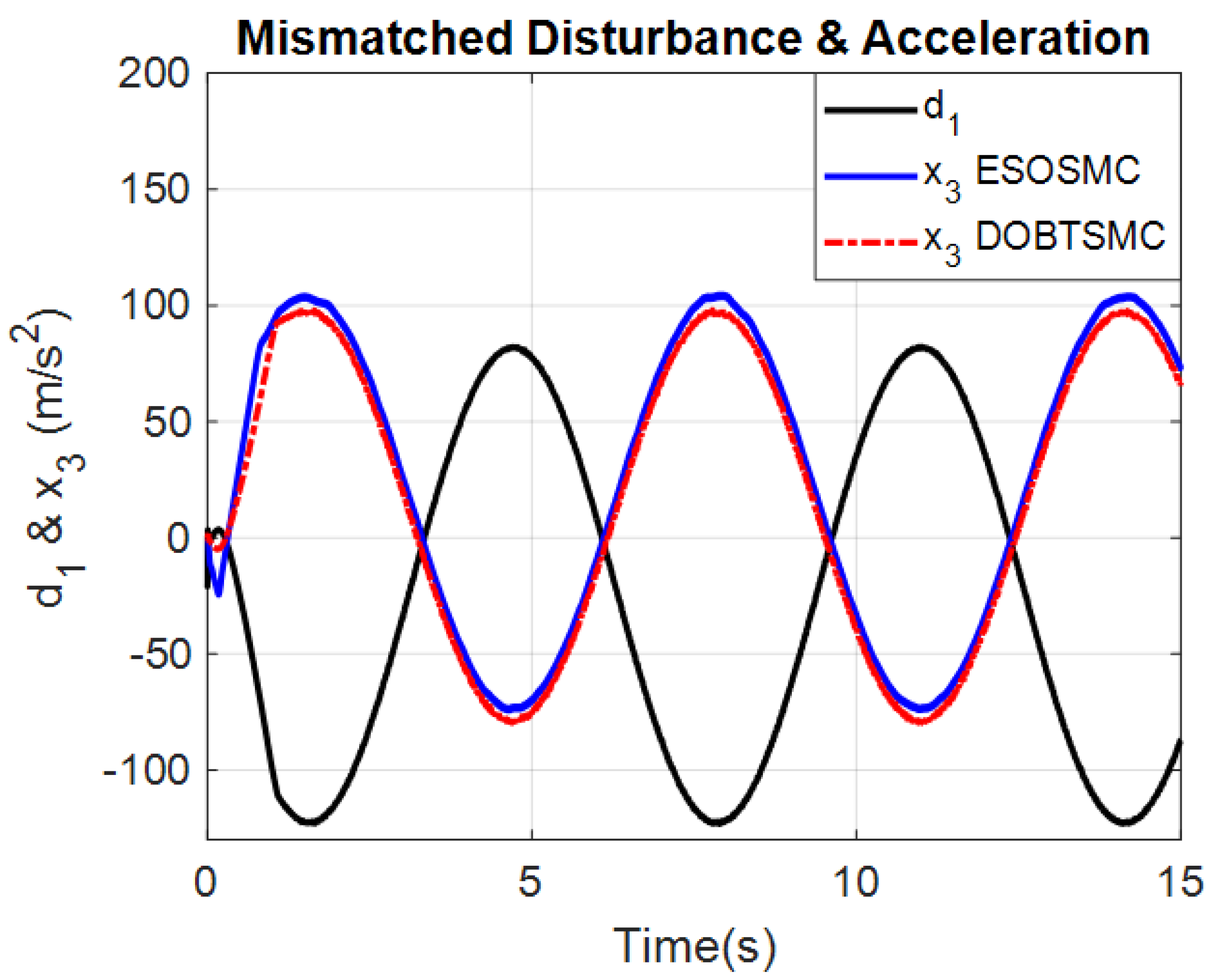
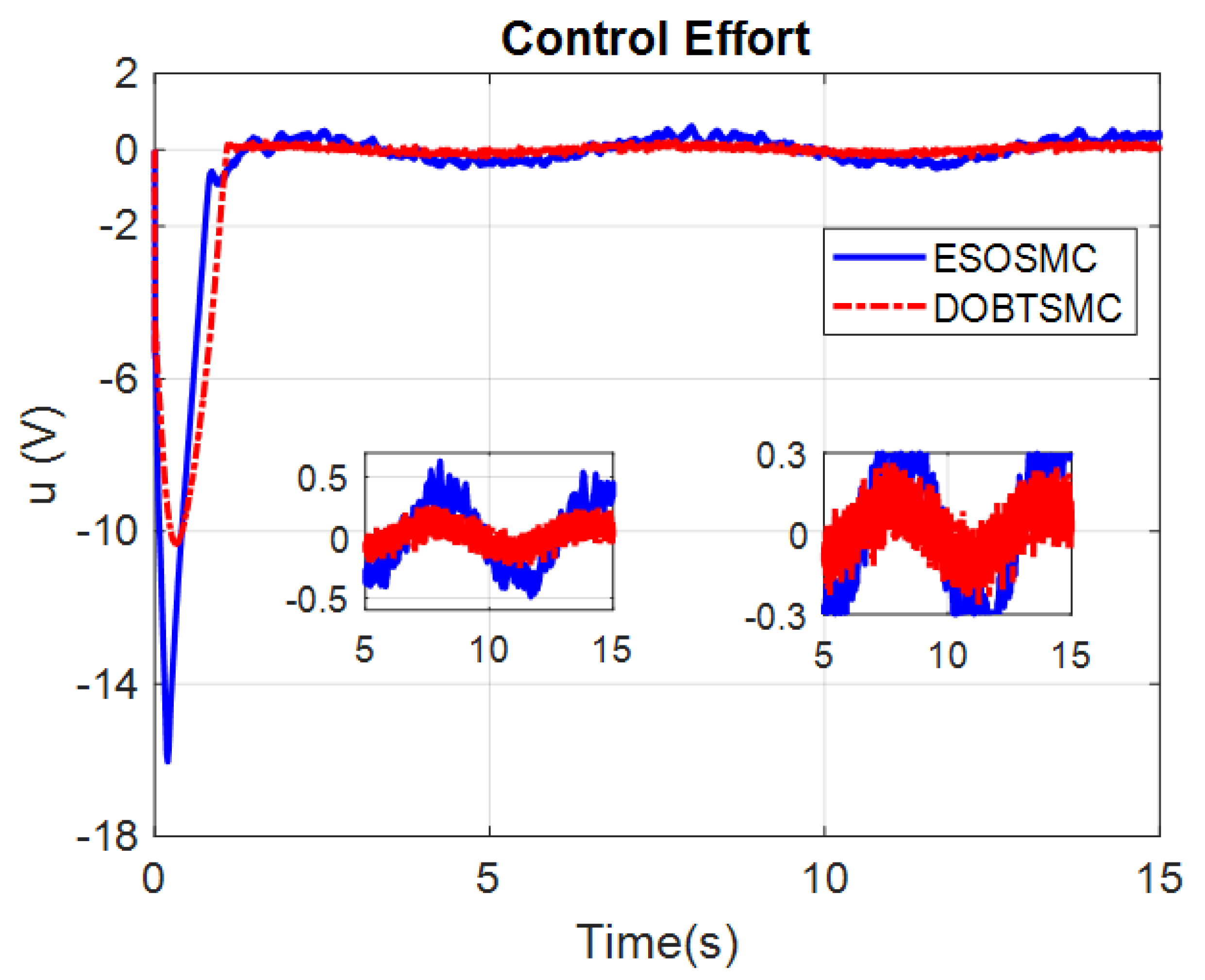
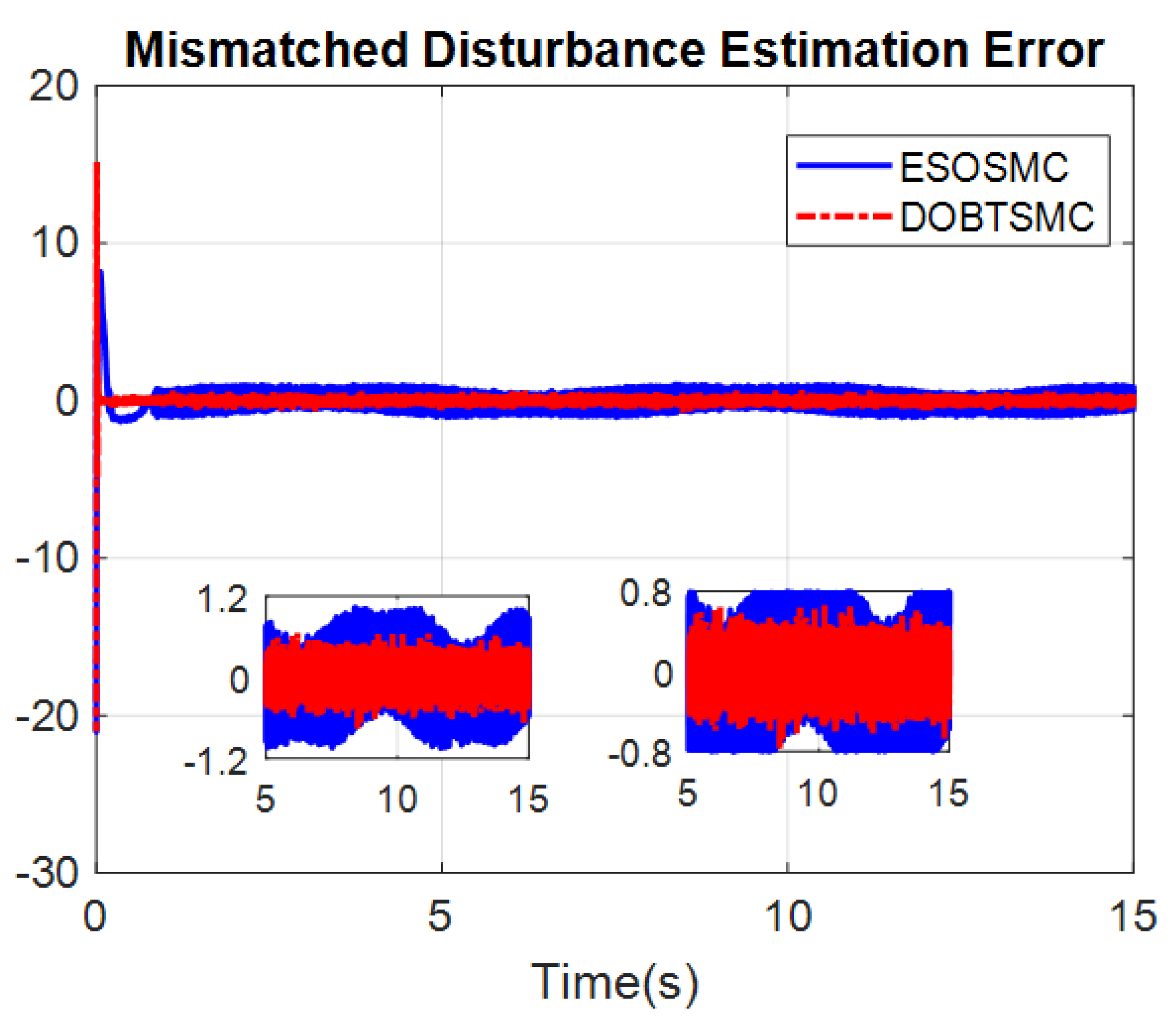
4. Simulations
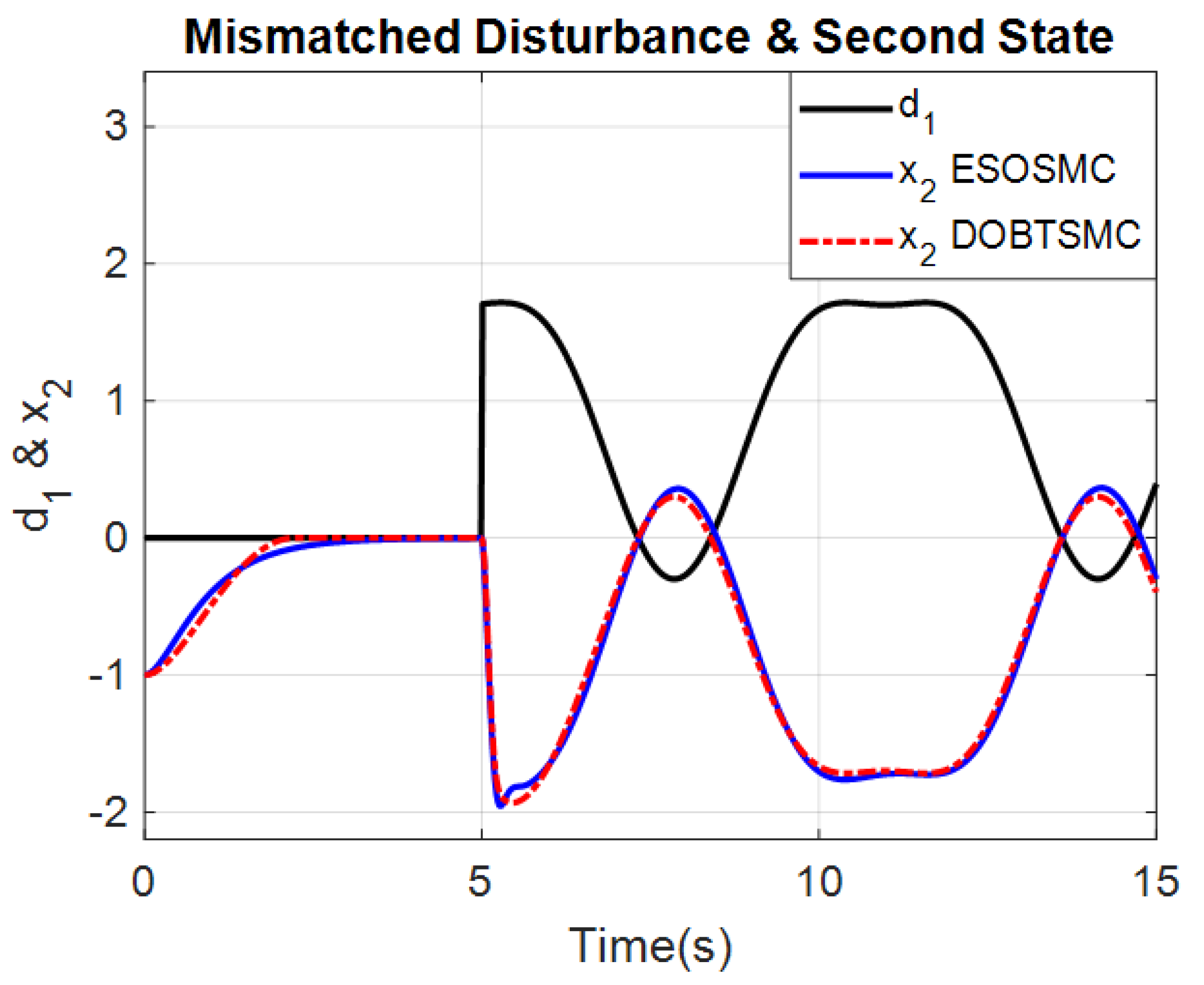
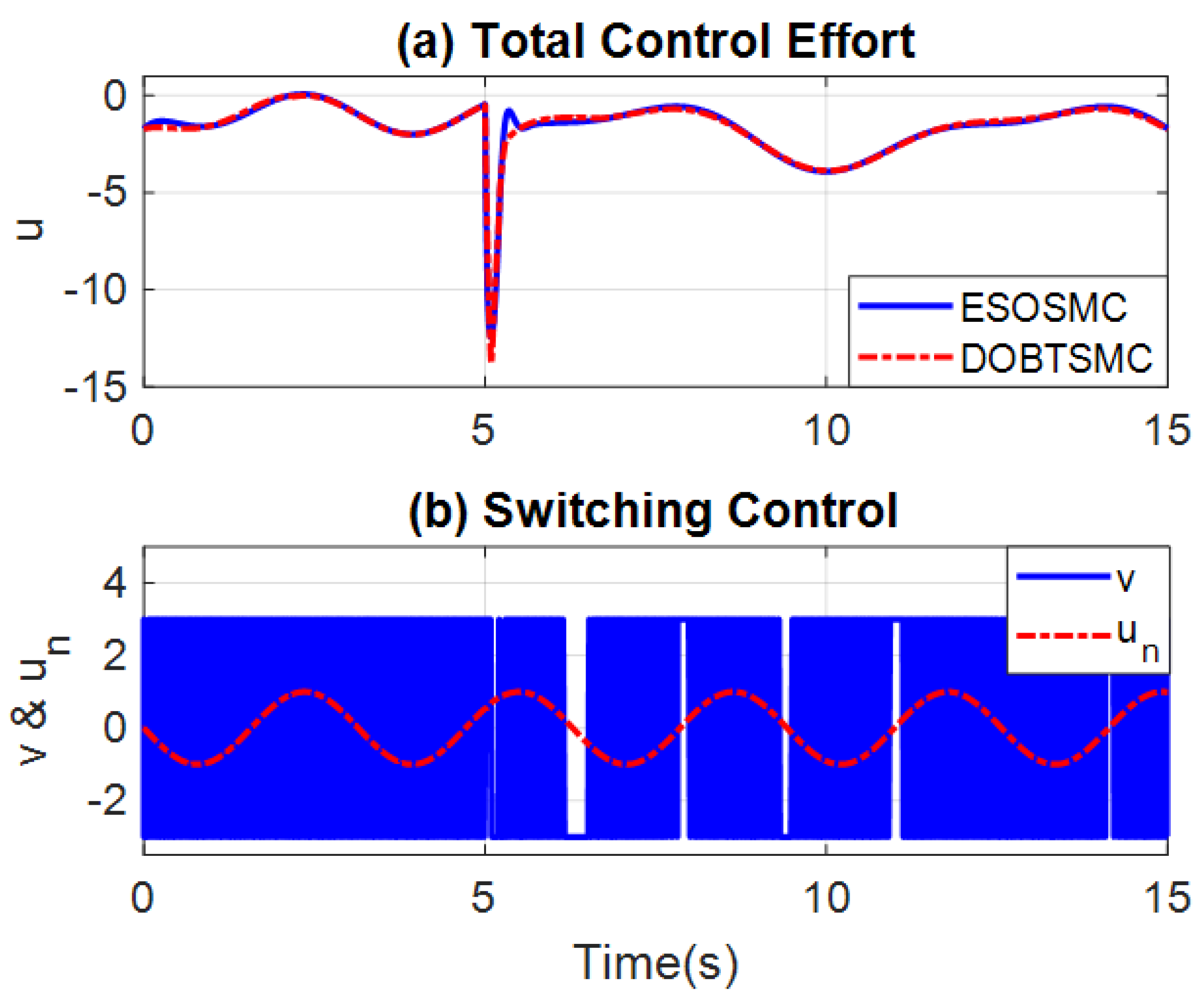
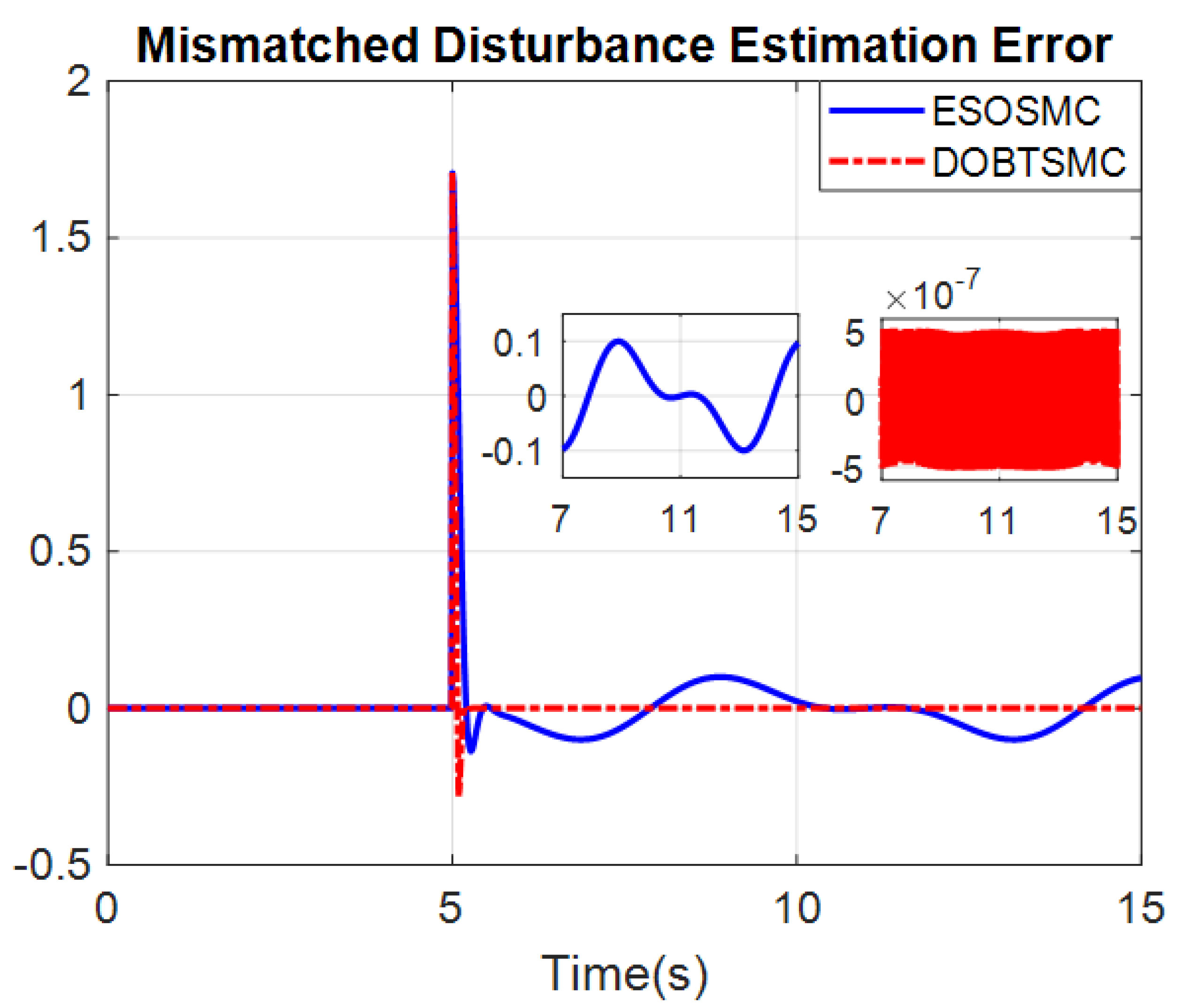
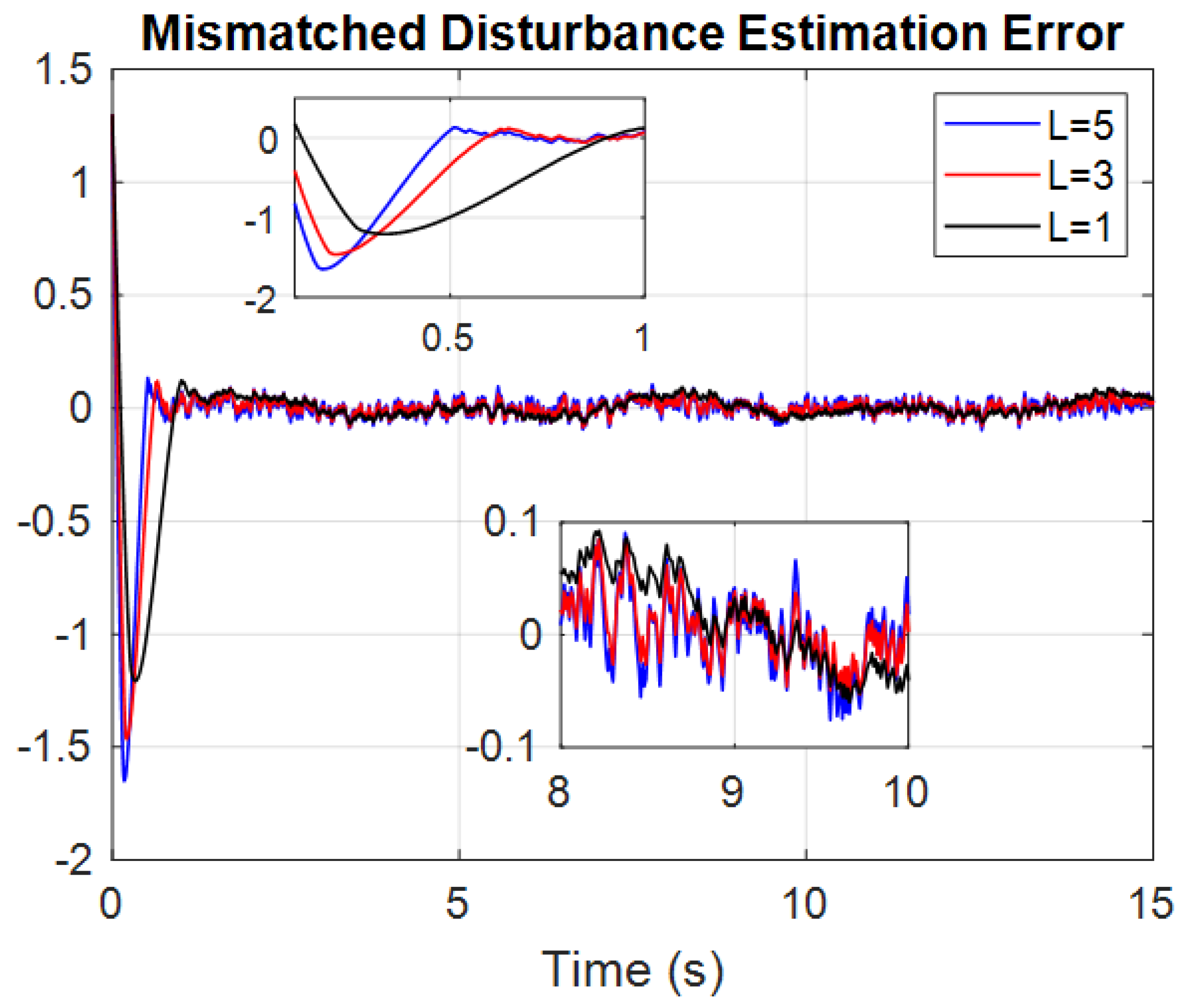
4.1. Numerical Example
4.2. Application to Electro Hydrostatic Actuator System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| SMC | Sliding Mode Control |
| TSMC | Terminal Sliding Mode Control |
| MAGLEV | Magnetic Levitation |
| PMSM | Permanent Magnet Synchronous Motor |
| EHA | Electro Hydrostatic Actuator |
| DOB | Disturbance Observer |
| ESOSMC | Extended State Observer based Sliding Mode Control |
| DOBTSMC | The proposed controller |
References
- Ginoya, D.; Shendge, P.; Phadke, S. Disturbance observer based sliding mode control of nonlinear mismatched uncertain systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 26, 98–107. [Google Scholar] [CrossRef]
- Jing, C.; Xu, H.; Niu, X. Adaptive sliding mode disturbance rejection control with prescribed performance for robotic manipulators. ISA Trans. 2019, 91, 41–51. [Google Scholar] [CrossRef]
- Asl, R.M.; Hagh, Y.S.; Palm, R. Robust control by adaptive Non-singular Terminal Sliding Mode. Eng. Appl. Artif. Intell. 2017, 59, 205–217. [Google Scholar] [CrossRef]
- Ye, H.; Wang, S. Trajectory Tracking Control for Nonholonomic Wheeled Mobile Robots with External Disturbances and Parameter Uncertainties. Int. J. Control Autom. Syst. 2020, 18, 3015–3022. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Lee, J. Lyapunov and Sliding Mode Based Leader-follower Formation Control for Multiple Mobile Robots with an Augmented Distance-angle Strategy. Int. J. Control Autom. Syst. 2019, 17, 1314–1321. [Google Scholar] [CrossRef]
- Jin, Z.; Liang, Z.; Wang, X.; Zheng, M. Adaptive Backstepping Sliding Mode Control of Tractor-trailer System with Input Delay Based on RBF Neural Network. Int. J. Control Autom. Syst. 2020, 19, 76–87. [Google Scholar] [CrossRef]
- Napole, C.; Barambones, O.; Derbeli, M.; Calvo, I. Advanced Trajectory Control for Piezoelectric Actuators Based on Robust Control Combined with Artificial Neural Networks. Appl. Sci. 2021, 11, 7390. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, Y.; Wang, X.; Chen, Q. Characteristic Model-based Adaptive Control with Genetic Algorithm Estimators for Four-PMSM Synchronization System. Int. J. Control Autom. Syst. 2020, 18, 1605–1616. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Yu, L. Reduced-order Generalized Proportional Integral Observer Based Continuous Dynamic Sliding Mode Control for Magnetic Levitation System with Time-varying Disturbances. Int. J. Control Autom. Syst. 2020, 19, 439–448. [Google Scholar] [CrossRef]
- Din, S.U.; Khan, Q.; Rehman, F.U.; Akmeliawanti, R. A Comparative Experimental Study of Robust Sliding Mode Control Strategies for Underactuated Systems. IEEE Access 2017, 6, 1927–1939. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Silaa, M.; Napole, C. Real-Time Implementation of a New MPPT Control Method for a DC-DC Boost Converter Used in a PEM Fuel Cell Power System. Actuators 2020, 9, 105. [Google Scholar] [CrossRef]
- Napole, C.; Derbeli, M.; Barambones, O. A global integral terminal sliding mode control based on a novel reaching law for a proton exchange membrane fuel cell system. Appl. Energy 2021, 301, 117473. [Google Scholar] [CrossRef]
- Chen, Z.; Tu, X.; Xing, L.; Fu, J.; Lozano, R.; Rogelio, L. A Special Kind of Sliding Mode Control for Nonlinear System with State Constraints. IEEE Access 2019, 7, 69998–70010. [Google Scholar] [CrossRef]
- Kamalesh, M.; Senthilnathan, N.; Bharatiraja, C. Design of a Novel Boomerang Trajectory for Sliding Mode Controller. Int. J. Control Autom. Syst. 2020, 18, 2917–2928. [Google Scholar] [CrossRef]
- Ye, D.; Zhang, H.; Tian, Y.; Zhao, Y.; Sun, Z. Fuzzy Sliding Mode Control of Nonparallel-ground-track Imaging Satellite with High Precision. Int. J. Control Autom. Syst. 2020, 18, 1617–1628. [Google Scholar] [CrossRef]
- Xu, S.S.-D.; Chen, C.-C.; Wu, Z.-L. Study of Nonsingular Fast Terminal Sliding-Mode Fault-Tolerant Control. IEEE Trans. Ind. Electron. 2015, 62, 3906–3913. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, M.; Zheng, X.; Han, F.; Yu, X. Full-order terminal sliding-mode control of MIMO systems with unmatched uncertainties. J. Frankl. Inst. 2018, 355, 653–674. [Google Scholar] [CrossRef]
- Levant, A. Chattering Analysis. IEEE Trans. Autom. Control 2010, 55, 1380–1389. [Google Scholar] [CrossRef]
- Kachroo, P.; Tomizuka, M. Chattering reduction and error convergence in the sliding-mode control of a class of nonlinear systems. IEEE Trans. Autom. Control 1996, 41, 1063–1068. [Google Scholar] [CrossRef] [Green Version]
- Bartolini, G.; Ferrara, A.; Usai, E. Chattering avoidance by second-order sliding mode control. IEEE Trans. Autom. Control 1998, 43, 241–246. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Levant, A. Principles of 2-sliding mode design. Automatica 2007, 43, 576–586. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.-X.; Pan, Y.-J.; Lee, T.-H. Sliding Mode Control with Closed-Loop Filtering Architecture for a Class of Nonlinear Systems. IEEE Trans. Circuits Syst. II Express Briefs 2004, 51, 168–173. [Google Scholar] [CrossRef]
- Tseng, M.-L.; Chen, M.-S. Chattering reduction of sliding mode control by low-pass filtering the control signal. Asian J. Control 2010, 12, 392–398. [Google Scholar] [CrossRef]
- Kawamura, A.; Itoh, H.; Sakamoto, K. Chattering reduction of disturbance observer based sliding mode control. IEEE Trans. Ind. Appl. 1994, 30, 456–461. [Google Scholar] [CrossRef]
- Mu, C.; He, H. Dynamic Behavior of Terminal Sliding Mode Control. IEEE Trans. Ind. Electron. 2017, 65, 3480–3490. [Google Scholar] [CrossRef]
- Corradini, M.L.; Cristofaro, A. Nonsingular terminal sliding-mode control of nonlinear planar systems with global fixed-time stability guarantees. Automatica 2018, 95, 561–565. [Google Scholar] [CrossRef]
- Rabiee, H.; Ataei, M.; Ekramian, M. Continuous nonsingular terminal sliding mode control based on adaptive sliding mode disturbance observer for uncertain nonlinear systems. Automatica 2019, 109, 108515. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, K.; Yan, F.; Chen, B. Adaptive super-twisting nonsingular fast terminal sliding mode control for cable-driven manipulators using time-delay estimation. Adv. Eng. Softw. 2018, 128, 113–124. [Google Scholar] [CrossRef]
- Feng, Y.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Yang, J.; Wu, B.; Li, Q. Finite-time disturbance observer based non-singular terminal sliding-mode control for pulse width modulation based DC–DC buck converters with mismatched load disturbances. IET Power Electron. 2016, 9, 1995–2002. [Google Scholar] [CrossRef]
- Utkin, V.; Shi, J. Integral sliding mode in systems operating under uncertainty conditions. In Proceedings of the 35th IEEE Conference on Decision and Control, Las Vegas, NV, USA, 13 December 2002; Volume 4, pp. 4591–4596. [Google Scholar] [CrossRef]
- Cao, W.-J.; Xu, J.-X. Nonlinear Integral-Type Sliding Surface for Both Matched and Unmatched Uncertain Systems. IEEE Trans. Autom. Control 2004, 49, 1355–1360. [Google Scholar] [CrossRef]
- Castanos, F.; Fridman, L. Analysis and Design of Integral Sliding Manifolds for Systems With Unmatched Perturbations. IEEE Trans. Autom. Control 2006, 51, 853–858. [Google Scholar] [CrossRef] [Green Version]
- Mondal, S.; Mahanta, C. Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty. ISA Trans. 2013, 52, 335–341. [Google Scholar] [CrossRef]
- Kwan, C.-M. Sliding mode control of linear systems with mismatched uncertainties. Automatica 1995, 31, 303–307. [Google Scholar] [CrossRef]
- Wen, C.-C.; Cheng, C.-C. Design of sliding surface for mismatched uncertain systems to achieve asymptotical stability. J. Frankl. Inst. 2008, 345, 926–941. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Yu, X. Sliding-Mode Control for Systems with Mismatched Uncertainties via a Disturbance Observer. IEEE Trans. Ind. Electron. 2012, 60, 160–169. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.D.; Phadke, S. Sliding Mode Control for Mismatched Uncertain Systems Using an Extended Disturbance Observer. IEEE Trans. Ind. Electron. 2013, 61, 1983–1992. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Xia, Y.; Zuo, Z.; Wang, Y. Disturbance Observer-Based Integral Sliding-Mode Control for Systems with Mismatched Disturbances. IEEE Trans. Ind. Electron. 2016, 63, 7040–7048. [Google Scholar] [CrossRef]
- Shi, S.-L.; Li, J.-X.; Fang, Y. Extended-State-Observer-Based Chattering Free Sliding Mode Control for Nonlinear Systems with Mismatched Disturbance. IEEE Access 2018, 6, 22952–22957. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Oh, H.; Kim, Y.; Moon, J. Disturbance Observer-Based Continuous Finite-Time Sliding Mode Control against Matched and Mismatched Disturbances. Complexity 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Chen, W.-H. Nonlinear Disturbance Observer-Enhanced Dynamic Inversion Control of Missiles. J. Guid. Control Dyn. 2003, 26, 161–166. [Google Scholar] [CrossRef]
- Su, J.; Yang, J.; Li, S. Continuous finite-time anti-disturbance control for a class of uncertain nonlinear systems. Trans. Inst. Meas. Control 2013, 36, 300–311. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Su, J.; Yu, X. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances. Automatica 2013, 49, 2287–2291. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Su, J.; Li, S.; Yu, X. High-Order Mismatched Disturbance Compensation for Motion Control Systems Via a Continuous Dynamic Sliding-Mode Approach. IEEE Trans. Ind. Inform. 2013, 10, 604–614. [Google Scholar] [CrossRef] [Green Version]
- Bhat, S.P.; Bernstein, D.S. Geometric homogeneity with applications to finite-time stability. Math. Control Signals Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Han, F.; Yu, X. Reply to “Comments on ‘Chattering free full-order sliding-mode control’ [Automatica 50 (2014) 1310–1314]”. Automatica 2016, 72, 255–256. [Google Scholar] [CrossRef]
- Bhat, S.; Bernstein, D. Finite-time stability of homogeneous systems. In Proceedings of the 1997 American Control Conference (Cat. No.97CH36041), Albuquerque, NM, USA, 6 June 1997. [Google Scholar] [CrossRef]
- Levant, A.; Livne, M. Globally convergent differentiators with variable gains. Int. J. Control 2018, 91, 1994–2008. [Google Scholar] [CrossRef]
- Levant, A. Homogeneity approach to high-order sliding mode design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Ba, D.X.; Dinh, T.Q.; Bae, J.; Ahn, K.K. An Effective Disturbance-Observer-Based Nonlinear Controller for a Pump-Controlled Hydraulic System. IEEE/ASME Trans. Mechatron. 2019, 25, 32–43. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D.; Yan, L. High-Accuracy Tracking Control of Hydraulic Rotary Actuators with Modeling Uncertainties. IEEE/ASME Trans. Mechatron. 2013, 19, 633–641. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Shin, D.; Chung, C.C. High-Gain Disturbance Observer-Based Backstepping Control With Output Tracking Error Constraint for Electro-Hydraulic Systems. IEEE Trans. Control Syst. Technol. 2014, 23, 787–795. [Google Scholar] [CrossRef]
- Merritt, H.E.; Pomper, V. Hydraulic control systems. J. Appl. Mech. 1968, 35, 200. [Google Scholar] [CrossRef]
- Ba, D.X.; Ahn, K.K.; Truong, D.Q.; Park, H.G. Integrated model-based backstepping control for an electro-hydraulic system. Int. J. Precis. Eng. Manuf. 2016, 17, 565–577. [Google Scholar] [CrossRef]




| Control Algorithm | Matched Disturbance Compensation | Mismatched Disturbance Compensation | Finite-Time Convergence |
|---|---|---|---|
| TSMC [30] | Yes | No | Yes |
| EOSMC [41] | Yes | Yes | No |
| The proposed | Yes | Yes | Yes |
| No. | Device | No. | Device |
|---|---|---|---|
| 1 | Hydraulic cylinder | 5 | Directional valve |
| 2 | Relief valves | 6 | Pilot check valve |
| 3 | Reservoir | 7 | Hydraulic pump |
| 4.1 | Check valve 4.1 | 8 | AC motor |
| 4.2 | Check valve 4.2 | 9 | AC motor driver |
| Symbol | Quantity and Unit |
|---|---|
| Displacement of the cylinder. | |
| Pressures inside the cylinder chambers. | |
| Bore- and rod- side areas of the cylinder. | |
| Relative mass of the motion system. | |
| Initial volumes of chamber 1 and 2. | |
| Active volume of chamber 1. | |
| Active volume of chamber 2. | |
| Effective bulk modulus of the fluid. | |
| Internal leakage coefficient. | |
| Displacement of the pump. | |
| Control gain of the motor driver. | |
| Volumetric efficiency of the pump. | |
| Driving voltage of the motor driver. | |
| Positive constants in the system model. | |
| Lumped disturbance in force dynamics. | |
| Lumped disturbances in pressure dynamics. |
| Parameter | Unit | Nominal (+ Variance) Value |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, D.G.; Tran, D.T.; Ahn, K.K. Disturbance Observer-Based Chattering-Attenuated Terminal Sliding Mode Control for Nonlinear Systems Subject to Matched and Mismatched Disturbances. Appl. Sci. 2021, 11, 8158. https://doi.org/10.3390/app11178158
Nguyen DG, Tran DT, Ahn KK. Disturbance Observer-Based Chattering-Attenuated Terminal Sliding Mode Control for Nonlinear Systems Subject to Matched and Mismatched Disturbances. Applied Sciences. 2021; 11(17):8158. https://doi.org/10.3390/app11178158
Chicago/Turabian StyleNguyen, Duc Giap, Duc Thien Tran, and Kyoung Kwan Ahn. 2021. "Disturbance Observer-Based Chattering-Attenuated Terminal Sliding Mode Control for Nonlinear Systems Subject to Matched and Mismatched Disturbances" Applied Sciences 11, no. 17: 8158. https://doi.org/10.3390/app11178158






