MHD Flow and Heat Transfer of Hybrid Nanofluid over an Exponentially Shrinking Surface with Heat Source/Sink

Abstract

In nanotechnology research, nanofluid technology contributes many applications to engineering applications and industry, such as power generation, solar collection, heat exchangers for cooling, and many more. However, there are still a few constraints in terms of heat transfer enhancement, although nanofluid properties show the best heat transfer rate compared with conventional fluids. Thus, this study was conducted for the purpose of investigating the behaviors of flow and heat transfer of hybrid nanofluid with carbon nanotubes (CNTs) on a permeable exponentially shrinking surface, as well as investigating the effects of a magnetic field and heat source/sink. This study was conducted by developing a mathematical model, which was the Tiwari–Das model for momentum and energy equations, and then transforming the model’s partial differential equations (PDEs) to ordinary differential equations (ODEs) using a similarity solution. Next, these equations were solved numerically using the MATLAB bvp4c boundary value problem solver. The authors particularly explored these behaviors with a few variations. Based on the results obtained, it was found that dual solutions exist in a specific range of the shrinking case, ${\lambda }_c<\lambda <-\lambda$ and that the critical point ${\lambda }_c$ also exists in a range of −1.5 < ${\lambda }_c$< −1 with different parameters. For the heat source/sink effect, the Nusselt number was higher when heat sink case ε < 0, whereas it decreased when the heat source case ε > 0. Therefore, this study deduced that the heat transfer rate of hybrid nanofluid (CNTs/Cu–water) is better than regular nanofluid (CNT–water) and conventional fluid (water). The present study took into consideration the problem of MHD flow and heat transfer analysis of a hybrid nanofluid towards an exponentially shrinking surface with the presence of heat source/sink and thermal radiation effects. The authors show that dual solutions exist within a specific range of values due to the shrinking case. The current work is predicted to have numerous benefits in equivalent real-world systems.

1. Introduction

In the past decade, there has been a global trend resulting from the discovery of hybrid nanofluid for heat transfer enhancement. The factor that influenced this increase in demand for a new efficient source was the need for heat transfer enhancement that could be applied to a few industries, including thermal power plants, solar energy, the chemical industry, manufacturing, and the processes industry. As an example application in the automobile industry, hybrid nanofluid is used as an alternative to conventional coolant in radiators. Generally, conventional fluids such as water, oil, and kerosene are used in radiators to transfer heat generated from the engine or cylinder to the surrounding area. Due to modern technological advances, hybrid nanofluids have experienced high demand for their use in heat exchange processes. There is such high demand because hybrid nanofluid has higher thermal conductivity than conventional fluid due to the intrinsic characteristics of nanoparticles.

It is well known that hybrid nanofluid is an extension of regular nanofluid. It is produced by adding another nanoparticle—known as a hybrid nanoparticle—into regular nanofluid. A few researchers have studied the properties of the boundary layer on a nonlinear surface, such as its exponential nature. Rohni et al. [1] investigated boundary layer flow and heat transfer over an exponentially shrinking vertical sheet with suction. They reported that the steady flow due to an exponentially shrinking sheet is possible when the mass suction parameter is S > 2.2667. Ara [2] investigated the effect of radiation on the boundary layer flow of an Eyring–Powell fluid over an exponentially shrinking sheet, finding that the amount of velocity generated due to exponential shrinking is greater than that of linear shrinking. Sandeep et al. [3] discussed the unsteady MHD radiative flow and heat transfer of a dusty nanofluid over an exponentially stretching surface. Aurangzaib et al. [4] examined micropolar fluid flow and heat transfer over an exponentially permeable shrinking sheet, noting that for Newtonian fluid, it is possible to obtain a steady similarity solution of boundary layer flow due to a linearly shrinking sheet with wall mass transfer if the wall mass suction parameter S is greater than or equal to 2 and that the flow due to an exponentially shrinking sheet is possible when S > 2.2667. Sathish Kumar et al. [5] presented a comparative analysis of magnetohydrodynamic (MHD) non-Newtonian fluids flow over an exponentially stretched sheet. Merkin et al. [6] considered stagnation-point flow and heat transfer over an exponentially stretching/shrinking cylinder. From this study’s observation, it was revealed that for the stretching case, the solution is unique, whereas in the shrinking case, the solutions are not unique, leading to dual solutions.

Additionally, Ur Rehman et al. [7] conducted a thermophysical analysis of the three-dimensional MHD stagnation-point flow of nanomaterial influenced by an exponentially stretching surface. Next, flow and heat transfer of nanofluid over an exponentially shrinking porous sheet with heat and mass fluxes was considered by [8], who mentioned that as in the case of an exponentially shrinking sheet, the generation of vorticity increases compared with that of a linearly shrinking sheet, so a higher value of suction is required to confine the generated vorticity within the boundary layer. Lund et al. [9] solved quadruple solutions of mixed convection flow of magnetohydrodynamic (MHD) nanofluid over exponentially vertical shrinking and stretching surfaces, including stability analysis.

Furthermore, recent studies on heat transfer in hybrid nanofluid are still relevant, even though it has been studied by researchers for a long time. Manjunatha et al. [10] investigated heat transfer enhancement in the boundary layer flow of hybrid nanofluids due to variable viscosity and natural convection. They concluded that hybrid nanofluid flow plays a more substantial role in the process of heat transfer than a regular nanofluid flow. Huminic and Huminic [11] reviewed hybrid nanofluids for heat transfer applications and mentioned that the deposition of nanoparticles and reduction in the thickness of the boundary layer were the main reasons for the enhancement in thermal performance. Bumataria et al. [12] presented current research aspects in mono and hybrid nanofluid-based heat pipe technologies. Recent research and experimental studies of the thermal conductivity of hybrid nanofluids were investigated by [13]. Next, [14] also reviewed hybrid nanofluid flow and heat transfer over backward and forward steps; the findings indicated that the features of hybrid nanofluids improve as the volume fraction and temperature increase and that they exhibit new characteristics in terms of heat transfer performance. A study by [15] described tailored silver/graphene nanoplatelet hybrid nanofluids for solar applications. The experimental and numerical study of heat transfer and friction factor of a plain tube with hybrid nanofluids was studied by [16]. The recent trend of nanofluid heat transfer machine learning research was applied to renewable energy by [17]. This study concluded that nanofluids could improve the heat transfer of the heat exchangers used in various energy systems, including renewable solar, wind, and geothermal energy. Alhajaj et al. [18] conducted an experimental and numerical approach regarding the flow of nanofluid and hybrid fluid in porous channels, and Hemmat Esfe et al. [19] reviewed the application of conventional and hybrid nanofluids in different machining processes.

Considering previous studies related to the boundary layer over nonlinear surfaces, such as exponential analyses, Bhattacharyya [20] investigated hybrid nanofluid flow induced by an exponentially shrinking sheet. They explained that vorticity occurs for the shrinking sheet flow. Thus, the similarity solutions do not exist, since vorticity could not be confined to the boundary layer. Mixed convection flow over an exponentially stretching/shrinking vertical surface in a hybrid nanofluid was studied by [21]. Moreover, Dero et al. [22] conducted a stability analysis of $Cu-C_6{H}_{9}Na{O}_7$ and $Ag-C_6{H}_{9}Na{O}_7$ nanofluids with the effect of viscous dissipation over stretching and shrinking surfaces using a single-phase model. It was observed that here, two possibilities exist: there is a unique solution when λ > λ_c, whereas when λ < λ_c, no solution exists. It should be noted that the λ_c indicates the critical point of the parameter λ where a solution exists. Khashi′ie et al. [23] presented flow and heat transfer past a permeable power-law deformable plate with orthogonal shear in a hybrid nanofluid. They mention that λ_c is also known as a separation point and is usually located in the shrinking region. Based on this study, the separation point can be extended when the volume fraction of copper nanoparticles and suction effect increase. A boost in suction and copper nanoparticles volume fraction can delay the separation. Khashi′ie et al. [23] also conducted a comparative analysis about flow and heat transfer of hybrid nanofluid over a permeable shrinking cylinder with Joule heating. Their results indicated that suction could hold the boundary layer separation by inducing the flow and increasing the heat transfer rate. Last but not least, Zainal et al. [24] investigated the heat generation/absorption effect on MHD flow of hybrid nanofluid over a bidirectional exponentially stretching/shrinking sheet. The stability of nanofluids has been discussed [25,26,27,28], whereby the performance of nanofluids can be significantly affected by channel orientations in micro dimensions. The dual solutions could justify the stability of the solution by performing a stability analysis. Numerically, the eigenvalues from the stability analysis indicated that the positive upper branch eigenvalues were physically stable compared with the negative values of the lower branch eigenvalues. Experimentally, the stability of nanofluids significantly indicated that the performance of working fluids and the preparation of nanofluids in order to maintain the thermophysical properties were very important [26].

Looking at the literature on MHD flow due to heat source/sink and thermal radiation, it is mentioned that the flow due to an exponentially shrinking boundary is still a relatively under-explored area. The investigation of boundary layer flow and heat transfer past an exponentially shrinking surface has gained more attention, as it finds important applications in many industries and manufacturing processes. Driven by the above reviews, the present paper was devoted to determining numerical solutions to MHD boundary layer flow and heat transfer of hybrid nanofluid over a permeable exponentially shrinking surface with a magnetic field, heat sink/source, and thermal radiation effect. This study also considered water as a base fluid, and carbon nanotubes (CNTs) including single-wall carbon nanotubes (SWCNTs) and multi-wall carbon nanotubes (MWCNTs) as nanoparticles, and copper (Cu) was considered as a hybrid nanoparticle. The results were obtained for several physical parameters, and they are also presented in tabular and graphical format. The present results obtained were compared with previously published results, indicating good agreement.

2. Mathematical Methods

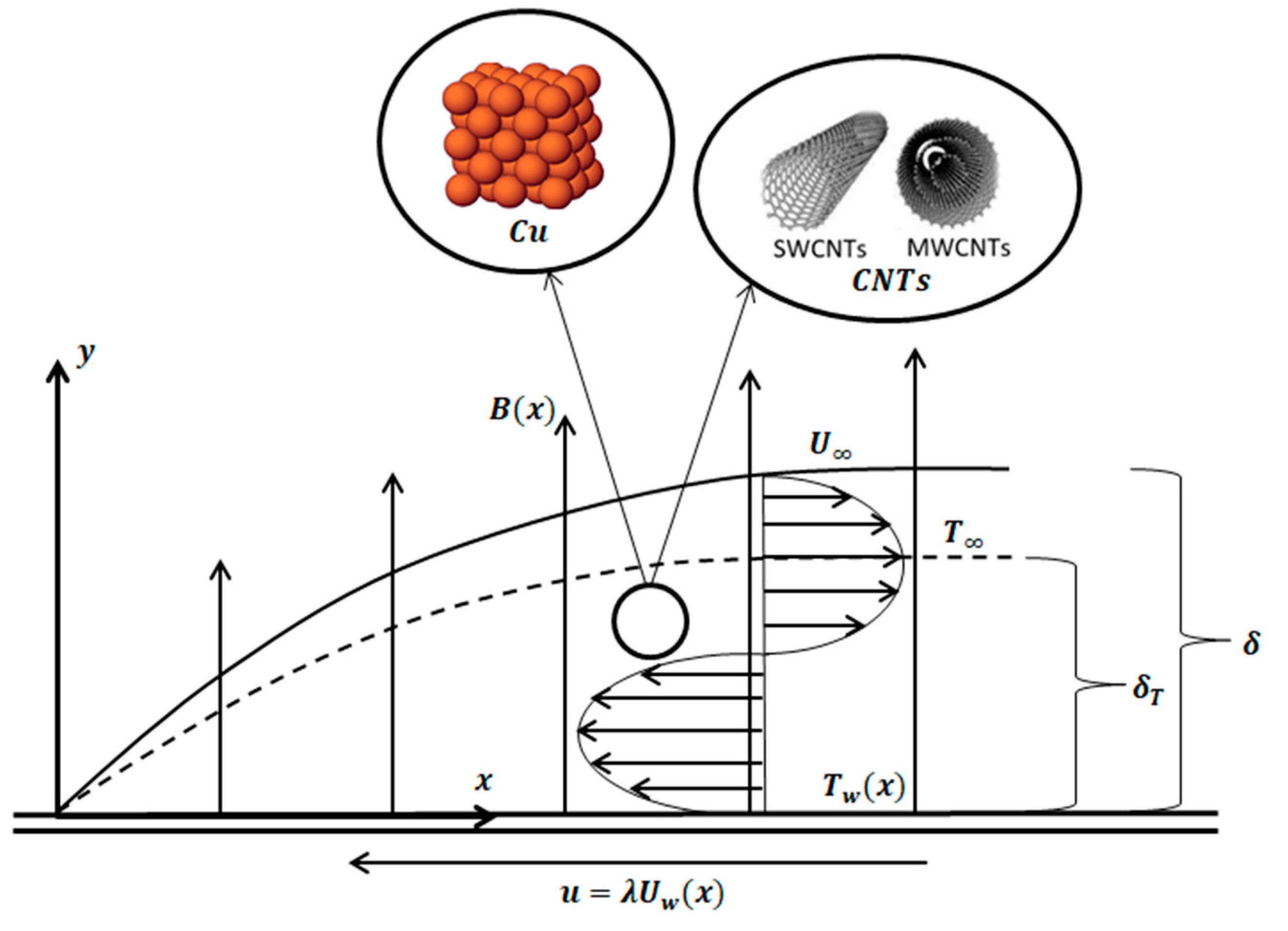
Consider a steady two-dimensional MHD flow and heat transfer of hybrid nanofluid along a permeable exponentially shrinking surface. As shown in Figure 1, the x direction is along the surface and the y direction is normal to it. The velocity wall is expressed as u_w(x) = U₀ e ^x/L, where U₀ is a constant velocity and L is the characteristic length of the surface. The induced magnetic field variable B(x) = B₀ e ^x/2L acts on the y direction, where B₀ is represented as an induced magnetic field constant. The dimensional heat sink/source is given as Q(x) = Q₀ e ^x/L, where Q₀ is the heat sink/source constant. The viscous dissipation effect is also ignored. Assume that the wall temperature of the exponentially shrinking/stretching surface is given as $T_w(x)=T_{\infty }+T_0{e}^{x/2L}$, where $T_{\infty }$ is the ambient temperature, and T₀ is the reference temperature when T₀ > 0, referred to as assisting flow, and T₀ < 0 is an opposing flow. Additionally, assume that the size of nanoparticles is uniform and small, with a nanosize of 10⁻⁹. The agglomeration of nanoparticles is neglected due to the synthesis of hybrid nanofluid as a stable compound. The impact of thermal radiation along the y axis with the convection heat transfer is integrated in the energy equation. Hence, the governing equations for continuity, momentum, and energy are given in Equations (1)–(3), respectively. All nomenclature in Equations (1)–(3) are illustrated in Nomenclature.

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\left[\frac{{\partial }^{2}u}{\partial y^2}\right]-\frac{{\sigma }_{hnf}{B}^2(x)u}{{\rho }_{hnf}}+gB\left(T-T_{\infty }\right)$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}-\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{\partial q_r}{\partial y}+\frac{Q(x)}{{\left(\rho C_p\right)}_{hnf}}\left(T-T_{\infty }\right)$$

(3)

where the heat flux of radiation, $q_r$, is described by using the Rosseland approximation:

$$q_r=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{\partial T^4}{\partial y}$$

(4)

where $\sigma$* is the Stefan–Boltzman constant, and k^* represents the mean absorption coefficient. The complication with this equation is that temperature appears to the fourth power, which makes the problem nonlinear in T and eliminates most hope of finding an analytical solution to the conduction problem. One way to deal with this is to linearize the radiation rate law via a first-order Taylor series expansion, assuming that the temperature difference is small enough in the flow. Thus, the expansion term T⁴ in the form of a Taylor series with ambient temperature, $T_{\infty }$, by neglecting a higher order to obtain the term in linear function is as follows:

$$T^4\cong 4T_{\infty }^{3}T-3T_{\infty }^4$$

(5)

From Equations (4) and (5):

$$\frac{\partial q_r}{\partial y}=-\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}}\frac{{\partial }^{2}T}{\partial y^2}$$

(6)

Using Equation (6), the new energy equation will be:

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\left(\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}+\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}}\right)\frac{{\partial }^{2}T}{\partial y^2}+\frac{Q(x)}{{\left(\rho C_p\right)}_{hnf}}\left(T-T_{\infty }\right)$$

(7)

Hence, a boundary condition for governing Equations (2), (3) and (7) is:

$$\begin{array}{l}u=\lambda u_w(x)=\lambda U_0{e}^{x/L},v=v_w(x),T=T_w(x)=T_{\infty }+T_0{e}^{x/2L} as y=0\\ u=0,T=T_{\infty } as y\to \infty \end{array}$$

(8)

where ${\nu }_w$(x) < 0 is velocity suction, whereas v_w(x) > 0 is velocity blowing. Next, the similarity solution is applied to the mathematical model as shown:

$$\psi =\sqrt{2{\nu }_f{U}_{0}L}{e}^{x/2L}f(\eta ),\eta =\sqrt{\frac{U_0}{2{\nu }_{f}L}}{e}^{x/2L}y,\theta (\eta )=\frac{T-T_{\infty }}{T_w-T_{\infty }}$$

(9)

where $\psi$ as a stream function is defined as $u=\raisebox{1ex}{$\partial \psi $}\!\left/ \!\raisebox{-1ex}{$\partial y$}\right.$ and $v=-\raisebox{1ex}{$\partial \psi $}\!\left/ \!\raisebox{-1ex}{$\partial x$}\right.$. Thus, u and v are obtained as:

$$\begin{array}{l}u=\frac{\partial \psi }{\partial y}=U_0{e}^{x/L}{f}^{\prime }(\eta ),\\ v=-\frac{\partial \psi }{\partial x}=-\sqrt{\frac{U_0{\nu }_f}{2L}}{e}^{x/2L}\left[\eta f^{\prime }(\eta )+f(\eta )\right]\end{array}$$

(10)

where (′) is differentiation with respect to $\eta$. It found that:

$$v_w(x)=-\sqrt{\frac{U_0{\nu }_f}{2L}}{e}^{x/2L}S$$

(11)

where ${\nu }_w$(x) is the mass flux surface, S is the mass flux parameter, $U_0$ is constant velocity, ${\nu }_f$ is kinematic viscosity, and L is the characteristic length surface. Additionally, it also considers the effective properties of hybrid nanofluid by performing a numerical analysis to identify the behavior of momentum and the thermal boundary layer on the permeable exponentially shrinking surface when nanoparticles are mixed with base fluid. Meanwhile, the effective properties of hybrid nanofluid, as described in the mathematical model, are shown in

Table 1. The effective properties of nanofluid types.

Thermophysical Properties	Regular Nanofluid CNT–Water s1 = CNT:n = 3	Hybrid Nanofluid CNT/Cu–Water s1 = CNT:s2 = Cu:n = 3
Density ($\mathrm{kg}/{\mathrm{m}}^3$)	${\rho }_{nf}=(1-{\phi }_1){\rho }_f+{\phi }_1{\rho }_{s1}$	${\rho }_{hnf}=(1-{\phi }_2)\left\{{\rho }_{nf}\right\}+{\phi }_2{\rho }_{s2}$
Heat capacity ($\mathrm{J}/\mathrm{K}$)	${\left(\rho C_p\right)}_{nf}=(1-{\phi }_1){\left(\rho C_p\right)}_f+{\phi }_1{\left(\rho C_p\right)}_{s1}$	${\left(\rho C_p\right)}_{hnf}=(1-{\phi }_2)\left\{{\left(\rho C_p\right)}_{nf}\right\}+{\phi }_2{\left(\rho C_p\right)}_{s2}$
Viscosity ($\mathrm{Ns}/{\mathrm{m}}^{-2}$)	${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-{\phi }_1\right)}^{2.5}}$	${\mu }_{hnf}=\frac{{\mu }_{nf}}{{\left(1-{\phi }_2\right)}^{2.5}}$
Thermal conductivity ($\mathrm{W}/\mathrm{Km}$)	$\frac{k_{nf}}{k_f}=\frac{k_{s1}+\left(n-1\right)k_f-\left(n-1\right){\phi }_1\left(k_f-k_{s1}\right)}{k_{s1}+\left(n-1\right)k_f+{\phi }_1\left(k_f-k_{s1}\right)}$	$\frac{k_{hnf}}{k_{nf}}=\frac{k_{s2}+\left(n-1\right)k_{nf}-\left(n-1\right){\phi }_2\left(k_{nf}-k_{s2}\right)}{k_{s2}+\left(n-1\right)k_{nf}+{\phi }_2\left(k_{nf}-k_{s2}\right)}$
Electrical conductivity ($\mathrm{W}/\mathrm{Km}$)	$\frac{{\sigma }_{nf}}{{\sigma }_f}=\frac{{\sigma }_{s1}+\left(n-1\right){\sigma }_f-\left(n-1\right){\phi }_1\left({\sigma }_f-{\sigma }_{s1}\right)}{{\sigma }_{s1}+\left(n-1\right){\sigma }_f+{\phi }_1\left({\sigma }_f-{\sigma }_{s1}\right)}$	$\frac{{\sigma }_{hnf}}{{\sigma }_{nf}}=\frac{{\sigma }_{s2}+\left(n-1\right){\sigma }_{nf}-\left(n-1\right){\phi }_2\left({\sigma }_{nf}-{\sigma }_{s2}\right)}{{\sigma }_{s2}+\left(n-1\right){\sigma }_{nf}+{\phi }_2\left({\sigma }_{nf}-{\sigma }_{s2}\right)}$

. As is well known, the effective thermal conductivity model, $k_{eff}$/$k_b$, and effective electrical conductivity, ${\sigma }_{eff}$/${\sigma }_b$, are based on the Hamilton and Crosser model, which is then modified to the Maxwell model when n = 3/m = 3 and where n is an empirical shape factor. The Maxwell model is needed because this model considers ideally spherical particles. The Maxwell theory is not considered a space distribution effect of particles on thermal conductivity and electrical conductivity.

Table 2. The thermophysical properties of nanoparticle, hybrid nanoparticle, and fluid.

Thermophysical Properties	Base Fluid	Hybrid Nanoparticle	Nanoparticle
	$\mathbf{Water}(\mathbf{Pr}=6.2)$	Copper (Cu)	SWCNT	MWCNT
$\rho$($\mathrm{kg}/{\mathrm{m}}^3$)	997.1	8933	2600	1600
$C_p$($\mathrm{J}/\mathrm{kg}\mathrm{K}$)	4179	385	425	796
$k$($\mathrm{W}/\mathrm{mK}$)	0.613	400	6600	3000
σ$\left(\mathrm{S}/\mathrm{m}\right)$	0.05	5.96 × 107	6.2 × 107	2.9 × 106

shows the properties of the nanoparticle, hybrid nanoparticle, and base fluid of different types. The values of fixed parameters in Table 2 were chosen based on the standard values used by many researchers [3,10,21].

Equation (9) is substituted into Equations (1), (2), (7), and (8) using similarity transformation, hence:

$$\frac{1}{{\left(1-{\phi }_1\right)}^{2.5}{\left(1-{\phi }_2\right)}^{2.5}}{f}^{‴}(\eta )-\frac{{\rho }_{hnf}}{{\rho }_f}\left(2f^{\prime 2}(\eta )-f(\eta )f^{″}(\eta )\right)-\frac{{\sigma }_{hnf}}{{\sigma }_f}M{f}^{\prime }(\eta )+Gr\theta =0$$

(12)

$$\frac{1}{\mathrm{Pr}}\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}Rd\right){\theta }^{″}(\eta )-\frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}\left(f^{\prime }(\eta )\theta (\eta )-f(\eta ){\theta }^{\prime }(\eta )\right)+\epsilon \theta (\eta )=0$$

(13)

with a boundary condition as follows:

$$\begin{array}{l}{f}^{\prime }(\eta )=\lambda ,f(\eta )=S,\theta (\eta )=1 as \eta =0\\ f^{\prime }(\eta )=0,\theta (\eta )=0 as \eta \to \infty \end{array}$$

(14)

The governing equation can be defined as follows:

$$\begin{array}{l}\begin{array}{ccc}\mathrm{Pr}=\frac{{\nu }_f}{{\alpha }_f},& M=\frac{2{\sigma }_f{B}_0^{2}L}{{\rho }_f{U}_0},& \epsilon =\frac{2Q_{0}L}{U_0{\left(\rho C_p\right)}_f}\end{array},\\ \begin{array}{cc}S=-\frac{v_w(x)}{\sqrt{\frac{U_0{\nu }_f}{2L}}}{e}^{-x/2L},& Rd=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k^{*}{k}_f}\end{array},Gr=g\beta \frac{\left(T_w-T_{\infty }\right)}{a^{2}x}\end{array}$$

(15)

In addition, the physical quantities considered in this study are skin friction coefficient, $C_f$, and Nusselt number, $N{u}_x$, which can be shown as follows:

$$\begin{array}{cc}{C}_f=\frac{{\tau }_w}{{\rho }_f{u}_w^2}& N{u}_x=\frac{2L{q}_w}{k_f\left(T_w-T_{\infty }\right)}\end{array}$$

(16)

Shear stress, ${\tau }_w$, and heat flux, $q_w$, from the surface can be defined as follows:

$$\begin{array}{cc}{\tau }_w={\mu }_{hnf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0}& q_w=\end{array}-k_{hnf}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}+{\left(q_r\right)}_{y=0}$$

(17)

By using the Reynold number coefficient, ${\mathrm{Re}}_x=2u_{w}L/{\nu }_f$, the local skin friction coefficient, ${\mathrm{Re}}_x^{1/2}{C}_f$, and local Nusselt number, ${\mathrm{Re}}_x^{-1/2}N{u}_x$, can be achieved as follows:

Local skin friction coefficient ${\mathrm{Re}}_x^{1/2}{C}_f$:

$${\mathrm{Re}}_x^{1/2}{C}_f=\frac{1}{{\left(1-{\phi }_1\right)}^{2.5}{\left(1-{\phi }_2\right)}^{2.5}}{f}^{″}(0)$$

(18)

Local number Nusselt ${\mathrm{Re}}_x^{-1/2}N{u}_x$:

$${\mathrm{Re}}_x^{-1/2}N{u}_x=-\left(\frac{k_{hnf}}{k_f}+\frac{4}{3}Rd\right){\theta }^{\prime }(0)$$

(19)

3. Numerical Analysis

The bvp4c codes start by finding the initial guess for the first and the second solution. The new variables are introduced to reduce the higher-order equations into first-order equations. The new variables are as follows:

$$f=y\left(1\right), f^{\prime }=y\left(2\right), f^{″}=y\left(3\right), g=y\left(4\right), g^{\prime }=y\left(5\right)$$

(20)

Therefore, Equations (12) and (13) are written as:

$$f^{‴}\to y^{\prime }\left(3\right)=\left[\frac{{\rho }_{hnf}}{{\rho }_f}\left(2f^{\prime 2}\left(\eta \right)-f\left(\eta \right)f{}^{″}\left(\eta \right)\right)+\frac{{\sigma }_{hnf}}{{\sigma }_f}Mf{}^{\prime }\left(\eta \right)-Gr\theta \left(\eta \right)\right]{\left(1-{\phi }_1\right)}^{2.5}{\left(1-{\phi }_2\right)}^{2.5}$$

(21)

$${\theta }^{″}\to y^{\prime }\left(5\right)=Pr\left[\frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}\left(f^{\prime }\left(\eta \right)\theta \left(\eta \right)-f\left(\eta \right)\theta {}^{\prime }\left(\eta \right)\right)-\epsilon \theta \left(\eta \right)\right]/\left[\frac{k_{hnf}}{k_f}+\frac{4}{3}Rd\right]$$

(22)

with boundary conditions:

$$ya\left(1\right)-S=0, ya\left(2\right)-\lambda =0, ya\left(4\right)-1=0, yb\left(2\right)=0, yb\left(4\right)=0$$

(23)

where a and b represent the coordinates on the surface when $\eta =0$, and the coordinates in the far field are at $\eta ={\eta }_{\infty }$, respectively. Further, the numerical finding has been obtained by guessing the inputs of pertinent parameters that satisfied the condition $f{}^{\prime }\left(\eta \right)\to 0$ and $\theta \left(\eta \right)\to 0$ as $\eta \to \infty$. The procedure is reiterated until the converged solution meets a tolerance limit of 10⁻⁶.

4. Results and Discussion

The bvp4c boundary value problem solver using MATLAB software was used to solve the governing nonlinear ordinary differential equation for boundary layer flow and heat transfer with its boundary condition. The three-stage Lobatto IIIa method is a numerical solution in bvp4c solver. The Lobatto IIIa method was proposed by Shampine. This method provides specified accuracy, where an initial guess is supplied at initial mesh points and changes step-size. According to Waini [21], the bvp4c solver produced satisfactory solutions compared with the shooting method and Keller box. The obtained results were validated by comparing the output with previously reported results, and it was shown that the comparison was in an excellent agreement with the published results. These numerical results are presented in the form of tables and graphs.

Next, parameter values ${\phi }_2$, M, $\epsilon$, Rd, and nanofluid types were selected to obtain numerical results for variation $\lambda$ in shrinking case $\lambda <0$. In this study, the Prandtl number value was set as Pr = 6.2, which shows that the water and nanoparticle types selected were carbon nanotubes (CNTs), which were single-wall CNTs and multi-wall CNTs, as well as copper (Cu). Next, the S parameter shows that the model is permeable and is considered to improve the suction rate, S > 0, and that the second solution is obtained when in a certain range, which is S > 2. Based on this study, this model depends on suction strength to control boundary layer separation on molecules that move slowly in flow. Meanwhile, the various numerical results of f″(0) and −$\theta$′(0) were compared with previous results reported by the authors of the related studies and are shown in

Table 3. Comparison of several of numerical results for f″(0) and −θ′(0) (λ = 1, S = 3, Pr = 0.7).

Author	f″(0)		−θ′(0)
	First Solution	Second Solution	First Solution	Second Solution
Ghosh and Mukhopadhyay [29]	2.39082	−0.97223	1.77124	0.84832
Hafidzuddin et al. [30]	2.3908	−0.9722	1.7712	0.8483
Iskandar et al. [31]	2.390814	−0.972247	1.771237	0.848316
Present result	2.390813487	−0.972247692	1.771237388	0.84831569

. Based on Table 3, each numerical result of the first and second solutions were compared and are shown to have achieved a good agreement, meaning that the numerical values of the present results are almost similar to the values of previous results, which are from [29,30,31]. The precision of the solutions to the boundary value problems found by using MATLAB bvp4c is comparable with previous studies, proving the compatibility of the numerical results in Table 3.

Apart from that,

Table 4. Comparison several of numerical results of −$\theta$′(0) for various parameters ($\lambda$ = 1, φ₁ = φ₂ = 0, Gr = 0).

Pr	M	Rd	ε	−θ′(0)
				Magyari and Keller [32]	El-Aziz [33]	Bidin and Nazar [34]	Ishak [35]	Iskandar [31]	Present Result
0.5	0	0	0	0.594338	0.594493			0.594339	0.596687601
1	0	0	0	0.954782	0.954785	0.9548	0.9548	0.954783	0.954810637
2	0	0	0			1.4714	1.4715	1.47146	1.471454035
3	0	0	0	1.869075	1.869074	1.8691	1.8691	1.869074	1.869068789
5	0	0	0	2.500135	2.500132		2.5001	2.500132	2.500127789
10	0	0	0	3.660379	3.660372		3.6604	3.660372	3.660369292
1	1	0	0				0.8611	0.861094	0.861508689
1	0	1	0			0.5315	0.5312	0.531158	0.535301194
1	1	1	0				0.4505	0.450536	0.461965494
1	1	1	−1						0.873201623
25	1	1	1						1.201645626

shows numerical results for −$\theta$′(0), which are compared with previous results [31,32,33,34,35]. Based on this table, it is proven that the present numerical results are almost identical to previous results and that they achieve good agreement. Based on the present results in Table 4, the higher value of the Prandtl number shows the increasing –$\theta$′(0) values, which causes the temperature boundary layer thickness to become thinner, demonstrating the improvement in the heat transfer process. Thus, heat transfer enhancement becomes better.

In general, Figure 2, Figure 3, Figure 4 and Figure 5 show the existence of the dual solution clearly, where the randomly shrinking case, ${\lambda }_c\le \lambda \le -\lambda$, can be observed. The unique solution exists at point ${\lambda }_c=\lambda$, where ${\lambda }_c$ is the critical point. In region ${\lambda }_c\le \lambda \le -\lambda$, the Tiwari–Das model was developed to describe the behavior of the MHD hybrid nanofluid flow and heat transfer on the permeable exponentially shrinking surface with a few parameters. A numerical solution does not exist in region ${\lambda }_c>\lambda$ because this case describes the incompatibility of the mathematical model in this region. The boundary condition separation from the exponentially uneven surface shows that the shrinking case causes the Tiwari–Das model, which was developed and used based on boundary layer approximation theory, to be invalid. The second solution obtained is limited over a certain range of $\lambda$ values, which is because the specific value of $\lambda$ cannot track the exact solution according to the relative error tolerance, which is limited. The first solution in Figure 2a shows that the increasing local skin friction coefficient, $R{e}_x^{1/2}{C}_f$, refers to f″(0) on the permeable exponentially shrinking surface when the volume fraction nanoparticle of copper ${\phi }_2$increases. Thus, the reduction in the momentum boundary layer thickness, $\delta$, coincides with the increase in value of ${\phi }_2$, causing an increase in $R{e}_x^{1/2}{C}_f$ when the ${\phi }_2$ value is increased. Therefore, the effect of shear stress on the permeable exponentially shrinking surface increases. In addition, the numerical solution that is shown in Figure 2b expresses the increase in the value of the local Nusselt number, $R{e}_x^{1/2}N{u}_x$, referred to as –$\theta$’(0) when the value of ${\phi }_2$ increases from 0 to 0.04 on a shrinking surface in region $\lambda$ < −1. This happens because of the synergy effect. In region −1 < $\lambda <0$, $R{e}_x^{1/2}N{u}_x$ values decrease when the ${\phi }_2$ value increases. This is because the shrinking strength $\lambda$ is not large enough. The thermal conductivity effect of hybrid nanofluid increases the heat flux on the exponentially shrinking surface in region $\lambda$ < −1, whereas the heat flux decreases in region −1 < $\lambda <0$. Thus, as the temperature gradient increases, the thermal boundary layer thickness ${\delta }_T$ becomes thin at region $\lambda$ < −1 when the value of ${\phi }_2$ increases, which ultimately increases the heat transfer rate of the exponentially shrinking surface.

Next, the upper and lower branches in Figure 3a also describe the increasing $R{e}_x^{1/2}{C}_f$ on the shrinking exponential surface when magnetic parameter M increases. This happened because the influence of higher Lorentz force $J\times B$ acts in same direction as the drift force or viscous force on the surface when in opposition to fluid flow. Moving the current density, J, is equivalent to fluid flow and the induced magnetic field moves normally or perpendicular to fluid flow according to the right-hand rule that was used to determine the direction of the physical quantity. This causes the skin friction on the surface to increase and the shear stress effect in the x axis to also increase. Therefore, the momentum boundary layer thickness over the permeable shrinking exponential surface becomes thin. Figure 3b describes the trend of the increasing value of $R{e}_x^{1/2}N{u}_x$ when the value of M is higher. Because of that, the higher heat flux on the permeable shrinking exponential surface that speeds up the heat exchange process with support from the Lorentz force contributes to the increasing value of $R{e}_x^{1/2}N{u}_x$. Thus, the temperature gradient increases, and the thermal boundary layer thickness decreases. As is well known, Figure 3 shows that the increasing values of M also cause shrinking of the surface region, and $\lambda$ < 0 is bigger, which is capable of slowing down the separation of boundary layers, while the critical value ${\lambda }_c$ becomes smaller. This is because the MHD effect acts in a way that is similar to the suction effect, S > 0, which controls the state of the boundary layer.

Additional parameters in the problem of this case study are the heat sink/source and the thermal radiation effect, the purpose of which are to diversify the behavior of the MHD hybrid nanofluid on an exponentially shrinking surface. The parameter of $\epsilon$ and Rd only affect heat transfer or the Nusselt number, $R{e}_x^{1/2}N{u}_x$, because the local skin friction coefficient, $R{e}_x^{1/2}{C}_f$, values are unchanged and it has been proved that they are not dependent on the effects of heat sink/source, $\epsilon$, and thermal radiation, Rd. Figure 4a presents the reduction in $R{e}_x^{1/2}N{u}_x$ value based on increasing $\epsilon$. This is because when the heat source of hybrid nanofluid $\epsilon >0$, the heat flux is lower on the permeable exponentially shrinking surface, and it slows down the heat exchange process. In fact, when heat sink occurs $\epsilon <0$, the heat flux is higher, and speeds up the heat exchange process. As a result, with the increase in the temperature gradient, the thermal boundary layer thickness ${\delta }_T$ becomes thin when the heat sink effect occurs $\epsilon <0$. An example of one application is that of a solar collector: when heat flux is higher, the heat exchange process is faster from the solar panel surface to the environment, which will increase the efficiency of the process of the solar collector. This is because the solar panel surface cools down quickly. In addition, Figure 4b shows the reduction in the $R{e}_x^{1/2}N{u}_x$ value over the permeable exponentially shrinking surface or region $\lambda$ < 0 for the first and second solution when the thermal radiation parameter Rd is higher. In addition, the radiation effect is dominant over fluid flow. If this situation is examined in more detail, we find that it happens because inertial force resists the influence of the weak buoyancy force to overcome the temperature distribution of the MHD hybrid nanofluid flow along the permeable exponentially shrinking case. Consequently, the temperature of the hybrid nanofluid in the shrinking case is $\lambda$ < 0 when the involvement of the higher thermal radiation effect decreases. Therefore, thermal boundary layer thickness increases because higher energy radiation is present in the flow velocity field.

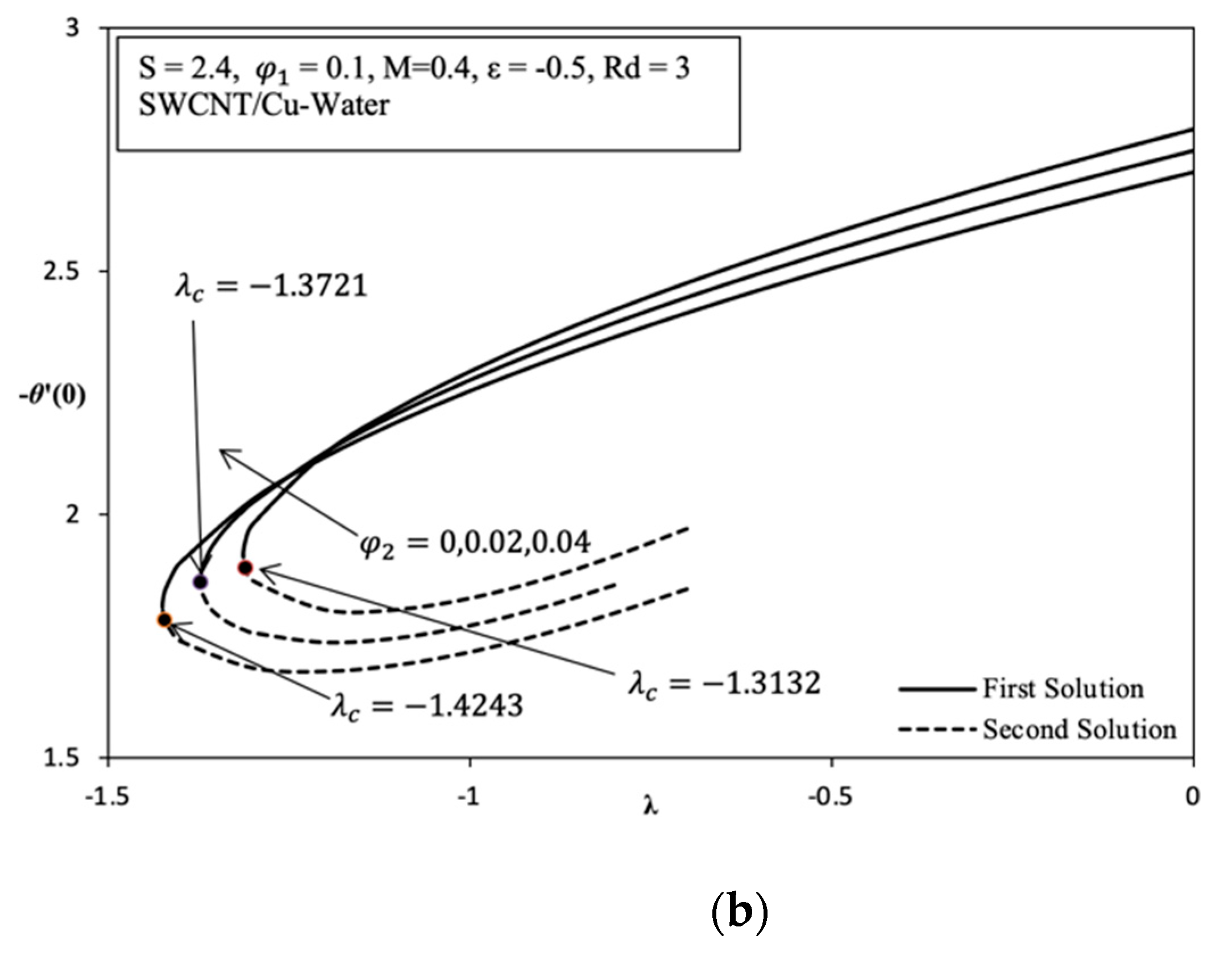
Subsequently, Figure 5a,b describes the value of $R{e}_x^{1/2}{C}_f$ and $R{e}_x^{1/2}N{u}_x$ with changes in the types of hybrids and regular nanofluid. Numerical results are produced for the purpose of studying the behavior of MHD flow and heat transfer with the different types of nanofluid used and for identifying the best nanofluid types for heat transfer enhancement. Based on Figure 5a, hybrid nanofluid SWCNT/Cu–water shows the highest value of $R{e}_x^{1/2}{C}_f$ compared with MWCNT/Cu–water and CNT–water. Regular nanofluid CNT–water, ${\phi }_2$ = 0, produces a lower value of $R{e}_x^{1/2}{C}_f$. Hybrid nanofluid SWCNT/Cu–water causes shear stress to become higher because this nanofluid is more viscous and its momentum boundary layer thickness is thin compared with MWCNT/Cu–water and CNT–water. Moreover, Figure 5b shows that SWCNT/Cu–water has the highest value of $R{e}_x^{1/2}N{u}_x$ compared with MWCNT/Cu–water and CNT–water when in the region of $\lambda$ < −1. This is because nanoparticles and fluid have different thermophysical properties that affect the heat transfer process and temperature gradient on the permeable exponentially shrinking surface, which is in the region of $\lambda$ < −1. Therefore, the thermal boundary layer thickness of SWCNT/Cu–water decreases compared with MWCNT/Cu–water and CNT–water. In light of the above fact, hybrid nanofluid shows better heat transfer enhancement than regular nanofluid.

Overall, the results indicate that variation in parameter $\lambda$ is able to obtain a critical value itself. Based on results presented in Figure 2, Figure 3, Figure 4 and Figure 5, the variation shows that different values of $\lambda$ increase shrinking strength and cause a significant increase in the value of $R{e}_x^{1/2}{C}_f$ but significantly reduce the value of $R{e}_x^{1/2}N{u}_x$.

Next, the dual solutions of the boundary layer velocity and temperature profiles are presented for various governing parameters. For the dual solutions of a boundary value problem, two different solutions are obtained under the same conditions by assuming different values of the missing initial conditions. From a physical point of view, it is important to know which solution is physically relevant. Unlike the second solution, we expect that the first solution is physically stable and frequently occurs in practice. In the present paper, we highlight the viability of the first solution only. Based on recent studies, stability analysis shows that the second solution is not stable due to the negative eigenvalues against the governing parameters where an initial growth of disturbance occurs, which means that the flow is unstable. Based on the volume fraction of hybrid nanoparticles in the existing CNT–water nanofluid, the first solution in Figure 6a shows an increasing value in velocity when the ${\phi }_2$ of copper increases. This situation can refer to the thermophysical properties of Cu in Table 2, where the high-density value of Cu increases the skin friction on the surface and hence makes it less viscous. Thus, a decrease in value in the momentum boundary layer thickness coincides with an increase in the value of ${\phi }_2$, as shown in Figure 6a. Therefore, the effect of shear stress on the exponentially permeable shrinking surface increases. The numerical solution shown in Figure 6b expresses the increase in temperature profile $\theta \left(\eta \right)$ when the value of ${\phi }_2$ increases from 0 to 0.04 towards a shrinking surface. This is due to the synergistic effect because the strength of the shrinking condition is not large enough. The heat conduction effect of hybrid nanofluids increases the heat flux on the exponentially shrinking surface in the region $\lambda <-1$. Thus, the temperature gradient increases and the thickness of the temperature boundary layer becomes thinner when the value of ${\phi }_2$ increases, as shown in Figure 6b, which ultimately increases the exponentially shrinking surface heat transfer rate.

Additional parameters in the problem of this study are the effect of heat absorption/generation and the effect of thermal radiation aimed at diversifying the MHD flow antics of hybrid nanofluids against exponentially shrinking surfaces. Generally, the parameters’ heat absorption/generation, ε, and thermal radiation, Rd, only affect the heat transfer because the value of the local skin friction coefficient is unchanged, and this proves that it does not depend on the ε and Rd. Based on Figure 7a, a decrease in the value of temperature occurs with the increase in the value of ε. This is because when heat generation occurs in hybrid nanofluids, a low heat flux occurs on the shrinking permeable exponential surface, and this will slow down the heat exchange process from that surface. In fact, when heat absorption occurs on hybrid nanofluids, a high heat flux occurs on the exponentially shrinking permeable surface, and this will accelerate the heat exchange process from that surface. As a result, the temperature gradient increases as the thickness of the temperature boundary layer becomes thinner when the effect of heat absorption, ε < 0, occurs, as shown in Figure 7a. Figure 7b shows the value of temperature increasing on the surface of the shrinking permeable exponential as the values of the radiation parameter Rd increase. In addition, the effect of radiation is dominant on thermal conduction. Furthermore, this situation occurs because inertial forces block the influence of weak buoyancy to overcome the MHD flow temperature distribution of hybrid nanofluids along the shrinking permeable exponential surface. As a result, the temperature of hybrid nanofluids over a shrinking sheet for $\lambda <0$ will shrink when the thermal radiation effect increases. Therefore, the temperature boundary layer thickness increases due to the high energy radiation in the flow field, as shown in Figure 7b.

5. Conclusions

This paper aimed to research the MHD flow and heat transfer of hybrid nanofluid on an exponentially shrinking surface with the heat source/sink and thermal radiation effects. After these numerical results were obtained, the behavior on flow and heat transfer in terms of the boundary layer were discovered when involving a few parameters. The results obtained were verified and compared with published results from other studies and the numerical data were found to be almost equivalent with those prior results. These results found that a dual solution exists when $\lambda >{\lambda }_c$. For the increasing values of φ₂ and M, the skin friction coefficient, f”(0), as well as the local Nusselt number, −$\theta$′(0), both increased when the parameter λ was near to the critical value ${\lambda }_c$. Based on the heat sink/source effect, ε, the heat transfer rate, −$\theta$′(0), continues to increase when a heat source exists, ε > 0, whereas there is a reduction in −$\theta$′(0) when a heat sink exists, ε < 0. The decrease in heat transfer rate, −$\theta$′(0), is obtained for both solutions when values of the parameter Rd are increased in a shrinking surface $\lambda$ < 0. These results showed that the skin friction coefficient, f″(0), as well as the local Nusselt number, −$\theta {}^{\prime }$(0), both increase more in hybrid nanofluid than in regular nanofluid. Thus, it was confirmed that hybrid nanofluid has better heat transfer enhancement than regular nanofluid.