Maximum Possible Cooling Rate in Ultrafast Chip Nanocalorimetry: Fundamental Limitations Due to Thermal Resistance at the Membrane/Gas Interface
Abstract
:1. Introduction
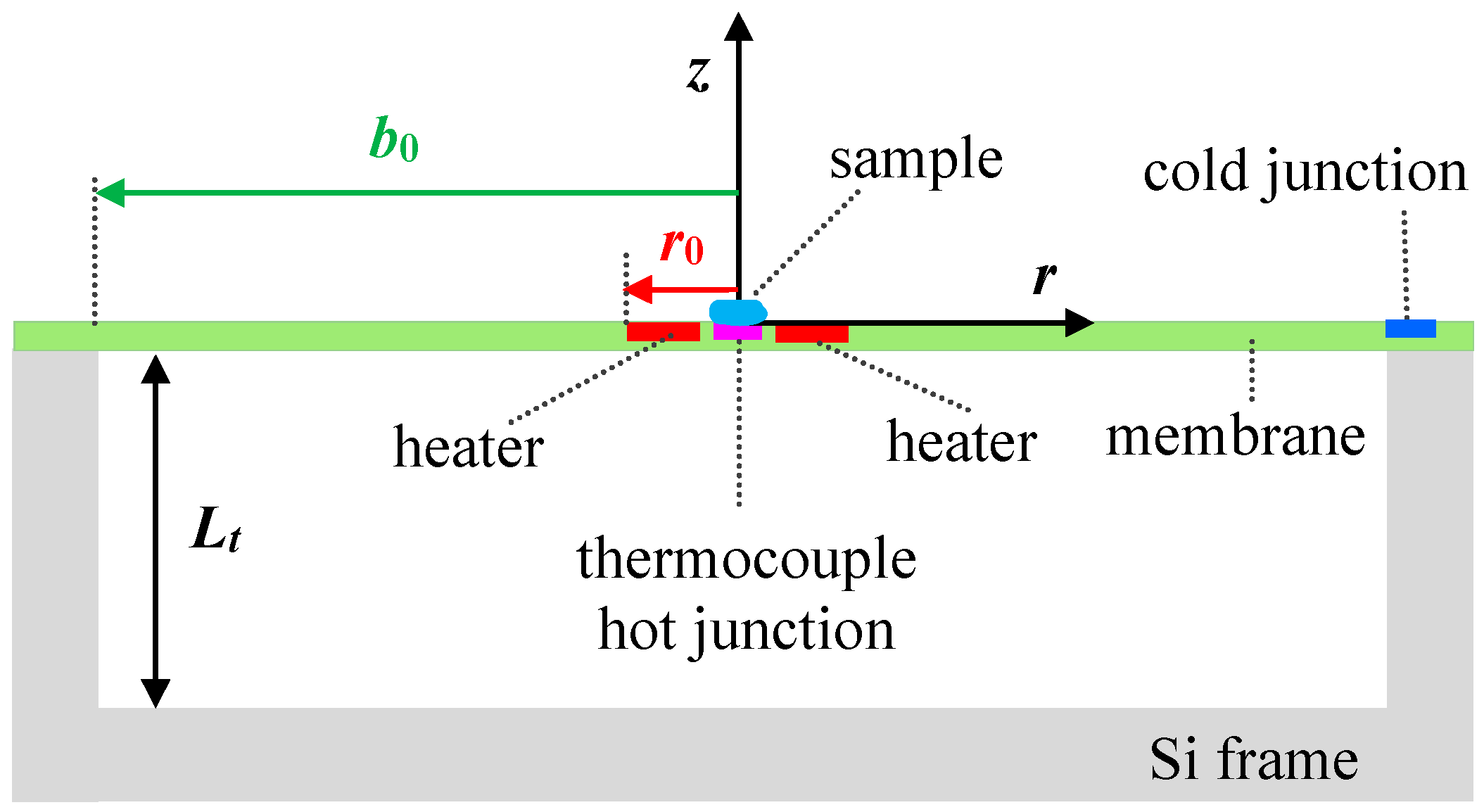
2. Membrane-Based Ultrafast Nanocalorimeter
3. Interfacial Thermal Resistance at the Membrane/Gas Interface
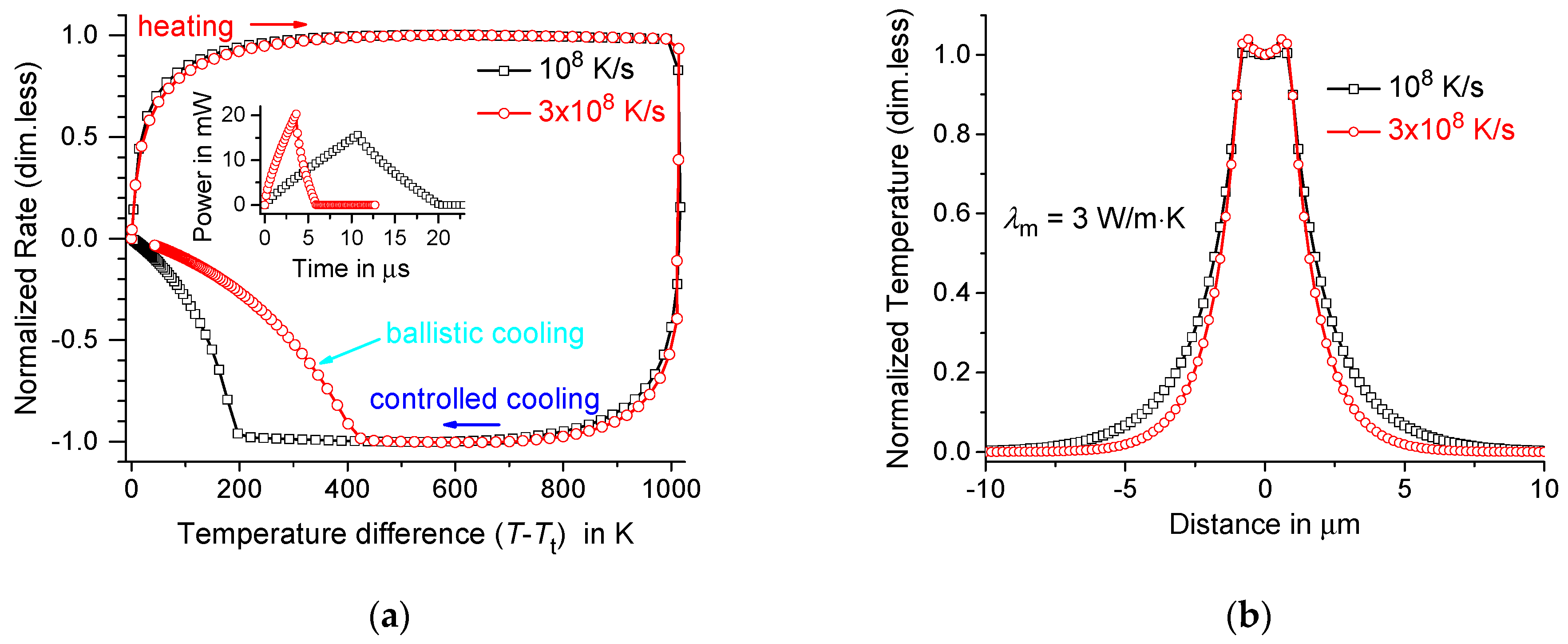
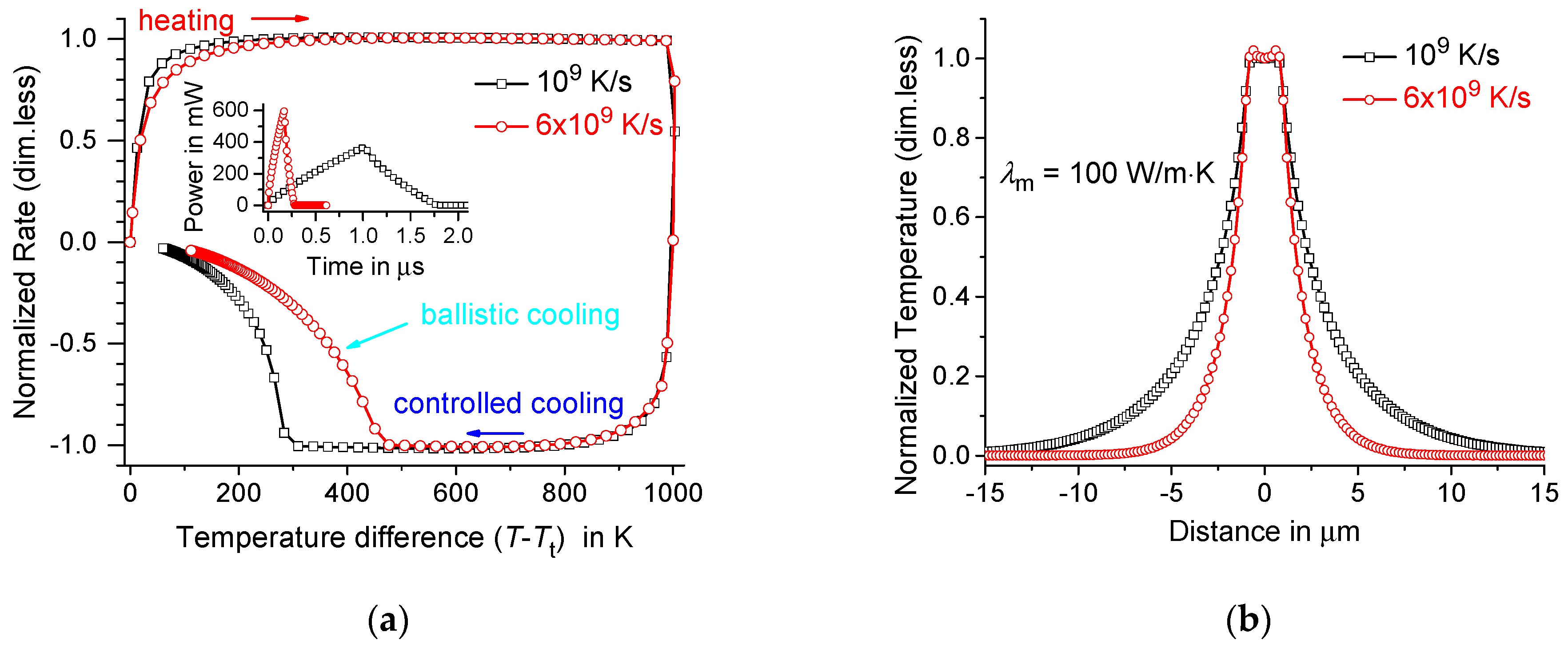
4. Maximum Possible Controlled Cooling Rate in the Membrane-Gas System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| distance from the center to the periphery of the membrane (m) | |
| , | specific heat of gas and membrane at constant (J/kgK) |
| , | thermal diffusivity of gas and membrane (m2/s) |
| membrane thickness (m) | |
| number of degrees of freedom of a gas molecule (dimensionless) | |
| acceleration of gravity (m/s2) | |
| thermal contact conductance (W/m2K) | |
| membrane/gas maximum thermal conductance (W/m2K) | |
| Grashof number (dimensionless) | |
| Boltzmann constant (J/K) | |
| mean-free-path (m) | |
| distance from the membrane hot zone to the thermostat (m) | |
| mass of a gas molecule (kg) | |
| Nusselt number (dimensionless) | |
| Prandtl number (dimensionless) | |
| pressure (Pa) | |
| heater power (W) | |
| heat flux through thermal contact (W/m2) | |
| temperature scan rate (K/s) | |
| maximum possible cooling rate (K/s) | |
| radius of the hot zone of the membrane (m) | |
| minimum radius of the hot zone (m) | |
| scan duration on heating (s) | |
| thermostat temperature (K) | |
| critical temperature difference of controlled cooling (K) | |
| average velocity of gas molecules (m/s) | |
| Greek Symbols | |
| heat transfer coefficient W/m2K | |
| convective contribution to the heat transfer coefficient W/m2K | |
| radiative contribution to the heat transfer coefficient W/m2K | |
| heat capacity ratio (dimensionless) | |
| temperature jump distance (m) | |
| scanning temperature range (K) | |
| temperature jump at the membrane/gas contact (K) | |
| membrane emissivity (dimensionless) | |
| thermal conductivity of gas and membrane (W/K · m) | |
| kinematic viscosity of gas (m2/s) | |
| density of gas and membrane (kg/m3) | |
| thermal accommodation coefficient (dimensionless) | |
| Stefan-Boltzmann constant (W/m2K4) | |
| time constant (s) | |
| thermal diffusion time (s) | |
| average time between collisions (s) | |
| time constant of nth component (s) | |
| reduced heat flux (K/s) | |
| nth Fourier component (K) | |
Appendix A. Radiative and Convective Contributions to Membrane Heat Loss
References
- Lai, S.L.; Guo, J.Y.; Petrova, V.; Ramanath, G.; Allen, L.H. Size-dependent melting properties of small tin particles: Nanocalorimetric measurements. Phys. Rev. Lett. 1996, 77, 99–102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Efremov, M.Y.; Schiettekatte, F.; Olson, E.A.; Kwan, A.T.; Lai, S.L.; Wisleder, T.; Greene, J.E.; Allen, L.H. Size-dependent melting point depression of nanostructures: Nanocalorimetric measurements. Phys. Rev. B 2000, 62, 10548–10557. [Google Scholar] [CrossRef] [Green Version]
- Efremov, M.Y.; Olson, E.A.; Zhang, M.; Lai, S.L.; Schiettekatte, F.; Zhang, Z.S.; Allen, L.H. Thin-film differential scanning nanocalorimetry: Heat capacity analysis. Thermochim. Acta 2004, 412, 13–23. [Google Scholar] [CrossRef]
- Zhang, M.; Wen, J.G.; Efremov, M.Y.; Olson, E.A.; Zhang, Z.S.; Hu, L.; de la Rama, L.P.; Kummamuru, R.; Kavanagh, K.L.; Ma, Z.; et al. Metastable phase formation in the Au-Si system via ultrafast nanocalorimetry. J. Appl. Phys. 2012, 111, 093516. [Google Scholar] [CrossRef]
- De La Rama, L.P.; Hu, L.; Ye, Z.; Efremov, M.Y.; Allen, L.H. Size effect and odd-even alternation in the melting of single and stacked AgSC n layers: Synthesis and nanocalorimetry measurements. J. Am. Chem. Soc. 2013, 135, 14286–14298. [Google Scholar] [CrossRef]
- Molina-Ruiz, M.; Lopeandía, A.F.; González-Silveira, M.; Anahory, Y.; Guihard, M.; Garcia, G.; Clavaguera-Mora, M.T.; Schiettekatte, F.; Rodríguez-Viejo, J. Formation of Pd2Si on single-crystalline Si (100) at ultrafast heating rates: An in-situ analysis by nanocalorimetry. Appl. Phys. Lett. 2013, 102, 143111. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.; De La Rama, L.P.; Hu, L.; Efremov, M.Y.; Allen, L.H. Nanocalorimetry study of the evolution of melting characteristics of single layer silver alkanethiolate lamella: Fast heating/cooling and electrical annealing. Thermochim. Acta 2015, 603, 69–78. [Google Scholar] [CrossRef]
- Ye, Z.; De La Rama, L.P.; Efremov, M.Y.; Zuo, J.M.; Allen, L.H. Approaching the size limit of organometallic layers: Synthesis and characterization of highly ordered silver-thiolate lamellae with ultra-short chain lengths. Dalton Trans. 2016, 45, 18954–18966. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; De La Rama, L.P.; Efremov, M.Y.; Sutrisno, A.; Allen, L.H. Critical Size for Bulk-to-Discrete Transition in 2D Aliphatic Layers: Abrupt Size Effect Observed via Calorimetry and Solid-State 13C NMR. J. Phys. Chem. C 2017, 121, 13916–13929. [Google Scholar] [CrossRef]
- Schick, C.; Mathot, V. Fast Scanning Calorimetry; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Yi, F.; LaVana, D.A. Nanocalorimetry: Exploring materials faster and smaller. Appl. Phys. Rev. 2019, 6, 031302. [Google Scholar] [CrossRef]
- Monnier, X.; Napolitano, S.; Cangialosi, D. Direct observation of desorption of a melt of long polymer chains. Nat. Commun. 2020, 11, 4354. [Google Scholar] [CrossRef]
- Monnier, X.; Marina, S.; Lopez de Pariza, X.; Sardón, H.; Martin, J.; Cangialosi, D. Physical Aging Behavior of a Glassy Polyether. Polymers 2021, 13, 954. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Zhao, B.; Vlassak, J.J.; Schick, C. Reprint of: Nanocalorimetry: Door opened for in situ material characterization under extreme non-equilibrium conditions. Prog. Mater. Sci. 2021, 120, 100819. [Google Scholar] [CrossRef]
- Simon, C.; Gao, J.; Mao, Y.; Wilde, G. Fast scanning calorimetric study of nucleation rates and nucleation transitions of Au-Sn alloys. Scr. Mater. 2017, 139, 13–16. [Google Scholar] [CrossRef]
- Mileva, D.; Wang, J.; Gahleitner, M.; Jariyavidyanont, K.; Androsch, R. New Insights into Crystallization of Heterophasic Isotactic Polypropylene by Fast Scanning Chip Calorimetry. Polymers 2020, 12, 1683. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Peng, Q.; Milkereit, B.; Springer, A.; Liu, D.; Rettenmayr, M.; Schick, C.; Keßler, O. Nucleation behaviour and microstructure of single Al-Si12 powder particles rapidly solidified in a fast scanning calorimeter. J. Mater. Sci. 2021, 56, 12881–12897. [Google Scholar] [CrossRef]
- Zhang, R.; Du, M.; Zhuravlev, E.; Androsch, R.; Schick, C. Surface crystal nucleation and growth in poly (ε-caprolactone): Atomic force microscopy combined with fast scanning chip calorimetry. Polymers 2021, 13, 2008. [Google Scholar] [CrossRef]
- Lapuk, S.E.; Mukhametzyanov, T.A.; Schick, C.; Gerasimov, A.V. Crystallization kinetics and glass-forming ability of rapidly crystallizing drugs studied by Fast Scanning Calorimetry. Int. J. Pharm. 2021, 599, 120427. [Google Scholar] [CrossRef]
- Lee, D.; Zhao, B.; Perim, E.; Zhang, H.; Gong, P.; Gao, Y.; Liue, Y.; Toher, C.; Curtarolo, S.; Schroers, J.; et al. Crystallization behavior upon heating and cooling in Cu50Zr50 metallic glass thin films. Acta Mater. 2016, 121, 68–77. [Google Scholar] [CrossRef] [Green Version]
- Minakov, A.; Morikawa, J.; Zhuravlev, E.; Ryu, M.; Schick, C. Thermal contact conductance at melting and crystallization of metal micro-droplets. Mater. Res. Express 2020, 7, 066524. [Google Scholar] [CrossRef]
- Minakov, A.; Morikawa, J.; Ryu, M.; Zhuravlev, E.; Schick, C. Variations of interfacial thermal conductance at melting and crystallization of an indium micro-particle in contact with a solid. Mater. Des. 2021, 201, 109475. [Google Scholar] [CrossRef]
- Minakov, A.; Morikawa, J.; Zhuravlev, E.; Ryu, M.; van Herwaarden, A.W.; Schick, C. High-speed dynamics of temperature distribution in ultrafast (up to 10^8 K/s) chip-nanocalorimeters, measured by infrared thermography of high resolution. J. Appl. Phys. 2019, 125, 054501. [Google Scholar] [CrossRef]
- Minakov, A.A.; van Herwaarden, A.W.; Wien, W.; Wurm, A.; Schick, C. Advanced non-adiabatic ultrafast nanocalorimetry and superheating phenomenon in linear polymers. Thermochim. Acta 2007, 461, 96–106. [Google Scholar] [CrossRef]
- Minakov, A.A.; Schick, C. Ultrafast thermal processing and nanocalorimetry at heating and cooling rates up to 1 MK/s. Rev. Sci. Instr. 2007, 78, 073902–073910. [Google Scholar] [CrossRef] [PubMed]
- Minakov, A.A.; Schick, C. Dynamics of the temperature distribution in ultra-fast thin-film calorimeter sensors. Thermochim. Acta 2015, 603, 205–217. [Google Scholar] [CrossRef]
- Zhuravlev, E.; Schick, C. Fast scanning power compensated differential scanning nano-calorimeter: 1. The device. Thermochim. Acta 2010, 505, 1–13. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics 10: Physical Kinetics, 1st ed.; Pergamon Press: Oxford, UK; Frankfurt, Germany, 1981. [Google Scholar] [CrossRef]
- Kennard, E.H. Kinetic Theory of Gases. In With an Introduction to Statistical Mechanics; McGraw-Hill Book Company, Inc.: New York, NY, USA; London, UK, 1938. [Google Scholar] [CrossRef]
- Madhusudana, C.V. Thermal Contact Conductance. Mechanical Engineering Series, 2nd ed.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Liang, Z.; Evans, W.; Keblinski, P. Equilibrium and nonequilibrium molecular dynamics simulations of thermal conductance at solid-gas interfaces. Phys. Rev. E 2013, 87, 022119. [Google Scholar] [CrossRef] [PubMed]
- Vincenti, W.G.; Kruger, C.H. Introduction to Physical Gas Dynamics; Wiley: New York, NY, USA, 1965. [Google Scholar]
- Lide, D.R. Crc Handbook of Chemistry and Physics, 90th ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Zhang, Z.M. Nano/Microscale Heat Transfer, 2nd ed.; Springer International Publishing: Singapore, 2020; ISBN 978-3-030-45039-7. [Google Scholar] [CrossRef]
- Minakov, A.A. Temperature gradients in ultrafast thin-film nanocalorimetry. Thermochim. Acta 2019, 677, 32–41. [Google Scholar] [CrossRef]
- Jacquot, A.; Chen, G.; Scherrer, H.; Dauscher, A.; Lenoir, B. Improvements of on-membrane method for thin-film thermal conductivity and emissivity measurements. Sens. Actuators A Phys. 2005, 117, 203–210. [Google Scholar] [CrossRef]
- Van Zwol, P.J.; Vles, D.F.; Voorthuijzen, W.P.; Peter, M.; Vermeulen, H.; Van der Zande, W.J.; Sturm, J.M.; van der Kruijs, R.W.E.; Bijkerk, F. Emissivity of freestanding membranes with thin metal coatings. J. Appl. Phys. 2015, 118, 213107. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics 6: Fluid Mechanics, 2nd ed.; Butterworth–Heinemann: Oxford, UK, 2000. [Google Scholar]
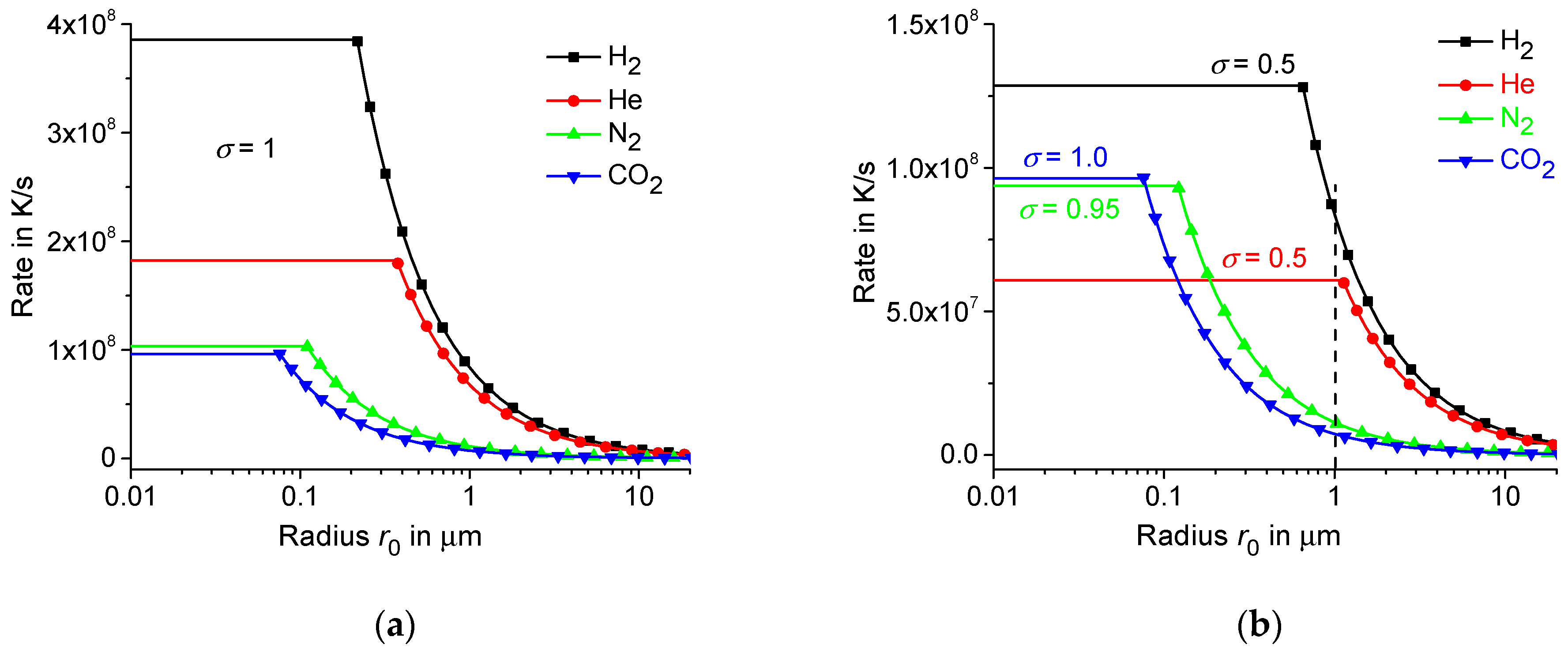

| Gas | Number of Degrees of Freedom of Gas Molecules | Mean Free Path of Gas Molecules | Temperature Jump Distance | Thermal Conductivity | Maximum Possible Parameter | Maximum Interfacial Thermal Conductance | Maximum Cooling Rate |
|---|---|---|---|---|---|---|---|
| Dimensionless | μm | μm | W/m·K | MW/m2K | MW/m2K | K/s | |
| H2 | 5 | 0.126 | 0.21 | 0.192 | 0.90 | 0.90 | 3.9 · 108 |
| He | 3 | 0.200 | 0.38 | 0.156 | 0.41 | 0.42 | 1.8 · 108 |
| N2 | 5 | 0.068 | 0.11 | 0.026 | 0.24 | 0.24 | 1.04 · 108 |
| CO2 | 6 | 0.045 | 0.07 | 0.017 | 0.22 | 0.22 | 0.96 · 108 |
| Gas | Thermal Accom-Modation Coefficient | Mean Free Path of Gas Molecules | Temperature Jump Distance | Thermal Conductivity | Maximum Possible Parameter | Maximum Interfacial Thermal Conductance | Maximum Cooling Rate |
|---|---|---|---|---|---|---|---|
| Dimensionless | μm | μm | W/m·K | MW/m2K | MW/m2K | K/s | |
| H2 | 0.7 | 0.126 | 0.40 | 0.192 | 0.48 | 0.48 | 2.1 · 108 |
| H2 | 0.5 | 0.126 | 0.64 | 0.192 | 0.30 | 0.30 | 1.3 · 108 |
| N2 | 0.95 | 0.068 | 0.12 | 0.026 | 0.21 | 0.22 | 0.9 · 108 |
| He | 0.5 | 0.200 | 1.13 | 0.156 | 0.14 | 0.14 | 0.6 · 108 |
| Gas | Mean Free Path | Thermal Diffusivity | Thermal Diffusion Time | Average Velocity of Gas Molecules | Average Time between Collisions |
|---|---|---|---|---|---|
| μm | m2/s | s | km/s | s | |
| H2 | 0.126 | 1.6 · 10−4 | 6.2 · 10−9 | 1.78 | 0.7 · 10−10 |
| He | 0.200 | 1.9 · 10−4 | 5.3 · 10−9 | 1.26 | 1.6 · 10−10 |
| N2 | 0.068 | 2.2 · 10−5 | 45 · 10−9 | 0.476 | 1.4 · 10−10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minakov, A.A.; Schick, C. Maximum Possible Cooling Rate in Ultrafast Chip Nanocalorimetry: Fundamental Limitations Due to Thermal Resistance at the Membrane/Gas Interface. Appl. Sci. 2021, 11, 8224. https://doi.org/10.3390/app11178224
Minakov AA, Schick C. Maximum Possible Cooling Rate in Ultrafast Chip Nanocalorimetry: Fundamental Limitations Due to Thermal Resistance at the Membrane/Gas Interface. Applied Sciences. 2021; 11(17):8224. https://doi.org/10.3390/app11178224
Chicago/Turabian StyleMinakov, Alexander A., and Christoph Schick. 2021. "Maximum Possible Cooling Rate in Ultrafast Chip Nanocalorimetry: Fundamental Limitations Due to Thermal Resistance at the Membrane/Gas Interface" Applied Sciences 11, no. 17: 8224. https://doi.org/10.3390/app11178224








