Next Article in Journal
Analyzing the Scientific Evolution of the Sustainable Development Goals
Previous Article in Journal
Fabrication of Circadian Light Meter with Non-Periodic Optical Filters to Evaluate the Non-Visual Effects of Light on Humans
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 11
Issue 18
10.3390/app11188285
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimation of Distances in 3D by Orthodontists Using Digital Models

by
Masrour Makaremi
1,2,* and
Bernard N’Kaoua
2
1
Handicap Activity Cognition Health, Bordeaux Population Health (BPH) U1219, Université de Bordeaux, 146 rue Léo Saignat, 33076 Bordeaux, France
2
Dentofacial Orthopedics Department, UFR des Sciences Odontologiques, 146 rue Léo Saignat, 33076 Bordeaux, France
*
Author to whom correspondence should be addressed.
Appl. Sci. 2021, 11(18), 8285; https://doi.org/10.3390/app11188285
Submission received: 13 June 2021 / Revised: 1 September 2021 / Accepted: 2 September 2021 / Published: 7 September 2021
(This article belongs to the Topic Advances in Dental Biomaterials and Oral Tissues Engineering)
Browse Figures
Versions Notes

Abstract

:
In the field of orthodontics, digital dental arch models are increasingly replacing plaster models in orthodontic diagnostics. This change in interface from physical plaster models to digital image-based models raises the question of how orthodontists interpret intra- and inter-arch relationships from an image on a screen. In particular, the issue of the accuracy of the distances estimated on numerical models is crucial since the estimation of distances is the basis of the therapeutic decision-making process. Studies have shown that distances were well estimated on plaster models, but no study has verified this point on numerical models. This is the question that our study addresses. The experimental protocol consisted of collecting estimates of measurements made by orthodontists using digital models. The reliability of these measurements was then assessed by comparing them to the actual physical distances. We asked 31 orthodontists (19 women and 12 men; an average age of 37 years) to generate 3D model-based measurements of seven different elements: mandibular congestion, the maxillary intermolar distance, Spee’s curve, 16/26 symmetry, the right canine class, overbite, and overjet. These values were then compared to the actual measurements calculated using Insignia® software (ORMCO Corporation: Brea, CA, USA), using single sample t-tests. This test makes it possible to compare a distance estimated by the participants with a reference value, which corresponds here to the real distance. The results indicate that, overall, the distance estimates made on the 3D models differ significantly from the actual distances measured using the Insignia® software. This was particularly so for mandibular crowding (test value = 0; t (30) = 10.74; p ≤ 0.01), test value = 1; t (30) = 6.23; p ≤ 0.01). Although no study has focused on distance estimation on numerical models in the field of orthodontics, our results agree with the conclusions of studies showing that distances are not estimated in the same way in real environments and virtual environments. Additional studies will make it possible to identify more clearly the parameters (individual factors, equipment, etc.), which make it possible to improve the estimation of distances in the practice of orthodontics. In any case, these studies are necessary to improve the training of future practitioners in the use of virtual models for decision-making and to support them in the digital transition.

1. Introduction

1.1. VR (Virtual Reality) and Medical Applications

For Ellis [1], VR is a human-machine interface that simulates a realistic environment, allowing the participants to interact with it. Ouramdane et al. [2] consider VR to be a technology that immerses one or more users in an artificial world representing a real or imaginary environment and which allows users to be actors capable of changing the properties of the environment and to interact with the various entities that comprise the simulated universe.
VR was initially considered to be a new gaming technology [3]. It has, however, proven to be useful in many areas such as commerce, education, the military, and architecture, among others. Today, medicine is one of the most important areas of application of virtual reality [4], for example, for diagnosis or therapeutic planning. Indeed, advances in medical imaging and advances in computing power have made simulated images much more realistic and much faster to generate, thus allowing the reconstruction of three-dimensional anatomical entities and offering practitioners the possibility to interact directly with this imagery [4].
Many fields of health are concerned, such as, for example, the treatment of a painful chronic handicap. Techniques using progressive motor imagery and VR can help manage the fear of moving or help make a movement that would normally be too painful [5]. VR is also used to treat anxiety disorders such as phobias [6], where an interactive space is created in which the patient is confronted with his situation or his phobic object. In addition, in the field of surgery, a remote control makes it possible to act on a virtual model by means of a virtual robot: the actions are first carried out in the virtual environment before being transmitted to the operator performing the operation, thereby allowing the procedure to be tested before being performed on the patient [7]. There are also various applications for the learning and training of medical personnel based on surgical simulators and software exploration of the human body [8].

1.2. VR in Orthopedic Dentofacial Orthodontics

The use of VR has also seen developments in the fields of orthopedic dento-facial orthodontics and orthognathic surgery. It played a major role in the initial and continuing training of practitioners. Indeed, the 3D acquisition of the different tissues of the head and neck provides a realistic platform for training in facial and dento-facial orthopedics [9]. For example, a new approach to virtual reality has been introduced and validated for cephalometric assessment by lateral view teleradiology [10]. A series of case studies using haptically activated computer-assisted cephalometry was performed. The authors showed that by providing tactile sensory feedback, errors in the cephalometric analysis were reduced, and tracking became more feasible and more intuitive. Another example is the use of the Voxel-Man simulator [11] in virtual apicoectomy, which revealed that, out of 53 medical dentistry students who performed a virtual apicoectomy, 51 had a positive evaluation of the impact of the simulation virtual as an additional modality in dental education.
Among clinical applications, techniques have been developed to obtain data on the soft and hard tissues of the maxillofacial area in order to produce virtual 3D models for analysis and surgical planning [12]. These techniques have overcome the disadvantages of 2D photographs and X-rays. Four main types of 3D imaging systems have been used to capture dental and orofacial structures, in particular conical beam tomography or CBCT, laser scanners, structured light scanners, and stereophotogrammetry [13].
Among these applications, one of the most important, in terms of impact and development, is computer-assisted 3D modeling of dental arches. Indeed, dental arch models are very useful for orthodontists [14]. They are an essential part of diagnostic information and are used to document the original condition, to design and measure the effect of treatment. They reduce the difficulty of 3D visualization of dental axes and positions during the clinical examination. Dental arch models have a central role in orthodontic practices around the world.
Until recently, plaster casts obtained from an imprint of the dental arches (Figure 1) were the only means to generate three-dimensional models to accurately represent the dental arches and malocclusions. 3D digital models have recently become a dematerialized alternative [15].
These models are electronic recordings of teeth and of the occlusion of a patient obtained with an intra-oral optical camera (Figure 1). The optical imprint of the dental arches is treated by software that draws a 3D projection, obtained from stereo-lithography (STL) files, on the computer screen. The features of the software allow the observer to change the view and to pivot or incline the image of the model. The software also allows measurement and storage of the circumferences of the arch, the diameter of the teeth, etc. Digital models have the advantage of electronic storage and remote access from multiple locations, thereby reducing the risk of loss or damage to the models. This VR technology can be considered to be part of VR as it represents two of its key characteristics:
−
Manipulate the imprints virtually on the screen. There is, therefore, a real-time interaction, which allows the user to modify the properties of the environment with which he interacts [11,16].
−
Deploy, thanks to the practitioner’s diagnosis and therapeutic projection, a cognitive activity in space created digitally by 3D models (which is another key element of VR) [2].
In these 3D models, the virtual environment is not immersive because the models are viewed on a computer screen. However, there are applications that allow you to create an immersive environment using a head-mounted virtual reality screen to view models [17]. Interaction with digital work models is performed using a mouse, most often a 2D mouse, although it is also possible to use a 3D mouse. Generally, 3D digital models of dental arches are, therefore, non-immersive with a low degree of interaction.

1.3. VR and the Evaluation of Distances

Although the use of digital models has increased greatly, there are still a number of unresolved questions when it comes to comparisons with real-life models. In particular, to ensure that the applications developed in Virtual Reality are efficient, it is important that the spatial properties of the virtual environment are perceived with precision. This finding is even more important when the actions performed in VR are supposed to be transferred to the real world. If the actions carried out in VR require recalibration in the real environment, this will lead to an increase in training and cost [18].
In this framework, research indicates that distance [19,20,21,22,23,24,25] and size [18,26,27,28] are underperceived in VR, in contrast to relatively accurate perception in the real world. Waller and Richardson [29] realized a review of 14 independent studies that examined distance estimation in immersive virtual environments [23,30,31,32,33,34,35,36,37,38,39,40,41]. They showed that the estimation of distances in immersive VEs were, on average, only 71% ± 8.2 of the modeled distance.
As pointed out by Waller and Richardson [29], although the causes of distance compression in immersive VEs were not fully understood [39,42], several recent investigations documented experimental manipulations that can attenuate or alleviate it. These manipulations include (a) asking users to estimate distances in a known familiar environment [32]; but see [23], (b) presenting the environment on a large projection screen instead of an HMD [35], (c) providing users with explicit feedback about their distance errors [36], and (d) providing users a brief period of interaction with the environment before having them make distance judgments [34,43].
Other authors show that the task used can eliminate this effect of compressing distances in VR. For example, Ref. [44] used an affordance judgment task and observed conservative answers or overestimation in both real and virtual environments. The methodology used by these authors involves a verbal indication that a particular action can or cannot be performed in a viewed environment. The results show that this type of VR task, which consists in deciding whether elements present in the environment are relevant to carry out a given action, gives estimates much closer to reality than the simpler and more passive tasks of size or distance estimate.
Indeed, in the study of [45], a task was carried out in two environments: a poor cue one with limited background cues and a rich cue one with textured background surfaces. The results show that the richness of the environment improves the estimation of distances and size of objects in a VR task.
All these studies show that the estimation of distances in a virtual environment is a complex problem, which depends on many parameters such as the more or less immersive nature of the environment, the familiarity with the environment, the more or less realistic character of the presented objects, the type of task to be performed (passive or actually actions to be performed), etc.
As we have indicated, in the medical field of orthodontics, distance estimation is at the center of the diagnosis and therapeutic follow-up of patients. The accuracy of these estimates is, therefore, a crucial issue from a quality-of-care perspective. Song et al. [46] published a study in which 69 orthodontists had to estimate, from 108 plaster molds, different variables, which included all the variables usually estimated by an orthodontist. The values were compared to the actual values measured with calipers. The results obtained revealed a statistically significant correlation between the objective measurements and the estimations carried out by the orthodontists. However, very few studies were carried out on virtual models, which are now widely used by professionals.

1.4. Objective of the Study

As we have seen, in the field of orthodontics, the digital transition means that professionals make therapeutic decisions by making distance estimations on digital models. However, no study has focused on the relevance of the estimates made, and in particular on the difference between estimated distances and actual distances.
In this context, the objective of our study was to use the methodology of Song et al. [46] (which these authors implemented on plaster models) to assess the relevance of estimating distances (intra and inter-arcs) using digital models. The experimental protocol consisted of collecting estimates of measurements made by orthodontists on digital models, then assessing the reliability of these measurements by comparing them to real distances.

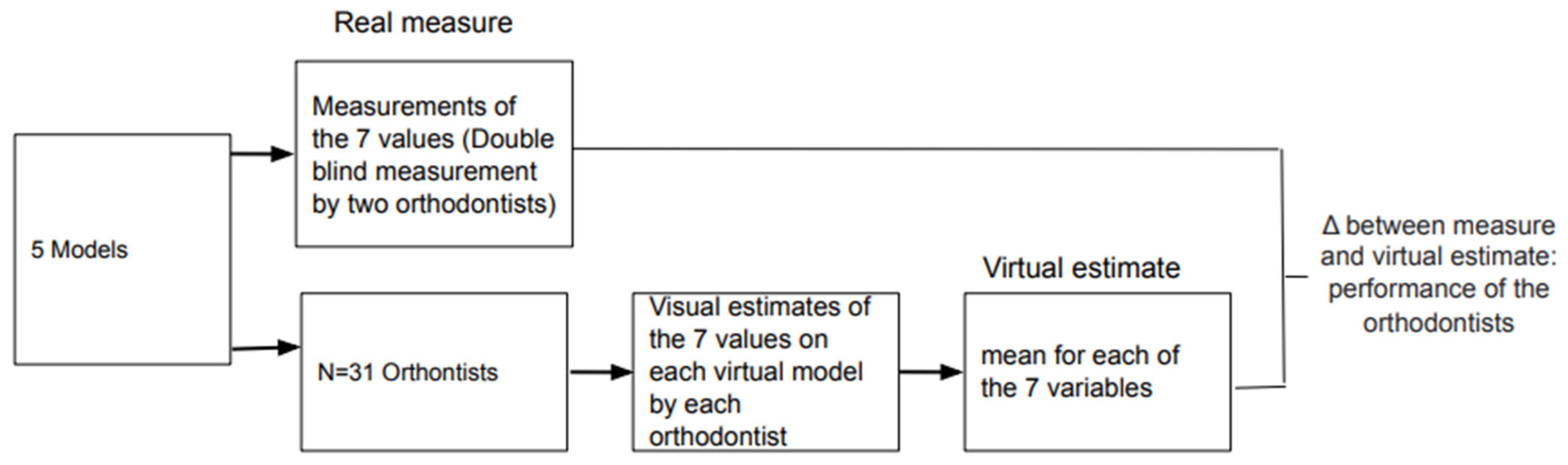
2. Method

2.1. Participants

The measurements were estimated by 31 orthodontists whose characteristics were as follows: all the practitioners began their specialization in dento-facial orthopedics and orthodontics in French universities. The distribution of the sample by sex was 19 women and 12 men, the average age of the participants was 37 years (±3.7). The number of years of exercise of the profession was distributed as follows: 0 to 5 years of professional practice (42%), 5 to 10 years (32%), and more than 10 years (26%). The objective of this research was explained to the practitioners, who gave their consent. The participants were recruited by an email sent to all orthodontic practices in the region. The participation was voluntary, and the experimentation was carried out in the participant’s office.

2.2. Materials

The estimations of distances were carried out on 5 3D digital models (obtained with Insignia® software), derived from 5 clinical cases (Figure 2). The choice of these 5 cases (also used in the study by Song et al.) was based on the objective of allowing the practitioners to make estimations on a varied panel of orthodontic malocclusions comprising all of the types of dental-maxillary dysmorphias in the three dimensions of space. The characteristics of the different malocclusions are reported Table 1.
The digital models were displayed on the same computer, by the same operator, and under the same conditions for each of the 31 practitioners. The participants had the option to change the orientation of the view of the model. The collection of distance estimates was carried out as follows: after observing the virtual models of each clinical case on the screen, the practitioner verbally gives their distance estimates for each of the 7 variables to the operator, who writes them down in a table.
The variables to be estimated:
For each of the models, each practitioner had to estimate 7 quantifiable variables. These estimates were carried out on the 5 virtual models mentioned (5 × 7 = 35 estimates by orthodontist) without the possibility of making direct measurements (they were only estimates). The variables selected were similar to those of the study by Song et al. [46]:
These variables were the following (Figure 3):
−
Crowding of the mandibular arch: the amount of space required for proper alignment of the teeth in the arch (volumetric reconstitution, intra-arch measurement);
−
Spee’s curve—the curve formed by the projection in a sagittal plane of the buccal cusps of the mandibular teeth (vertical dimension, intra-arch measurement);
−
Antero-posterior symmetry of the first permanent maxillary molars (teeth 16 and 26) while taking their mesial side as a reference (sagittal dimension, intra-arch measurement);
−
Inter-molar distance of 16/26 (horizontal dimension, intra-arch measurement): distance separating the mesiobuccal cusp of the first permanent maxillary molars (teeth 16 and 26);
−
Right canine class according to Angle’s classification [47] based on the mesiodistal relationship of the teeth (sagittal dimension, inter-arch measurement);
−
Overjet of 11/41—the gap as assessed on to the occlusal plane between the buccal side of the mandibular incisors and the occlusal edges of the central maxillary incisors (sagittal dimension, inter-arch measurement);
−
Alignment of 11/41—Alignment of the mandibular incisors by their opposing maxillaries (vertical dimension, inter-arch measurement).
The question that we wanted to address was the performance of the orthodontist’s estimate compared to the measurements made with software whose reliability in this regard has been demonstrated and which can, therefore, serve as a reference. Indeed, the reliability and precision of the measurements made using different software have already been demonstrated [47,48,49]. The actual measurements were calculated for each case by the same operator using the Insignia® software (ORMCO Corporation: Brea, CA, USA) and then verified by a second operator.
For each of the 7 variables, the difference in the absolute value between the estimation of the measurement by the practitioner and the measurement of the variable carried using the Insignia® software was determined.
A flowchart of the procedure is shown in Figure 4.

2.3. Statistical Analyses

As the objective was to compare the estimates made by orthodontists with the measurements made with the Insignia® software, we performed a single sample t-test. This test is generally used to compare the average of a sample for a specific variable (here, the average of the orthodontist’s estimates) with a population average or with a theoretical reference average (here, the measurement carried out by the Insignia® software).
For each estimated variable (i.e., the 7 variables presented above), the difference between the estimate made by the practitioners and the actual distance was tested. The actual distance was reduced to 0 (since the estimated measurements have been subtracted from the actual measurements). For each variable measured, the difference between the estimated measurements and the real distance (here reduced to 0) was assessed using a single sample t-test. First, the theoretical value of 0 was used. If the t-test was not significant, it meant that the estimated value was not significantly different from the actual value. If the t-test was significant, it meant that the estimated value was significantly different from the actual value. Secondly, we performed the same analysis using a reference value equal to 1 (i.e., 1 cm more than the actual value equal to 0). Again, if the t-test was significant, it meant that the estimation error made by the practitioner was greater than 1 cm.

3. Results

The results obtained for each model are reported in Table 2.
On the basis of the single t-test results, the 7 variables fell into 3 groups: (1) variables for which the estimates were not significantly different from the real values; in this case, the estimated value was not significantly different from the actual value; (2) variables for which the estimates were significantly different from the actual value 0 but not from the value 1; in this case, the estimation error was greater than 0 but less than 1 cm; (3) variables for which the estimation error was significantly different from the value 1; in this case, the estimation error was greater than 1 cm (Table 3). Table 3 (power column) also shows the power of each result for a β risk of 20%. The column values indicate the minimum sample size for the conclusion at H0 to be strong enough. The column values indicate the minimum sample size for the conclusion at H0 to be strong enough. This power analysis show that the size samples were sufficient for all the significant results, with the exception of the right canine class variable for a theoretical value of 0 (but for this same variable, the size sample is sufficient for a value theoretical of 1).
−
Variables for which the estimates were not significantly different from the real values. This was the case for the following 3 variables:
The overjet (t (30) = −1.60; p = 0.11);
The curve of Spee (t (30) = −1.33; p = 0.19);
The inter-molar distance (t (29) = 0.39; p = 0.69).
−
Variables for which the estimates were significantly different from the actual value 0 but not from the value 1. This was the case for the following 3 variables:
The 16/26 symmetry: value = 0 (t (30) = −9.65; p ≤ 0.01), but with a test value = 1 (t (30) = −0.66; p = 0.51);
The over bite: test value = 0 (t (30) = −5.40; p ≤ 0.01), but with a test value = 1 (t (30) = 0.64; p = 0.52);
The right canine class: test value = 0 (t (30) = 3.19; p = ≤ 0.01), but with a test value = 1 (t (30) = −0.51; p = 0.61).
−
Variables for which the estimation error was significantly different from the value 1. This was the case only for the mandibular discrepancy variable: test value = 0 (t (30) = −10.74; p ≤ 0.01), test value = 1 (t (30) = 6.23; p ≤ 0.01).

4. Discussion

The objective of our study was to find out if, for seven variables of interest, the estimation of distances carried out on numerical models was significantly different (or not) from the real distance (here, reduced to the value 0). For the variables whose estimates were significantly different from the real distance (comparison between the measurements carried out by the practitioners and the theoretical mean of 0), we also checked whether this difference between the estimates and the real value was greater than 1 cm (comparison between the measurements made by practitioners and the theoretical average of 1).
Of the seven variables studied, three were associated with distances estimated to be significantly greater than the real distance, and for one variable, the difference was greater than 1 cm.
These results question the reliability of the use of numerical models for decision-making, in particular in borderline cases. The relevant elements for this discussion are the difference in the estimation of distances between virtual and real models, the way in which our results can be discussed in the light of the work on the estimation of distances in virtual environments, and the perspectives of this study as part of further investigations.
The results obtained in the study by Song et al. [46] on real models revealed a statistically significant correlation between the objective measurements and the estimates made by orthodontists for all the variables (the same variables as those used in our study).
Thus, with only the virtual model (i.e., other than a situation where the practitioner can manipulate real physical models), the estimate was less reliable for four of the seven variables, in particular the estimate of the mandibular crowding.
The results of our study are in keeping with the various studies in the literature regarding the estimation of distances in a digital environment in terms of the presence of bias in the estimation of distances in a virtual environment [25,50,51,52,53].
In terms of crowding of the mandibular arch, which is the amount of space required for proper alignment of the teeth on the arch, this is the variable estimated in the least precise way. One of the explanations could be the difficulty for the practitioner to perform a three-dimensional mental reconstruction from the virtual model to estimate the space required for aligning the teeth from the malposed teeth. It is of particular interest to note that it was in case no. 5 that the accuracy was less good, that is to say, where the estimation of the crowding requires reconstitution of the shape of the arch based on the initial malpositions that were substantial before estimation of the lack of space for alignment of the teeth on the arch. For this particular case, the performance of the practitioners was particularly poor, with a relatively large standard deviation (σ = 7.47), while the value of the variable was low (Table 2). The large standard deviation between the estimated value and the actual value in case no. 5 can be explained by the study by [54], who showed the difficulty of maintaining attention and, therefore, the efficacy of the process beyond a certain degree of complexity of a 3D image. This appears to be illustrated by the difficulty of the estimation of the crowding.
Future work should also study the role of calibration. This is a very important point. The contribution of calibration to visual perception in VR has been established by numerous works [43,55,56]. For example, Ref. [56] showed the effects of calibration to visual and proprioceptive information on near filed distance judgments in 3D user interface. One method of calibration that could be experienced would allow viewing the error that they made on the different estimation of distance, and they allow the participant to correct the response. If this work were conclusive, the calibration training programs could have a positive impact on the performance of practitioners. Studies on these different points will allow the development of educational materials to employ a wider range of stimuli to support the training of practitioners in the use of virtual models for decision-making and also to optimize the interaction of the practitioner with the virtual environment. For example, one image with a particular mandibular discrepancy can be transformed to create a number of stimuli with a continuum of different mandibular discrepancies.
Another aspect of estimating values in a virtual environment that needs to be explored in our study is the mental workload necessary to estimate distances in a virtual environment [57] and, therefore, in this context, on 3D digital orthodontic models. According to the experience of users and practitioners, the mental workload required for the analysis of virtual models seems to be greater than that required for physical models. This increase in mental load accentuated the difficulty of transition between real models and virtual models. This feeling is widely shared (interview with the participants in our study after the experiment) and needs to be documented.
In this context, the main limitations of our study are, therefore, that, as we have just seen, we did not measure the mental load associated with the estimates to be made, but also, we did not take into account the number of years of professional experience (evaluation of the effect of expertise on the estimation of distances), and we did not compare the estimates made on the numerical models with the estimates made on the same plaster models (our comparison focused on the real distance and not on the estimate made on plaster models). The future investigations, which we are in the process of carrying out, are intended to answer all of these questions.
The future investigations, which we are in the process of carrying out, are intended to answer these main questions.
In addition, the difficulties related to digital models also appear to be due to the fact that practitioners handle the actual models to estimate distances. As a result, the transition of real models to virtual models involves a paradigm shift, with a loss of haptic range for the practitioner who can no longer manipulate the models with his hands. This observation may be linked to the different studies showing dissociation of neuronal routes related to the seizure or perception of objects [58,59,60,61]. Another interesting perspective would then be to study the estimation of distances on digital models by proposing to practitioners a more realistic manipulation device than that used in our study (computer mouse), such as a glove or an articulated arm.

5. Conclusions

3D digital models of dental arches can be considered a non-immersive virtual reality characterized by a low degree of interaction. These models are now widely used to carry out diagnoses, but the estimation of distances by the user (orthodontist) carried out on this type of digital model, and which constitutes a determining factor in the therapeutic decision-making, had not yet been studied.
It is within this framework that we conducted our study. Our results of distance estimations on numerical models showed that four of the seven variables tested were associated with a lack of precision in the estimation of distances, the size of the mandibular arch being the least well-estimated variable.
Although no studies have been carried out in the field of orthodontia, the lack of precision in the estimation of measurements made on virtual 3D models corresponds to what has been described in studies relating to distance estimations in digital environments.
Other studies in preparation will be necessary to understand better the variables (related to professionals, equipment, type of models, etc.) likely to affect the estimation of distances and, therefore, the therapeutic decision-making. Such studies are fundamental in particular for improving the training of professionals in the use of new digital tools. These objectives can be best addressed through a multidisciplinary approach [62], in order to help keep the expertise and perception of the practitioner at the center of decision-making, thus ensuring a successful digital transition.

Author Contributions

Conceptualization, M.M. and B.N.; methodology, M.M.; software, M.M.; validation, M.M. and B.N.; formal analysis, B.N.; investigation, M.M.; resources, M.M.; data curation, M.M.; writing—original draft preparation, M.M. and B.N.; writing—review and editing, B.N.; visualization, M.M.; supervision, B.N.; project administration, M.M.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Institutional Ethics Committee of University of Bordeaux.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The study data can be obtained by email request to the authors.

Acknowledgments

Charpentier Valentine; Marcy Benoit; Gibaudon Lionel.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Stephen, R.E. What are virtual environments? IEEE Comput. Graph. Appl. 1994, 1, 17–22. [Google Scholar]
  2. Ouramdane, N.; Otmane, S.; Mallem, M. Interaction 3D en Réalité Virtuelle-Etat de l’art. Tech. Sci. Inform. 2009, 28, 1017–1049. [Google Scholar] [CrossRef]
  3. Engler, C.E. Affordable VR by 1994. Comput. Gaming World 1992, 1, 80–82. [Google Scholar]
  4. Li, L.; Yu, F.; Shi, D.; Shi, J.; Tian, Z.; Yang, J.; Wang, X.; Jiang, Q. Application of virtual reality technology in clinical medicine. Am. J. Transl. Res. 2017, 9, 3867–3880. [Google Scholar] [PubMed]
  5. Baldominos, A.; Saez, Y.; del Pozo, C.G. An approach to physical rehabilitation using state-of-the-art virtual reality and motion tracking technologies. Procedia Comput. Sci. 2015, 64, 10–16. [Google Scholar] [CrossRef] [Green Version]
  6. Li, A.; Montaño, Z.; Chen, V.J.; Gold, J.I. Virtual reality and pain management: Current trends and future directions. Pain Manag. 2011, 1, 147–157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  7. Satava, R.M.; Jones, S.B. Virtual environments for medical training and education. Presence Teleoperators Virtual Environ. 1997, 6, 139–146. [Google Scholar] [CrossRef]
  8. Ackerman, M.J. The visible human project. Proc. IEEE 1998, 86, 504–511. [Google Scholar] [CrossRef]
  9. Ayoub, A.; Pulijala, Y. The application of virtual reality and augmented reality in Oral & Maxillofacial Surgery. BMC Oral. Health 2019, 19, 1–8. [Google Scholar]
  10. Medellín-Castillo, H.I.; Govea-Valladares, E.H.; Pérez-Guerrero, C.N.; Gil-Valladares, J.; Lim, T.; Ritchie, J.M. The evaluation of a novel haptic-enabled virtual reality approach for computer-aided cephalometry. Comput. Methods Programs Biomed. 2016, 130, 46–53. [Google Scholar] [CrossRef]
  11. Wu, F.; Chen, X.; Lin, Y.; Wang, C.; Wang, X.; Shen, G.; Qin, J.; Heng, P.-A. A virtual training system for maxillofacial surgery using advanced haptic feedback and immersive workbench. Int. J. Med Robot. Comput. Assist. Surg. 2014, 10, 78–87. [Google Scholar] [CrossRef]
  12. Kwon, H.B.; Park, Y.S.; Han, J.S. Augmented reality in dentistry: A current perspective. Acta Odontol. Scand. 2018, 76, 497–503. [Google Scholar] [CrossRef] [PubMed]
  13. Ayoub, A.F.; Xiao, Y.; Khambay, B.; Siebert, J.P.; Hadley, D. Towards building a photo-realistic virtual human face for craniomaxillofacial diagnosis and treatment planning. Int. J. Oral Maxillofac. Surg. 2007, 36, 423–428. [Google Scholar] [CrossRef] [PubMed]
  14. Marcel, T.J. Three-dimensional on-screen virtual models. Am. J. Orthod. Dentofac. Orthop. 2001, 119, 666–668. [Google Scholar] [CrossRef] [PubMed]
  15. Kravitz, N.D.; Groth, C.; Jones, P.E.; Graham, J.W.; Redmond, W.R. Intraoral digital scanners. J. Clin. Orthod. 2014, 48, 337–347. [Google Scholar]
  16. Lanier, J. A Vintage Virtual Reality Interview, 1988. In Interview by Adam Heilbrun of Jaron Lanier, Published; 1988; Available online: https://philpapers.org/rec/LANAVV (accessed on 1 September 2021).
  17. TootyVR—Application de VR Dentaire. 2020. Available online: https://www.tootyvr.com/ (accessed on 1 September 2021).
  18. Siegel, Z.D.; Kelly, J.W. Walking through a virtual environment improves perceived size within and beyond the walked space. Atten. Percept. Psychophys. 2017, 79, 39–44. [Google Scholar] [CrossRef]
  19. El Jamiy, F.; Marsh, R. Distance estimation in virtual reality and augmented reality: A survey. In Proceedings of the 2019 IEEE International Conference on Electro Information Technology (EIT), Brookings, SD, USA, 20–22 May 2019; IEEE: New York, NY, USA, 2019; pp. 063–068. [Google Scholar]
  20. Swan, J.E.; Kuparinen, L.; Rapson, S.; Sandor, C. Visually perceived distance judgments: Tablet-based augmented reality versus the real world. Int. J. Hum.-Comput. Interact. 2017, 33, 576–591. [Google Scholar] [CrossRef]
  21. Bodenheimer, B.; Meng, J.; Wu, H.; Narasimham, G.; Rump, B.; McNamara, T.P.; Carr, T.H.; Rieser, J.J. Distance estimation in virtual and real environments using bisection. In Proceedings of the 4th Symposium on Applied Perception in Graphics and Visualization, Tubingen, Germany, 25–27 July 2007; pp. 35–40. [Google Scholar]
  22. Kuhl, S.A.; Thompson, W.B.; Creem-Regehr, S.H. HMD calibration and its effects on distance judgments. ACM Trans. Appl. Percept. 2009, 6, 1–20. [Google Scholar] [CrossRef]
  23. Messing, R.; Durgin, F.H. Distance perception and the visual horizon in head-mounted displays. ACM Trans. Appl. Percept. 2005, 2, 234–250. [Google Scholar] [CrossRef]
  24. Steinicke, F.; Bruder, G.; Hinrichs, K.; Lappe, M.; Ries, B.; Interrante, V. Transitional environments enhance distance perception in immersive virtual reality systems. In Proceedings of the 6th Symposium on Applied Perception in Graphics and Visualization, Chania, Greece, 30 September–2 October 2009; pp. 19–26. [Google Scholar]
  25. Ziemer, C.J.; Plumert, J.M.; Cremer, J.F.; Kearney, J.K. Estimating distance in real and virtual environments: Does order make a difference? Atten. Percept. Psychophys. 2009, 71, 1095–1106. [Google Scholar] [CrossRef] [PubMed]
  26. Kelly, J.W.; Donaldson, L.S.; Sjolund, L.A.; Freiberg, J.B. More than just perception-action recalibration: Walking through a virtual environment causes rescaling of perceived space. Atten. Percept. Psychophys. 2013, 75, 1473–1485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Kunz, B.R.; Creem-Regehr, S.H.; Thompson, W.B. Does perceptual-motor calibration generalize across two different forms of locomotion? Investigations of walking and wheelchairs. PLoS ONE 2013, 8, e54446. [Google Scholar] [CrossRef] [Green Version]
  28. Stefanucci, J.K.; Creem-Regehr, S.H.; Thompson, W.B.; Lessard, D.A.; Geuss, M.N. Evaluating the accuracy of size perception on screen-based displays: Displayed objects appear smaller than real objects. J. Exp. Psychol. Appl. 2015, 21, 215. [Google Scholar] [CrossRef] [PubMed]
  29. Waller, D.; Richardson, A.R. Correcting distance estimates by interacting with immersive virtual environments: Effects of task and available sensory information. J. Exp. Psychol. Appl. 2008, 14, 61. [Google Scholar] [CrossRef] [PubMed]
  30. Durgin, F.H.; Gigone, K.; Scott, R. Perception of visual speed while moving. J. Exp. Psychol. Hum. Percept. Perform. 2005, 31, 339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  31. Henry, D.; Furness, T. Spatial perception in virtual environments: Evaluating an architectural application. In Proceedings of the IEEE Virtual Reality Annual International Symposium, Seattle, WA, USA, 18–22 September 1993; pp. 33–40. [Google Scholar]
  32. Interrante, V.; Ries, B.; Anderson, L. Distance perception in immersive virtual environments, revisited. In Proceedings of the IEEE Virtual Reality Conference (VR 2006), Alexandria, VA, USA, 25–29 March 2006; pp. 3–10. [Google Scholar]
  33. Knapp, J.M.; Loomis, J.M. Limited field of view of head-mounted displays is not the cause of distance underestimation in virtual environments. Presence Teleoperators Virtual Environ. 2004, 13, 572–577. [Google Scholar] [CrossRef]
  34. Mohler, B.J.; Creem-Regehr, S.H.; Thompson, W.B. The influence of feedback on egocentric distance judgments in real and virtual environments. In Proceedings of the 3rd Symposium on Applied Perception in Graphics and Visualization, Boston, MA, USA, 28–29 July 2006; pp. 9–14. [Google Scholar]
  35. Plumert, J.M.; Kearney, J.K.; Cremer, J.F.; Recker, K. Distance perception in real and virtual environments. ACM Trans. Appl. Percept. 2005, 2, 216–233. [Google Scholar] [CrossRef]
  36. Richardson, A.R.; Waller, D. The effect of feedback training on distance estimation in virtual environments. Appl. Cogn. Psychol. 2005, 19, 1089–1108. [Google Scholar] [CrossRef] [Green Version]
  37. Sahm, C.S.; Creem-Regehr, S.H.; Thompson, W.B.; Willemsen, P. Throwing versus walking as indicators of distance perception in similar real and virtual environments. ACM Trans. Appl. Percept. 2005, 2, 35–45. [Google Scholar] [CrossRef]
  38. Sinai, M.J.; Krebs, W.K.; Darken, R.P.; Rowland, J.H.; McCarley, J.S. Egocentric distance perception in a virutal environment using a perceptual matching task. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Los Angeles, CA, USA, 1 September 1999; SAGE Publications: Los Angeles, CA, USA, 1999; Volume 43, pp. 1256–1260. [Google Scholar]
  39. Thompson, W.B.; Willemsen, P.; Gooch, A.A.; Creem-Regehr, S.H.; Loomis, J.M.; Beall, A.C. Does the quality of the computer graphics matter when judging distances in visually immersive environments? Presence 2004, 13, 560–571. [Google Scholar] [CrossRef]
  40. Willemsen, P.; Gooch, A.A. Perceived egocentric distances in real, image-based, and traditional virtual environments. In Proceedings of the IEEE Virtual Reality 2002, Orlando, FL, USA, 24–28 March 2002; pp. 275–276. [Google Scholar]
  41. Witmer, B.G.; Sadowski, W.J., Jr. Nonvisually guided locomotion to a previously viewed target in real and virtual environments. Hum. Factors 1998, 40, 478–488. [Google Scholar] [CrossRef]
  42. Loomis, J.M.; Knapp, J.M. Visual perception of egocentric distance in real and virtual environments. Virtual Adapt. Environ. 2003, 11, 21–46. [Google Scholar]
  43. Richardson, A.R.; Waller, D. Interaction with an immersive virtual environment corrects users’ distance estimates. Hum. Factors 2007, 49, 507–517. [Google Scholar] [CrossRef]
  44. Geuss, M.; Stefanucci, J.; Creem-Regehr, S.; Thompson, W.B. Can I pass? Using affordances to measure perceived size in virtual environments. In Proceedings of the 7th Symposium on Applied Perception in Graphics and Visualization, Los Angeles, CA, USA, 23–24 July 2010; pp. 61–64. [Google Scholar]
  45. Murgia, A.; Sharkey, P.M. Estimation of distances in virtual environments using size constancy. Int. J. Virtual Real. 2009, 8, 67–74. [Google Scholar] [CrossRef]
  46. Song, G.Y.; Jiang, R.P.; Zhang, X.Y.; Liu, S.Q.; Yu, X.N.; Chen, Q.; Weng, X.R.; Wu, W.Z.; Su, H.; Ren, C.; et al. Validation of subjective and objective evaluation methods for orthodontic treatment outcome. J. Peking Univ. Health Sci. 2015, 47, 90–97. [Google Scholar]
  47. Campbell, S.; Goldstein, G. Angle’s Classification—A Prosthodontic Consideration: Best Evidence Consensus Statement. J. Prosthodont. 2021, 30 (Suppl. 1), 67–71. [Google Scholar] [CrossRef]
  48. Rossini, G.; Parrini, S.; Castroflorio, T.; Deregibus, A.; Debernardi, C.L. Diagnostic accuracy and measurement sensitivity of digital models for orthodontic purposes: A systematic review. Am. J. Orthod. Dentofac. Orthop. 2016, 149, 161–170. [Google Scholar] [CrossRef]
  49. Kumar, A.A.; Phillip, A.; Kumar, S.; Rawat, A.; Priya, S.; Kumaran, V. Digital model as an alternative to plaster model in assessment of space analysis. J. Pharm. Bioallied Sci. 2015, 7 (Suppl. 2), S465. [Google Scholar] [CrossRef] [PubMed]
  50. Reuschl, R.P.; Heuer, W.; Stiesch, M.; Wenzel, D.; Dittmer, M.P. Reliability and validity of measurements on digital study models and plaster models. Eur. J. Orthod. 2016, 38, 22–26. [Google Scholar] [CrossRef] [Green Version]
  51. Priot, A.E.; Charbonneau, M.; Paillé, D. Spatial constraints for 3D perception in Helmet-Mounted Displays. In Head-and Helmet-Mounted Displays XIII: Design and Applications; International Society for Optics and Photonics: Bellingham, WA, USA, 2008; Volume 6955, p. 69550G. [Google Scholar]
  52. Aglioti, S.; DeSouza, J.F.; Goodale, M.A. Size-contrast illusions deceive the eye but not the hand. Curr. Biol. 1995, 5, 679–685. [Google Scholar] [CrossRef] [Green Version]
  53. Pavani, F.; Boscagli, I.; Benvenuti, F.; Rabuffetti, M.; Farnè, A. Are perception and action affected differently by the Titchener circles illusion? Exp. Brain Res. 1999, 127, 95–101. [Google Scholar] [CrossRef]
  54. Kenyon, R.V.; Phenany, M.; Sandin, D.; Defanti, T. Accommodation and size-constancy of virtual objects. Ann. Biomed. Eng. 2008, 36, 342–348. [Google Scholar] [CrossRef]
  55. Frey, J.; Hachet, M.; Lotte, F. EEG-based neuroergonomics for 3D user interfaces: Opportunities and challenges. Trav. Hum. 2017, 80, 73–92. [Google Scholar] [CrossRef] [Green Version]
  56. Kelly, J.W.; Hammel, W.W.; Siegel, Z.D.; Sjolund, L.A. Recalibration of perceived distance in virtual environments occurs rapidly and transfers asymmetrically across scale. IEEE Trans. Vis. Comput. Graph. 2014, 20, 588–595. [Google Scholar] [CrossRef]
  57. Ebrahimi, E.; Altenhoff, B.M.; Pagano, C.C.; Babu, S.V. Carryover effects of calibration to visual and proprioceptive information on near field distance judgments in 3d user interaction. In Proceedings of the 2015 IEEE Symposium on 3D User Interfaces (3DUI), Arles, France, 23–24 March 2015; pp. 97–104. [Google Scholar]
  58. Trabucco, J.T.; Rottigni, A.; Cavallo, M.; Bailey, D.; Patton, J.; Marai, G.E. User perspective and higher cognitive task-loads influence movement and performance in immersive training environments. BMC Biomed. Eng. 2019, 1, 21. [Google Scholar] [CrossRef] [Green Version]
  59. Goodale, M.A.; Milner, A.D.; Jakobson, L.S.; Carey, D.P. A neurological dissociation between perceiving objects and grasping them. Nature 1991, 349, 154–156. [Google Scholar] [CrossRef]
  60. Goodale, M.A.; Westwood, D.A. An evolving view of duplex vision: Separate but interacting cortical pathways for perception and action. Curr. Opin. Neurobiol. 2004, 14, 203–211. [Google Scholar] [CrossRef]
  61. Goodale, M.A.; Meenan, J.P.; Bülthoff, H.H.; Nicolle, D.A.; Murphy, K.J.; Racicot, C.I. Separate neural pathways for the visual analysis of object shape in perception and prehension. Curr. Biol. 1994, 4, 604–610. [Google Scholar] [CrossRef]
  62. Makaremi, M. The role of cognitive sciences in orthodontic treatments: Optimizing the interface between practitioners and new technologies. J. Dentofac. Anom. Orthod. 2016, 19, 410. [Google Scholar] [CrossRef]
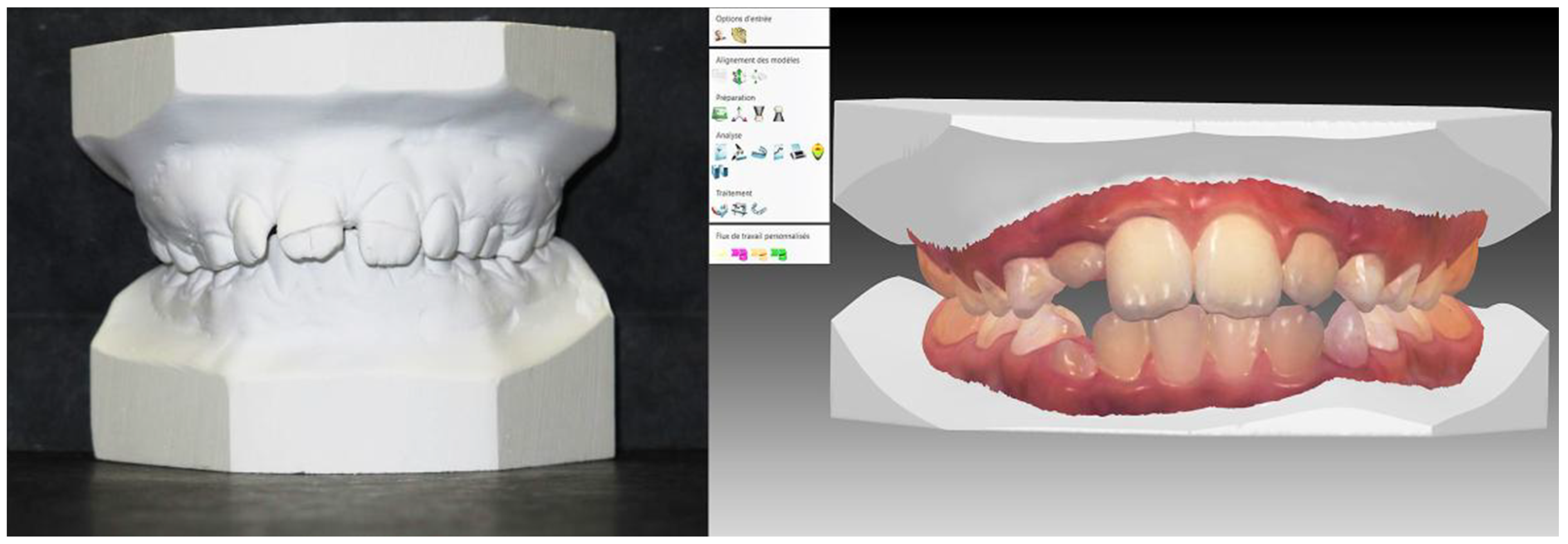
Applsci 11 08285 g001 550
Figure 1. Plaster and 3D digital orthodontic working models.
Figure 1. Plaster and 3D digital orthodontic working models.
Applsci 11 08285 g001
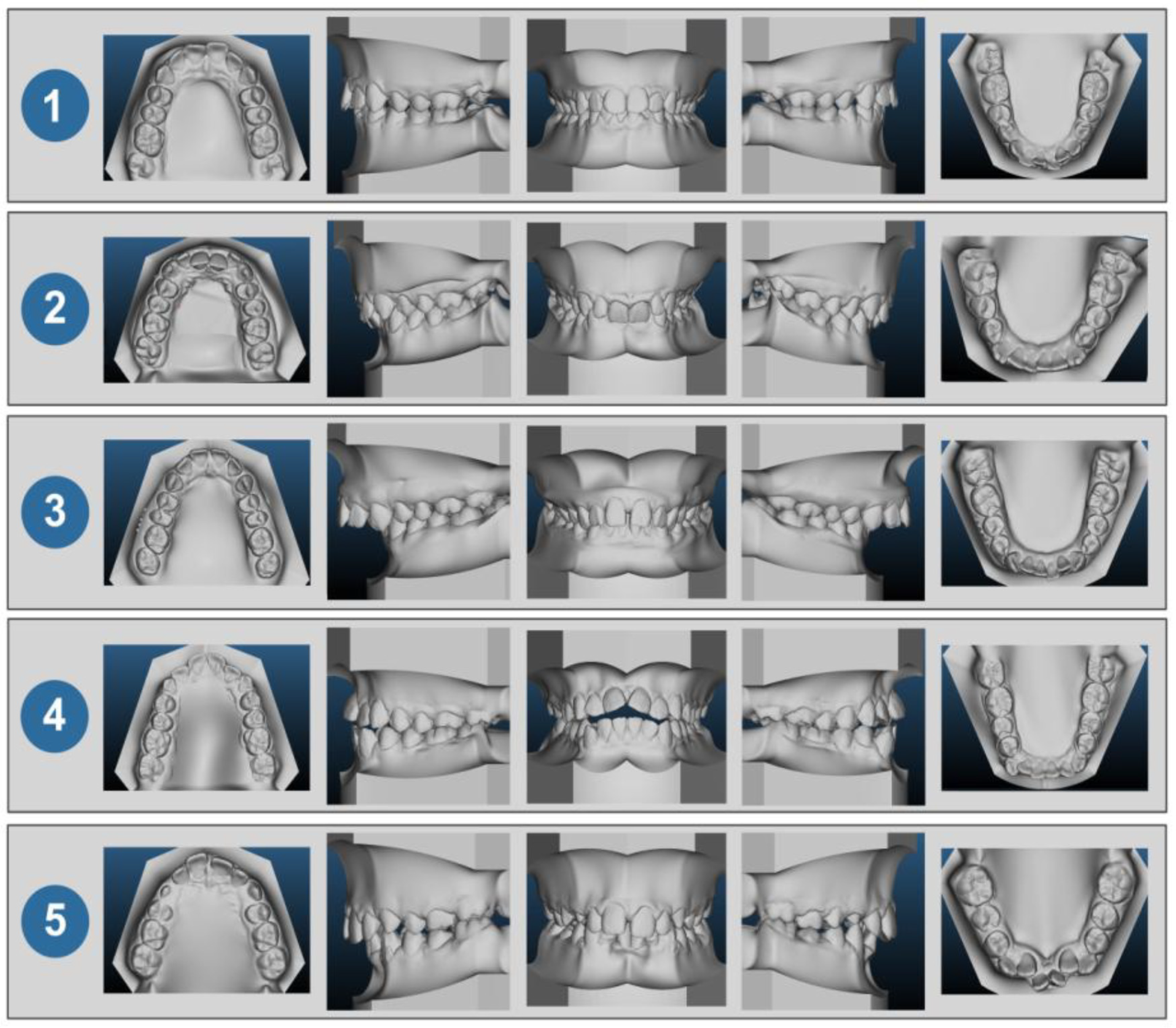
Applsci 11 08285 g002 550
Figure 2. The five clinical cases used for distance estimation.
Figure 2. The five clinical cases used for distance estimation.
Applsci 11 08285 g002
Applsci 11 08285 g003 550
Figure 3. Presentation of the seven estimated variables.
Figure 3. Presentation of the seven estimated variables.
Applsci 11 08285 g003
Applsci 11 08285 g004 550
Figure 4. Flowchart of the procedure.
Figure 4. Flowchart of the procedure.
Applsci 11 08285 g004
Table
Table 1. Presentation of the five clinical cases used in our study.
Table 1. Presentation of the five clinical cases used in our study.
Case no. 1Class I with moderate crowding of the arch
Case no. 2Class II with pronounced incisor supraclusion
Case no. 3Class II with a significantly increased overjet
Case no. 4Class II incisor infraclusion
Case no. 5Class II with malposition of the mandibular incisors
Table
Table 2. Means and standard deviation for each model. ×1 represent the machine values, ×2 is the mean of the measurement. σ is the standard deviation.
Table 2. Means and standard deviation for each model. ×1 represent the machine values, ×2 is the mean of the measurement. σ is the standard deviation.
Case No. 1Case No. 2Case No. 3Case No. 4Case No. 5
Mandibular Discrepancy×1: −3×1: 0.5×1: −3×1: −3.5×1: 2.5
×2: −2.73×2: −2.35×2: −3.55×2: −4.44×2: −4.60
σ: 1.43σ: 3.21×1: −3×1: −3.5×1: 2.5
Intermolar Distance×1: 36×1: 37×1: 36.5×1: 40×1: 40
×2: 38.10×2: 38.6×2: 38×2: 36.6×2: 41
σ: 7.82σ: 8.22σ: 8.73σ: 8.11σ: 8.36
Spee Curve×1: 2×1: 1.5×1: 2.5×1: 2×1: 2.5
×2: 2.42×2: 1.66×2: 2.47×2: 1.03×2: 2.2
σ: 0.81σ: 0.90σ: 0.86σ: 1.07σ: 0.87
16/26 Symetric ×1: 3×1: 1×1: 1×1: 0×1: 1.5
×2: 1.52×2: 0.32×2: 0.11×2: −0.32×2: 0.19
σ: 1.80 σ: 0.97σ: 1.19σ: 0.77σ: 1.60
Right Canine Class×1: 6×1: 1×1: 8×1: −4×1: 2
×2: 5.45×2: 3.24×2: 7.34×2: −2.75×2: 2.95
σ: 1.47σ: 2.57σ: 2.19σ: 3.08σ: 1.36
Over Jet×1: 1.5×1: 3.5×1: 14×1: 3×1: 4.5
×2: 1.45×2: 4.32×2: 10.94×2: 2.97×2: 5.08
σ: 1.23σ: 1.81σ: 4.47σ: 1.04σ: 1.96
Over Bite×1: 7×1: 5×1: 5×1: −5×1: 4
×2: 6.27×2: 3.52×2: 9.55×2: 4.18×2: 3.63
σ: 1.60σ: 1.80σ: 1.11σ: 2.05σ: 0.97
Table
Table 3. Results of the one-sample test for all of the variables. This table shows the mean value, standard deviation, t-test value, and the significance for each variable. The upper table presents results with 0 cm as a reference value. The lower table presents results with 1 cm as a reference value (only significant variables with the value 0 are tested with the value 1).
Table 3. Results of the one-sample test for all of the variables. This table shows the mean value, standard deviation, t-test value, and the significance for each variable. The upper table presents results with 0 cm as a reference value. The lower table presents results with 1 cm as a reference value (only significant variables with the value 0 are tested with the value 1).
t = 0MeanStandard DeviationtSig.Power (0.8)
Mandibular Discrepancy−2.231.15−10.74≤0.015
Right Canine Class0.621.083.19≤0.0148
Spee Curve−0.130.58−1.330.19313
Intermolar Distance0.567.790.390.693049
Over Bite−0.650.66−5.40≤0.0117
Over Jet−0.341.20−1.600.11197
16/26 Symetric−0.930.53−9.65≤0.016
t = 1MeanStandard DeviationtSig.Power (0.8)
Mandibular Discrepancy2.251.116.23≤0.014
Right Canine Class0.920.84−0.510.6114
Over Bite0.800.440.640.525
16/26 Symetric0.930.53−0.660.516
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Makaremi, M.; N’Kaoua, B. Estimation of Distances in 3D by Orthodontists Using Digital Models. Appl. Sci. 2021, 11, 8285. https://doi.org/10.3390/app11188285

AMA Style

Makaremi M, N’Kaoua B. Estimation of Distances in 3D by Orthodontists Using Digital Models. Applied Sciences. 2021; 11(18):8285. https://doi.org/10.3390/app11188285

Chicago/Turabian Style

Makaremi, Masrour, and Bernard N’Kaoua. 2021. "Estimation of Distances in 3D by Orthodontists Using Digital Models" Applied Sciences 11, no. 18: 8285. https://doi.org/10.3390/app11188285

APA Style

Makaremi, M., & N’Kaoua, B. (2021). Estimation of Distances in 3D by Orthodontists Using Digital Models. Applied Sciences, 11(18), 8285. https://doi.org/10.3390/app11188285

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop