Soft Computing Techniques for Appraisal of Potentially Toxic Elements from Jalandhar (Punjab), India
Abstract
:1. Introduction
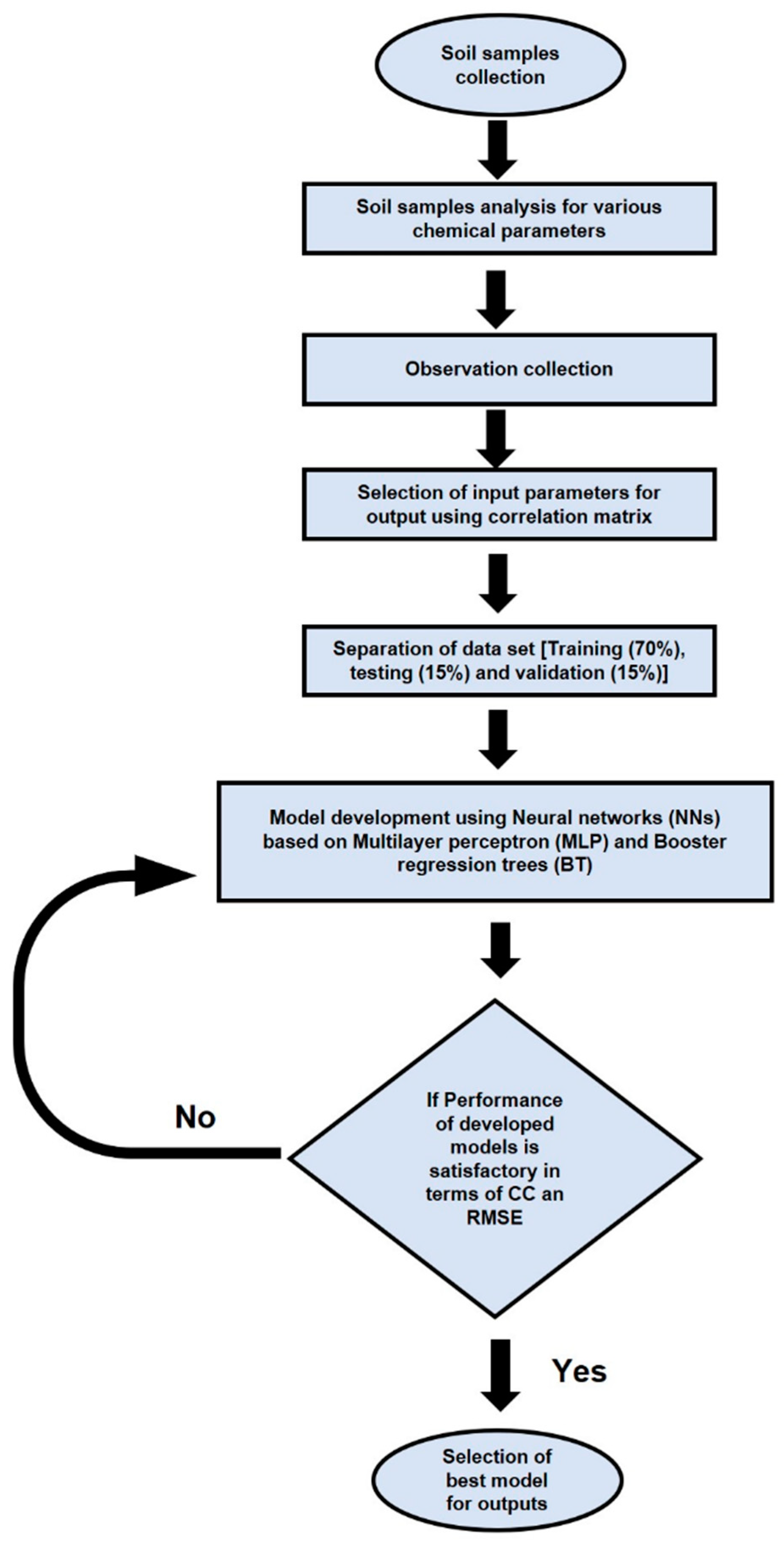
2. Materials and Methods
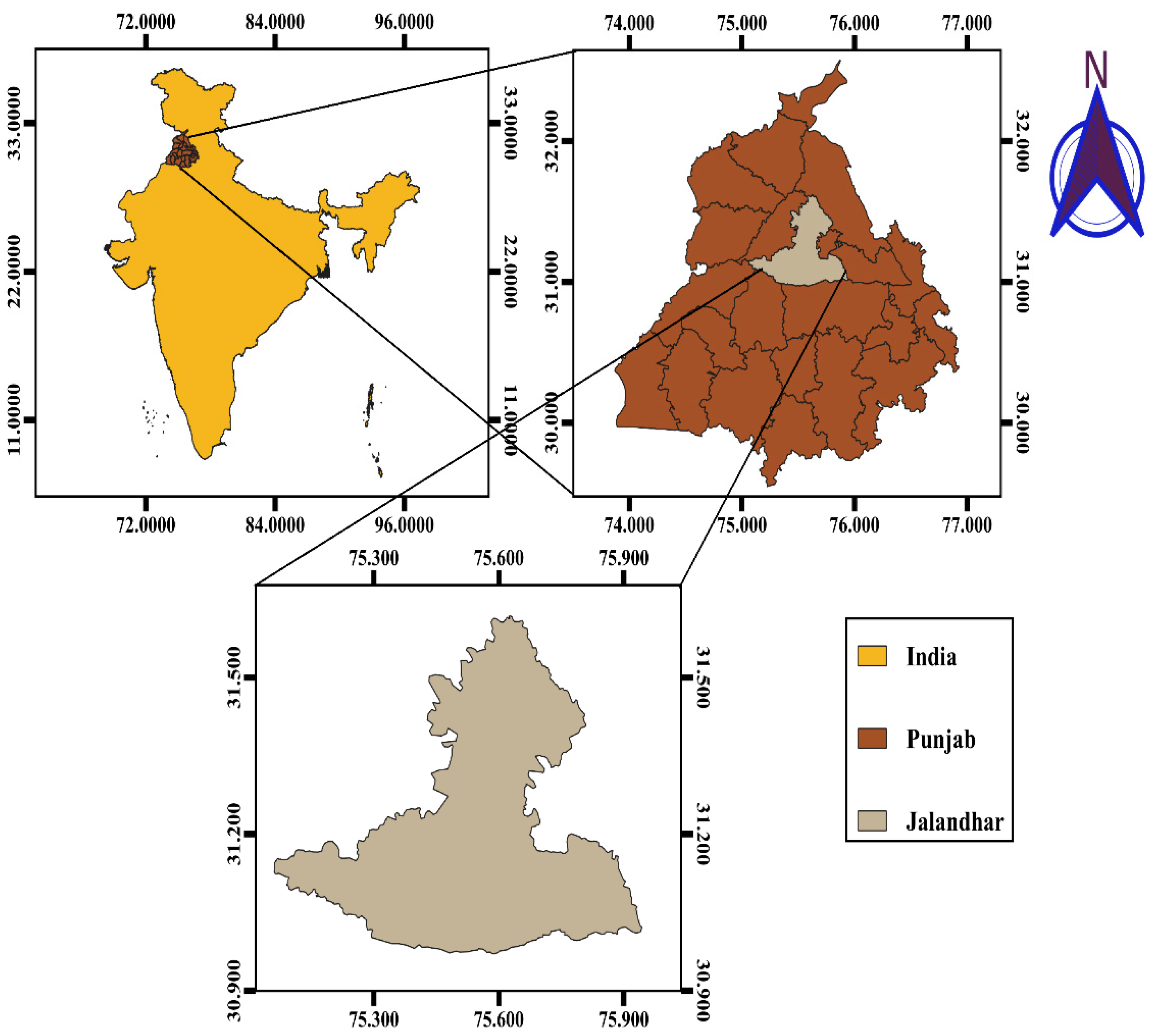
2.1. Study Area
2.2. Soil Sampling and Analysis of Chemical Properties of Soil
2.3. Stepwise Regression for Input Selection
2.4. Modeling Techniques
2.5. Model Performance Assessing Parameters:
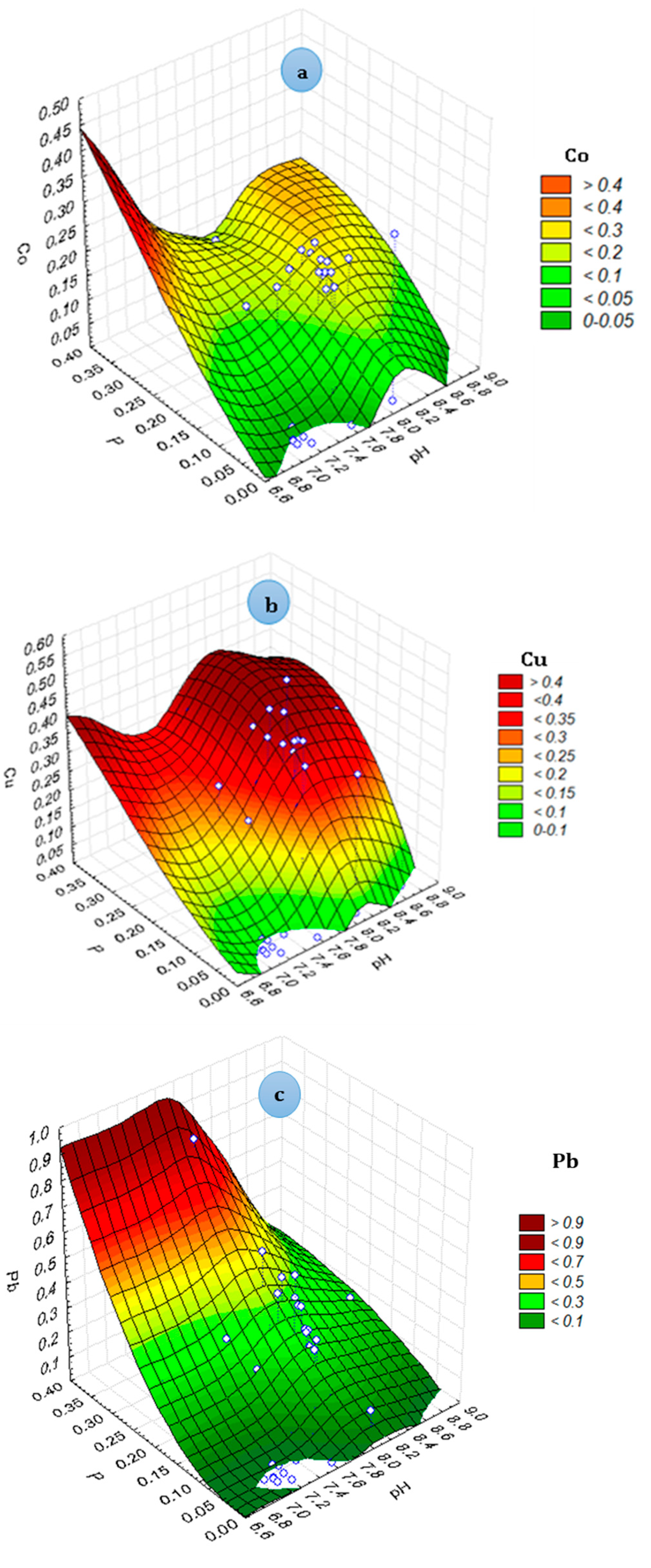
3. Results and Discussion
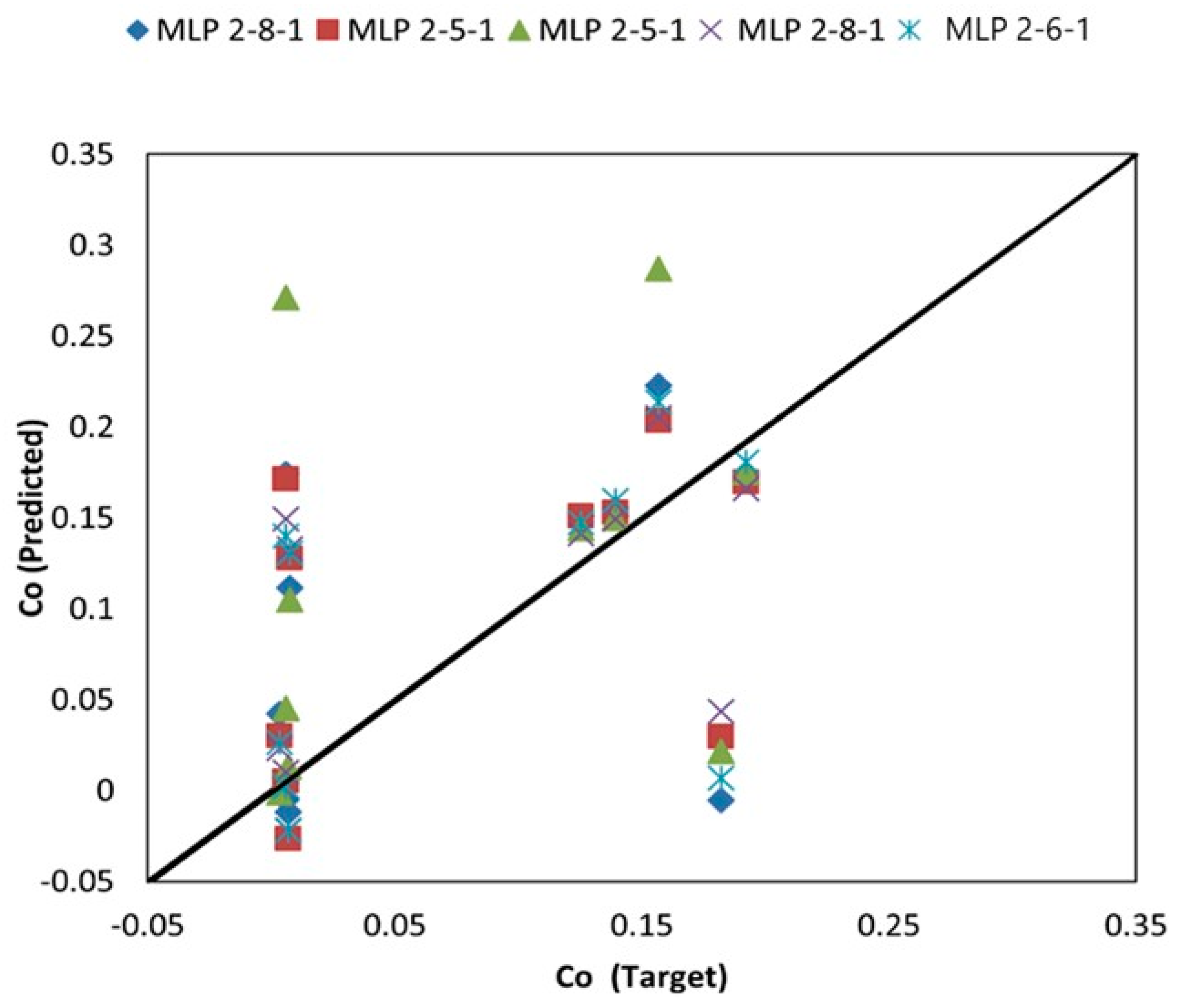
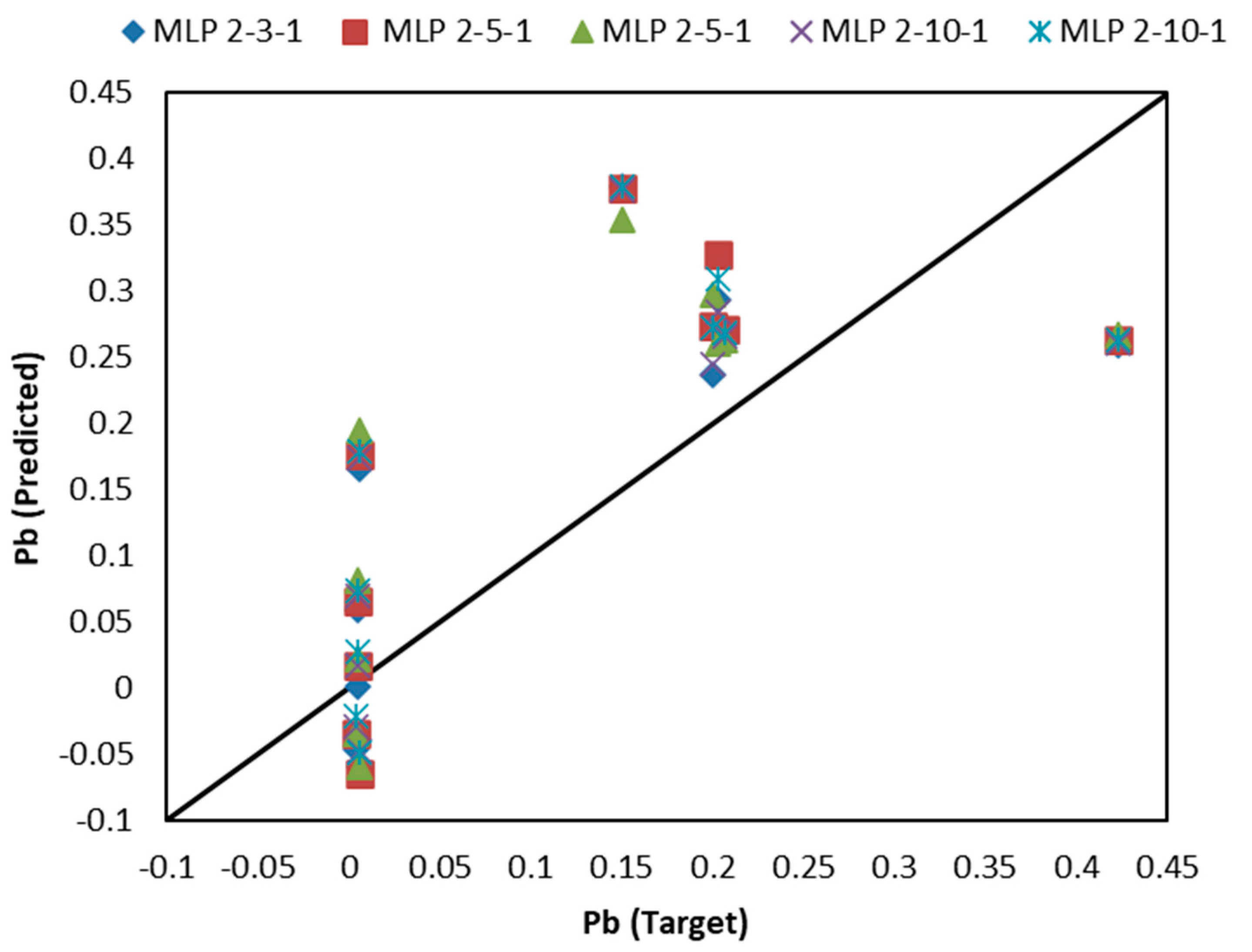
3.1. Results of MLP-Based Models
3.2. Results of BT-Based Models
3.3. Intercomparison of Applied Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dogra, N.; Sharma, M.; Sharma, A.; Keshavarzi, A.; Minakshi, B.R.; Kumar, V. Pollution assessment and spatial distribution of roadside agricultural soils: A case study from India. Int. J. Environ. Res. Public Health 2020, 30, 146–159. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Sharma, A.; Kaur, P.; Sidhu, G.P.S.; Bali, A.S.; Bhardwaj, R.; Cerda, A. Pollution assessment of heavy metals in soils of India and ecological risk assessment: A state-of-the-art. Chemosphere 2019, 216, 449–462. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; López-Vicente, M.; Kumar, V.; Rodríguez-Seijo, A.; Valkó, O.; Rojas, C.; Pourghasemi, H.R.; Salvati, L.; Bakr, N.; Vaudour, E.; et al. Soil science challenges in a new era: A transdisciplinary overview of relevant topics. Air Soil Water Res. 2020, 13, 1178622120977491. [Google Scholar] [CrossRef]
- Panagos, P.; Van Liedekerke, M.; Yigini, Y.; Montanarella, L. Contaminated sites in Europe: Review of the current situation based on data collected through a European network. J. Environ. Public Health 2013, 2013, 158764. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Sharma, A.; Kaur, P.; Kumar, R.; Keshavarzi, A.; Bhardwaj, R.; Thukral, A.K. Assessment of soil properties from catchment areas of Ravi and Beas rivers: A review. Geol. Ecol. Landsc. 2019, 3, 149–157. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Kumar, V. Spatial distribution and potential ecological risk assessment of heavy metals in agricultural soils of Northeastern, Iran. Geol. Ecol. Landsc. 2019, 4, 87–103. [Google Scholar] [CrossRef] [Green Version]
- Harter, R.D.; Naidu, R. An assessment of environmental and solution parameter impact on trace-metal sorption by soils. Soil Sci. Soc. Am. J. 2001, 65, 597–612. [Google Scholar] [CrossRef]
- Peakall, D.; Burger, J. Methodologies for assessing exposure to metals: Speciation, bioavailability of metals, and ecological host factors. Ecotox. Environ. Saf. 2003, 56, 110–121. [Google Scholar] [CrossRef]
- Tóth, G.; Hermann, T.; Da Silva, M.R.; Montanarella, L. Heavy metals in agricultural soils of the European Union with implications for food safety. Environ. Int. 2016, 88, 299–309. [Google Scholar] [CrossRef] [PubMed]
- Hou, D.; O’Connor, D.; Igalavithana, A.D.; Alessi, D.S.; Luo, J.; Tsang, D.C.W.; Sparks, D.L.; Yamauchi, Y.; Rinklebe, J.; Ok, Y.S. Metal contamination and bioremediation of agricultural soils for food safety and sustainability. Nat. Rev. Earth Environ. 2020, 1, 366–381. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Kumar, V. Ecological risk assessment and source apportionment of heavy metal contamination in agricultural soils of Northeastern Iran. Int. J. Environ. Health Res. 2019, 29, 544–560. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.P.; Cheng, B.Y.; Shyu, G.S.; Chang, T.K. Combining a finite mixture distribution model with indicator kriging to delineate and map the spatial patterns of soil heavy metal pollution in Chunghua County, central Taiwan. Environ. Pollut. 2010, 158, 235–244. [Google Scholar] [CrossRef]
- Rodríguez-Seijo, A.; Andrade, M.L.; Vega, F.A. Origin and spatial distribution of metals in urban soils. J. Soils Sediments 2017, 17, 1514–1526. [Google Scholar] [CrossRef]
- Wang, Q.; Xie, Z.; Li, F. Using ensemble models to identify and apportion heavy metal pollution sources in agricultural soils on a local scale. Environ. Pollut. 2015, 206, 227–235. [Google Scholar] [CrossRef]
- Sihag, P.; Keshavarzi, A.; Kumar, V. Comparison of different approaches for modelling of heavy metal estimations. SN Appl. Sci. 2019, 1, 780. [Google Scholar] [CrossRef] [Green Version]
- Michel, K.; Roose, M.; Ludwig, B. Comparison of different approaches for modelling heavy metal transport in acidic soils. Geoderma 2007, 140, 207–214. [Google Scholar] [CrossRef]
- Naderi, A.; Delavar, M.A.; Kaboudin, B.; Sadegh, A.M. Assessment of spatial distribution of soil heavy metals using ANN-GA, MSLR and satellite imagery. Environ. Monit. Assess. 2017, 189, 214. [Google Scholar] [CrossRef]
- Ma, J.; Chen, Y.; Weng, L.; Peng, H.; Liao, Z.; Li, Y. Source Identification of Heavy Metals in Surface Paddy Soils Using Accumulated Elemental Ratios Coupled with MLR. Int. J. Environ. Res. Public Health 2021, 18, 2295. [Google Scholar] [CrossRef] [PubMed]
- Toriz-Robles, N.; Ramírez-Guzmán, M.E.; Fernández-Ordoñez, Y.M.; Soria-Ruiz, J.; Ybarra, M. Comparison of linear and nonlinear models to estimate the risk of soil contamination. Agrociencia 2019, 53, 269–283. [Google Scholar]
- Zhang, M.; Wang, X.; Liu, C.; Lu, J.; Qin, Y.; Mo, Y.; Xiao, P.; Liu, Y. Quantitative source identification and apportionment of heavy metals under two different land use types: Comparison of two receptor models APCS-MLR and PMF. Environ. Sci. Pollut. Res. 2020, 27, 42996–43010. [Google Scholar] [CrossRef]
- Deng, M.H.; Zhu, Y.; Shao, K.; Zhang, Q.; Ye, G.H.; Shen, J. Metals source apportionment in farmland soil and the prediction of metal transfer in the soil-rice-human chain. J. Environ. Manag. 2020, 260, 110092. [Google Scholar] [CrossRef] [PubMed]
- Gholami, R.; Kamkar-Rouhani, A.; Ardejani, F.D.; Maleki, S. Prediction of toxic metals concentration using artificial intelligence techniques. Appl. Water Sci. 2011, 1, 125–134. [Google Scholar] [CrossRef]
- Sengorur, B.; Dogan, E.; Koklu, R.; Samandar, A. Dissolved oxygen estimation using artificial neural network for water quality control. Fresen. Environ. Bull. 2006, 15, 1064–1067. [Google Scholar]
- Kuo, J.; Hsieh, M.; Lung, W.; She, N. Using artificial neural network for reservoir eutriphication prediction. Ecol. Model. 2007, 200, 171–177. [Google Scholar] [CrossRef]
- Palani, S.; Liong, S.; Tkalich, P. An ANN application for water quality forecasting. Marin. Pollut. Bull. 2008, 56, 1586–1597. [Google Scholar] [CrossRef] [PubMed]
- Hanbay, D.; Turkoglu, I.; Demir, Y. Prediction of wastewater treatment plant performance based on wavelet packet decomposition and neural networks. Expert. Syst. Appl. 2008, 34, 1038–1043. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Chenard, J.F.; Caissie, D. Stream temperature modelling using neural networks: Application on Catamaran Brook, New Brunswick, Canada. Hydrol. Process. 2008, 22, 3361–3372. [Google Scholar] [CrossRef]
- Dogan, E.; Sengorur, B.; Koklu, R. Modeling biochemical oxygen demand of the Melen River in Turkey using an artificial neural network technique. J. Environ. Manag. 2009, 90, 1229–1235. [Google Scholar] [CrossRef]
- Chen, H.Y.; Yuan, X.Y.; Li, T.Y.; Sun, H.; Ji, J.F.; Wang, C. Characteristics of heavy metal transfer and their influencing factors in different soil–crop systems of the industrialization region, China. Ecotoxicol. Environ. Saf. 2016, 126, 193–201. [Google Scholar] [CrossRef]
- Mu, T.; Wu, T.; Zhou, T.; Li, Z.; Ouyang, Y.; Jiang, J.; Zhou, D.; Hou, J.Y.; Wang, Z.Y.; Luo, Y.M.; et al. Geographical variation in arsenic, cadmium, and lead of soils and rice in the major rice producing regions of China. Sci. Total Environ. 2020, 677, 373–381. [Google Scholar] [CrossRef]
- Kumar, V.; Kothiyal, N.C. Distribution behavior and carcinogenic level of some polycyclic aromatic hydrocarbons in roadside soil at major traffic intercepts within a developing city of India. Environ. Monit. Assess. 2012, 184, 6239–6252. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Sharma, A.; Minakshi, B.R.; Thukral, A.K. Temporal distribution, source apportionment, and pollution assessment of metals in the sediments of Beas river, India. Hum. Ecol. Risk Assess. 2018, 24, 2162–2181. [Google Scholar] [CrossRef]
- PSCST. Punjab State Council for Science & Technology, Chandigarh. Available online: http://punenvis.nic.in/index2.aspx?slid=205&mid=1&langid=1&sublinkid=62 (accessed on 21 February 2021).
- Singh, A.; Sharma, C.S.; Jeyaseelan, A.T.; Chowdary, V.M. Spatio–temporal analysis of groundwater resources in Jalandhar district of Punjab state, India. Sustain. Water Resour. Manag. 2015, 1, 293–304. [Google Scholar]
- Jackson, M.L. Soil Chemical Analysis; Prentice Hall of India. Pvt. Ltd.: New Delhi, India, 1967. [Google Scholar]
- Olsen, S.R.; Cole, C.V.; Watanabe, F.S.; Dean, L.A. Estimation of Available Phosphorus by Extraction with Sodium Bicarbonate (Circular 39); USDA: Washington, DC, USA, 1954. [Google Scholar]
- Tucker, B.B.; Kurtz, L.T. Calcium and Magnesium Determinations by EDTA Titrations. Soil. Sci. Soc. Am. J. 1961, 25, 27–29. [Google Scholar] [CrossRef]
- Nelson, D.W.; Sommers, L.E. Total Carbon, Organic Carbon, and Organic Matter. In Methods of Soil Analysis; Page, A.L., Ed.; ASA and SSSA: Madisson, WI, USA, 1982; pp. 539–579. [Google Scholar]
- Fausset, L.V. (Ed.) Fundamentals of Neural Networks: Architectures, Algorithms and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Park, Y.S.; Lek, S. Chapter 7-Artificial Neural Networks: Multilayer Perceptron for Ecological Modeling. In Developments in Environmental Modelling; Jørgensen, S.E., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 28, pp. 123–140. [Google Scholar]
- Shiri, J.; Keshavarzi, A.; Kisi, O.; Iturraran-Viveros, U.; Bagherzadeh, A.; Mousavi, R.; Karimi, S. Modeling soil cation exchange capacity using soil parameters. Comput. Electron. Agric. 2017, 135, 242–251. [Google Scholar] [CrossRef]
- Shiri, J.; Keshavarzi, A.; Kisi, O.; Karimi, S.; Iturraran-Viveros, U. Modeling soil bulk density through a complete data scanning procedure: Heuristic alternatives. J. Hydrol. 2017, 549, 592–602. [Google Scholar] [CrossRef]
- Ozel, H.U.; Gemici, B.T.; Gemici, E.; Ozel, H.B.; Cetin, M.; Sevik, H. Application of artificial neural networks to predict the heavy metal contamination in the Bartin River. Environ. Sci. Poll. Res. 2020, 27, 42495–42512. [Google Scholar] [CrossRef] [PubMed]
- Bąk, Ł.; Szeląg, B.; Sałata, A.; Studziński, J. Modeling of Heavy Metal (Ni, Mn, Co, Zn, Cu, Pb, and Fe) and PAH Content in Stormwater Sediments Based on Weather and Physico-Geographical Characteristics of the Catchment-Data-Mining Approach. Water 2019, 11, 626. [Google Scholar] [CrossRef] [Green Version]
- El Badaoui, H.; Abdallaoui, A.; Manssouri, I.; Lancelot, L. Application of the artificial neural networks of MLP type for the prediction of the levels of heavy metals in Moroccan aquatic sediments. Int. J. Comput. Eng. Res. 2013, 3, 75–81. [Google Scholar]
- Falamaki, A. Artificial neural network application for predicting soil distribution coefficient of nickel. J. Environ. Radio. 2013, 115, 6–12. [Google Scholar] [CrossRef]
- Covelo, E.F.; Matías, J.M.; Vega, F.A.; Reigosa, M.J.; Andrade, M.L. A tree regression analysis of factors determining the sorption and retention of heavy metals by soil. Geoderma 2008, 147, 75–85. [Google Scholar] [CrossRef]
- Vega, F.A.; Matías, J.M.; Andrade, M.L.; Reigosa, M.J.; Covelo, E.F. Classification and regression trees (CARTs) for modelling the sorption and retention of heavy metals by soil. J. Hazard. Mater. 2009, 167, 615–624. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Yuan, Z.; Zhong, Y.; Yang, L.; Hu, X.; Zhang, Y. An improved gradient boosting regression tree estimation model for soil heavy metal (arsenic) pollution monitoring using hyperspectral remote sensing. Appl. Sci. 2019, 9, 1943. [Google Scholar] [CrossRef] [Green Version]
- Hu, B.; Xue, J.; Zhou, Y.; Shao, S.; Fu, Z.; Li, Y.; Shi, Z. Modelling bioaccumulation of heavy metals in soil-crop ecosystems and identifying its controlling factors using machine learning. Environ. Pollut. 2020, 262, 114308. [Google Scholar] [CrossRef]
- Guevara, M.; Olmedo, G.F.; Stell, E.; Yigini, Y.; Aguilar, D.Y.; Arellano, H.C.; Vargas, R. No silver bullet for digital soil mapping: Country-specific soil organic carbon estimates across Latin America. Soil 2018, 4, 173–193. [Google Scholar] [CrossRef] [Green Version]
- Ge, X.; Wang, J.; Ding, J.; Cao, X.; Zhang, Z.; Liu, J.; Li, X. Combining UAV-based hyperspectral imagery and machine learning algorithms for soil moisture content monitoring. PeerJ 2019, 7, 6926. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, S.; Wang, Y.; Valbuena, R.; Wu, Y.; Kutia, M.; Shi, Y. Tighten the Bolts and Nuts on GPP Estimations from Sites to the Globe: An Assessment of Remote Sensing Based LUE Models and Supporting Data Fields. Remote Sens. 2021, 13, 168. [Google Scholar] [CrossRef]






| Variables | Units | Mean | Minimum | Median | Maximum | SD | CV | Skewness |
|---|---|---|---|---|---|---|---|---|
| pH | 7.76 | 6.70 | 7.88 | 8.80 | 0.41 | 0.05 | −0.21 | |
| C | % | 3.66 | 1.78 | 3.51 | 6.70 | 0.99 | 0.27 | 0.80 |
| P | mg kg−1 | 128.97 | 7.00 | 132.85 | 355.20 | 74.94 | 0.58 | 0.44 |
| Ca | meq 100g−1 | 0.19 | 0.05 | 0.14 | 0.93 | 0.15 | 0.79 | 3.68 |
| Mg | meq 100g−1 | 0.17 | 0.02 | 0.15 | 0.90 | 0.13 | 0.74 | 3.37 |
| Co | mg kg−1 | 0.10 | 0.01 | 0.11 | 0.36 | 0.09 | 0.91 | 0.37 |
| Cu | mg kg−1 | 0.51 | 0.01 | 0.19 | 12.79 | 1.99 | 3.89 | 5.77 |
| Pb | mg kg−1 | 0.23 | 0.01 | 0.15 | 5.83 | 0.70 | 2.98 | 7.68 |
| Models | Training | Testing | Validation | ||||
|---|---|---|---|---|---|---|---|
| Run | CC | RMSE | CC | RMSE | CC | RMSE | |
| MLP 2-8-1 | 10 | 0.8676 | 0.0453 | 0.7226 | 0.0416 | 0.4026 | 0.0082 |
| MLP 2-5-1 | 10 | 0.8574 | 0.0469 | 0.7107 | 0.0162 | 0.4582 | 0.0070 |
| MLP 2-5-1 | 25 | 0.9075 | 0.0383 | 0.7645 | 0.0148 | 0.3138 | 0.0125 |
| MLP 2-8-1 | 25 | 0.8547 | 0.0474 | 0.7186 | 0.0193 | 0.5119 | 0.0060 |
| MLP 2-6-1 | 25 | 0.8511 | 0.0479 | 0.6662 | 0.0144 | 0.4769 | 0.0070 |
| Models | Training | Testing | Validation | ||||
|---|---|---|---|---|---|---|---|
| Run | CC | RMSE | CC | RMSE | CC | RMSE | |
| MLP 2-4-1 | 25 | 0.9407 | 0.0557 | 0.7420 | 0.0878 | 0.6635 | 0.1440 |
| MLP 2-10-1 | 25 | 0.9488 | 0.0519 | 0.7366 | 0.0891 | 0.8626 | 0.0943 |
| MLP 2-7-1 | 25 | 0.9331 | 0.0591 | 0.7554 | 0.0874 | 0.7883 | 0.0564 |
| MLP 2-5-1 | 25 | 0.9372 | 0.0573 | 0.7264 | 0.0901 | 0.6828 | 0.0903 |
| MLP 2-9-1 | 25 | 0.9463 | 0.0531 | 0.7393 | 0.0886 | 0.5610 | 0.0686 |
| Models | Training | Testing | Validation | ||||
|---|---|---|---|---|---|---|---|
| Run | CC | RMSE | CC | RMSE | CC | RMSE | |
| MLP 2-3-1 | 25 | 0.8561 | 0.0938 | 0.3529 | 0.1078 | 0.7132 | 0.0128 |
| MLP 2-5-1 | 25 | 0.8465 | 0.0104 | 0.3490 | 0.1084 | 0.7113 | 0.0142 |
| MLP 2-5-1 | 10 | 0.8378 | 0.0243 | 0.3602 | 0.1052 | 0.7119 | 0.0129 |
| MLP 2-10-1 | 25 | 0.8562 | 0.0231 | 0.3706 | 0.1071 | 0.7114 | 0.0126 |
| MLP 2-10-1 | 10 | 0.8518 | 0.0066 | 0.3563 | 0.1079 | 0.7095 | 0.0137 |
| Output | Training | Testing | Validation | |||
|---|---|---|---|---|---|---|
| CC | RMSE | CC | RMSE | CC | RMSE | |
| Co | 0.9159 | 0.0376 | 0.7092 | 0.0455 | 0.9062 | 0.0343 |
| Cu | 0.9600 | 0.0478 | 0.8646 | 0.0755 | 0.8539 | 0.0854 |
| Pb | 0.8000 | 0.1175 | 0.6450 | 0.0791 | 0.7064 | 0.1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, V.; Sihag, P.; Keshavarzi, A.; Pandita, S.; Rodríguez-Seijo, A. Soft Computing Techniques for Appraisal of Potentially Toxic Elements from Jalandhar (Punjab), India. Appl. Sci. 2021, 11, 8362. https://doi.org/10.3390/app11188362
Kumar V, Sihag P, Keshavarzi A, Pandita S, Rodríguez-Seijo A. Soft Computing Techniques for Appraisal of Potentially Toxic Elements from Jalandhar (Punjab), India. Applied Sciences. 2021; 11(18):8362. https://doi.org/10.3390/app11188362
Chicago/Turabian StyleKumar, Vinod, Parveen Sihag, Ali Keshavarzi, Shevita Pandita, and Andrés Rodríguez-Seijo. 2021. "Soft Computing Techniques for Appraisal of Potentially Toxic Elements from Jalandhar (Punjab), India" Applied Sciences 11, no. 18: 8362. https://doi.org/10.3390/app11188362
APA StyleKumar, V., Sihag, P., Keshavarzi, A., Pandita, S., & Rodríguez-Seijo, A. (2021). Soft Computing Techniques for Appraisal of Potentially Toxic Elements from Jalandhar (Punjab), India. Applied Sciences, 11(18), 8362. https://doi.org/10.3390/app11188362








