Tailorable Brillouin Light Scattering in a Lithium Niobate Waveguide
Abstract
:1. Introduction
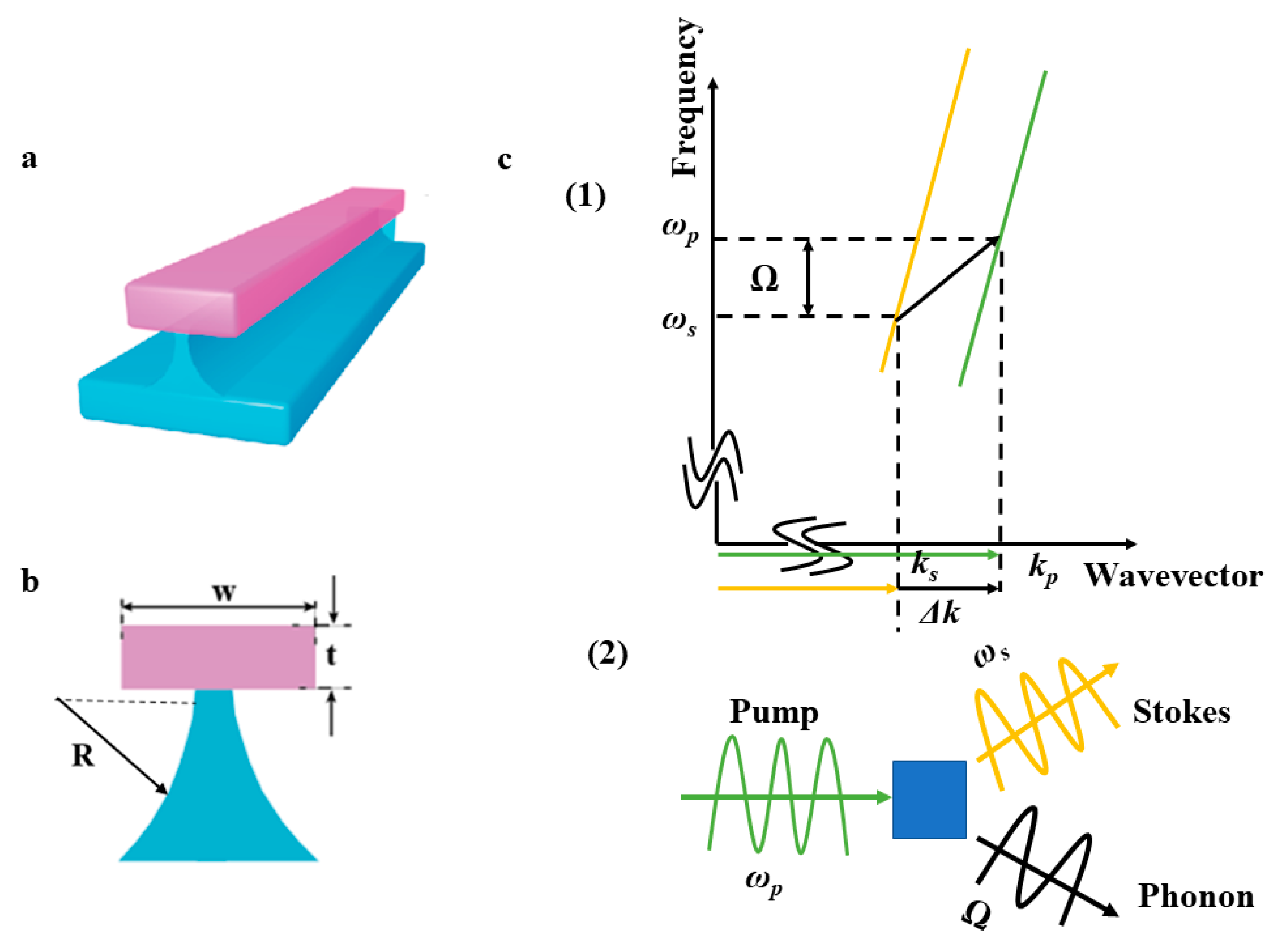
2. Materials and Methods
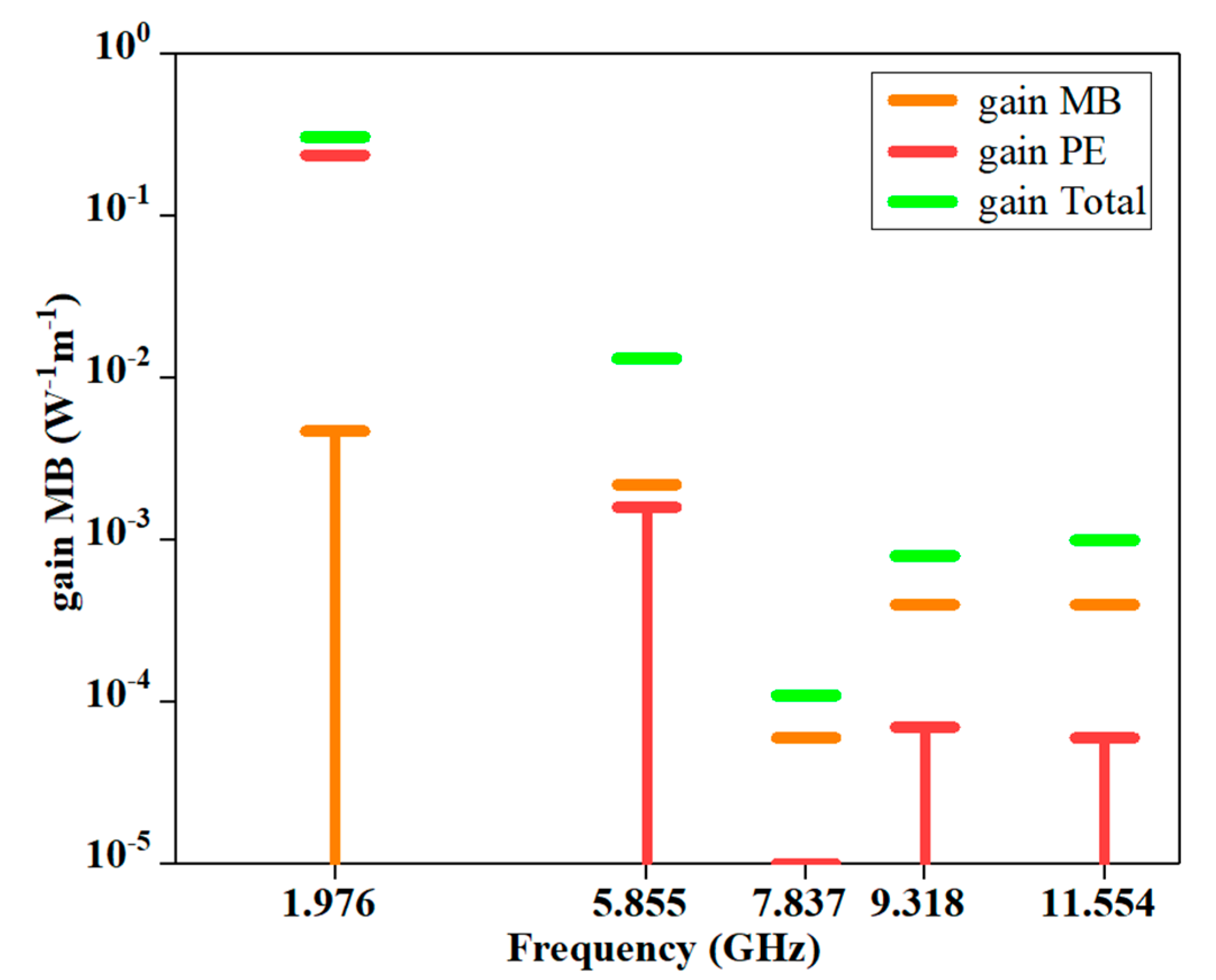
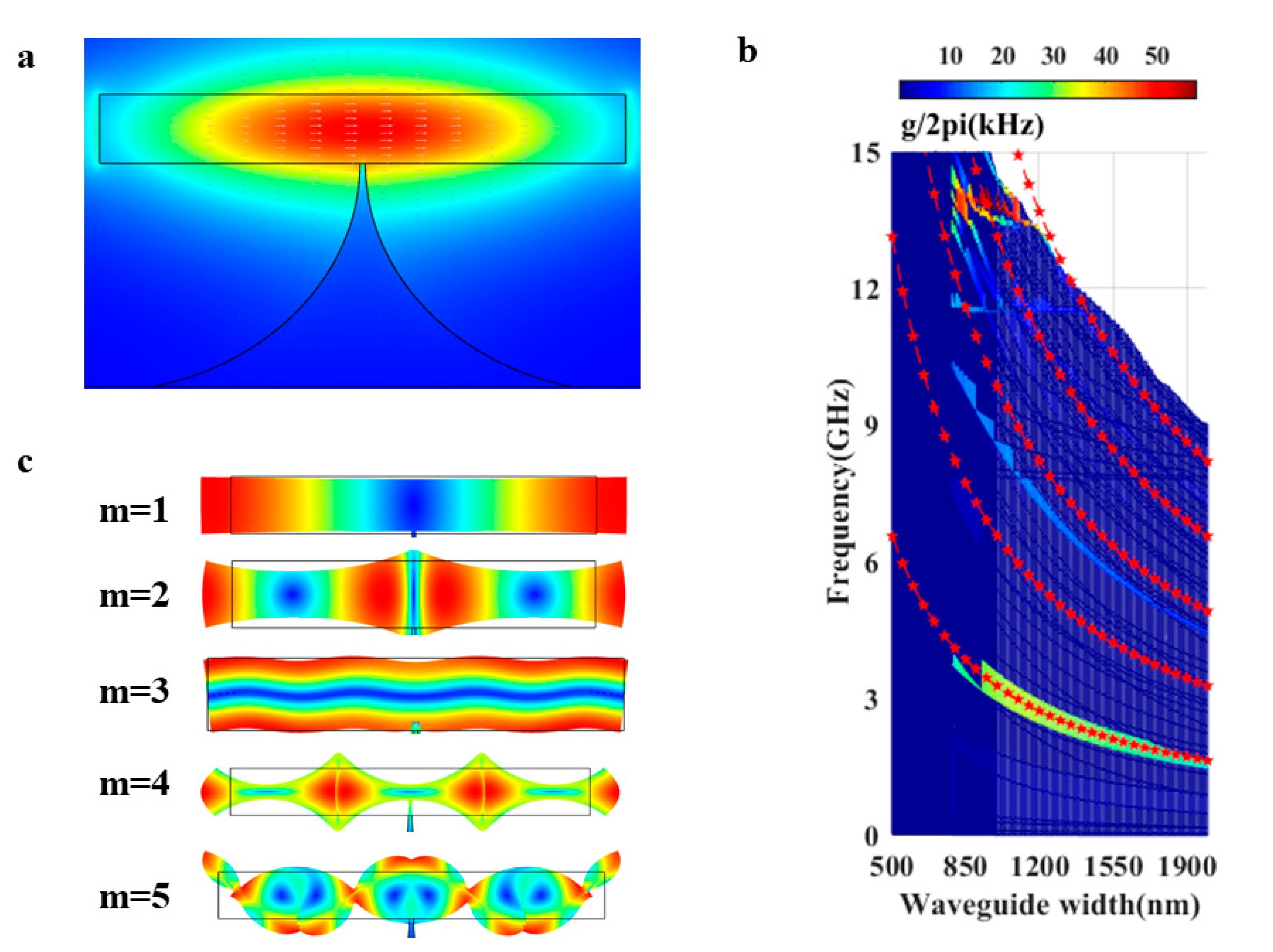
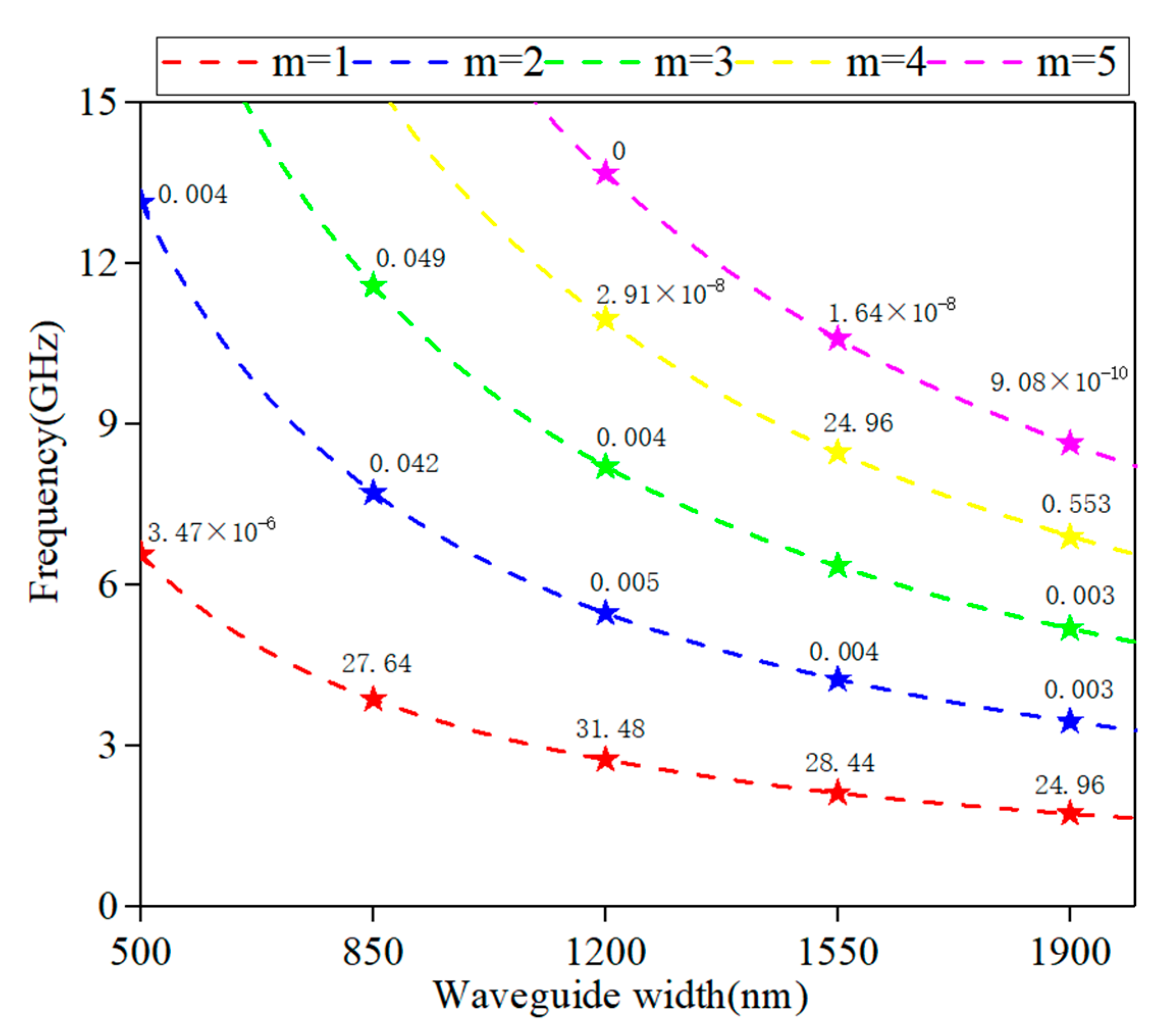
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lang, Z.; Yuangang, L.; Yangyang, F.; Haixia, M.; Chaolin, D. Design of a hybrid on-chip waveguide with giant backward stimulated Brillouin scattering. Opt. Express 2019, 27, 24953. [Google Scholar]
- Eggleton, B.J.; Poulton, C.G.; Rakich, P.T.; Steel, M.J.; Bahl, G. Brillouin integrated photonics. Nat. Photonics 2019, 13, 664–677. [Google Scholar] [CrossRef]
- Liu, Y.; Choudhary, A.; Marpaung, D.; Eggleton, B.J. Integrated microwave photonic filters. Adv. Opt. Photonics 2020, 12, 485–555. [Google Scholar] [CrossRef]
- Bai, Z.; Williams, R.J.; Kitzler, O.; Sarang, S.; Spence, D.J.; Wang, Y.; Lu, Z.; Mildren, R.P. Diamond Brillouin laser in the visible. APL photonics 2020, 5, 031301. [Google Scholar] [CrossRef]
- Bai, Z.; Yuan, H.; Liu, Z.; Xu, P.; Gao, Q.; Williams, R.J.; Kitzler, O.; Mildren, R.P.; Wang, Y.; Lu, Z. Stimulated Brillouin scattering materials, experimental design and applications: A review. Opt. Mater. 2018, 75, 626–645. [Google Scholar] [CrossRef]
- Florez, O.; Jarschel, P.F.; Espinel, Y.; Cordeiro, C.; Alegre, T.M.; Wiederhecker, G.S.; Dainese, P. Brillouin scattering self-cancellation. Nat. Commun. 2016, 7, 11759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kabakova, I.V.; Pant, R.; Choi, D.Y.; Debbarma, S.; Luther-Davies, B.; Madden, S.J.; Eggleton, B.J. Narrow linewidth Brillouin laser based on chalcogenide photonic chip. Opt. Lett. 2013, 38, 3208–3211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jouybari, S.N. Brillouin gain enhancement in nano-scale photonic waveguide. Photonics Nanostruct. Fundam. Appl. 2018, 29, 8–14. [Google Scholar] [CrossRef]
- Niu, Y.; Lin, C.; Liu, X.; Chen, Y.; Zhu, S. Optimizing the efficiency of a periodically poled lnoi waveguide using in situ monitoring of the ferroelectric domains. Appl. Phys. Lett. 2020, 116, 101104. [Google Scholar] [CrossRef]
- Poulton, C.G.; Pant, R.; Eggleton, B.J. Acoustic confinement and Stimulated Brillouin Scattering in integrated optical waveguides. J. Opt. Soc. Am. B Opt. Phys. 2013, 30, 2657–2664. [Google Scholar] [CrossRef]
- Wong, K.-K. Properties of Lithium Niobate; INSPEC/IEE: London, UK, 2002; p. 28. [Google Scholar]
- Parameswaran, K.R.; Route, R.K.; Kurz, J.R.; Roussev, R.V.; Fejer, M.M.; Fujimura, M. Highly efficient second-harmonic generation in buried waveguides formed by annealed and reverse proton exchange in periodically poled lithium niobate. Opt. Lett. 2002, 27, 179–181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, G.D.; Batchko, R.G.; Tulloch, W.M.; Fejer, M.M.; Byer, R.L. 42%-efficient single-pass cw second-harmonic generation in periodically poled lithium niobate. Opt. Lett. 1997, 22, 1834–1836. [Google Scholar] [CrossRef] [PubMed]
- Tanzilli, S.; Tittel, W.; Riedmatten, H.D.; Zbinden, H.; Baldi, P.; Demicheli, M.; Ostrowsky, D.; Gisin, N. PPLN waveguide for quantum communication. Eur. Phys. J. D 2002, 18, 155–160. [Google Scholar] [CrossRef] [Green Version]
- Langrock, C.; Diamanti, E.; Roussev, R.V.; Yamamoto, Y.; Fejer, M.M.; Takesue, H. Highly efficient single-photon detection at communication wavelengths by use of upconversion in reverse-proton-exchanged periodically poled LiNbO3waveguides. Opt. Lett. 2005, 30, 1725–1727. [Google Scholar] [CrossRef] [PubMed]
- Tanzilli, S.; Tittel, W.; Halder, M.; Alibart, O.; Baldi, P.; Gisin, N.; Zbinden, H. A photonic quantum information interface. Nature 2005, 437, 116–120. [Google Scholar] [CrossRef] [PubMed]
- Damzen, M.J.; Vlad, V.I.; Babin, V.; Mocofanescu, A. Stimulated Brillouin Scattering: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2010; pp. 26–27. [Google Scholar]
- Mirnaziry, S.R.; Wolff, C.; Steel, M.J.; Eggleton, B.J.; Poulton, C.G. Stimulated Brillouin scattering in silicon/chalcogenide slot waveguides. Opt. Express 2016, 24, 4786. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: Cambridge, MA, USA, 2007; pp. 355–383. [Google Scholar]
- Qiu, W.; Rakich, P.T.; Shin, H.; Dong, H.; Soljačić, M.; Wang, Z. Stimulated Brillouin scattering in nanoscale silicon step-index waveguides: A general framework of selection rules and calculating SBS gain. Opt. Express 2013, 21, 31402–31419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aryanfar, I.; Wolff, C.; Steel, M.J.; Eggleton, B.J.; Poulton, C.G. Mode conversion using stimulated Brillouin scattering in nanophotonic silicon waveguides. Opt. Express 2014, 22, 29270–29282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, Z.; Sun, X. Giant enhancement of stimulated Brillouin scattering with engineered phoxonic crystal waveguides. Opt. Express 2018, 26, 1255–1267. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Qiu, W.; Jarecki, R.; Cox, J.A.; Iii, R.; Starbuck, A.; Zheng, W.; Rakich, P.T. Tailorable stimulated Brillouin scattering in nanoscale silicon waveguides. Nat. Commun. 2013, 4, 1944. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peter, T.R.; Cox, J.A.; Shin, H.; Zheng, W.; Potter, R.C. Traveling-wave photon-phonon coupling as the basis for new signal processing technologies. In Proceedings of the SPIE Defense and Security Symposium, Baltimore, MD, USA, 5–9 May 2014. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Yu, Y.; Li, Y.; Bai, Z.; Wang, G.; Li, K.; Song, C.; Wang, Z.; Li, S.; Wang, Y.; et al. Tailorable Brillouin Light Scattering in a Lithium Niobate Waveguide. Appl. Sci. 2021, 11, 8390. https://doi.org/10.3390/app11188390
Wang W, Yu Y, Li Y, Bai Z, Wang G, Li K, Song C, Wang Z, Li S, Wang Y, et al. Tailorable Brillouin Light Scattering in a Lithium Niobate Waveguide. Applied Sciences. 2021; 11(18):8390. https://doi.org/10.3390/app11188390
Chicago/Turabian StyleWang, Wuyue, Yu Yu, Yunfei Li, Zhenxu Bai, Gong Wang, Kai Li, Changyu Song, Zhiyong Wang, Sensen Li, Yulei Wang, and et al. 2021. "Tailorable Brillouin Light Scattering in a Lithium Niobate Waveguide" Applied Sciences 11, no. 18: 8390. https://doi.org/10.3390/app11188390
APA StyleWang, W., Yu, Y., Li, Y., Bai, Z., Wang, G., Li, K., Song, C., Wang, Z., Li, S., Wang, Y., Lu, Z., Li, Y., Liu, T., & Yan, X. (2021). Tailorable Brillouin Light Scattering in a Lithium Niobate Waveguide. Applied Sciences, 11(18), 8390. https://doi.org/10.3390/app11188390







