Ionic Conductivity and Dielectric Relaxation of NASICON Superionic Conductors at the Near-Cryogenic Regime †
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Solid-State Reaction (SSR) Synthesis Protocol and Post-Synthesis Processing
2.2. Instrumentation and Characterization Methods
3. Results and Discussion
3.1. Preliminary Material Characterization: Effects of Processing Parameters
3.1.1. Particle Size Distribution, Microporosity, and Thermal Profiles
3.1.2. Macro- and Microstructure Phase Investigations
3.2. Ionic Conductivity and Dielectric Relaxation Investigations
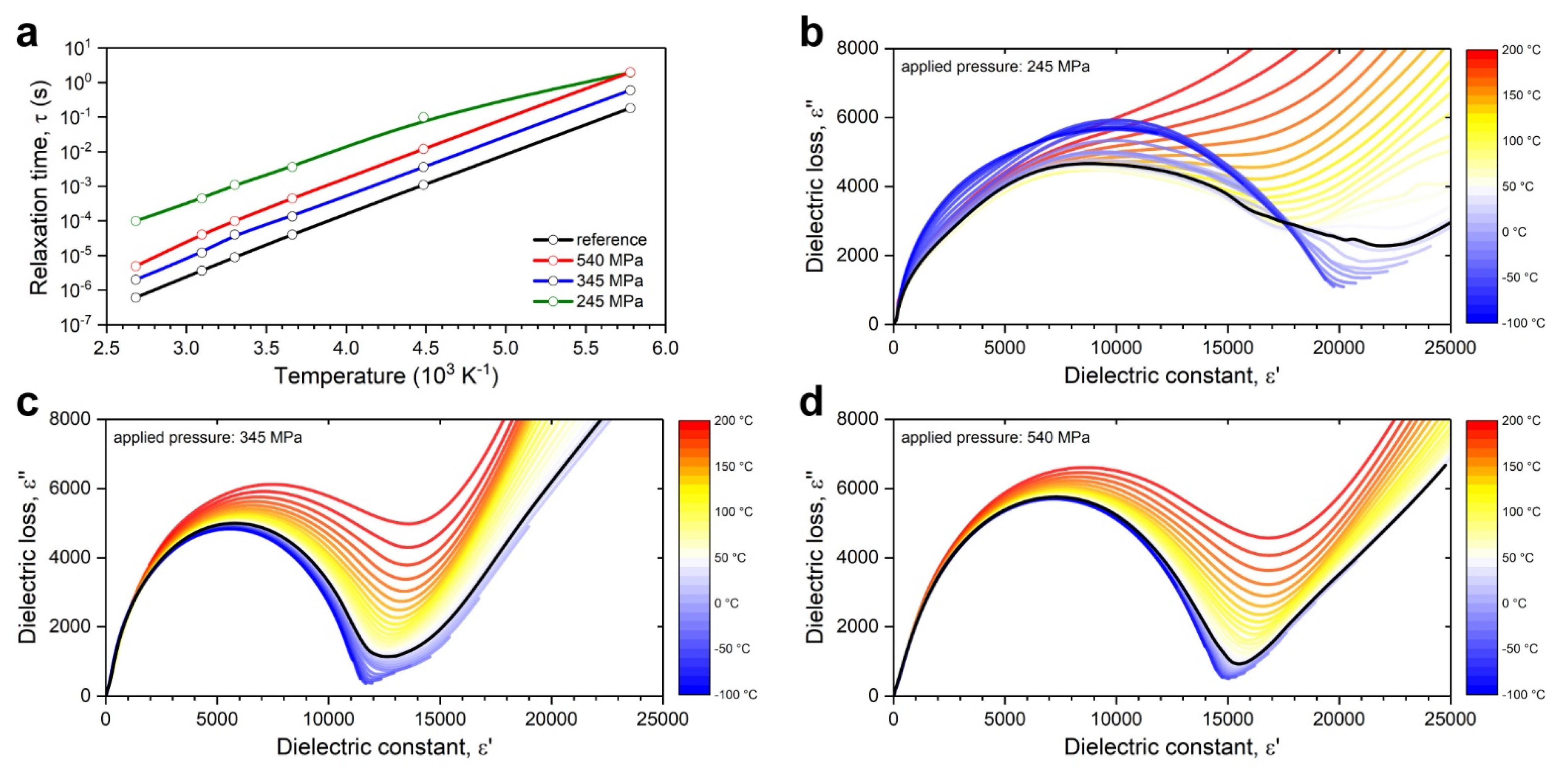
3.2.1. Broadband Ionic Conductivity Measurements
3.2.2. Broadband Dielectric Permittivity Measurements
4. Conclusions
- Precursor particle size (nano- vs. micron-sized particles) is not necessarily of critical importance, provided that ball-milling has been performed rigorously to arrive at monomodal but polydisperse distributions of NASICON precursors;
- Excess zirconia contamination can be modestly controlled, but not fully suppressed due to the high sintering temperature, by applying selected isostatic pressure levels during pellet formation in order to minimize the zirconia crystallite size; excessive pressure levels (>345 MPa) reverse this trend by dispersing zirconia particles over a wider phase distribution, although a higher packing order of the material is induced;
- Low pressure levels (<345 MPa) may cause inhomogeneity and mechanical stability issues due to zirconia accretion and poor packing order, reflecting negatively on the ionic conductivity of the system;
- Low pressure levels may also result in significant hysteresis between relaxation and ionic transport activation energies, with a lower energy barrier for relaxation causing early dissipation of energy and thus diminishing ionic conductivity;
- The high-frequency permittivity limit ε∞ may be assessed by dielectric permittivity scans near the cryogenic regime without having to access high frequencies to negate dipole contributions to polarization;
- Phase-space mappings have identified a correlated high ionic conductivity band with its corresponding relaxation band in the dissipation factor spectra, both propagating diagonally in tandem frequency and temperature dependency; and
- Phase-space mappings of the dissipation factor revealed a secondary relaxation band that can be associated with the monoclinic-to-rhombohedral lattice transition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anantharamulu, N.; Rao, K.K.; Rambabu, G.; Kumar, B.V.; Radha, V.; Vithal, M. A wide-ranging review on Nasicon type materials. J. Mater. Sci. 2011, 46, 2821–2837. [Google Scholar] [CrossRef]
- Whittingham, M.S.; Huggins, R.A. Measurement of sodium ion transport in beta alumina using reversible solid electrodes. J. Chem. Phys. 1971, 54, 414–416. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Hong, H.P.; Kafalas, J.A. Fast Na+-ion transport in skeleton structures. Mater. Res. Bull. 1976, 11, 203–220. [Google Scholar] [CrossRef]
- Hong, H.P. Crystal structures and crystal chemistry in the system Na1+xZr2SixP3−xO12. Mater. Res. Bull. 1976, 11, 173–182. [Google Scholar] [CrossRef]
- Gordon, R.S.; Miller, G.R.; McEntire, B.J.; Beck, E.D.; Rasmussen, J.R. Fabrication and characterization of Nasicon electrolytes. Solid State Ion. 1981, 3, 243–248. [Google Scholar] [CrossRef]
- Kohler, H.; Schulz, H. Single crystal investigations on NASICON Na/1 + z/Zr/2− y/Si/x/P/3− x/0/12/; 0 ≤ y ≤ 3/4, 0 ≤ z ≤ 0 comparison of the compounds x = 1.24 and x = 3. Solid State Ion. 1983, 9, 795–798. [Google Scholar] [CrossRef]
- Kohler, H.; Schulz, H.; Melnikov, O. Composition and conduction mechanism of the NASICON structure X-ray diffraction study on two crystals at different temperatures. Mater. Res. Bull. 1983, 18, 1143–1152. [Google Scholar] [CrossRef]
- Nicholas, V.A.; Johnson, P.J.; Kingon, A.I. Conductivity measurements in the Nasicon system. Solid State Ion. 1985, 17, 351–357. [Google Scholar] [CrossRef]
- Kohler, H.; Schulz, H. NASICON solid electrolytes: Part I—The Na+-diffusion path and its relation to the structure. Mater. Res. Bull. 1985, 20, 1461–1471. [Google Scholar] [CrossRef]
- Kohler, H.; Schulz, H. NASICON solid electrolytes: Part II—X-ray diffraction experiments on sodium-zirconium-phosphate single crystals at 295K and at 993K. Mater. Res. Bull. 1986, 21, 23–31. [Google Scholar] [CrossRef]
- Kreuer, K.D.; Kohler, H.; Warhus, U.; Schulz, H. NASICON solid electrolytes: Part III—Sodium conductivity enhancement along domain and grain boundaries. Mater. Res. Bull. 1986, 21, 149–159. [Google Scholar] [CrossRef]
- Kreuer, K.D.; Warhus, U. NASICON solid electrolytes: Part IV—Chemical durability. Mater. Res. Bull. 1986, 21, 357–363. [Google Scholar] [CrossRef]
- Didisheim, J.J.; Prince, E.; Wuensch, B.J. Neutron Rietveld analysis of structural changes in NASICON solid solutions Na1+xZr2SixP3−xO12 at elevated temperatures: X = 1.6 and 2.0 at 320 °C. Solid State Ion. 1986, 18, 944–958. [Google Scholar] [CrossRef]
- Rudolf, P.; Jorgensen, J.; Clearfield, A. A time-of-flight neutron powder Rietveld refinement study at elevated temperature on a monoclinic near-stoichiometric NASICON. J. Solid State Chem. 1988, 72, 100–112. [Google Scholar] [CrossRef]
- Lightfoot, P.; Woodcock, D.A.; Jorgensen, J.D.; Short, S. Low thermal expansion materials: A comparison of the structural behaviour of La0.33Ti2(PO4)3, Sr0.5Ti2(PO4)3 and NaTi2(PO4)3. Int. J. Inorg. Mater. 1999, 1, 53–60. [Google Scholar] [CrossRef]
- Saito, Y.; Maruyama, T. Recent developments of the sensors for carbon oxides using solid electrolytes. Solid State Ion. 1988, 28, 1644–1647. [Google Scholar] [CrossRef]
- Yao, S.; Shimizu, Y.; Miura, N.; Yamazoe, N. Solid electrolyte CO2 sensor using binary carbonate electrode. Chem. Lett. 1990, 19, 2033–2036. [Google Scholar] [CrossRef]
- Scheetz, B.E.; Agrawal, D.K.; Breval, E.; Roy, R. Sodium zirconium phosphate (NZP) as a host structure for nuclear waste immobilization: A review. Waste Manag. 1994, 14, 489–505. [Google Scholar] [CrossRef]
- Balagopal, S.; Landro, T.; Zecevic, S.; Sutija, D.; Elangovan, S.; Khandkar, A. Selective sodium removal from aqueous waste streams with NASICON ceramics. Sep. Purif. Technol. 1999, 15, 231–237. [Google Scholar] [CrossRef]
- Bragard, M.; Soltau, N.; Thomas, S.; De Doncker, R.W. The balance of renewable sources and user demands in grids: Power electronics for modular battery energy storage systems. IEEE Trans. Power Electron. 2010, 25, 3049–3056. [Google Scholar] [CrossRef]
- Dunn, B.; Kamath, H.; Tarascon, J.M. Electrical energy storage for the grid: A battery of choices. Science 2011, 334, 928–935. [Google Scholar] [CrossRef] [Green Version]
- Castillo, A.; Gayme, D.F. Grid-scale energy storage applications in renewable energy integration: A survey. Energy Convers. Manag. 2014, 87, 885–894. [Google Scholar] [CrossRef]
- Hueso, K.B.; Armand, M.; Rojo, T. High temperature sodium batteries: Status, challenges and future trends. Energy Env. Sci. 2013, 6, 734–749. [Google Scholar] [CrossRef]
- Noguchi, Y.; Kobayashi, E.; Plashnitsa, L.S.; Okada, S.; Yamaki, J.I. Fabrication and performances of all solid-state symmetric sodium battery based on NASICON-related compounds. Electrochim. Acta 2013, 101, 59–65. [Google Scholar] [CrossRef]
- Lalère, F.; Leriche, J.B.; Courty, M.; Boulineau, S.; Viallet, V.; Masquelier, C.; Seznec, V. An all-solid state NASICON sodium battery operating at 200 °C. J. Power Sources 2014, 247, 975–980. [Google Scholar] [CrossRef]
- Crabtree, G.; Kocs, E.; Trahey, L. The energy-storage frontier: Lithium-ion batteries and beyond. MRS Bull. 2015, 40, 1067–1078. [Google Scholar] [CrossRef] [Green Version]
- Guin, M.; Tietz, F. Survey of the transport properties of sodium superionic conductor materials for use in sodium batteries. J. Power Sources 2015, 273, 1056–1064. [Google Scholar] [CrossRef]
- Guin, M.; Tietz, F.; Guillon, O. New promising NASICON material as solid electrolyte for sodium-ion batteries: Correlation between composition, crystal structure and ionic conductivity of Na3+xSc2SixP3-xO12. Solid State Ion. 2016, 293, 18–26. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, L.; Qi, X.; Lu, Y.; Wu, F.; Zhao, J.; Yu, Y.; Hu, Y.S.; Chen, L. Solid-state sodium batteries. Adv. Energy Mater. 2018, 8, 1703012. [Google Scholar] [CrossRef]
- Ruan, Y.; Guo, F.; Liu, J.; Song, S.; Jiang, N.; Cheng, B. Optimization of Na3Zr2Si2PO12 ceramic electrolyte and interface for high performance solid-state sodium battery. Ceram. Int. 2019, 45, 1770–1776. [Google Scholar] [CrossRef]
- Wang, Y.; Song, S.; Xu, C.; Hu, N.; Molenda, J.; Lu, L. Development of solid-state electrolytes for sodium-ion battery–A short review. Nano Mater. Sci. 2019, 1, 91–100. [Google Scholar] [CrossRef]
- Kim, J.K.; Lee, E.; Kim, H.; Johnson, C.; Cho, J.; Kim, Y. Rechargeable seawater battery and its electrochemical mechanism. ChemElectroChem 2015, 2, 328–332. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Kim, H.; Park, S.; Seo, I.; Kim, Y. Na ion-conducting ceramic as solid electrolyte for rechargeable seawater batteries. Electrochim. Acta 2016, 191, 1–7. [Google Scholar] [CrossRef]
- Bae, H.; Park, J.S.; Senthilkumar, S.T.; Hwang, S.M.; Kim, Y. Hybrid seawater desalination-carbon capture using modified seawater battery system. J. Power Sources 2019, 410, 99–105. [Google Scholar] [CrossRef]
- Hwang, S.M.; Park, J.S.; Kim, Y.; Go, W.; Han, J.; Kim, Y.; Kim, Y. Rechargeable seawater batteries—From concept to applications. Adv. Mater. 2019, 31, 1804936. [Google Scholar] [CrossRef]
- Lee, C. Understanding Structural Degradation of NASICON Solid Electrolyte for Stable Seawater Batteries. Master’s Thesis, Department of Energy Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan, Korea, 2019. [Google Scholar]
- Bohnke, O.; Ronchetti, S.; Mazza, D. Conductivity measurements on nasicon and nasicon-modified materials. Solid State Ion. 1999, 122, 127–136. [Google Scholar] [CrossRef]
- Fuentes, R.O.; Figueiredo, F.M.; Marques, F.M.B.; Franco, J.I. Influence of microstructure on the electrical properties of NASICON materials. Solid State Ion. 2001, 140, 179. [Google Scholar] [CrossRef]
- Fergus, J.W. Ion transport in sodium ion conducting solid electrolytes. Solid State Ion. 2012, 227, 102–112. [Google Scholar] [CrossRef]
- Ignaszak, A.; Pasierb, P.; Gajerski, R.; Komornicki, S. Synthesis and properties of Nasicon-type materials. Thermochim. Acta 2005, 426, 7–14. [Google Scholar] [CrossRef]
- Naqash, S.; Ma, Q.; Tietz, F.; Guillon, O. Na3Zr2(SiO4)2(PO4) prepared by a solution-assisted solid state reaction. Solid State Ion. 2017, 302, 83–91. [Google Scholar] [CrossRef]
- Ejehi, F.; Marashi, S.P.H.; Ghaani, M.R.; Haghshenas, D.F. The synthesis of NASICON-type ZrNb(PO4)3 structure by the use of Pechini method. Ceram. Int. 2012, 38, 6857–6863. [Google Scholar] [CrossRef]
- Novikova, S.A.; Larkovich, R.V.; Chekannikov, A.A.; Kulova, T.L.; Skundin, A.M.; Yaroslavtsev, A.B. Electrical conductivity and electrochemical characteristics of Na3V2(PO4)3-based NASICON-type materials. Inorg. Mater. 2018, 54, 794–804. [Google Scholar] [CrossRef]
- Meunier, M.; Izquierdo, R.; Hasnaoui, L.; Quenneville, E.; Ivanov, D.; Girard, F.; Morin, F.; Yelon, A.; Paleologou, M. Pulsed laser deposition of superionic ceramic thin films: Deposition and applications in electrochemistry. Appl. Surf. Sci. 1998, 127, 466–470. [Google Scholar] [CrossRef]
- Pérez-Estébanez, M.; Isasi-Marín, J.; Rivera-Calzada, A.; León, C.; Nygren, M. Spark plasma versus conventional sintering in the electrical properties of Nasicon-type materials. J. Alloy. Compd. 2015, 651, 636–642. [Google Scholar] [CrossRef]
- Bell, N.S.; Edney, C.; Wheeler, J.S.; Ingersoll, D.; Spoerke, E.D. The influences of excess sodium on low-temperature NASICON synthesis. J. Am. Ceram. Soc. 2014, 97, 3744–3748. [Google Scholar] [CrossRef]
- Park, H.; Jung, K.; Nezafati, M.; Kim, C.S.; Kang, B. Sodium ion diffusion in NASICON (Na3Zr2Si2PO12) solid electrolytes: Effects of excess sodium. ACS Appl. Mater. Interfaces 2016, 8, 27814–27824. [Google Scholar] [CrossRef]
- Park, H.; Kang, M.; Park, Y.C.; Jung, K.; Kang, B. Improving ionic conductivity of Nasicon (Na3Zr2Si2PO12) at intermediate temperatures by modifying phase transition behavior. J. Power Sources 2018, 399, 329–336. [Google Scholar] [CrossRef]
- Naqash, S.; Tietz, F.; Yazhenskikh, E.; Müller, M.; Guillon, O. Impact of sodium excess on electrical conductivity of Na3Zr2Si2PO12 + xNa2O ceramics. Solid State Ion. 2019, 336, 57–66. [Google Scholar] [CrossRef]
- Narayanan, S.; Reid, S.; Butler, S.; Thangadurai, V. Sintering temperature, excess sodium, and phosphorous dependencies on morphology and ionic conductivity of NASICON Na3Zr2Si2PO12. Solid State Ion. 2019, 331, 22–29. [Google Scholar] [CrossRef]
- Samiee, M.; Radhakrishnan, B.; Rice, Z.; Deng, Z.; Meng, Y.S.; Ong, S.P.; Luo, J. Divalent-doped Na3Zr2Si2PO12 natrium superionic conductor: Improving the ionic conductivity via simultaneously optimizing the phase and chemistry of the primary and secondary phases. J. Power Sources 2017, 347, 229–237. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K.; Noi, K.; Hayashi, A.; Tatsumisago, M. Low temperature sintering of Na1+xZr2SixP3−xO12 by the addition of Na3BO3. Scr. Mater. 2018, 145, 67–70. [Google Scholar] [CrossRef]
- Oh, J.A.S.; He, L.; Plewa, A.; Morita, M.; Zhao, Y.; Sakamoto, T.; Song, X.; Zhai, W.; Zeng, K.; Lu, L. Composite NASICON (Na3Zr2Si2PO12) solid-state electrolyte with enhanced Na+ ionic conductivity: Effect of liquid phase sintering. ACS Appl. Mater. Interfaces 2019, 11, 40125–40133. [Google Scholar] [CrossRef] [PubMed]
- Jalalian-Khakshour, A.; Phillips, C.O.; Jackson, L.; Dunlop, T.O.; Margadonna, S.; Deganello, D. Solid-state synthesis of NASICON (Na3Zr2Si2PO12) using nanoparticle precursors for optimisation of ionic conductivity. J. Mater. Sci. 2020, 55, 2291–2302. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.M.; Lee, S.T.; Lee, D.H.; Lee, S.H.; Han, S.S.; Lim, S.K. Effect of particle size on the density and ionic conductivity of Na3Zr2Si2PO12 NASICON. J. Ceram. Process. Res. 2015, 16, 49–53. [Google Scholar]
- Zangina, T.; Hassan, J.; Matori, K.A.; Ahmadu, U.; See, A. Sintering behavior, ac conductivity and dielectric relaxation of Li1.3Ti1.7Al0.3(PO4)3 NASICON compound. Results Phys. 2016, 6, 719–725. [Google Scholar] [CrossRef] [Green Version]
- Martin, U.; Boysen, H.; Frey, F. Neutron powder investigation of tetragonal and cubic stabilized zirconia, TZP and CSZ, at temperatures up to 1400 K. Acta Crystallogr. B Struct. Sci. Cryst. 1993, 49, 403–413. [Google Scholar] [CrossRef]
- Jolley, A.G.; Taylor, D.D.; Schreiber, N.J.; Wachsman, E.D. Structural investigation of monoclinic-rhombohedral phase transition in Na3Zr2Si2PO12 and doped NASICON. J. Am. Ceram. Soc. 2015, 98, 2902–2907. [Google Scholar] [CrossRef]
- Donohue, M.D.; Aranovich, G.L. Adsorption hysteresis in porous solids. J. Colloid Interface Sci. 1998, 205, 121–130. [Google Scholar] [CrossRef]
- Bottom, R. Thermogravimetric Analysis. In Principles and Applications of Thermal Analysis, 1st ed.; Gabbott, P., Ed.; John Wiley & Sons—Blackwell Publishing: Oxford, UK, 2008; pp. 87–118. ISBN 978-1-4051-3171-1. [Google Scholar] [CrossRef]
- Bukun, N. Superionic transitions in NASICON-type solid electrolytes. Ionics 1996, 2, 63–68. [Google Scholar] [CrossRef]
- Guerrant, G.O.; Brown, D.E. Thermal stability, thermal decomposition of high-analysis fertilizers based on ammonium phosphate. J. Agric. Food Chem. 1965, 13, 493–497. [Google Scholar] [CrossRef]
- Morimoto, T.; Nagao, M.; Imai, J. The adsorption of water on SiO2, Al2O3, and SiO2·Al2O3. The relation between the amounts of physisorbed and chemisorbed water. Bull. Chem. Soc. Jpn. 1971, 44, 1282–1288. [Google Scholar] [CrossRef] [Green Version]
- Nogami, M. Glass preparation of the ZrO2-SiO2 system by the sol-gel process from metal alkoxides. J. Non-Cryst. Solids 1985, 69, 415–423. [Google Scholar] [CrossRef]
- Leonova, L.S.; Tkacheva, N.S.; Bukun, N.G. Effect of the nature of a sodium-conducting solid electrolyte on the impedance of its interface with the SmCo0.8Ti0.2O3 oxide electrode in an oxygen atmosphere. Russ. J. Electrochem. 2002, 38, 596–601. [Google Scholar] [CrossRef]
- Colomban, P.; Mouchon, E. Phase transition in, thermal history and expansion of NASICON, solid solution and lithium derivative ceramics and of SiC (mullite) fibers-NASICON composites. Solid State Ion. 1994, 73, 209–220. [Google Scholar] [CrossRef]
- Govindaraj, G.; Mariappan, C.R. Synthesis, characterization and ion dynamic studies of NASICON type glasses. Solid State Ion. 2002, 147, 49–59. [Google Scholar] [CrossRef]
- Mariappan, C.R.; Govindaraj, G. Ac conductivity, dielectric studies and conductivity scaling of NASICON materials. Mater. Sci. Eng. B 2002, 94, 82–88. [Google Scholar] [CrossRef]
- Mudenda, S.; Kale, G.M. New insight into the electrical properties and ion dynamics of screen printed NASICON thick films. J. Mater. Chem. A 2015, 3, 12268–12275. [Google Scholar] [CrossRef] [Green Version]
- Arya, A.; Sharma, A.L. Temperature and salt-dependent dielectric properties of blend solid polymer electrolyte complexed with LiBOB. Macromol. Res. 2019, 27, 334–345. [Google Scholar] [CrossRef]
- Greenhoe, B.M.; Hassan, M.K.; Wiggins, J.S.; Mauritz, K.A. Universal power law behavior of the AC conductivity versus frequency of agglomerate morphologies in conductive carbon nanotube-reinforced epoxy networks. J. Polym. Sci. B Polym. Phys. 2016, 54, 1918–1923. [Google Scholar] [CrossRef]
- Mauritz, K.A. Dielectric relaxation studies of ion motions in electrolyte-containing perfluorosulfonate ionomers. 4. Long-range ion transport. Macromolecules 1989, 22, 4483–4488. [Google Scholar] [CrossRef]
- Anjali; Patial, B.S.; Thakur, N. On the AC-conduction mechanism in Se-Te-Pb amorphous chalcogenide system: A detailed study through frequency-dependent imaginary part of AC conductivity. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2020; p. 080050. [Google Scholar] [CrossRef]
- Almond, D.P.; Duncan, G.K.; West, A.R. The determination of hopping rates and carrier concentrations in ionic conductors by a new analysis of ac conductivity. Solid State Ion. 1983, 8, 159–164. [Google Scholar] [CrossRef]
- Bounar, N.; Benabbas, A.; Ropa, P.; Carru, J.C. Synthesis and ionic conductivity of NASICON-structured LiTi2-xSnx(PO4)3 anode material for lithium-ion batteries. Adv. Mater. Process. Technol. 2017, 3, 241–249. [Google Scholar] [CrossRef]
- Dyre, J.C.; Schrøder, T.B. Universality of ac conduction in disordered solids. Rev. Mod. Phys. 2000, 72, 873–892. [Google Scholar] [CrossRef] [Green Version]
- Schrøder, T.B.; Dyre, J.C. Ac hopping conduction at extreme disorder takes place on the percolating cluster. Phys. Rev. Lett. 2008, 101, 025901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tarasov, A.; Titov, K. On the use of the Cole–Cole equations in spectral induced polarization. Geophys. J. Int. 2013, 195, 352–356. [Google Scholar] [CrossRef]

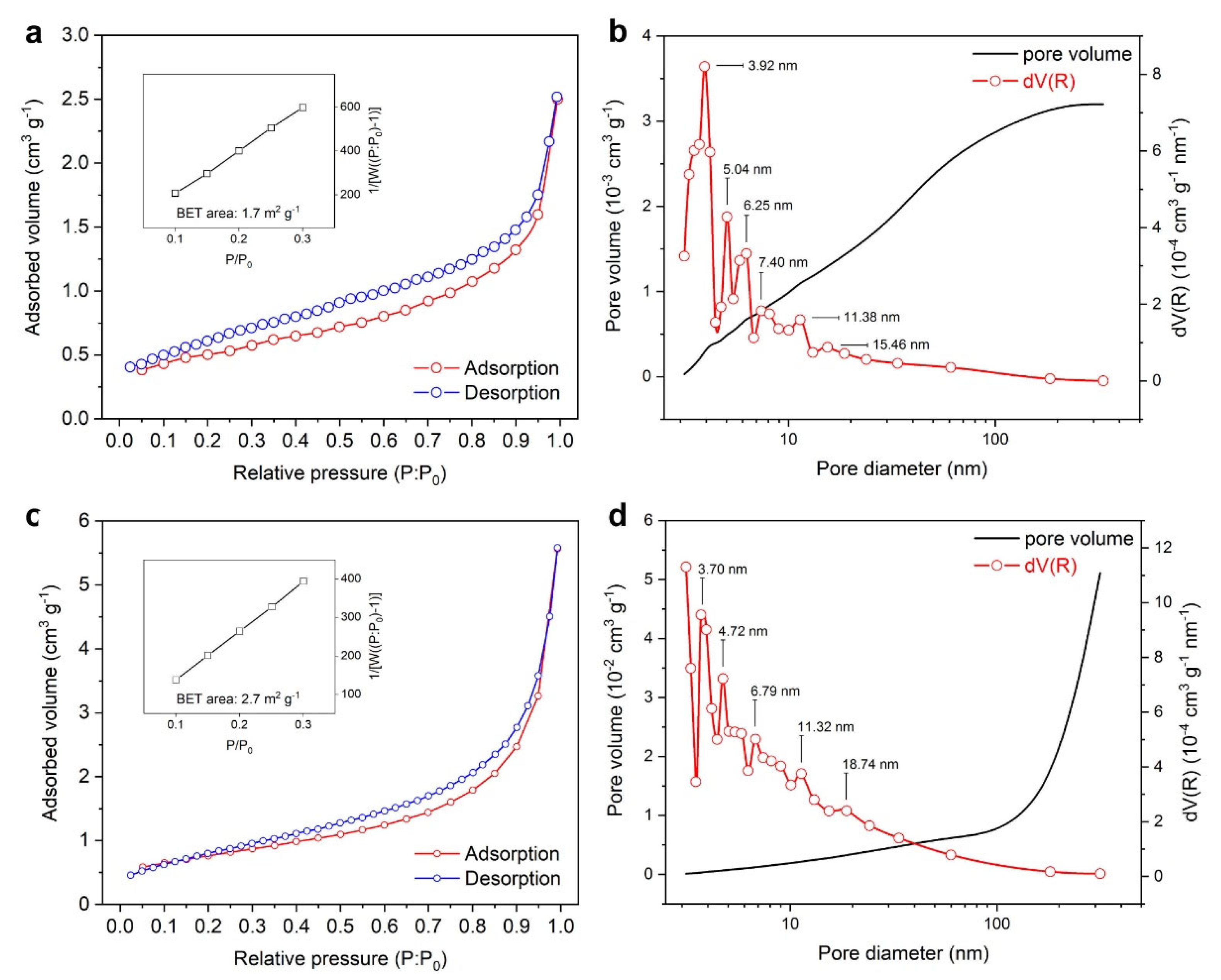
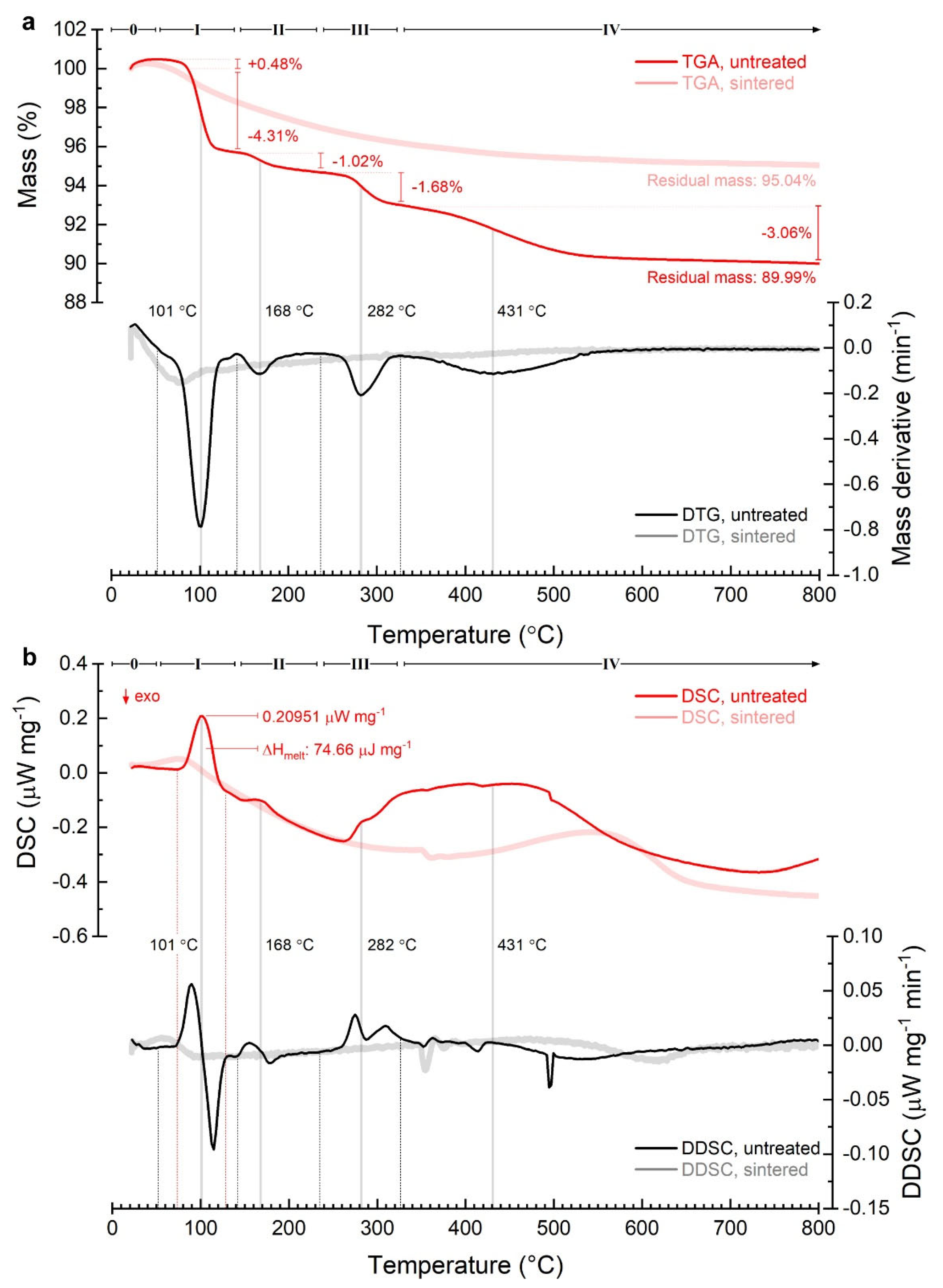

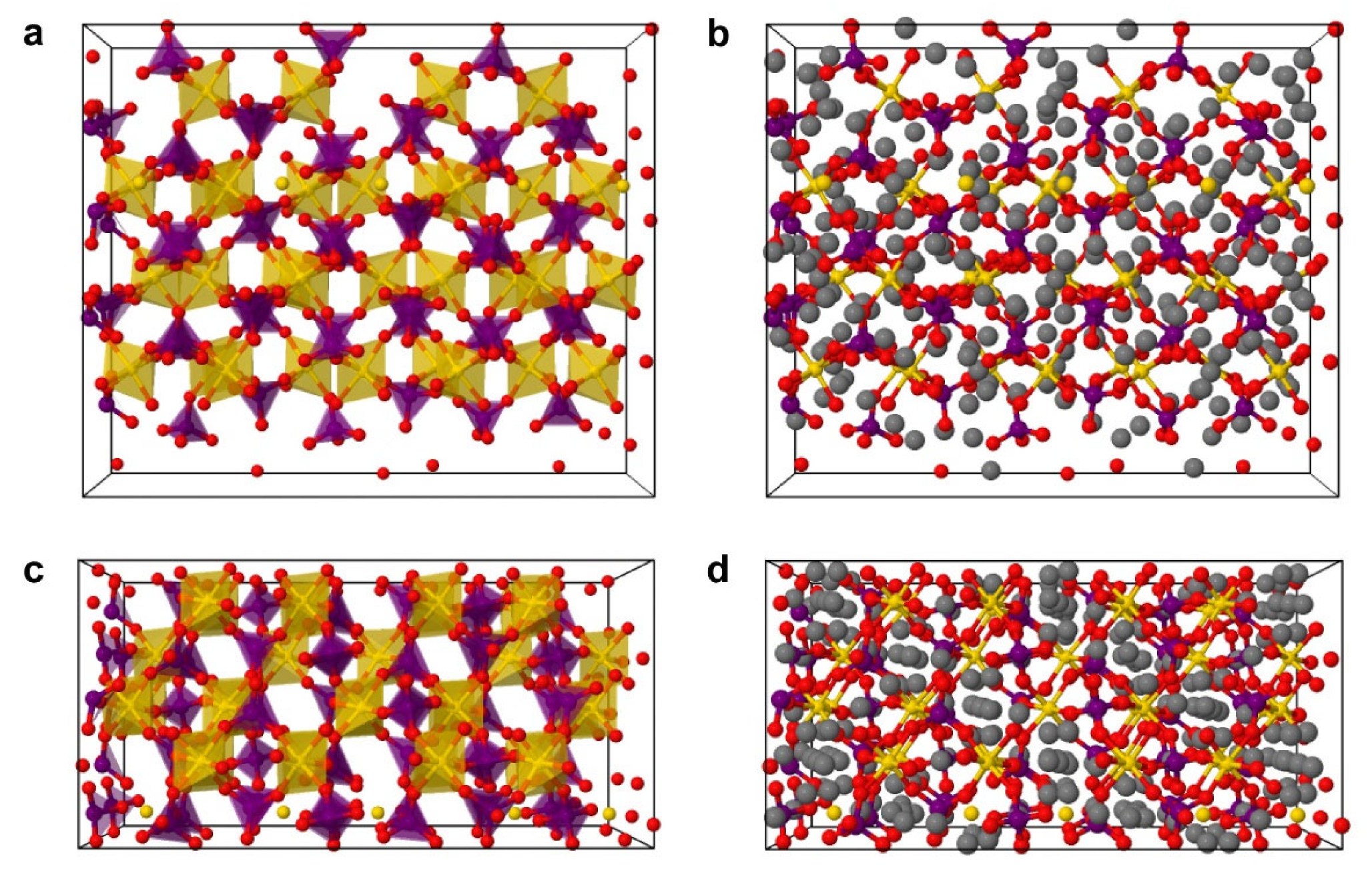
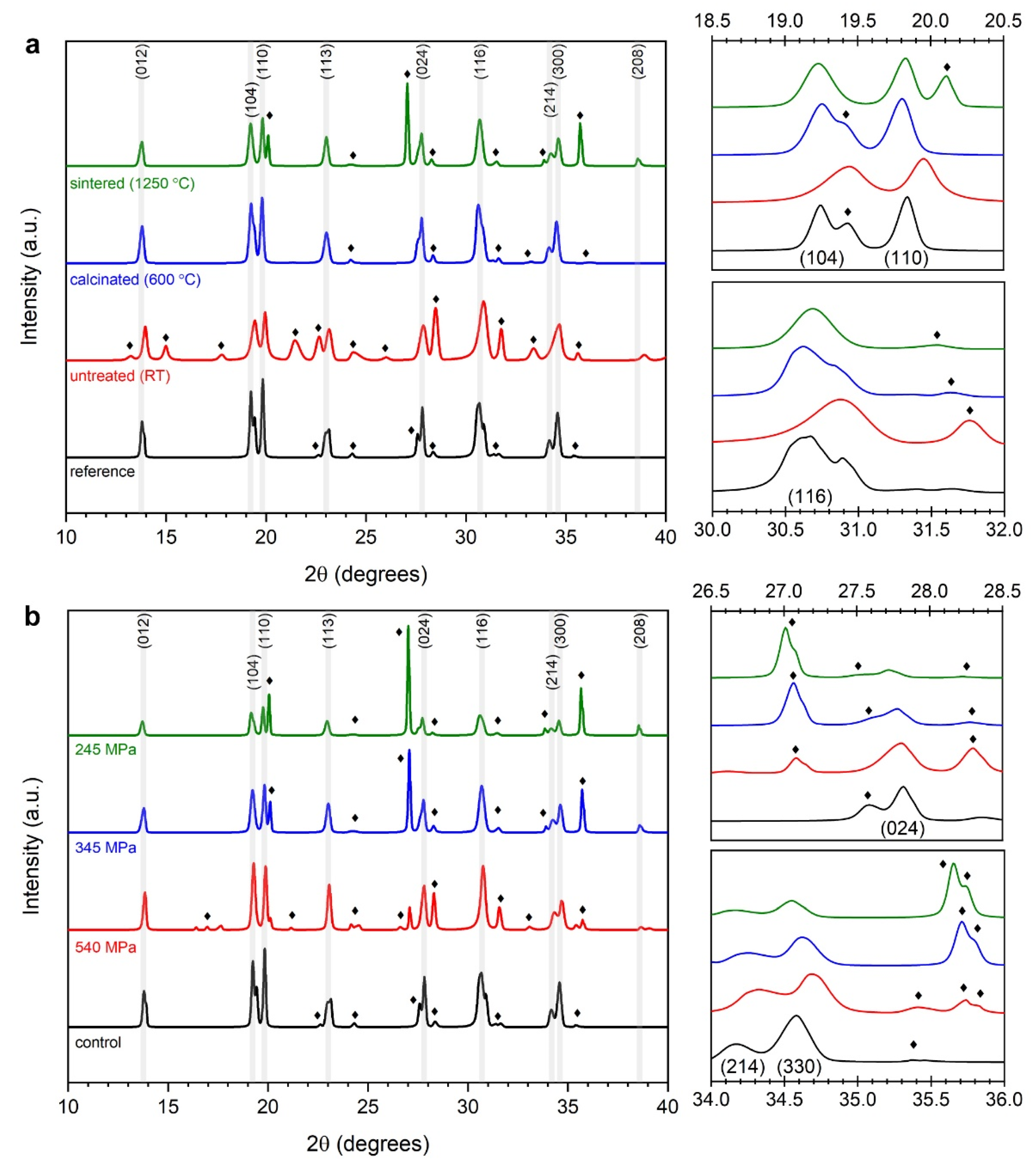

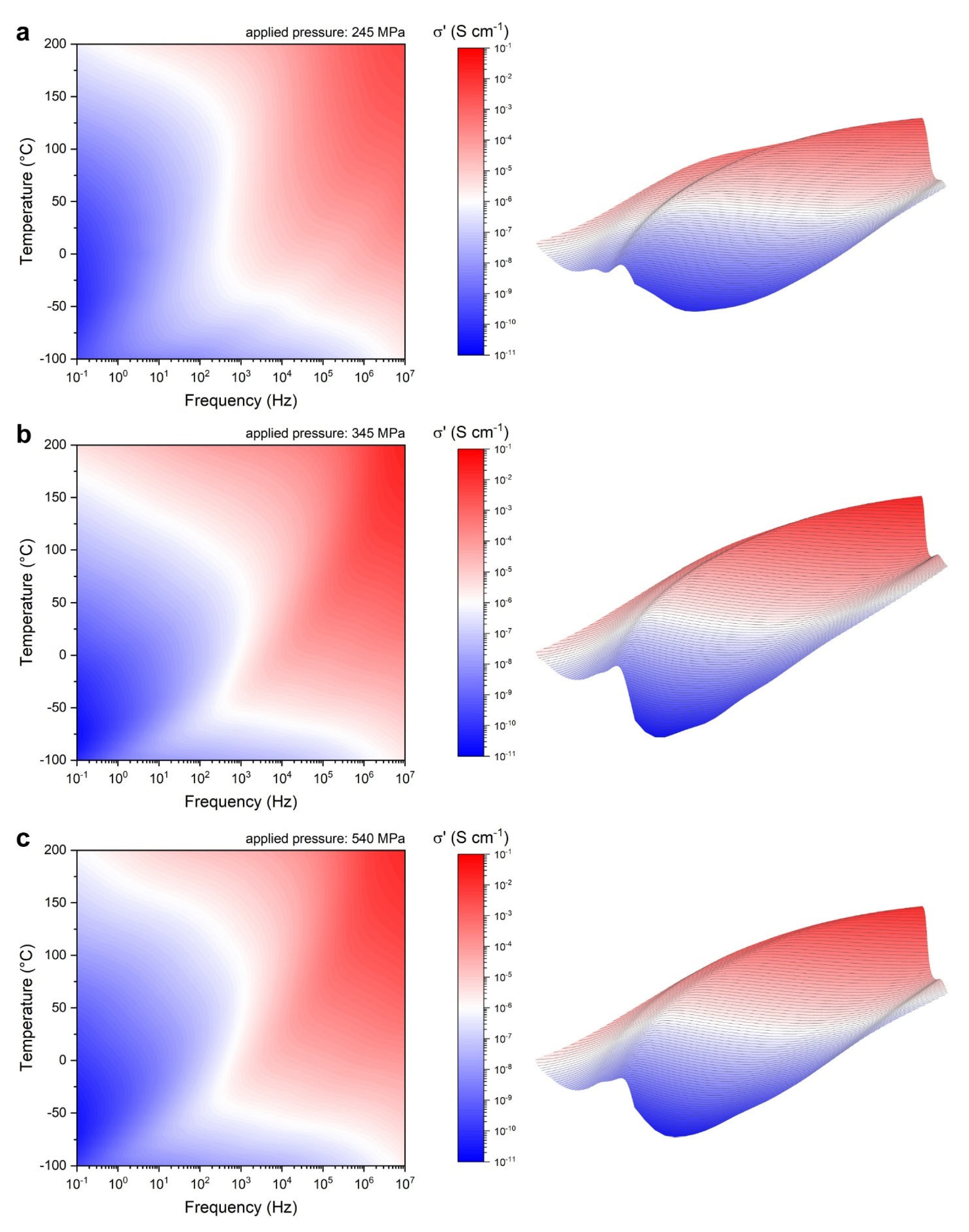
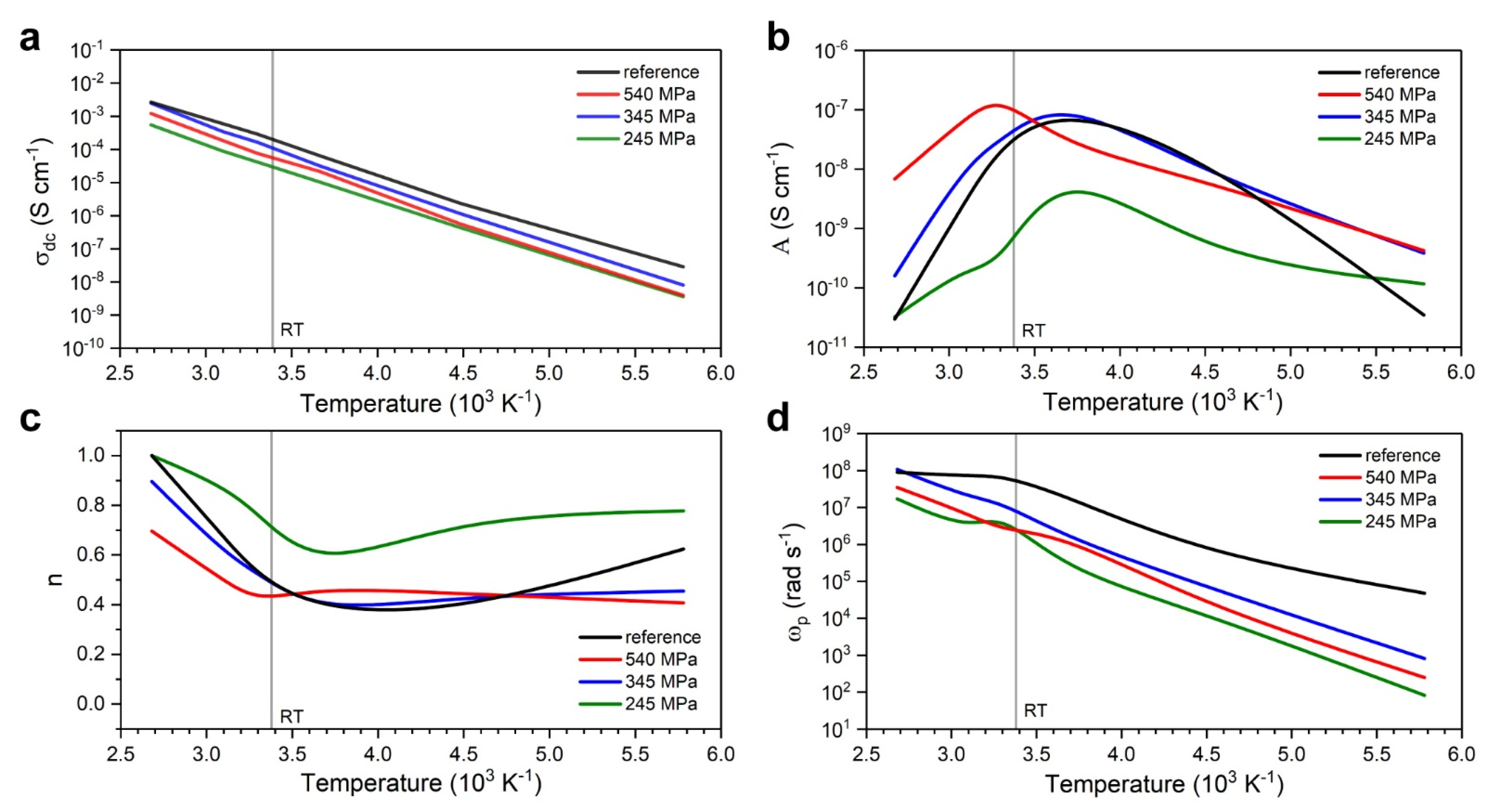
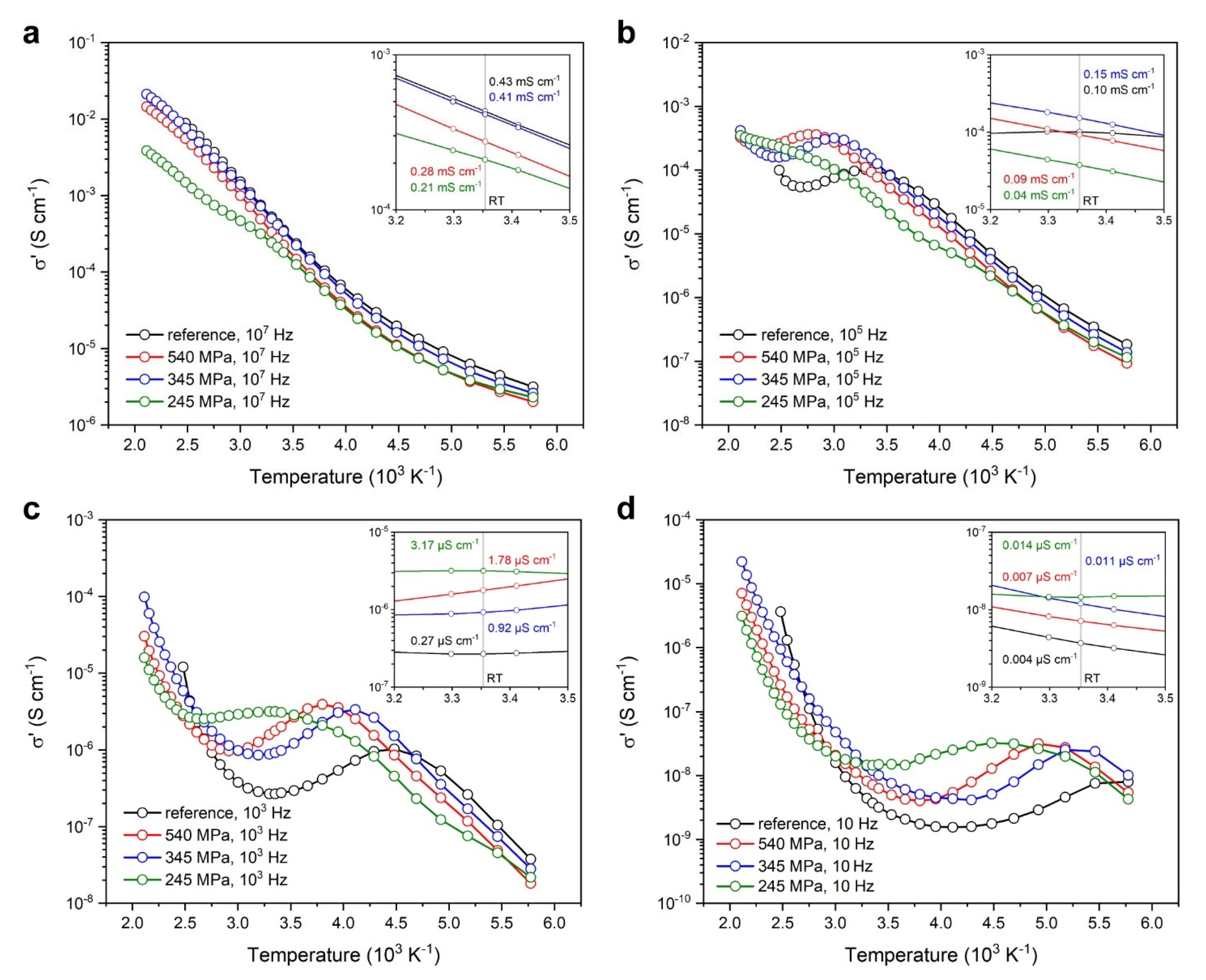
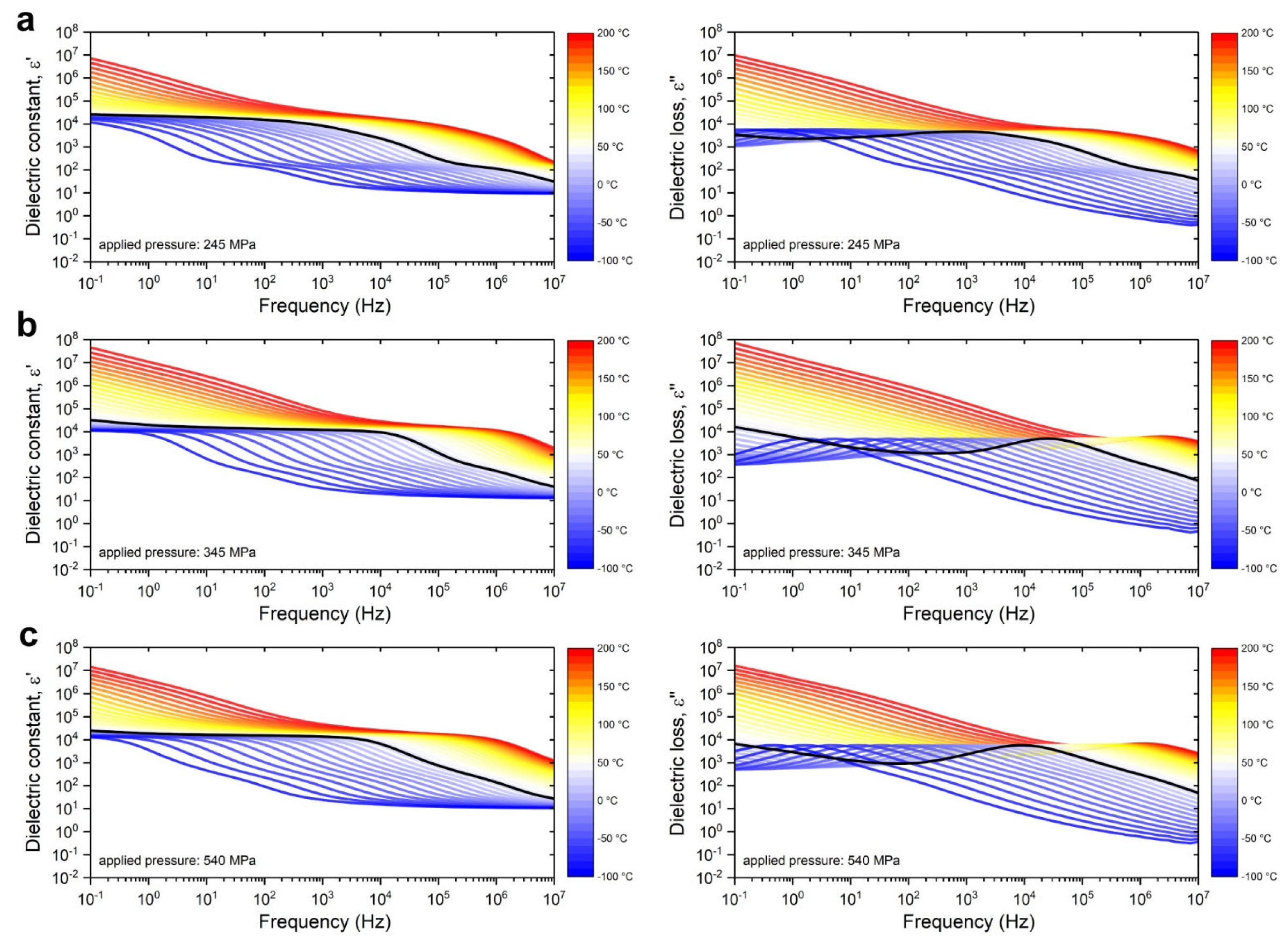

| Processing Stage | Dmode [nm] | Daverage [nm] | D10 [nm] | D50 [nm] | D90 [nm] | CV [%] | PI [%] | RMS [–] |
|---|---|---|---|---|---|---|---|---|
| Untreated | 1563.8 | 1636.1 | 1262.3 | 1591.2 | 2002.4 | 17.5 | 46.5 | 0.00249 |
| Sintered | 1363.2 | 1799.9 | 908.9 | 1635.9 | 2817.3 | 42.1 | 116.7 | 0.02643 |
| Peak Signature | Untreated (RT|80 °C) | Calcinated (600 °C) | Sintered (1250 °C) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2θ | Miller | d | FWHM | Size | d | FWHM | Size | d | FWHM | Size |
| [deg.] | (h k l) | [Å] | [deg.] | [Å] | [Å] | [deg.] | [Å] | [Å] | [deg.] | [Å] |
| 13.8 | 012 | 6.341 | 0.226 | 369 | 6.414 | 0.216 | 387 | 6.453 | 0.186 | 448 |
| 19.2 | 104 | 4.564 | 0.337 | 250 | 4.572 | 0.144 | 585 | 4.634 | 0.185 | 454 |
| 19.8 | 110 | 4.448 | 0.194 | 435 | 4.481 | 0.161 | 524 | 4.492 | 0.121 | 695 |
| 23.0 | 113 | 3.840 | 0.316 | 268 | 3.864 | 0.264 | 320 | 3.872 | 0.215 | 393 |
| 28.2 | 024 | 3.134 | 0.253 | 338 | 3.147 | 0.135 | 635 | 3.159 | 0.105 | 813 |
| 30.7 | 116 | 2.896 | 0.442 | 195 | 2.923 | 0.310 | 277 | 2.925 | 0.300 | 287 |
| 34.1 | 241 | 2.684 | 0.357 | 243 | 2.626 | 0.234 | 371 | 2.627 | 0.250 | 347 |
| 34.6 | 300 | 2.584 | 0.452 | 193 | 2.597 | 0.204 | 426 | 2.595 | 0.160 | 544 |
| 38.7 | 208 | 2.314 | 0.357 | 246 | – | – | – | 2.334 | 0.092 | 951 |
| Peak Signature | Low Pressure (245 MPa) | Medium Pressure (345 MPa) | High Pressure (540 MPa) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2θ | Miller | d | FWHM | Size | d | FWHM | Size | d | FWHM | Size |
| [deg.] | (h k l) | [Å] | [deg.] | [Å] | [Å] | [deg.] | [Å] | [Å] | [deg.] | [Å] |
| 20.1 | – | 4.425 | 0.092 | 920 | 4.413 | 0.109 | 774 | 4.441 | 0.101 | 834 |
| 27.0 | – | 3.299 | 0.078 | 1095 | 3.292 | 0.078 | 859 | 3.290 | 0.088 | 974 |
| 28.3 | – | 3.159 | 0.105 | 813 | 3.154 | 0.149 | 574 | 3.152 | 0.135 | 634 |
| 35.7 | – | 2.516 | 0.084 | 1039 | 2.513 | 0.099 | 884 | 2.510 | 0.101 | 864 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiliakos, A.; Iordache, M.; Marinoiu, A. Ionic Conductivity and Dielectric Relaxation of NASICON Superionic Conductors at the Near-Cryogenic Regime. Appl. Sci. 2021, 11, 8432. https://doi.org/10.3390/app11188432
Tiliakos A, Iordache M, Marinoiu A. Ionic Conductivity and Dielectric Relaxation of NASICON Superionic Conductors at the Near-Cryogenic Regime. Applied Sciences. 2021; 11(18):8432. https://doi.org/10.3390/app11188432
Chicago/Turabian StyleTiliakos, Athanasios, Mihaela Iordache, and Adriana Marinoiu. 2021. "Ionic Conductivity and Dielectric Relaxation of NASICON Superionic Conductors at the Near-Cryogenic Regime" Applied Sciences 11, no. 18: 8432. https://doi.org/10.3390/app11188432







