Non-Classic Atmospheric Optical Turbulence: Review
Abstract
:1. Introduction
1.1. Early Studies
1.2. Kolmogorov Theory (1941–1942)
1.3. Batchelor-Leigh-Kraichnan Theory
2. Measurements and Synthesis
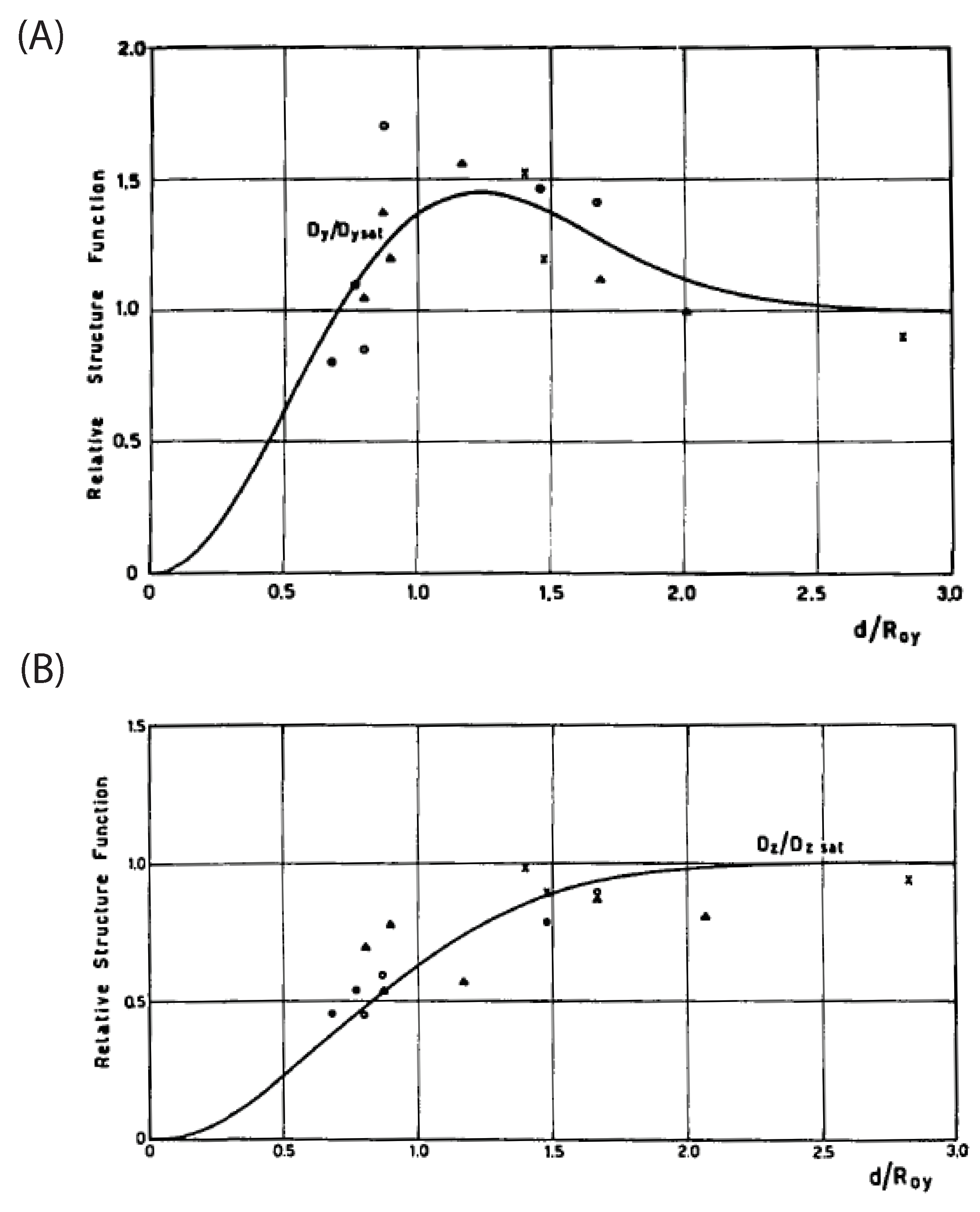
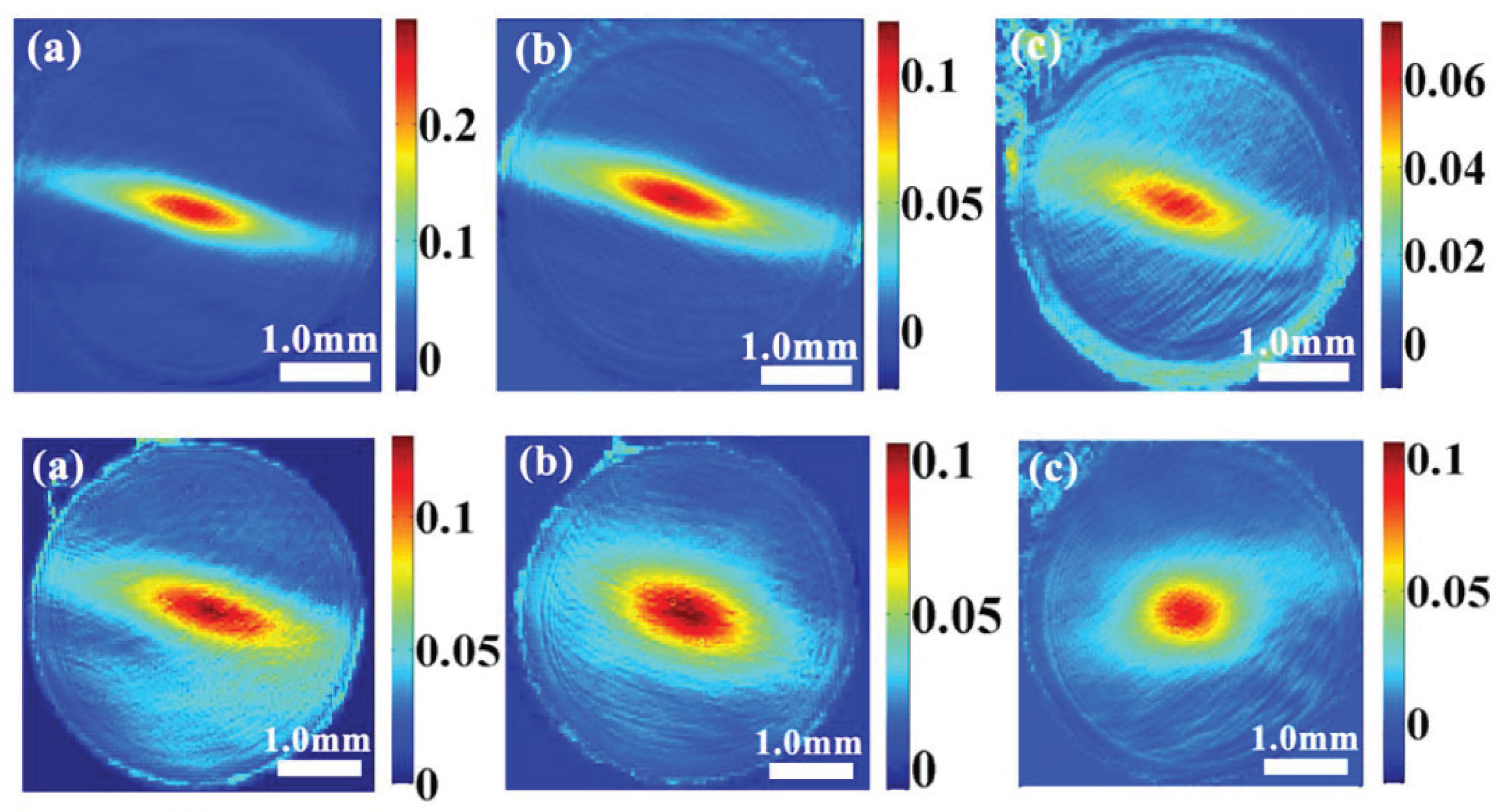
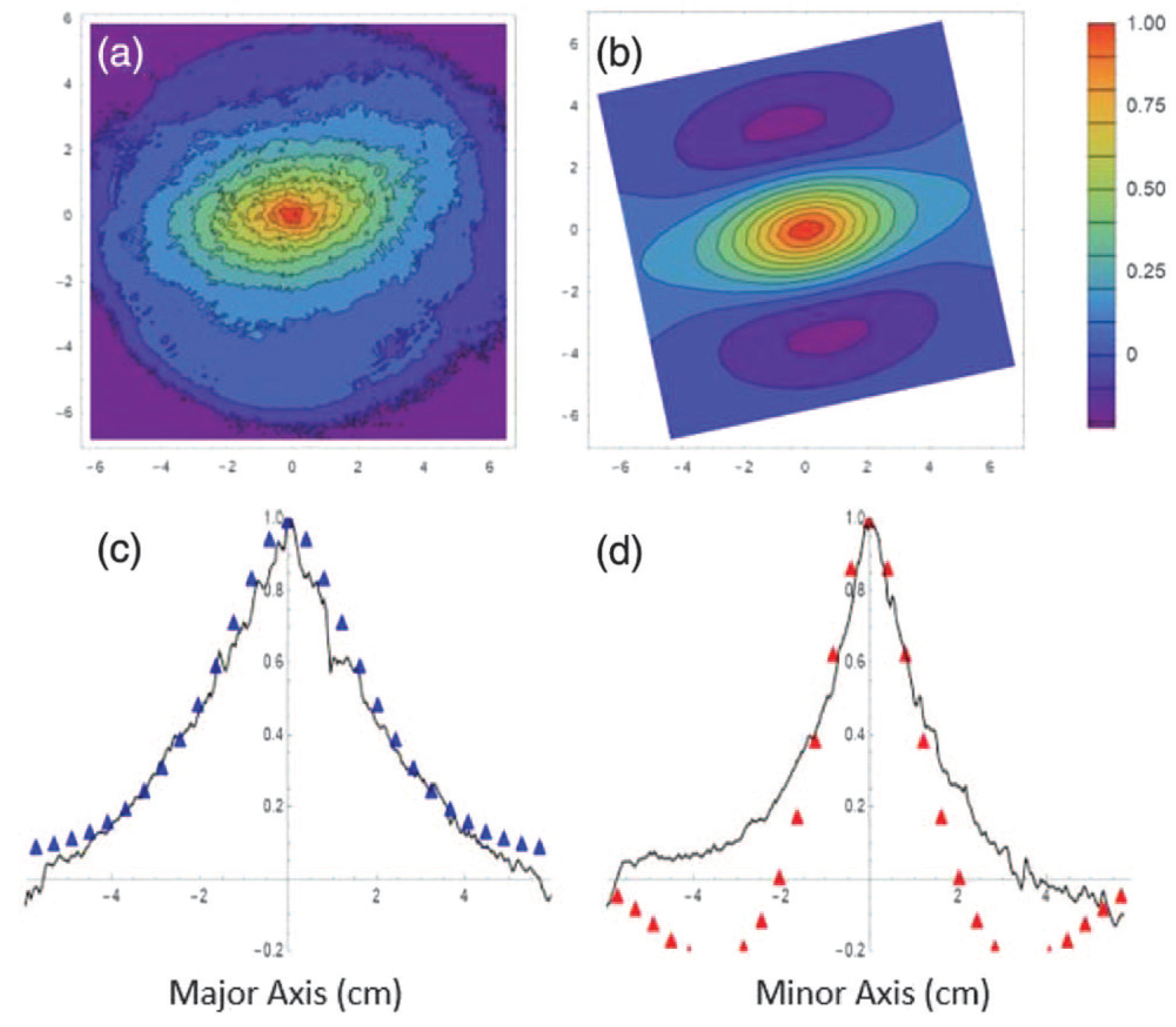
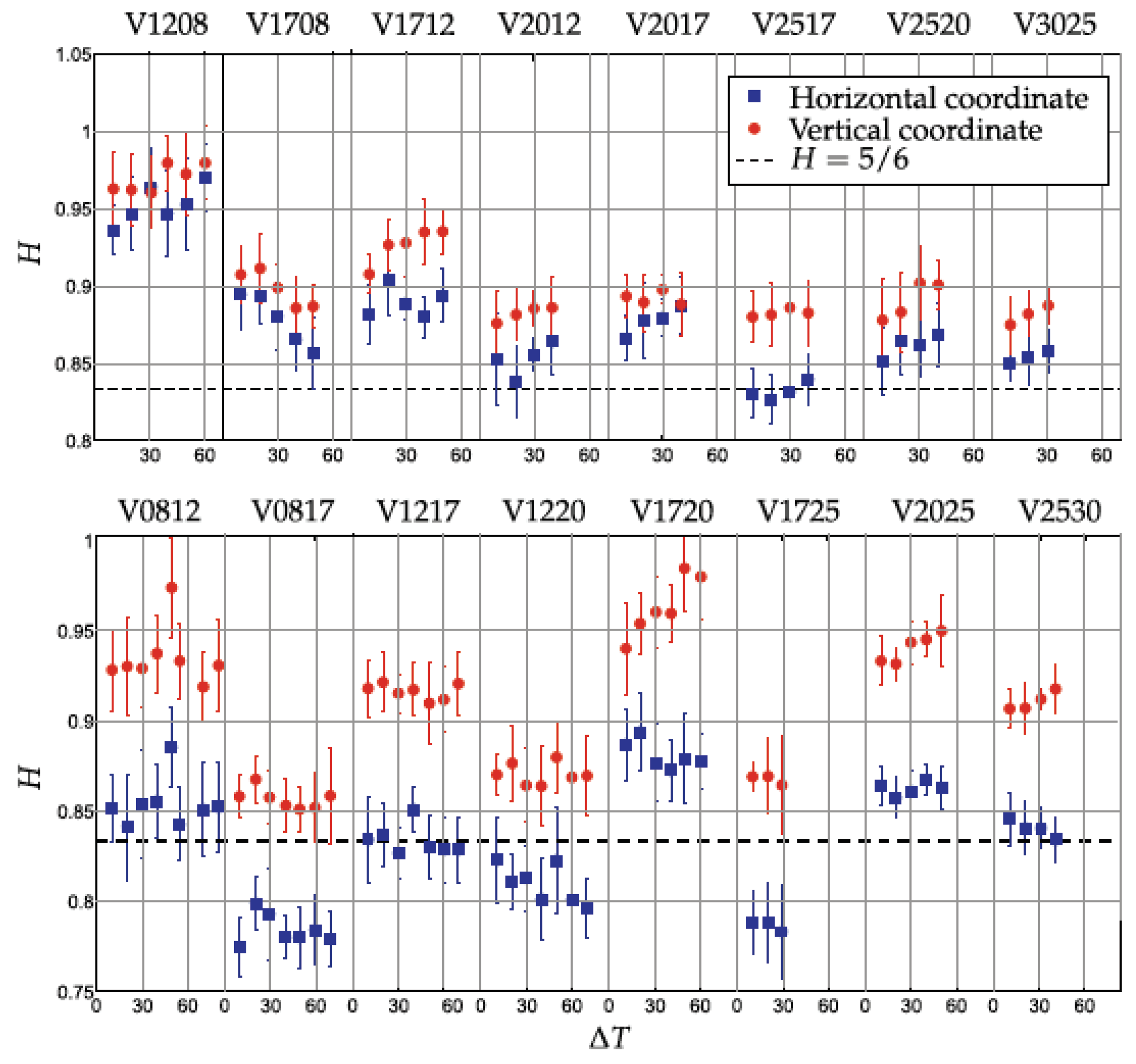
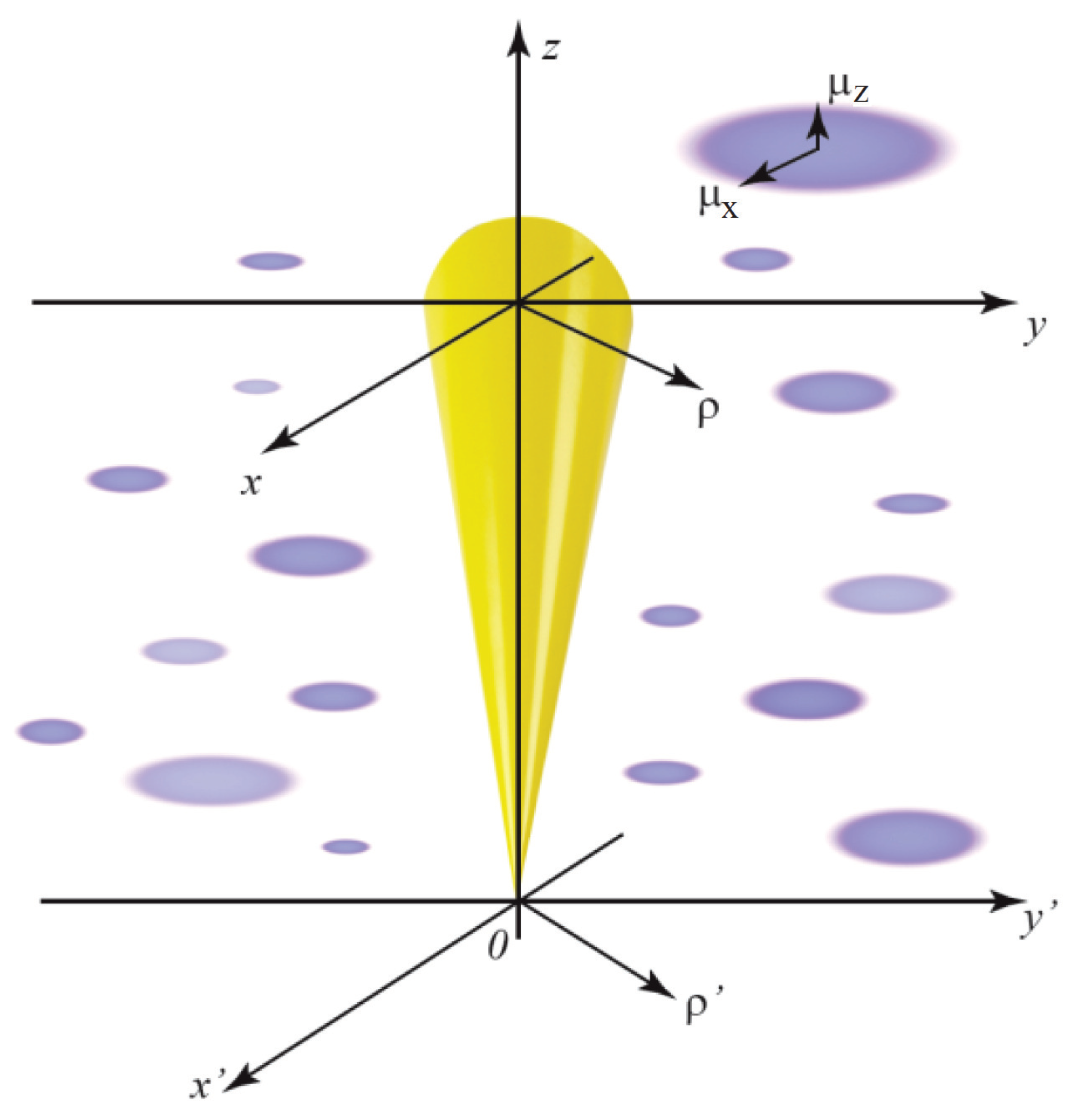
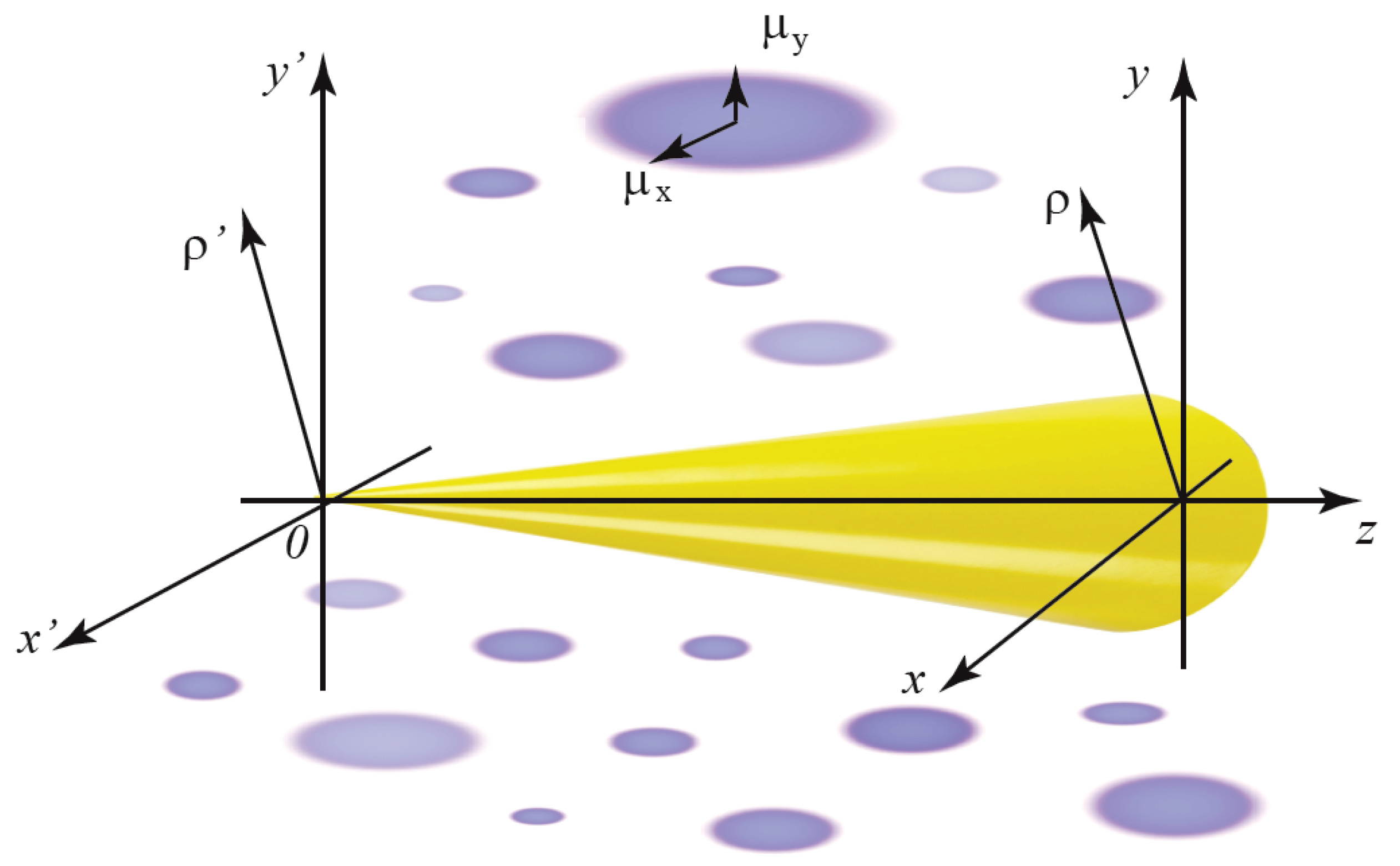
2.1. Anisotropic Turbulence
2.2. Non-Kolmogorov Power Law
2.3. Presence of Refractive Index Gradients
2.4. Deep Turbulence Effects
2.5. Non-Classic Turbulence Emulators
3. Theoretical Modeling of Optical Turbulence
3.1. Obukhov-Corrsin Theory
3.2. Non-Kolmogorov Turbulence
3.3. Anisotropic Turbulence
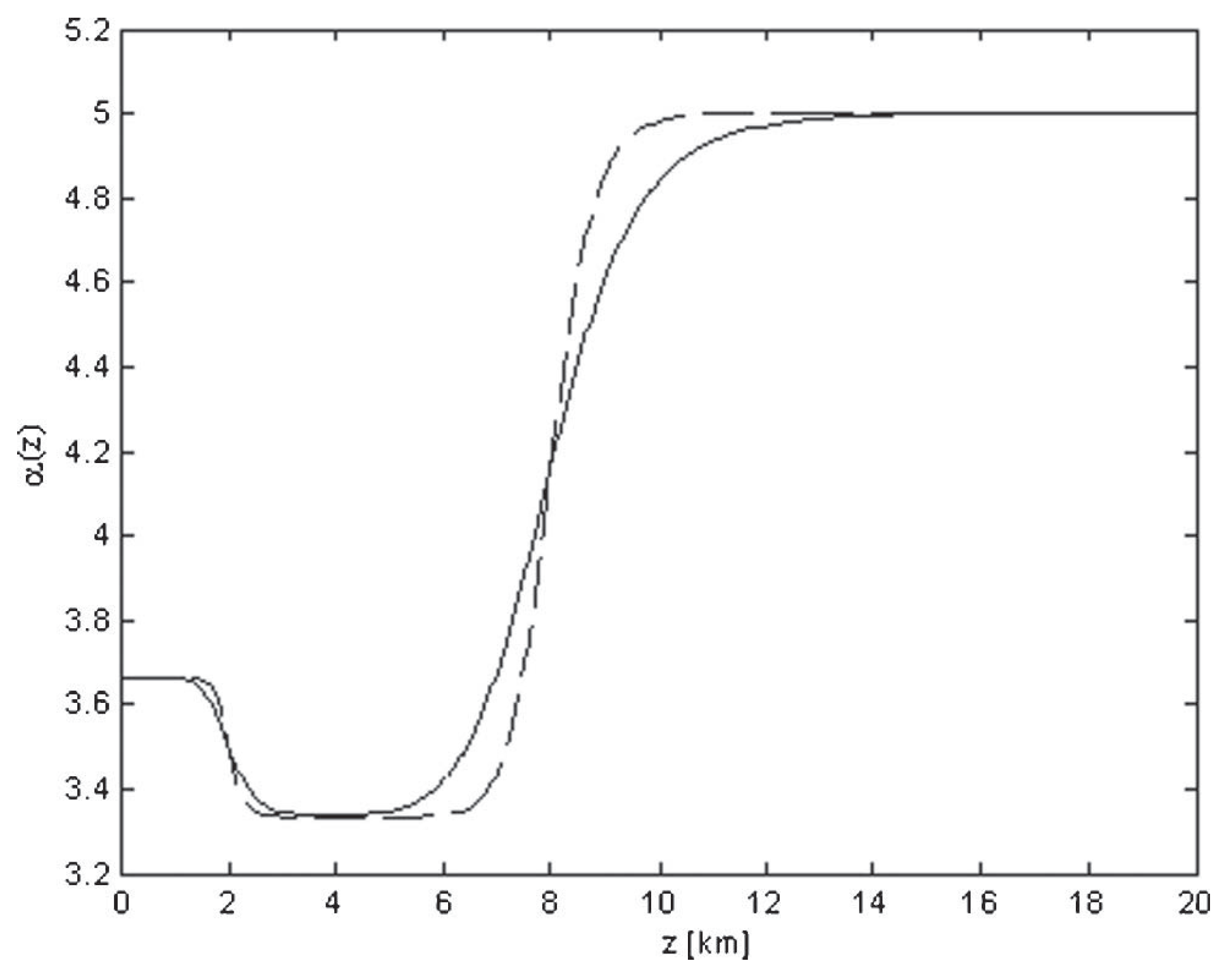
3.4. Jet-Stream Turbulence
3.5. Coherent Turbulence
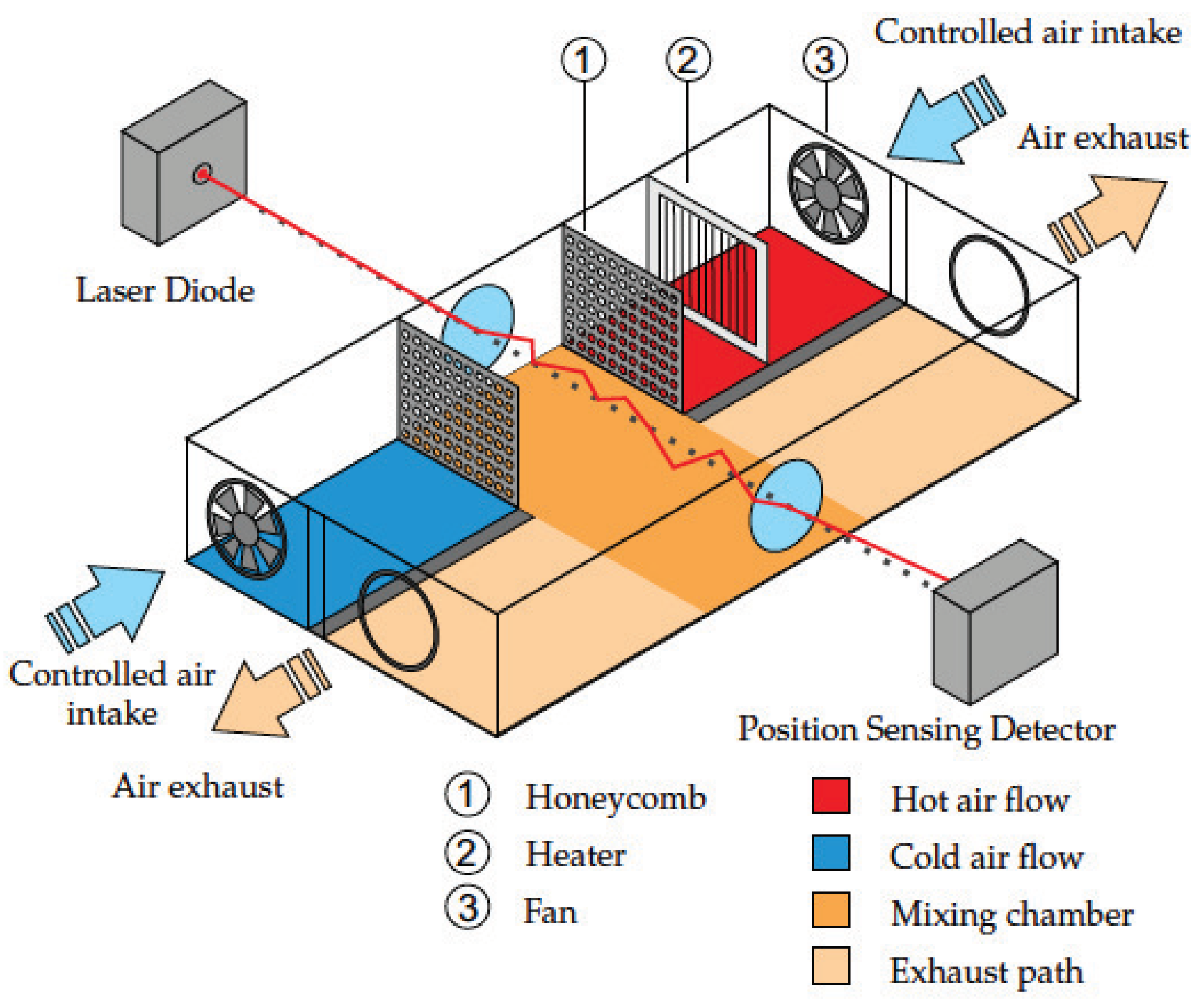
4. SLM/DMD Benchtop Simulations
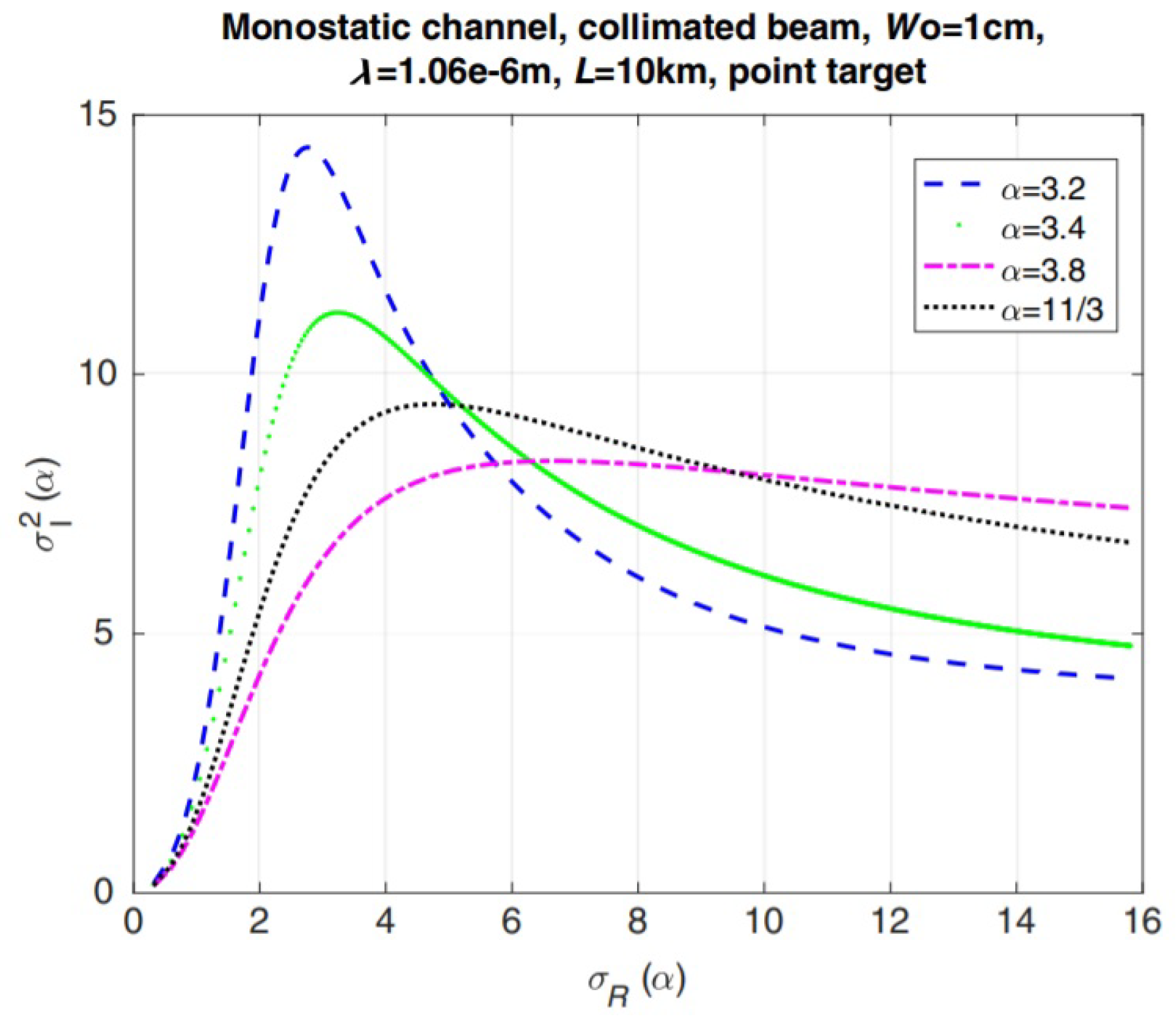
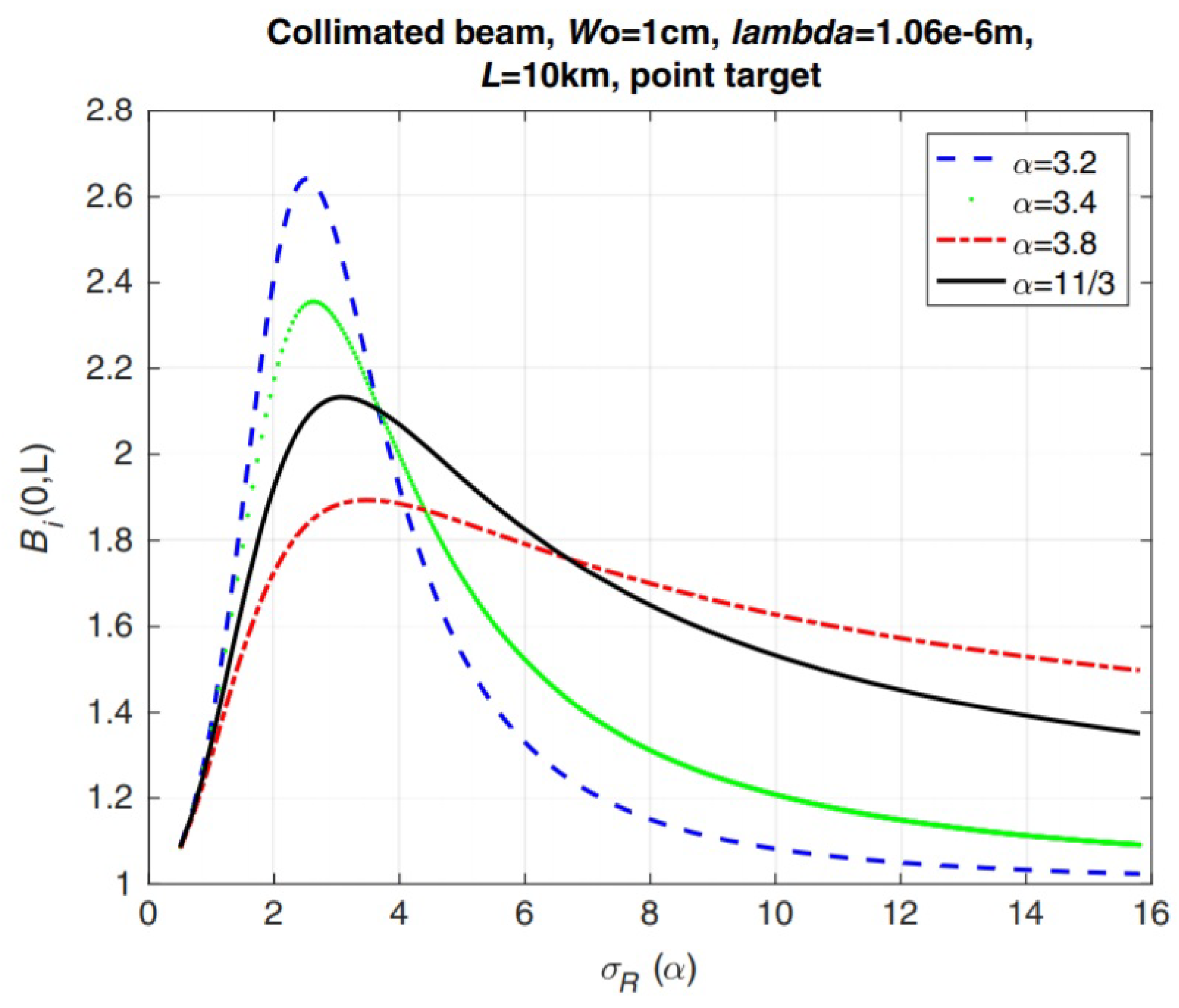
5. Theoretical Predictions for Non-Classic Turbulence-Light Interactions
6. Influence in Applications
6.1. Wireless Optical Communications
6.1.1. Aperture-Averaged Scintillation of a Gaussian Beam
6.1.2. Probability of Fade
6.1.3. Mean-Signal-to-Noise Ratio
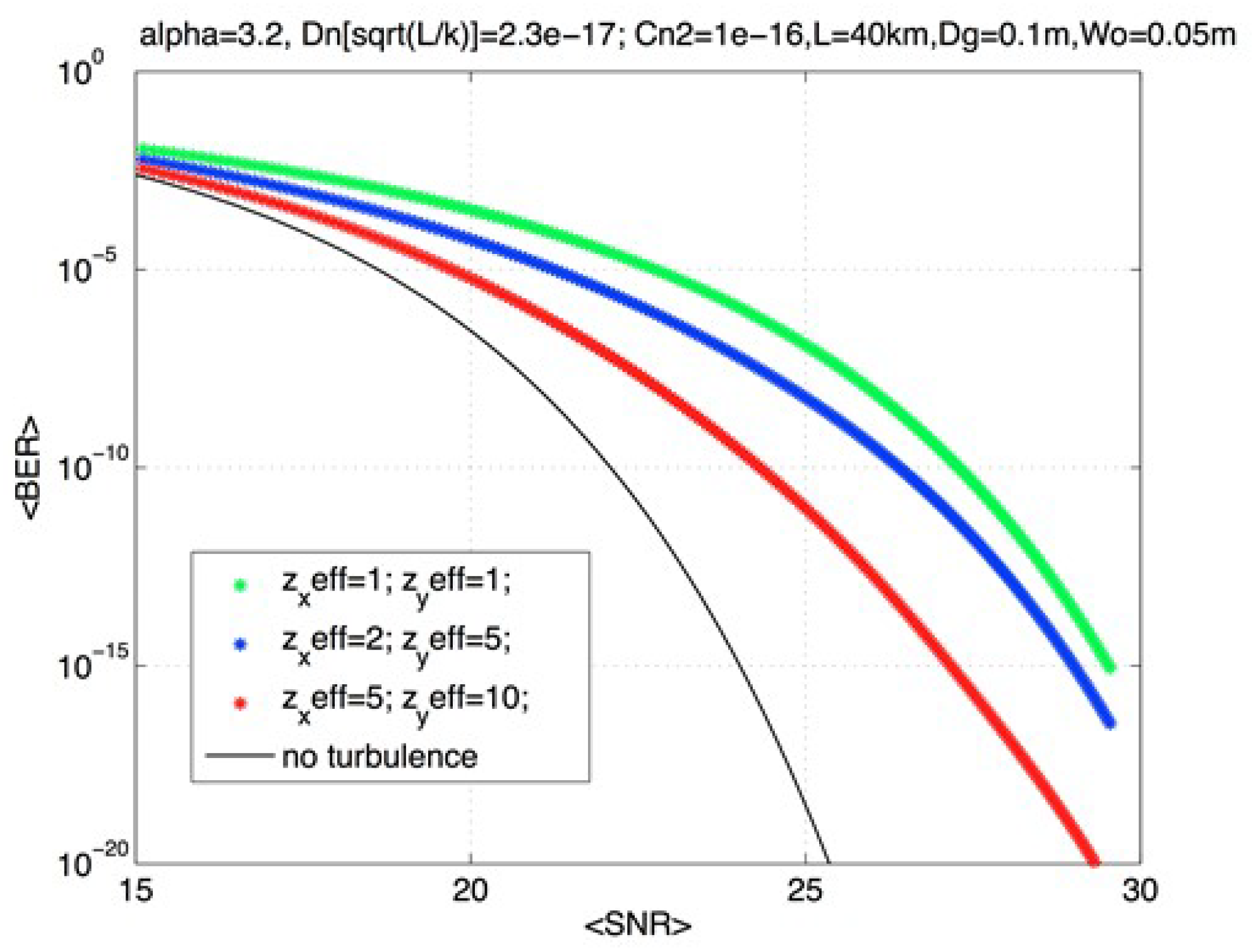
6.1.4. Mean Bit-Error Rate
6.2. LIDARs
6.3. Imaging Systems
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Euler, L. Principes généraux du mouvement des fluides. [The General Principles of the Movement of Fluids]. Mém. Acad. Sci. Berl. 1757, 11, 274–315. [Google Scholar]
- Stokes, G.G. On some cases of fluid motion. Trans. Camb. Phil. Soc. 1843, 8, 105–137. [Google Scholar]
- Stokes, G.G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Trans. Camb. Phil. Soc. 1851, 9, 8–106. [Google Scholar]
- Reynolds, O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. 1883, 174, 935–982. [Google Scholar]
- Richardson, L.F. Weather Prediction by Numerical Processes; Cambridge University Press: Boston, MA, USA, 2008; pp. 154–196. [Google Scholar]
- Prandtl, L. Berichtüber Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 1925, 5, 136–139. [Google Scholar] [CrossRef]
- Taylor, G.I. Statistical theory of turbulence. Part 1. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1935, 151, 421–444. [Google Scholar]
- De Karman, T.; Howarth, L. On the Statistical Theory of Isotropic Turbulence. Proc. R. Soc. Lond. A 1938, 164, 192–215. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Grundbegriffe der Wahrscheinlichkeitsrechnung; Springer: Berlin/Heidelberg, Germany, 1933. [Google Scholar]
- Kolmogorov, A.N. La transformation de Laplace dans les espaces lineaires. C. R. Acad. Sci. Paris 1935, 200, 1717–1718. [Google Scholar]
- Millionshchikov, M.D. Decay of homogeneous isotropic turbulence in a viscous incompressible fluids. Dokl. Akad. Nauk SSSR 1939, 22, 236–240. [Google Scholar]
- Millionshchikov, M.D. Theory of homogeneous isotropic turbulence. Izv. Akad. Nauk SSSR Ser. Geogr. Geojiz. 1941, 5, 433–446. [Google Scholar]
- Kolmogorov, A.N. Local structure of turbulence in an incompressible fluid at very high Reynolds numbers. Dokl. Akad. Nauk SSSR 1941, 30, 299–303. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Logarithmically normal distribution of the size of particles under fragmentation. Dokl. Akad. Nauk SSSR 1941, 31, 99–101. [Google Scholar]
- Kolmogorov, A.N. Decay of isotropic turbulence in an incompressible viscous fluid. Dokl. Akad. Nauk SSSR 1941, 31, 538–541. [Google Scholar]
- Kolmogorov, A.N. Energy dissipation in locally isotropic turbulence. Dokl. Akad. Nauk SSSR 1941, 32, 19–21. [Google Scholar]
- Kolmogorov, A.N. Equations of turbulent motion of an incompressible fluid. Izv. Akad. Nauk SSSR Ser. Fiz. 1942, 6, 56–58. [Google Scholar]
- Obukhov, A.M. Sound scattering in a turbulent flow. Dokl. Akad. Nauk SSSR 1941, 30, 611–614. [Google Scholar]
- Obukhov, A.M. Spectral energy distribution in a turbulent flow. Izv. Akad. Nauk SSSR Ser. Geogr. Geojiz. 1941, 5, 453–466. [Google Scholar]
- Obukhov, A.M. On the theory of atmospheric turbulence. Izv. Akad. Nauk SSSR Ser. Fiz. 1942, 6, 59–63. [Google Scholar]
- Kraichnan, R.H. Inertial ranges in two-dimensional turbulence. Phys. Fluids 1942, 10, 1417–1423. [Google Scholar] [CrossRef] [Green Version]
- Leith, C.E. Diffusion approximation for two-dimensional turbulence. Phys. Fluids 1968, 11, 671–672. [Google Scholar] [CrossRef]
- Batchelor, G.K. Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 1969, 12, 233–239. [Google Scholar] [CrossRef]
- Batchelor, G.K. Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 1959, 5, 113–133. [Google Scholar] [CrossRef]
- Alexakis, A.; Biferale, L. Cascades and transitions in turbulent flows. Phys. Rep. 2018, 767, 1–101. [Google Scholar] [CrossRef] [Green Version]
- Muschinski, A.; Wode, C. First in situ evidence for coexisting submeter temperature and humidity sheets in the lower free troposphere. J. Atmos. Sci. 1998, 55, 2893–2906. [Google Scholar] [CrossRef]
- Muschinski, A. Optical propagation through non-overturning, undulating temperature sheets in the atmosphere. J. Opt. Soc. Am. A 2016, 33, 793–800. [Google Scholar] [CrossRef]
- Monin, A.C.; Yaglom, A.M. Statistical Hydromechanics. Mechanics of Turbulence; Nauka: Moscow, Russia, 1967; Volume 2. (In Russian) [Google Scholar]
- Balsley, B.B.; Jensen, M.L.; Frehlich, R.G.; Meillier, Y.; Muschinski, A. Extreme gradients in the nocturnal boundary layer: Structure, evolution, and potential causes. J. Atmos. Sci. 2003, 60, 2496–2508. [Google Scholar] [CrossRef] [Green Version]
- Muschinski, A.; Frehlich, R.G.; Balsley, B.B. Small-scale and large-scale intermittency in the nocturnal boundary layer and the residual layer. J. Fluid Mech. 2004, 515, 319–351. [Google Scholar] [CrossRef] [Green Version]
- Biferale, L.; Procaccia, I. Anisotropic contribution to the statistics of the atmospheric boundary layer. Phys. Rep. 2005, 414, 43–164. [Google Scholar] [CrossRef] [Green Version]
- Consortini, A.A.; Ronchi, L.; Stefanutti, L. Investigation of atmospheric turbulence by narrow laser beams. Appl. Opt. 1970, 9, 2543–2547. [Google Scholar] [CrossRef]
- Grechko, G.M.; Gurvich, A.S.; Kan, V.; Kireev, S.V.; Savchenko, S.A. Anisotropy of spatial structures in the middle atmosphere. Adv. Space Res. 1992, 12, 169–175. [Google Scholar] [CrossRef]
- Dalaudier, F.; Sidi, C. Direct evidence of “Sheets” in the Armospheric Temperature field. J. Atmos. Sci. 1994, 51, 237–248. [Google Scholar] [CrossRef] [Green Version]
- Belen’kii, M.S.; Karis, S.J.; Osmon, C.L.; Brown, J.M., II; Fugate, R.Q. Experimental evidence of the effects of non-Kolmogorov turbulence and anisotropy of turbulence. In Proceedings of the SPIE, 18th Congress of the International Commission for Optics, San Francisco, CA, USA, 2–6 August 1999; Volume 3749. [Google Scholar]
- Robert, C.; Conan, J.M.; Michau, V.; Renard, J.B.; Dalaudier, F. Retrieving parameters of the anisotropic refractive index fluctuations spectrum in the stratosphere from balloon-borne observations of stellar scintillation. J. Opt. Soc. Am. 2008, 25, 379–393. [Google Scholar] [CrossRef]
- Wang, F.; Toselli, I.; Li, J.; Korotkova, O. Measuring anisotropy ellipse of atmospheric turbulence by intensity correlations of laser light. Opt. Lett. 2017, 42, 1129–1132. [Google Scholar] [CrossRef] [PubMed]
- Beason, M.; Smith, C.; Coffaro, J.; Belichki, S.; Spychalsky, J.; Titus, F.; Crabbs, R.; Andrews, L.; Phillips, R. Near ground measure and theoretical model of plane wave covariance of intensity in anisotropic turbulence. Opt. Lett. 2018, 43, 2607–2610. [Google Scholar] [CrossRef] [PubMed]
- Beason, M.; Coffaro, J.; Smith, C.; Spychalsky, J.; Belichki, S.; Titus, F.; Sanzone, F.; Berry, B.; Crabbs, R.; Andrews, L.; et al. Evolution of near-ground optical turbulence over concrete runway throughout multiple days in summer and winter. J. Opt. Soc. Am. A 2018, 35, 1393–1400. [Google Scholar] [CrossRef]
- Wu, C.; Paulson, D.A.; Rzasa, J.R.; Davis, C.C. Light field camera study of near-ground turbulence anisotropy and observation of small outer-scales. Opt. Lett. 2020, 45, 1156–1159. [Google Scholar] [CrossRef]
- Kyrazis, D.T.; Wissler, J.B.; Keating, D.B.; Preble, A.J.; Bishop, K.P. Measurement of optical turbulence in the upper troposphere and lower stratosphere. Proc. SPIE 1994, 2120, 43–55. [Google Scholar]
- Kyrazis, D.T.; Eaton, F.D.; Black, D.J.; Black, W.T.; Black, R.A. The balloon ring: A high-performance, low-cost instrumentation platform for measuring atmospheric turbulence profiles. Proc. SPIE 2009, 7463, 3–4. [Google Scholar]
- Gladysz, S.; Stein, K.; Sucher, E.; Sprung, D. Measuring non-Kolmogorov turbulence. Proc. SPIE 2013, 8890, 889013. [Google Scholar]
- Basu, S.; McCrae, J.; Pollock, Z.; He, P.; Nunalee, C.; Basu, S.; Voelz, D.; Fiorino, S. Comparison of atmospheric refractive index gradient variations derived from time-lapse imagery and mesoscale modeling. In Proceedings of the Imaging and Applied Optics 2015, OSA Technical Digest, PM1C.4, Arlington, VA, USA, 7–11 June 2015. [Google Scholar]
- Kulikov, V.A.; Vorontsov, M.A. Analysis of the joint impact of atmospheric turbulence and refractivity on laser beam propagation. Opt. Express 2017, 25, 28524–28535. [Google Scholar] [CrossRef]
- McDaniel, A.; Mahalov, A. Stochastic mirage phenomenon in a random medium. Opt. Lett. 2017, 42, 2002–2005. [Google Scholar] [CrossRef]
- Lachinova, S.L.; Vorontsov, M.A. Giant irradiance spikes in laser beam propagation in volume turbulence: Analysis and impact. J. Opt. 2016, 18, 025608. [Google Scholar] [CrossRef]
- Funes, G.; Olivares, F.; Weinberger, C.G.; Carrasco, Y.D.; Nuñez, L.; Pérez, D.G. Synthesis of anisotropic optical turbulence at the laboratory. Opt. Lett. 2016, 41, 5696–5699. [Google Scholar] [CrossRef]
- Obukhov, A.M. The structure of the temperature field in a turbulent flow. Izv. Akad. Nauk SSSR Ser. Geogr. Geofiz. 1949, 13, 58–69. [Google Scholar]
- Corrsin, S. On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 1951, 22, 469–473. [Google Scholar] [CrossRef]
- Tatarskii, V.I. Wave Propagation in a Turbulent Medium; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Tatarskii, V.I. The Effects of the Turbulent Atmosphere on Wave Propagation; Israel Program for Scientific Translation: Jerusalem, Israel, 1971. [Google Scholar]
- Frehlich, R.G. Laser scintillation measurements of the temperature spectrum in the atmospheric surface layer. J. Atmos. Sci. 1992, 49, 1494–1509. [Google Scholar] [CrossRef]
- Andrews, L.C. An analytical model for the refractive index power spectrum and its application to optical scintillations in the atmosphere. J. Mod. Opt. 1992, 39, 1849–1853. [Google Scholar] [CrossRef]
- Muschinski, A. Temperature variance dissipation equation and its relevance for optical turbulence modeling. J. Opt. Soc. Am. A 2015, 32, 2195–2200. [Google Scholar] [CrossRef] [PubMed]
- Hill, R.J.; Clifford, S.F. Modified spectrum of atmospheric temperature fluctuations and its application to optical propagation. J. Opt. Soc. Am. 1978, 68, 892–899. [Google Scholar] [CrossRef]
- Hill, R.J. Models of the scalar spectrum for turbulent advection. J. Fluid Mech. 1978, 88, 541–562. [Google Scholar] [CrossRef]
- Grayshan, K.S.; Vetelino, F.S.; Young, C.Y. A marine atmospheric spectrum for laser propagation. Waves Rand. Compl. Med. 2008, 18, 173–184. [Google Scholar] [CrossRef]
- Bolgiano, B., Jr. Structure of turbulence in stratified media. J. Geophys. Res. 1962, 67, 3015–3023. [Google Scholar] [CrossRef]
- Stribling, B.E.; Welsh, B.M.; Roggemann, M.C. Optical propagation in non-Kolmogorov atmospheric turbulence. Proc. SPIE 1995, 2471, 181–196. [Google Scholar]
- Toselli, I.; Andrews, L.C.; Phillips, R.L.; Ferrero, V. Free-space optical system performance for laser beam propagation through non-Kolmogorov turbulence. Opt. Eng. 2008, 47, 026003. [Google Scholar]
- Zilberman, A.; Golbraikh, E.; Kopeika, N.S. Propagation of electromagnetic waves in Kolmogorov and non-Kolmogorov atmospheric turbulence: Three-layer altitude model. Appl. Opt. 2008, 47, 6385–6391. [Google Scholar] [CrossRef] [PubMed]
- Zilberman, A.; Golbraikh, E.; Kopeika, N.S.; Virtser, A.; Kupershmidt, I.; Shtemler, Y. Lidar study of aerosol turbulence characteristics in the troposphere: Kolmogorov and non-Kolmogorov turbulence. Atmos. Res. 2008, 88, 66–77. [Google Scholar] [CrossRef]
- Golbraikh, E.; Branover, H.; Kopeika, N.S.; Zilberman, A. Non-Kolmogorov atmospheric turbulence and optical signal propagation. Nonlin. Process. Geophys. 2006, 13, 297–301. [Google Scholar] [CrossRef]
- Beland, R.R. Some aspects of propagation through weak isotropic non-Kolmogorov turbulence. Proc. SPIE 1995, 2375, 6–16. [Google Scholar]
- Boreman, G.B.; Dainty, C. Zernike expansions for non-Kolmogorov turbulence. J. Opt. Soc. Am. A 1996, 13, 517–522. [Google Scholar] [CrossRef]
- Orlov, V.; Voitsekhovich, V. Karhunen–Loeve functions for non-Kolmogorov turbulence. J. Turbulence 2017, 18, 560–568. [Google Scholar] [CrossRef]
- Kon, A.I. Qualitative theory of amplitude and phase fluctuations in a medium with anisotropic turbulent irregularity. Waves Rand. Compl. Media 1994, 4, 297–306. [Google Scholar] [CrossRef]
- Toselli, I.; Agrawal, B.; Restaino, S. Light propagation through anisotropic turbulence. J. Opt. Soc. Am. A 2011, 28, 483–488. [Google Scholar] [CrossRef] [Green Version]
- Andrews, L.C.; Phillips, R.L.; Crabbs, R.; Leclerc, T. Deep turbulence propagation of a Gaussian-beam wave in anisotropic non-Kolmogorov turbulence. Proc. SPIE 2013, 8874, 887401. [Google Scholar]
- Andrews, L.C.; Phillips, R.L.; Crabbs, R. Propagation of a Gaussian-beam wave in general anisotropic turbulence. Proc. SPIE 2014, 9224, 922402. [Google Scholar]
- Toselli, I. Introducing the concept of anisotropy at different scales for modeling optical turbulence. J. Opt. Soc. Am. A 2014, 31, 1868–1875. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Xue, B.; Zhou, F. Generalized anisotropic turbulence spectra and application in the optical waves’ propagation through anisotropic turbulence. Opt. Express 2015, 23, 30088–30103. [Google Scholar] [CrossRef] [PubMed]
- Sjöqvist, L. Laser beam propagation in jet engine plume environments: A review. Proc. SPIE 2008, 7115, 71150C. [Google Scholar]
- Sirazetdinov, V.S. Experimental study and numerical simulation of laser beams propagation through the turbulent aerojet. Appl. Opt. 2008, 47, 975–985. [Google Scholar] [CrossRef] [PubMed]
- Lukin, V.P.; Bol’basova, L.A.; Nosov, V.V. Comparison of Kolmogorov’s and coherent turbulence. Appl. Opt. 2014, 53, B231–B236. [Google Scholar] [CrossRef] [PubMed]
- Lukin, V.P.; Nosov, E.V.; Nosov, V.V.; Torgaev, A.V. Causes of non-Kolmogorov turbulence in the atmosphere. Appl. Opt. 2016, 55, B163–B168. [Google Scholar] [CrossRef]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation, with Examples in MATLAB; SPIE Press: Bellingham, WA, USA, 2010. [Google Scholar]
- Phillips, J.D.; Goda, M.E.; Schmidt, J. Atmospheric turbulence simulation using liquid crystal light modulators. Proc. SPIE 2005, 5894, 589406. [Google Scholar]
- Bos, J.P.; Roggemann, M.C.; Gudimetla, V.S.R. Anisotropic non-Kolmogorov turbulence phase screens with variable orientation. Appl. Opt. 2015, 54, 2039–2045. [Google Scholar] [CrossRef]
- Toselli, I.; Korotkova, O.; Xiao, X.; Voelz, D.G. SLM-based laboratory simulations of Kolmogorov and non-Kolmogorov anisotropic turbulence. Appl. Opt. 2015, 54, 4740–4744. [Google Scholar] [CrossRef] [PubMed]
- Voelz, D. Computational Fourier Optics: A MatLab Tutorial; SPIE Press: Bellingham, WA, USA, 2011. [Google Scholar]
- Charnotskii, M. Intensity fluctuations of flat-topped beam in non-Kolmogorov weak turbulence: Comment. J. Opt. Soc. Am. A 2012, 29, 1838–1840. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Voelz, D.G.; Toselli, I.; Korotkova, O. Gaussian beam propagation in anisotropic turbulence along horizontal links: Theory, simulation, and laboratory implementation. Appl. Opt. 2016, 55, 4079–4084. [Google Scholar] [CrossRef]
- Wang, F.; Korotkova, O.; Toselli, I. Two spatial light modulator system for laboratory simulation of random beam propagation in random media. Appl. Opt. 2016, 55, 1112–1117. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O. Random Light Beams: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Yura, H.T. Mutual Coherence function of a finite cross section optical beam propagating in a turbulent medium. Appl. Opt. 1972, 11, 1399–1406. [Google Scholar] [CrossRef]
- Korotkova, O.; Shchepakina, E. Color changes in stochastic light fields propagating in non-Kolmogorov turbulence. Opt. Lett. 2010, 35, 3772–3774. [Google Scholar] [CrossRef]
- Mei, Z. Light sources generating self-splitting beams and their propagation in non-Kolmogorov turbulence. Opt. Express 2014, 22, 13029–13040. [Google Scholar] [CrossRef]
- Shchepakina, E.; Korotkova, O. Second-order statistics of stochastic electromagnetic beams propagating through non-Kolmogorov turbulence. Opt. Express 2010, 18, 10650–10658. [Google Scholar] [CrossRef]
- Wu, G.; Guo, H.; Yu, S.; Luo, B. Spreading and direction of Gaussian-Schell model beam through a non-Kolmogorov turbulence. Opt. Lett. 2010, 35, 715–717. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Cui, Z.; Qu, J. Propagation of elegant Laguerre–Gaussian beam in non-Kolmogorov turbulence. Opt. Express 2011, 19, 21163–21173. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Yuan, Y.; Qu, J.; Huang, W. Propagation properties of Laguerre-Gaussian correlated Schell-model beam in non-Kolmogorov turbulence. Opt. Express 2016, 22, 10682–10693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Min, Y.; Toselli, I.; Korotkova, O. Propagation of electromagnetic stochastic beams in anisotropic turbulence. Opt. Express 2014, 22, 31608–31619. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Wang, F.; Korotkova, O. Random optical beam propagation in anisotropic turbulence along horizontal links. Opt. Express 2016, 24, 24422–24434. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Korotkova, O.; Zhao, D.; Pan, L. Gaussian Schell-model beams propagating in the jet engine exhaust. Opt. Express 2020, 28, 1037–1050. [Google Scholar] [CrossRef]
- Chen, C.; Yang, H.; Lou, Y.; Tong, S.; Liu, R. Temporal broadening of optical pulses propagating through non-Kolmogorov turbulence. Opt. Express 2012, 20, 7749–7757. [Google Scholar] [CrossRef]
- Kotiang, S.; Choi, J. Temporal frequency spread of optical wave propagation through anisotropic non-Kolmogorov turbulence. J. Opt. 2015, 17, 125606. [Google Scholar] [CrossRef]
- Toselli, I.; Korotkova, O. General scale-dependent anisotropic turbulence and its impact on free space optical communication system performance. J. Opt. Soc. Am. A 2015, 32, 1017–1025. [Google Scholar] [CrossRef]
- Toselli, I.; Gladysz, S. Efficiency of adaptive optics correction for Gaussian beams propagating through non-Kolmogorov turbulence. In Proceedings of the Imaging and Applied Optics 2014, OSA Technical Digest (Online), PM3E.6, Seattle, WA, USA, 13–17 July 2014. [Google Scholar]
- Banakh, V.A.; Mironov, L.V. LIDAR in a Turbulent Atmosphere; Artech House: Dedham, MS, USA, 1987. [Google Scholar]
- Toselli, I.; Wang, F.; Korotkova, O. LIDAR systems operating in a non-Kolmogorov turbulent atmosphere. Waves Rand. Compl. Med. 2018, 29, 743–758. [Google Scholar] [CrossRef]
- Toselli, I.; Gladysz, S.; Fillimonov, G. Scintillation analysis of LIDAR systems operating in weak-to-strong non-Kolmogorov turbulence: Unresolved target case. J. Appl. Remote Sens. 2018, 12, 42407–42416. [Google Scholar] [CrossRef]
- Rao, C.; Jiang, W.; Ling, N. Spatial and temporal characterization of phase fluctuations in non-Kolmogorov atmospheric turbulence. J. Mod. Opt. 2000, 47, 1111–1126. [Google Scholar] [CrossRef]
- Kopeika, N.S.; Zilberman, A.; Golbraikh, E. Imaging and communications through non-Kolmogorov turbulence. Proc. SPIE 2009, 7463, 746307. [Google Scholar]
- Cui, L.; Xue, B.; Cao, X.; Dong, J.; Wang, J. Generalized atmospheric turbulence MTF for wave propagating through non-Kolmogorov turbulence. Opt. Express 2010, 18, 21269–21283. [Google Scholar] [PubMed]
- Cui, L. Atmosphere turbulence MTF models in moderate-to-strong anisotropic turbulence. Optik 2017, 130, 68–75. [Google Scholar] [CrossRef]




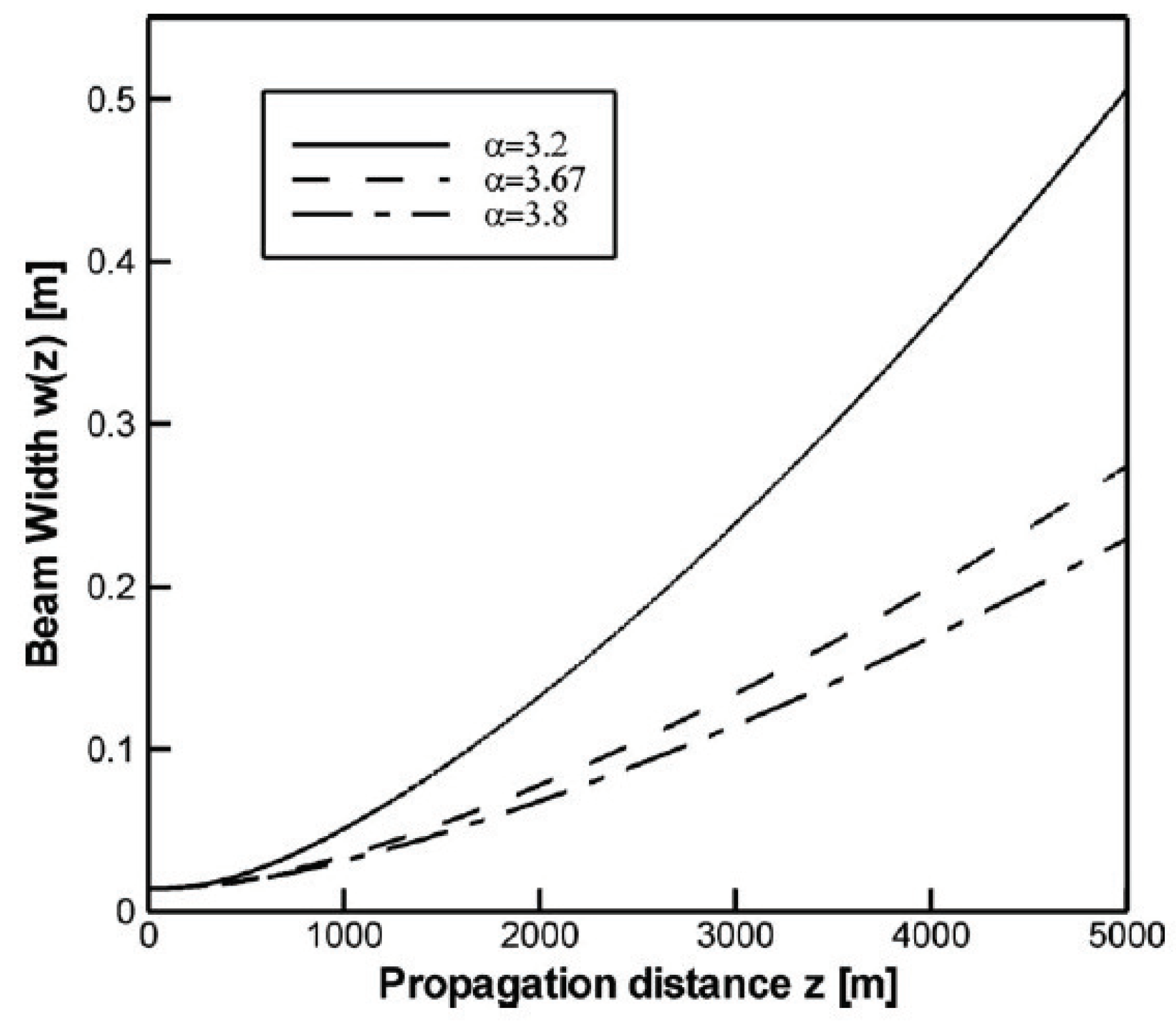
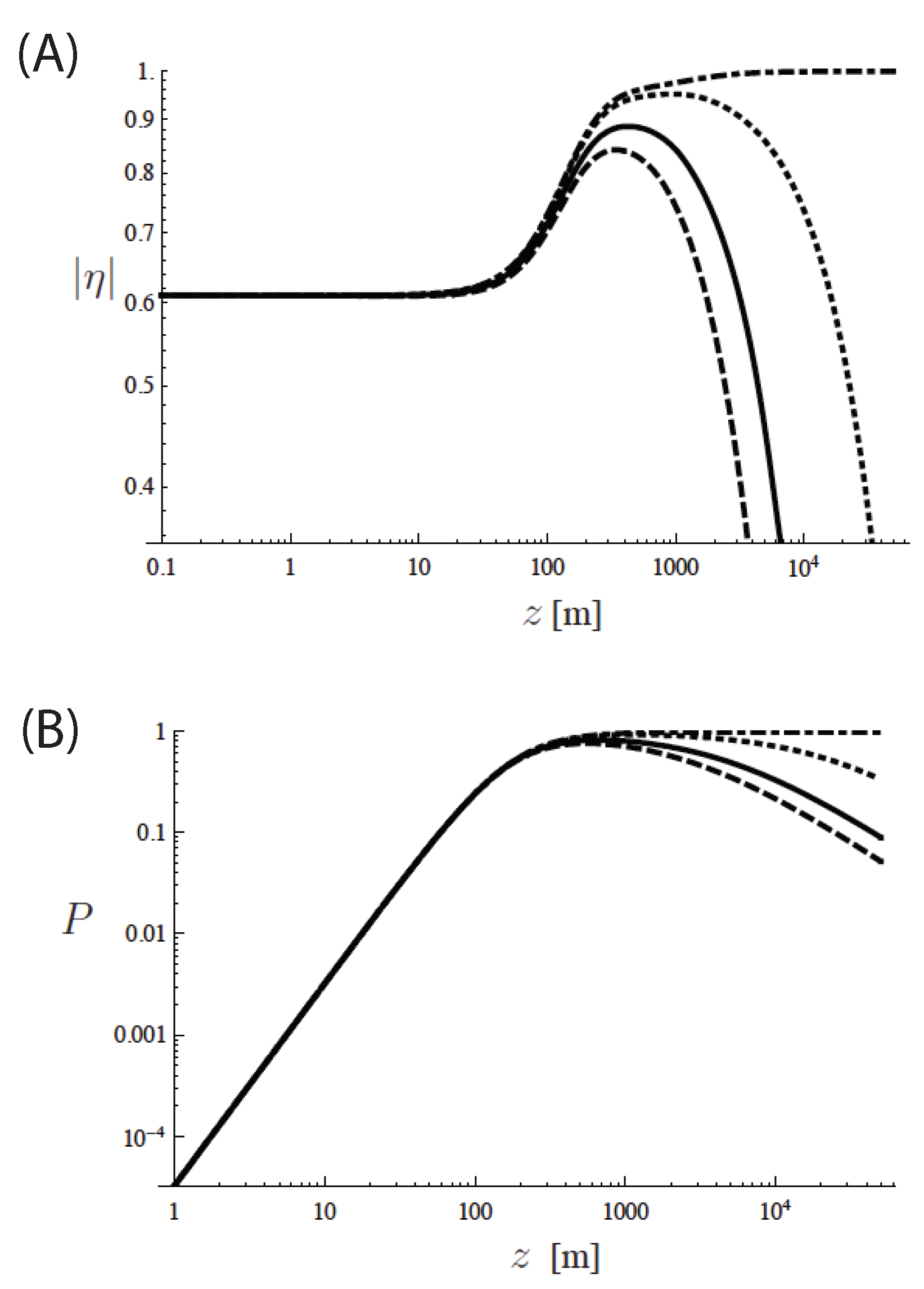
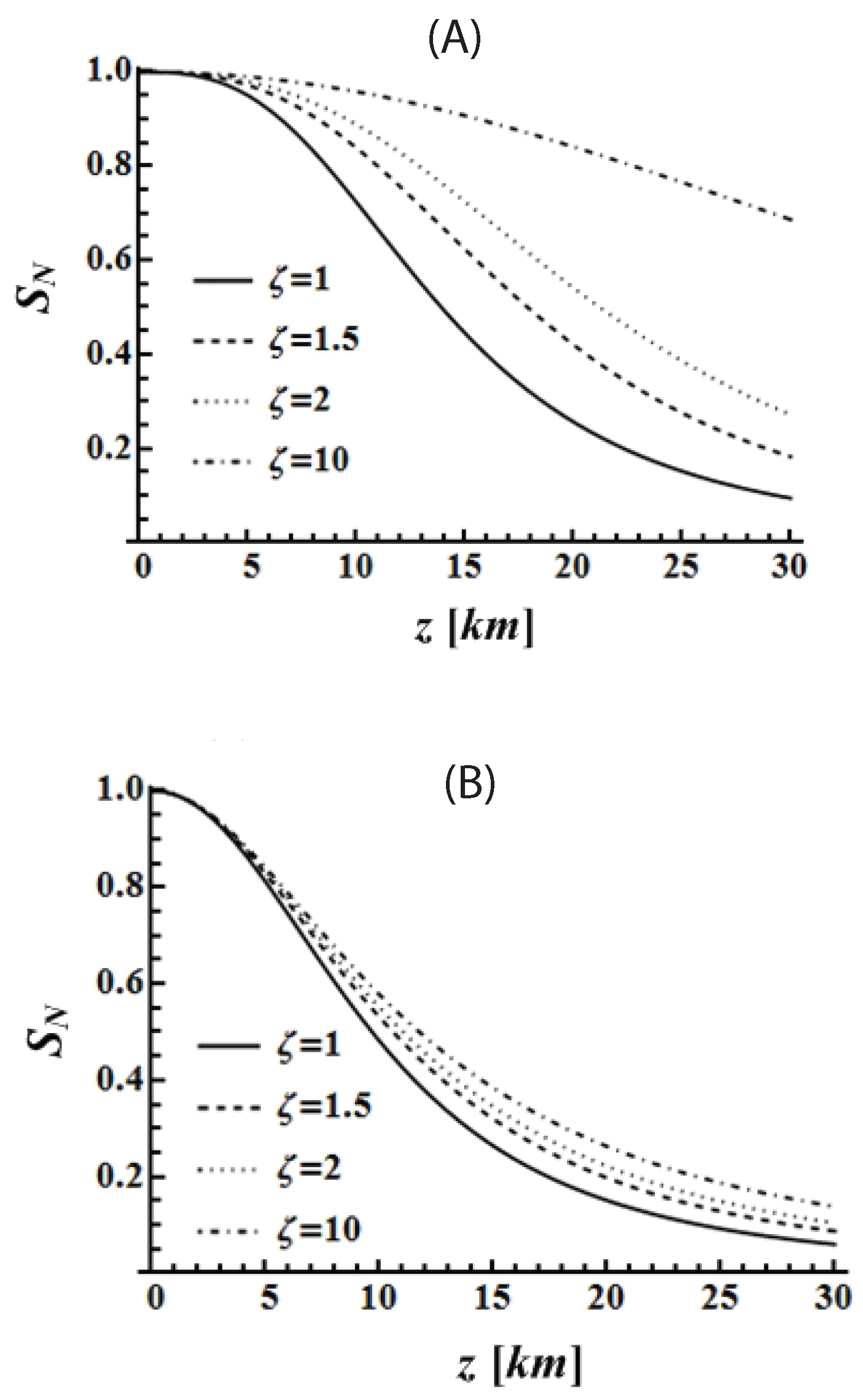



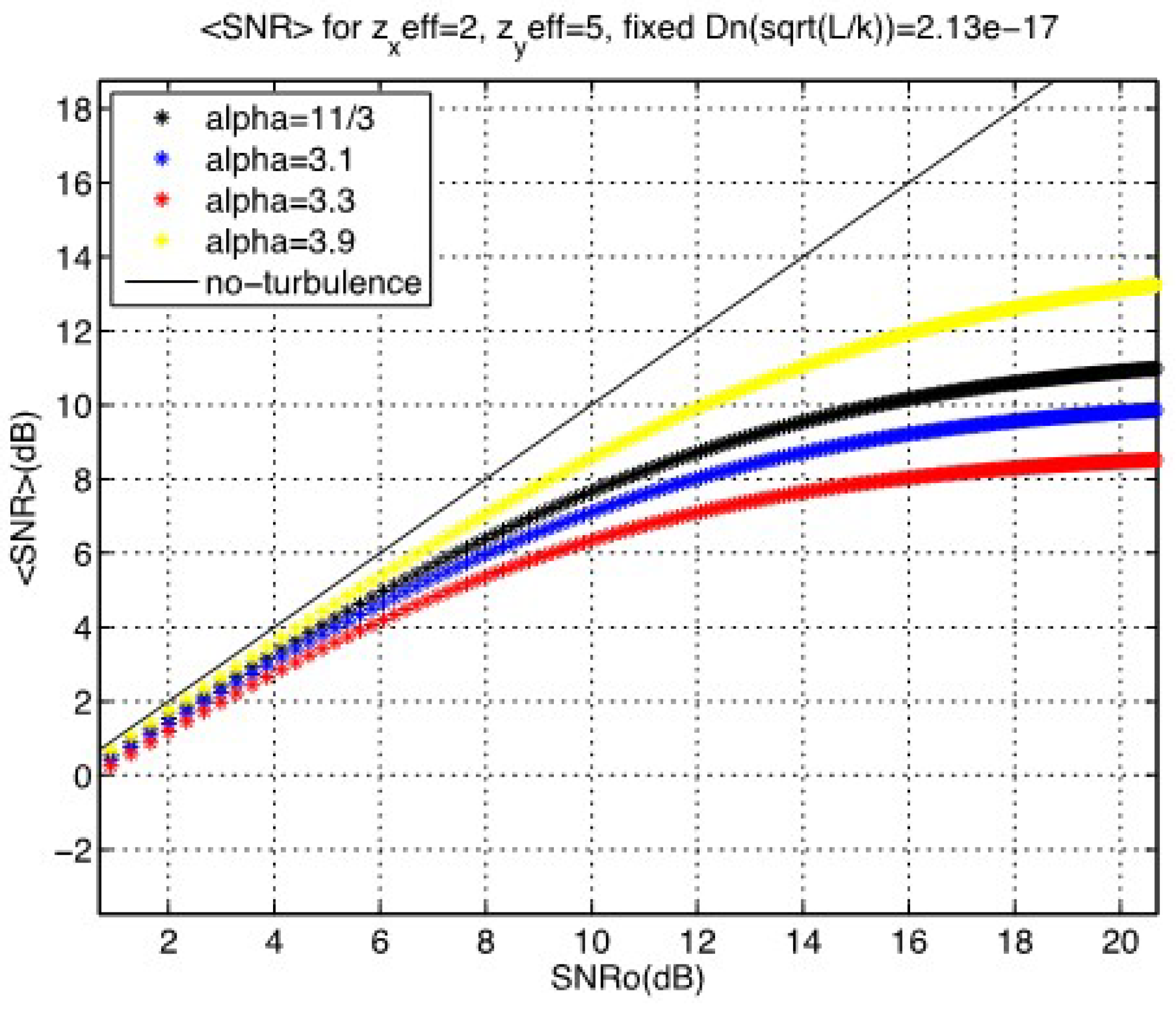

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korotkova, O.; Toselli, I. Non-Classic Atmospheric Optical Turbulence: Review. Appl. Sci. 2021, 11, 8487. https://doi.org/10.3390/app11188487
Korotkova O, Toselli I. Non-Classic Atmospheric Optical Turbulence: Review. Applied Sciences. 2021; 11(18):8487. https://doi.org/10.3390/app11188487
Chicago/Turabian StyleKorotkova, Olga, and Italo Toselli. 2021. "Non-Classic Atmospheric Optical Turbulence: Review" Applied Sciences 11, no. 18: 8487. https://doi.org/10.3390/app11188487
APA StyleKorotkova, O., & Toselli, I. (2021). Non-Classic Atmospheric Optical Turbulence: Review. Applied Sciences, 11(18), 8487. https://doi.org/10.3390/app11188487




