Optical Turbulence Profile Forecasting and Verification in the Offshore Atmospheric Boundary Layer
Abstract
:1. Introduction
2. Optical Turbulence Forecasting
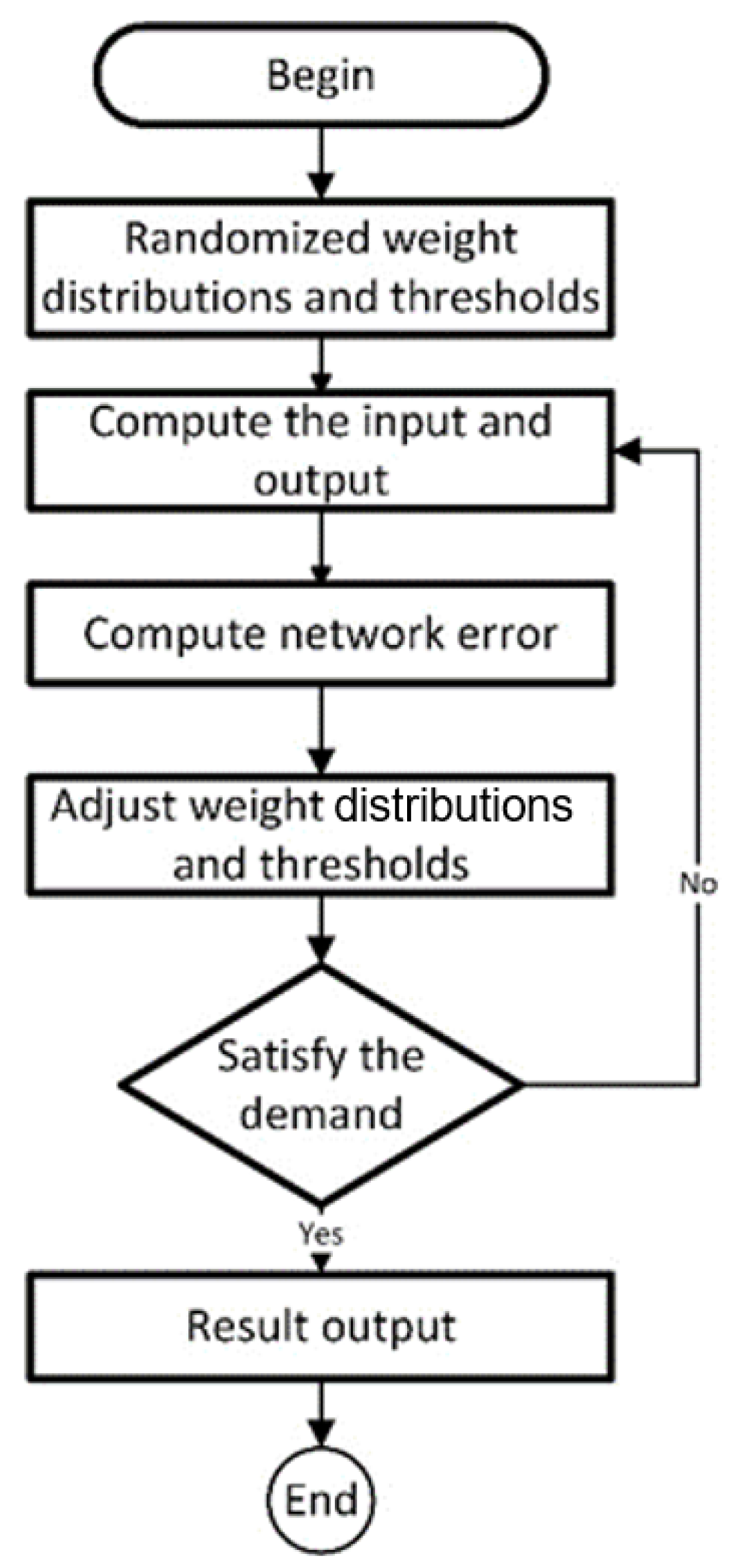
2.1. BPNN
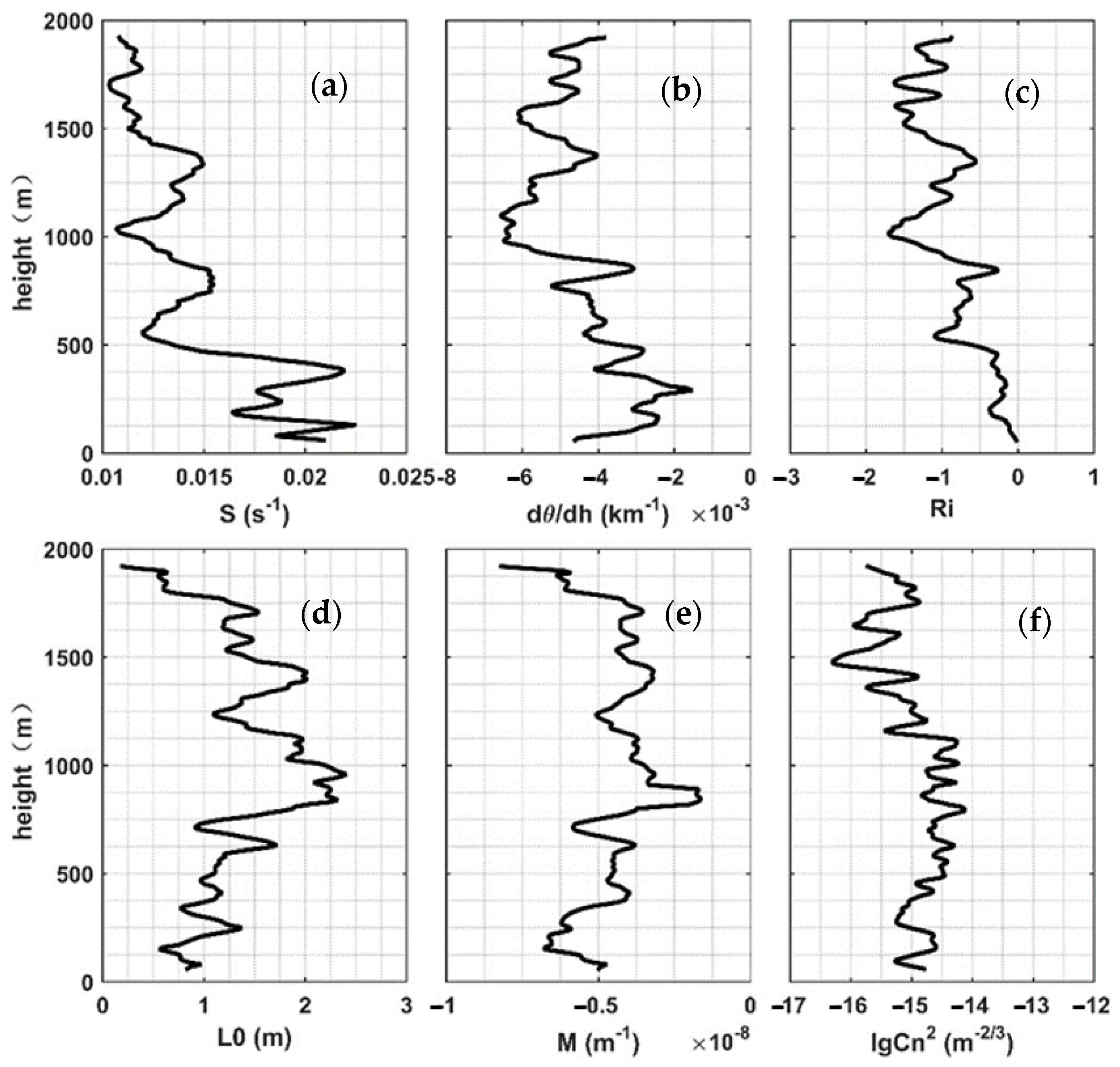
2.2. Estimation Model
2.3. Method of Statistical Analysis
2.4. Integrated Astroclimatic Parameters
3. Results and Discussion
3.1. Principle of and Measurement
3.2. Setting Up of Contrast Experiments
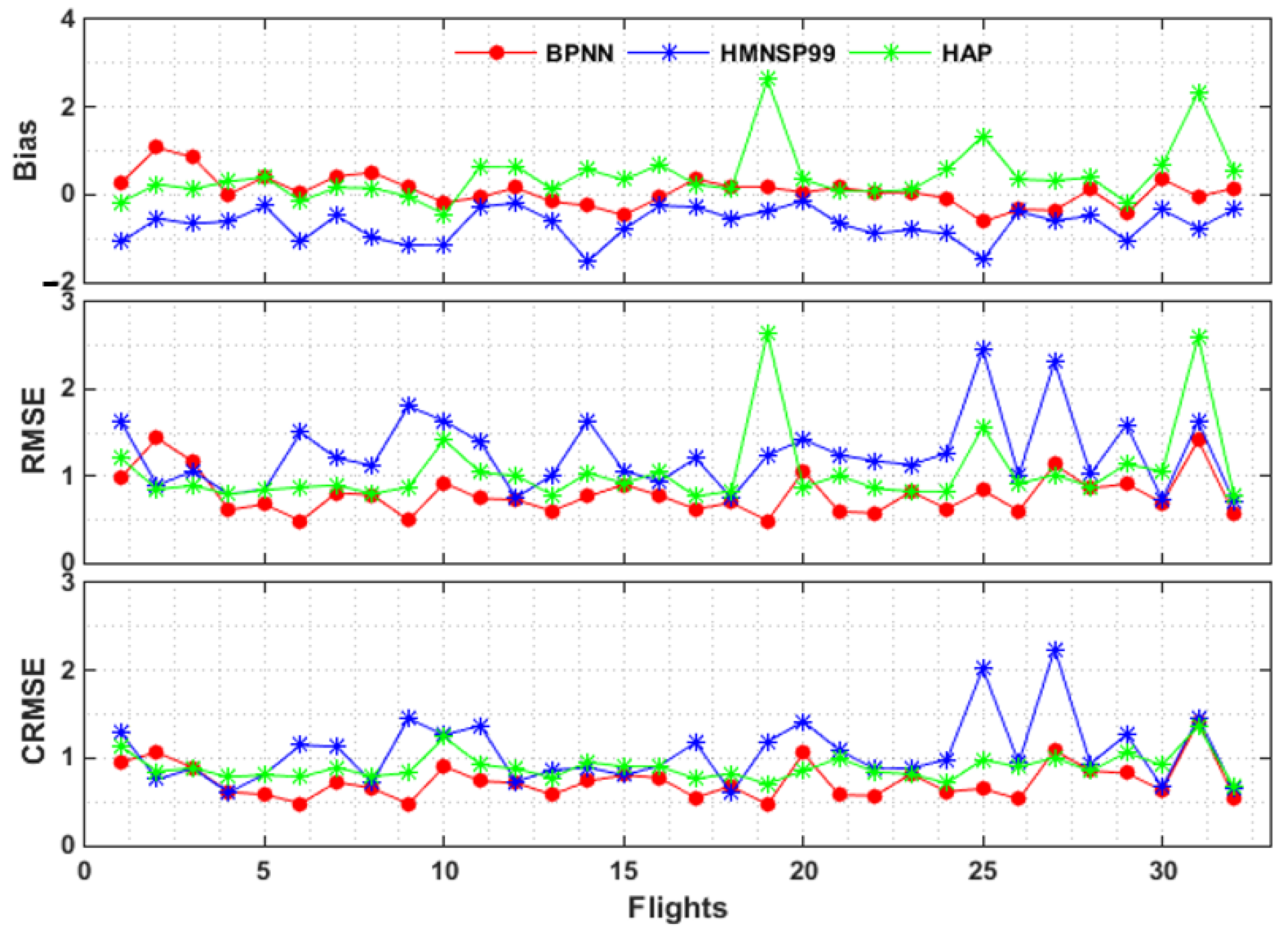
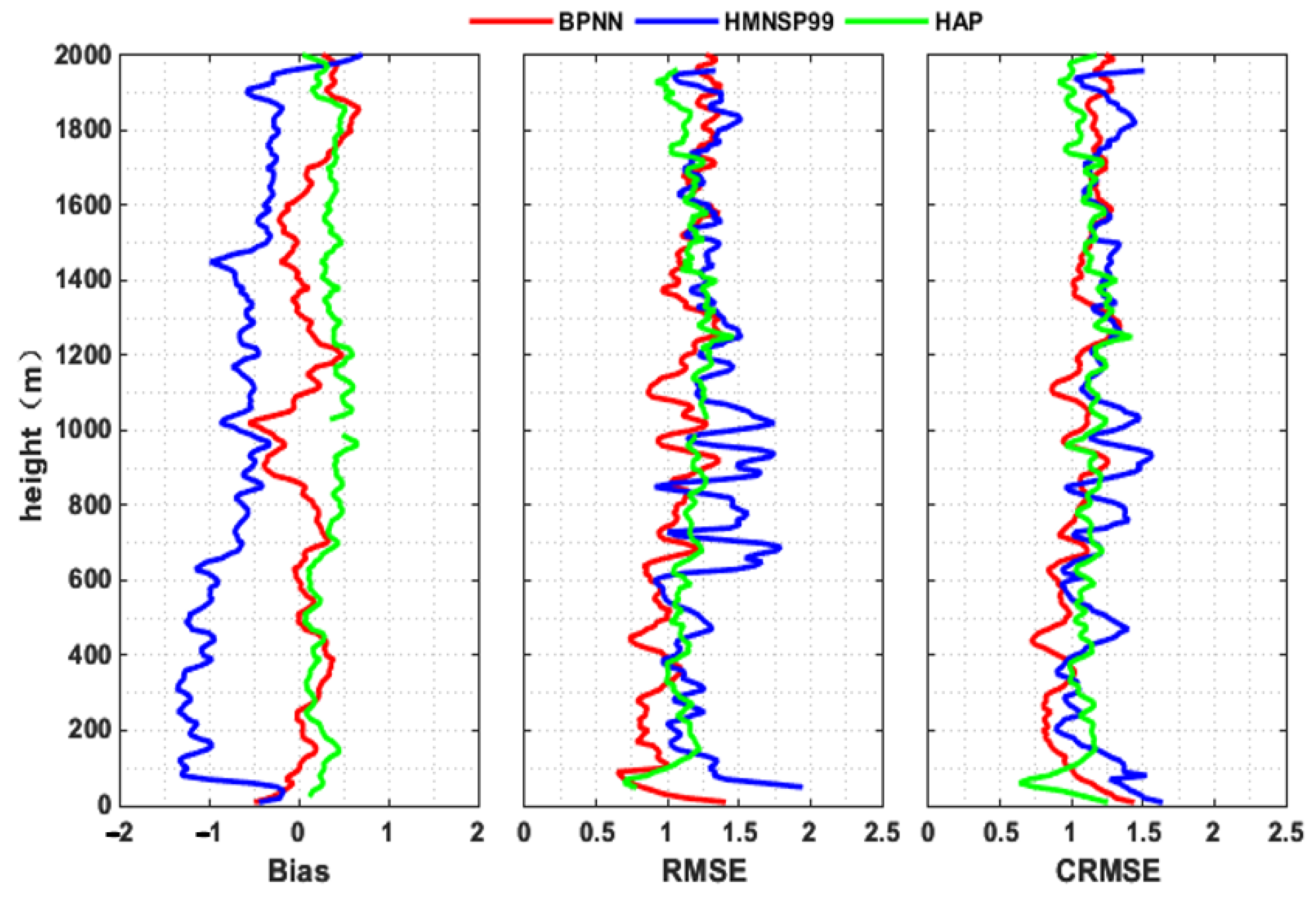
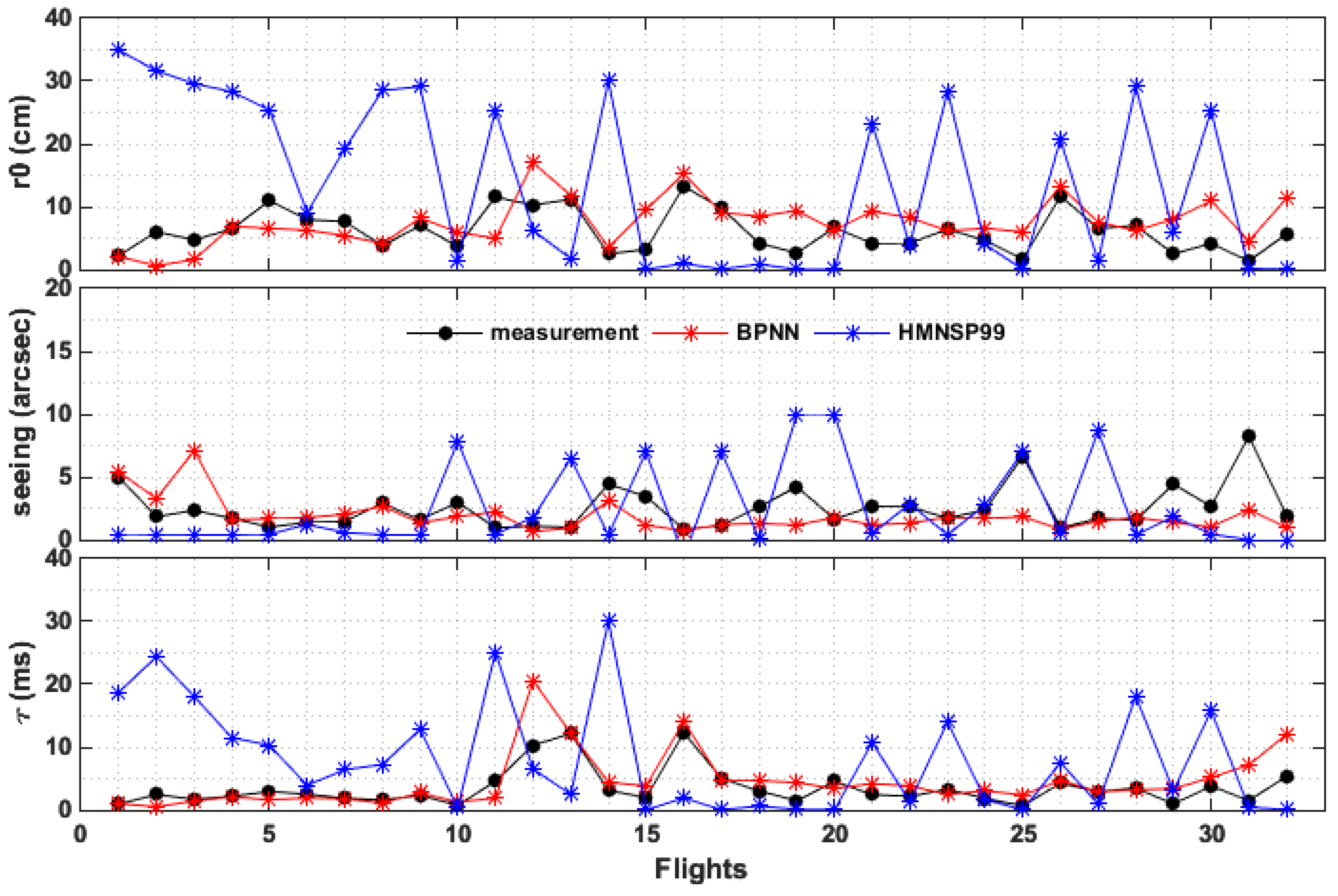
3.3. Overall Approach to Performances
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stull, R. An Introduction To Boundary Layer Meteorology; Kluwer Academic Publishers: Norwell, MA, USA, 1988; Volume 13, pp. 1–2. [Google Scholar]
- Andrews, L.; Phillips, R. Laser Beam Propagation through Random Media; SPIE Optical Engineering Press: Bellingham, DC, USA, 2005. [Google Scholar] [CrossRef]
- Wang, Y.; Basu, S. Utilizing the Kantorovich metric for the validation of optical turbulence predictions. Opt. Lett. 2016, 41, 4008–4011. [Google Scholar] [CrossRef]
- Song, T.; Cai, Z.; Liu, Y.; Zhao, M.; Fang, Y.; Zhang, X.; Wang, J.; Li, X.; Song, Q.; Du, Z. Daytime optical turbulence profiling with a profiler of the differential solar limb. Mon. Not. R. Astron. Soc. 2020, 499, 1909–1917. [Google Scholar] [CrossRef]
- Shen, H.; Yu, L.; Jing, X.; Tan, F. Method for Measuring the Second-Order Moment of Atmospheric Turbulence. Atmosphere 2021, 12, 564. [Google Scholar] [CrossRef]
- Chabé, J.; Aristidi, E.; Ziad, A.; Lantéri, H.; Fanteï-Caujolle, Y.; Giordano, C.; Borgnino, J.; Marjani, M.; Renaud, C. PML: A generalized monitor of atmospheric turbulence profile with high vertical resolution. Appl. Opt. 2020, 59, 7574–7584. [Google Scholar] [CrossRef] [PubMed]
- Shikhovtsev, A.; Kiselev, A.; Kovadlo, P.; Kolobov, D.; Lukin, V.; Tomin, V. Method for Estimating the Altitudes of Atmospheric Layers with Strong Turbulence. Atmos. Ocean. Opt. 2020, 33, 295–301. [Google Scholar] [CrossRef]
- Vernin, J.; Barletti, R.; Ceppatelli, G.; Paternò, L.; Righini, A.; Speroni, N. Optical remote sensing of atmospheric turbulence: A comparison with simultaneous thermal measurements. Appl. Opt. 1979, 18, 243–247. [Google Scholar] [CrossRef]
- Anand, N.; Sunilkumar, K.; Satheesh, S.; Moorthy, K.K. Entanglement of near-surface optical turbulence to atmospheric boundary layer dynamics and particulate concentration: Implications for optical wireless communication systems. Appl. Opt. 2020, 59, 1471–1483. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C. The Kansas and Minnesota experiments. Bound.-Layer Meteorol. 1990, 50, 31–47. [Google Scholar] [CrossRef]
- Van Iersel, M.; Paulson, D.A.; Wu, C.; Ferlic, N.A.; Rzasa, J.R.; Davis, C.C.; Walker, M.; Bowden, M.; Spychalsky, J.; Titus, F. Measuring the turbulence profile in the lower atmospheric boundary layer. Appl. Opt. 2019, 58, 6934–6941. [Google Scholar] [CrossRef]
- Coulman, C.E. A quantitative treatment of solar ‘seeing’, II. Sol. Phys. 1974, 34, 491–506. [Google Scholar] [CrossRef]
- Coulman, C.E. Vertical profiles of small-scale temperature structure in the atmosphere. Bound.-Layer Meteorol. 1973, 4, 169–177. [Google Scholar] [CrossRef]
- Bufton, J. Correlation of Microthermal Turbulence Data with Meteorological Soundings in the Troposphere. J. Atmos. Sci. 1973, 30, 83–87. [Google Scholar] [CrossRef]
- Bufton, J. Comparison of Vertical Profile Turbulence Structure with Stellar Observations. Appl. Opt. 1973, 12, 1785–1793. [Google Scholar] [CrossRef]
- Azouit, M.; Vernin, J. Optical Turbulence Profiling with Balloons Relevant to Astronomy and Atmospheric Physics. Publ. Astron. Soc. Pac. 2005, 117, 536–543. [Google Scholar] [CrossRef]
- McHugh, J.; Jumper, G.; Chun, M. Balloon Thermosonde Measurements over Mauna Kea and Comparison with Seeing Measurements. Publ. Astron. Soc. Pac. 2008, 120, 1318–1324. [Google Scholar] [CrossRef]
- Miller, M.; Zieske, P. Turbulence Environment Characterization; Avco-Everett Research Lab.: Everett, MA, USA, 1979; 135p. [Google Scholar]
- Good, R.E.; Beland, R.R.; Murphy, E.A.; Brown, J.H.; Dewan, E.M. Atmospheric models of optical turbulence. Proc. SPIE 1988, 928, 165–186. [Google Scholar] [CrossRef]
- Jumper, G.; Beland, R. Progress in the Understanding and Modeling of Atmospheric Optical Turbulence. In Proceedings of the 31st Plasmadynamics and Lasers Conference, Denver, CO, USA, 19–22 June 2000. [Google Scholar] [CrossRef]
- Beland, R.R.; Brown, J.H. A deterministic temperature model for stratospheric optical turbulence. Phys. Scr. 1988, 37, 419–423. [Google Scholar] [CrossRef]
- Hufnagel, R.; Stanley, N. Modulation Transfer Function Associated with Image Transmission through Turbulent Media. JOSA 1964, 54, 52–60. [Google Scholar] [CrossRef]
- Tatarski, V.L. Wave Propagation in a Turbulent Medium; Silverman, R.A., Translator; McGraw-Hill: New York, NY, USA, 1961; Volume 134, 285p. [Google Scholar] [CrossRef]
- Felton, B.; Alliss, R. Improved climatological characterization of optical turbulence for free-space optical communications. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 21–25 August 2011; Volume 8162. [Google Scholar] [CrossRef]
- Kovadlo, P.G.; Lukin, V.P.; Shikhovtsev, A.Y. Development of the Model of Turbulent Atmosphere at the Large Solar Vacuum Telescope Site as Applied to Image Adaptation. Atmos. Ocean. Opt. 2019, 32, 202–206. [Google Scholar] [CrossRef]
- Zhang, R.; Jing, J.; Tao, J.; Hsu, S.C.; Wang, G.; Cao, J.; Lee, C.S.L.; Zhu, L.; Chen, Z.; Zhao, Y.; et al. Chemical characterization and source apportionment of PM2.5 in Beijing: Seasonal perspective. Atmos. Chem. Phys. 2013, 13, 7053–7074. [Google Scholar] [CrossRef] [Green Version]
- Suárez Gómez, S.; Gonzalez, C.; Alonso, E.; Santos, J.D.; Rodríguez, M.; Morris, T.; Osborn, J.; Basden, A.; Bonavera, L.; González, J.; et al. Experience with Artificial Neural Networks Applied in Multi-object Adaptive Optics. Publ. Astron. Soc. Pac. 2019, 131, 108012. [Google Scholar] [CrossRef]
- Lohani, S.; Glasser, R.T. Turbulence correction with artificial neural networks. Opt. Lett. 2018, 43, 2611–2614. [Google Scholar] [CrossRef]
- Pelliccioni, A.; Tirabassi, T. Air dispersion model and neural network: A new perspective for integrated models in the simulation of complex situations. Environ. Model. Softw. 2006, 21, 539–546. [Google Scholar] [CrossRef]
- Tracey, B.D.; Duraisamy, K.; Alonso, J.J. A Machine Learning Strategy to Assist Turbulence Model Development. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Wang, Y.; Basu, S. Using an artificial neural network approach to estimate surface-layer optical turbulence at Mauna Loa, Hawaii. Opt. Lett. 2016, 41, 2334–2337. [Google Scholar] [CrossRef]
- Su, C.; Wu, X.; Luo, T.; Wu, S.; Qing, C. Adaptive niche-genetic algorithm based on backpropagation neural network for atmospheric turbulence forecasting. Appl. Opt. 2020, 59, 3699–3705. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Tatarski, V.I.; Silverman, R.A.; Chako, N. Wave Propagation in a Turbulent Medium. Phys. Today 1961, 14, 46. [Google Scholar] [CrossRef]
- Beland, R.R. Propagation through atmospheric optical turbulence. Atmos. Propag. Radiat. 1993, 2, 157–232. [Google Scholar]
- Han, Y.; Wu, X.; Luo, T.; Qing, C.; Yang, Q.; Jin, X.; Liu, N.; Wu, S.; Su, C. New statistical model based on first radiosonde turbulence observation over Lhasa. J. Opt. Soc. Am. A 2020, 37, 995–1001. [Google Scholar] [CrossRef]
- Ruggiero, F.H.; Debenedictis, D.A. Forecasting optical turbulence from mesoscale numerical weather prediction models. In Proceedings of the DoD High Performance Modernization Program Users Group Conference; Austin, Texas, USA: 10–14 June 2002.
- Andrews, L.C.; Phillips, R.L.; Wayne, D.; Leclerc, T.; Sauer, P.; Crabbs, R.; Kiriazes, J. Near-ground vertical profile of refractive-index fluctuations. In Proceedings of the SPIE Defense, Security, and Sensing, Orlando, FL, USA, 13–17 April 2009. [Google Scholar]
- Masciadri, E.; Lascaux, F.; Fini, L. MOSE: Operational forecast of the optical turbulence and atmospheric parameters at European Southern Observatory ground-based sites—I. Overview and vertical stratification of atmospheric parameters at 0–20 km. Mon. Not. R. Astron. Soc. 2013, 436, 1968–1985. [Google Scholar] [CrossRef] [Green Version]
- Roddier, F.; Gilli, J.M.; Lund, G. On the origin of speckle boiling and its effects in stellar speckle interferometry. J. Opt. 2000, 13, 263. [Google Scholar] [CrossRef]
- Fried, D.L. Optical Resolution through a Randomly Inhomogeneous Medium for Very Long and Very Short Exposures. J. Opt. Soc. Am. 1966, 56, 1372–1379. [Google Scholar] [CrossRef]
- Shao, S.; Qin, F.; Liu, Q.; Xu, M.; Cheng, X. Turbulent Structure Function Analysis Using Wireless Micro-Thermometer. IEEE Access 2020, 8, 123929–123937. [Google Scholar] [CrossRef]
- Lawrence, R.S.; Ochs, G.R.; Clifford, S.F. Measurements of atmospheric turbulence relevant to optical propagatian. J. Opt. Soc. Am. 1970, 60, 826–830. [Google Scholar] [CrossRef]
- Tatarskii, V.I. The Effects of the Turbulent Atmosphere on Wave Propagation; Israel Program for Scientific Translations: Jerusalem, Israel, 1971. [Google Scholar]
- Xiaoqing, W.U.; Qiguo, T.; Peng, J.; Bo, C.; Qing, C.; Jun, C.A.I.; Xinmiao, J.I.N.; Hongyan, Z. A new method of measuring optical turbulence of atmospheric surface layer at Antarctic Taishan Station with ultrasonic anemometer. Adv. Polar Sci. 2015, 26, 305. [Google Scholar] [CrossRef]
- Qing, C.; Wu, X.; Li, X.; Zhu, W.; Qiao, C.; Rao, R.; Mei, H. Use of weather research and forecasting model outputs to obtain near-surface refractive index structure constant over the ocean. Opt. Express 2016, 24, 13303–13315. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Li, X.B.; Zhan, G.W.; Wu, P.F.; Xu, C.Y.; Qing, C.; Wu, X.Q. A new model for the profiles of optical turbulence outer scale and Cn2 on the coast. Wuli Xuebao/Acta Phys. Sin. 2018, 67, 014206. [Google Scholar] [CrossRef]
- Ellrod, G.P.; Lester, P.F.; Ehernberger, L.J. Clear Air Turbulence. In Encyclopedia of Atmospheric Sciences; Holton, J.R., Ed.; Academic Press: Oxford, UK, 2003; pp. 393–403. [Google Scholar] [CrossRef]
- McGrath-Spangler, E.L.; Denning, A.S. Global seasonal variations of midday planetary boundary layer depth from CALIPSO space-borne LIDAR. J. Geophys. Res. Atmos. 2013, 118, 1226–1233. [Google Scholar] [CrossRef]
- Sathyanadh, A.; Prabhakaran, T.; Patil, C.; Karipot, A. Planetary boundary layer height over the Indian subcontinent: Variability and controls with respect to monsoon. Atmos. Res. 2017, 195, 44–61. [Google Scholar] [CrossRef]
- Sudeepkumar, B.L.; Babu, C.A.; Varikoden, H. Atmospheric boundary layer height and surface parameters: Trends and relationships over the west coast of India. Atmos. Res. 2020, 245, 105050. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Shao, S.; Liu, Q.; Sun, G.; Han, Y.; Weng, N. Optical Turbulence Profile Forecasting and Verification in the Offshore Atmospheric Boundary Layer. Appl. Sci. 2021, 11, 8523. https://doi.org/10.3390/app11188523
Xu M, Shao S, Liu Q, Sun G, Han Y, Weng N. Optical Turbulence Profile Forecasting and Verification in the Offshore Atmospheric Boundary Layer. Applied Sciences. 2021; 11(18):8523. https://doi.org/10.3390/app11188523
Chicago/Turabian StyleXu, Manman, Shiyong Shao, Qing Liu, Gang Sun, Yong Han, and Ningquan Weng. 2021. "Optical Turbulence Profile Forecasting and Verification in the Offshore Atmospheric Boundary Layer" Applied Sciences 11, no. 18: 8523. https://doi.org/10.3390/app11188523
APA StyleXu, M., Shao, S., Liu, Q., Sun, G., Han, Y., & Weng, N. (2021). Optical Turbulence Profile Forecasting and Verification in the Offshore Atmospheric Boundary Layer. Applied Sciences, 11(18), 8523. https://doi.org/10.3390/app11188523






