Physically Consistent Scar Tissue Dynamics from Scattered Set of Data: A Novel Computational Approach to Avoid the Onset of the Runge Phenomenon
Abstract
:1. Introduction
2. Methods
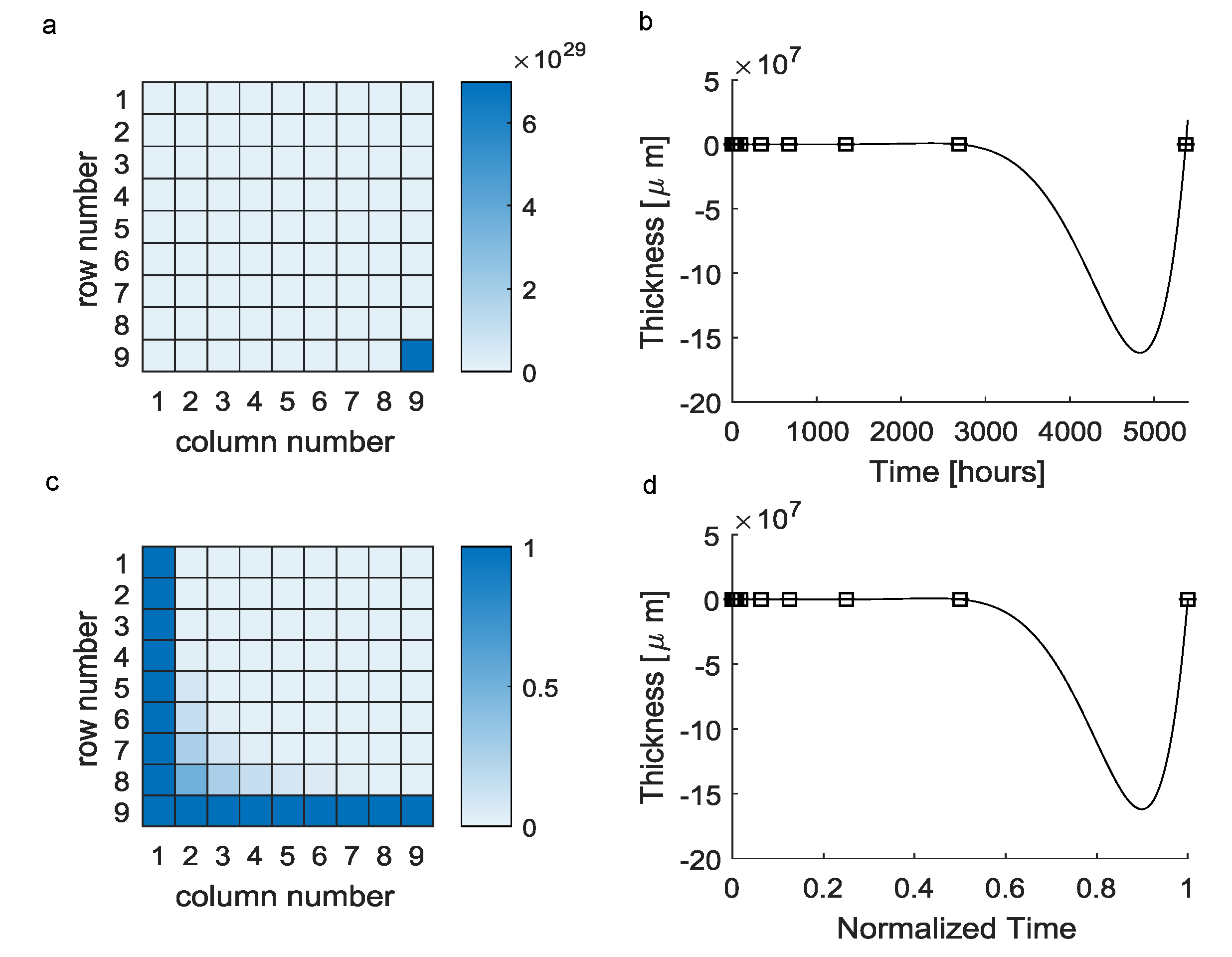
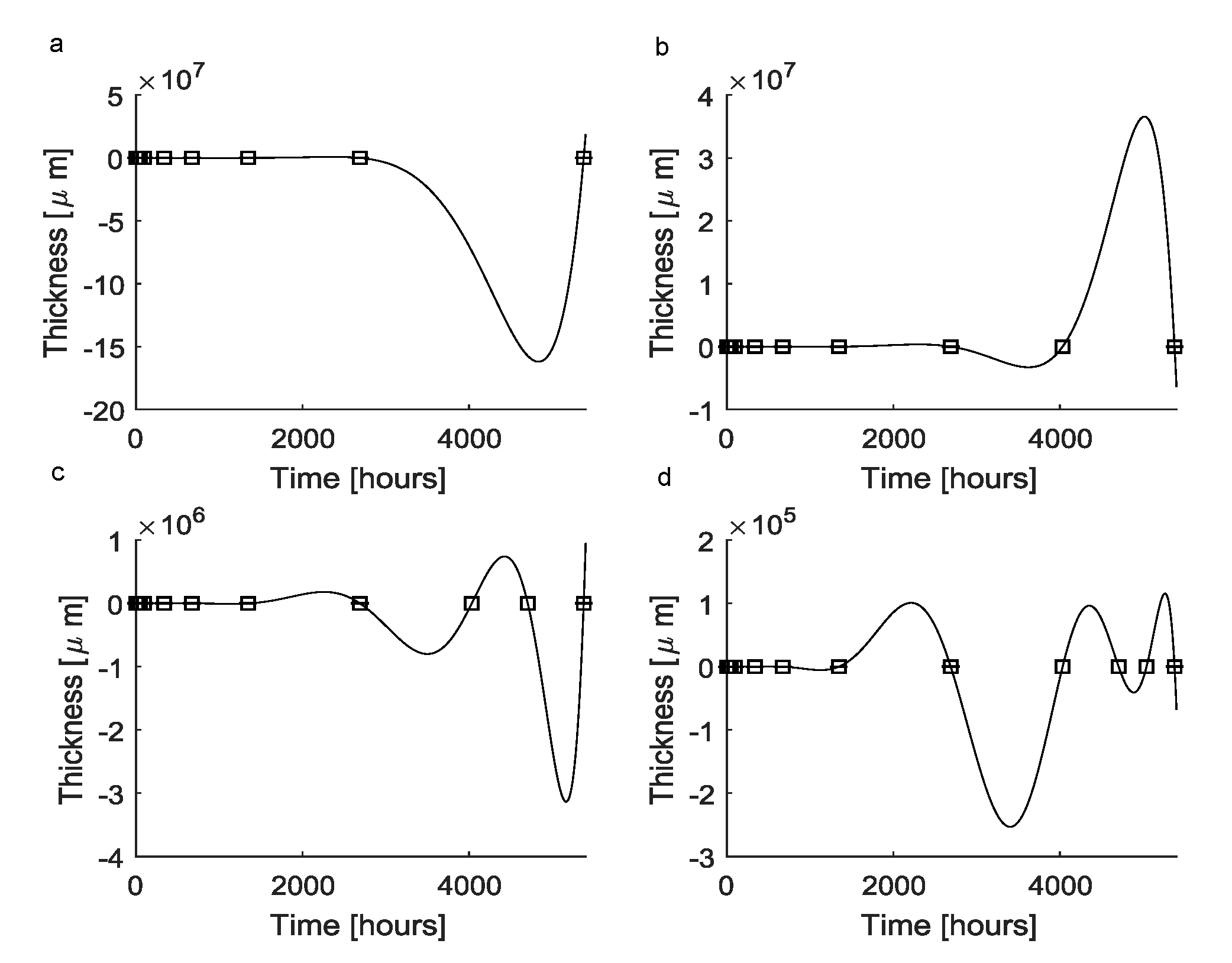
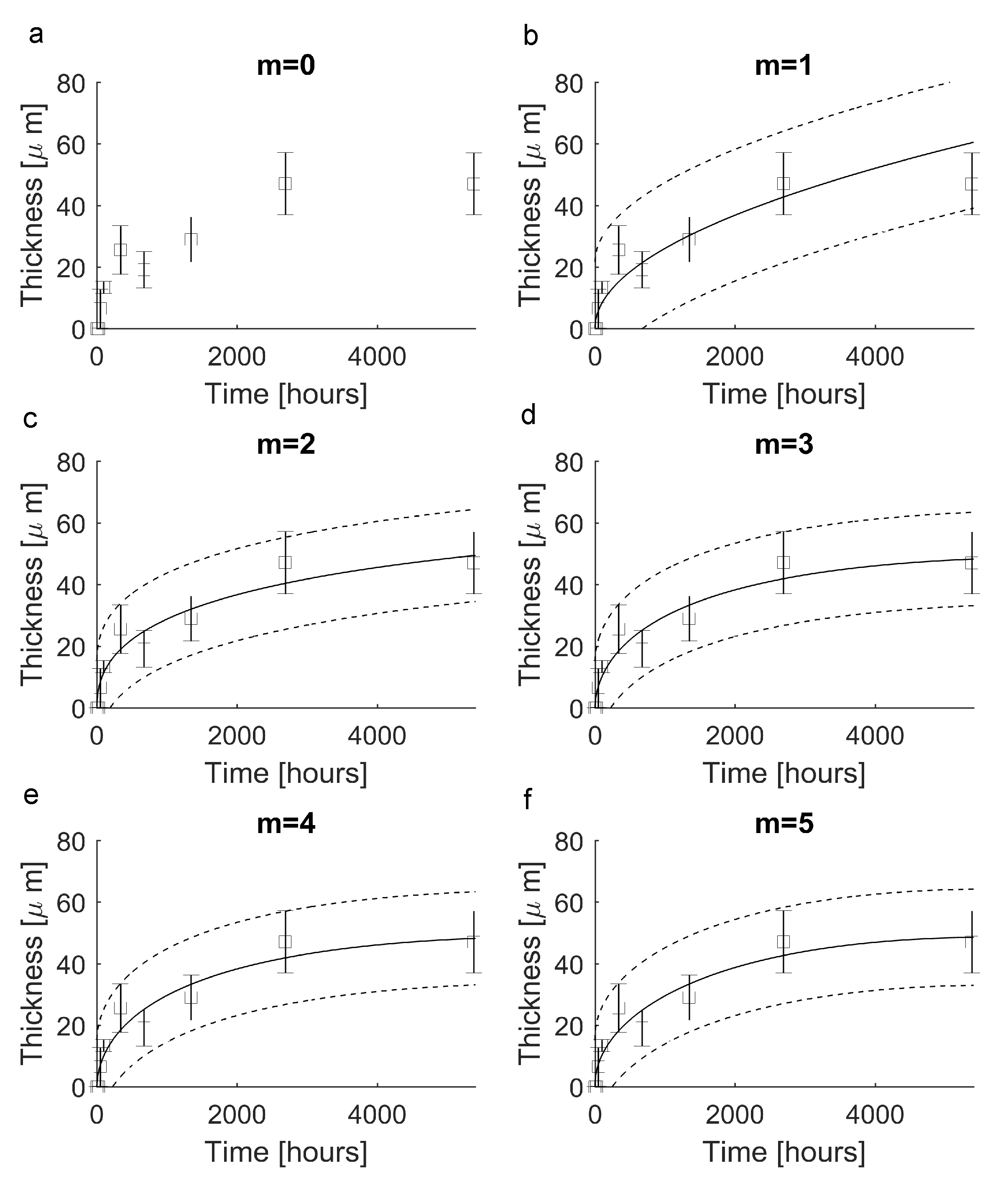
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
References
- Navarro, X.; Krueger, T.B.; Lago, N.; Micera, S.; Stieglitz, T.; Dario, P. A critical review of interfaces with the peripheral nervous system for the control of neuroprostheses and hybrid bionic systems. J. Peripher. Nerv. Syst. 2005, 10, 229–258. [Google Scholar] [CrossRef] [PubMed]
- Lago, N.; Yoshida, K.; Koch, K.P.; Navarro, X. Assessment of Biocompatibility of Chronically Implanted Polyimide and Platinum Intrafascicular Electrodes. IEEE Trans. Biomed. Eng. 2007, 54, 281–290. [Google Scholar] [CrossRef] [PubMed]
- Badia, J.; Raspopovic, S.; Carpaneto, J.; Micera, S.; Navarro, X. Spatial and Functional Selectivity of Peripheral Nerve Signal Recording With the Transversal Intrafascicular Multichannel Electrode (TIME). IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 20–27. [Google Scholar] [CrossRef]
- Cutrone, A.; Sergi, P.N.; Bossi, S.; Micera, S. Modelization of a self-opening peripheral neural interface: A feasibility study. Med. Eng. Phys. 2011, 33, 1254–1261. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Lewinsky, I.; Nielsen, M.; Hylleberg, M. Implantation mechanics of tungsten microneedles into peripheral nerve trunks. Med. Biol. Eng. Comput. 2007, 45, 413–420. [Google Scholar] [CrossRef]
- Sergi, P.N.; Jensen, W.; Micera, S.; Yoshida, K. In vivo interactions between tungsten microneedles and peripheral nerves. Med. Eng. Phys. 2012, 34, 747–755. [Google Scholar] [CrossRef] [Green Version]
- Sergi, P.N.; Jensen, W.; Yoshida, K. Interactions among biotic and abiotic factors affect the reliability of tungsten microneedles puncturing in vitro and in vivo peripheral nerves: A hybrid computational approach. Mater. Sci. Eng. C 2016, 59, 1089–1099. [Google Scholar] [CrossRef] [PubMed]
- Lago, N.; Udina, E.; Ramachandran, A.; Navarro, X. Neurobiological Assessment of Regenerative Electrodes for Bidirectional Interfacing Injured Peripheral Nerves. IEEE Trans. Biomed. Eng. 2007, 54, 1129–1137. [Google Scholar] [CrossRef]
- FitzGerald, J.J.; Lago, N.; Benmerah, S.; Serra, J.; Watling, C.P.; Cameron, R.E.; Tarte, E.; Lacour, S.P.; McMahon, S.B.; Fawcett, J.W. A regenerative microchannel neural interface for recording from and stimulating peripheral axonsin vivo. J. Neural Eng. 2012, 9, 016010. [Google Scholar] [CrossRef]
- Ciofani, G.; Sergi, P.N.; Carpaneto, J.; Micera, S. A hybrid approach for the control of axonal outgrowth: Preliminary simulation results. Med. Biol. Eng. Comput. 2011, 49, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Romaus-Sanjurjo, D.; Ledo-García, R.; Fernández-López, B.; Hanslik, K.; Morgan, J.R.; Barreiro-Iglesias, A.; Rodicio, M.C. GABA promotes survival and axonal regeneration in identifiable descending neurons after spinal cord injury in larval lampreys. Cell Death Dis. 2018, 9, 663. [Google Scholar] [CrossRef]
- Mahar, M.; Cavalli, V. Intrinsic mechanisms of neuronal axon regeneration. Nat. Rev. Neurosci. 2018, 19, 323–337. [Google Scholar] [CrossRef]
- Fogli, B.; Corthout, N.; Kerstens, A.; Bosse, F.; Klimaschewski, L.; Munck, S.; Schweigreiter, R. Imaging axon regeneration within synthetic nerve conduits. Sci. Rep. 2019, 9, 10095. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.M.; Defife, K.; Mcnally, A.; Collier, T.; Jenney, C. Monocyte, macrophage and foreign body giant cell interactions with molecularly engineered surfaces. J. Mater. Sci. Mater. Med. 1999, 10, 579–588. [Google Scholar] [CrossRef]
- Luttikhuizen, D.T.; Harmsen, M.C.; Luyn, M.J.V. Cellular and Molecular Dynamics in the Foreign Body Reaction. Tissue Eng. 2006, 12, 1955–1970. [Google Scholar] [CrossRef] [PubMed]
- Sunderland, S. The intraneural topography of the radial, median and ulnar nerves. Brain 1945, 68, 243–299. [Google Scholar] [CrossRef] [PubMed]
- Sunderland, S. The connective tissues of peripheral nerves. Brain 1965, 88, 841–854. [Google Scholar] [CrossRef] [PubMed]
- Lundborg, G. The intrinsic vascularization of human peripheral nerves: Structural and functional aspects. J. Hand Surg. Am. 1979, 4, 34–41. [Google Scholar] [CrossRef]
- Lundborg, G. Intraneural microcirculation. Orthop. Clin. N. Am. 1988, 19, 1–12. [Google Scholar] [CrossRef]
- Zochodne, D.W.; Huang, Z.X.; Ward, K.K.; Low, P.A. Guanethidine-induced adrenergic sympathectomy augments endoneurial perfusion and lowers endoneurial microvascular resistance. Brain Res. 1990, 519, 112–117. [Google Scholar] [CrossRef]
- Stolinski, C. Structure and composition of the outer connective tissue sheaths of peripheral nerve. J. Anat. 1995, 186 Pt 1, 123–130. [Google Scholar]
- Millesi, H.; Zoch, G.; Reihsner, R. Mechanical properties of peripheral nerves. Clin. Orthop. Relat. Res. 1995, 314, 76–83. [Google Scholar] [CrossRef]
- Topp, K.S.; Boyd, B.S. Structure and biomechanics of peripheral nerves: Nerve responses to physical stresses and implications for physical therapist practice. Phys. Ther. 2006, 86, 92–109. [Google Scholar] [CrossRef] [PubMed]
- Green, R.A.; Lovell, N.H.; Wallace, G.G.; Poole-Warren, L.A. Conducting polymers for neural interfaces: Challenges in developing an effective long-term implant. Biomaterials 2008, 29, 3393–3399. [Google Scholar] [CrossRef] [PubMed]
- Grill, W.M.; Norman, S.E.; Bellamkonda, R.V. Implanted Neural Interfaces: Biochallenges and Engineered Solutions. Annu. Rev. Biomed. Eng. 2009, 11, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Carpaneto, J.; Cutrone, A.; Bossi, S.; Sergi, P.; Citi, L.; Rigosa, J.; Rossini, P.M.; Micera, S. Activities on PNS neural interfaces for the control of hand prostheses. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 4637–4640. [Google Scholar]
- Anderson, J.M.; Rodriguez, A.; Chang, D.T. Foreign body reaction to biomaterials. Semin. Immunol. 2008, 20, 86–100. [Google Scholar] [CrossRef] [Green Version]
- Christensen, M.; Pearce, S.; Ledbetter, N.; Warren, D.; Clark, G.; Tresco, P. The foreign body response to the Utah Slant Electrode Array in the cat sciatic nerve. Acta Biomater. 2014, 10, 4650–4660. [Google Scholar] [CrossRef]
- Andrade, J.D.; Hlady, V. Plasma Protein Adsorption: The Big Twelvea. Ann. N. Y. Acad. Sci. 1987, 516, 158–172. [Google Scholar] [CrossRef]
- Jenney, C.R.; Anderson, J.M. Adsorbed serum proteins responsible for surface dependent human macrophage behavior. J. Biomed. Mater. Res. 2000, 49, 435–447. [Google Scholar] [CrossRef]
- Richardson, D.L.; Pepper, D.S.; Kay, A.B. Chemotaxis for Human Monocytes by Fibrinogen-derived Peptides. Br. J. Haematol. 1976, 32, 507–514. [Google Scholar] [CrossRef]
- Smiley, S.T.; King, J.A.; Hancock, W.W. Fibrinogen Stimulates Macrophage Chemokine Secretion Through Toll-Like Receptor 4. J. Immunol. 2001, 167, 2887–2894. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Szaba, F.M.; Smiley, S.T. Roles for thrombin and fibrin(ogen) in cytokine/chemokine production and macrophage adhesion in vivo. Blood 2002, 99, 1053–1059. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Jennings, T.; Eaton, J.W. Mast Cells Mediate Acute Inflammatory Responses to Implanted Blomaterials. Pediatr. Res. 1997, 41, 116. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.M. Multinucleated giant cells. Curr. Opin. Hematol. 2000, 7, 40–47. [Google Scholar] [CrossRef]
- Gori, M.; Vadalà, G.; Giannitelli, S.M.; Denaro, V.; Di Pino, G. Biomedical and Tissue Engineering Strategies to Control Foreign Body Reaction to Invasive Neural Electrodes. Front. Bioeng. Biotechnol. 2021, 9, 411. [Google Scholar] [CrossRef]
- Ward, W.K. A Review of the Foreign-body Response to Subcutaneously-implanted Devices: The Role of Macrophages and Cytokines in Biofouling and Fibrosis. J. Diabetes Sci. Technol. 2008, 2, 768–777. [Google Scholar] [CrossRef] [Green Version]
- Nachemson, A.K.; Lundborg, G.; Myrhage, R.; Rank, F. Nerve regeneration and pharmacological suppression of the scar reaction at the suture site. An experimental study on the effect of estrogen-progesterone, methylprednisolone-acetate and cis-hydroxyproline in rat sciatic nerve. Scand. J. Plast. Reconstr. Surg. 1985, 19, 255–260. [Google Scholar] [CrossRef]
- Bora, F.W.; Richardson, S.; Black, J. The biomechanical responses to tension in a peripheral nerve. J. Hand Surg. 1980, 5, 21–25. [Google Scholar] [CrossRef]
- Layton, B.E.; Sastry, A.M. A Mechanical Model for Collagen Fibril Load Sharing in Peripheral Nerve of Diabetic and Nondiabetic Rats. J. Biomech. Eng. 2005, 126, 803–814. [Google Scholar] [CrossRef] [PubMed]
- Layton, B.E.; Sastry, A.M. Equal and local-load-sharing micromechanical models for collagens: Quantitative comparisons in response of non-diabetic and diabetic rat tissue. Acta Biomater. 2006, 2, 595–607. [Google Scholar] [CrossRef] [PubMed]
- Main, E.K.; Goetz, J.E.; Rudert, M.J.; Goreham-Voss, C.M.; Brown, T.D. Apparent transverse compressive material properties of the digital flexor tendons and the median nerve in the carpal tunnel. J. Biomech. 2011, 44, 863–868. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Hu, S.; Tan, J.S.; Myer, C.; Njus, N.M.; Xia, Z. In vitro and in vivo mechanical properties of human ulnar and median nerves. J. Biomed. Mater. Res. A 2013, 101, 2718–2725. [Google Scholar] [CrossRef]
- Giannessi, E.; Stornelli, M.R.; Sergi, P.N. A unified approach to model peripheral nerves across different animal species. PeerJ 2017, 5, e4005. [Google Scholar] [CrossRef] [Green Version]
- Giannessi, E.; Stornelli, M.R.; Sergi, P.N. Fast in silico assessment of physical stress for peripheral nerves. Med. Biol. Eng. Comput. 2018. [Google Scholar] [CrossRef]
- Giannessi, E.; Stornelli, M.R.; Coli, A.; Sergi, P.N. A Quantitative Investigation on the Peripheral Nerve Response within the Small Strain Range. Appl. Sci. 2019, 9, 1115. [Google Scholar] [CrossRef] [Green Version]
- Giannessi, E.; Stornelli, M.R.; Sergi, P.N. Strain stiffening of peripheral nerves subjected to longitudinal extensions in vitro. Med. Eng. Phys. 2020, 76, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Sergi, P.N. Deterministic and Explicit: A Quantitative Characterization of the Matrix and Collagen Influence on the Stiffening of Peripheral Nerves Under Stretch. Appl. Sci. 2020, 10, 6372. [Google Scholar] [CrossRef]
- Yoshida, K.; Horch, K. Selective stimulation of peripheral nerve fibers using dual intrafascicular electrodes. IEEE Trans. Biomed. Eng. 1993, 40, 492–494. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Jovanović, K.; Stein, R.B. Intrafascicular electrodes for stimulation and recording from mudpuppy spinal roots. J. Neurosci. Methods 2000, 96, 47–55. [Google Scholar] [CrossRef]
- de la Oliva, N.; Navarro, X.; del Valle, J. Time course study of long-term biocompatibility and foreign body reaction to intraneural polyimide-based implants. J. Biomed. Mater. Res. Part A 2018, 106, 746–757. [Google Scholar] [CrossRef] [Green Version]
- de la Oliva, N.; del Valle, J.; Delgado-Martínez, I.; Mueller, M.; Stieglitz, T.; Navarro, X. Long-Term Functionality of Transversal Intraneural Electrodes is Improved by Dexamethasone Treatment. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 457–464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Szostak, K.M.; Grand, L.; Constandinou, T.G. Neural Interfaces for Intracortical Recording: Requirements, Fabrication Methods, and Characteristics. Front. Neurosci. 2017, 11, 665. [Google Scholar] [CrossRef] [Green Version]
- Guadarrama-Santana, A.; Garcia-Valenzuela, A. Determination of Thickness and Dielectric Constant of Coatings from Capacitance Measurements. IEEE Instrum. Meas. Mag. 2007, 10, 26–31. [Google Scholar] [CrossRef]
- Davis, P. Interpolation and Approximation; Blaisdell: New York, NY, USA, 1963. [Google Scholar]
- Conte, S.; de Boor, C. Elementary Numerical Analysis: An Algorithmic Approach, 3rd ed.; Mcgraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- de la Oliva, N.; Mueller, M.; Stieglitz, T.; Navarro, X.; del Valle, J. On the use of Parylene C polymer as substrate for peripheral nerve electrodes. Sci. Rep. 2018, 8, 5965. [Google Scholar] [CrossRef]
- De la Oliva, N.; Navarro, X.; del Valle, J. Dexamethasone Reduces the Foreign Body Reaction to Intraneural Electrode Implants in the Peripheral Nerve of the Rat. Anat. Rec. 2018, 301, 1722–1733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phillips, G. Two Millenia of Mathematics from Archimedes to Gauss; Springer: New York, NY, USA, 2000. [Google Scholar]
- Phillips, G. Interpolation and Approximation by Polynomials; Springer: New York, NY, USA, 2003. [Google Scholar]
- Stengle, G. Chebyshev interpolation with approximate nodes of unrestricted multiplicity. J. Approx. Theory 1989, 57, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Ibrahimoglu, B.A. A fast algorithm for computing the mock-Chebyshev nodes. J. Comput. Appl. Math. 2020, 373, 112336. [Google Scholar] [CrossRef]
- Poirier, D.J. Piecewise Regression Using Cubic Splines. J. Am. Stat. Assoc. 1973, 68, 515–524. [Google Scholar] [CrossRef]
- Lucas, T.R. Error Bounds for Interpolating Cubic Splines Under Various End Conditions. SIAM J. Numer. Anal. 1974, 11, 569–584. [Google Scholar] [CrossRef]
- Sergi, P.N.; Valle, J.D.; Oliva, N.D.L.; Micera, S.; Navarro, X. A data-driven polynomial approach to reproduce the scar tissue outgrowth around neural implants. J. Mater. Sci. Mater. Med. 2020, 31, 59. [Google Scholar] [CrossRef] [PubMed]


| Elements of the a Vector | Value |
|---|---|
| 0 | |
| −0.276 | |
| +0.015 | |
| Elements | Total Time Points = 9 + 1 | Total Time Points = 9 + 2 | Total Time Points = 9 + 3 |
|---|---|---|---|
| 0 | 0 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sergi, P.N.; De la Oliva, N.; del Valle, J.; Navarro, X.; Micera, S. Physically Consistent Scar Tissue Dynamics from Scattered Set of Data: A Novel Computational Approach to Avoid the Onset of the Runge Phenomenon. Appl. Sci. 2021, 11, 8568. https://doi.org/10.3390/app11188568
Sergi PN, De la Oliva N, del Valle J, Navarro X, Micera S. Physically Consistent Scar Tissue Dynamics from Scattered Set of Data: A Novel Computational Approach to Avoid the Onset of the Runge Phenomenon. Applied Sciences. 2021; 11(18):8568. https://doi.org/10.3390/app11188568
Chicago/Turabian StyleSergi, Pier Nicola, Natalia De la Oliva, Jaume del Valle, Xavier Navarro, and Silvestro Micera. 2021. "Physically Consistent Scar Tissue Dynamics from Scattered Set of Data: A Novel Computational Approach to Avoid the Onset of the Runge Phenomenon" Applied Sciences 11, no. 18: 8568. https://doi.org/10.3390/app11188568
APA StyleSergi, P. N., De la Oliva, N., del Valle, J., Navarro, X., & Micera, S. (2021). Physically Consistent Scar Tissue Dynamics from Scattered Set of Data: A Novel Computational Approach to Avoid the Onset of the Runge Phenomenon. Applied Sciences, 11(18), 8568. https://doi.org/10.3390/app11188568






