Reinforcement Learning and Physics
Abstract
:1. Introduction
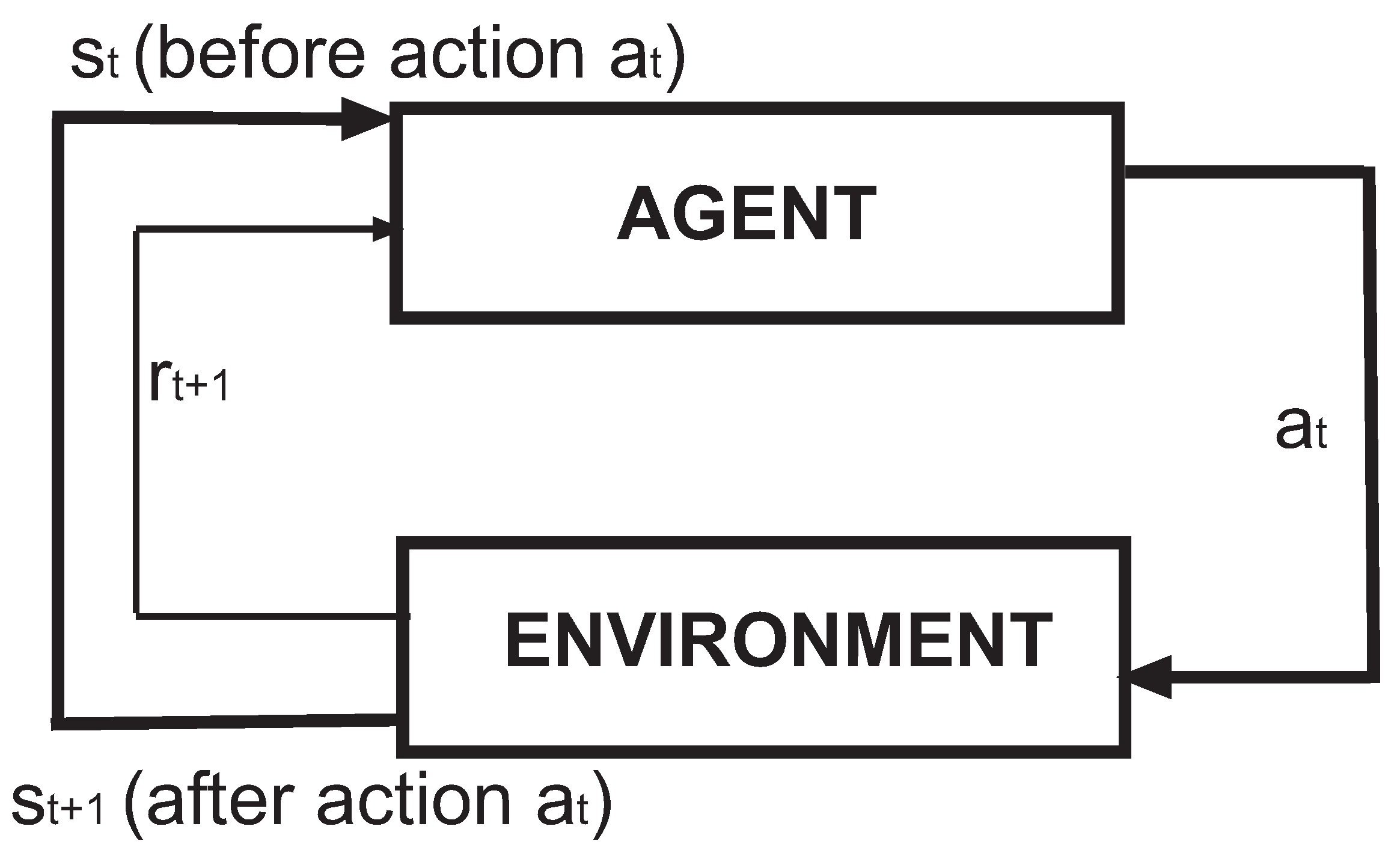
2. Reinforcement Learning and Physics
- Dynamic programming (DP): it makes use of the Bellman equation [19] when a complete model of the environment is available.
- MonteCarlo (MC) methods [17]: They do not need a model of the environment but only sample sequences of states, actions and rewards. is computed when an episode finishes, and accordingly updated.
- Temporal difference methods (TD) [20]: They do not require an environment model, either. The values of are updated using information from the environment ( and ) as well as estimations of .
2.1. Standard Reinforcement Learning for Physics Research
2.2. Quantum Reinforcement Learning
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Theodoridis, S. Machine Learning: A Bayesian and Optimization Perspective; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Mathur, P. Machine Learning Applications Using Python: Cases Studies from Healthcare, Retail and Finance; APress: New York, NY, USA, 2014. [Google Scholar]
- Martín-Guerrero, J.D.; Lisboa, P.J.G.; Vellido, A. Physics and machine learning: Emerging paradigms. In Proceedings of the ESANN 2016 European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 27–29 April 2016; pp. 319–326. [Google Scholar]
- Schütt, K.T.; Chmiela, S.; von Lilienfeld, O.A.; Tkatchenko, A.; Tsuda, K.; Müller, K.-R. Machine Learning meets Quantum Physics; Lecture Notes in Physics; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Nielsen, M.; Chuang, I.L.S. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2020, 5549, 195–202. [Google Scholar] [CrossRef]
- Muñoz-Gil, G.; Garcia-March, M.A.; Manzo, C.; Martín-Guerrero, J.D.; Lewenstein, M. Single trajectory characterization via machine learning. New J. Phys. 2020, 22, 013010. [Google Scholar] [CrossRef]
- Melko, R.G.; Carleo, G.; Carrasquilla, J.; Cirac, J.I. Restricted Boltzmann machines in quantum physics. Nat. Phys. 2019, 15, 887–892. [Google Scholar] [CrossRef]
- Andreassen, A.; Feige, I.; Fry, C.; Schwartz, M.D. JUNIPR: A framework for unsupervised machine learning in particle physics. Eur. Phys. J. C 2019, 2, 102. [Google Scholar] [CrossRef]
- Swischuk, R.; Mainini, L.; Peherstorfer, B.; Willcox, K. Projection-based model reduction: Formulations for physics-based machine learning. Comput. Fluids 2019, 179, 704–707. [Google Scholar] [CrossRef]
- Ren, K.; Chew, Y.; Zhang, Y.F.; Fuh, J.Y.H.; Bi, G.J. Thermal field prediction for laser scanning paths in laser aided additive manufacturing by physics-based machine learning. Comput. Meth. Appl. Mech. Eng. 2020, 362, 112734. [Google Scholar] [CrossRef]
- Tiersch, M.; Ganahl, E.J.; Briegel, H.J. Adaptive quantum computation in changing environments using projective simulation. Sci. Rep. 2012, 5, 12874. [Google Scholar] [CrossRef] [Green Version]
- Wigley, P.B.; Everitt, P.J.; van den Hengel, A.; Bastian, J.W.; Sooriyabandara, M.A.; McDonald, G.C.; Hardman, K.S.; Quinlivan, C.D.; Manju, P.; Kuhn, C.C.N.; et al. Fast machine-learning online optimization of ultra-cold-atom experiments. Sci. Rep. 2012, 6, 25890. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palittapongarnpim, P.; Wittek, P.; Sanders, B.C. Controlling Adaptive Quantum Phase Estimation with Scalable Reinforcement Learning. In Proceedings of the 24th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN-16), Bruges, Belgium, 27–29 April 2016; pp. 327–332. [Google Scholar]
- Ding, Y.; Ban, Y.; Martín-Guerrero, J.D.; Solano, E.; Casanova, J.; Chen, X. Breaking adiabatic quantum control with deep learning. Phys. Rev. A 2021, 103, L040401. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning, 4th ed.; MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming and Optimal Control: Volume II; Athenas Scientific: Belmont, MA, USA, 2001. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Zhang, T.; Mo, H. Reinforcement learning for robot research: A comprehensive review and open issues. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211007305. [Google Scholar] [CrossRef]
- Gómez-Pérez, G.; Martín-Guerrero, J.D.; Soria-Olivas, E.; Balaguer-Ballester, E.; Palomares, A.; Casariego, N. Assigning discounts in a marketing campaign by using reinforcement learning and neural networks. Expert Syst. Appl. 2009, 36, 8022–8031. [Google Scholar] [CrossRef]
- Martín-Guerrero, J.D.; Gomez, F.; Soria-Olivas, E.; Schmidhuber, J.; Climente-Martí, M.; Jiménez-Torres, N.V. A Reinforcement Learning approach for Individualizing Erythropoietin Dosages in Hemodialysis Patients. Expert Syst. Appl. 2009, 36, 9737–9742. [Google Scholar] [CrossRef]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602. [Google Scholar] [CrossRef] [Green Version]
- Fösel, T.; Tighineanu, P.; Weiss, T.; Marquardt, F. Reinforcement Learning with Neural Networks for Quantum Feedback. Phys. Rev. X 2018, 8, 031084. [Google Scholar] [CrossRef] [Green Version]
- Bukov, M.; Day, A.G.R.; Sels, D.; Weinberg, P.; Polkovnikov, A.; Mehta, P. Reinforcement Learning in Different Phases of Quantum Control. Phys. Rev. X 2018, 8, 031086. [Google Scholar] [CrossRef] [Green Version]
- Melnikov, A.A.; Nautrup, H.P.; Krenn, M.; Dunjko, V.; Tiersch, M.; Zeilinger, A.; Briegel, H.J. Active learning machine learns to create new quantum experiments. Proc. Natl. Acad. Sci. USA 2018, 115, 1221–1226. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Martín-Guerrero, J.D.; Sanz, M.; Magdalena-Benedicto, R.; Chen, X.; Solano, E. Retrieving Quantum Information with Active Learning. Phys. Rev. Lett. 2020, 124, 140504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjel, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Nguyen, V.; Orbell, S.B.; Lennon, D.T.; Moon, H.; Vigneau, F.; Camenzind, L.C.; Yu, L.; Zumbühl, D.M.; Briggs, G.A.D.; Osborne, M.A.; et al. Deep reinforcement learning for efficient measurement of quantum devices. npj Quantum Inform. 2021, 7, 100. [Google Scholar] [CrossRef]
- Zhang, X.M.; Wei, Z.; Asad, R.; Yang, X.C.; Wang, X. When does reinforcement learning stand out in quantum control? A comparative study on state preparation. npj Quantum Inform. 2019, 5, 85. [Google Scholar] [CrossRef]
- Zheng, A.; Zhou, D.L. Deep reinforcement learning for quantum gate control. Europhys. Lett. 2019, 126, 60002. [Google Scholar]
- Whitelam, S.; Jacobson, D.; Tamblyn, I. Evolutionary reinforcement learning of dynamical large deviations. J. Chem. Phys. 2020, 153, 044113. [Google Scholar] [CrossRef] [PubMed]
- Garnier, P.; Viquerat, J.; Rabault, J.; Larcher, A.; Kuhnle, A.; Hachem, E. A review on deep reinforcement learning for fluid mechanics. Comput. Fluids 2021, 225, 104973. [Google Scholar] [CrossRef]
- Nousiainen, J.; Rajani, C.; Kasper, M.; Helin, T. Adaptive optics control using model-based reinforcement learning. Opt. Express 2021, 29, 15327–15344. [Google Scholar] [CrossRef]
- Beeler, C.; Yahorau, U.; Coles, R.; Mills, K.; Whitelam, S.; Tamblyn, I. Optimizing thermodynamic trajectories using evolutionary and gradient-based reinforcement learning. arXiv 2019, arXiv:1903.08453. [Google Scholar]
- Rose, D.C.; Mair, J.F.; Garrahan, J.P. A reinforcement learning approach to rare trajectory sampling. New J. Phys. 2021, 23, 013013. [Google Scholar] [CrossRef]
- Lamata, L. Quantum machine learning and quantum biomimetics: A perspective. Mach. Learn. Sci. Technol. 2020, 1, 033002. [Google Scholar] [CrossRef]
- Dong, D.; Chen, C.; Li, H.; Tarn, T.-J. Quantum Reinforcement Learning. IEEE Trans. Syst. Man Cybern. B 2008, 38, 1207. [Google Scholar] [CrossRef] [Green Version]
- Paparo, G.D.; Dunjko, V.; Makmal, A.; Martin-Delgado, M.A.; Briegel, H.J. Quantum speedup for active learning agents. Phys. Rev. X 2014, 4, 031002. [Google Scholar] [CrossRef]
- Dunjko, V.; Taylor, J.M.; Briegel, H.J. Quantum-enhanced machine learning. Phys. Rev. Lett. 2016, 117, 130501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lamata, L. Basic protocols in quantum reinforcement learning with superconducting circuits. Sci. Rep. 2017, 7, 1609. [Google Scholar] [CrossRef] [Green Version]
- Cárdenas-López, F.A.; Lamata, L.; Retamal, J.C.; Solano, E. Multiqubit and multilevel quantum reinforcement learning with quantum technologies. PLoS ONE 2018, 13, e0200455. [Google Scholar]
- Albarrán-Arriagada, F.; Retamal, J.C.; Solano, E.; Lamata, L. Measurement-based adaptation protocol with quantum reinforcement learning. Phys. Rev. A 2018, 98, 042315. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Albarrán-Arriagada, F.; Retamal, J.C.; Wang, Y.T.; Liu, W.; Ke, Z.J.; Meng, Y.; Li, Z.P.; Tang, J.S.; Solano, E.; et al. Reconstruction of a Photonic Qubit State with Reinforcement Learning. Adv. Quantum Technol. 2019, 2, 1800074. [Google Scholar] [CrossRef]
- Olivares-Sánchez, J.; Casanova, J.; Solano, E.; Lamata, L. Measurement-based adaptation protocol with quantum reinforcement learning in a Rigetti quantum computer. Quantum Rep. 2020, 2, 293. [Google Scholar] [CrossRef]
- Albarrán-Arriagada, F.; Retamal, J.C.; Solano, E.; Lamata, L. Reinforcement learning for semi-autonomous approximate quantum eigensolver. Mach. Learn. Sci. Technol. 2020, 1, 015002. [Google Scholar] [CrossRef]
- Lamata, L. Quantum Reinforcement Learning with Quantum Photonics. Photonics 2021, 8, 33. [Google Scholar] [CrossRef]
- Spagnolo, M.; Morris, J.; Piacentini, S.; Antesberger, M.; Massa, F.; Ceccarelli, F.; Crespi, A.; Osellame, R.; Walther, P. Experimental quantum memristor. arXiv 2021, arXiv:2105.04867. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín-Guerrero, J.D.; Lamata, L. Reinforcement Learning and Physics. Appl. Sci. 2021, 11, 8589. https://doi.org/10.3390/app11188589
Martín-Guerrero JD, Lamata L. Reinforcement Learning and Physics. Applied Sciences. 2021; 11(18):8589. https://doi.org/10.3390/app11188589
Chicago/Turabian StyleMartín-Guerrero, José D., and Lucas Lamata. 2021. "Reinforcement Learning and Physics" Applied Sciences 11, no. 18: 8589. https://doi.org/10.3390/app11188589
APA StyleMartín-Guerrero, J. D., & Lamata, L. (2021). Reinforcement Learning and Physics. Applied Sciences, 11(18), 8589. https://doi.org/10.3390/app11188589






