Influence of the Motion of a Spring Pendulum on Energy-Harvesting Devices
Abstract
:1. Introduction
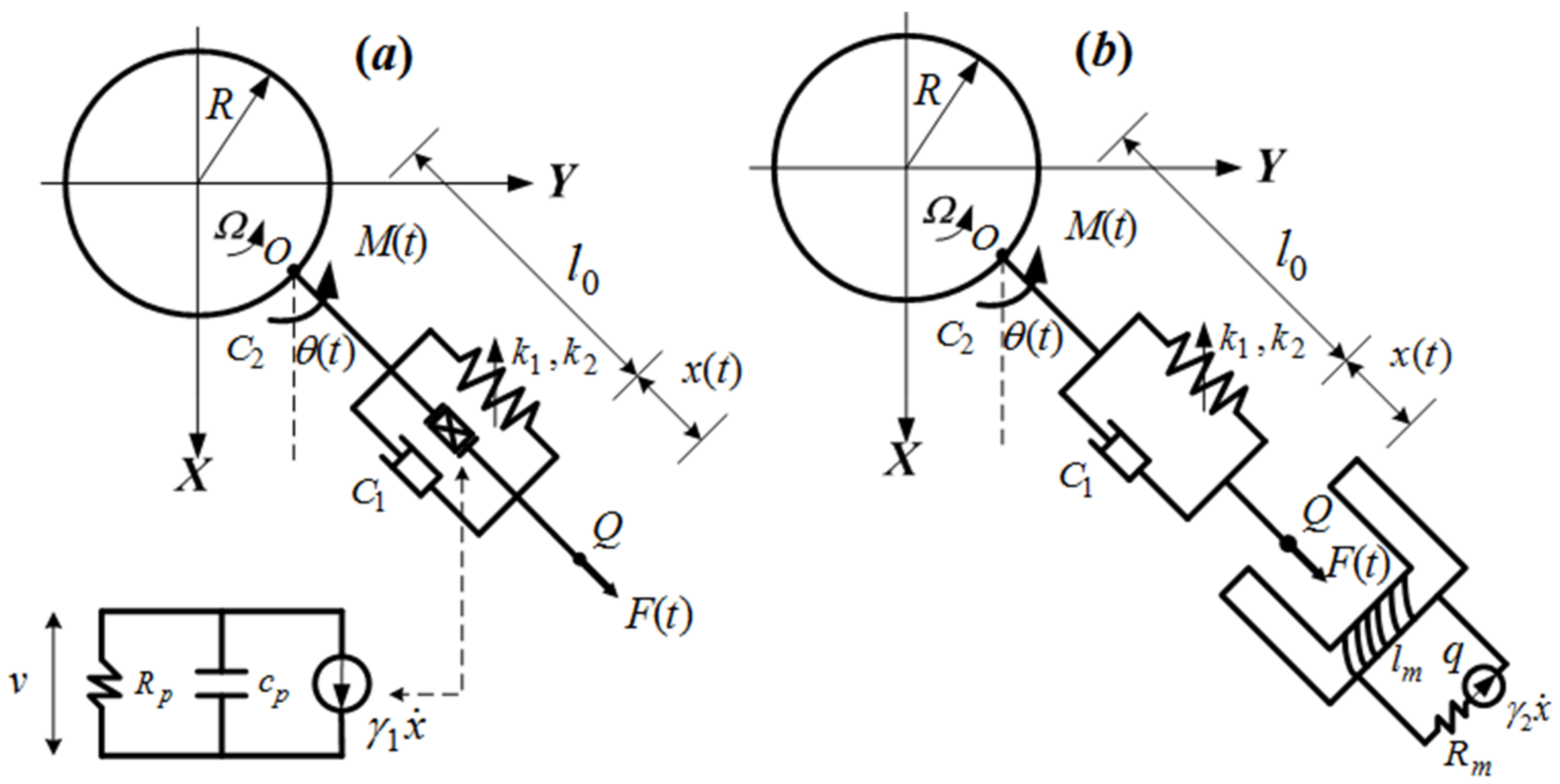
2. Dynamical Modeling
3. The Proposed Method
4. Vibrations and Resonance Conditions
5. Steady-State Solutions
6. Stability Analysis
7. Energy-Harvesting Device Performance
8. Conclusions
- 1.
- A 2DOF nonlinear damped vibrating spring pendulum system moving in a circular path with a stationary angular velocity, in which it is connected with energy-harvesting devices, was investigated as a novel model.
- 2.
- The governing equations were derived using Lagrange’s equation and solved asymptotically using the AMS to obtain results with high accuracy.
- 3.
- The solvability conditions were acquired in light of the resonance cases.
- 4.
- The achieved ME was solved to obtain two nonlinear algebraic equations in terms of the amplitudes and the detuning parameters.
- 5.
- The time histories of the dynamical motion, the resonance curves responses, and the solutions at the steady-state cases were graphed to reveal the excellent impact of the selected values of the model parameters on the motion.
- 6.
- The achieved asymptotic solutions were verified compared with the numerical results that reveal the high solidity between them.
- 7.
- The damping coefficients and excitation amplitudes that influence the output voltage, current, and power were checked. Moreover, the output power of the systems was reviewed according to the response of excitation frequency.
- 8.
- The nonlinear stability of the ME was examined through the stability and instability areas for the frequency response curves. In addition, the nonlinear analysis for the nonlinear amplitudes of these equations is presented.
- 9.
- Electrical energy was generated from piezoelectric and electromagnetic devices.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols and Abbreviations | Description |
| and | External harmonic force and torque. |
| and | Damping coefficients. |
| and | Linear and nonlinear stiffness coefficients. |
| Spring’s normal length. | |
| Gravitational acceleration. | |
| and | The elongation and swaying angle of the spring. |
| and | Output voltage and current. |
| Radius of the circular path. | |
| Angular velocity. | |
| Suspension point of the dynamical system. | |
| Axes in the plane. | |
| Potential and kinetic energies. | |
| Linear coupling coefficients for the piezoelectric and electromagnetic circuits. | |
| and | Resistive loads of the piezoelectric circuit and electromagnetic one. |
| and | Capacitance of the piezoelectric and the inductance of the coil. |
| Small parameter. | |
| Amplitudes. | |
| Modified phases. | |
| and | Frequencies. |
| Amplitudes of harmonic force and torque. | |
| Detuning parameters. | |
| EH | Energy harvesting. |
| PEH | Piezoelectric energy harvester. |
| FEM | Finite element method. |
| DOF | Degrees of freedom. |
| AMS | Approach of multiple scales. |
| EOM | Equations of motion. |
| ODEs | Ordinary differential equations. |
| ME | Modulation equations. |
References
- Priya, S.; Inman, D.J. (Eds.) Energy Harvesting Technologies; Springer: New York, NY, USA, 2008. [Google Scholar]
- Anton, S.; Sodano, H. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Beeby, S.P.; Cao, Z.; Almussallam, A. 11- Kinetic, thermoelectric and solar energy harvesting technologies for smart textiles. In Multidisciplinary Know-How for Smart-Textiles Developers; Woodhead Publishing: Cambridge, UK, 2013; pp. 306–328. [Google Scholar]
- Glynne-Jones, P.; Tudor, M.J.; Beeby, S.P.; White, N.M. An electromagnetic, vibration-powered generator for intelligent sensor systems. Sens. Actuators A 2004, 110, 344–349. [Google Scholar] [CrossRef] [Green Version]
- Owens, B.A.M.; Mann, B.P. Linear and nonlinear electromagnetic coupling models in vibration-based energy harvesting. J. Sound Vib. 2012, 331, 922–937. [Google Scholar] [CrossRef]
- Cepnik, C.; Radler, O.; Rosenbaum, S.; Ströhla, T.; Wallrabe, U. Effective optimization of electromagnetic energy harvesters through direct computation of the electromagnetic coupling. Sens. Actuators A 2011, 167, 416–421. [Google Scholar] [CrossRef]
- Gholikhania, M.; Nasouri, R.; Tahami, S.A.; Legette, S.; Dessouky, S.; Montoya, A. Harvesting kinetic energy from roadway pavement through an electromagnetic speed bump. Appl. Energy 2019, 250, 503–511. [Google Scholar] [CrossRef]
- Gao, L.; Lu, S.; Xie, W.; Chen, X.; Wu, L.; Wang, T.; Wang, A.; Yue, C.; Tong, D.; Lei, W.; et al. A self-powered and self-functional tracking system based on triboelectric-electromagnetic hybridized blue energy harvesting module. Nano Energy 2020, 72, 104684. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, Y.; Ma, J.; Zhu, H.; Cao, X.; Wang, N.; Wang, Z.L. Harvesting wind energy: A hybridized design of pinwheel by coupling triboelectrification and electromagnetic induction effects. Nano Energy 2019, 60, 641–648. [Google Scholar] [CrossRef]
- Fan, K.; Tan, Q.; Liu, H.; Zhang, Y.; Cai, M. Improved energy harvesting from low-frequency small vibrations through a monostable piezoelectric energy harvester. Mech. Syst. Signal Process. 2019, 117, 594–608. [Google Scholar] [CrossRef]
- Li, X.; Upadrashta, D.; Yu, K.; Yang, Y. Analytical modeling and validation of multi-mode piezoelectric energy harvester. Mech. Syst. Signal Process. 2019, 124, 613–631. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Dhote, S.; Li, H.; Yang, Z. Multi-frequency responses of compliant orthoplanar spring designs for widening the bandwidth of piezoelectric energy harvesters. Int. J. Mech. Sci. 2019, 157–158, 684–691. [Google Scholar] [CrossRef]
- Hsieh, J.; Lin, D.T.W.; Lin, C. The development and optimization of an innovative piezoelectric energy harvester on the basis of vapor-induced vibrations. Mech. Syst. Signal Process. 2019, 131, 649–658. [Google Scholar] [CrossRef]
- Kim, J.; Byun, S.; Lee, S.; Ryu, J.; Cho, S.; Oh, C.; Kim, H.; No, K.; Ryu, S.; Lee, Y.M.; et al. Cost-effective and strongly integrated fabric-based wearable piezoelectric energy harvester. Nano Energy 2020, 75, 104992. [Google Scholar] [CrossRef]
- Saxena, S.; Sharma, R.; Pant, B.D. Piezoelectric layer length and thickness variation effects on displacement, von-Mises stress and electric potential generated by cantilever type piezoelectric energy harvester. Mater. Today Proc. 2020, 30, 23–27. [Google Scholar] [CrossRef]
- Saxena, S.; Sharma, R.; Pant, B.D. Effect of seismic mass thickness on the resonance frequency of cantilever type piezoelectric energy harvester. Mater. Today Proc. 2020, 30, 88–92. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design and testing of a new dual-axial under floor piezoelectric energy harvester. Sens. Actuators A 2020, 303, 111858. [Google Scholar] [CrossRef]
- Alkasassbeh, M.; Omar, Z.; Mebarek-Oudina, F.; Raza, J.; Chamkha, A. Heat transfer study of convective fin with temperature-dependent internal heat generation by hybrid block method. Heat Transf.-Asian Res. 2019, 48, 1225–1244. [Google Scholar] [CrossRef]
- Farhan, M.; Omar, Z.; Mebarek-Oudina, F.; Raza, J.; Shah, Z.; Choudhari, R.V.; Makinde, O.D. Implementation of the one-step one-hybrid block method on the nonlinear equation of a circular sector oscillator. Comput. Math. Model. 2020, 31, 116–132. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z. Nonlinear analysis of axially loaded piezoelectric energy harvesters with flexoelectricity. Int. J. Mech. Sci. 2020, 173, 105473. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1144. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Qiu, J.; Zhou, S.; Ji, H.; Chen, Y.; Li, S. A piezoelectric spring pendulum oscillator used for multi-directional an ultra-low frequency vibration energy harvesting. Appl. Energy 2018, 231, 600–614. [Google Scholar] [CrossRef]
- Hu, G.; Tang, L.; Das, R.; Marzocca, P. A two-degree-of-freedom piezoelectric energy harvester with stoppers for achieving enhanced performance. Int. J. Mech. Sci. 2018, 149, 500–507. [Google Scholar] [CrossRef]
- Sun, S.; Tse, P.W. Modeling of a horizontal asymmetric U-shaped vibration-based piezoelectric energy harvester (U-VPEH). Mech. Syst. Signal Process. 2019, 114, 467–485. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Broadband piezoelectric power generation on high energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Wang, X.; Liang, X.; Hao, Z.; Du, H.; Zhang, N.; Qian, M. Comparison of electromagnetic and piezoelectric vibration energy harvesters with different interface circuits. Mech. Syst. Signal Process. 2016, 72–73, 906–924. [Google Scholar] [CrossRef]
- Karami, M.A.; Inman, D.J. Equivalent damping and frequency change for linear and nonlinear hybrid vibrational energy harvesting systems. J. Sound Vib. 2011, 330, 5583–5597. [Google Scholar] [CrossRef]
- Karama, M.; Hamdi, M.; Habbad, M. Energy harvesting in a nonlinear energy sink absorber using delayed resonators. Nonlinear Dyn. 2021, 105, 113–129. [Google Scholar] [CrossRef]
- Kecik, K.; Mitura, A. Theoretical and experimental investigations of a pseudo-magnetic levitation system for energy harvesting. Sensors 2020, 20, 1623. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kecik, K. Simultaneous vibration mitigation and energy harvesting from a pendulum-type absorber. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105479. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Starosta, R. Resonances in a kinematically driven nonlinear system asymptotic analysis. Math. Eng. Sci. Aerosp. 2010, 1, 1–10. [Google Scholar]
- Awrejcewicz, J.; Starosta, R.; Kaminska, G. Asymptotic analysis of resonances in nonlinear vibrations of the 3-dof pendulum. Differ. Equ. Dyn. Syst. 2013, 21, 123–140. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A.; Abouhmr, M.K. On the vibrational analysis for the motion of a harmonically damped rigid body pendulum. Nonlinear Dyn. 2018, 91, 2485–2502. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A.; Abohamer, M.K. On the motion of a harmonically excited damped spring pendulum in an elliptic path. Mech. Res. Commun. 2019, 95, 23–34. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A. Chaotic responses of a harmonically excited spring pendulum moving in circular path. Nonlinear Anal. RWA 2009, 10, 3196–3202. [Google Scholar] [CrossRef]
- Bek, M.A.; Amer, T.S.; Almahalawy, A.; Elameer, A.S. The asymptotic analysis for the motion of 3DOF dynamical system close to resonances. Alex. Eng. J. 2021, 60, 3539–3551. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A.; Hassan, S.S.; Elbendary, S. The stability analysis for the motion of a nonlinear damped vibrating dynamical system with three-degrees-of-freedom. Results Phys. 2021, 28, 104561. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A.; Hassan, S.S. The dynamical analysis for the motion of a harmonically two degrees of freedom damped spring pendulum in an elliptic trajectory. Alex. Eng. J. 2021. [Google Scholar] [CrossRef]
- El-Sabaa, F.M.; Amer, T.S.; Gad, H.M.; Bek, M.A. On the motion of a damped rigid body near resonances under the influence of harmonically external force and moments. Results Phys. 2020, 19, 103352. [Google Scholar] [CrossRef]
- Rajasekar, S.; Sanjuan, M.A. Nonlinear Resonances; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Abady, I.M.; Amer, T.S.; Gad, H.M.; Bek, M.A. The asymptotic analysis and stability of 3DOF nonlinear damped rigid body pendulum near resonance. Ain Shams Eng. J. 2021. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Perturbations Methods; Wiley-VCH Verlag GmbH and Co. KGaA: Weinheim, Germany, 2004. [Google Scholar]
- Bek, M.A.; Amer, T.S.; Sirwah, M.A.; Awrejcewicz, J.; Arab, A.A. The vibrational motion of a spring pendulum in a fluid flow. Results Phys. 2020, 19, 103465. [Google Scholar] [CrossRef]


































Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abohamer, M.K.; Awrejcewicz, J.; Starosta, R.; Amer, T.S.; Bek, M.A. Influence of the Motion of a Spring Pendulum on Energy-Harvesting Devices. Appl. Sci. 2021, 11, 8658. https://doi.org/10.3390/app11188658
Abohamer MK, Awrejcewicz J, Starosta R, Amer TS, Bek MA. Influence of the Motion of a Spring Pendulum on Energy-Harvesting Devices. Applied Sciences. 2021; 11(18):8658. https://doi.org/10.3390/app11188658
Chicago/Turabian StyleAbohamer, Mohamed K., Jan Awrejcewicz, Roman Starosta, Tarek S. Amer, and Mohamed A. Bek. 2021. "Influence of the Motion of a Spring Pendulum on Energy-Harvesting Devices" Applied Sciences 11, no. 18: 8658. https://doi.org/10.3390/app11188658






