Modelling of Evenness of Runways as an Element of Sustainable Airport Maintenance
Abstract
:1. Introduction
- has sufficient surface roughness (important for accelerating and decelerating aircraft) —otherwise, roughness must be ensured by appropriate measures (grooming),
- the horizontal slope may be:
- ○
- between 1 and 1.5% for airports with code letter C, D, E and F, and between 1 and 2% for airports with code letter A and B. In terms of elevation, individual sections of the runway may deviate from the runway centerline for runway code numbers 3 and 4
- ○
- less than 1% in the first quarter, less than 0,8% in the last quarter and less than 1.25% in the remaining quarters. For runways with code numbers 2 and 4, a tolerance of less than 2% shall apply everywhere. Changes from two consecutive slopes may be less than 1.5% for code number 3 and 4 airports and less than 2% for code number 1 and 2 airports. There is also a rule concerning the transition between different slopes, namely a change of slope of less than 0.1% per 30 m for code number 4 airports, of less than 0.2% per 30 m for code number 3 airports and of less than 0.4% per 30 m for code numbers 1 and 2 airports is allowed.
- the cross slope of the runway shall provide drainage of the runway. The installation of additional vegetation can help with this, as it artificially directs rainwater outside the airport runway.
The Purpose of the Research
2. Methods for Measuring the Evenness of Airport Runways
2.1. Methods for Modelling the Evenness of Airport Runways
- approximation with regression plane,
- inverse distance weighted interpolation (IWD) and
- interpolation based on triangulated irregular network (TIN).
2.1.1. Approximation with Regression Plane
- D—the distance between the plain and centroid of the cloud of point,
- a, b, c—the parameters in the equation of the plain
- x-x coordinate of the point
- y-y coordinate of the point
- H–normal orthometric altitude or altitude
2.1.2. Inverse Distance Weighted Interpolation (IDW)
2.1.3. Interpolation Based on Triangulated Irregular Network (TIN)
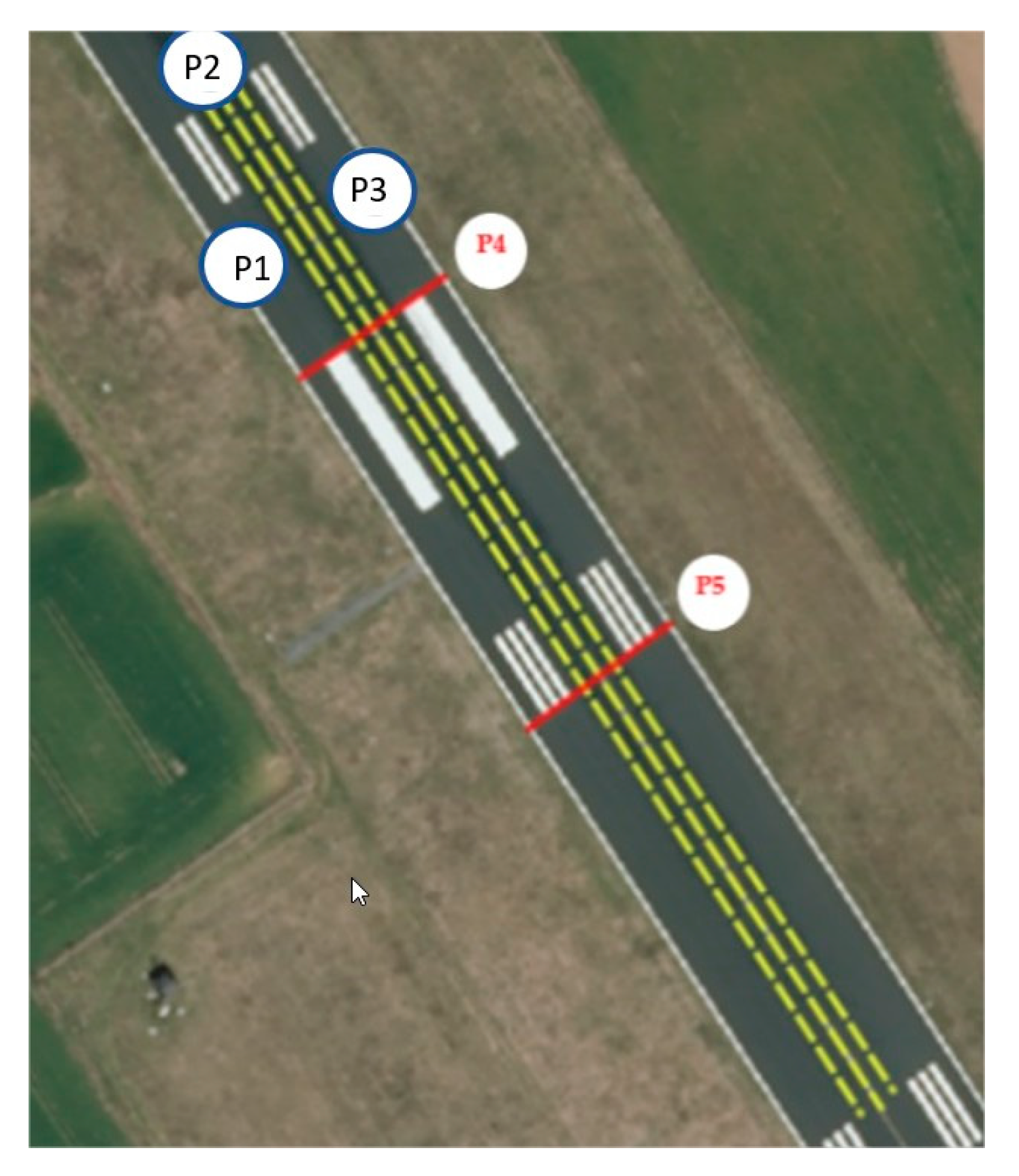
3. Experiment
4. Results
4.1. Approximation with Regression Plane
4.2. Inverse Distance Weighted Interpolation (IDW)
4.3. Interpolation Based on Triangulated Irregular Network (TIN)
5. Discussion
- regression plane approximation (RR): The method allows for the calculation of the elevation of each selected point of the regression plane. Since the regression plane is continuous, the alignments of the measured runway irregularities are likely to be large. Comparison with the average linear slope shows the best fit (MAX < 3 mm, Mean < 7 mm, SE < 0,1mm on longitudinal cross-sections and MAX < 9 mm, Mean < 5 mm, SE < 3 mm on other selected cross-sections). An additional disadvantage of this method is the longer post-processing (a few hours) and, of course, the processing of the results with the MatLab program, which is not public, but was made for the purposes of this research.
- linear triangular irregular network interpolation (TIN): A method of creating an elevation model using TIN interpolation is a tool included in every major GIS (public tool). The basic elements of the model are flat triangular surfaces whose nodes are determined by the measured elevation points. The use of the model, therefore, promotes the consideration that the model accounts as much as possible for the measured irregularities in slope evenness and most likely approximates the actual slope condition. Comparison with the average linear slope shows the good fit (MAX < 30 mm, Mean < 5 mm, SE < 0.1 mm on longitudinal cross-sections and MAX < 100 mm, Mean < 4 mm, SE < 3 mm on other selected cross-sections). The creation of a model is relatively fast and simple; the understanding of the results is guaranteed. All tools for further processing TIN are publicly available.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jackson, P.T.G.; Nelson, C.J.; Schiefele, J.; Obara, B. Runway detection in High Resolution remote sensing data. In Proceedings of the 9th International Symposium on Image and Signal Processing and Analysis (ISPA), Zagreb, Croatia, 7–9 September 2015. [Google Scholar]
- Lee, M.-H.; Chou, C.-P.; Li, K.-H. Automatic measurement of runway grooving construction for pavement skid evaluation. Autom. Constr. 2009, 18, 856–863. [Google Scholar] [CrossRef]
- Moon, S.; Yang, B.; Kim, J.; Seo, J. Effectiveness of remote control for a concrete surface grinding machine. Autom. Constr. 2010, 19, 734–741. [Google Scholar] [CrossRef]
- Taleghani, M.; Taleghani, A. Hierachy of Sustainablility Management System. Available online: https://www.researchgate.net/publication/343548430_Hierarchy-of-Sustainability-Management-System (accessed on 17 March 2021).
- Choi, T.-M.; Chiu, C.H.; Chan, H.K. Risk management of logistics systems. Transp. Res. Part E Logist. Transp. Rev. 2016, 90, 1–6. [Google Scholar] [CrossRef]
- Bensassi, S.; Márquez-Ramos, L.; Martinez-Zarzoso, I.; Suárez-Burguet, C. Relationship between logistics infrastructure and trade: Evidence from Spanish regional exports. Transp. Res. Part A Policy Pract. 2015, 72, 47–61. [Google Scholar] [CrossRef]
- Tsai, M.-C.; Su, Y.-S. Political risk assessment on air logistics hub developments in Taiwan. J. Air Transp. Manag. 2002, 8, 373–380. [Google Scholar] [CrossRef]
- ICAO. Aerodrome Design Manual, Part 1 Runway, 4th ed.; ICAO: Montreal, QC, Canada, 2020. [Google Scholar]
- Micco, A.; Serebrisky, T. Infrastructure, Competition Regimes, and Air Transport Costs: Cross-Country Evidence; Policy Research Working Paper Series 3355; World Bank: Washington, DC, USA, 2004. [Google Scholar]
- Bogoyavlenskiy, A. The analysis of measurements of flatness of the artificial surfaces of the runway of civil aerodrome. World Meas. 2018. [Google Scholar] [CrossRef]
- Barbarella, M.; De Blasiis, M.R.; Fiani, M.; Santoni, M. A LiDAR application for the study of taxiway surface evenness and slope. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, II-5, 65–72. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, K.P.; El-Sheimy, N. Mobile Mapping Systems—State of The Art and Future Trends. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 10. [Google Scholar]
- Samsonov, S.V.; D’Oreye, N.; Gonzalez, P.J.; Tiampo, K.; Ertolahti, L.; Clague, J.J. Rapidly accelerating subsidence in the Greater Vancouver region from two decades of ERS-ENVISAT-RADARSAT-2 DInSAR measurements. Remote. Sens. Environ. 2014, 143, 180–191. [Google Scholar] [CrossRef] [Green Version]
- Mao, X.; Yuan, C.; Gan, J. Incorporating Dynamic Traffic Distribution into Pavement Maintenance Optimization Model. Sustainability 2019, 11, 2488. [Google Scholar] [CrossRef] [Green Version]
- Kelemen, M.; Polishchuk, V.; Gavurová, B.; Andoga, R.; Szabo, S.; Yang, W.; Christodoulakis, J.; Gera, M.; Kozuba, J.; Kaľavský, P.; et al. Educational Model for Evaluation of Airport NIS Security for Safe and Sustainable Air Transport. Sustainability 2020, 12, 6352. [Google Scholar] [CrossRef]
- Ciampoli, L.B.; Gagliardi, V.; Ferrante, C.; Calvi, A.; D’Amico, F.; Tosti, F. Displacement Monitoring in Airport Runways by Persistent Scatterers SAR Interferometry. Remote Sens. 2020, 12, 3564. [Google Scholar] [CrossRef]
- Ding, W.; Wu, J. An Airport Knowledge-Based Method for Accurate Change Analysis of Airport Runways in VHR Remote Sensing Images. Remote Sens. 2020, 12, 3163. [Google Scholar] [CrossRef]
- Brtnický, M.; Pecina, V.; Baltazár, T.; Vašinová Galiová, M.; Baláková, L.; Bęś, A.; Radziemska, M. Environmental Impact Assessment of Potentially Toxic Elements in Soils Near the Runway at the International Airport in Central Europe. Sustainability 2020, 12, 7224. [Google Scholar] [CrossRef]
- Svigkas, N.; Loupasakis, C.; Papoutsis, I.; Kontoes, C.; Alatza, S.; Tzampoglou, P.; Tolomei, C.; Spachos, T. InSAR Campaign Reveals Ongoing Displacement Trends at High Impact Sites of Thessaloniki and Chalkidiki, Greece. Remote Sens. 2020, 12, 2396. [Google Scholar] [CrossRef]
- Cai, Y.; Ma, J.; Yan, W.; Zhang, W.; An, Y. Aircraft Detection Using Phase-Sensitive Optical-Fiber OTDR. Sensors 2021, 21, 5094. [Google Scholar] [CrossRef]
- Wesolowski, M.; Iwanowski, P. Evaluation of Natural Airfield Pavements Condition Based on the Airfield Pavement Condition Index (APCI). Appl. Sci. 2021, 11, 6139. [Google Scholar] [CrossRef]
- Baldo, N.; Miani, M.; Rondinella, F.; Celauro, C. A Machine Learning Approach to Determine Airport Asphalt Concrete Layer Moduli Using Heavy Weight Deflectometer Data. Sustainability 2021, 13, 8831. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, L.; Deng, K.; Wang, M.; Xu, Y.; Zheng, M.; Luo, Q. An Adaptive Offset-Tracking Method Based on Deformation Gradients and Image Noises for Mining Deformation Monitoring. Remote Sens. 2021, 13, 2958. [Google Scholar] [CrossRef]
- Dai, K.; Shi, X.; Gou, J.; Hu, L.; Chen, M.; Zhao, L.; Dong, X.; Li, Z. Diagnosing Subsidence Geohazard at Beijing Capital International Airport, from High-Resolution SAR Interferometry. Sustainability 2020, 12, 2269. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-H.; Chou, C.-P. Effects of Airport Pavement-Profile Wavelength on Aircraft Vertical Responses. Transp. Res. Rec. J. Transp. Res. Board 2004, 1889, 83–93. [Google Scholar] [CrossRef]
- Šoštarić, M.; Vidović, K.; Jakovljević, M.; Lale, O. Data-Driven Methodology for Sustainable Urban Mobility Assessment and Improvement. Sustainability 2021, 13, 7162. [Google Scholar] [CrossRef]
- Pittenger, D.M. Evaluating Sustainability of Selected Airport Pavement Treatments with Life-Cycle Cost, Raw Material Consumption, and Greenroads Standards. Transp. Res. Rec. J. Transp. Res. Board 2011, 2206, 61–68. [Google Scholar] [CrossRef]
- Di Mascio, P.; Moretti, L. Implementation of a pavement management system for maintenance and rehabilitation of airport surfaces. Case Stud. Constr. Mater. 2019, 11, e00251. [Google Scholar] [CrossRef]
- De Luca, M.; Dell’Acqua, G. Runway surface friction characteristics assessment for Lamezia Terme airfield pavement management system. J. Air Transp. Manag. 2014, 34, 1–5. [Google Scholar] [CrossRef]
- Ghosh, R.; Schilling, T.; Wicke, K. Theoretical framework of systems design for the air transportation system including an inherently quantitative philosophy of scenario development. J. Air Transp. Manag. 2017, 58, 58–67. [Google Scholar] [CrossRef] [Green Version]
- Gendreau, M.; Soriano, P. Airport pavement management systems: An appraisal of existing methodologies. Transp. Res. Part A: Policy Pract. 1998, 32, 197–214. [Google Scholar] [CrossRef]
- D’Apuzzo, M.; Festa, B.; Giuliana, G.; Mancini, L.; Nicolosi, V. The Evaluation of Runway Surface Properties: A New Approach. Proc. Soc. Behav. Sci. 2012, 53, 1192–1201. [Google Scholar] [CrossRef]
- Đapo, A. Obrada i Intrepretacija Geodetskih mjerenja na Geodinamičkoj mreži Grada Zagreba. Master’s Thesis, University of Zagreb, Zagreb, Croatia, 2005. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote. Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Pribičević, B.; Medak, D.; Đapo, A. Densification of the Zagreb Geodynamic Network in the area of northeast Medvednica. Geod. List 2007, 61, 247–258. [Google Scholar]
- Mileusnic, M.; Parlov, J.; Bacani, A.; Durn, G. Conceptual model for groundwater status and risk assessment—Case study of the Zagreb aquifer system. Geol. Croat. 2013, 66, 55–76. [Google Scholar]
- Osmanoğlu, B.; Sunar, F.; Wdowinski, S.; Cabral-Cano, E. Time series analysis of InSAR data: Methods and trends. ISPRS J. Photogramm. Remote. Sens. 2016, 115, 90–102. [Google Scholar] [CrossRef]
- Wang, W. Protocol Based Pavement Cracking Measurement with 1 mm 3D Pavement Surface Model. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 2015. [Google Scholar]
- Kamath, V.R.; Martinez, J.C. Generic representation of 3D motion paths in dynamic animations of simulated construction processes. Autom. Constr. 2008, 17, 188–200. [Google Scholar] [CrossRef]
- Khoemarga, K.V.; Tajudin, A.N. Structural design of Airport runway Case study: Jos Orno Imsula MOA Airport; Conference Series Materials Science and Engineering, 852. In Proceedings of the 2nd Tarumanagara International Conference on the Applications of Technology and Engineering (TICATE), Jakarta, Indonesia, 21–22 November 2019. [Google Scholar]
- Becek, K.; Koppe, W.; Kutoğlu, H. Evaluation of Vertical Accuracy of the WorldDEMTM Using the Runway Method. Remote. Sens. 2016, 8, 934. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, H.; Correia, P.L. Automatic Road Crack Detection and Characterization. IEEE Trans. Intell. Transp. Syst. 2013, 14, 155–168. [Google Scholar] [CrossRef]
- Mokhtari, S.; Wu, L.; Yun, H.-B. Comparison of Supervised Classification Techniques for Vision-Based Pavement Crack Detection. Transp. Res. Rec. J. Transp. Res. Board 2016, 2595, 119–127. [Google Scholar] [CrossRef]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic Road Crack Detection Using Random Structured Forests. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- Wang, P.; Hu, Y.; Dai, Y.; Tian, M. Asphalt Pavement Pothole Detection and Segmentation Based on Wavelet Energy Field. Math. Probl. Eng. 2017, 2017, 1604130. [Google Scholar] [CrossRef] [Green Version]
- Peng, L.; Chao, W.; Shuangmiao, L.; Baocai, F. Research on Crack Detection Method of Airport Runway Based on Twice-Threshold Segmentation. In Proceedings of the 5th International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 18–20 September 2015. [Google Scholar]
- Fernández, A.C.; Rodríguez-Lozano, F.J.; Villatoro, R.; Olivares, J.; Palomares, J.M. Efficient pavement crack detection and classification. EURASIP J. Image Video Process. 2017, 2017, 39. [Google Scholar] [CrossRef]
- He, L.; Lin, H.; Zou, Q.; Zhang, D. Accurate measurement of pavement deflection velocity under dynamic loads. Autom. Constr. 2017, 83, 149–162. [Google Scholar] [CrossRef]
- Li, W.; Huyan, J.; Tighe, S.L.; Ren, Q.-Q.; Sun, Z.-Y. Three-Dimensional Pavement Crack Detection Algorithm Based on Two-Dimensional Empirical Mode Decomposition. J. Transp. Eng. Part B Pavements 2017, 143, 04017005. [Google Scholar] [CrossRef]
- De Souza, N.M.; Filha, A.T.A. A systematic airport runway maintenance and inspection policy based on a delay time modelling approach. Autom. Constr. 2020, 110, 103039. [Google Scholar] [CrossRef]
- Kovačič, B.; Doler, D.; Sever, D. Innovative Business Model for the Management of Airports in Purpose to Identify Runway Damage in Time. Sustainability 2021, 13, 613. [Google Scholar] [CrossRef]
- Kovačič, B.; Doler, D.; Sever, D. The Innovative Model of Runway Sustainable Management on Smaller Regional Airports. Sustainability 2021, 13, 652. [Google Scholar] [CrossRef]
- Kovačič, B.; Želodec, D.; Doler, D. Prototype of the Runway Monitoring Process at Smaller Airports: Edvard Rusjan Airport Maribor. Processes 2020, 8, 1689. [Google Scholar] [CrossRef]
- Mitas, L.; Mitasova, H. Spatial Interpolation. In Geographic Information Systems: Principles, Techniques, Management and Applications, 2nd ed.; Longley, P.A., Goodchild, M.F., Maguire, D.J., Rhind, D.W., Eds.; Wiley: Hoboken, NJ, USA, 2005; Volume 1, Part 2, Chapter 34; ISBN 978-0-471-73545-8. [Google Scholar]
- Penrose, R.A. Generalized inverse for matrices. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef] [Green Version]
- Doler, D. Inoviran Model Kontinuiranega Spremljanja Deformacij Letaliških Vzletno Pristajalnih Stez. Ph.D. Thesis, Univerza v Mariboru, Maribor, Slovenia, 2020. [Google Scholar]
- Achilleos, G. The Inverse Distance Weighted interpolation method and error propagation mechanism—Creating a DEM from an analogue topographical map. J. Spat. Sci. 2011, 56, 283–304. [Google Scholar] [CrossRef]
- Delaunay, B. Sur la sphère vide. Izv. Akad. Nauk SSSR Otd. Mat. i Estestv. Nauk 1934, 7, 1–2. [Google Scholar]
- Mann, S. Cubic Precision Clough-Tocher Interpolation; Computer Science Department of University of Waterloo: Waterloo, ON, Canada, 1998; Report CS-98-15. [Google Scholar]








| Regression Plane Parameters | a | b | c | D |
|---|---|---|---|---|
| R3 | −0.0112926570 | −0.0050969835 | 1 | 7,265.5263 |
| Parameter accuracy | ||||
| R3 | 1.5154 × 10−5 | 1.1416 × 10−5 | 1 | 1 |
| No. | Case | p | Average Computer Time (s) | Range of File (MB) | Comment |
|---|---|---|---|---|---|
| 1 | IDW1 | 2 | 1705 | 49.139 | Expected and sensible solution |
| 2 | IDW2 | 1 | 406.9 | 49.138 | p = 1 => inappropriate parameter. The results are not within expectations. |
| 3 | IDW3 | 10 | 1697.01 | 49.061 | Expected and sensible solution |
| No. | Case | p | Average Computer Time (s) | Range of File (MB) | Comment |
|---|---|---|---|---|---|
| 1 | TIN1 | linear | 1.43 | 33.679 | Expected and sensible solution |
| 2 | TIN2 | cubic | 1.76 | 30.314 | Comprehensibility of the model is not guarantee |
| Cross-Section | Model | s [‰] | Descriptive Statistics [m] | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Median | SE | SD | V (m2] | Max | |||
| P1 S = 2.18‰ | IDW1 | 2.18 | 0.01509 | 0.01493 | 0.00022 | 0.00788 | 0.00006 | 0.03197 |
| IDW3 | 2.23 | 0.00941 | 0.00928 | 0.00015 | 0.00543 | 0.00002 | 0.02732 | |
| TIN1 | 2.18 | 0.00412 | 0.00345 | 0.00009 | 0.00314 | 0.00001 | 0.01339 | |
| RR | 2.14 | 0.00428 | 0.00359 | 0.00008 | 0.00302 | 0.00001 | 0.01019 | |
| P2 * S = 2.06‰ | IDW1 | 2.17 | 0.00376 | 0.00264 | 0.00011 | 0.00356 | 0.00001 | 0.02257 |
| IDW3 | 2.19 | 0.00774 | 0.00791 | 0.00013 | 0.00435 | 0.00001 | 0.01959 | |
| TIN1 | 2.18 | 0.00431 | 0.00415 | 0.00007 | 0.00269 | 0.00001 | 0.01440 | |
| RR | 2.14 | 0.00164 | 0.00164 | 0.00001 | 0.00055 | 0.00001 | 0.00260 | |
| P3 ** S = 2.18‰ | IDW1 | 2.16 | 0.00761 | 0.00732 | 0.00014 | 0.00458 | 0.00002 | 0.01795 |
| IDW3 | 2.21 | 0.00909 | 0.00817 | 0.00018 | 0.00603 | 0.00003 | 0.02126 | |
| TIN1 | 2.21 | 0.00455 | 0.00389 | 0.00009 | 0.00336 | 0.00001 | 0.02291 | |
| RR | 2.17 | 0.00111 | 0.00091 | 0.00002 | 0.00078 | <0.00001 | 0.00266 | |
| Cross-Section | Model | s [‰] | Descriptive Statistics [m] | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Median | SE | SD | V | Max | |||
| P4 S = 8.46‰ | IDW1 | 8.16 | 0.03669 | 0.03459 | 0.00137 | 0.01323 | 0.00017 | 0.09093 |
| IDW3 | 8.74 | 0.04380 | 0.03485 | 0.00351 | 0.03389 | 0.00114 | 0.12133 | |
| TIN1 | 8.67 | 0.03906 | 0.03366 | 0.00323 | 0.03119 | 0.00097 | 0.09810 | |
| RR | 8.26 | 0.04032 | 0.04018 | 0.00260 | 0.02513 | 0.00063 | 0.08340 | |
| P5 S = 7.95‰ | IDW1 | 7.80 | 0.04216 | 0.04166 | 0.00129 | 0.01254 | 0.00015 | 0.08801 |
| IDW3 | 7.91 | 0.04473 | 0.03956 | 0.00307 | 0.02984 | 0.00089 | 0.11181 | |
| TIN1 | 7.89 | 0.04229 | 0.04082 | 0.00263 | 0.02556 | 0.00065 | 0.09024 | |
| RR | 8.19 | 0.04123 | 0.04040 | 0.00283 | 0.02750 | 0.00075 | 0.08936 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sever, D.; Doler, D.; Kovačič, B. Modelling of Evenness of Runways as an Element of Sustainable Airport Maintenance. Appl. Sci. 2021, 11, 8697. https://doi.org/10.3390/app11188697
Sever D, Doler D, Kovačič B. Modelling of Evenness of Runways as an Element of Sustainable Airport Maintenance. Applied Sciences. 2021; 11(18):8697. https://doi.org/10.3390/app11188697
Chicago/Turabian StyleSever, Drago, Damjan Doler, and Boštjan Kovačič. 2021. "Modelling of Evenness of Runways as an Element of Sustainable Airport Maintenance" Applied Sciences 11, no. 18: 8697. https://doi.org/10.3390/app11188697







