Research on the Inertial Migration Characteristics of Bi-Disperse Particles in Channel Flow
Abstract
:1. Introduction
2. Materials and Methods
2.1. Lattice Boltzmann Method
2.2. Repulsive Force Model
2.3. Problem Definition
3. Validation
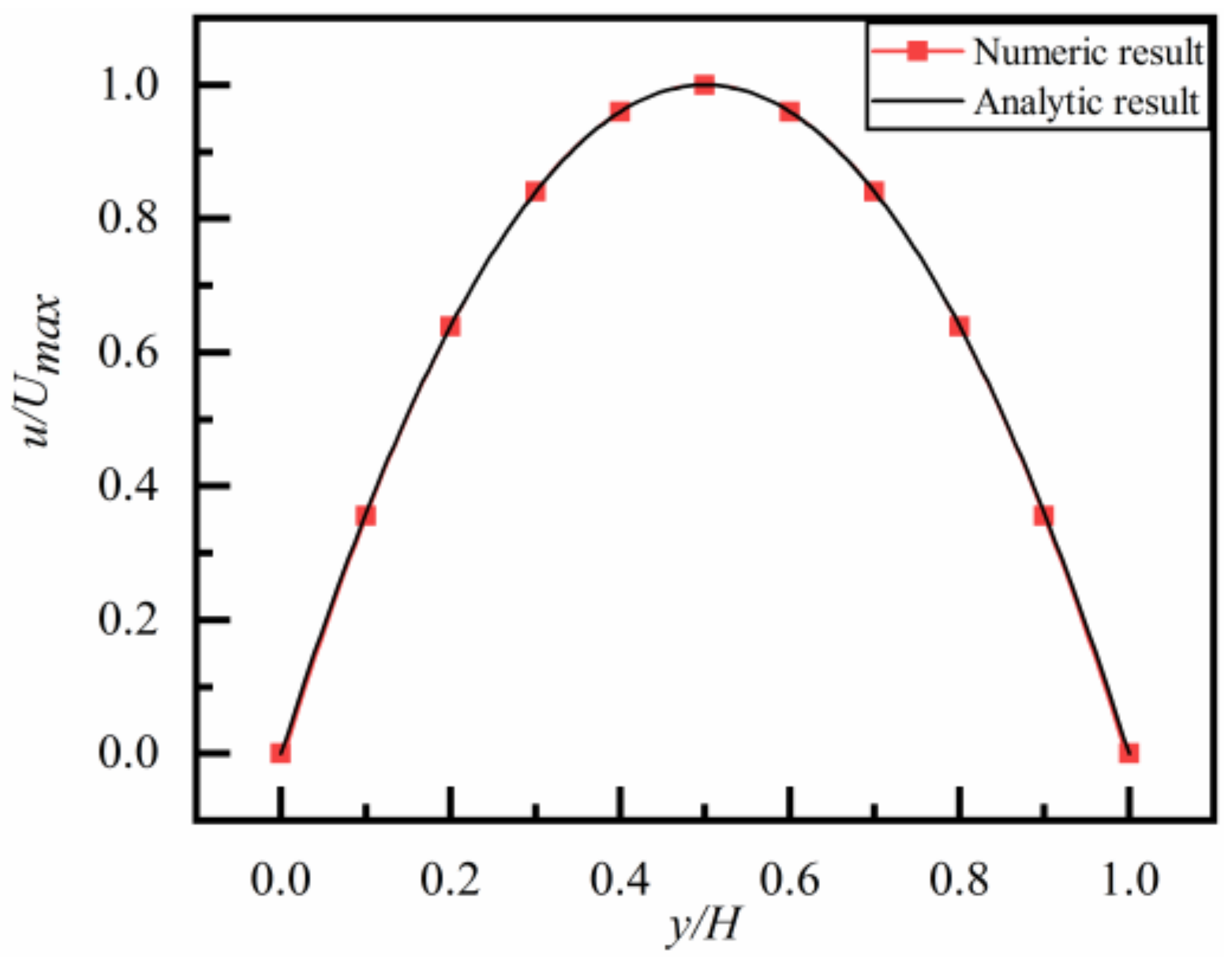
3.1. Velocity Profile in a Poiseuille Flow
3.2. Trajectory of a Particle in Shear Flow
3.3. Trajectory of a Particle in Poiseuille Flow
4. Results and Discussion
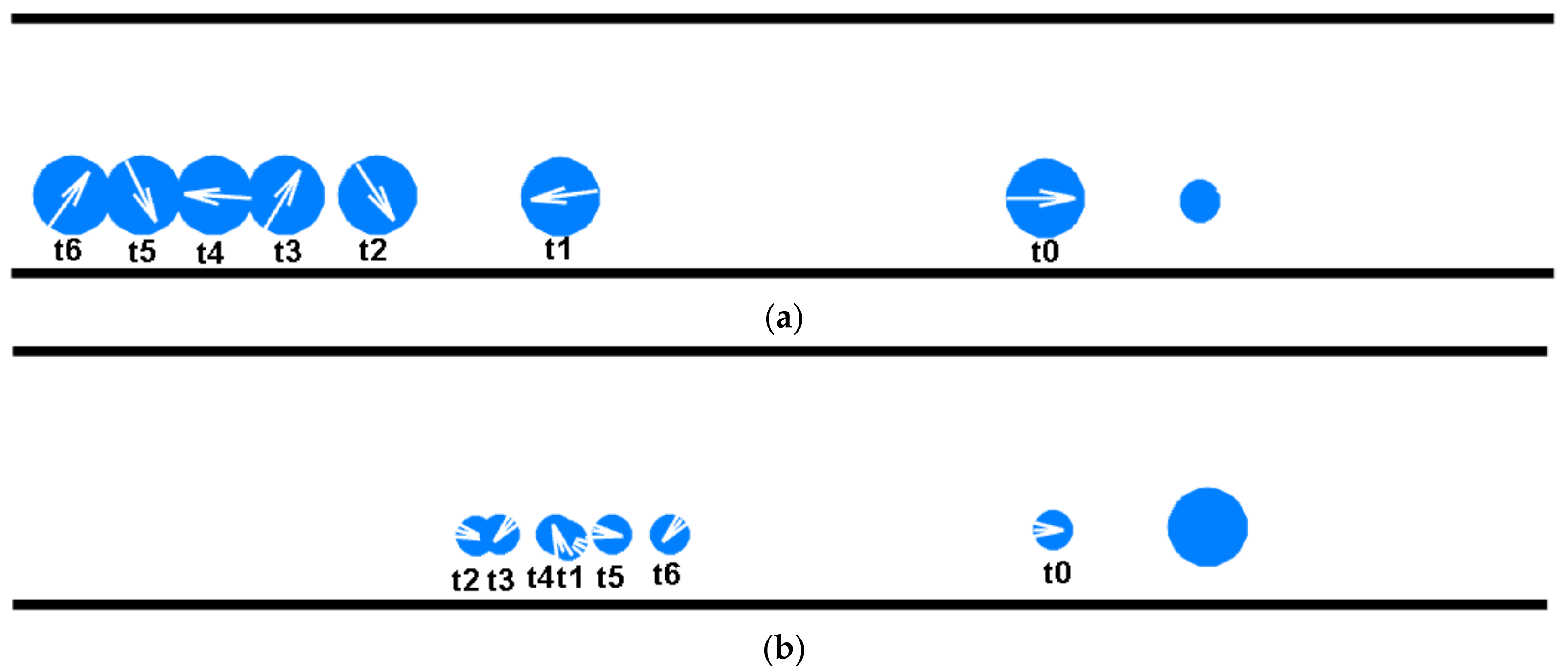
4.1. A Pair of Single-Scale Particles
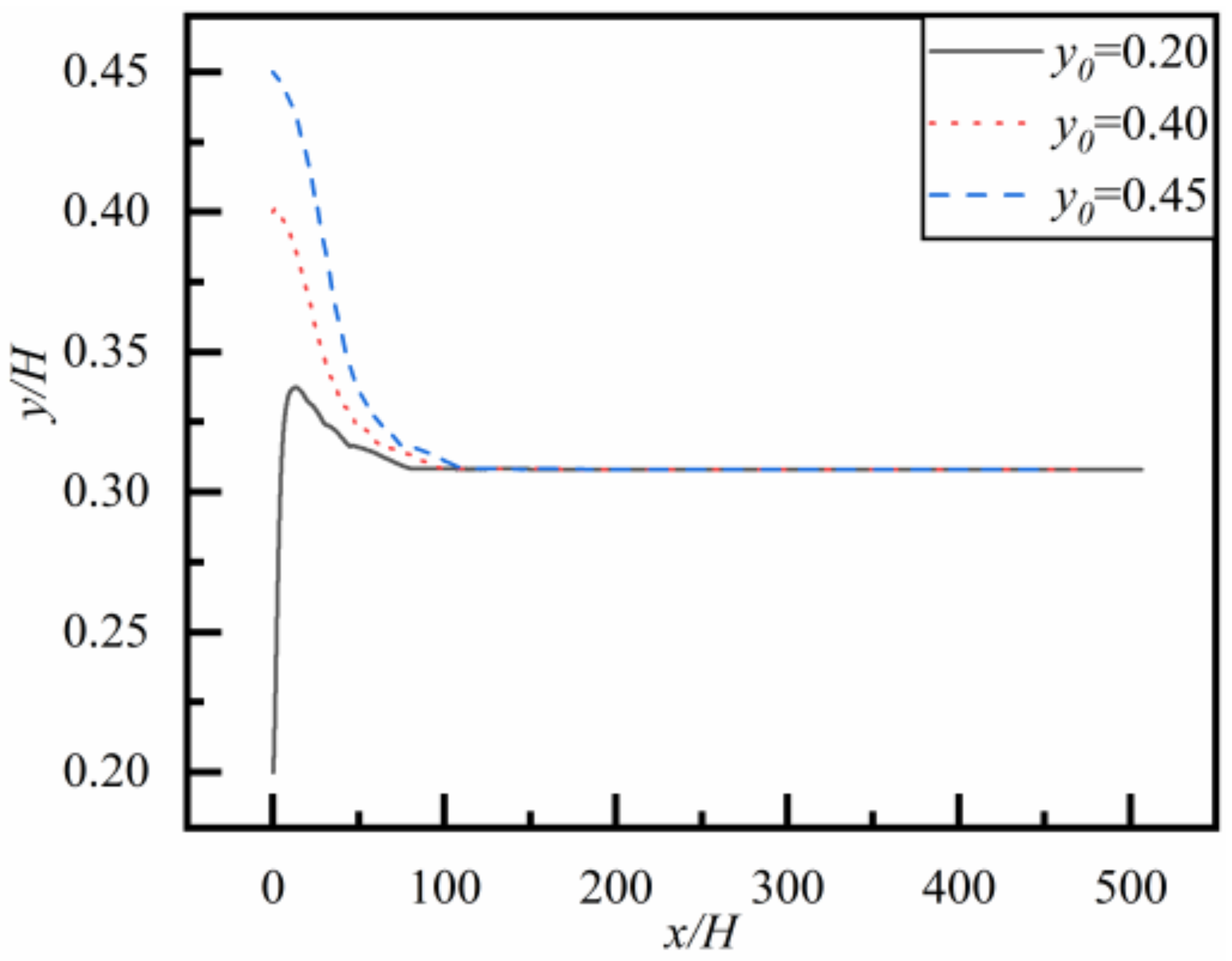
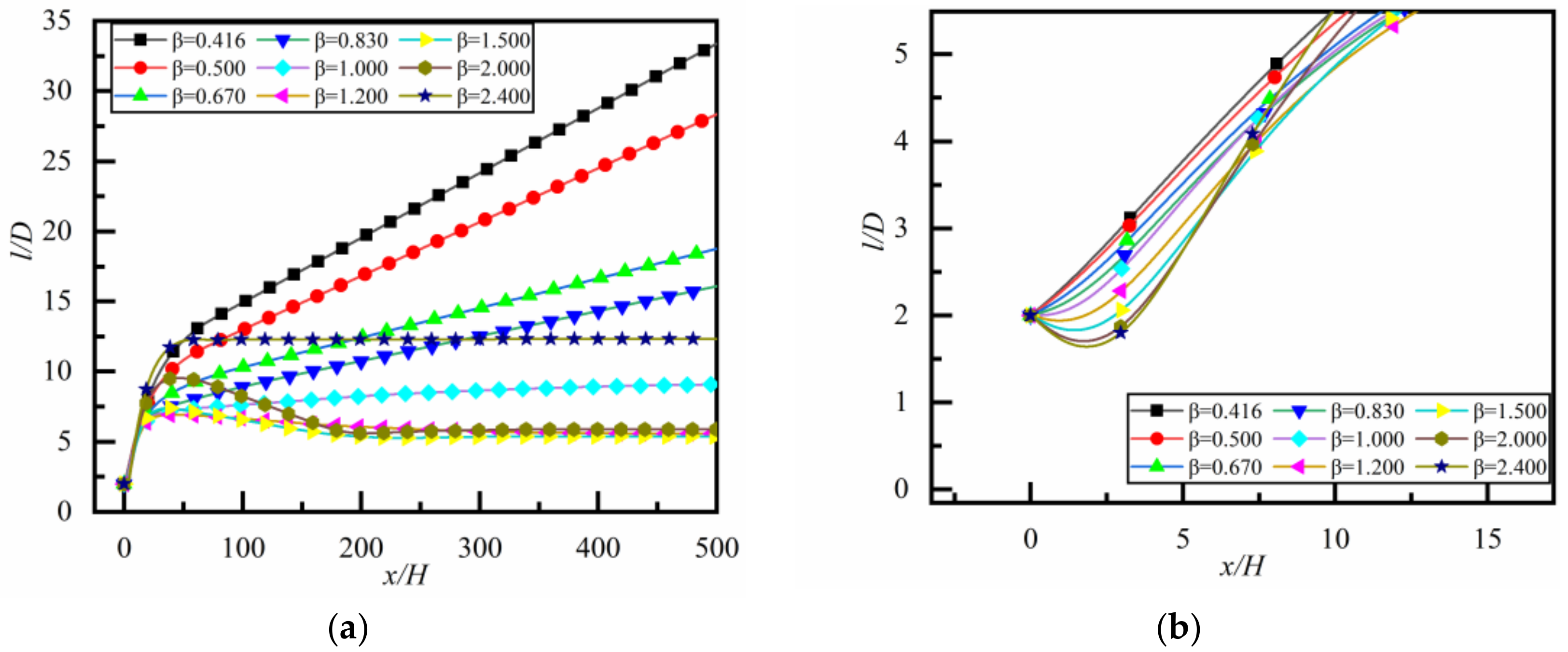
4.1.1. The Effect of Initial Spacing
4.1.2. Effect of Blocking Ratio
4.2. A Pair of Dual-Scale Particles
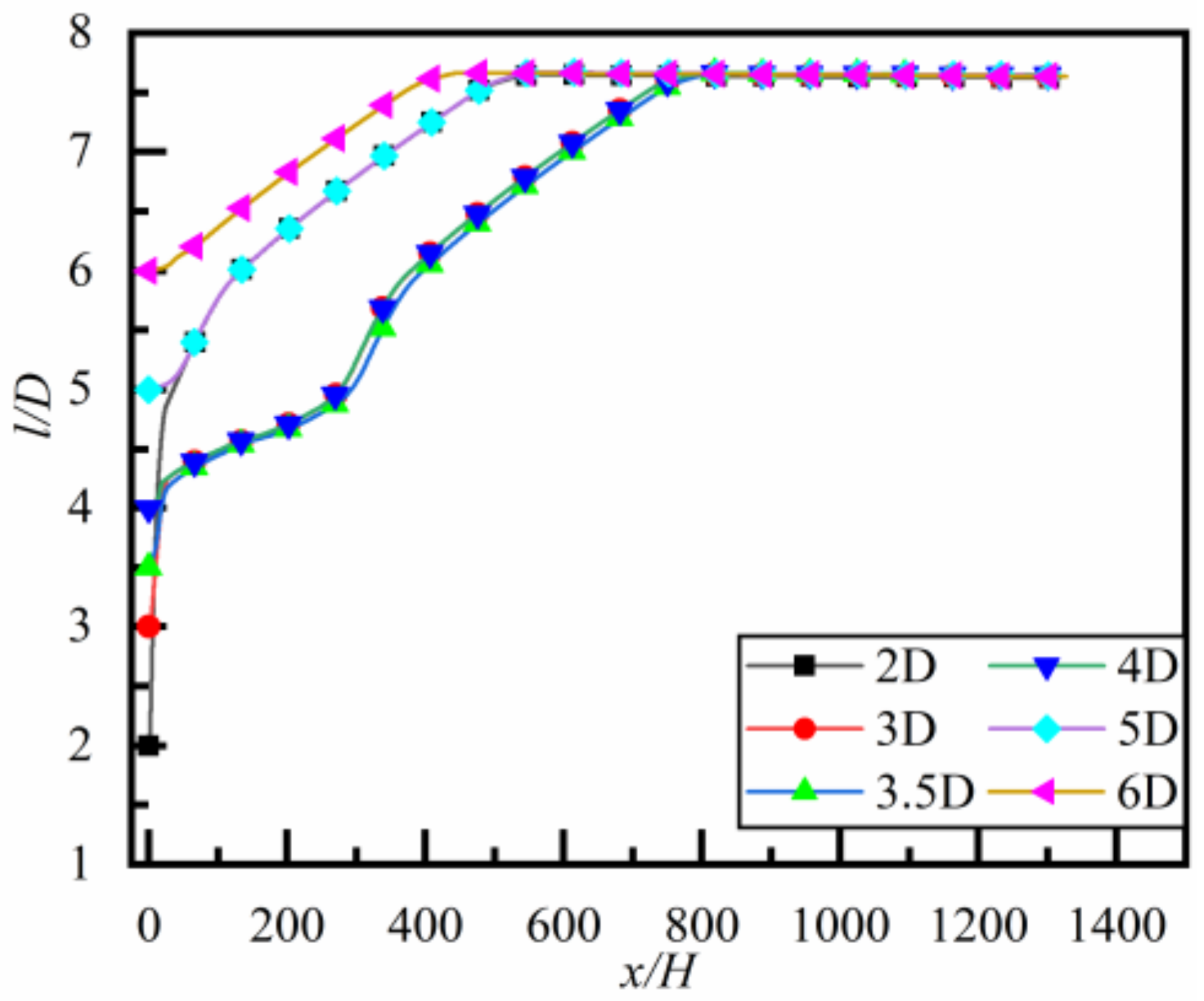
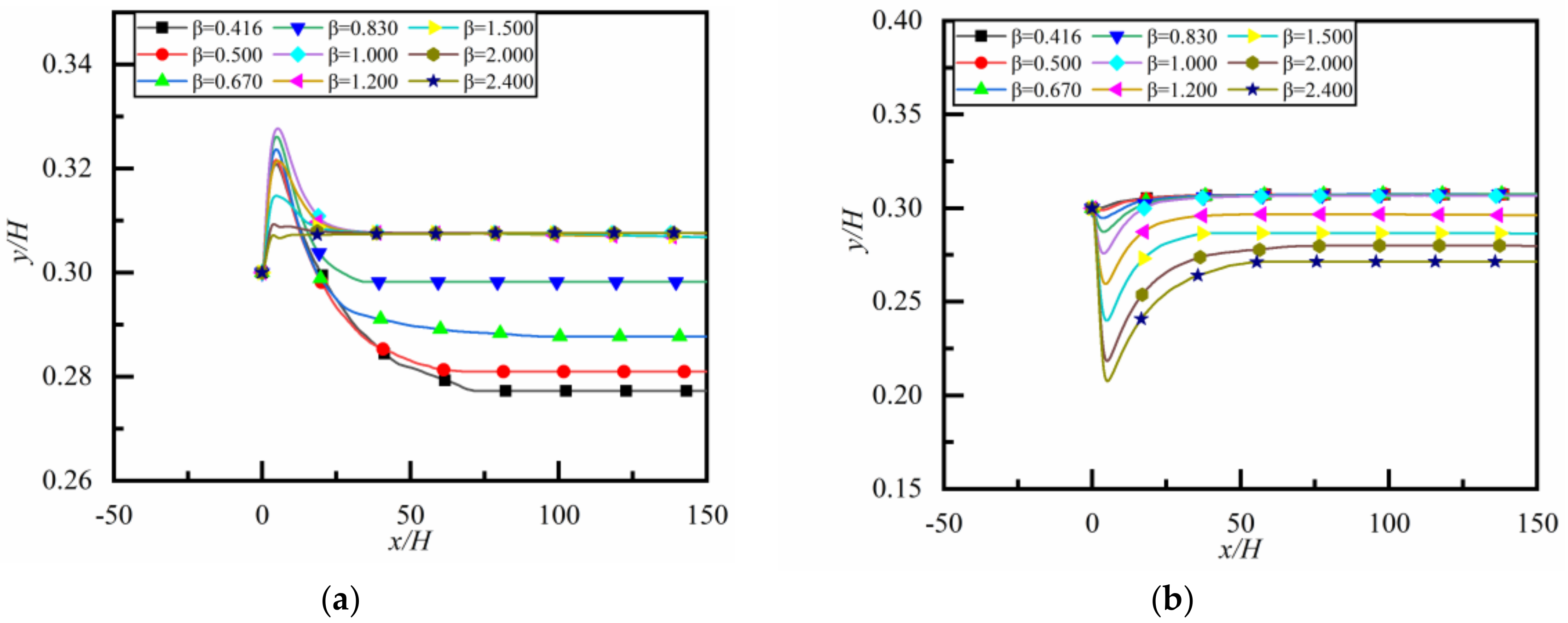
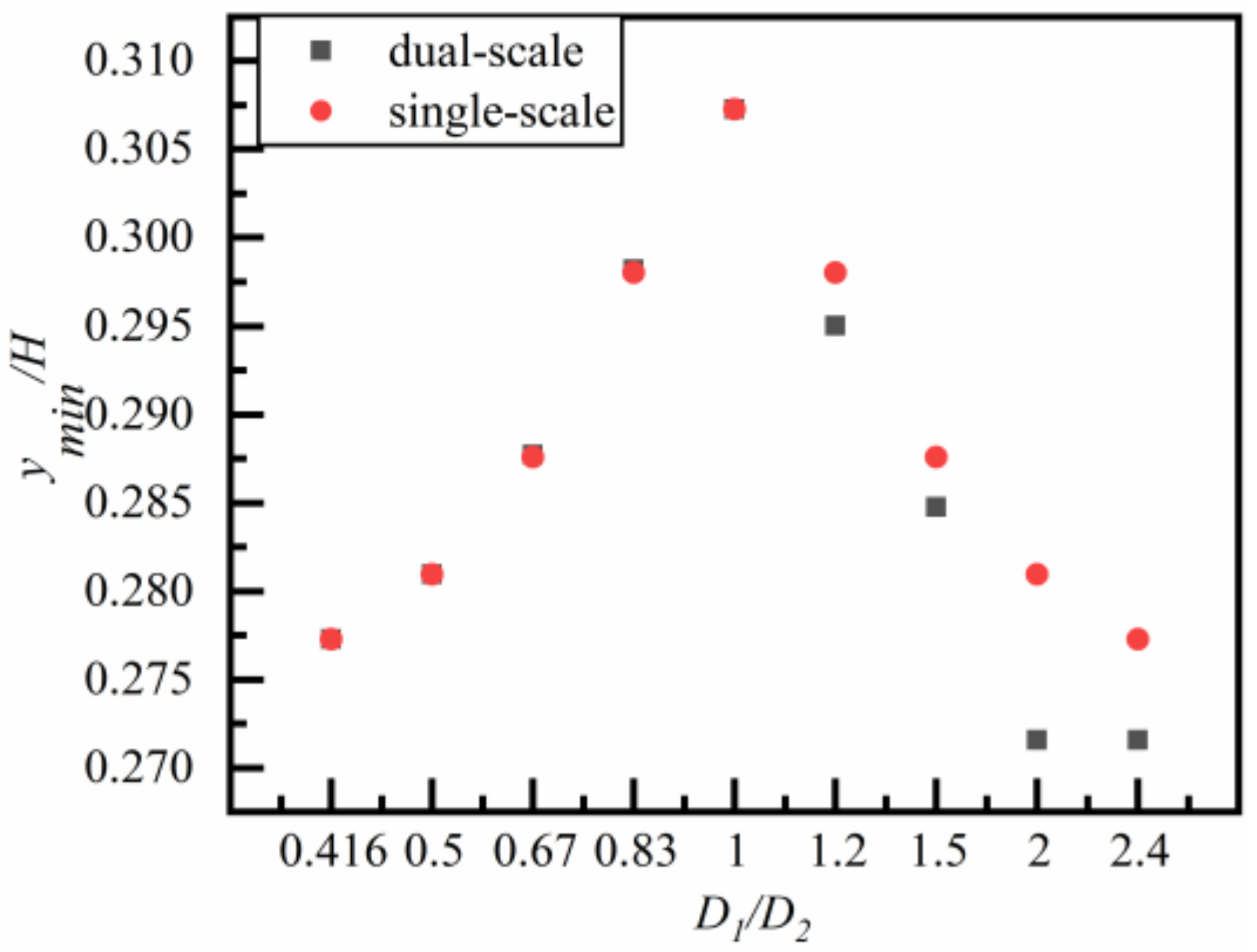
4.2.1. Effect of Size Ratio of Particles
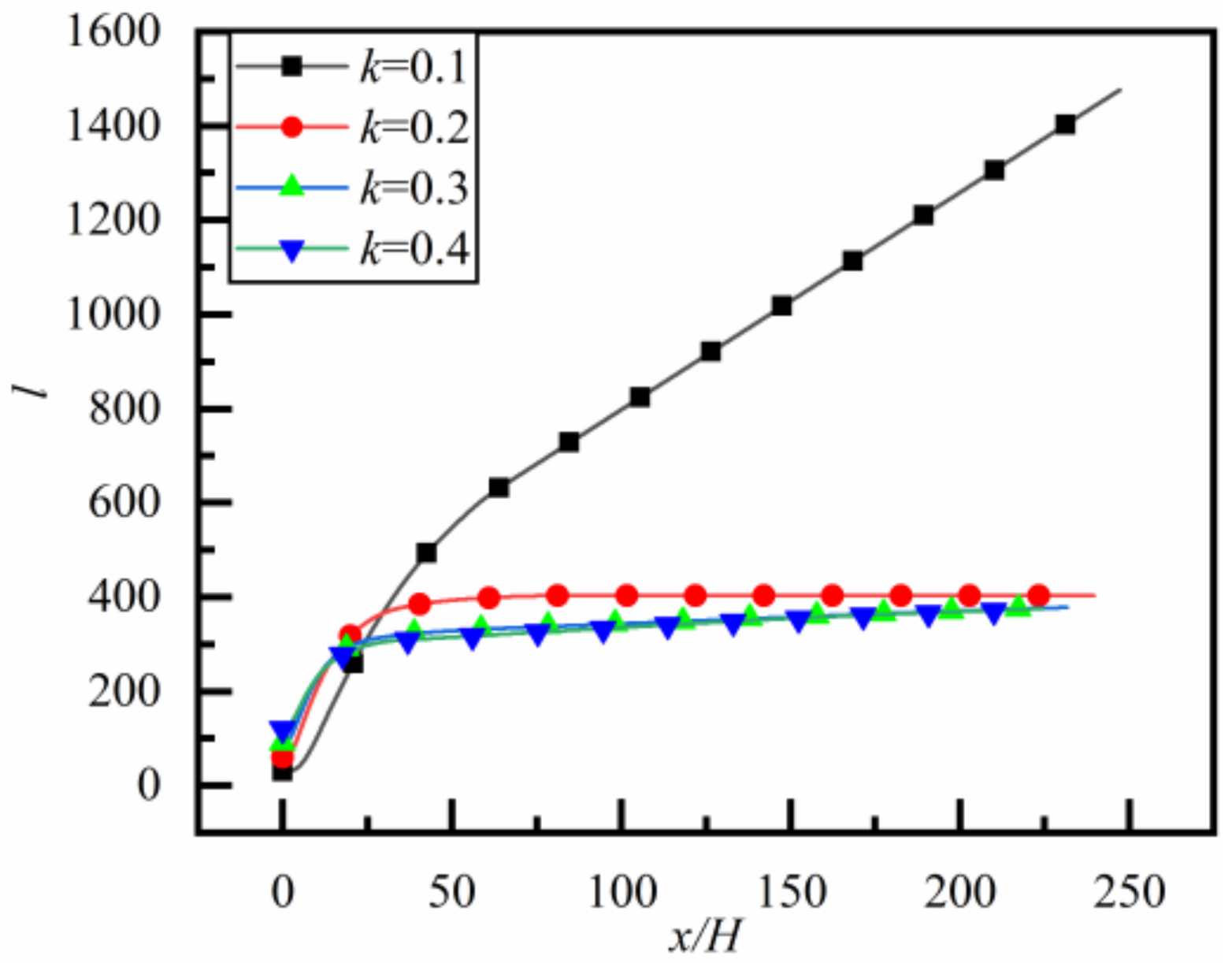
4.2.2. Effect of Reynolds Number
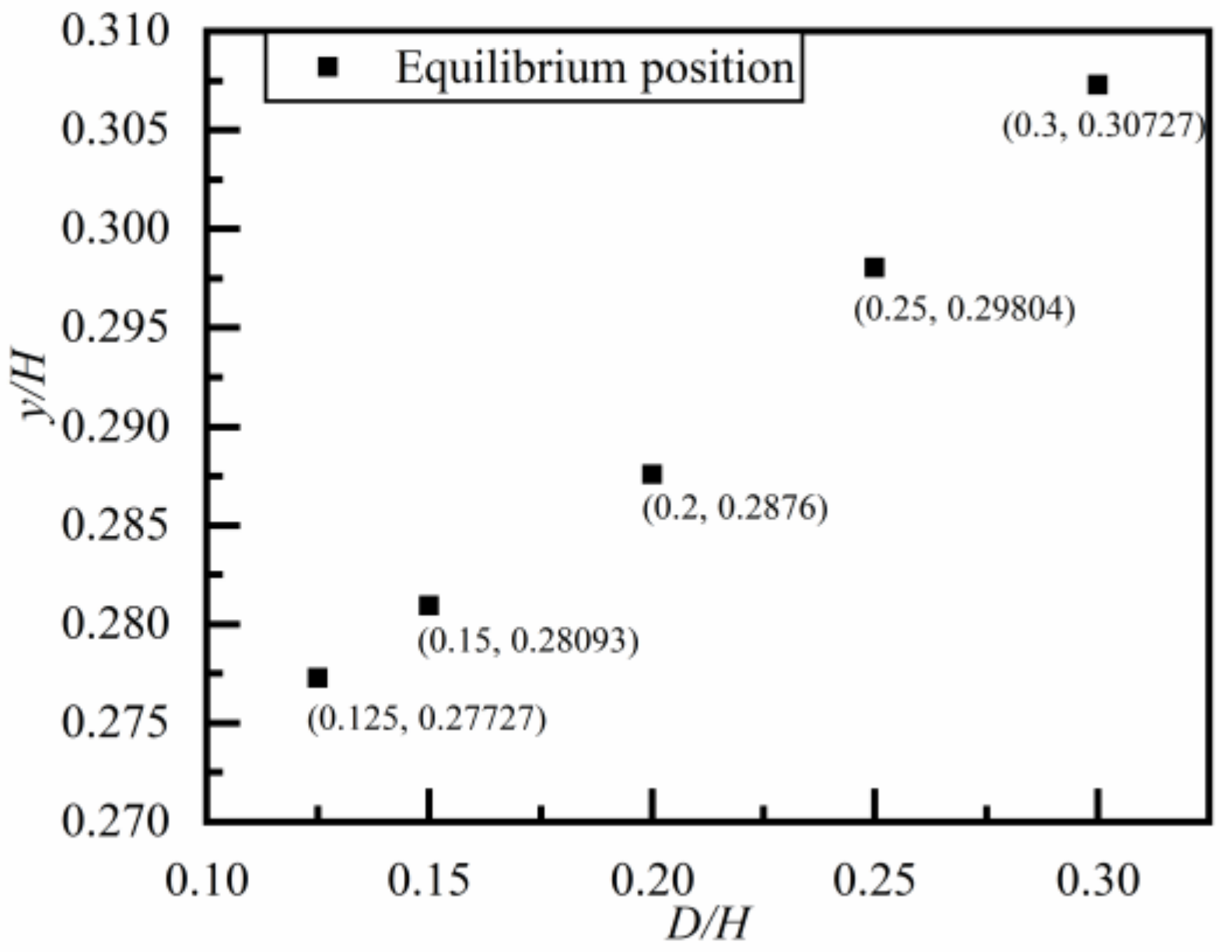
4.3. The Equilibrium Position of the Particles
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Zhang, J.; Tang, F.; Li, W.; Wang, X. Design of a Single-Layer Microchannel for Continuous Sheathless Single-Stream Particle Inertial Focusing. Anal. Chem. 2018, 90, 1786–1794. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, S.; Zhang, J.; Yuan, D.; Li, W. Hybrid microfluidics combined with active and passive approaches for continuous cell separation. Electrophoresis 2017, 38, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Godino, N.; Jorde, F.; Lawlor, D.; Jaeger, M.; Duschl, C. Purification of microalgae from bacterial contamination using a disposable inertia-based microfluidic device. J. Micromech. Microeng. 2015, 25, 84002. [Google Scholar] [CrossRef]
- Xuan, X.; Zhu, J.; Church, C. Particle focusing in microfluidic devices. Microfluid. Nanofluid. 2010, 9, 1–16. [Google Scholar] [CrossRef]
- Segré, G.; Silberberg, A. Radial particle displacements in poiseuille flow of suspensions. Nature 1961, 189, 209. [Google Scholar] [CrossRef]
- Lee, W.; Amini, H.; Stone, H.A.; Di Carlo, D. Dynamic self-assembly and control of microfluidic particle crystals. Proc. Natl. Acad. Sci. USA 2010, 107, 22413–22418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matas, J.; Glezer, V.; Guazzelli, É.; Morris, J.F. Trains of particles in finite-Reynolds-number pipe flow. Phys. Fluids 2004, 16, 4192–4195. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Magaud, P.; Baldas, L.; Lafforgue, C.; Abbas, M.; Colin, S. Self-ordered particle trains in inertial microchannel flows. Microfluid. Nanofluid. 2017, 21, 154. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J.; Ku, X. Inertial migration of circular particles in Poiseuille flow of a power-law fluid. Phys. Fluids 2019, 31, 72206. [Google Scholar]
- Hu, X.; Lin, J.; Chen, D.; Ku, X. Stability condition of self-organizing staggered particle trains in channel flow. Microfluid. Nanofluidics 2020, 24, 1–12. [Google Scholar] [CrossRef]
- Morris, J.F. High-speed trains: In microchannels? J. Fluid Mech. 2016, 792, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Mach, A.J.; Di Carlo, D. Continuous scalable blood filtration device using inertial microfluidics. Biotechnol. Bioeng. 2010, 107, 302–311. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Papautsky, I. Fundamentals of inertial focusing in microchannels. Lab Chip 2013, 13, 1121–1132. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Magaud, P.; Lafforgue, C.; Colin, S.; Baldas, L. Inertial lateral migration and self-assembly of particles in bidisperse suspensions in microchannel flows. Microfluid. Nanofluid. 2019, 23, 93. [Google Scholar] [CrossRef]
- Qian, Y.H.; Dhumieres, D.; Lallemand, P. Lattice Bgk Models for Navier-Stokes Equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- He, Y.L.; Wang, Y.; Li, Q. Theory and Application of Lattice Boltzmann Method; Science Press: Beijing, China, 2009. [Google Scholar]
- He, X.Y.; Shan, X.W.; Doolen, G.D. Discrete Boltzmann equation model for nonideal gases. Phys. Rev. E 1998, 57, R13–R16. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Glowinski, R.; Pan, T.W.; Hesla, T.I.; Joseph, D.D.; Périaux, J. A Fictitious Domain Approach to the Direct Numerical Simulation of Incompressible Viscous Flow past Moving Rigid Bodies: Application to Particulate Flow. J. Comput. Phys. 2001, 169, 363–426. [Google Scholar] [CrossRef] [Green Version]
- Feng, Z.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Lin, J.; Hu, X. Research on the Inertial Migration Characteristics of Bi-Disperse Particles in Channel Flow. Appl. Sci. 2021, 11, 8800. https://doi.org/10.3390/app11198800
Chen D, Lin J, Hu X. Research on the Inertial Migration Characteristics of Bi-Disperse Particles in Channel Flow. Applied Sciences. 2021; 11(19):8800. https://doi.org/10.3390/app11198800
Chicago/Turabian StyleChen, Dongmei, Jianzhong Lin, and Xiao Hu. 2021. "Research on the Inertial Migration Characteristics of Bi-Disperse Particles in Channel Flow" Applied Sciences 11, no. 19: 8800. https://doi.org/10.3390/app11198800





