Nonlinear Doubly Wiener Constant-Stress Accelerated Degradation Model Based on Uncertainties and Acceleration Factor Constant Principle
Abstract
:1. Introduction
2. Nonlinear Wiener Process with Covariates
2.1. Nonlinear Wiener Process
2.2. Deducing Relation of Parameters in the ADT for Nonlinear Wiener Model
3. Modeling and Parameter Estimation in CSADT
3.1. ADT with Random Effects
3.2. Acceleration Degradation Process Modeling with Measurement Errors
3.3. Parameter Estimation
4. Numerical Examples
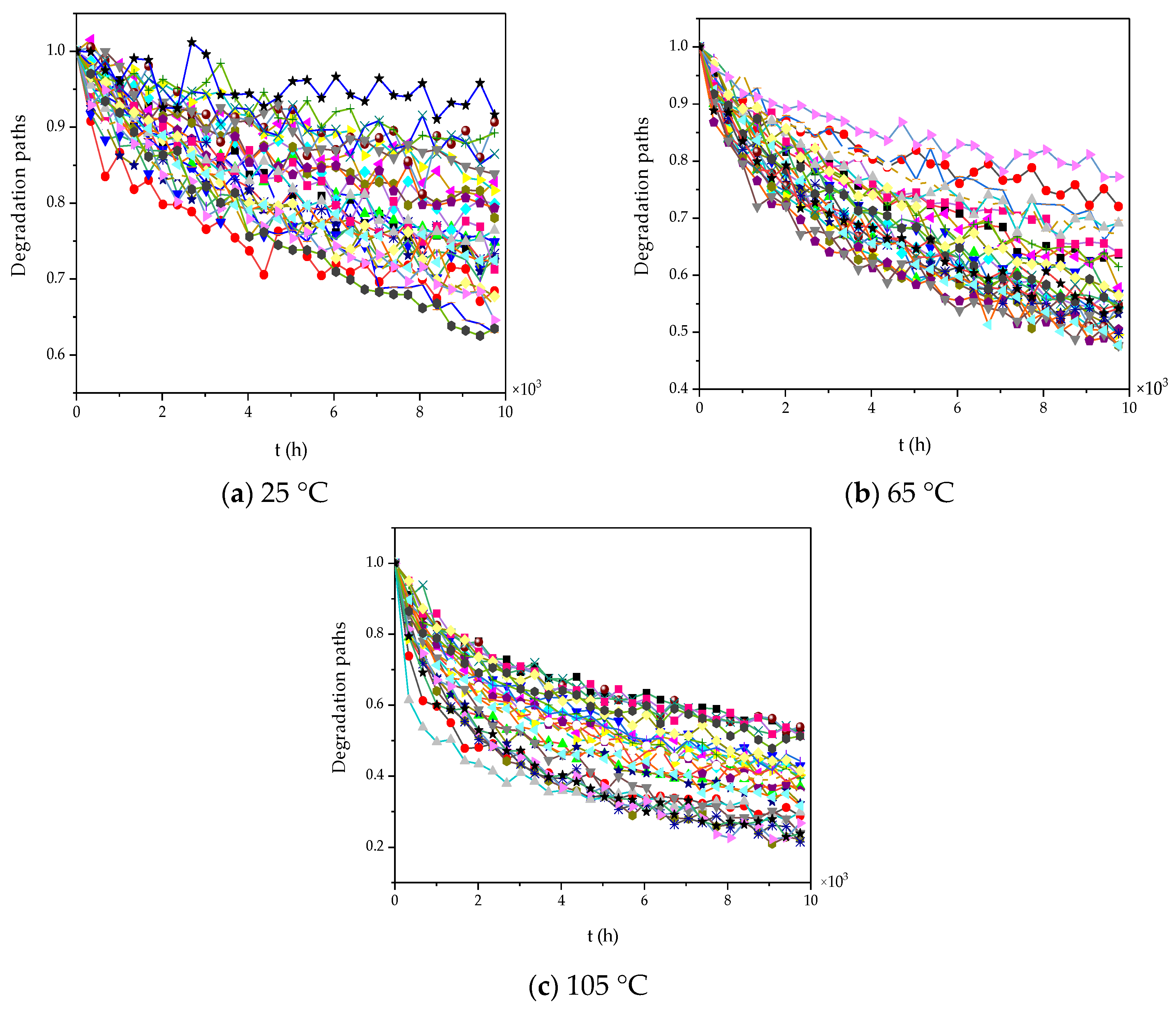
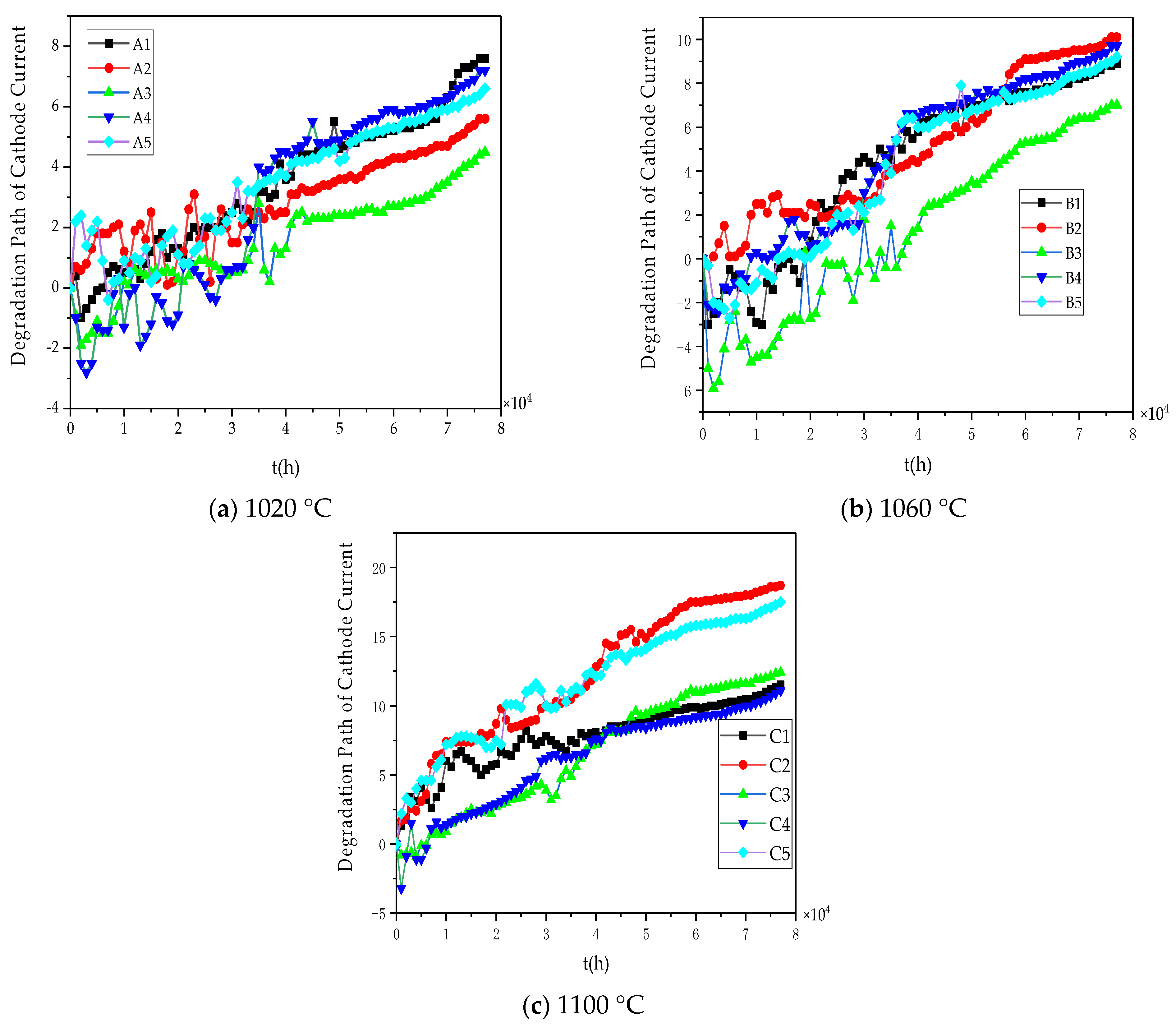
4.1. Model Verification
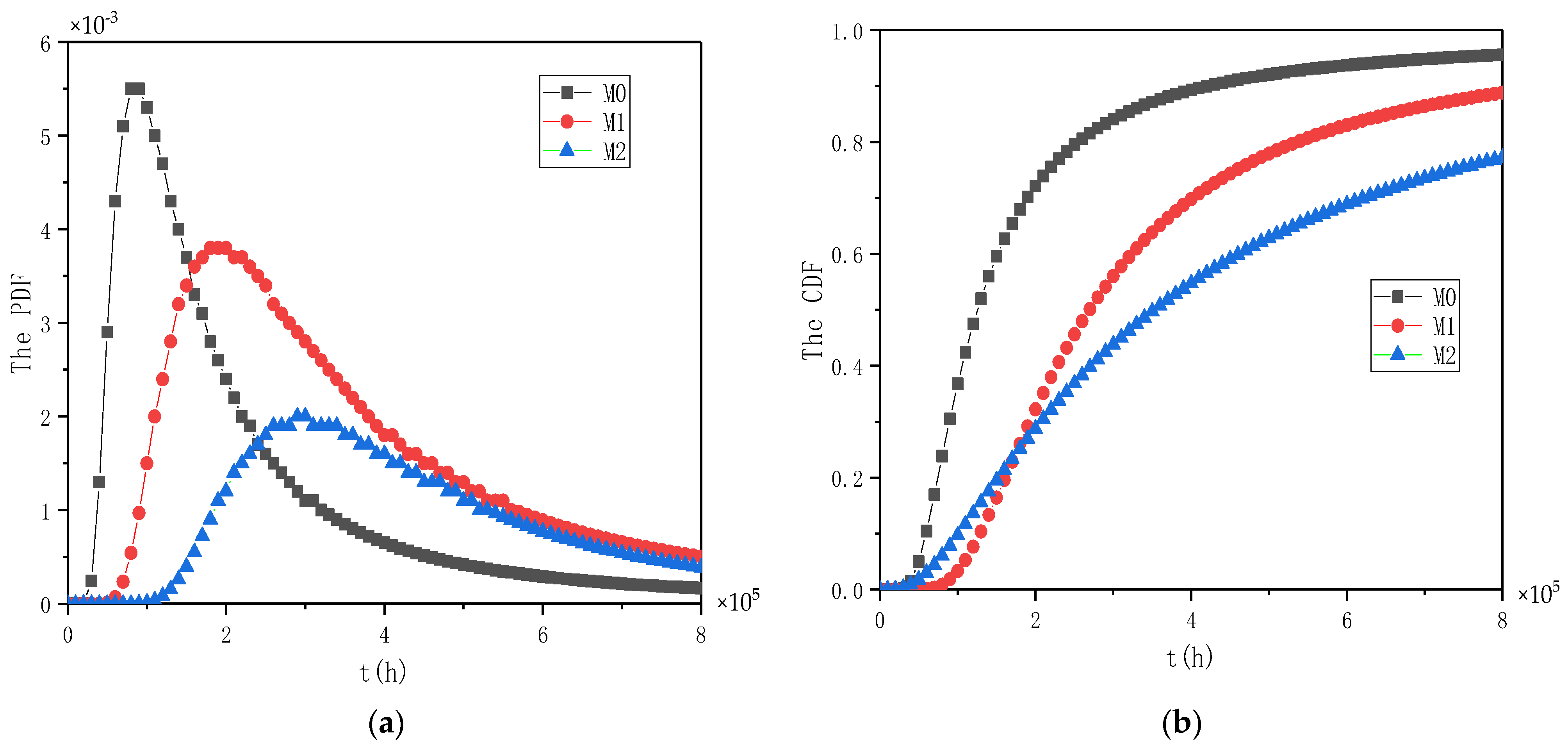
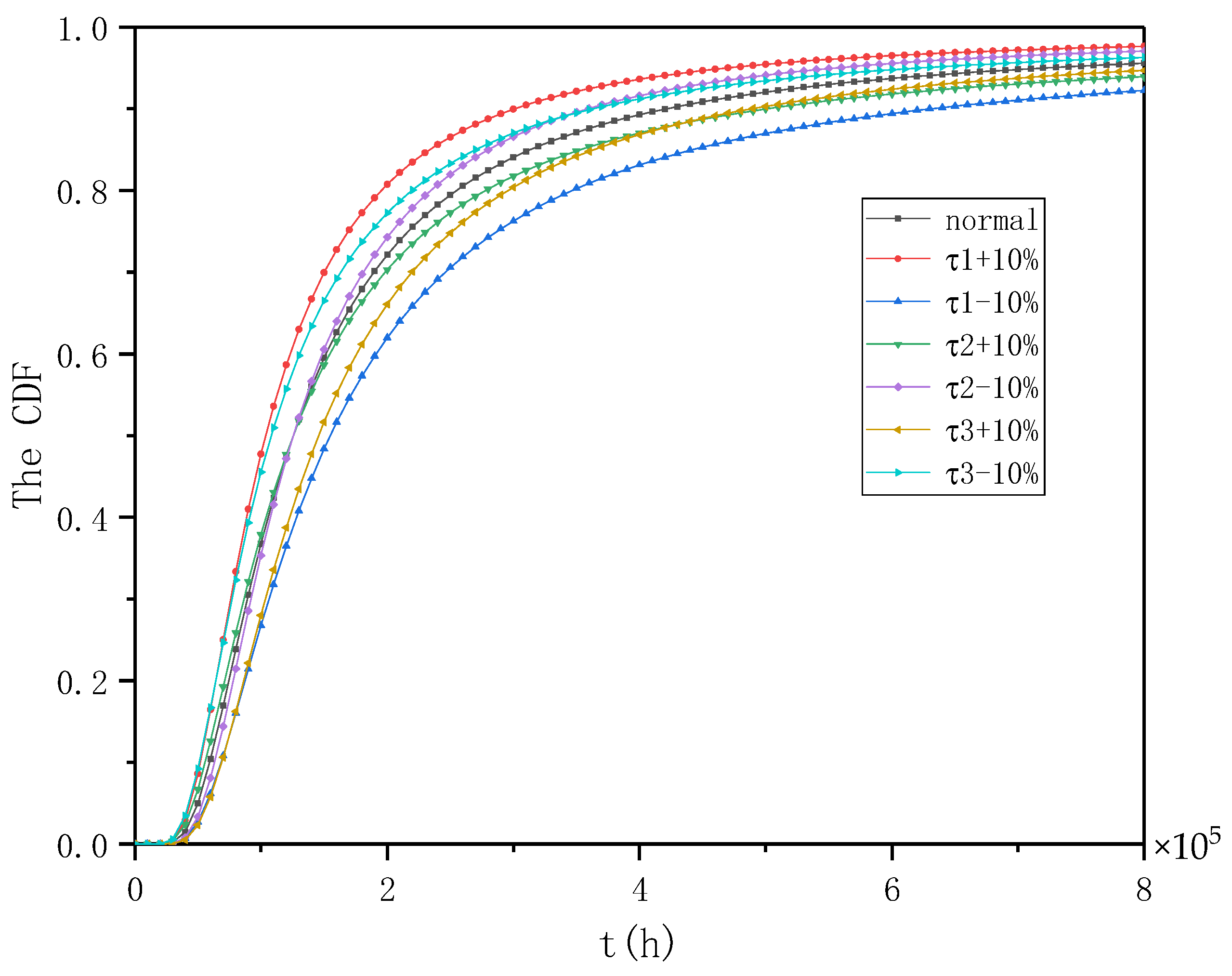
4.2. Case Application and Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meeker, W.Q.; Escobar, L.A. Accelerated degradation tests: Modeling and analysis. Technometrics 1998, 40, 89–99. [Google Scholar] [CrossRef]
- Lu, C.; Meeker, W. Using degradation measures to estimate a time-to -failure distribution. Technometrics 1993, 35, 161–174. [Google Scholar] [CrossRef]
- Tang, S.; Guo, X.; Yu, C.; Xue, H.; Zhou, Z. Accelerated degradation tests modeling based on the nonlinear Wiener process with random effect. Math. Probl. Eng. 2014, 2014, 560726. [Google Scholar] [CrossRef]
- Onar, A.; Padgett, W.J. Acceleratedtest models with the inverse Gaussian distribution. J. Stat. Plan. Inference 2000, 89, 119–133. [Google Scholar] [CrossRef]
- Tsai, T.-R.; Lio, Y.L.; Jiang, N. Optimal decisions on the accelerated degradation test plan under the Wiener process. Qual. Technol. Quant. Manag. 2014, 11, 461–470. [Google Scholar] [CrossRef]
- Ye, Z.-S.; Xie, M. Stochastic modeling and analysis of degradation for highly reliable products. Appl. Stoch. Models Bus. Ind. 2015, 31, 16–32. [Google Scholar] [CrossRef]
- Tang, L.C.; Yang, G.; Xie, M. Planning of step-stress accelerated degradation test. In Proceedings of the Annual Symposium Reliability and Maintainability, 2004-RAMS, Los Angeles, CA, USA, 26–29 January 2004; pp. 287–292. [Google Scholar]
- Wang, X.; Balakrishman, N.; Guo, B. Residual life estimation based on a generalized Wiener degradation process. Reliab. Eng. Syst. Saf. 2014, 124, 13–23. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, P.; Guo, B.; Cheng, Z. Real-time reliability evaluation with a general Wiener process-based degradation model. Qual. Reliab. Eng. Int. 2014, 30, 205–220. [Google Scholar] [CrossRef]
- Ye, Z.S.; Chen, N.; Shen, Y. A new class of Wiener process models for degradation analysis. Reliab. Eng. Syst. Saf. 2013, 112, 38–47. [Google Scholar] [CrossRef]
- Park, C.; Padgett, W.J. Accelerated degradation models for failure based on geometric Brownian motion and gamma processes. Lifetime Data Anal. 2005, 11, 511–527. [Google Scholar] [CrossRef]
- Wang, L.; Pan, R.; Li, X.; Jiang, T. A Bayesian reliability sevalution method with integrated accelerated degradation testing and field information. Reliab. Eng. Syst. Saf. 2013, 112, 38–47. [Google Scholar] [CrossRef]
- Liao, H.T.; Elsayed, E.A. Reliability inference for field conditions from accelerated degradation testing. Nav. Res. Logist. 2006, 53, 576–587. [Google Scholar] [CrossRef]
- Whitmore, G.A.; Schenkelberg, F. Modeling accelerated degradation data using Wiener diffusion with A time scale transformation. Lifetime Data Anal. 1997, 3, 27–45. [Google Scholar] [CrossRef]
- Tang, S. Step stress accelerated degradation process modeling and remaining useful life estimation. J. Mech. Eng. 2014, 50, 16–33. [Google Scholar] [CrossRef]
- Chen, Z.; Li, S.; Pan, E. Optimal Constant-Stress Accelerated Degradation Test Plans Using Nonlinear Generalized Wiener Process. Math. Probl. Eng. 2016, 2016, 9283295. [Google Scholar] [CrossRef]
- Peng, C.Y.; Tseng, S.T. Mis-specification analysis of linear degradation models. IEEE Trans. Reliab. 2009, 58, 444–455. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.; Hu, C.H.; Zhou, D.H.; Pecht, M.G. Remaining useful life estimation based on a nonlinear diffusion degradation process. IEEE Trans. Reliab. 2012, 61, 50–67. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.; Hu, C.H.; Chen, M.Y.; Zhou, D.H. A Wiener–Process-based degradation model with a recursive filter algorithm for remaining useful life estimation. Mech. Syst. Signal Process. 2013, 35, 219–237. [Google Scholar] [CrossRef]
- Tsai, C.C.; Tseng, S.T. Mis-specification analyses of gamma and Wiener degradation processes. J. Stat. Plan. Inference 2011, 11, 3725–3735. [Google Scholar] [CrossRef]
- Pieruschka, E. Relation between Lifetime Distribution and the Stress Level Causing Failure; Lockheed Missiles and Space Division: Sunnyvale, CA, USA, 1961. [Google Scholar]
- Nelson, W.B. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Wang, H.W.; Teng, K.N.; Zhou, Y. Design an optimal accelerated-stress reliability acceptance test plan based on acceleration factor. IEEE Trans. Reliab. 2018, 67, 1008–1018. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Si, X.S.; Hu, C.H.; Zhang, Q.; Li, T.M.; Xu, C.Q. Planning repeated degradation testing for products with three-source variability. IEEE Trans. Reliab. 2016, 65, 640–647. [Google Scholar] [CrossRef]
- Wang, H.W.; Teng, F. Accelerated Degradation Data Modeling and Statistical Analysis Methods and Engineering Applications; Science Press: Beijing, China, 2020. [Google Scholar]
- Hamada, M.S.; Wilson, A.; Reese, C.S. Bayesian Reliability; Springer: Berlin, Germany, 2008. [Google Scholar]
- Sharma, R.K.; Choudhury, A.R.; Arya, S.; Ghosh, S.K.; Srivastava, V. Design and Experimental Evaluation of Dual-Anode Electron Gun and PPM Focusing of Helix TWT. IEEE Trans. Electron Devices 2015, 62, 3419–3425. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.W.; Yu, S.; Wang, Y.; Zhang, H. Life Test Studies on Dispenser Cathode with Dual-Layer Porous Tungsten. IEEE Trans. Electron Devices 2014, 61, 2983–2988. [Google Scholar] [CrossRef]
- Ishibori, K.; Mita, N.; Yamamoto, K. A 10 W, 20 GHz-band traveling-wave tube amplifier for communications satellite. Rev. Electr. Commun. Lab. 1983, 31, 634–641. [Google Scholar]
- Feltham, S.J.; Kornfeld, G.; Lotthammer, R.; Stevenson, J.L. Life test studies on MM-cathodes. IEEE Trans. Electron Devices 1990, 37, 2558–2563. [Google Scholar] [CrossRef]
| Accelerated Models | Drift Parameter | Diffusion Parameter | Acceleration Factor |
|---|---|---|---|
| Arrhenius models | |||
| Eyring models | |||
| Inverse Power models |
| 1.0223 | 0.2915 | 1934.6 | 0.032 | / | 0.036 | 4511.7 | −9011.4 | |
| 1.2889 | 0.3120 | 1831.7 | / | 0.0071 | 0.027 | 4241.6 | −8473.2 | |
| 1.3781 | 0.0001 | 1853.1 | / | 0.026 | / | 3691.2 | −7374.4 |
| 0.1092 | 0.0387 | 932 | 0.000020 | / | 0.00268 | 2146.9 | −4283.8 | 25.34 a | |
| 0.0923 | 0.0316 | 1200 | / | 0.034 | 0.00951 | 1976.4 | −3942.8 | 27.48 a | |
| 0.1281 | 0.03 | 1678 | / | 0.29 | / | 1389.7 | −2771.4 | 28.28 a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Su, X.; Wang, J. Nonlinear Doubly Wiener Constant-Stress Accelerated Degradation Model Based on Uncertainties and Acceleration Factor Constant Principle. Appl. Sci. 2021, 11, 8968. https://doi.org/10.3390/app11198968
Wang X, Su X, Wang J. Nonlinear Doubly Wiener Constant-Stress Accelerated Degradation Model Based on Uncertainties and Acceleration Factor Constant Principle. Applied Sciences. 2021; 11(19):8968. https://doi.org/10.3390/app11198968
Chicago/Turabian StyleWang, Xiaoning, Xiaobao Su, and Jinjing Wang. 2021. "Nonlinear Doubly Wiener Constant-Stress Accelerated Degradation Model Based on Uncertainties and Acceleration Factor Constant Principle" Applied Sciences 11, no. 19: 8968. https://doi.org/10.3390/app11198968
APA StyleWang, X., Su, X., & Wang, J. (2021). Nonlinear Doubly Wiener Constant-Stress Accelerated Degradation Model Based on Uncertainties and Acceleration Factor Constant Principle. Applied Sciences, 11(19), 8968. https://doi.org/10.3390/app11198968






