Intermittent FOCV Using an I-V Curve Tracer for Minimizing Energy Loss
Abstract
:1. Introduction
2. Conventional MPPT Algorithms
2.1. Perturb and Observe (P & O)
2.2. Successive Approximate Register (SAR)
2.3. Combined Algorithm Based on the Adaptively Binary-Weighted Search (ABWS) and the Monotonically Decreased Step (MDS)
2.4. Fractional Open-Circuit Voltage (FOCV)
3. Proposed FOCV MPPT Algorithm
3.1. Scan Phase
3.1.1. Current-To-Voltage (I2V) Converter and Voltage-To-PWM (V2PWM) Converter
3.1.2. Multiplier
3.2. Set Phase
3.2.1. Sample and Hold (S & H)
3.2.2. Proposed FOCV
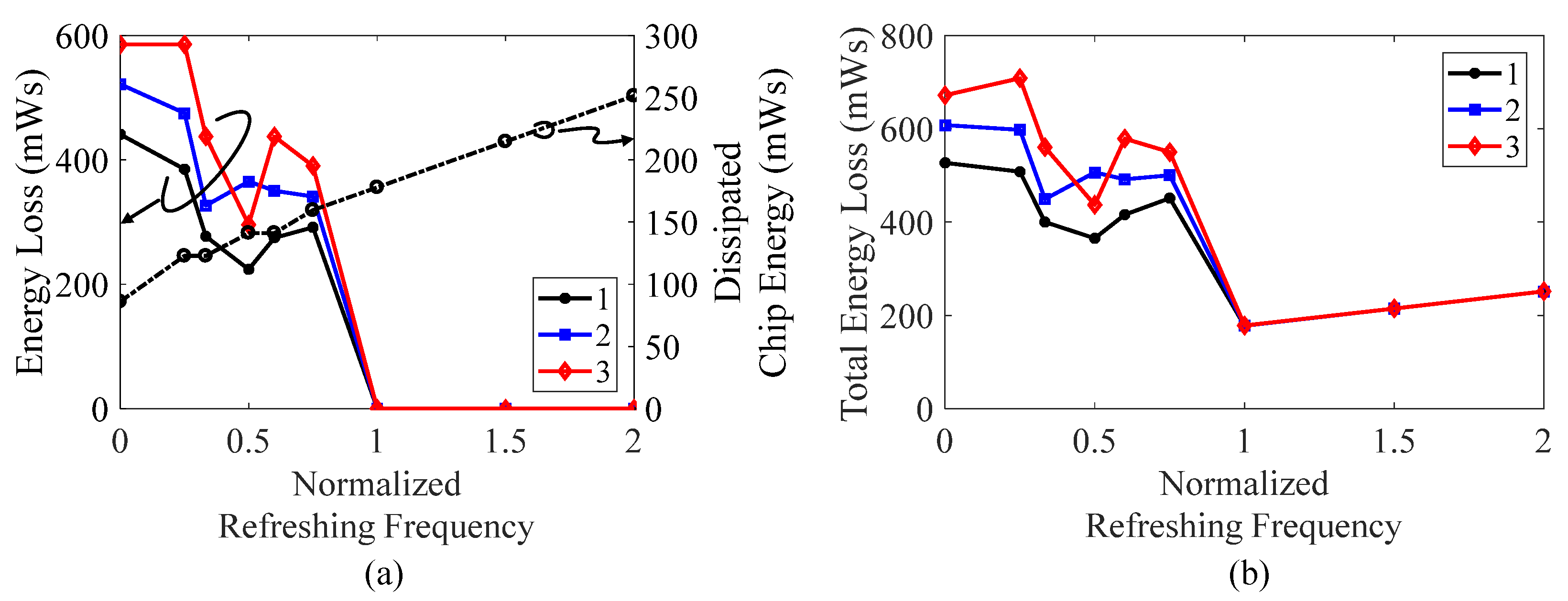
4. Simulation Results
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, K.; Yu, J.; Hsu, J.; Zahedi, S.; Lee, D.; Friedman, J.; Kansal, A.; Raghunathan, V.; Srivastava, M. Heliomote: Enabling Long-lived Sensor Networks through Solar Energy Harvesting. In Proceedings of the 3rd International Conference on Embedded Networked Sensor Systems, San Diego, CA, USA, 2–4 November 2005. [Google Scholar]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy Harvesting Vibration Sources for Microsystems Applications. Meas. Sci. Technol. 2006, 17, 175–195. [Google Scholar] [CrossRef]
- Wu, L.; Ha, D.S. A Self-Powered Piezoelectric Energy Harvesting Circuit with an Optimal Flipping Time SSHI and Maximum Power Point Tracking. IEEE Trans. Circuits Syst. II Express Briefs 2019, 10, 1758–1762. [Google Scholar] [CrossRef]
- Lawrence, E.E.; Snyder, G.J. A Study of Heat Sink Performance in Air and Soil for Use in a Thermoelectric Energy Harvesting Device. In Proceedings of the Twenty-First International Conference on Thermoelectrics, Long Beach, CA, USA, 29 August 2002. [Google Scholar]
- Sher, H.A.; Murtaza, A.F.; Noman, A.; Addoweesh, K.E.; Al-Haddad, K.; Chiaberge, M. A New Sensorless Hybrid MPPT Algorithm Based on Fractional Short-Circuit Current Measurement and P&O MPPT. IEEE Trans. Sustain. Energy 2015, 6, 1426–1434. [Google Scholar]
- Kim, H.; Kim, S.; Kwon, C.; Min, Y.; Kim, C.; Kim, S. An Energy-Efficient Fast Maximum Power Point Tracking Circuit in an 800-uW Photovoltaic Energy Harvester. IEEE Trans. Power Electron. 2013, 28, 2927–2935. [Google Scholar] [CrossRef]
- Liu, S.; Dougal, R.A. Dynamic Multiphysics Model for Solar Array. IEEE Trans. Energy Convers. 2002, 17, 285–294. [Google Scholar]
- Hong, Y.; Pham, S.N.; Yoo, T.; Chae, K.; Baek, K.; Kim, Y.S. Efficient Maximum Power Point Tracking for a Distributed PV System under Rapidly Changing Environmental Conditions. IEEE Trans. Power Electron. 2015, 30, 4209–4218. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef] [Green Version]
- Masoum, M.A.S.; Dehbonei, H.; Fuchs, E.F. Theoretical and Experimental Analyses of Photovoltaic Systems with Voltage- and Current-Based Maximum Power-Point Tracking. IEEE Trans. Energy Convers. 2002, 17, 514–522. [Google Scholar] [CrossRef] [Green Version]
- Brunelli, D.; Moser, C.; Thiele, L.; Benini, L. Design of a Solar-Harvesting Circuit for Batteryless Embedded Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 11, 2519–2528. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wang, C.; Lil, Z.; Sheng, X.; Lee, H.G.; Chang, N.; Yang, H. Storage-Less and Converter-Less Photovoltaic Energy Harvesting with Maximum Power Point Tracking for Internet of Things. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2016, 35, 173–186. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Ha, D.S. Energy Harvesting Circuit for Indoor Light based on the FOCV and P&O Schemes with an Adaptive Fraction Approach. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 10–21 October 2020. [Google Scholar]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of Perturb and Observe Maximum Power Point Tracking Method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Krishlnan, M.M.; Bharath, K.R. A Novel Sensorless Hybrid MPPT Method Based on FOCV Measurement and P&O MPPT Technique for Solar PV Applications. In Proceedings of the 2019 International Conference on Advances in Computing and Communication Engineering (ICACCE), Sathyamangalam, India, 4–6 April 2019. [Google Scholar]
- Canadian_Solar-Datasheet- BiHiKu_CS3W-PB-AG_High Efficiency_(1000 V & 1500 V). Available online: https://www.canadiansolar.com/wp-content/uploads/2019/12/Canadian_Solar-Datasheet-BiHiKu_CS3W-PB-AG_High-Efficiency_1000V1500V_EN-2.pdf (accessed on 27 June 2021).
- JKM395-415M-54HL4-V-F1-30-CN.ai. Available online: https://www.jinkosolar.com/uploads/JKM395-415M-54HL4-V-F1-30-CN.pdf (accessed on 27 June 2021).
- JKM440-460M-60HL4-(V)-F1-CN.ai. Available online: https://www.jinkosolar.com/uploads/JKM440-460M-60HL4-(V)-F1-CN.pdf (accessed on 27 June 2021).
- PS-M A Datasheet_TALLMAX_DE06X.05(II)_EN_2020_PA2_web. Available online: https://static.trinasolar.com/sites/default/files/US_Datasheet_DE06X.05(II)_NA_2021_PA3.pdf (accessed on 27 June 2021).
- Download | Panasonic Solar HIT | Life Solutions | Business | Panasonic Global. Available online: http://panasonic.net/lifesolutions/solar/download/index.html (accessed on 27 June 2021).
- VBHN330_325SJ47_EN.pdf. Available online: http://europe-solarstore.com/download/panasonic/VBHN330_325SJ47_EN.pdf (accessed on 20 August 2021).
- PS-M- Small Size Datasheet_TallmaxM_DEG15VC.20(II)_EN_2020_PA1_web. Available online: http://static.trinasolar.com/sites/default/files/Datasheet_Bifacial%20DEG15VC.20%28II%29_2021_B.pdf (accessed on 27 June 2021).
- Datasheets. Available online: http://q-cells.com/kr/main/service/download/datasheets~datasheets~.html?page=1 (accessed on 27 June 2021).
- Canadian_solar-Datasheet- HiKu_CS3N-MS_(1000 V & 1500 V)_EN. Available online: https://static.csisolar.com/wp-content/uploads/sites/2/2019/12/13140918/CS-Datasheet-HiKu_CS3N-MS_v2.8C25_AU-black-frame25-years-product-warranty.pdf (accessed on 27 June 2021).
- JAM72S10 400-420 MR. Available online: https://www.jasolar.com//uploadfile/2020/0605/20200605034219227.pdf (accessed on 27 June 2021).
- JAM60S10 330-350 MR. Available online: https://www.jasolar.com//uploadfile/2020/0605/20200605033853385.pdf (accessed on 27 June 2021).
- LR5-66HBD 475-500M. Available online: http://en.longi-solar.com/uploads/attach/20210507/60950dbad3c23.pdf (accessed on 27 June 2021).
- LGiLE-T-TMD-059-108 LR5-72HBD 525-545M. Available online: http://en.longi-solar.com/uploads/attach/20210512/609b53096a2a1.pdf (accessed on 27 June 2021).
- EN_Ultra_S_STP455S_B72_Vnh.pdf. Available online: http://suntech-power.com/wp-content/uploads/download/product-specification/EN_Ultra_S_STP455S_B72_Vnh.pdf (accessed on 27 June 2021).
- EN_Ultra_V_STP550S_C72_Vmh.pdf. Available online: http://suntech-power.com/wp-content/uploads/download/product-specification/EN_Ultra_V_STP550S_C72_Vmh.pdf (accessed on 27 June 2021).
- 83e8173f1203f01571b4170ae1827bbe.pdf. Available online: http://www.tw-solar.com/en/Uploads/20210409/83e8173f1203f01571b4170ae1827bbe.pdf (accessed on 27 June 2021).
- 2230b50c83aaf4092bd129beb1352d3d.pdf. Available online: http://www.tw-solar.com/en/Uploads/20210409/2230b50c83aaf4092bd129beb1352d3d.pdf (accessed on 27 June 2021).
- 2e414aeb51a11620dc-45d1a08f722a1e.pdf. Available online: http://www.tw-solar.com/en/Uploads/20210409/2e414aeb51a11620dc45d1a08f722a1e.pdf (accessed on 27 June 2021).
- Weather in April 2021 in Furnace Creek (Death Valley), California, USA. Available online: http://timeanddate.com/weather/usa/furnace-creek-death-valley/historic?month=4&year=2021 (accessed on 16 August 2021).
- Weather in July 2021 in Seoul, South Korea. Available online: http://timeanddate.com/weather/south-korea/seoul/historic?month=7&year=2021 (accessed on 17 August 2021).
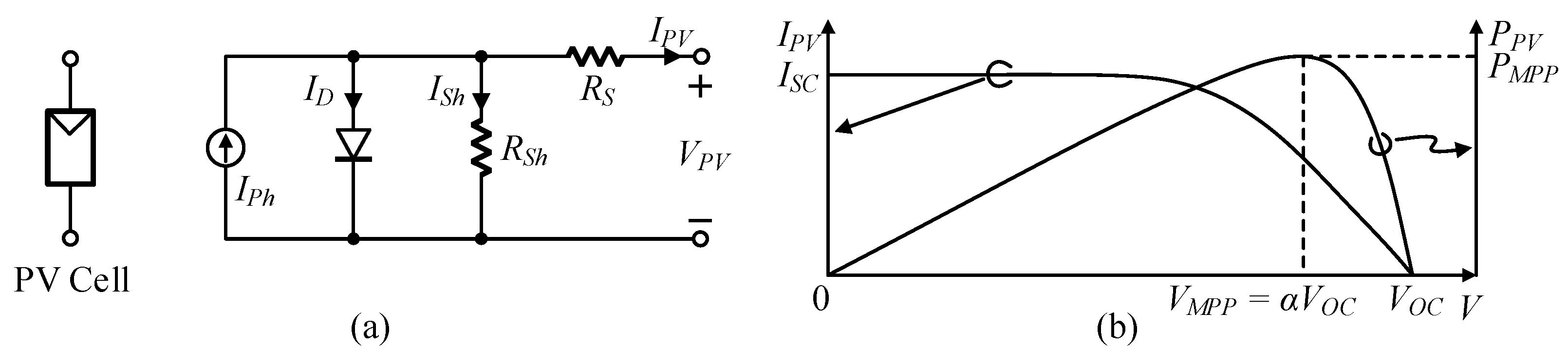























Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Im, Y.C.; Kwak, S.S.; Park, J.; Kim, Y.S. Intermittent FOCV Using an I-V Curve Tracer for Minimizing Energy Loss. Appl. Sci. 2021, 11, 9006. https://doi.org/10.3390/app11199006
Im YC, Kwak SS, Park J, Kim YS. Intermittent FOCV Using an I-V Curve Tracer for Minimizing Energy Loss. Applied Sciences. 2021; 11(19):9006. https://doi.org/10.3390/app11199006
Chicago/Turabian StyleIm, Yun Chan, Seung Soo Kwak, Jonghyun Park, and Yong Sin Kim. 2021. "Intermittent FOCV Using an I-V Curve Tracer for Minimizing Energy Loss" Applied Sciences 11, no. 19: 9006. https://doi.org/10.3390/app11199006





