A Novel Dual-Wavelength Method for Evaluating Temperature Effect in Fiber-Optic SPR Sensors

Abstract

The temperature effect is one of the critical factors to induce the resonance wavelength shift in fiber-optic surface plasmon resonance (SPR) sensors, which leads to the inaccuracy measurement of refractive index (RI) in practical applications. In this study, a novel dual-wavelength method is presented for fiber-optic SPR sensors to measure the changes of RI and temperature simultaneously in real time. A typical model of an SPR-based fiber optical sensor is constructed for theoretical analysis of temperature effect. Both the thermo-optic effect in the fiber core and phonon–electron scattering along with electron–electron scattering in the metal layer are studied systematically in the theoretical model. The linear and independent relationship, about the dependence of defined output signals on the RI and temperature, is validated by a theoretical calculation in specific dual wavelengths. A proof-of-concept experiment is conducted to demonstrate the capability of the presented dual-wavelength technique. The experimental results indicate that the presented dual-wavelength method is technically feasible and can be applied for practical application. Since the presented method only depends on the full advantages of the transfer spectrum data, it can be applied directly to the conventional single-channel fiber-optic SPR without any specific design structure of the sensor probe. The proposed method provides a new way to detect the RI under different thermal conditions and could lead to a better design for the fiber-optic SPR sensors.

1. Introduction

Surface plasmon resonance (SPR) is a phenomenon that involves the absorption of p-polarized light by the surface electrons of a metal film [1,2]. The changes of refractive index (RI) on the surface of metal film can be measured based on the SPR effect to reveal the properties of analytes in real time. The SPR has become an important optical biosensing technology due to the advantages of miniaturization, remote sensing capabilities, anti-electromagnetic radiation, and label-free and real-time monitoring [3,4]. Therefore, a fiber-optic sensor using the SPR (also called fiber-optic SPR sensor) can be designed with different molecular sensor layers on the metal surface. The fiber-optic SPR sensor is a novel bio-chemical sensor that can be applied broadly in the fields of biomolecular interaction analysis, chemical/biological analytes detection and medical diagnostics [5,6,7,8]. It is capable of detecting tiny RI changes of an analyte or other physical quantities that equivalently convert to RI changes [9,10]. However, the performance of fiber-optic SPR sensors is always disturbed by several physical parameters, such as the external environment parameters and the condition of the analyte, in practical application. All of the physical parameters result in the wavelength shift of fiber-optic SPR sensor. The application of fiber-optic SPR sensors is limited by the accurate detection of wavelength shift. In all the interference parameters, the temperature of the measuring object is one of the critical factors for the fiber-optic SPR sensor and needs to be carefully considered for ensuring the stability and accuracy of the sensor. Previous studies have proven that the temperature of the detecting situation has multiple influences on the performance of the SPR sensor and may lead to incorrect measurements [11,12,13,14]. For a fiber-based SPR sensor, the temperature influence on the measurement generally includes two main aspects: the property changes from detecting the analyte and the sensor structure parameters. Therefore, the spectrum resonance shift could be caused by the changes of the RI and temperature simultaneously [15,16], leading to the major technological problem of discriminating between the RI-induced and temperature-induced SPR changes. As a result, it poses a substantial challenge for the applications of fiber-optic SPR sensors.

In order to eliminate the uncertainty of RI measurement of fiber-optic SPR sensor caused by temperature perturbation, an alternative method is to measure RI and temperature simultaneously. Several methods have been proposed to extract two different parameters from the output signal of the conventional fiber SPR sensing probe. These methods can be summarized into four categories: (i) measurements at two different fluid channels (one of the channels is taken as the reference for the measurement); (ii) angular spectroscopy at two different wavelengths [17] corresponding to the angle intensity interrogation mode; (iii) wavelength spectroscopy at two different angles [18] corresponding to the wavelength interrogation mode; (iv) multi-mode SPR spectroscopy [19]. However, it is not easy to apply these methods in practice. To this end, a common approach is to design the sensing structure by a pair of cascaded or embedded fiber devices. Typically, a double-channel SPR with one of them taking as a reference is proposed and applied. However, this method is not suitable for fabricating compact sensors or, in general, requiring a complicated fabrication process and specialized equipment [20]. In addition, Velázquez-González et al. proposed a gold-coated MM–SM–MM fiber structure to measure the RI and temperature simultaneously [21]. With the design of the single-mode fiber section inserted between two multimode fibers in sensor probes, the sensitive section was partially covered with an analyte to generate two SPR resonance dips in the transmission spectrum. Therefore, a complex fiber optic sensor probe structure is expected to carry out in the experiment.

To this end, we present and demonstrate a novel dual-wavelength method for simultaneous measurement of the RI and temperature variation in this paper. Compared to other types of fiber-optic SPR sensors with temperature self-compensation [22,23,24], our proposed method can be directly applied to the traditional fiber SPR probe. In the dual-wavelength technique, the dependence of the defined output signals at two dual-wavelengths on RI and temperature are linear and independent with each other. Therefore, there are two main advantages of the dual-wavelength technique. Firstly, the probe of the fiber-optic SPR sensor is a single channel rather than a dual-channel. Secondly, the structure is just the same as the traditional fiber SPR sensor. Therefore, this technique can be applied to the traditional fiber SPR sensor, and no extra structure changes is needed in the sensor probe section. The only requirement is to launch the sensor probe with two suitable wavelengths of lights. This makes the dual-wavelength technique more suitable for practical application. In this paper, a systematic theoretical analysis is conducted for the temperature effect in fiber-optic SPR sensors. Based on the analysis, a theoretical calculation and the corresponding numerical analysis are conducted to validate the change of light reflectance signals with a pair of specific wavelengths due to the resonance wavelength shift. In some specific dual wavelengths, the dependence of the defined output signals on the RI and temperature is linear and independent of them. An experimental platform is constructed to verify the dual-wavelength technique. The proof-of-concept experiment arrangement is as simple and robust as the conventional single-channel fiber-optic SPR sensor. The experimental results demonstrate that the presented dual-wavelength method is feasible in technology and can be used in practical applications.

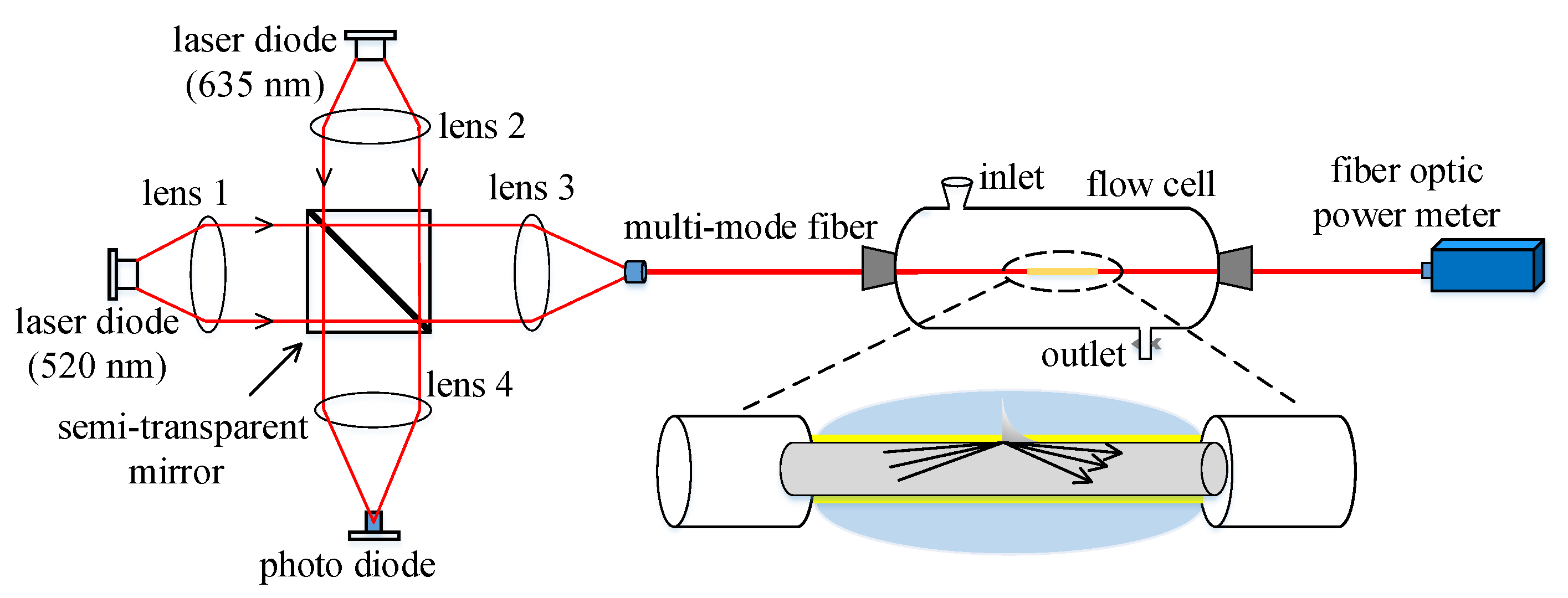
2. Material and Methods

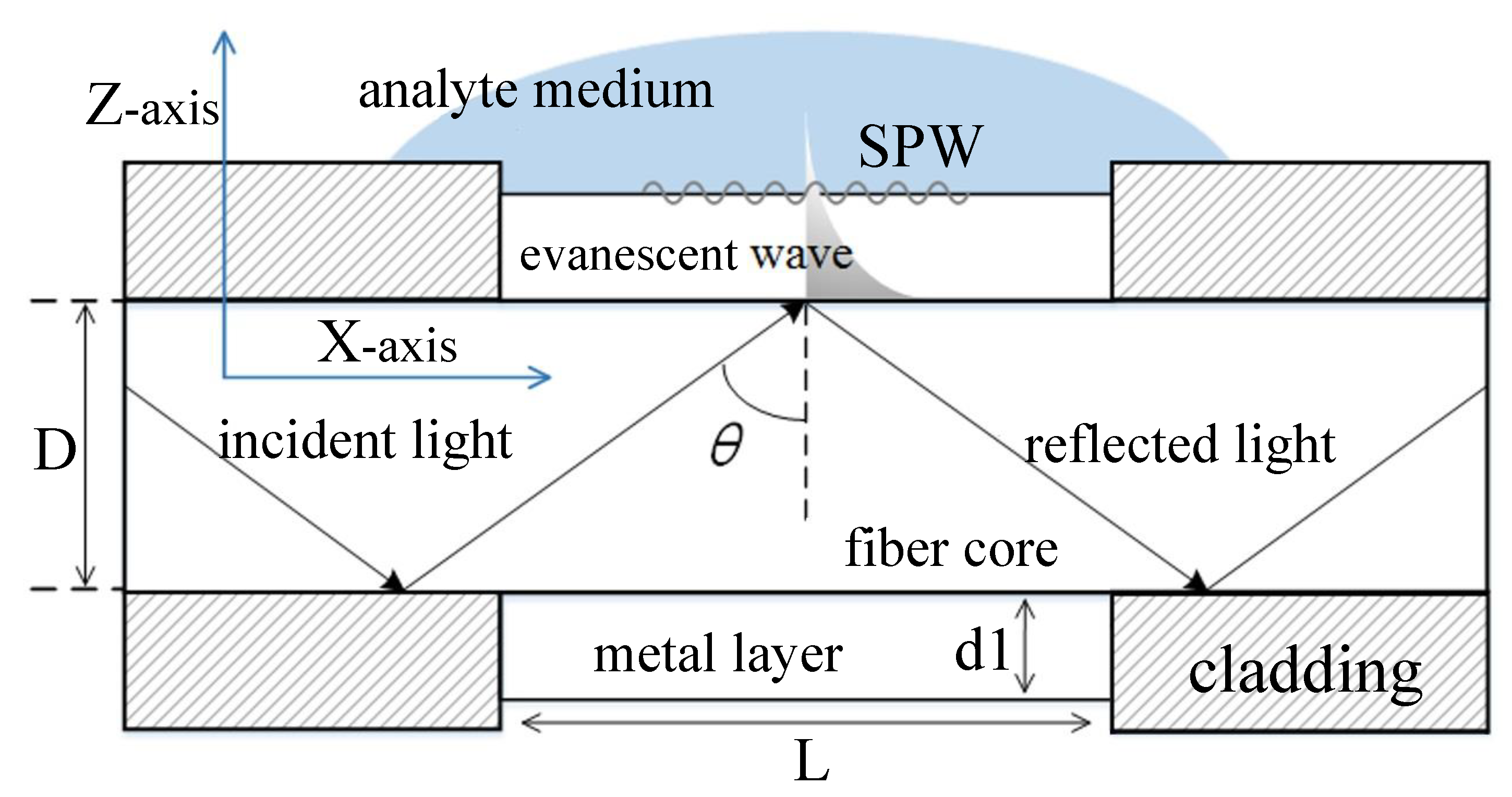
2.1. The Model of Fiber-Optic SPR Sensor

A typical model of an SPR-based fiber-optic sensor can be constructed with the structure shown in Figure 1. A small portion of the cladding is firstly removed and the exposed fiber core is then coated with a metal layer. Therefore, an analyte medium (dielectric analyte) is surrounded on the metal layer that has been detected. When a beam of light is inserted into the optical fiber, the metal–dielectric interface supports an electromagnetic wave called the surface plasmon wave (SPW). In the SPR-based fiber optical sensor model, the temperature effects on SPR can be equivalent to the changes in the physical parameters of the sensing structure, i.e., the metal layer and fiber core. Therefore, combining the phonon–electron scattering along with electron–electron scattering (in the metal layer) and phenomena of thermo-optic (in the fiber core) with the multi-layer matrix method, a complete theoretical model can be constructed to investigate the multiple temperature effects on a fiber-optic SPR sensor.

2.2. Temperature Effect on Metal Layer

The theoretical analysis of the temperature effect on a metal layer is described as follows. Firstly, the complex and frequency-dependent dielectric function of a metal sensor layer can be presented by the Drude model [25] as Equation (1):

$$\epsilon \left(\omega \right)=1-\frac{{\omega }_p^2}{\omega \left(\omega +i{\omega }_c\right)}$$

(1)

where the ${\omega }_c$ and ${\omega }_p$ are the collision frequency and plasma frequency, respectively.

Then, temperature (T) dependence of the plasma frequency (${\omega }_p$) can be calculated according to the volumetric effects [26] as Equation (2):

$${\omega }_p={\omega }_{p0}{\left[1+{\gamma }_e\left(T-T_0\right)\right]}^{-1/2}$$

(2)

where ${\omega }_{p0}$ is the plasma frequency at a reference temperature $T_0$ and ${\gamma }_e$ is the expansion coefficient of the metal layer.

In addition, the impact of temperature (T) on the collision frequency (${\omega }_c$) occurs through two main factors: namely, phonon–electron scattering (${\omega }_{cp}$) and electron–electron scattering (${\omega }_{ce}$). Therefore, the combined effect ${\omega }_c$ can be represented as Equation (3)

$${\omega }_c={\omega }_{cp}+{\omega }_{ce}$$

(3)

1.

${\omega }_{cp}$ can be simulated with the Holstein model of phonon–electron scattering [27]:

$${\omega }_{cp}\left(T\right)={\omega }_0\left[\frac{2}{5}+4{\left(\frac{T}{T_D}\right)}^5{\int }_0^{T_D/\phantom{T_{D}T}T}\frac{z^{4}dz}{e^z-1}\right]$$

(4)

where ${\omega }_0$ is a constant related to the electric conductivity of metal and can be determined from the static limit of the equation [28]. $T_D$ is the Debye temperature of the metal.

2.

${\omega }_{ce}$ can be presented by the Lawrence model using the Born approximation and Thomas–Fermi screening of the Coulomb interaction [29] as:

$${\omega }_{ce}\left(T\right)=\frac{1}{6}{\pi }^4\frac{\Gamma \Delta }{\hslash E_F}\left[{\left(k_{B}T\right)}^2+{\left(\frac{\hslash \omega }{4{\pi }^2}\right)}^2\right]$$

(5)

where $\Gamma$, $\Delta$, ℏ, $E_F$, and $k_B$ are the Fermi surface average of scattering probability, fractional Umklapp scattering, Planck’s constant, Fermi energy, and Boltzmann constant, respectively.

Besides, temperature effects also affect the thickness of the metal layer. According to [30], the metal film only expands in the normal direction with a corrected thermal-expansion coefficient. Hence, the temperature dependence of the thickness of the metal layer d can be expressed as Equation (6):

$$d=d_0\left[1+{\gamma }^{\prime }\left(T-T_0\right)\right]=d_0\left[1+\gamma \frac{1+\mu }{1-\mu }\left(T-T_0\right)\right]$$

(6)

where $\mu$ is the Poisson’s number, $\gamma$ is the linear expansion coefficient of the sensor metal, and ${\gamma }^{\prime }$ is the corrected thermal expansion coefficient. $T_0$ is the reference temperature as in Equation (2).

2.3. Temperature Dependence of the Optical Fiber for Wave-Interrogation Mode

In this study, the optical fiber is considered as a step index multimode fiber. The central core of the optical fiber is made of fused silica. Therefore, the dependence of its RI can be expressed by the Sellmeier relation as Equation (7):

$$n_1\left(\lambda \right)=\sqrt{1+\frac{A_1{\lambda }^2}{{\lambda }^2-{B_1}^2}+\frac{A_2{\lambda }^2}{{\lambda }^2-{B_2}^2}+\frac{A_3{\lambda }^2}{{\lambda }^2-{B_3}^2}}$$

(7)

where $\lambda$ denotes the wavelength of incident light. The coefficients $A_1$, $A_2$, $A_3$, $B_1$, $B_2$, and $B_3$ are constants with certain numeric values.

Meanwhile, the RI variation of the fiber core ($n_{\lambda }$) with temperature is another factor which needs to be taken into account. The temperature effect on the fiber core can be expressed as Equations (8) and (9) [31]:

$$R={\lambda }^2/\phantom{{\lambda }^2\left({\lambda }^2-{\lambda }_{ig}^2\right)}\left({\lambda }^2-{\lambda }_{ig}^2\right)$$

(8)

$$2n\left(\lambda \right)\frac{dn}{dT}\left(\lambda \right)=GR+H{R}^2$$

(9)

where ${\lambda }_{ig}$ represents the band gap wavelength in units of $\mathsf{\mu }\mathrm{m}$. $dn/dT$ is the thermo-optic coefficient for silica.

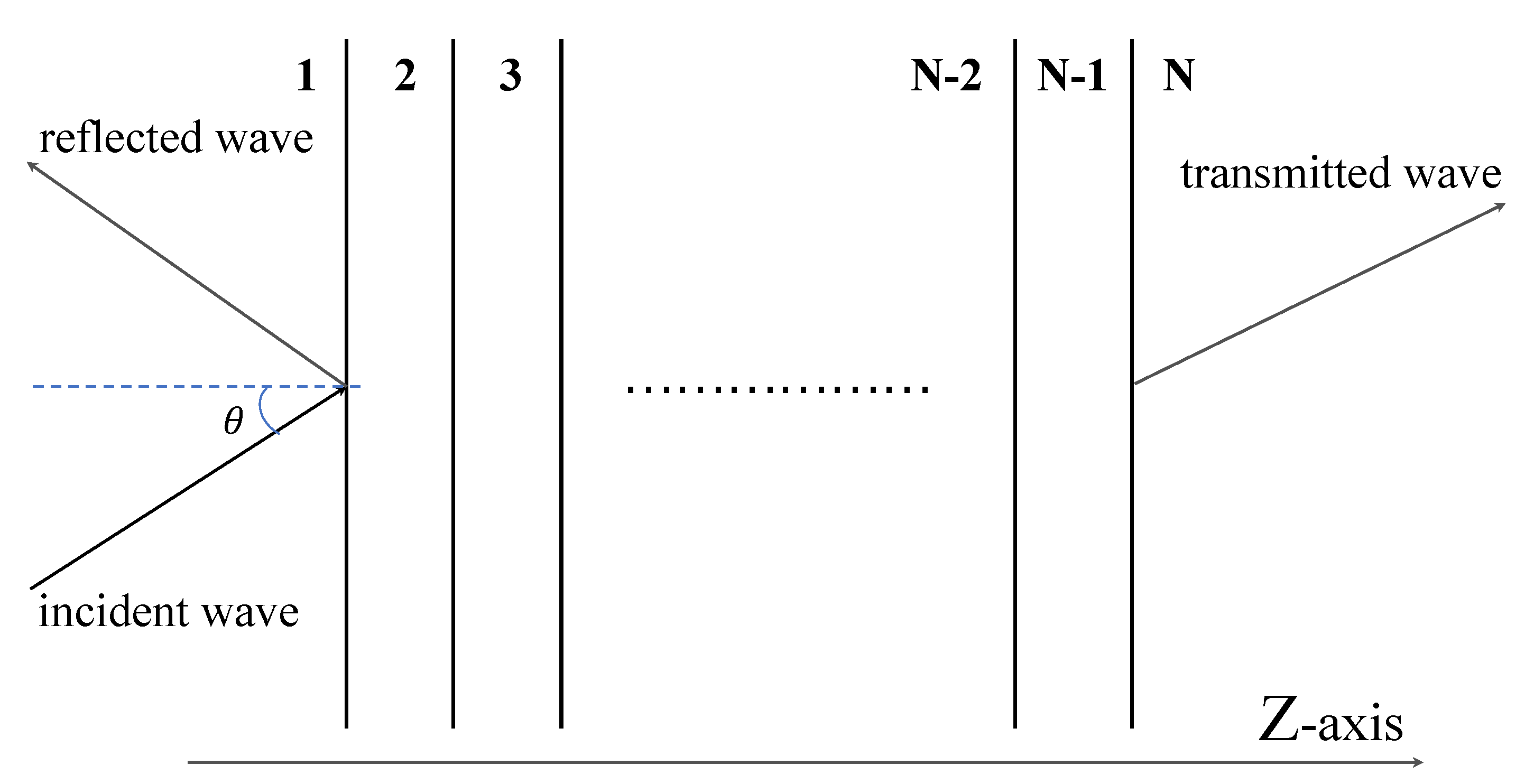
2.4. Multi-Layer Matrix Method

In general, the fiber sensor based on the SPR can be considered as an N-layer model [32,33,34]. To simplify the model, all the layers are assumed to be uniform, isotropic, non-magnetic, and stacked along the z-axis, as shown in Figure 2. Here, we use the matrix method to obtain the expression for the reflected light intensity of p-polarized incident light.

For the $n\mathrm{th}$ medium layer, the thickness, dielectric constant, and permeability are defined as $d_n$, ${\epsilon }_n$, and ${\mu }_n$. The tangential fields at the first boundary ($Z=Z_1=0$) and the final boundary ($Z=Z_{N-1}$) are related by the relation of Equation (10):

$$\left[\begin{array}{c}{E}_1\\ H_1\end{array}\right]=M\left[\begin{array}{c}{E}_{N-1}\\ H_{N-1}\end{array}\right]$$

(10)

where, $E_1$, $H_1$, and $E_{N-1}$, $H_{N-1}$ are the tangential components of electric and magnetic fields at the boundary of the first layer and the $N\mathrm{th}$ layer, respectively. Here, M is the characteristic matrix for the multilayer structure and can be given by Equation (11):

$$M={\prod }_{n=2}^{N-1}{M}_n$$

(11)

Herein,

$$M_n=\left[\begin{array}{cc}cos{\beta }_n& \frac{-isin{\beta }_n}{q_n}\\ -i{q}_{n}sin{\beta }_n& cos{\beta }_n\end{array}\right]$$

(12)

with the coefficients:

$${\beta }_n=\frac{1}{\lambda }2\pi d_n\sqrt{{\epsilon }_n-n_1^2{sin}^2\theta }$$

(13)

where $\lambda$ is the free space wavelength and $n_1$ is the RI of the first layer.

In transverse-electric (TE, s-polarized) models,

$$q_n=\sqrt{{\epsilon }_n-n_1^2{sin}^2\theta }$$

(14)

In transverse-magnetic (TM, p-polarized) models,

$$q_n=\frac{q_n}{{\epsilon }_n}$$

(15)

The reflection amplitude for polarized incident light can be calculated by Equation (16):

$$r=\frac{\left(M_{11}+M_{12}{q}_N\right)q_1-\left(M_{21}+M_{22}{q}_N\right)}{\left(M_{11}+M_{12}{q}_N\right)q_1+\left(M_{21}+M_{22}{q}_N\right)}$$

(16)

Therefore, the final reflection intensity of unpolarized wave containing TE and TM modes can be given by Equation (17):

$$R=\frac{1}{2}\left({\left|r_{TE}\right|}^2+{\left|r_{TM}\right|}^2\right)$$

(17)

2.5. Transmitted Power for SPR-Based Fiber-Optical Sensor

The modal power corresponding to the incident angle $\theta$ can be expressed as [35,36]:

$$p\left(\theta \right)=\frac{n_1^{2}sin\theta cos\theta }{{\left(1-n_1^2{cos}^2\theta \right)}^2}$$

(18)

Based on the reflectance value for a single reflection at the core/metal interface, the normalized transmitted power of unpolarized light can be calculated by Equation (19):

$$p=\frac{{\int }_{{\theta }_{cr}}^{\pi /\phantom{\pi 2}2}{R}^{N}p\left(\theta \right)d\theta }{{\int }_{{\theta }_{cr}}^{\pi /\phantom{\pi 2}2}p\left(\theta \right)d\theta }$$

(19)

where N represents the number of reflections that a ray undergoes in the fiber sensing area. ${\theta }_{cr}$ is the critical angle. The N and ${\theta }_{cr}$ can be expressed as in Equations (20) and (21):

$$N=\frac{L}{Dtg\theta }$$

(20)

$${\theta }_{cr}={sin}^{-1}\left(\frac{n_{cl}}{n_1}\right)$$

(21)

where L and D are the length and core diameter of the fiber sensing region, as shown in Figure 1. $n_{cl}$ and $n_1$ are the refractive indices of the cladding and core.

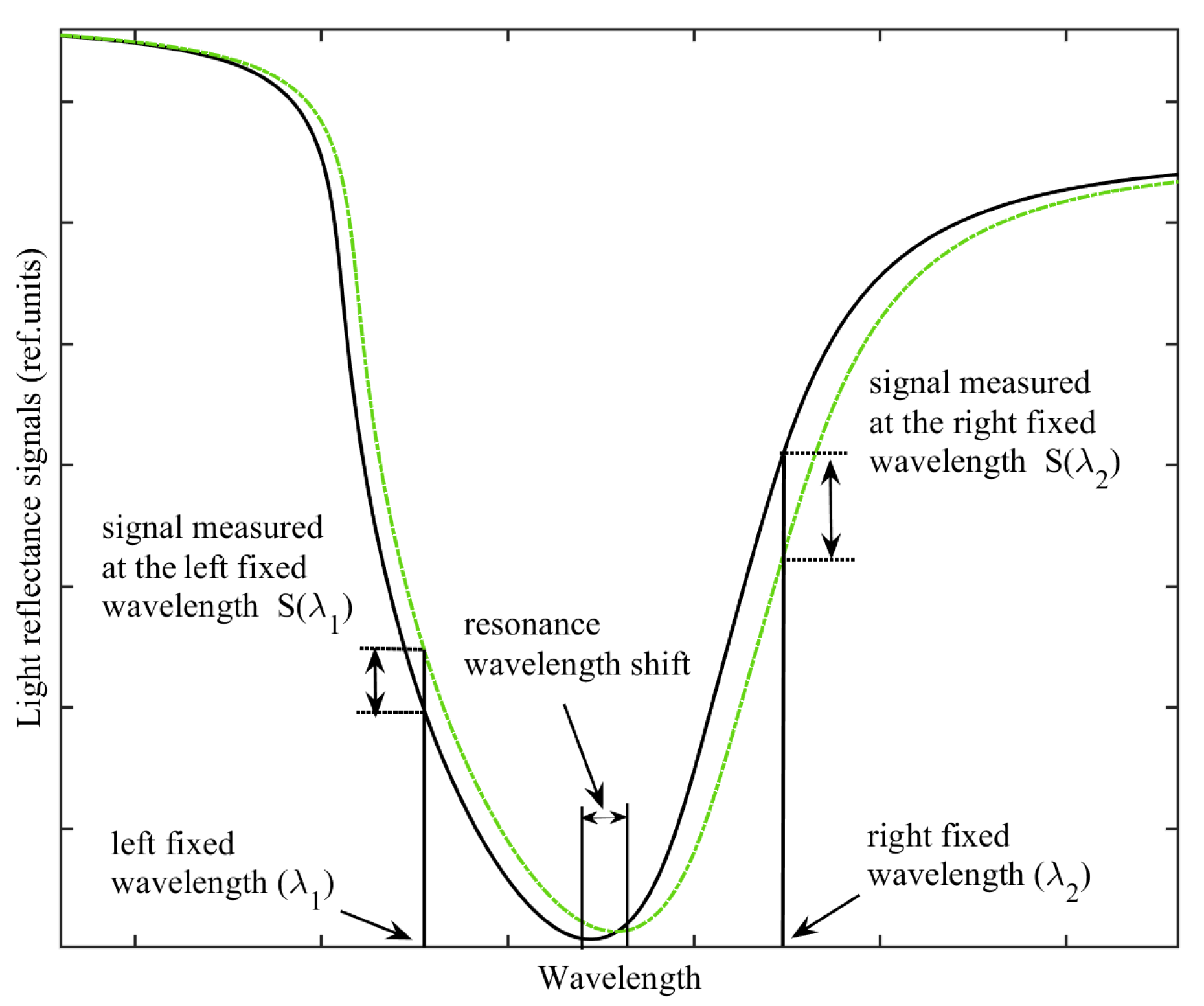
3. The Principle of Dual-Wavelength Method and Theoretical Calculation of Fiber-Optic SPR Sensor

Based on the model of fiber-optic SPR sensor illustrated in Section 2.1, the functional relationship between the output light intensity and the wavelength of incident light is fitted as shown in Figure 3. The solid curve represents a typical resonance spectrum of the fiber-optic SPR sensor. The resonance curve exhibits a valley and the signal of light reflectance gets its minimum value in a characteristic wavelength. However, the surface-plasmon wave of the fiber-optic SPR sensor will be changed due to the variation of RI or temperature of an analyte, which in turn leads to the variation of resonance incident wave vector. The original resonance curve could shift to the dotted line as shown in Figure 3 with a resonance wavelength drift. The conventional method to obtain the variation is to detect the resonance dip in the transmission spectrum. However, the temperature effect cannot be ruled out, which results in the bias of detection result.

Inspired by the dual-incident angle technique for the prism-based SPR sensor [37,38,39,40], a dual-wavelength method is presented for the fiber-optic SPR sensor in this paper. Based on the theoretical analysis and the resonance characteristics of the fiber-optic SPR sensor, we present a linear model between the change of reflectance transmission signal and the change of RI/temperature of the analyte with two specific incident wavelengths. The two specific incident wavelengths (${\lambda }_1$ and ${\lambda }_2$) are chosen on the opposite sides of the resonance curve. The light reflectance signal at wavelength ${\lambda }_1$ is denoted as $S\left({\lambda }_1\right)$, and the light reflectance signal at wavelength ${\lambda }_2$ is denoted as $S\left({\lambda }_2\right)$. Compared with the traditional fiber-optic SPR detection method which just exploits the resonance wavelength obtained at the dip of transmission spectrum, the presented dual-wavelength measurement takes full advantage of the data obtained at both ${\lambda }_1$ and ${\lambda }_2$ and offers two output signals to indicate the variations in temperature and RI. Based on the assumption of the original dual-wavelength method, the selection principle of the wavelengths is that the dependence of the defined output signals on RI and temperature are linear and independent of each other in the detection range of both RI and temperature. In order to find two fixed wavelengths that meet these conditions for practical applications, the RI and temperature effects are analyzed in detail. Figure 4 shows the resonance spectra of the analyte with RI range from 1.333 to 1.340, and the temperature is set at 310 K. As shown in the Figure 4, the resonance spectrum shifts to the right side as RI increasing. In wavelength range 1, the lines of the resonance spectra are almost parallel to each other. The same phenomenon appears in the wavelength range 2. Therefore, a linear relationship between the RI and reflectance signal can be established in the two wavelength ranges. The right fixed wavelength can be chosen in range 1, and the left fixed wavelength can be chosen in range 2.

In order to investigate the feasibility of the dual-wavelength method for the simultaneous measurement of the changes of RI and temperature, a theoretical calculation and numerical analysis are conducted to quantify the output signal, i.e., light intensity, of a fiber-optic SPR sensor with different temperature and RI. In our simulation, the core of a multimode fiber is coated with gold film. The thickness of the gold sensor film is assumed to be 50 nm. The numerical aperture (NA) of the optical fiber is set to 0.36. Temperature variation is in the range of 290–320 K and the interval of variation of the RI is set to 1.333–1.338 RIU. The two characteristic wavelengths ${\lambda }_1=495$ nm and ${\lambda }_2=575$ nm are sought for the evaluation of temperature effect and RI on the fiber-optic SPR sensor. The dependence of output signal on temperature and RI is analyzed based on the model analysis in Section 2. Hence, the theoretical analysis and numerical calculation are carried out to quantitative analysis of the variations of temperature and RI simultaneously. The dependence of reflectance signals on RI and temperature are simulated at the wavelengths ${\lambda }_1=495$ nm and ${\lambda }_2=575$ nm, as shown in Figure 5. It is obvious that the reflectance signals $S\left({\lambda }_1\right)$ and $S\left({\lambda }_2\right)$ are linear with both RI and temperature. For example, the reflectance signal $S\left({\lambda }_1\right)$ increases linearly with RI at a temperature of 300 K, while the linear decrease of the signal $S\left({\lambda }_2\right)$ is with RI at the temperature of 300 K. Besides, the absolute slope of $S\left({\lambda }_2\right)$ is larger than that of $S\left({\lambda }_1\right)$, which reveals that the change of reflectance signal at ${\lambda }_2$ is faster than ${\lambda }_1$ to RI variation. In other words, the constructed fiber-optic SPR sensor is more sensitive to RI at the ${\lambda }_2$. Meanwhile, another feature is that the linear variation of the reflectance signals $S\left(\lambda \right)$ with temperature is less significant than RI. It demonstrates that the reflectance signal is less sensitive to temperature. The variation of the output signal mainly depends on the change of RI. In summary, the relationship between the output signal change versus RI and temperature variation is approximately linear with different slopes depending upon the light wavelength used in the measurement.

For the detailed scenario, Figure 6 shows the output signal changes versus the RI at different temperatures. It is obvious that the dependence of the $S\left({\lambda }_1\right)$ (or $S\left({\lambda }_2\right)$) on the RI is nearly the same at T = 290 K (T is the value of temperature) and T= 320 K. The difference in the slope of the signal versus RI is negligible compared to either of the two slopes. It clearly suggests that, for the two defended sensor outputs, the dependence of the output signal on RI is almost independent with temperature. Another important observation is that the spacings between the curve pairs of T = 290 K and T = 320 K are different. The spacing of ${\lambda }_1$ is larger than the spacing of ${\lambda }_2$, which reveals that the signal is less sensitive to temperature variation at the signal of $S\left({\lambda }_2\right)$. As the curves show in Figure 6, the linear sensitivities between output signals versus the RI are −21.6454/ RIU and 9.2836/RIU for $S\left({\lambda }_2\right)$ and $S\left({\lambda }_1\right)$, respectively. Figure 7 shows the change of the output signal versus the temperature with RI equalling n = 1.333 RIU (n is the value of RI) and n = 1.338 RIU. Similarly, two important key features can be obviously found from these curves. Firstly, the spacings between the curve pairs of n = 1.333 RIU and n = 1.338 RIU for $S\left({\lambda }_1\right)$ and $S\left({\lambda }_2\right)$ are larger than its counterpart in Figure 6 because of the significant RI dependence and low temperature sensitivity. Secondly, it is clearly observed that, for both of the output signals, the slopes of the output signal versus temperature for n = 1.333 RIU and n = 1.338 RIU are nearly equal. This means that, for the two signals, the temperature dependence of the output is approximately independent with RI. The small detectable sensitivities between output signals versus the temperature are −2.8672/${10}^4$ K and −5.3535/${10}^4$ K, respectively.

Based on the above analysis, the dependence of the two output signals, defined by the dual-wavelength technique, on RI and temperature can be viewed as linear and independent with each other. Therefore, the variation of the two defined output signals with the simultaneous changes in RI and temperature can be expressed as:

$$\left(\begin{array}{c}\Delta S\left({\lambda }_1\right)\\ \Delta S\left({\lambda }_2\right)\end{array}\right)=K\left(\begin{array}{c}\Delta n\\ \Delta T\end{array}\right)$$

(22)

$$K=\left(\begin{array}{cc}{k}_{n1}& k_{T1}\\ k_{n2}& k_{T2}\end{array}\right)$$

(23)

where $\Delta S\left({\lambda }_1\right)$ and $\Delta S\left({\lambda }_2\right)$ are the output changes of the two defined signals. $\Delta n$ and $\Delta T$ represent the RI variation and temperature change, respectively. K is the sensitivity matrix, taking into account the cross-sensitivity between the changes of RI and temperature. The sensitivity matrix K is composed of the linear fitting coefficients between the output signals versus the RI and temperature as shown in Figure 6 and Figure 7. However, the changes of RI and temperature are invisible in an actual sensing case of measuring the resonance spectrum to detect the variations of RI and temperature. Therefore, by the inverse matrix of K and measuring the defined output signals at the dual wavelengths, the changes of RI and temperature can be calculated simultaneously as:

$$\left(\begin{array}{c}\Delta n\\ \Delta T\end{array}\right)=K^{-1}\left(\begin{array}{c}\Delta S\left({\lambda }_1\right)\\ \Delta S\left({\lambda }_2\right)\end{array}\right)=\left(\begin{array}{cc}0.0201& -0.0376\\ -0.1519& -0.0651\end{array}\right)\left(\begin{array}{c}\Delta S\left({\lambda }_1\right)\\ \Delta S\left({\lambda }_2\right)\end{array}\right)$$

(24)

With the full use of the detected spectrum data, both the variations in RI and temperature can be obtained with the dual-wavelength method. Further, this technique can be applied with traditional single-channel fiber-optic SPR sensors and extended to a detection situation of both the transmission-based and the reflection-based fiber-optic SPR probes.

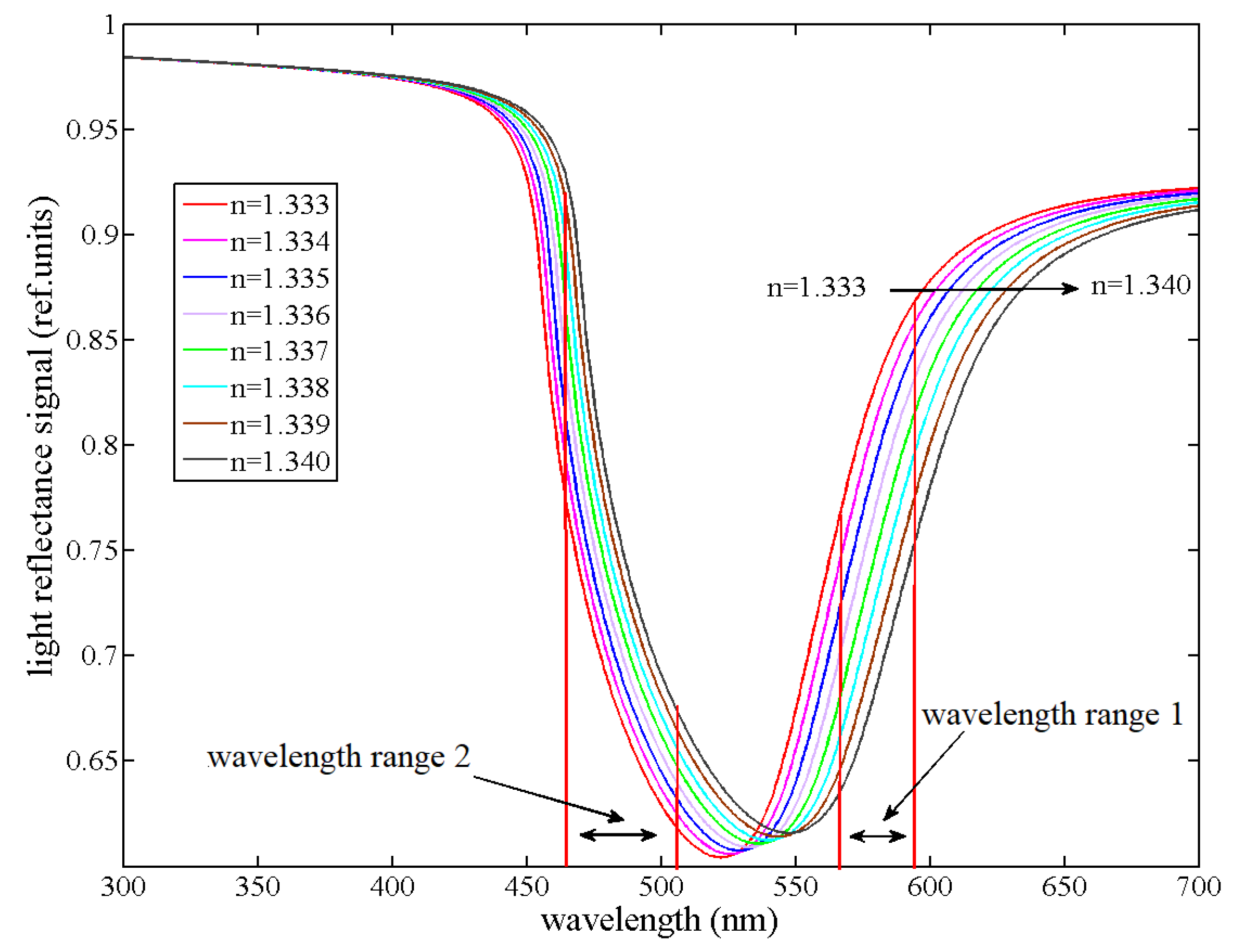
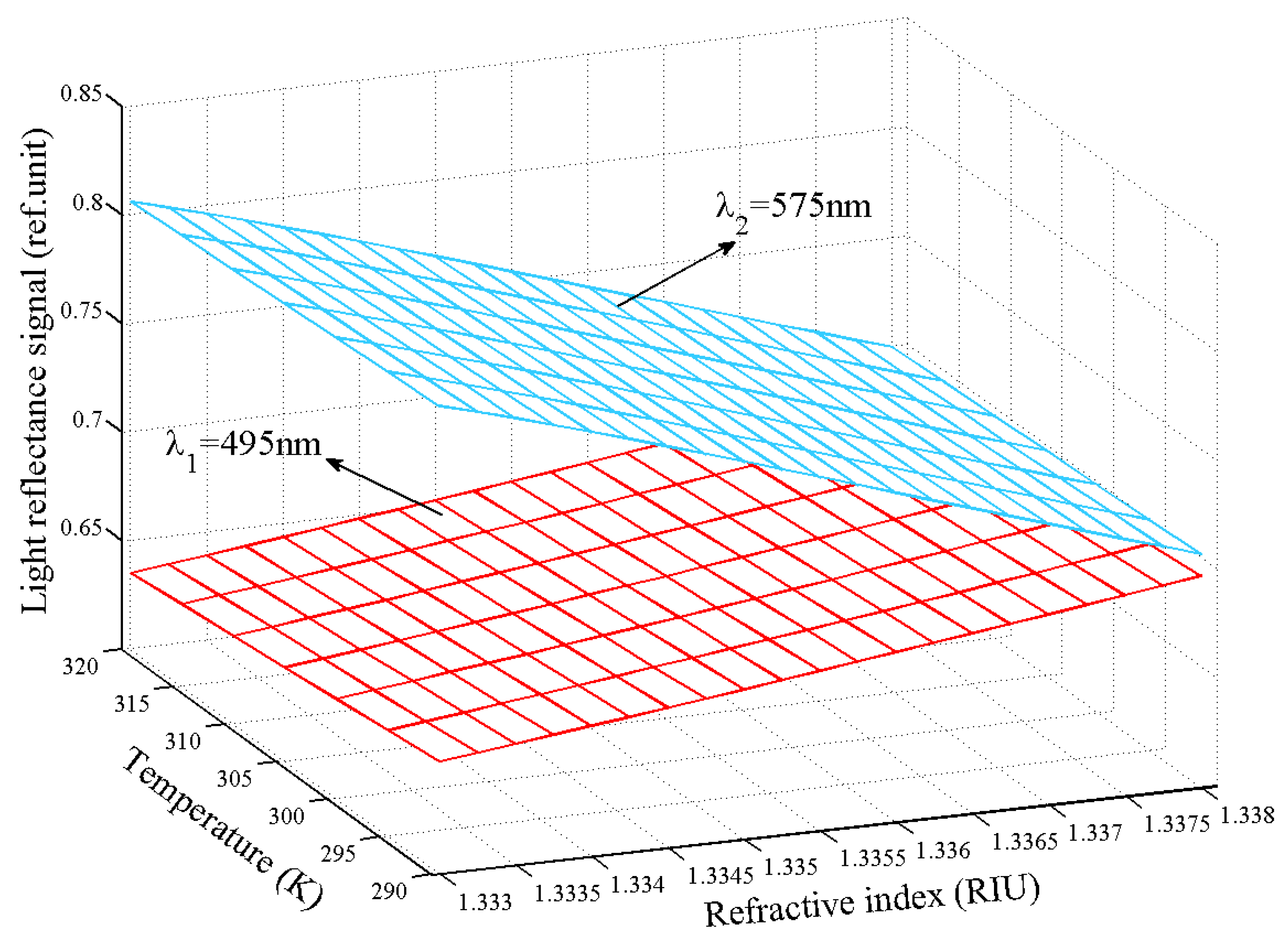
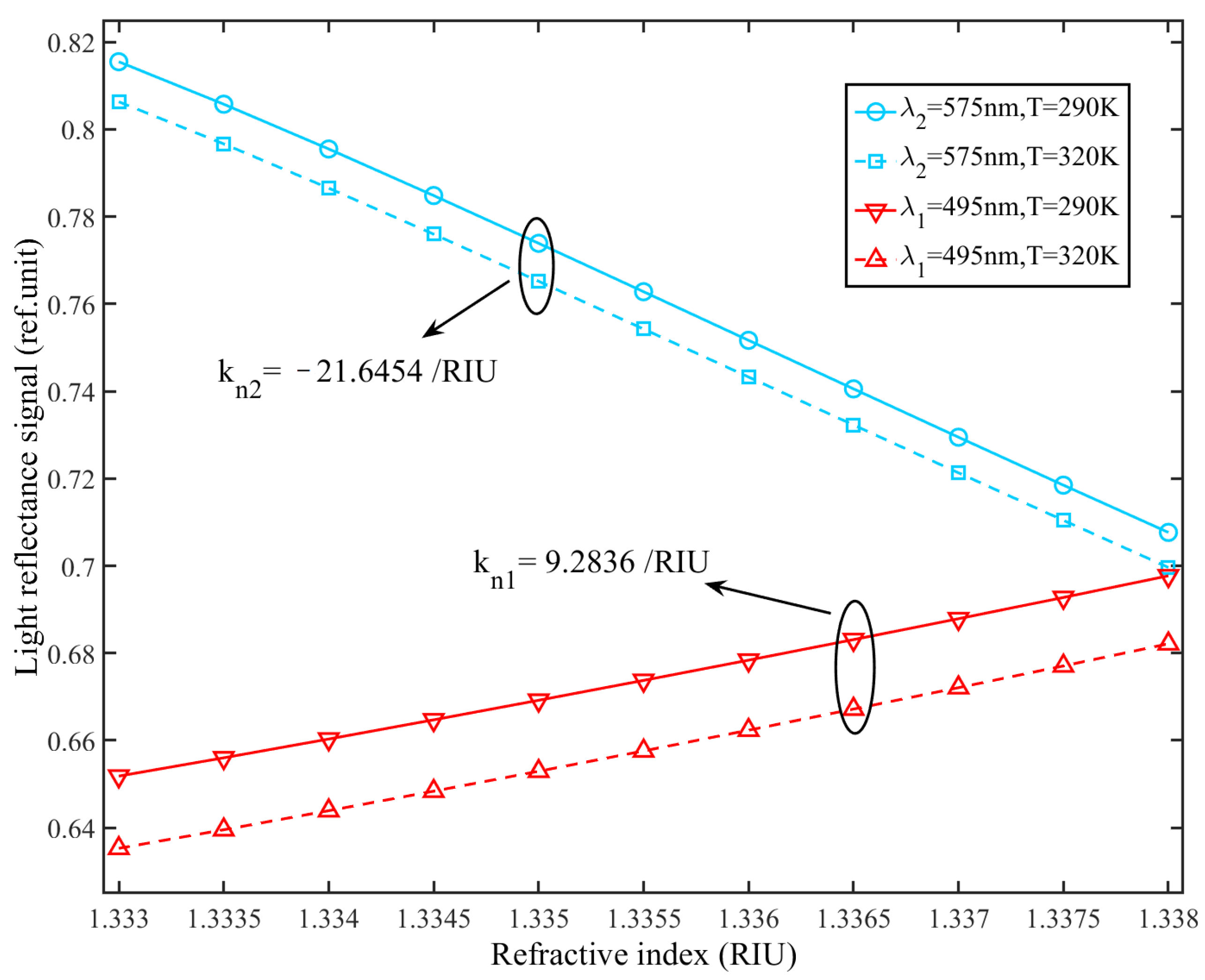
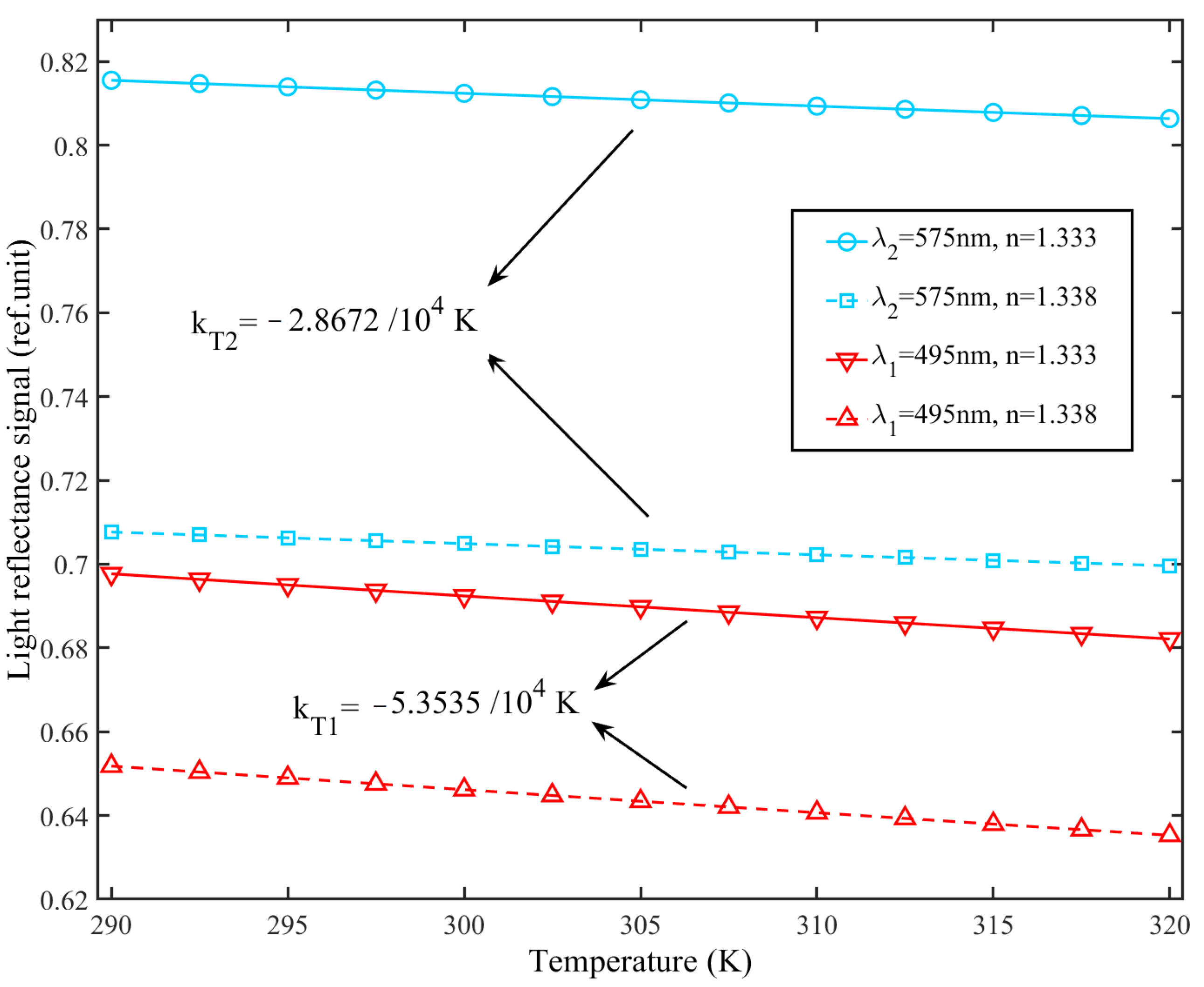
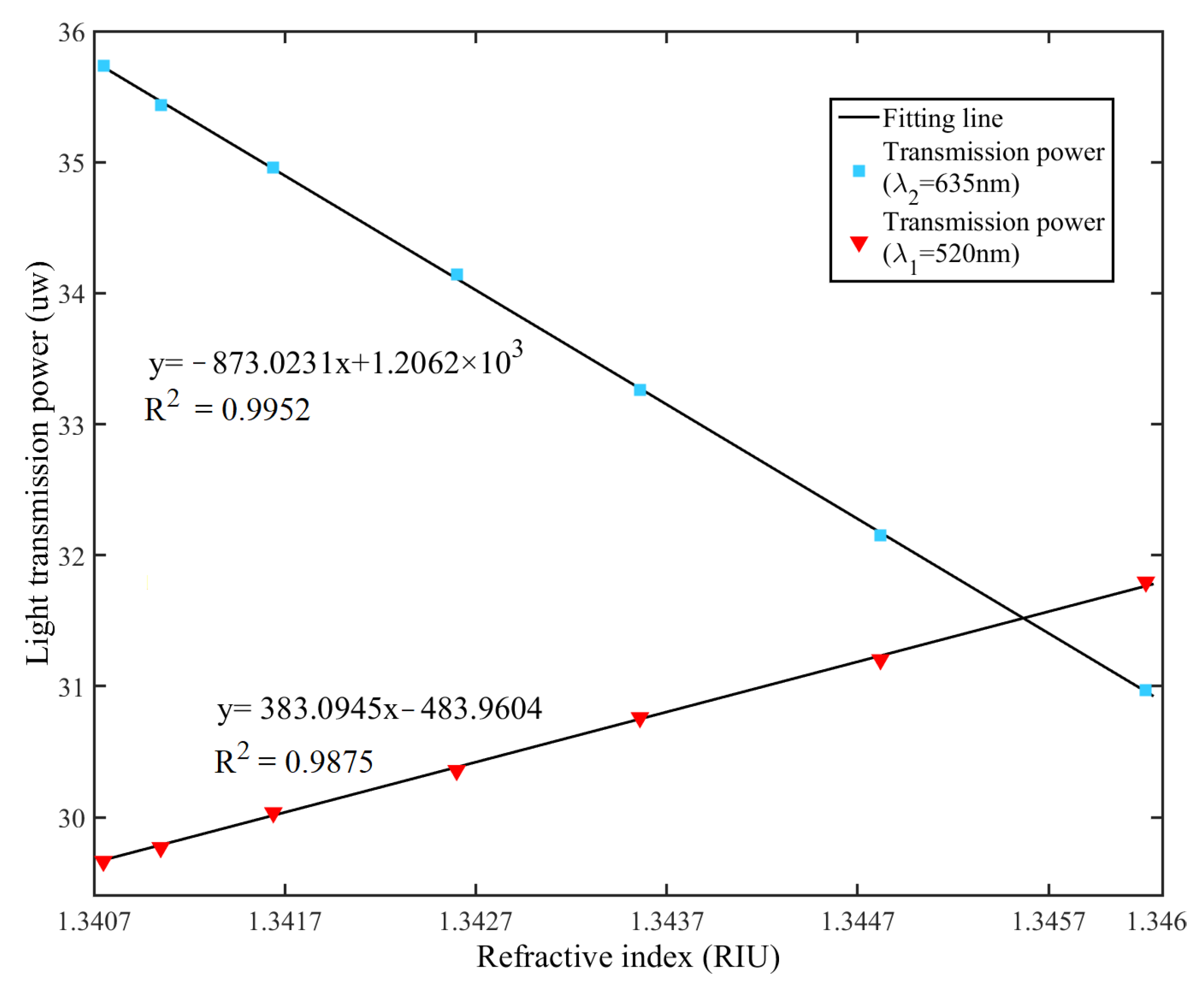
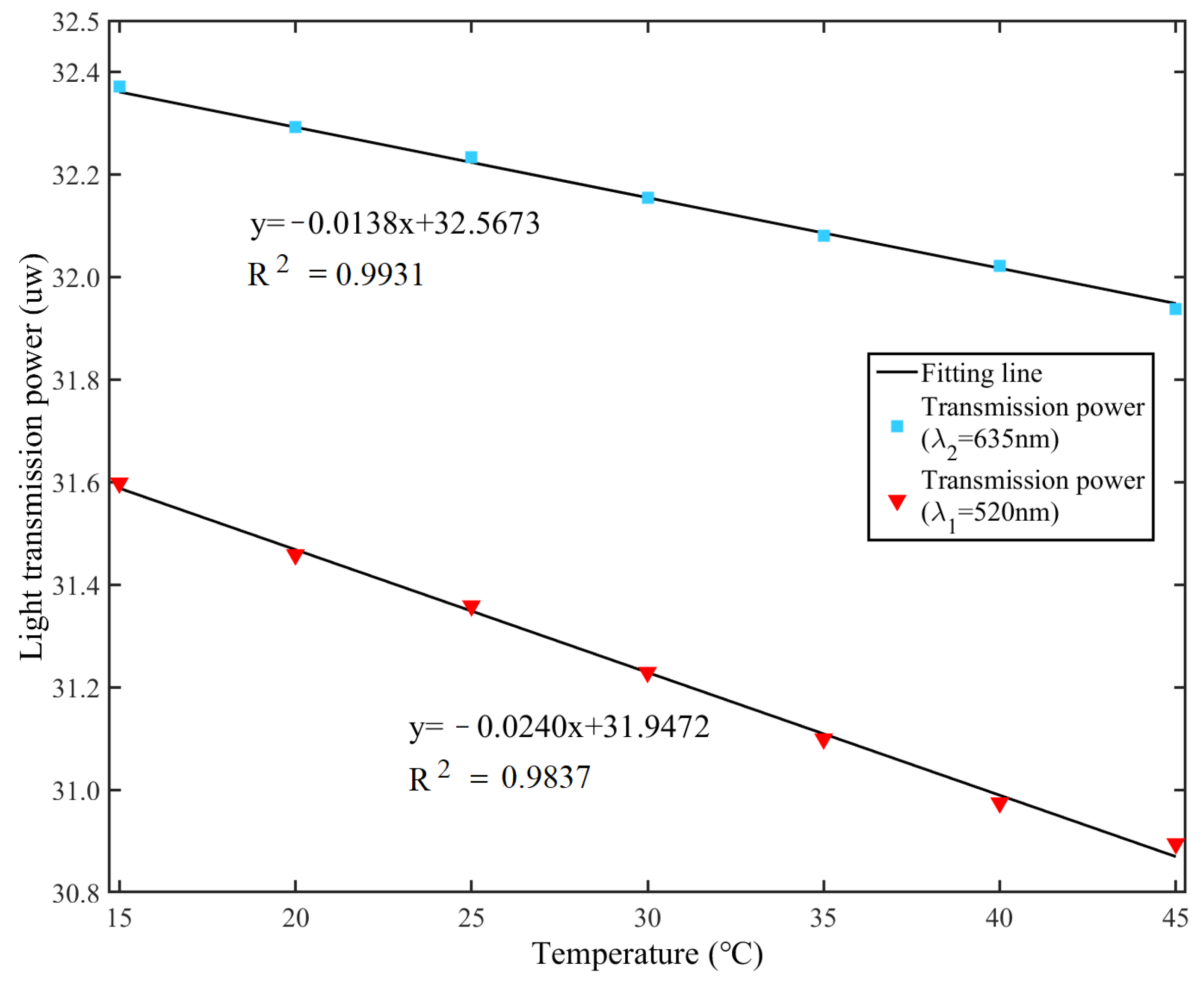
4. Experimental Results and Discussion

Based on the above-mentioned dual-wavelength method, the approach can be directly applied to the conventional fiber-optic SPR sensor. A proof-of-concept experiment is carried out with a typical transmission-based fiber-optic SPR sensor. The schematic of the transmission-based fiber-optic SPR is shown in Figure 8. Two laser diodes with the center wavelengths of 520 nm and 635 nm light up in turns. The light beams interflow into the two exiting directions through a semi-permeable mirror. One direction of the light is directly recorded by a photoelectric detector as the reference to eliminate the influence caused by the fluctuation of light source. The other one is the detecting light coupled into the optical fiber with the lens 3. The light passes through the SPR sensing probe portion and is detected with a fiber-optic power meter (PM20A, Thorlabs). A step index multimode fiber (core: 200 μm, 0.37NA) is used as the light transmission medium with cladding of 10 mm length removed. Then, the unclad fiber core is coated with gold film of a thickness of 50 nm using vacuum magnetic sputtering rotary technique.

The experimental platform can provide an exact measurement of transmission power variation caused by SPR sensing at the two detecting wavelengths. Different concentrations of aqueous NaCl solution are used as the analytes and confirm the RI with an Abel refractive index-measuring instrument in the experiment. The change of temperature is controlled by a hot plate. Therefore, a proof-of-concept experiment is carried out to demonstrate the capability of the proposed dual-wavelength method after the optical arrangement.

Figure 9 depicts the relationship between the output signal versus analyte RI when the temperature is fixed at 30 °C. Obviously, there is a significant linear relationship between output signal and the RI. With the RI changing from 1.3407 RIU to 1.3462 RIU, the signal at ${\lambda }_2=635$ nm decreases from 35.7258 uw to 30.9591 uw while the signal at ${\lambda }_1=520$ nm increases from 29.6735 uw to 31.7652 uw, corresponding to the slopes of −873.0231 uw/RIU and 383.0945 uw/RIU, respectively. Figure 10 shows the dual-wavelength signals’ variation versus temperature with the RI of 1.3448 RIU. With the increase in temperature, both of the output signals decrease slightly, resulting in the detectable slopes of −0.0240 uw/°C for $S\left({\lambda }_2\right)$ and $-0.0138$ uw/°C for $S\left({\lambda }_2\right)$, respectively. Due to the fitting lines measured in the calibration progress, the sensitivity matrix can be obtained with the linear coefficients. Therefore, with the proposed dual-wavelength technique and the inverse of linear sensitivity matrix, both the RI and temperature variations can be measured as:

$$\left(\begin{array}{c}\Delta n\\ \Delta T\end{array}\right)=K^{-1}\left(\begin{array}{c}\Delta S\left({\lambda }_1\right)\\ \Delta S\left({\lambda }_2\right)\end{array}\right)=\left(\begin{array}{cc}5.2593& -9.1466\\ -33.2716& -14.6001\end{array}\right)\left(\begin{array}{c}\Delta S\left({\lambda }_1\right)\\ \Delta S\left({\lambda }_2\right)\end{array}\right)$$

(25)

Here, $\Delta n$ and $\Delta T$ are the RI variation and temperature change of the analyte in units of ${10}^{-4}$ RIU and °C. $\Delta S\left({\lambda }_1\right)$ and $\Delta S\left({\lambda }_2\right)$ are the variations of defined output signals at ${\lambda }_1=520$ nm and ${\lambda }_2=635$ nm, respectively.

For the experimental setup used to verify the new technique, the sensor works in the intensity-interrogation mode. The detection limit is dependent on the composite resolutions of the fiber intensity detector, metal thickness, and RI detecting range. In general, a conventional SPR sensor based on multimode fiber has the RI resolutions of $7.69\times {10}^{-5}$ RIU with the wavelength sensitivity of 2600 nm/RIU and spectrometer resolutions of 0.2 nm [41]. Compared to the traditional multimode fiber SPR sensor, our proposed detecting method using two fixed wavelengths can improve the resolution and signal-to-noise ratio of measurements.

5. Conclusions

In this paper, we analyze the temperature effect on the performance of fiber-optic SPR sensors in theory. Based on theoretical analysis, a novel dual-wavelength method is presented to simultaneously measure the changes of RI and temperature. The detailed theoretical calculation is carried out to analyze the temperature effects on the performance of the SPR-based fiber-optic sensor. We then experimentally demonstrate the effectiveness and capability of the proposed dual-wavelength technique. The proof-of-concept experiment arrangement is as simple and robust as the conventional single-channel fiber-optic SPR sensor. The dual-wavelength technique is practical and convenient for various applications, which makes full use of the signals at two fixed wavelengths without need of extra sensing structure design. With the dual-wavelength technique, the RI change can be distinguished from the temperature interference. Therefore, the proposed dual-wavelength technique may further extend the potential of the fiber-optic SPR sensor and pave a way to optimize the performance against temperature interference.