Temporal Convolution Network Based Joint Optimization of Acoustic-to-Articulatory Inversion
Abstract
:1. Introduction
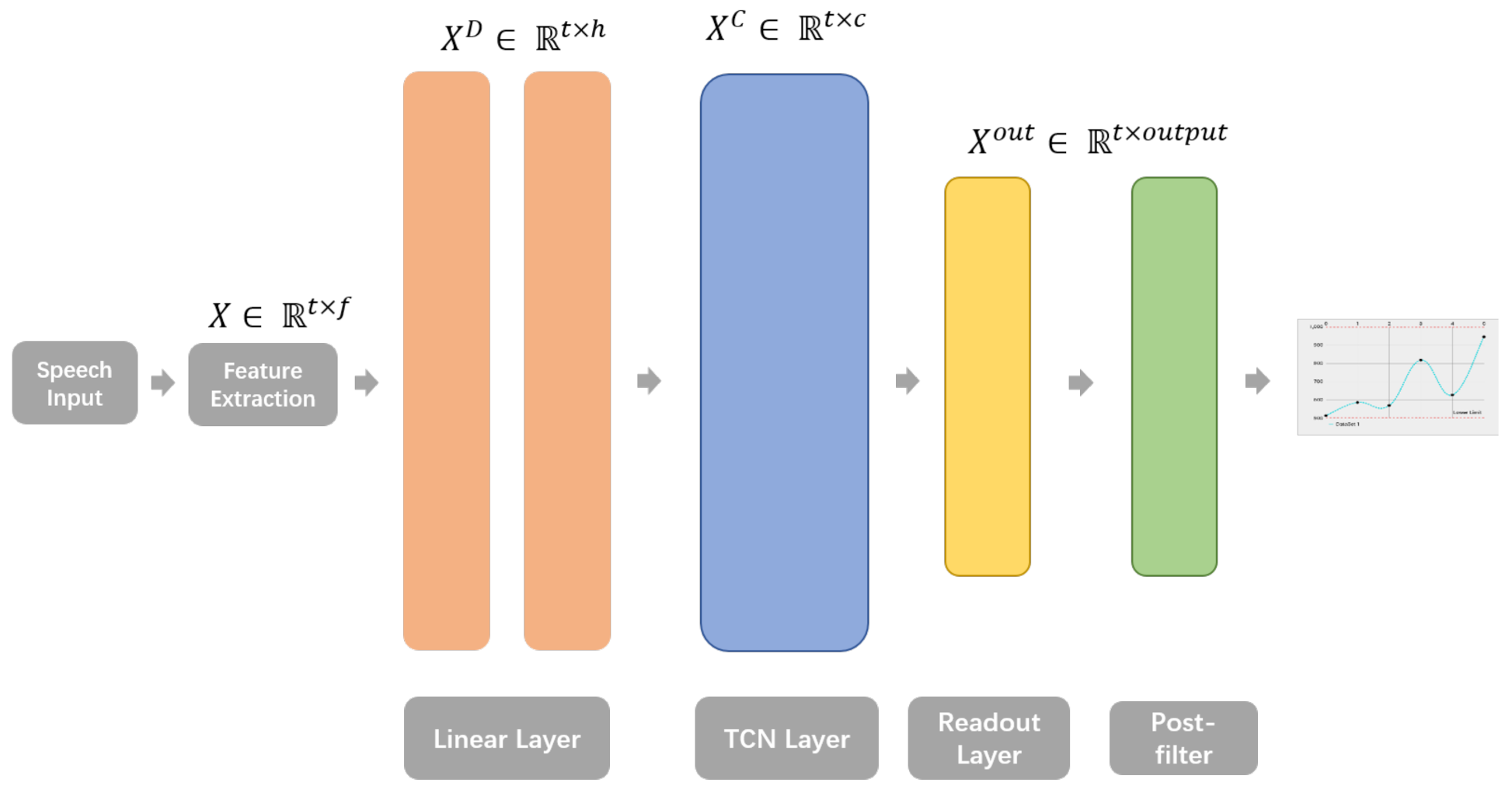
2. Methods
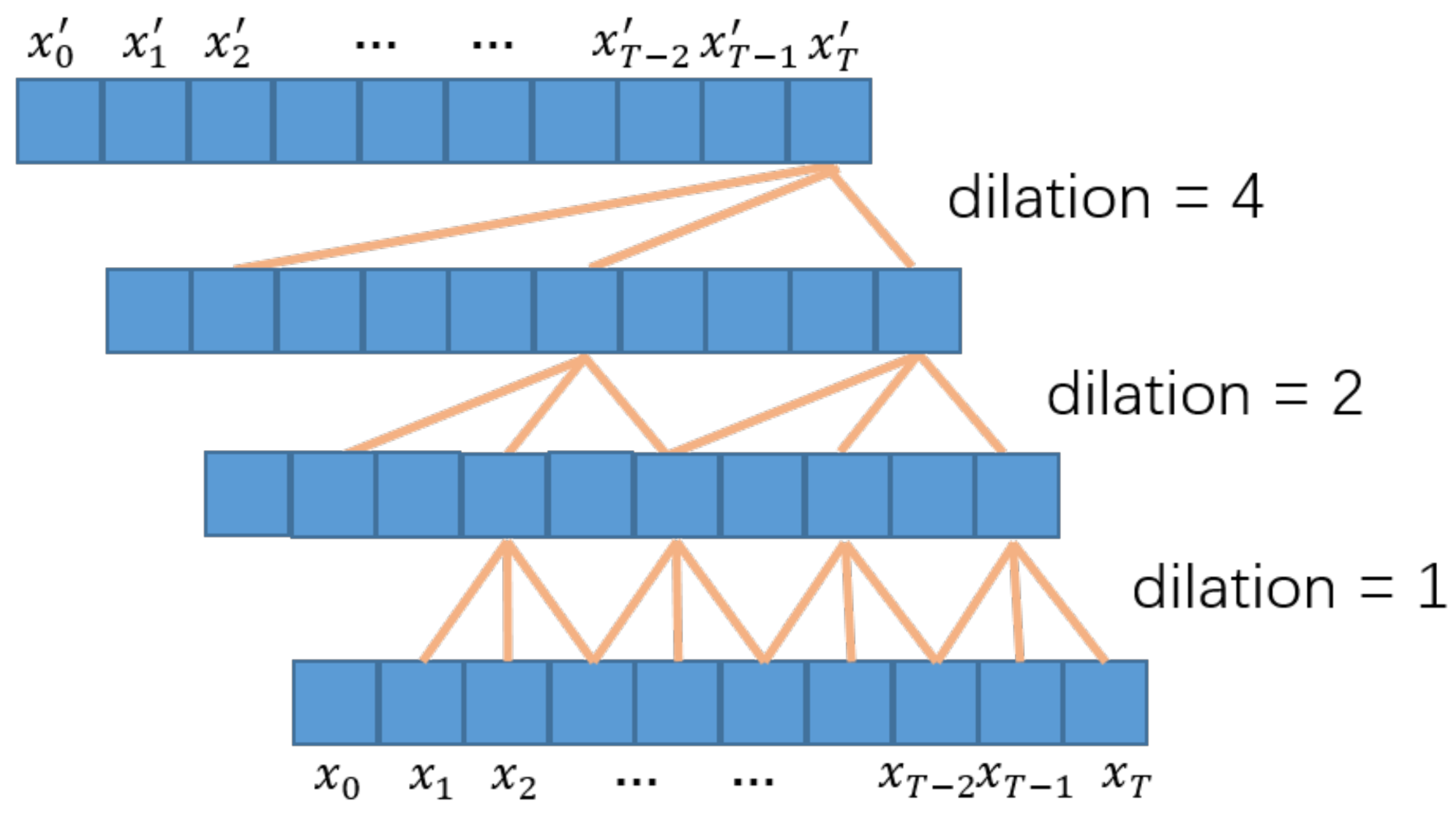
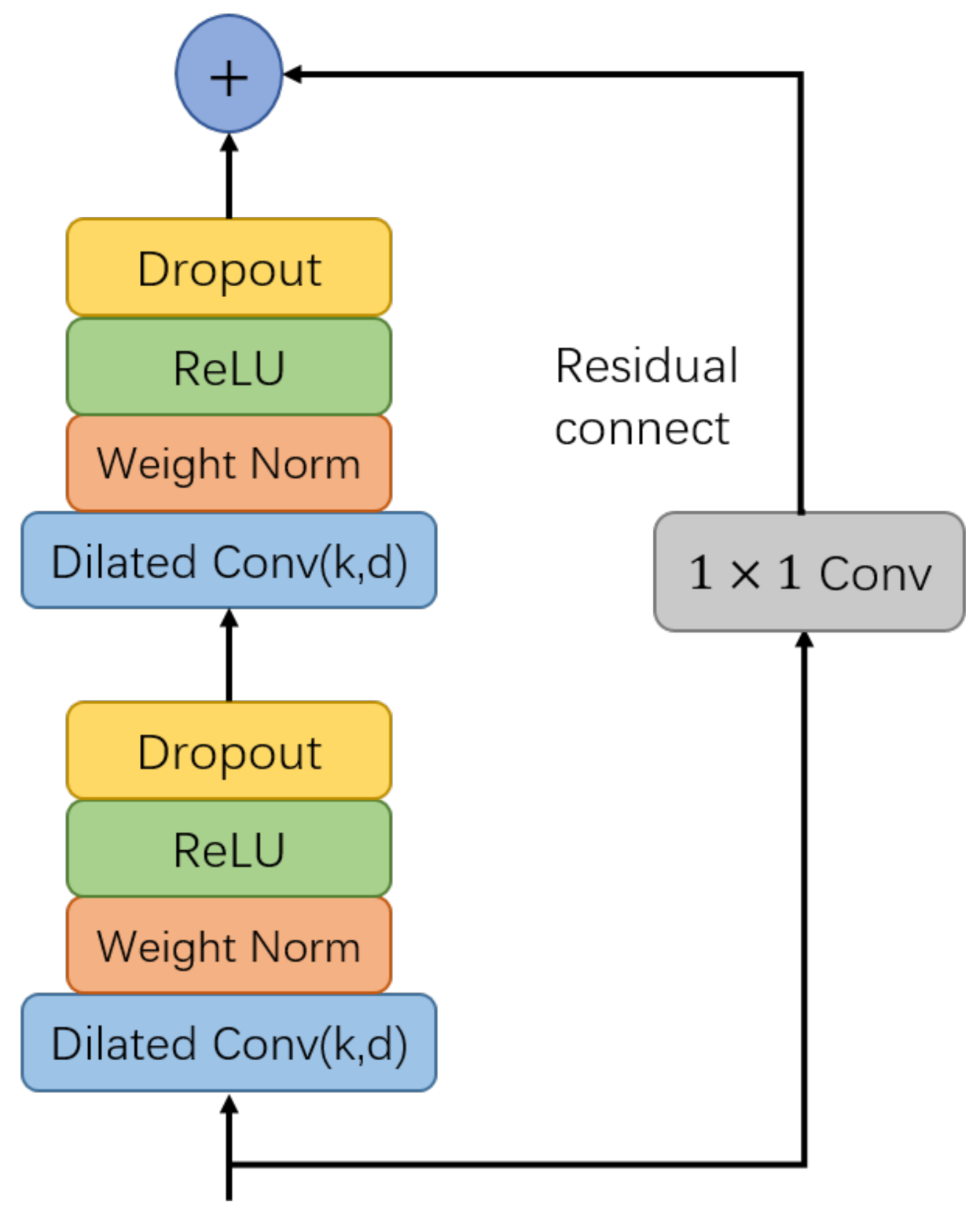
2.1. Temporal Convolution Network
2.2. Joint Optimization Target Fuction
3. Dataset
3.1. Dataset Description
3.2. Articulatory Features
3.3. Vocal Tract Variables
4. Experimental Setup
4.1. Feature Extraction
4.2. Model Parameters
5. Results
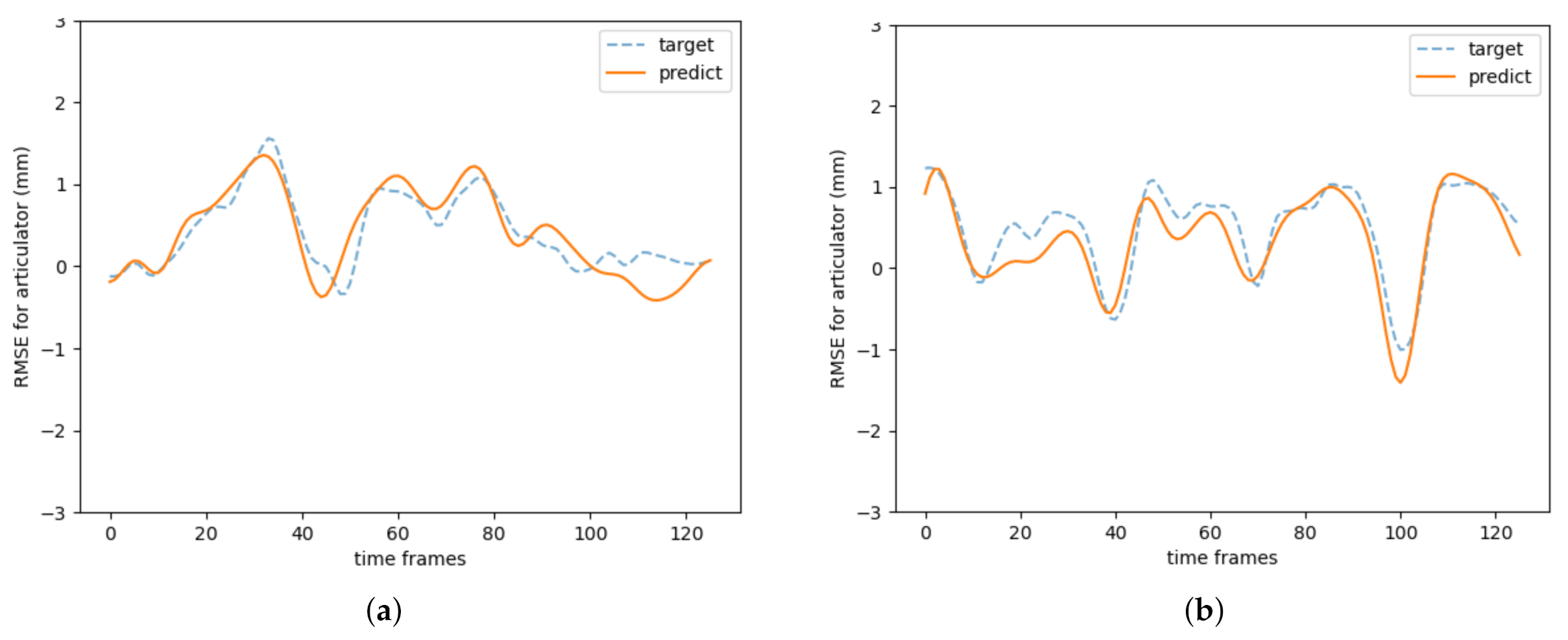
5.1. TCN Model vs. Bi-LSTM
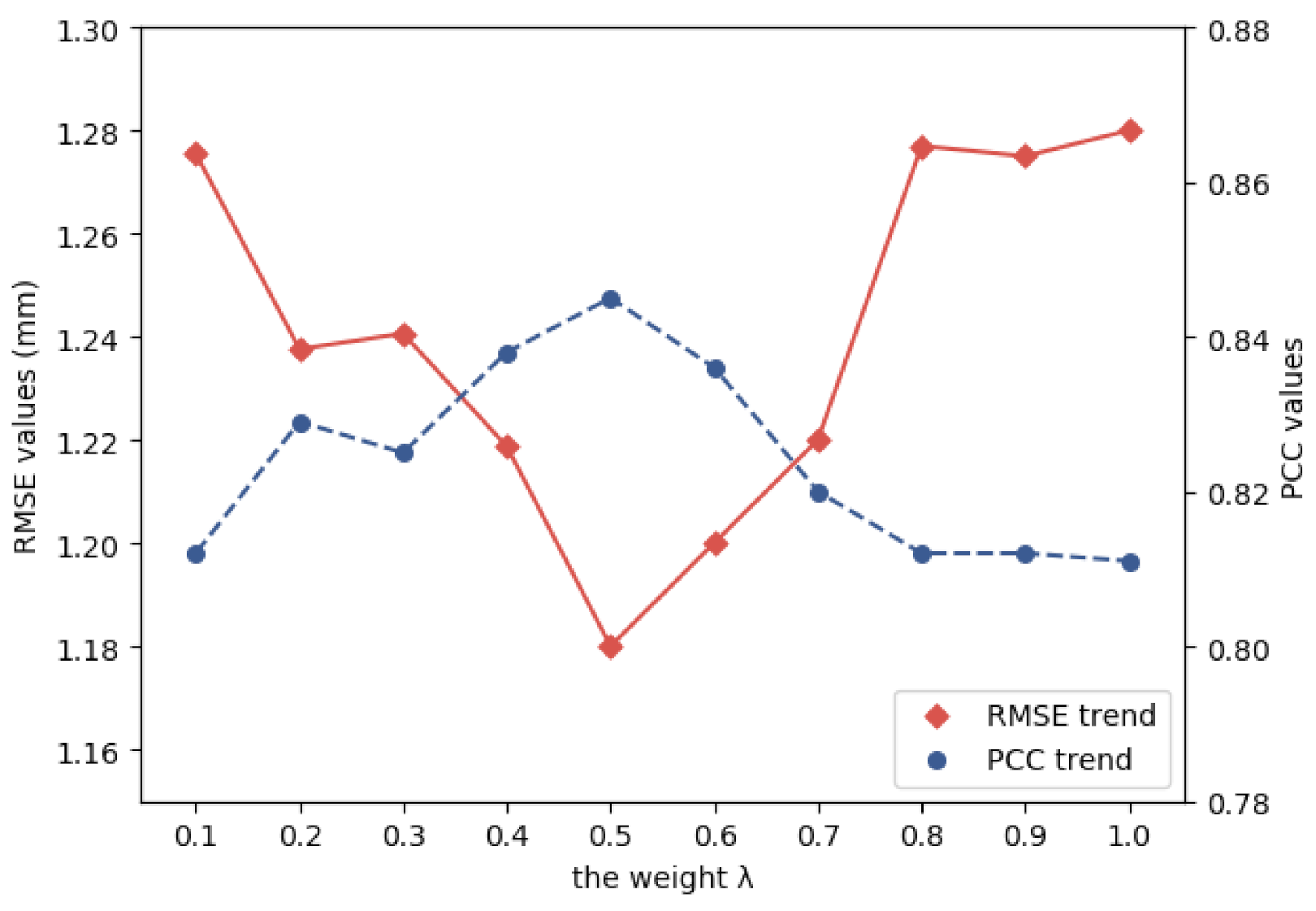
5.2. Weight Analysis of Target Function
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AAI | Acoustic-to-Articulatory Inversion |
| Bi-LSTM | Bi-directional Long Short Term Memory |
| TCN | Temporal Convolution Network |
| RMSE | Root Mean Square Error |
| PCC | Pearson Correlation Coefficient |
| ASR | Automatic Speech Recognition |
| CALL | Computer-Aided Language Learning |
| EMA | Electro-Magnetic Articulography |
| rtMRI | real-time Magnetic Resonance Imaging |
| GMM | Gaussian Mixture Model |
| HMM | Hidden Markov Model |
| DNN | Deep Neural Networks |
| MDN | Mixture Density Networks |
| RNN | Recurrent Neural Networks |
| CNN | Convolution Neural Networks |
| MFCC | Mel-Frequency Cepstral Coefficients |
References
- Qin, C.; Carreira-Perpiñán, M.Á. An empirical investigation of the nonuniqueness in the acoustic-to-articulatory mapping. In Proceedings of the Eighth Annual Conference of the International Speech Communication Association, Antwerp, Belgium, 27–31 August 2007. [Google Scholar]
- Kirchhoff, K.; Fink, G.A.; Sagerer, G. Combining acoustic and articulatory feature information for robust speech recognition. Speech Commun. 2002, 37, 303–319. [Google Scholar] [CrossRef]
- Mitra, V.; Sivaraman, G.; Bartels, C.; Nam, H.; Wang, W.; Espy-Wilson, C.; Vergyri, D.; Franco, H. Joint modeling of articulatory and acoustic spaces for continuous speech recognition tasks. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 5205–5209. [Google Scholar]
- Yu, J.; Markov, K.; Matsui, T. Articulatory and spectrum information fusion based on deep recurrent neural networks. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 742–752. [Google Scholar] [CrossRef]
- Mitra, V.; Sivaraman, G.; Nam, H.; Espy-Wilson, C.; Saltzman, E.; Tiede, M. Hybrid convolutional neural networks for articulatory and acoustic information based speech recognition. Speech Commun. 2017, 89, 103–112. [Google Scholar] [CrossRef]
- Richmond, K.; Ling, Z.; Yamagishi, J. The use of articulatory movement data in speech synthesis applications: An overview—Application of articulatory movements using machine learning algorithms. Acoust. Sci. Technol. 2015, 36, 467–477. [Google Scholar] [CrossRef] [Green Version]
- Cao, B.; Kim, M.J.; van Santen, J.P.H.; Mau, T.; Wang, J. Integrating Articulatory Information in Deep Learning-Based Text-to-Speech Synthesis. In Proceedings of the Interspeech 2017, Stockholm, Sweden, 20–24 August 2017; pp. 254–258. [Google Scholar]
- Aryal, S.; Gutierrez-Osuna, R. Accent conversion through cross-speaker articulatory synthesis. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 7694–7698. [Google Scholar]
- Yılmaz, E.; Mitra, V.; Sivaraman, G.; Franco, H. Articulatory and bottleneck features for speaker-independent ASR of dysarthric speech. Comput. Speech Lang. 2019, 58, 319–334. [Google Scholar] [CrossRef] [Green Version]
- Hahm, S.; Wang, J. Parkinson’s condition estimation using speech acoustic and inversely mapped articulatory data. In Proceedings of the Sixteenth Annual Conference of the International Speech Communication Association, Dresden, Germany, 6–10 September 2015. [Google Scholar]
- Jones, D.K. Development of Kinematic Templates for Automatic Pronunciation Assessment Using Acoustic-to-Articulatory Inversion; Marquette University: Milwaukee, WI, USA, 2017. [Google Scholar]
- Lin, J.; Li, W.; Gao, Y.; Xie, Y.; Chen, N.F.; Siniscalchi, S.M.; Zhang, J.; Lee, C.-H. Improving Mandarin tone recognition based on DNN by combining acoustic and articulatory features using extended recognition networks. J. Signal Process. Syst. 2018, 90, 1077–1087. [Google Scholar] [CrossRef]
- Duan, R.; Kawahara, T.; Dantsuji, M.; Zhang, J. Articulatory modeling for pronunciation error detection without non-native training data based on DNN transfer learning. IEICE Trans. Inf. Syst. 2017, 100, 2174–2182. [Google Scholar] [CrossRef] [Green Version]
- Tiede, M.; Espy-Wilson, C.Y.; Goldenberg, D.; Mitra, V.; Nam, H.; Sivaraman, G. Quantifying kinematic aspects of reduction in a contrasting rate production task. J. Acoust. Soc. Am. 2017, 141, 3580. [Google Scholar] [CrossRef]
- Westbury, J.R.; Turner, G.; Dembowski, J. X-ray Microbeam Speech Production Database User’s Handbook; Waisman Center on Mental Retardation and Human Development: Madison, WI, USA, 1994. [Google Scholar]
- Narayanan, S.; Nayak, K.; Lee, S.; Sethy, A.; Byrd, D. An approach to real-time magnetic resonance imaging for speech production. J. Acoust. Soc. Am. 2004, 115, 1771–1776. [Google Scholar] [CrossRef] [PubMed]
- Atal, B.S.; Chang, J.J.; Mathews, M.V.; Tukey, J.W. Inversion of articulatory-to-acoustic transformation in the vocal tract by a computer-sorting technique. J. Acoust. Soc. Am. 1978, 63, 1535–1555. [Google Scholar] [CrossRef] [PubMed]
- Dusan, S.; Deng, L. Acoustic-to-articulatory inversion using dynamical and phonological constraints. In Proceedings of the 5th Seminar on Speech Production, Kloster Seeon, Germany, 1–4 May 2000; pp. 237–240. [Google Scholar]
- Toda, T.; Black, A.; Tokuda, K. Acoustic-to-articulatory inversion mapping with Gaussian mixture model. In Proceedings of the Eighth International Conference on Spoken Language Processing, Jeju-si, Korea, 4–8 October 2004. [Google Scholar]
- Zhang, L.; Renals, S. Acoustic-articulatory modeling with the trajectory HMM. IEEE Signal Process. Lett. 2008, 15, 245–248. [Google Scholar] [CrossRef] [Green Version]
- Tobing, P.L.; Kameoka, H.; Toda, T. Deep acoustic-to-articulatory inversion mapping with latent trajectory modeling. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 1274–1277. [Google Scholar]
- Uria, B.; Murray, I.; Renals, S.; Richmond, K. Deep architectures for articulatory inversion. In Proceedings of the Thirteenth Annual Conference of the International Speech Communication Association, Portland, Oregon, 9–13 September 2012. [Google Scholar]
- Richmond, K. Trajectory mixture density networks with multiple mixtures for acoustic-articulatory inversion. In Proceedings of the International Conference on Nonlinear Speech Processing, Paris, France, 22–25 May 2007; pp. 263–272. [Google Scholar]
- Liu, P.; Yu, Q.; Wu, Z.; Kang, S.; Meng, H.; Cai, L. A deep recurrent approach for acoustic-to-articulatory inversion. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 4450–4454. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Parrot, M.; Millet, J.; Dunbar, E. Independent and Automatic Evaluation of Speaker-Independent Acoustic-to-Articulatory Reconstruction. In Proceedings of the Interspeech 2020, Shanghai, China, 25–29 October 2020. [Google Scholar]
- Sivaraman, G.; Mitra, V.; Nam, H.; Tiede, M.; Espy-Wilson, C. Unsupervised speaker adaptation for speaker independent acoustic to articulatory speech inversion. J. Acoust. Soc. Am. 2019, 146, 316–329. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, S.; Toutios, A.; Ramanarayanan, V.; Lammert, A.; Kim, J.; Lee, S.; Nayak, K.; Kim, Y.-C.; Zhu, Y.; Goldstein, L.; et al. Real-time magnetic resonance imaging and electromagnetic articulography database for speech production research (TC). J. Acoust. Soc. Am. 2014, 136, 1307–1311. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| RMSE (SD) | PCC | Params | |
|---|---|---|---|
| Bi-LSTM | 1.44 (0.46) mm | 0.770 | 11.0 M |
| TCN-512channel | 1.09 (0.32) mm | 0.873 | 9.9 M |
| TCN-256channel | 1.18 (0.40) mm | 0.845 | 2.5 M |
| TCN-128channel | 1.30 (0.46) mm | 0.801 | 0.6 M |
| Weight | RMSE | PCC | Weight | RMSE | PCC |
|---|---|---|---|---|---|
| 0.1 | 1.276 | 0.812 | 0.6 | 1.200 | 0.836 |
| 0.2 | 1.238 | 0.829 | 0.7 | 1.220 | 0.820 |
| 0.3 | 1.241 | 0.825 | 0.8 | 1.285 | 0.812 |
| 0.4 | 1.219 | 0.838 | 0.9 | 1.275 | 0.812 |
| 0.5 | 1.180 | 0.845 | 1 | 1.280 | 0.811 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, G.; Huang, Z.; Wang, L.; Zhang, P. Temporal Convolution Network Based Joint Optimization of Acoustic-to-Articulatory Inversion. Appl. Sci. 2021, 11, 9056. https://doi.org/10.3390/app11199056
Sun G, Huang Z, Wang L, Zhang P. Temporal Convolution Network Based Joint Optimization of Acoustic-to-Articulatory Inversion. Applied Sciences. 2021; 11(19):9056. https://doi.org/10.3390/app11199056
Chicago/Turabian StyleSun, Guolun, Zhihua Huang, Li Wang, and Pengyuan Zhang. 2021. "Temporal Convolution Network Based Joint Optimization of Acoustic-to-Articulatory Inversion" Applied Sciences 11, no. 19: 9056. https://doi.org/10.3390/app11199056
APA StyleSun, G., Huang, Z., Wang, L., & Zhang, P. (2021). Temporal Convolution Network Based Joint Optimization of Acoustic-to-Articulatory Inversion. Applied Sciences, 11(19), 9056. https://doi.org/10.3390/app11199056






