Elastic Properties Estimation of Masonry Walls through the Propagation of Elastic Waves: An Experimental Investigation
Abstract
:1. Introduction
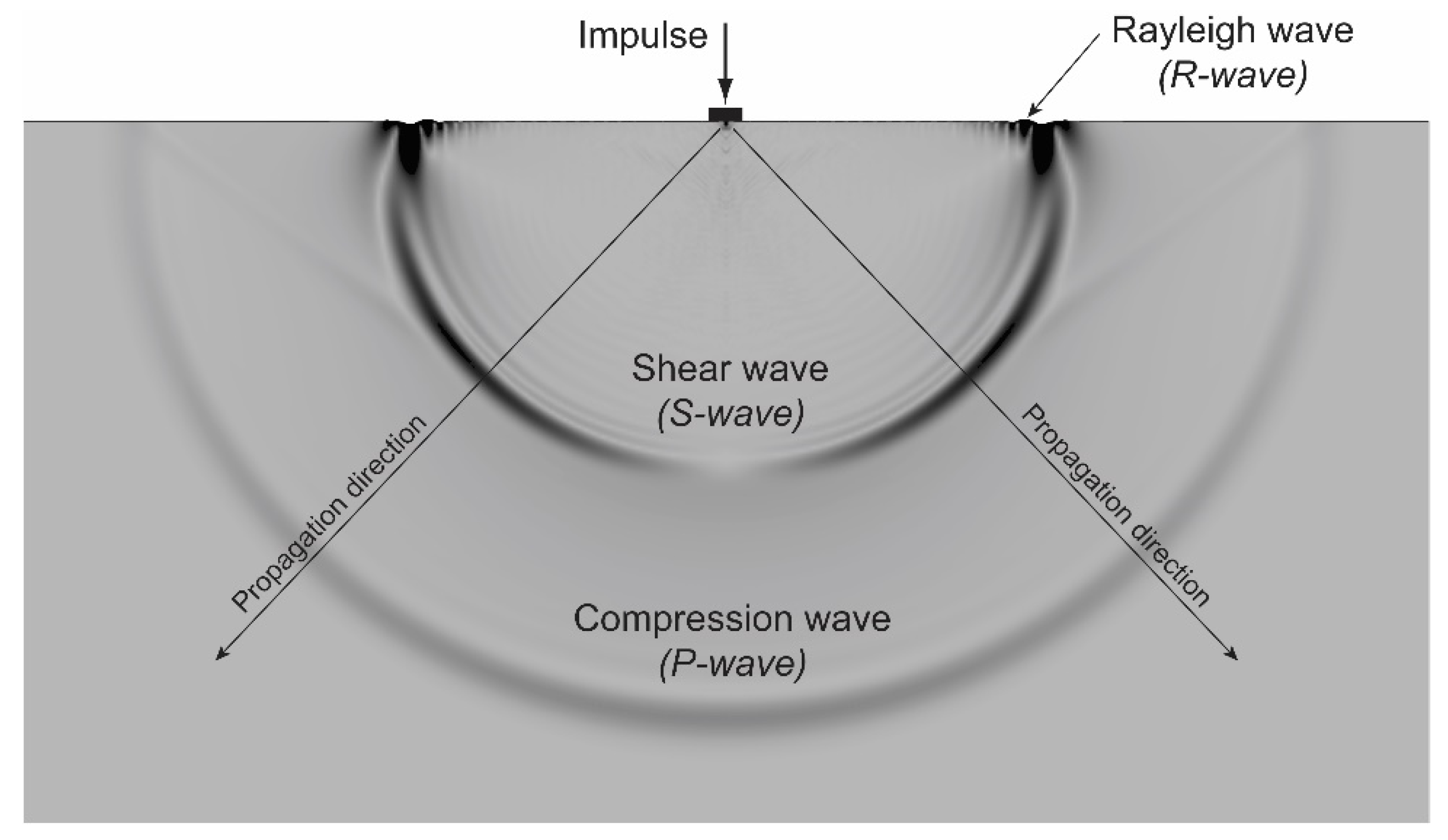
2. Waves Propagation in Isotropic Homogeneous Elastic Media. Basic Theoretical Concepts
3. Materials and Methods
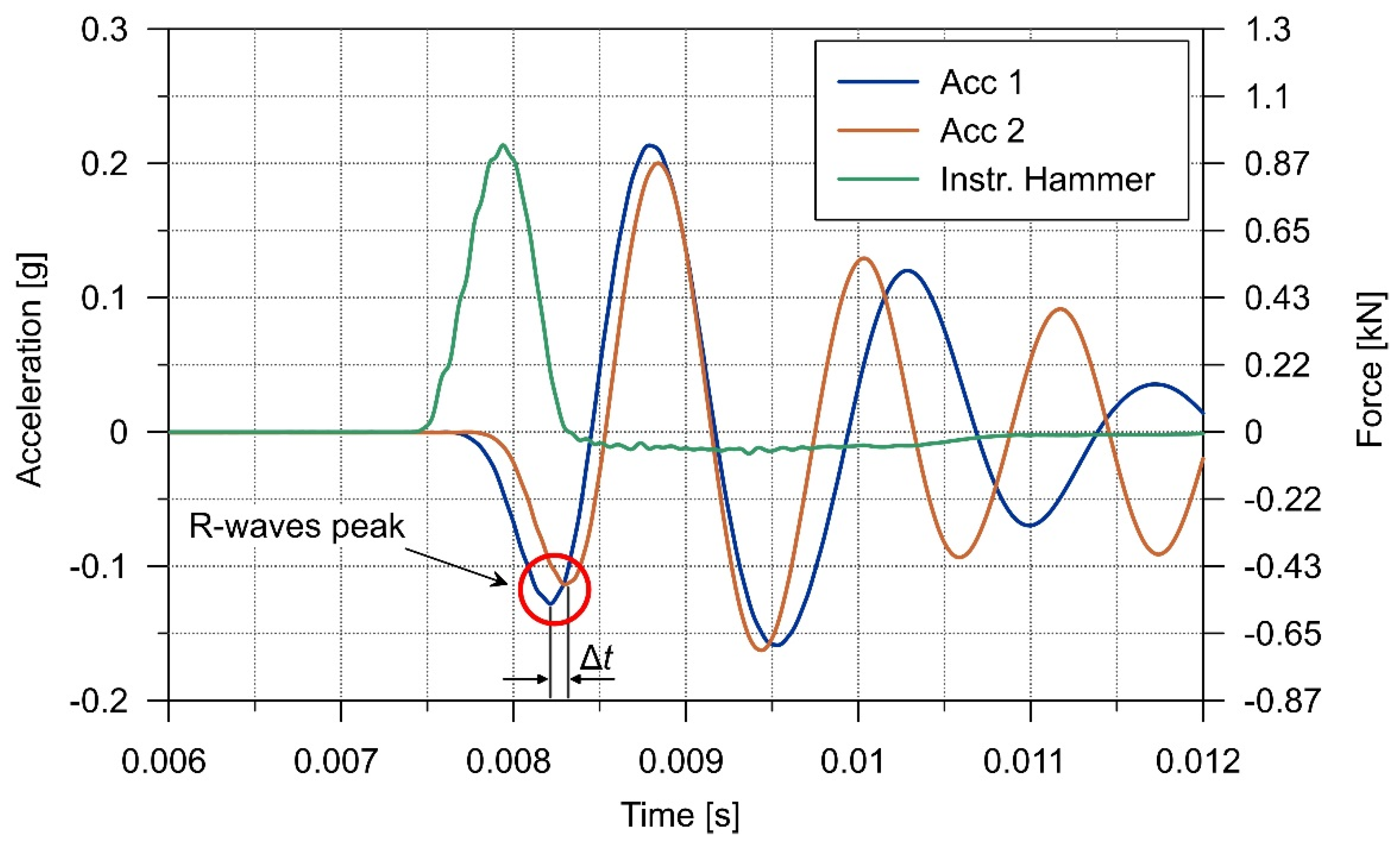
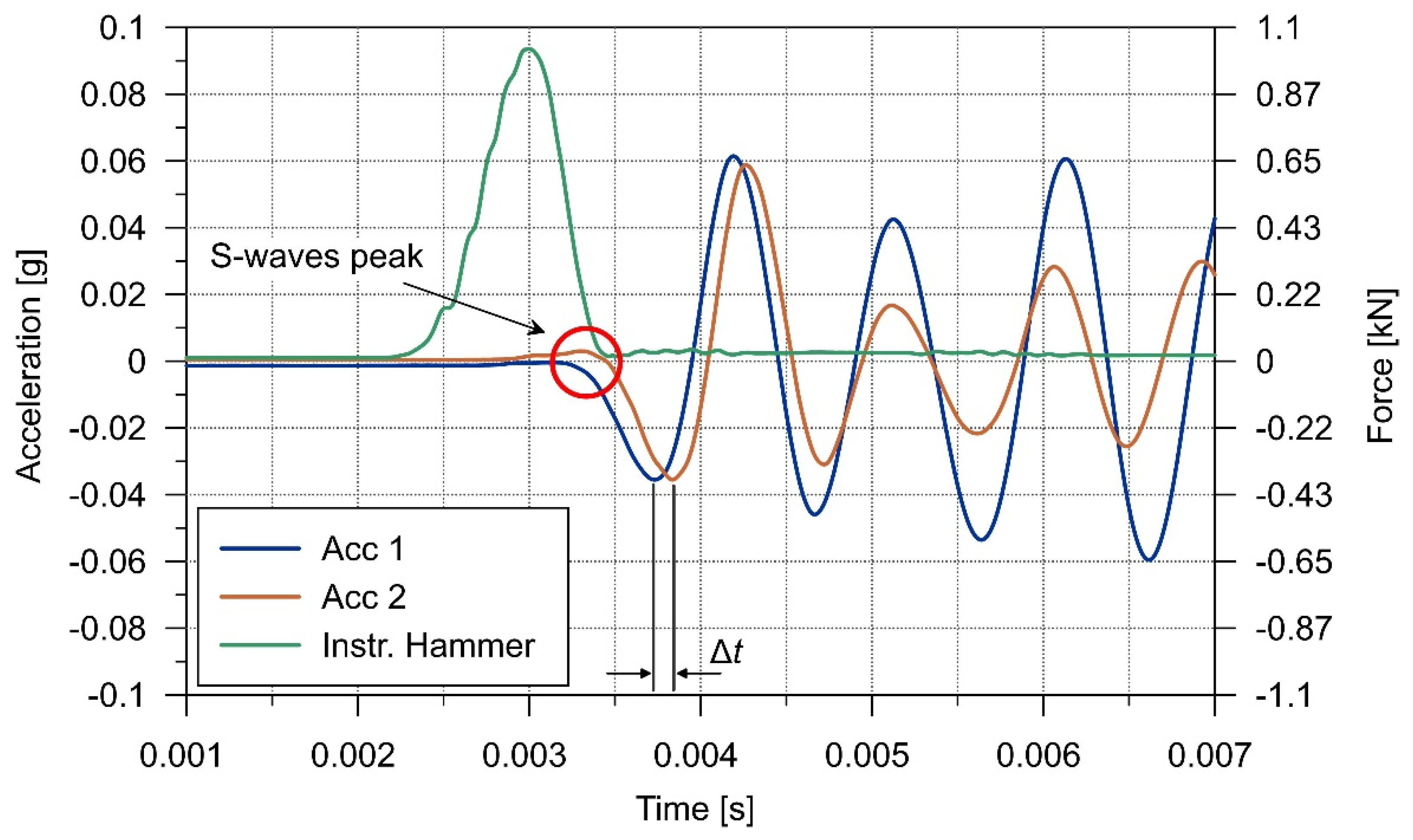
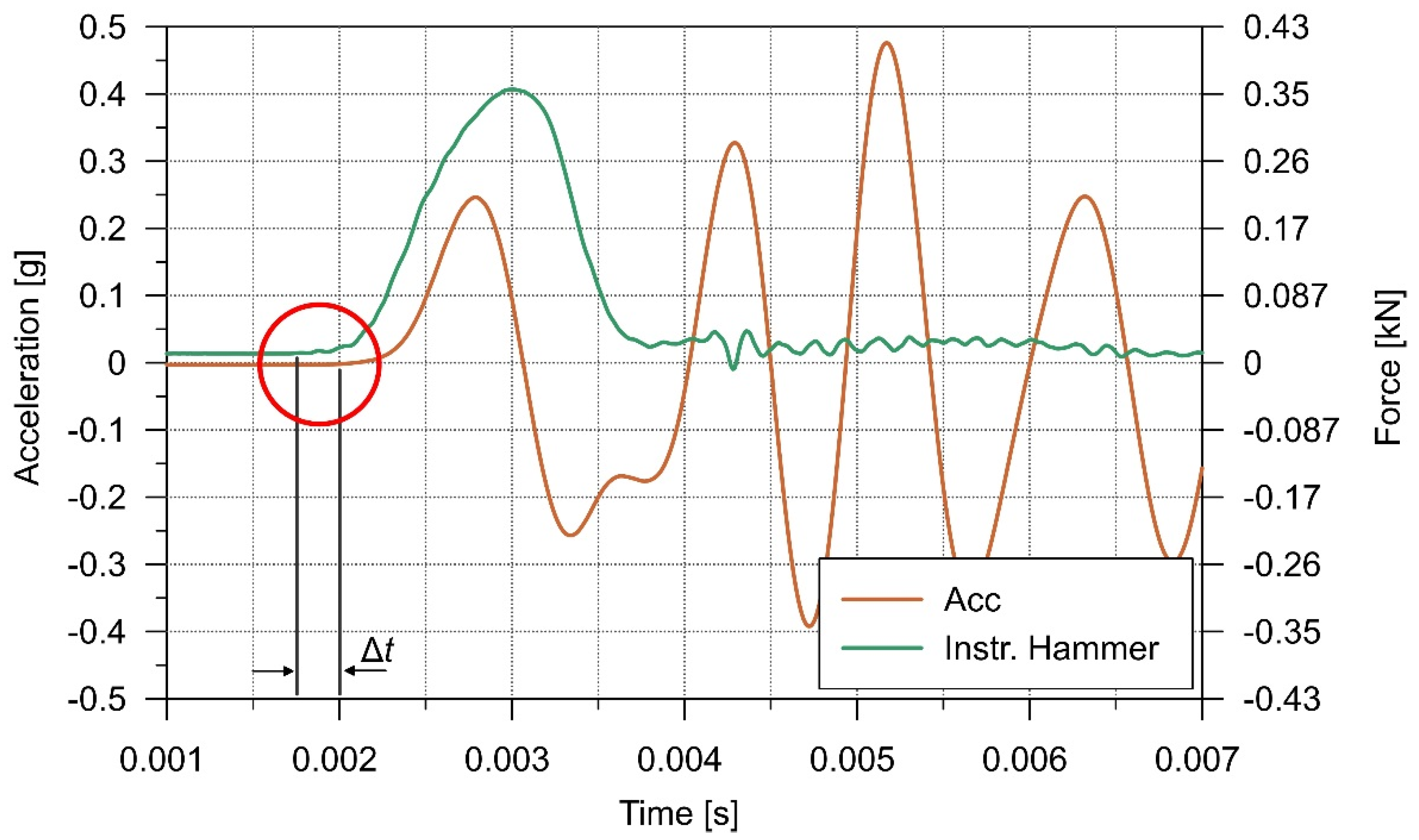
3.1. Experimental Setup and Test Procedure
3.2. Preliminary Tests on Concrete Materials
4. Estimation of Elastic Parameters on Masonry Panel
4.1. Experimental Tests Layout
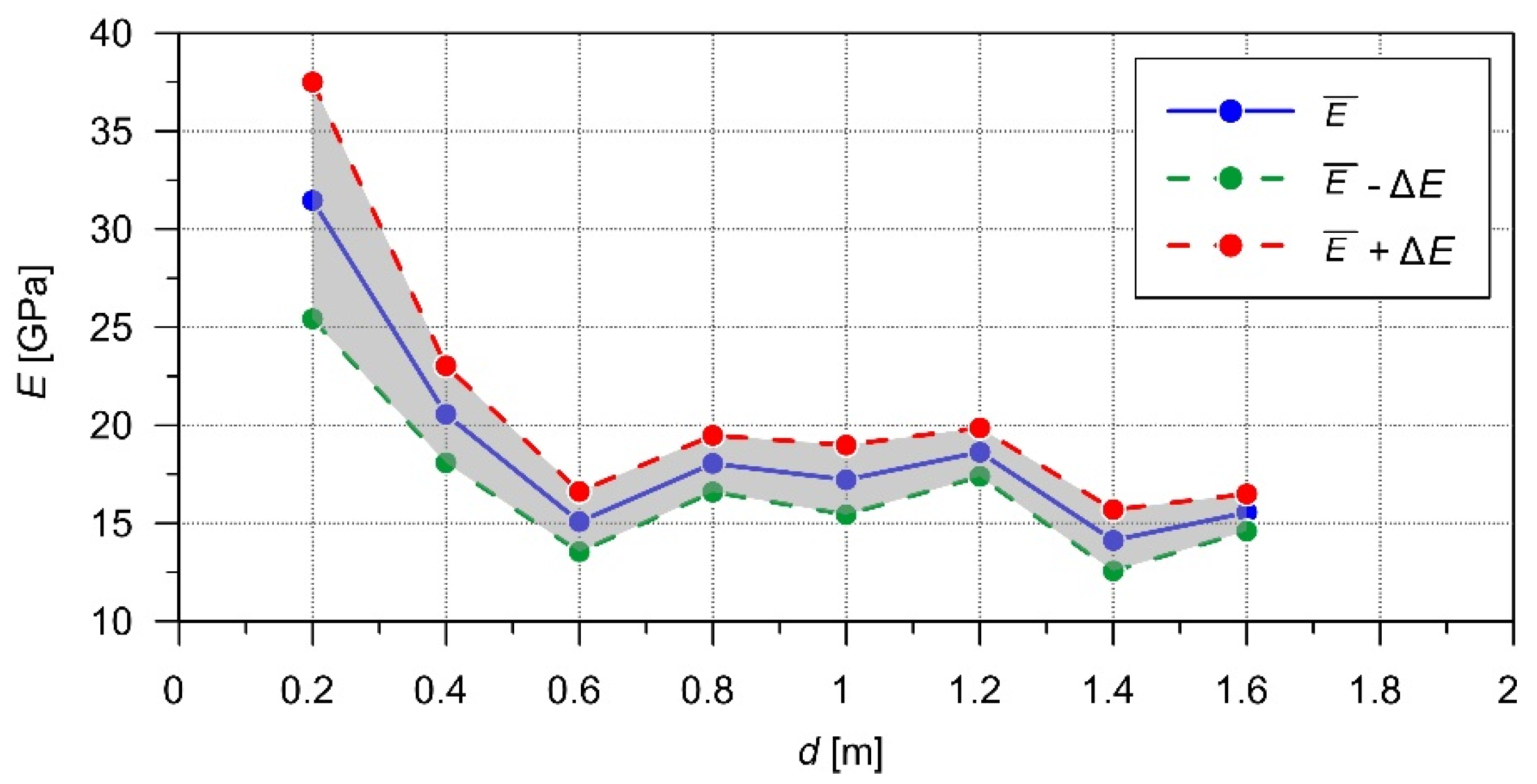
4.2. Analysis of the Results
5. Final Remarks
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cavalagli, N.; Kita, A.; Castaldo, V.L.; Pisello, A.L.; Ubertini, F. Hierarchical environmental risk mapping of material degradation in historic masonry buildings: An integrated approach considering climate change and structural damage. Constr. Build. Mater. 2019, 215, 998–1014. [Google Scholar] [CrossRef]
- Hao, L.; Herrera-Avellanosa, D.; Del Pero, C.; Troi, A. What are the implications of climate change for retrofitted historic buildings? A literature review. Sustainability 2020, 12, 7557. [Google Scholar] [CrossRef]
- Sesana, E.; Gagnon, A.S.; Ciantelli, C.; Cassar, J.; Hughes, J.J. Climate change impacts on cultural heritage: A literature review. Wiley Interdiscip. Rev. Clim. Chang. 2021, 12, e710. [Google Scholar] [CrossRef]
- Livingston, R.A. Nondestructive Testing of Historic Structures. Arch. Mus. Inform. 1999, 13, 249–271. [Google Scholar] [CrossRef]
- Bosiljkov, V.; Uranjek, M.; Žarnić, R.; Bokan-Bosiljkov, V. An integrated diagnostic approach for the assessment of historic masonry structures. J. Cult. Herit. 2010, 11, 239–249. [Google Scholar] [CrossRef]
- Uranjek, M.; Bosiljkov, V.; Žarnić, R.; Bokan-Bosiljkov, V. In situ tests and seismic assessment of a stone-masonry building. Mater. Struct. Mater. Constr. 2012, 45, 861–879. [Google Scholar] [CrossRef]
- Gil, E.; Mas, A.; Lerma, C.; Torner, M.E.; Vercher, J. Non-destructive Techniques Methodologies for the Detection of Ancient Structures under Heritage Buildings. Int. J. Archit. Herit. 2021, 15, 1457–1473. [Google Scholar] [CrossRef]
- Milani, G.; Esquivel, Y.W.; Lourenço, P.B.; Riveiro, B.; Oliveira, D.V. Characterization of the response of quasi-periodic masonry: Geometrical investigation, homogenization and application to the Guimarães castle, Portugal. Eng. Struct. 2013, 56, 621–641. [Google Scholar] [CrossRef] [Green Version]
- Jasiński, R.; Drobiec, Ł.; Mazur, W. Validation of Selected non-destructive methods for determining the compressive strength of masonry units made of autoclaved aerated concrete. Materials 2019, 12, 389. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Aparicio, L.J.; Bautista-De Castro, Á.; Conde, B.; Carrasco, P.; Ramos, L.F. Non-destructive means and methods for structural diagnosis of masonry arch bridges. Autom. Constr. 2019, 104, 360–382. [Google Scholar] [CrossRef]
- Biscarini, C.; Catapano, I.; Cavalagli, N.; Ludeno, G.; Pepe, F.A.; Ubertini, F. UAV photogrammetry, infrared thermography and GPR for enhancing structural and material degradation evaluation of the Roman masonry bridge of Ponte Lucano in Italy. NDT E Int. 2020, 115, 102287. [Google Scholar] [CrossRef]
- Curulli, A.; Montesperelli, G.; Ronca, S.; Cavalagli, N.; Ubertini, F.; Padeletti, G.; Vecchio Ciprioti, S. A multidisciplinary approach to the mortars characterization from the Town Walls of Gubbio (Perugia, Italy). J. Therm. Anal. Calorim. 2020, 142, 1721–1737. [Google Scholar] [CrossRef]
- Gusella, V.; Cluni, F.; Liberotti, R. Feasibility of a thermography nondestructive technique for determining the quality of historical frescoed masonries: Applications on the templar church of San Bevignate. Appl. Sci. 2021, 11, 281. [Google Scholar] [CrossRef]
- Jasiński, R.; Stebel, K.; Kielan, P. Use of the AE effect to determine the stresses state in AAC masonry walls under compression. Materials 2021, 14, 3459. [Google Scholar] [CrossRef]
- Pepi, C.; Cavalagli, N.; Gusella, V.; Gioffrè, M. An integrated approach for the numerical modeling of severely damaged historic structures: Application to a masonry bridge. Adv. Eng. Softw. 2021, 151, 102935. [Google Scholar] [CrossRef]
- Qixian, L.; Bungey, J.H. Using compression wave ultrasonic transducers to measure the velocity of surface waves and hence determine dynamic modulus of elasticity for concrete. Constr. Build. Mater. 1996, 10, 237–242. [Google Scholar] [CrossRef]
- Carino, N.J. The Impact-Echo Method: An Overview. In Proceedings of the World Structural Engineering Congress, ASCE NIST, Gaithersburg, MD, USA, 21–23 May 2001. [Google Scholar]
- Sansalone, M.; Carino, N.J. Impact-Echo: A Method for Flaw Detection in Concrete Using Transient Stress Waves, NBSIR 86-3452; US Department of Commerce, National Bureau of Standards, Center for Building Technology, Structures Division: Springfield, VA, USA, 1986. [Google Scholar]
- Song, F.; Huang, G.L.; Kim, J.H.; Haran, S. On the study of surface wave propagation in concrete structures using a piezoelectric actuator/sensor system. Smart Mater. Struct. 2008, 17, 055024. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Papadopoulos, N.A.; Angeli, G.M.; Karayannis, C.G.; Liolios, A.A.; Providakis, C.P. Damage Evaluation in Shear-Critical Reinforced Concrete Beam using Piezoelectric Transducers as Smart Aggregates. Open Eng. 2015, 5, 373–384. [Google Scholar] [CrossRef]
- Karayannis, C.G.; Voutetaki, M.E.; Chalioris, C.E.; Providakis, C.P.; Angeli, G.M. Detection of flexural damage stages for RC beams using Piezoelectric sensors (PZT). Smart Struct. Syst. 2015, 15, 997–1018. [Google Scholar] [CrossRef]
- Park, J.Y.; Yoon, Y.G.; Oh, T.K. Prediction of concrete strength with P-, S-, R-wave velocities by support vector machine (SVM) and artificial neural network (ANN). Appl. Sci. 2019, 9, 4053. [Google Scholar] [CrossRef] [Green Version]
- Grazzini, A. Sonic and Impact Test for Structural Assessment of Historical Masonry. Appl. Sci. 2019, 9, 5148. [Google Scholar] [CrossRef] [Green Version]
- Luchin, G.; Ramos, L.F.; D’Amato, M. Sonic Tomography for Masonry Walls Characterization. Int. J. Archit. Herit. 2020, 14, 589–604. [Google Scholar] [CrossRef]
- Cascante, G.; Najjaran, H.; Crespi, P. Novel Methodology for Nondestructive Evaluation of Brick Walls: Fuzzy Logic Analysis of MASW Tests. J. Infrastruct. Syst. 2008, 14, 117–128. [Google Scholar] [CrossRef]
- Miranda, L.; Cantini, L.; Guedes, J.; Binda, L.; Costa, A. Applications of Sonic Tests to Masonry Elements: Influence of Joints on the Propagation Velocity of Elastic Waves. J. Mater. Civ. Eng. 2013, 25, 667–682. [Google Scholar] [CrossRef]
- Miranda, L.; Cantini, L.; Guedes, J.; Costa, A. Assessment of mechanical properties of full-scale masonry panels through sonic methods. Comparison with mechanical destructive tests. Struct. Control Heal. Monit. 2016, 23, 503–516. [Google Scholar] [CrossRef]
- Verstrynge, E.; Lacidogna, G.; Accornero, F.; Tomor, A. A review on acoustic emission monitoring for damage detection in masonry structures. Constr. Build. Mater. 2021, 268, 121089. [Google Scholar] [CrossRef]
- Lacidogna, G.; Manuello, A.; Niccolini, G.; Carpinteri, A. Acoustic emission monitoring of Italian historical buildings and the case study of the Athena temple in Syracuse. Archit. Sci. Rev. 2015, 58, 290–299. [Google Scholar] [CrossRef]
- Manning, E.; Ramos, L.F.; Fernandes, F.M. Direct Sonic and Ultrasonic Wave Velocity in Masonry under Compressive Stress. In Proceedings of the 9th International Masonry Conference, Guimarães, Portugal, 7–9 July 2014. [Google Scholar]
- Valluzzi, M.R.; Cescatti, E.; Cardani, G.; Cantini, L.; Zanzi, L.; Colla, C.; Casarin, F. Calibration of sonic pulse velocity tests for detection of variable conditions in masonry walls. Constr. Build. Mater. 2018, 192, 272–286. [Google Scholar] [CrossRef]
- Mesquita, E.; Martini, R.; Alves, A.; Antunes, P.; Varum, H. Non-destructive characterization of ancient clay brick walls by indirect ultrasonic measurements. J. Build. Eng. 2018, 19, 172–180. [Google Scholar] [CrossRef]
- Mesquita, E.; Martini, R.; Alves, A.; Mota, L.; Rubens, T.; Antunes, P.; Varum, H. Heterogeneity detection of Portuguese–Brazilian masonries through ultrasonic velocities measurements. J. Civ. Struct. Health Monit. 2018, 8, 847–856. [Google Scholar] [CrossRef]
- Šejnoha, J.; Šejnoha, M.; Zeman, J.; Sýkora, J.; Vorel, J. Mesoscopic study on historic masonry. Struct. Eng. Mech. 2008, 30, 99–117. [Google Scholar] [CrossRef]
- Lombardo, M.; Zeman, J.; Šejnoha, M.; Falsone, G. Stochastic modeling of chaotic masonry via mesostructural characterization. Int. J. Multiscale Comput. Eng. 2009, 7, 171–185. [Google Scholar]
- Cavalagli, N.; Cluni, F.; Gusella, V. Evaluation of a Statistically Equivalent Periodic Unit Cell for a quasi-periodic masonry. Int. J. Solids Struct. 2013, 50, 4226–4240. [Google Scholar] [CrossRef] [Green Version]
- Cavalagli, N.; Cluni, F.; Gusella, V. Failure surface of quasi-periodic masonry by means of Statistically Equivalent Periodic Unit Cell approach. Meccanica 2018, 53, 1719–1736. [Google Scholar] [CrossRef] [Green Version]
- Cluni, F.; Gusella, V.; Vinti, G. Masonry elastic characteristics assessment by thermographic images. Meccanica 2019, 54, 1339–1349. [Google Scholar] [CrossRef] [Green Version]
- Tiberti, S.; Milani, G. 2D pixel homogenized limit analysis of non-periodic masonry walls. Comput. Struct. 2019, 219, 16–57. [Google Scholar] [CrossRef]
- Cluni, F.; Costarelli, D.; Gusella, V.; Vinti, G. Reliability increase of masonry characteristics estimation by a sampling algorithm applied to thermographic digital images. Probabilistic Eng. Mech. 2020, 60, 103022. [Google Scholar] [CrossRef]
- Tiberti, S.; Milani, G. 3D voxel homogenized limit analysis of single-leaf non-periodic masonry. Comput. Struct. 2020, 229, 106186. [Google Scholar] [CrossRef]
- Krejčí, T.; Koudelka, T.; Bernardo, V.; Šejnoha, M. Effective elastic and fracture properties of regular and irregular masonry from nonlinear homogenization. Comput. Struct. 2021, 254, 106580. [Google Scholar] [CrossRef]
- Kolsky, H. Stress Waves in Solids, 1st ed.; Oxford University Press: Oxford, UK, 1953. [Google Scholar]
- Ewing, W.M.; Jardetzky, W.S.; Press, F. Elastic Waves in Layered Media, 1st ed.; McGraw-Hill: New York, NY, USA, 1957. [Google Scholar]
- Viktorov, I.A. Rayleigh and Lamb Waves: Physical Theory and Applications; Plenum Press: New York, NY, USA, 1967. [Google Scholar]
- EN 1992-1-1 (2004): Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization, CEN-CENELEC Management Centre: Brussels, Belgium, 2004.
- Cavalagli, N.; Gusella, V. Dome of the Basilica of Santa Maria degli Angeli in Assisi: Static and dynamic assessment. Int. J. Archit. Herit. 2015, 9, 157–175. [Google Scholar] [CrossRef]
- Italian Ministery of Infrastructure and Transport. Istruzioni per L′applicazione Dell′«Aggiornamento Delle “Norme Tecniche per le Costruzioni”» di cui al Decreto Ministeriale 17 Gennaio 2018. CIRCOLARE 21 Gennaio 2019, n. 7 C.S.LL.PP, (GU n.35 del 11-2-2019-Suppl. Ordinario n. 5); Istituto Poligrafico e Zecca dello Stato: Roma, Italy, 2019. [Google Scholar]






| Wall | [kg/m3] | ν [−] | d [m] | N Samples | [m/s] | [m/s] | Conf. Int. 95% [m/s] | E [MPa] |
|---|---|---|---|---|---|---|---|---|
| CLS1 | 2400 | 0.2 | 0.20 | 14 | 2053 | 231 | ±132 | 29,226 ± 3886 |
| CLS2 | 2400 | 0.2 | 0.20 | 41 | 2131 | 621 | ±196 | 31,464 ± 6048 |
| 0.40 | 37 | 1722 | 303 | ±101 | 20,556 ± 2477 | |||
| 0.60 | 34 | 1475 | 210 | ±73 | 15,076 ± 1536 | |||
| 0.80 | 29 | 1613 | 166 | ±63 | 18,040 ± 1441 | |||
| 1.00 | 24 | 1576 | 188 | ±79 | 17,216 ± 1773 | |||
| 1.20 | 19 | 1639 | 112 | ±54 | 18,629 ± 1241 | |||
| 1.40 | 14 | 1428 | 134 | ±77 | 14,125 ± 1562 | |||
| 1.60 | 5 | 1498 | 39 | ±45 | 15,547 ± 946 |
| d [m] | N Samples | [m/s] | [m/s] | Conf. Int. 95% [m/s] |
|---|---|---|---|---|
| 0.20 | 35 | 626 | 295 | ±101 |
| 0.40 | 20 | 540 | 99 | ±46 |
| 0.60 | 11 | 548 | 60 | ±40 |
| 0.80 | 3 | 521 | 23 | ±43 |
| d [m] | N Samples | [m/s] | [m/s] | Conf. Int. 95% [m/s] |
|---|---|---|---|---|
| 0.25 | 50 | 2072 | 515 | ±146 |
| 1.95 | 5 | 2074 | 45 | ±52 |
| [m/s] | [m/s] | ν [−] | E [MPa] |
|---|---|---|---|
| 544 ± 43 | 2073 ± 100 | 0.47 ÷ 0.48 | 880 ÷ 1290 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marazzani, J.; Cavalagli, N.; Gusella, V. Elastic Properties Estimation of Masonry Walls through the Propagation of Elastic Waves: An Experimental Investigation. Appl. Sci. 2021, 11, 9091. https://doi.org/10.3390/app11199091
Marazzani J, Cavalagli N, Gusella V. Elastic Properties Estimation of Masonry Walls through the Propagation of Elastic Waves: An Experimental Investigation. Applied Sciences. 2021; 11(19):9091. https://doi.org/10.3390/app11199091
Chicago/Turabian StyleMarazzani, Jacopo, Nicola Cavalagli, and Vittorio Gusella. 2021. "Elastic Properties Estimation of Masonry Walls through the Propagation of Elastic Waves: An Experimental Investigation" Applied Sciences 11, no. 19: 9091. https://doi.org/10.3390/app11199091
APA StyleMarazzani, J., Cavalagli, N., & Gusella, V. (2021). Elastic Properties Estimation of Masonry Walls through the Propagation of Elastic Waves: An Experimental Investigation. Applied Sciences, 11(19), 9091. https://doi.org/10.3390/app11199091







