Abstract
We present a new spatial compounding method to improve the contrast of ultrasonic images for non-delayed sequential beamforming (NDSB). Sequential beamforming adopts more than one beamformer to reconstruct B-mode images which has the advantage of simple front-end electronics and fast data transfer rate. Via field pattern analysis, we propose a compounding method where two more sub-images can be reconstructed along with the NDSB sub-image. These sub-images can be seen as being produced with different transmit origins; thus, their summation enhances image contrast. Image quality was analyzed in terms of spatial resolution, contrast ratio (CR), and contrast-to-noise ratio (CNR). The proposed compounding method improves the lateral resolution up to 41%. In vitro results confirm a 13.0-dB CR and 4.0-dB CNR improvement. In vivo results reveal 10.9-dB and 6.0-dB improvement in CR and CNR for cross-section jugular vein and 8.0-dB and 4.5-dB improvement in CR and CNR for the longitudinal-section carotid artery.
1. Introduction
Synthetic aperture focusing technique (SAFT) was first introduced for the single-element transducer. A ‘virtual source’ concept is used by treating the focus point as a point source emitting spherical waves towards and away from the transducer [1,2]. Improved resolution is obtained for areas away from the focus. For linear array, similar algorithms have been introduced [3,4,5,6,7,8].
Although the image quality is significantly improved, the computational cost of synthetic aperture beamformer is heavy. The work of Nguyen [6] showed that the size of the beamformed image is 30 mm × 30 mm. The computation time for a traditional synthetic aperture beamformer is 59 min, and the advanced synthetic aperture beamformer takes 145 min, whereas dynamic focusing takes 42 s with an O() computation complexity ( denotes the number of transducer element and denotes the number of time samples). The requirement of real-time imaging demands the beamformer to be computationally efficient while retaining the image quality.
A dual-stage beamformer combining an advanced beamformer and traditional delay-and-sum (DAS) beamformer has been proposed to enhance the resolution and contrast [9,10]. A dual-stage beamformer (or termed ‘sequential beamforming’) has also been addressed in the context of synthetic aperture imaging [11,12,13]. A sequential beamforming algorithm termed non-delayed sequential beamforming (NDSB) is developed to simplify the front-end electronics design [13]. In the first stage, the received signals are directly summed without delay. In the second stage, the high-resolution image is reconstructed based on the two-way travel path. The authors proved this new approach can achieve a comparable imaging quality with a simpler receive electronic front-end than dynamic receive focusing (DRF). Due to the lack of focusing in the first beamformer, NDSB requires a large transmit opening angle to combine more data to generate a high-resolution image in the second stage. This means a large number of active elements. Even so, the contrast of NDSB is still inferior to dynamic receive focusing.
Spatial compounding can enhance image contrast by combining limited-correlating images of the same region-of-interest (ROI). To generate the limited-correlating images, we can mechanically translate the transducer, or electrically activate different transmit elements, or apply different transmit apodization [14,15]. To date, spatial compounding methods have not been applied to sequential beamforming in synthetic aperture imaging.
Here, a new spatial compounding method is proposed for NDSB. Spatiotemporal analysis of the pressure field is performed. By modeling the transmit sub-aperture as a continuous curved aperture, the pressure field can be characterized by three excitation signals with different transmit origins and different time delays. Sub-images can be reconstructed based on the propagation path of the corresponding excitation signals. Because these excitation signals are spatially separated, the reconstructed sub-images carry different spatial frequencies and thus decorrelate from each other. Spatial compounding can be done via summing these sub-images. The proposed compounding method improves contrast ratio and contrast-to-noise ratio in-vitro, and in-vivo.
2. Materials and Methods
2.1. Non-Delayed Sequential Beamforming
Non-delayed sequential beamforming introduced in [13] proposes a new dual-stage beamformer. A low-resolution image (LRI) is produced by the direct summation of channel data at the first stage. A second beamformer then reconstructs a high-resolution image (HRI) using the LRI. The time-of-flight (TOF) for the NDSB is shown in Figure 1, which is given as
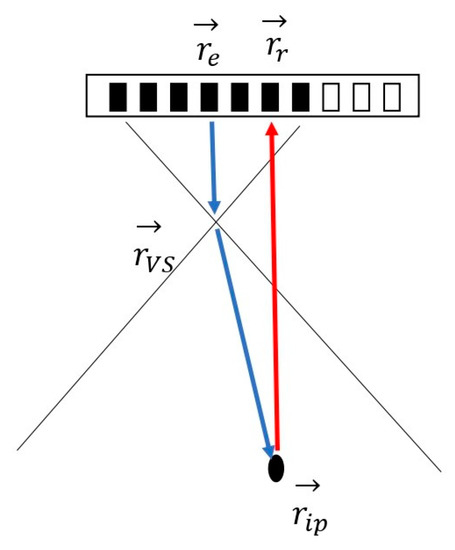
Figure 1.
Wave propagation path for NDSB. , , and denote the positions of the virtual source, the receive element, the transmit origin, and the imaging point, respectively. The blue arrows indicate the transmit path, and the red arrows indicate the receive path. The active elements are indicated as black.
In the equations, , , and denote the positions of the virtual source, the receive element, the transmit origin, and the imaging point, respectively. is the speed of sound. To reconstruct in the HRI, a time-delay is applied to the LRI data at the lateral position :
where is the focus depth. The high-resolution image can be written as
where denotes the high-resolution image for NDSB, is the apodization function, and denotes the low-resolution image.
2.2. Pressure Field Analysis
The spatiotemporal impulse response of the transmit sub-aperture is used to extract excitation signals which correspond to different transmit configurations [6]. For simplicity, we consider only the region where the spherical wave assumption is valid.
We make some assumptions: all elements of the transducer share the same electromechanical impulse response with uniform directivity function, and the discrete transmit sub-aperture is modeled as a continuous curved aperture. The pressure field of the imaging area can be obtained through a spatiotemporal impulse response [16].
Assuming a sinusoidal excitation and a rigid baffle, the pressure field for point at time can be written as
where is the equilibrium density of the medium, and in the equation can be given by [16].
where is the distance from the point to the aperture, and is the corresponding angle in the polar coordinates.
Integrating the above equation over the aperture surface, the pressure field for the point above the focus in Figure 2a can be expressed as
where and are associated with and .
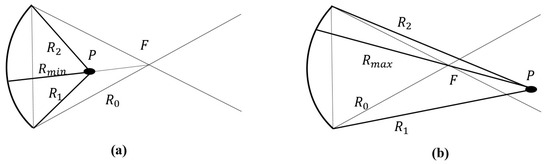
Figure 2.
Geometries for calculating pressure field of transmit sub-aperture for spatial point in front of the focus (a) and behind the focus (b).
For the point below the focus in Figure 2b, the pressure can be expressed as
where is associated with .
Equations (7) and (8) show that the transmit wave shape can be characterized by three spherical waves. The total field is a combination of the three pulses with different transmit origins and different time delays. NDSB selects the excitation signal with the highest energy to do the reconstruction which is denoted as in Equation (7) and in Equation (8). On the other hand, beamforming can also be performed under two other excitation signals from the two ends of the aperture. Because the three excitation signals are from different origins, their corresponding beamformed images are therefore spatially decorrelated. Compounding can be done by summing these images together.
To reconstruct the image originated from the two transmit aperture ends, the wave propagation path needs to be adjusted.
The TOF corresponds to the excitation signal emitted from the ends of the active aperture can be expressed as
Figure 3a presents the TOF to generate the image corresponds to the left end of the active aperture, and Figure 3b corresponds to the right end. To produce HRI at , the delay time is also adjusted as
where denotes the lateral position of the left/right end of the active aperture. The high-resolution image is denoted as and using Equation (2).
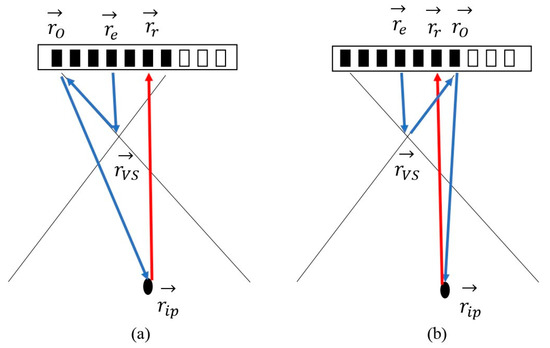
Figure 3.
Wave propagation path for (a) left end of the active aperture and (b) right end of the active aperture. , , and denote the positions of the virtual source, the receive element, the transmit origin, and the imaging point, respectively. denotes the position for the end of the active aperture. The blue arrows indicate the transmit path, and the red arrows indicate the receive path. The active elements are indicated as black.
Here we produce two compound images using the three high-resolution images (, and ): summation of and gets compound image 1 (denoted as Comp1). Summation of , and gets compound image 2 (denoted as Comp2).
2.3. Experiment Setup
The Verasonics Vantage 256 scanner (Redmond, WA, USA) and a L11-4v linear array were used to collect experimental data. The array has a 6.25-MHz central frequency, 128 elements, 67% bandwidth, and 0.3-mm pitch size. The excitation signal is a 1-cycle sinusoid tone burst at the central frequency. Transmit F-number (F #, defined as the ratio between focal length and the aperture diameter) is set to 0.75 for all experiments. During transmission, the number of the active elements is 16, boxcar apodization is used for every transmit event. The focused beam is translated by an element pitch in the lateral direction of 0.3 mm. The transmit focus is always on the centerline of the active aperture. During reception, all 128 elements are active to collect radio-frequency data. The raw data are sampled at 25 Msamples/s, resulting in a 0.078 mm-axial sampling distance. The Verasonics system stores 4096 samples of each receiver signal which covers data ranging from 3 mm to 34 mm in depth. Off-line processing is performed to produce the final images. B-mode images were obtained through Hilbert transform and log-compression. A phantom made of nylon threads of 0.2-mm diameter immersed in water was used for the quantification of the lateral resolution, and a lab-made cyst phantom is used to quantify realistic image contrast. In vivo imaging is performed to image the long-section and cross-section of the carotid artery.
2.4. Evaluation
Two proposed compound images are present, denoted as Comp1 and Comp2. To provide a fair comparison, both NDSB and DAS images are shown.
The reconstructed images are evaluated in terms of resolution and image contrast. The resolution is quantified by imaging a point target. We define the resolution as the full-width-at-half-maximum (FWHM) in the lateral and axial direction. The performance of image contrast is evaluated in terms of contrast ratio (CR) which is defined as
where denotes the mean intensities of the measured cyst and denotes the mean intensities of the measured background.
The contrast-to-noise ratio (CNR) value is also used which is defined as
The unit of CR and CNR is decibel (dB).
3. Results
3.1. Resolution
To measure the ability of the proposed beamformer to resolve a point target, a phantom made of nylon threads of 0.2-mm diameter was immersed in water. The distance between the target to the transducer surface is 15.1 mm. Four beamformers are used and the results are compared. Figure 4 presents the beamformed images with a 30-dB dynamic range. It can be seen that NDSB produces a slightly larger point spread function (PSF) compared with DAS. It can be seen in Figure 4c,d that the side lobes for proposed beamformers are slightly asymmetric. The reason is in Section 2.2 we assume the pressure field contributions from the two aperture ends are equal. But for real discrete transmit sub-aperture, these contributions might not be perfectly the same. Weighting strategy can be used for each contribution, but the design of weighting parameters is beyond the scope of current work. The proposed compound method in Figure 4c,d improves the resolution of NDSB. Figure 5 plots the lateral and axial profile of the beamformed point target. The detailed resolution in the lateral and axial direction is in Table 1. The proposed Comp1 method provides the best resolution in both directions, which is 1.37 mm in the lateral direction and 0.43 mm in the axial direction. The proposed two compounding methods (Comp1, Comp2) outperform DAS and NDSB in terms of resolution.

Figure 4.
B-mode images of a point target. (a) DAS image (b) NDSB image (c) Comp1 image (d) Comp2 image.
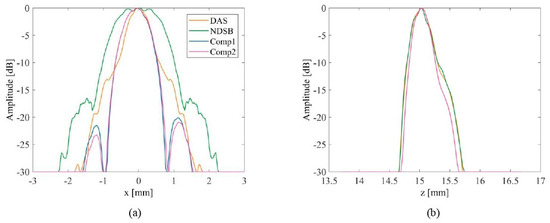
Figure 5.
Lateral and axial profile of beamformed point target. (a) lateral profiles (b) axial profile.

Table 1.
Lateral and axial resolution for point target.
3.2. Contrast
To test the robustness of the beamformers in terms of phase aberration. A lab-made cyst phantom is used to compare image contrast under different beamformers. This phantom has a random background and two anechoic cysts. The left cyst is centered at (x, z) = (−8, 22) mm and the right one is centered at (x, z) = (4, 18) mm. The anechoic cysts are surrounded by randomly placed scatterers, the attenuation coefficient is 0.6 dB/MHz/cm and the speed of sound within the phantom is 1539–1550 m/s.
The beamformed images are shown in Figure 6. For CR and CNR calculation, the measured cyst region is enclosed in the white circle and the background in the white rectangle in Figure 6. The background region with uniform speckle patterns shares the same centerline as the measured cyst and contains no particular bright reflectors. The detailed CR and CNR values are given in Table 2.

Figure 6.
B-mode images of experiment cyst phantom. (a) DAS image (b) NDSB image (c) Comp1 image (d) Comp2 image.

Table 2.
Contrast-ratio and Contrast-to-noise ratio for Figure 6.
From the beamformed images, we can find cyst region enclosed by the white circle gets cleaner after compounding. In Table 2, Comp2 has the better CR performance which is 11.1 dB higher than DAS and 13.0 dB higher than NDSB. CNR value also validates the improvement in image contrast. Comp2 gives the best CNR value which provides 3.9-dB and 4.0-dB improvement compared to DAS and NDSB, respectively.
3.3. In Vivo Imaging
To test the robustness of the proposed compounding method in clinical circumstances, we acquired in vivo data from a 26-year-old volunteer using the Verasonics scanner. This data was obtained with appropriate ethical clearance and informed consent. During the experiment, the probe and the human object are kept still to eliminate large motion artifacts.
Figure 7 shows the in vivo images. The image contains the transverse view of two vessels in the neck, including the jugular vein and the carotid artery. We choose the region inside the jugular vein to calculate CR and CNR values. The ROI is enclosed in the white circle in Figure 7. The background is depicted in the white rectangular which is within the tissue region in the thyroid gland. After compounding, the contrast for the jugular vein improves. The measured CR and CNR are shown in Table 3.

Figure 7.
B-mode images of cross-section carotid artery and the jugular vein in 50-dB range. (a) DAS image (b) NDSB image (c) Comp1 image (d) Comp2 image.

Table 3.
Contrast-ratio and Contrast-to-noise ratio for Figure 7.
From Table 3, the proposed Comp2 gives the best CR and CNR performance, Comp1 also gives similar performance. Comp2 outperforms DAS by 9.7 dB and 5.2 dB in terms of CR and CNR. Compared with NDSB, the compounding method provides up to 10.9-dB and 6-dB improvement in CR and CNR, respectively.
The longitudinal section beamformed images of the carotid artery are shown in Figure 8. Visually, the contrast within the carotid artery improves with the proposed method. The ROI is chosen within the carotid artery depicted in the white circle in Figure 8. The background region is within the white rectangular. The measured CR and CNR are shown in Table 4.

Figure 8.
B-mode images of the longitudinal-section carotid artery in 50-dB range. (a) DAS image (b) NDSB image (c) Comp1 image (d) Comp2 image.

Table 4.
Contrast-ratio and Contrast-to-noise ratio for Figure 8.
From Table 4, the proposed Comp2 gives the best CR and CNR performance, Comp2 outperforms DAS by 6.4 dB and 1.4 dB in terms of CR and CNR. Compared with NDSB, the compounding method provides up to 8.0-dB and 4.5-dB improvement in CR and CNR, respectively.
4. Discussion
This paper exploits a spatial compounding method for non-delayed sequential beamforming. Our proposed method depends on theoretical modeling of the transmit pressure field. As a result, two beamformed images originated from two ends of the transmit aperture can be produced using the same received signals. From the in vitro results, our proposed compounding images significantly improve the image contrast without sacrificing the resolution. In vivo studies also demonstrate the robustness of our proposed compounding methods. Image contrast is greatly enhanced in both the longitudinal and cross-section carotid artery images.
The aim of NDSB is to simplify the front-end architecture and retain the beamformer’s quality comparable to DRF. The image quality is highly affected by the transmit F#: smaller F# results in better resolution and contrast. Small F# means larger transmit opening angle. This ensures more data in the low-resolution image can be synthesized to generate a pixel point in the high-resolution image. The optimal F# is set to 0.75 in [13]. With this setting, degrading lateral resolution is found at shallow depth (<40 mm) and inferior contrast (CR, CNR) compared with DRF.
In this work, the transmit F# is also 0.75. NDSB produces inferior image quality (lateral resolution, CR, CNR) compared to DAS. This conclusion is the same in [13]. The proposed compounding improves the resolution and image contrast by summation of limited-correlated images. The effect of transmit F# to the compounding method is illustrated in Figure 9. Two transmit F# are compared: 0.75 and 3. To measure the lateral resolution, the same point target in Figure 4 is used. The result is shown in Figure 9a. The y-label is the ratio of lateral resolution of NDSB, Comp1, and Comp2 to that of DAS in certain transmit F#. When the F# increases, the lateral resolution of the compound method degrades. To address the image contrast, we image the carotid artery same in Figure 7. The ratio of CR and CNR (to that of DAS) in terms of transmit F# is plotted in Figure 9b. We can find the same conclusion: when F# increases, the image contrast also degrades. This is easily understood: a larger F# means a smaller active aperture given the same focus depth. The transmit origins for the contributing signal get closer and the beamformed images carry almost the same spatial frequencies. The summation of these images gives limited improvement compared with a small F# (larger active aperture). The computation time to reconstruct an image of 30 mm × 30 mm is 7.2 s for DAS, 8.5 s for NDSB, 18.5 s for Comp1, and 19.2 s for Comp2.
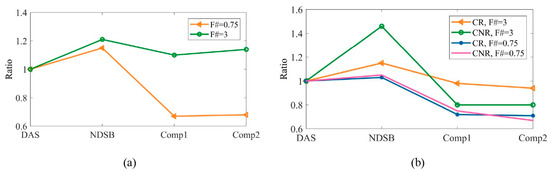
Figure 9.
Comparison of transmit F# to (a) lateral resolution and (b) image contrast (CR, CNR).
5. Conclusions
In this work, we propose two spatial compounding methods for a sequential beamforming algorithm named non-delay sequential beamforming (NDSB). Pressure field analysis indicates different sub-images can be beamformed under different transmit configurations. The summation of these sub-images produces a compound final image. In vitro and in vivo studies are carried out to quantify the proposed compounding methods. The results show the proposed compounding methods significantly improve the target detectability: in vitro results confirm a 13.0-dB better CR and 4.0-dB better CNR compared with NDSB. In vivo imaging of cross-section jugular vein reveals 10.9-dB and 6.0-dB improvement in CR and CNR using the proposed method. For the longitudinal-section carotid artery, the compounding method provides up to 8.0-dB and 4.5-dB improvement in CR and CNR, respectively.
Author Contributions
Conceptualization, L.W. and S.L.; methodology, S.L.; software, S.L.; validation, S.L.; resources, L.W.; writing, L.W. and S.L. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Institutional Review Board of City University of Hong Kong.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.
Acknowledgments
This work is partially supported by the National Natural Science Foundation of China (NSFC) (81627805, 61805102); Research Grants Council of the Hong Kong Special Administrative Region (11215817).
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Passmann, C.; Ermert, H. A 100-MHz ultrasound imaging system for dermatologic and ophthalmologic diagnostics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 545–552. [Google Scholar] [CrossRef]
- Karaman, M.; Li, P.-C.; O’Donnell, M. Synthetic aperture imaging for small scale systems. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 429–442. [Google Scholar] [CrossRef]
- Bae, M.-H.; Jeong, M.-K. A study of synthetic-aperture imaging with virtual source elements in B-mode ultrasound imaging systems. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 1510–1519. [Google Scholar] [CrossRef] [PubMed]
- Bae, M.-H.; Jeong, M.-K. Bidirectional pixel based focusing in conventional B-mode ultrasound imaging. Electron. Lett. 1998, 34, 2105–2107. [Google Scholar] [CrossRef]
- Kim, C.; Yoon, C.; Park, J.-H.; Lee, Y.; Kim, W.H.; Chang, J.M.; Choi, B.I.; Song, T.-K.; Yoo, Y.-M. Evaluation of ultrasound synthetic aperture imaging using bidirectional pixel-based focusing: Preliminary phantom and in vivo breast study. IEEE Trans. Biomed. Eng. 2013, 60, 2716–2724. [Google Scholar] [PubMed]
- Nguyen, N.Q.; Prager, R.W. High-resolution ultrasound imaging with unified pixel-based beamforming. IEEE Trans. Med. Imaging 2015, 35, 98–108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, N.Q.; Prager, R.W. Minimum variance approaches to ultrasound pixel-based beamforming. IEEE Trans. Med. Imaging 2016, 36, 374–384. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, N.Q.; Prager, R.W. Ultrasound pixel-based beamforming with phase alignments of focused beams. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 937–946. [Google Scholar] [CrossRef] [PubMed]
- Mozaffarzadeh, M.; Sadeghi, M.; Mahloojifar, A.; Orooji, M. Double-stage delay multiply and sum beamforming algorithm applied to ultrasound medical imaging. Ultrasound Med. Biol. 2018, 44, 677–686. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, C.-C. A Study of Double-Stage DMAS and p-DMAS for Their Relation in Baseband Ultrasound Beamforming. Biomed. Signal. Process. Control 2020, 60, 101964. [Google Scholar] [CrossRef]
- Kortbek, J.; Jensen, J.A.; Gammelmark, K.L. Sequential beamforming for synthetic aperture imaging. Ultrasonics 2013, 53, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Arendt Jensen, J. Synthetic aperture flow imaging using dual stage beamforming: Simulations and experiments. J. Acoust. Soc. Am. 2013, 133, 2014–2024. [Google Scholar] [CrossRef] [PubMed]
- Bera, D.; Bosch, J.G.; Verweij, M.D.; de Jong, N.; Vos, H.J. Dual stage beamforming in the absence of front-end receive focusing. Phys. Med. Biol. 2017, 62, 6631. [Google Scholar] [CrossRef] [PubMed]
- Trahey, G.E.; Smith, S.W.; Von Ramm, O. Speckle pattern correlation with lateral aperture translation: Experimental results and implications for spatial compounding. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1986, 33, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Wilhjelm, J.E.; Jensen, M.; Brandt, T.; Sahl, B.; Martinsen, K.; Jespersen, S.K.; Falk, E. Some imaging strategies in multi-angle spatial compounding. In Proceedings of the 2000 IEEE Ultrasonics Symposium. Proceedings. An International Symposium (Cat. No. 00CH37121), San Juan, PR, USA, 22–25 October 2000; pp. 1615–1618. [Google Scholar]
- Cobbold, R.S. Foundations of Biomedical Ultrasound; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).