Shafting Torsional Vibration Analysis of 1000 MW Unit under Electrical Short-Circuit Fault
Abstract
:1. Introduction
2. Solving of Torsional Vibration Natural Frequency of Shafting
3. Construction of Electrical Short-Circuit Fault Model
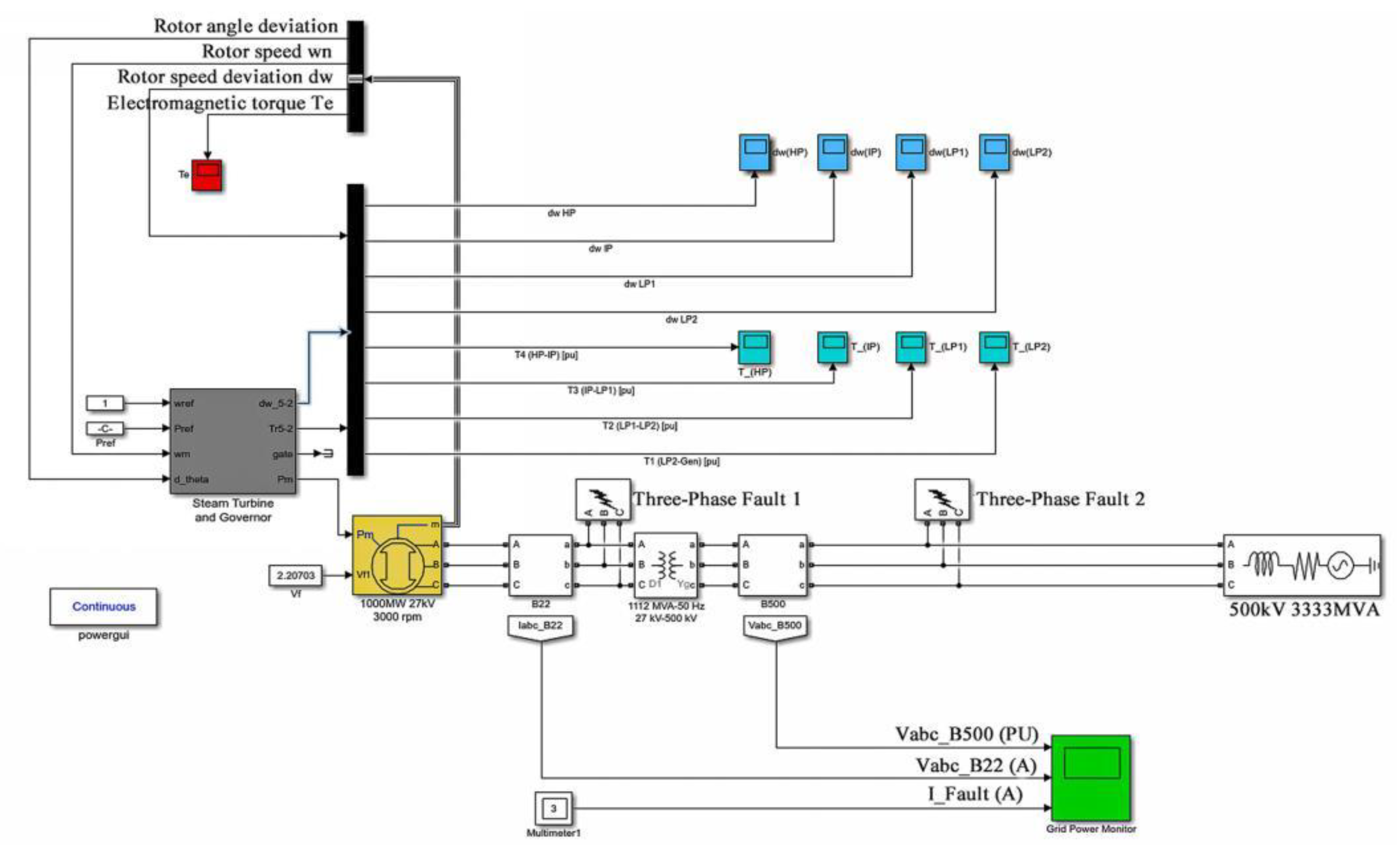
3.1. SIMULINK Electric Short-Circuit System Simulation Model
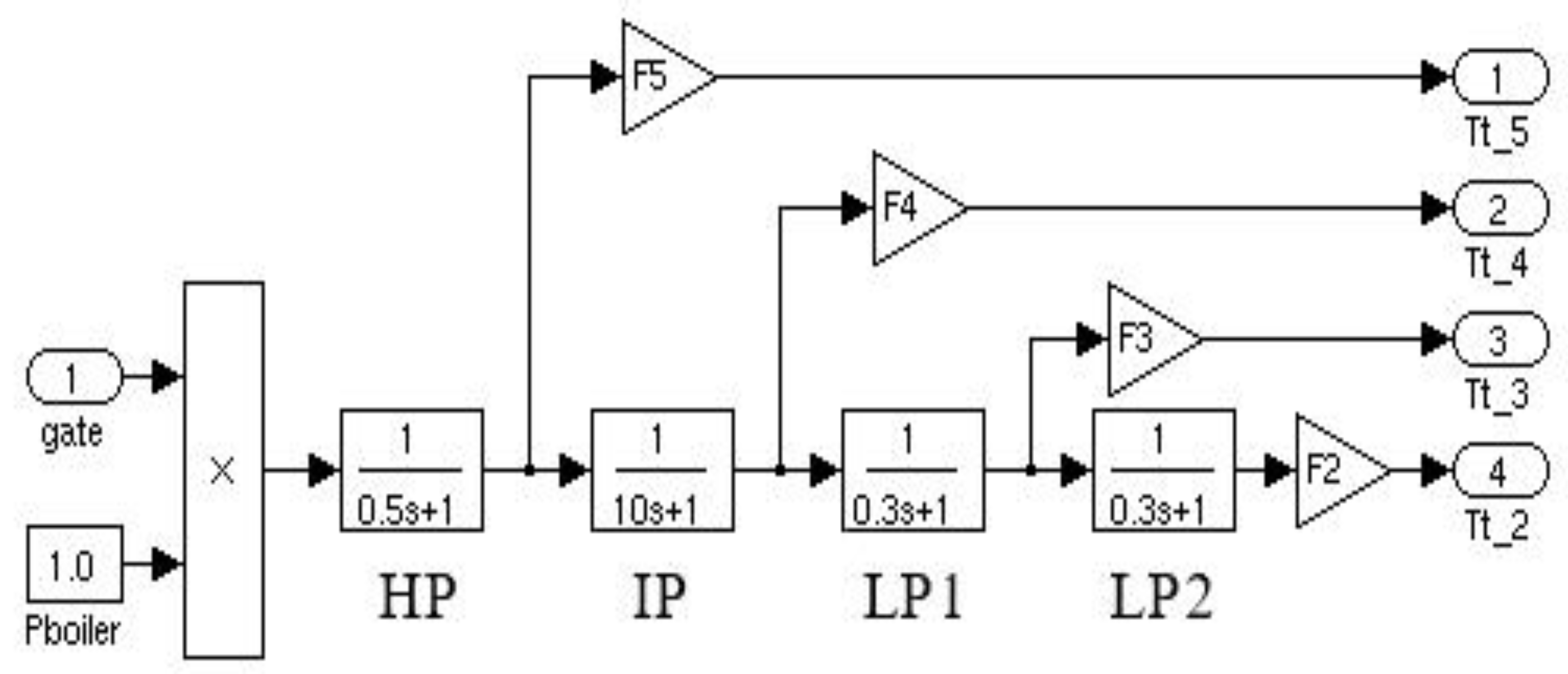
3.2. SIMULINK Turbine Generator Unit Model
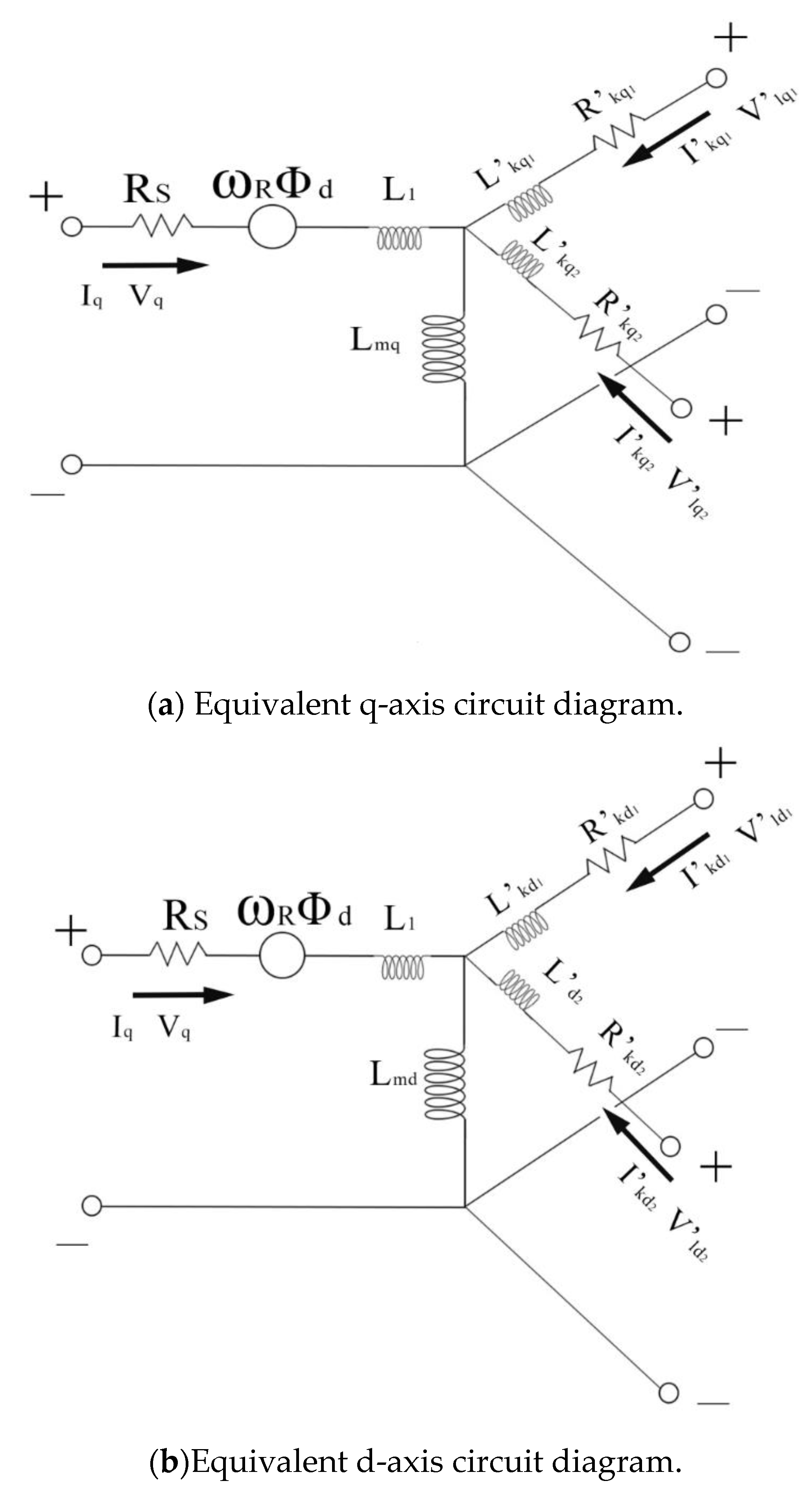
3.3. SIMULINK Synchronous Generator Model
4. Electrical Short-Circuit Fault Simulation Analysis
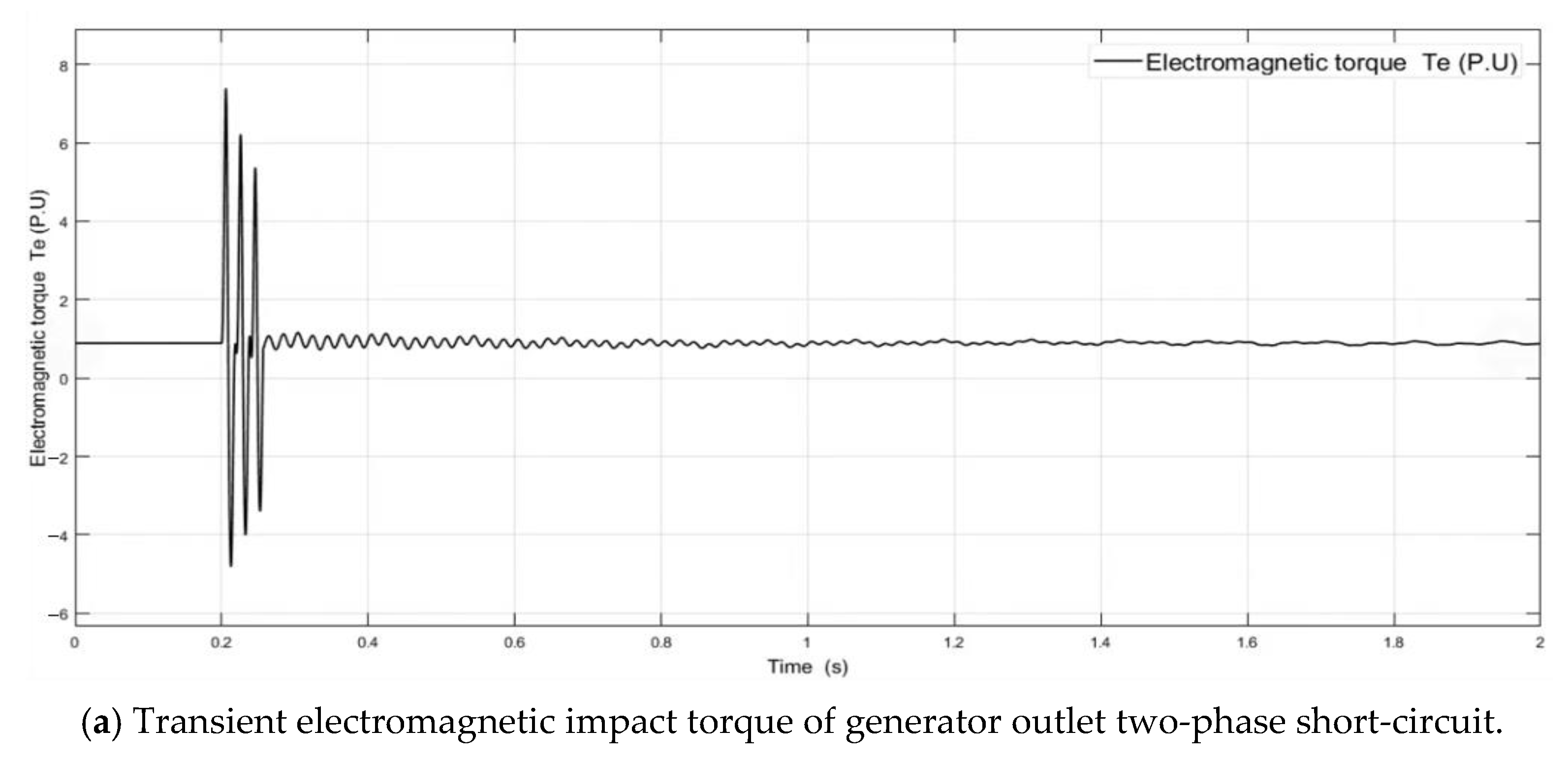
4.1. Simulation Analysis of Generator Terminals Two-Phase Short-Circuit
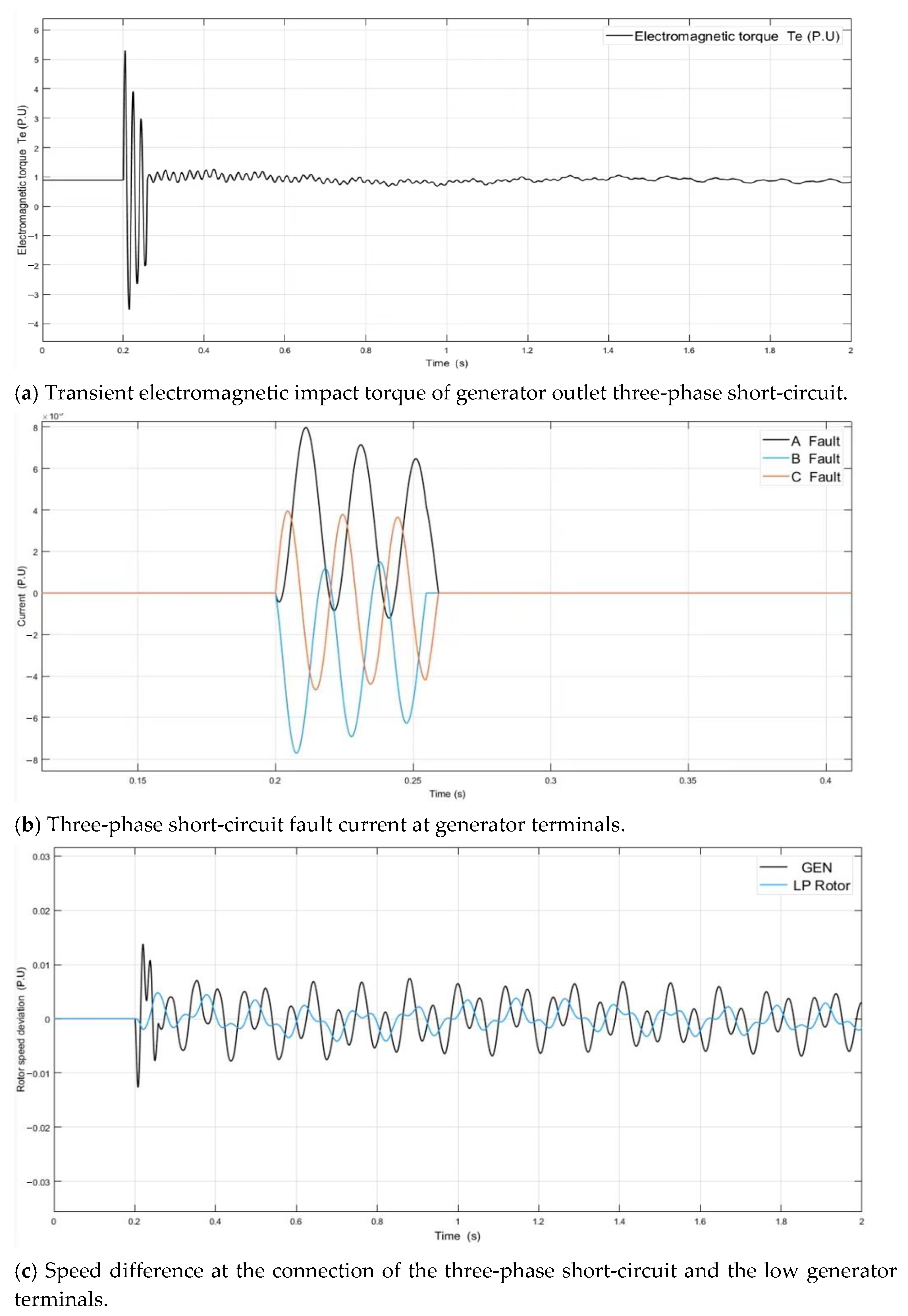
4.2. Simulation Analysis of Generator Terminal’s Three-Phase Short-Circuit
4.3. Simulation Analysis of Two-Phase Short-Circuit on the Power Grid Side
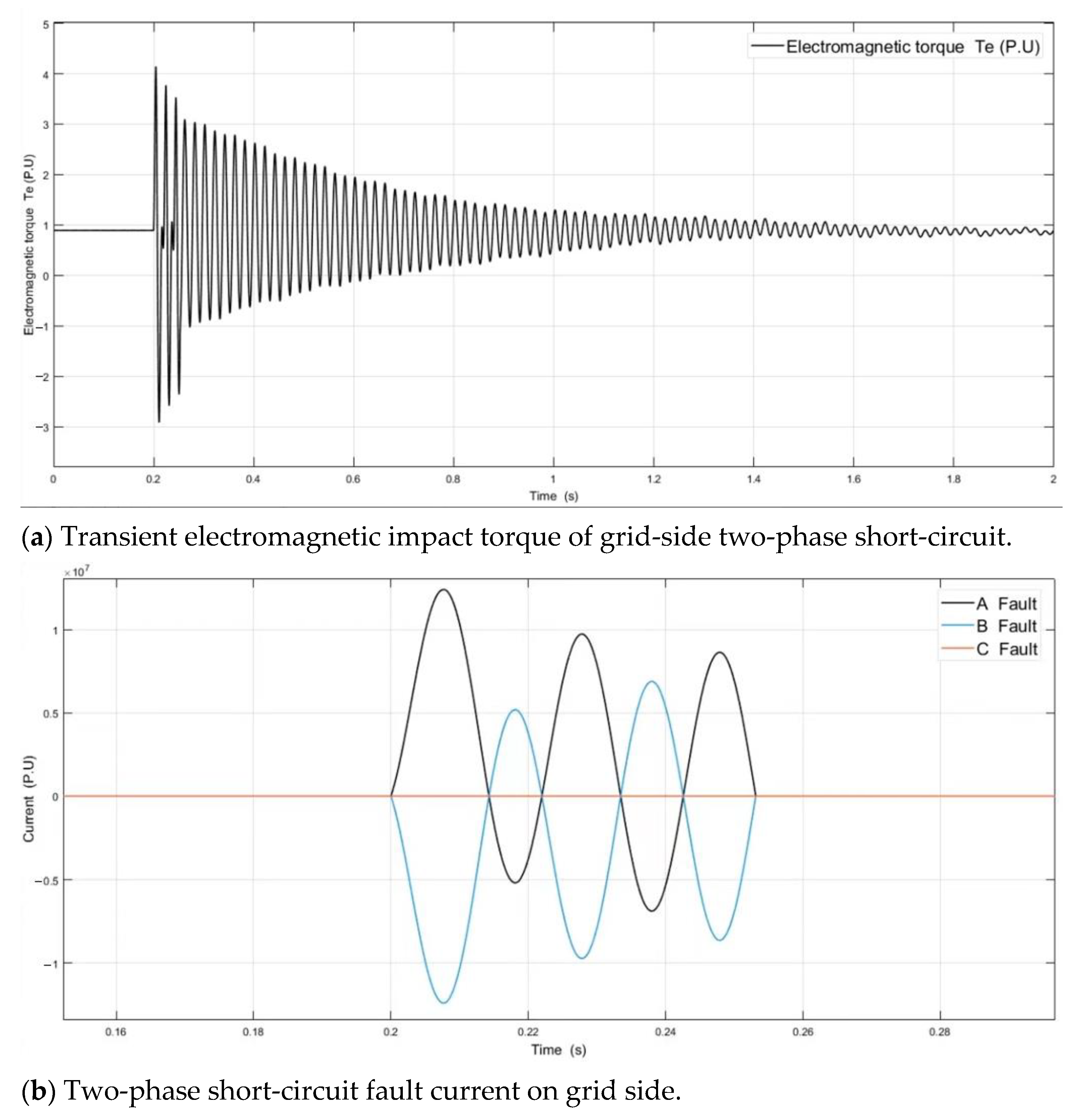
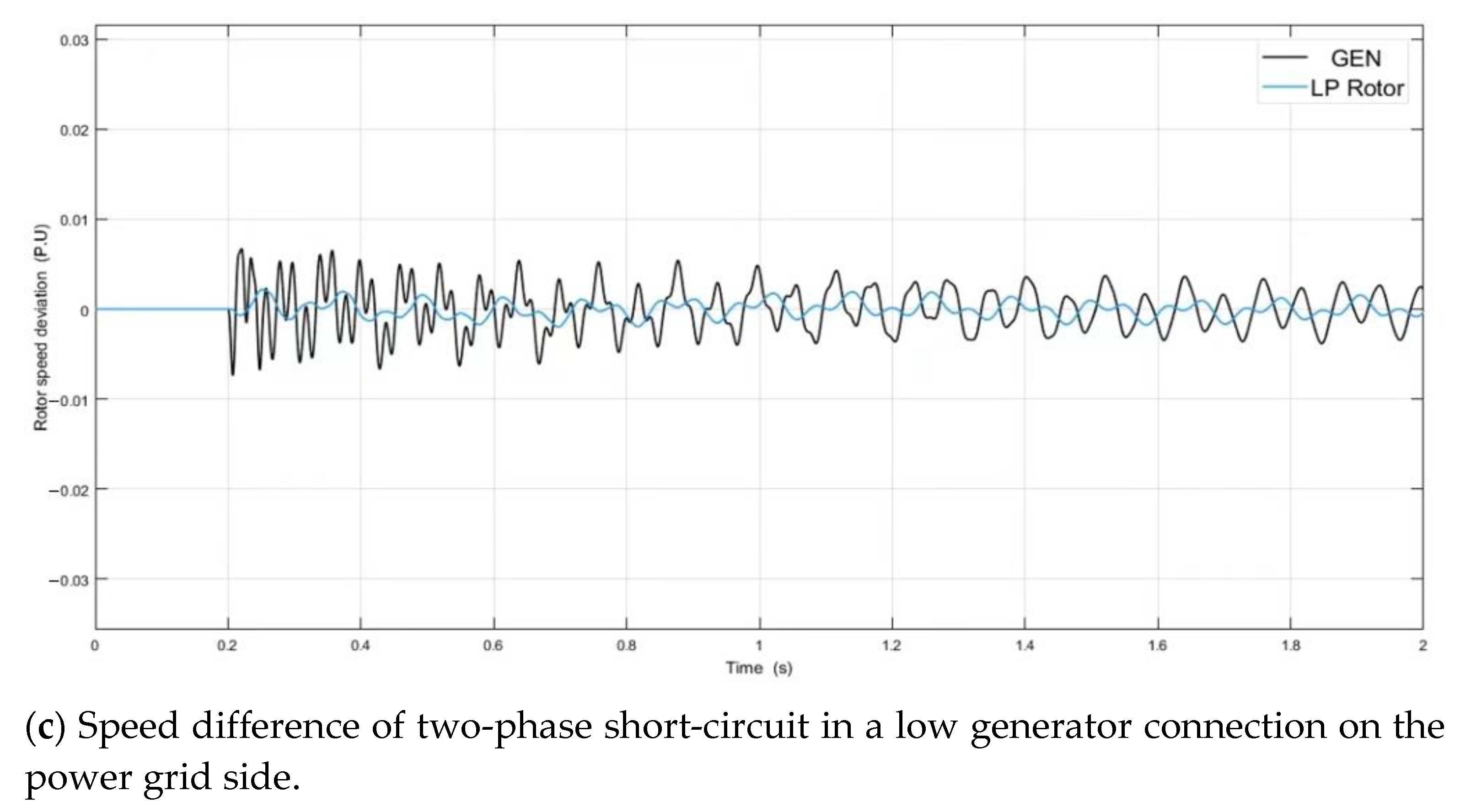
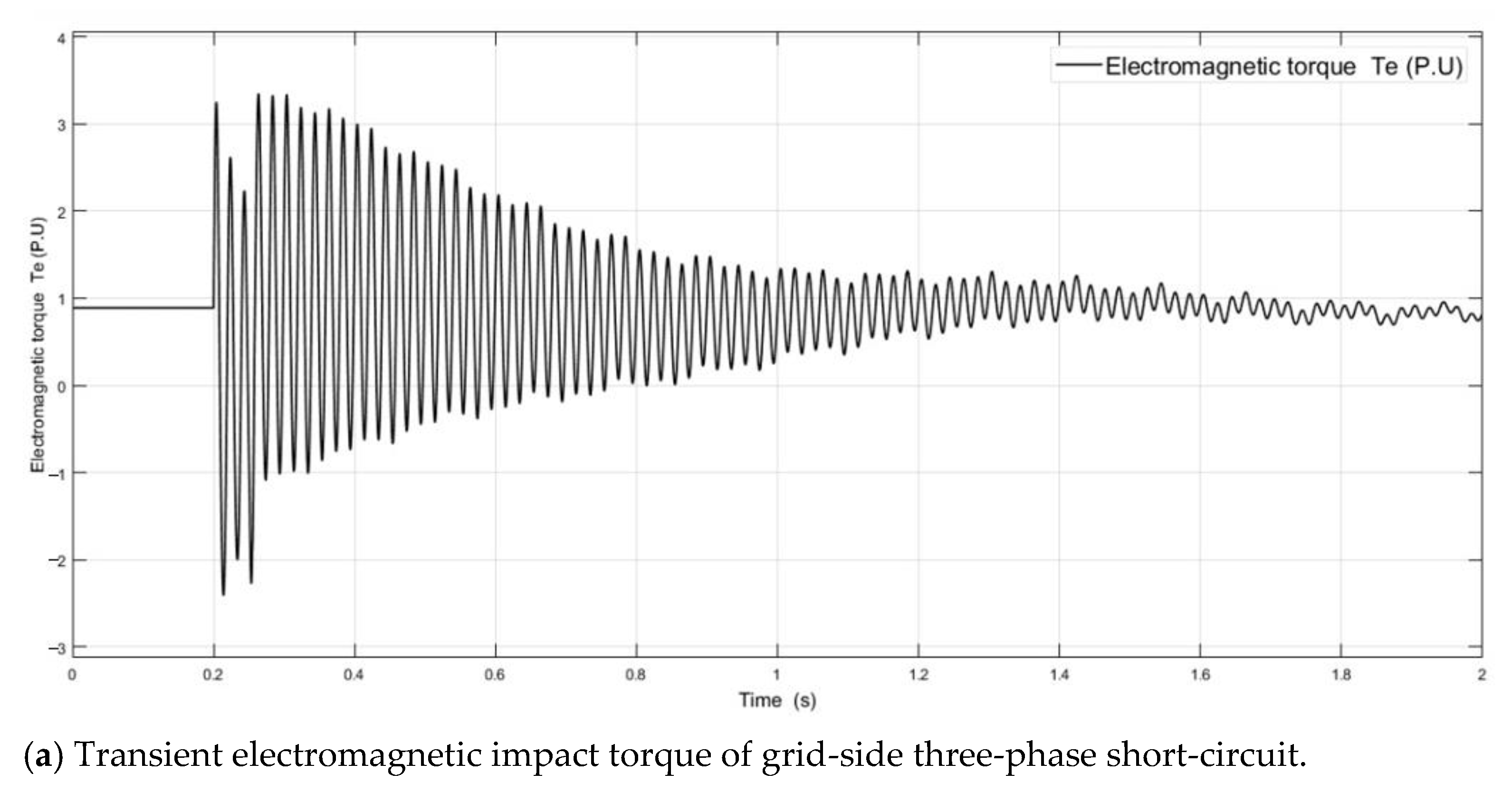
4.4. Simulation Analysis of Three-Phase Short-Circuit on the Power Grid Side
5. Analysis of Short-Circuit Fault Simulation Data
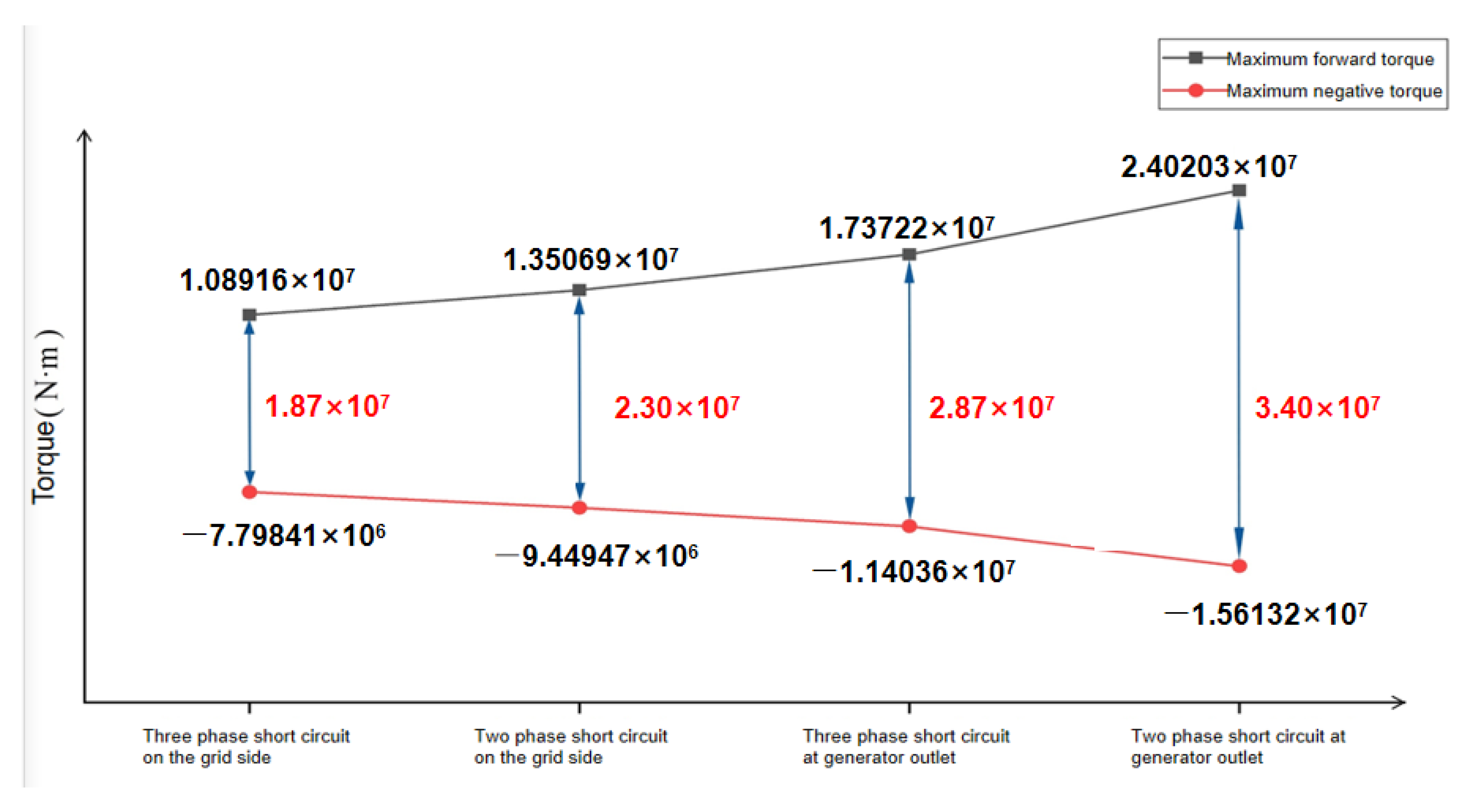
5.1. Electromagnetic Torque Analysis of Short-Circuit Fault
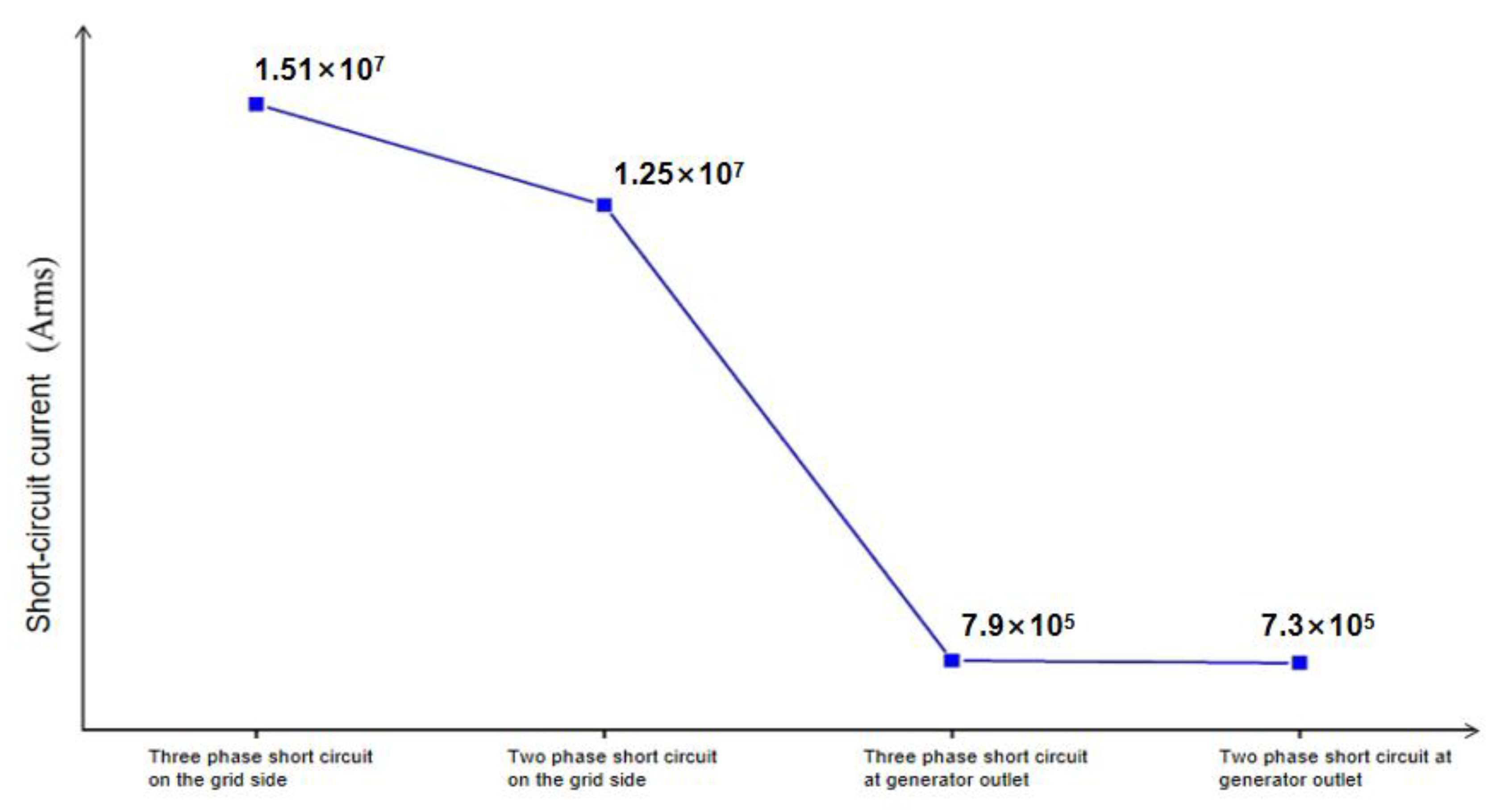
5.2. Short-Circuit Fault Current Analysis
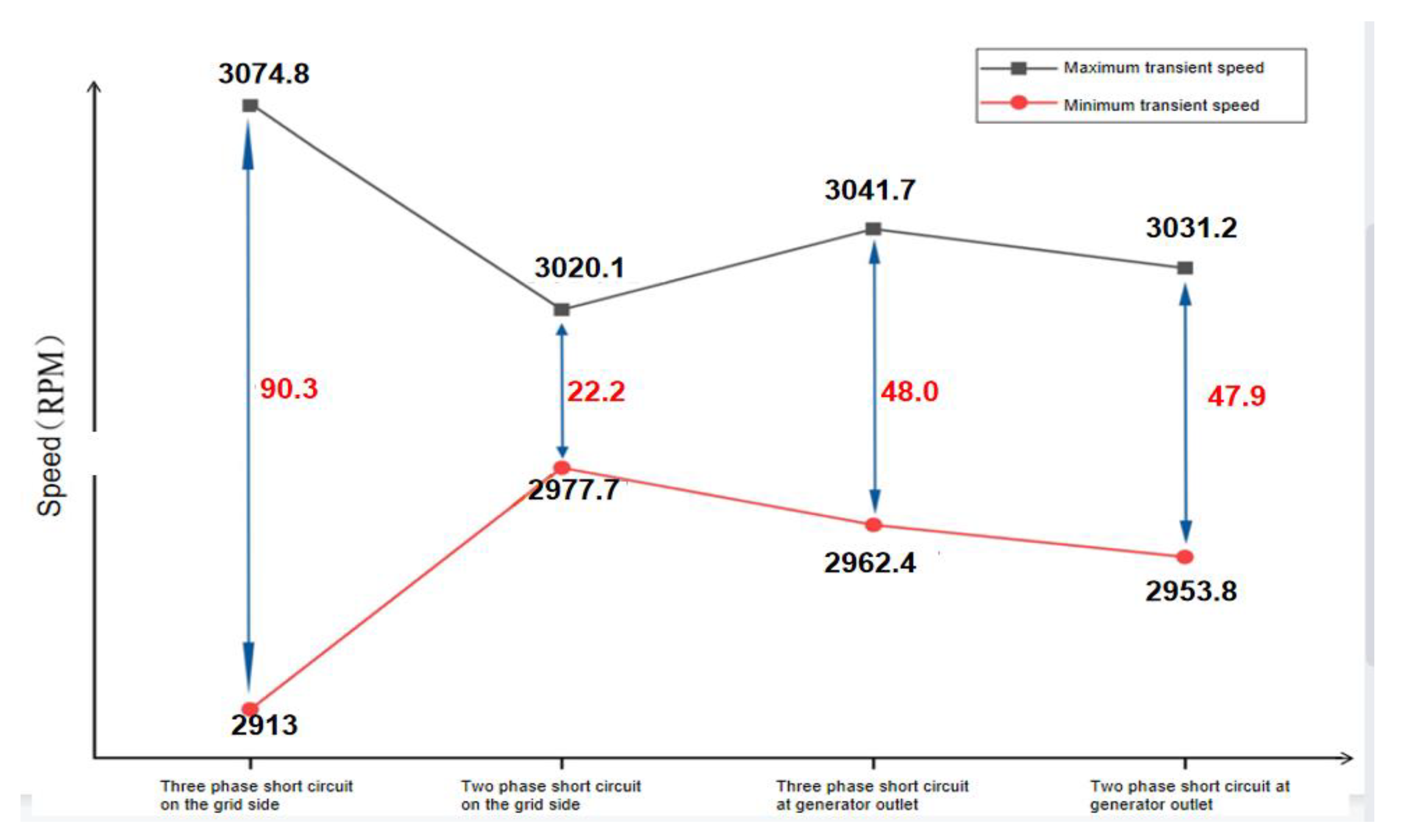
5.3. Analysis of Speed Difference at a Low-Frequency Connection of the Short-Circuit Fault
6. Conclusions
- In terms of the transient electromagnetic torque impact value, the two-phase short-circuit fault of the generator terminals was the largest, the three-phase short-circuit fault of the grid side was the smallest, and the electromagnetic torque impact value of the generator terminals under fault was greater than that of the grid side. The transient electromagnetic impact torque caused by a two-phase short-circuit at the same fault point was greater than that caused by a three-phase short-circuit;
- The transient impulse current under three-phase short-circuit at any fault point is greater than that under two-phase short-circuit. The impact current of a grid-side short-circuit fault is much larger than the generator terminals’ short-circuit fault. The speed fluctuation between rotors and the fluctuation difference caused by the three-phase short-circuit on the grid side are the largest;
- Four kinds of fault with transient electromagnetic force alternating frequencies, excluding the natural frequency of the unit shaft torsional vibration, will not give rise to short-circuit fault time domain shaft torsional resonance. However, the potential impact of the residual small fluctuation of torque in the rotor system after the fault is removed needs further analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, M.H.; Pham, X.D.; Vuong, Q.D. Torsional Vibration Stress and Fatigue Strength Analysis of Marine Propulsion Shafting System Based on Engine Operation Patterns. J. Mar. Sci. Eng. 2020, 8, 613. [Google Scholar] [CrossRef]
- Rajkiran, U.; Vinoth, A.; Jegadeesan, K.; Shravankumar, C. Lateral and torsional vibration analysis of composite shaft. IOP Conf. Ser. Mater. Sci. Eng. 2020, 912, 022040. [Google Scholar] [CrossRef]
- Chow, J.H.; Javid, S.H.; Sanchez-Gasca, J.J.; Bowler, C.E.J.; Edmonds, J.S. Torsional model identification for turbine-generators. IEEE Trans. Energy Convers. 1986, 4, 83–91. [Google Scholar] [CrossRef]
- Fairbairn, R.E.; Jennings, G.D.; Harley, R.G. Turbogenerator torsional mechanical modal parameter identification from on-line measurements. IEEE Trans. Power Syst. 1991, 6, 1389–1395. [Google Scholar] [CrossRef]
- Li, Z.Y.; Tian, S.J.; Zhang, Y.F.; Li, H.; Lu, M. Active Control of Drive Chain Torsional Vibration for DFIG-Based Wind Turbine. Energies 2019, 12, 1744. [Google Scholar] [CrossRef] [Green Version]
- Masayuki, W.; Hiroyuki, I.; Kazuma, S.; Yasunori, M.; Yoshihisa, U.; Yoshihide, K. Analysis of Turbine Generator Shaft Torsional Vibration Caused by Self-Commutated Converters. Electr. Eng. Jpn. 2015, 193, 9–17. [Google Scholar]
- Masayuki, W.; Ueno, Y.; Yasunori, M.; Hiroyuki, I.; Yoshihisa, U.; Yasuhiro, U. A Dynamical Model for Customer’s Gas Turbine Generator in Industrial Power Systems. IFAC Proc. Vol. 2009, 42, 203–208. [Google Scholar]
- Tang, G.J.; Chen, X.J. Analysis of torsional vibration inherent characteristics of rotating machinery shafting. Steam Turbine Technol. 2010, 52, 339–341, 344. [Google Scholar]
- Zhao, T.Y.; Cui, Y.S.; Pan, H.G.; Yuan, H.Q.; Yang, J. Free vibration analysis of a functionally graded graphene nanoplatelet reinforced disk-shaft assembly with whirl motion. Int. J. Mech. Sci. 2021, 197. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Yuan, H.Q.; Yang, W.J.; Sun, H.G. Genetic particle swarm parallel algorithm analysis of optimization arrangement on mistuned blades. Eng. Optim. 2017, 49, 2095–2116. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, Z.Y.; Zhao, Z.; Xie, L.Y.; Yuan, H.Q. Modeling and free vibration analysis of rotating hub-blade assemblies reinforced with graphene nanoplatelets. J. Strain Anal. Eng. Des. 2021. [Google Scholar] [CrossRef]
- Liu, J.H.; Huang, S.H.; Lu, J.D. Dynamic frequency study on torsional vibration of large turbo-generator shaft. Therm. Power Eng. 2005, 3, 234–238, 328–329. [Google Scholar]
- Liu, J.H.; Huang, S.H.; Lu, J.D. Research on torsional vibration frequency of single mass disk rotor. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2005, 8, 12–15. [Google Scholar]
- Liu, J.H.; Huang, S.H.; Lu, J.D. Dynamic frequency problem of torsional vibration of turbine mechanical shafting. Shanghai Steam Turbine 2003, 4, 237–239. [Google Scholar]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Pan, H.G.; Cai, Y. Free vibration analysis of a rotating graphene nanoplatelet reinforced pre-twist blade-disk assembly with a setting angle. Appl. Math. Model. 2021, 93, 578–596. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, L.P.; Pan, H.G.; Yang, J.; Sritawat, K. Coupled free vibration of a functionally graded pre-twisted blade-shaft system reinforced with graphene nanoplatelets. Compos. Struct. 2020, 262, 113362. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Yang, J. Coupled Free Vibration of Spinning Functionally Graded Porous Double-Bladed Disk Systems Reinforced with Graphene Nanoplatelets. Materials 2020, 13, 5610. [Google Scholar] [CrossRef]
- Pan, H.G.; Wu, Y.S.; Zhao, T.Y. Study on Influence of Multi-Parameter Variation of Bladed Disk System on Vibration Characteristics. Appl. Sci. 2021, 11, 3084. [Google Scholar] [CrossRef]
- Pan, H.G.; Wu, Y.S.; Zhou, J.N.; Fu, Y.M.; Liang, X.; Zhao, T.Y. Free Vibration Analysis of a Graphene-Reinforced Porous Composite Plate with Different Boundary Conditions. Materials 2021, 14, 3879. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Goran, A.; Anjan, B.; Claudio, C.; Nikos, H.; David, H.; Alex, S.; Carson, T.; et al. Definition and Classification of Power System Stability. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Mazana, A.; Jose, R.M.; Luis, R.L.; Kundur, P. Multilevel MATE for Efficient Simultaneous Solution of Control Systems and Nonlinearities in the OVNI Simulator. IEEE Trans. Power Syst. 2006, 21, 1250–1259. [Google Scholar]
- Venkata, S.S.; Sukumar, B.; Jason, S.; Kundur, P. Continue Your Learning. IEEE Power and Energy Mag. 2010, 8, 36–43. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Wang, Y.Q.; Pan, H.G. Vibration characteristics of graphene nanoplatelet reinforced disk-shaft rotor with eccentric mass. Mech. Adv. Mater. Struct. 2021, 1–21. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Yang, Y.F.; Pan, H.G.; Zhang, H.Y.; Yuan, H.Q. Free vibration analysis of a spinning porous nanocomposite blade reinforced with graphene nanoplatelets. J. Strain Anal. Eng. Des. 2021, 56, 574–586. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Liu, Z.F.; Pan, H.G.; Zhang, H.Y.; Yuan, H.Q. Vibration Characteristics of Functionally Graded Porous Nanocomposite Blade-disk-shaft Rotor System Reinforced with Graphene Nanoplatelets. Appl. Compos. Mater. 2021, 28, 717–731. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Wang, Y.X.; Yu, Y.X.; Cai, Y.; Wang, Y.Q. Modeling and vibration analysis of a spinning assembled beam–plate structure reinforced by graphene nanoplatelets. Acta Mech. 2021, 1–17. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Wang, Y.X.; Pan, H.G.; Yuan, H.Q.; Cai, Y. Nonlinear forced vibration analysis of spinning shaft-disk assemblies under sliding bearing supports. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Wang, X.Y.; Pan, H.G.; Gao, X.S. Analytical solution for vibration characteristics of rotating graphene nanoplatelet-reinforced plates under rub-impact and thermal shock. Adv. Compos. Lett. 2020, 29. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Li, H.G.; Sun, H.G. Parallel intelligent algorithm analysis of optimization arrangement on mistuned blades based on compute unified device architecture. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 233, 2207–2218. [Google Scholar] [CrossRef]
- Li, Z.J.; Zhao, T.Y.; Kou, H.J.; Zhang, H.; Yuan, H.Q. Vibration characteristics of multi-stage blade–disk–shaft integrated structure with three-dimensional crack. J. Vib. Eng. Technol. 2021, 9, 597–611. [Google Scholar] [CrossRef]
- Kacejko, P.; Machowski, J. Modelling of phase shifting transformers in short circuit calculations. Prz. Elektrotechniczny 2017, 93, 1–5. [Google Scholar]
- Gryszpanowicz, K.; Machowski, J.; Robak, S. Overload emergency state control of transmission network based on generation curtailment. Prz. Elektrotechniczny 2016, 92, 275–280. [Google Scholar]
- Navid, A.; Seyyedmilad, E.; Juri, J.; Hermann, W.D. Saturable and Decoupled Constant-Parameter VBR Model for Six-Phase Synchronous Machines in State-Variable Simulation Programs. IEEE Trans. Energy Convers. 2019, 34, 1868–1880. [Google Scholar]
- Navid, A.; Seyyedmilad, E.; Mehrdad, C.; Juri, J.; Hermann, W.D. Constant-Parameter Voltage-Behind-Reactance Model of Six-Phase Synchronous Machines. IEEE Trans. Energy Convers. 2017, 32, 548–559. [Google Scholar]
- Navid, A.; Seyyedmilad, E.; Mehrdad, C.; Juri, J.; Hermann, W.D. Voltage-behind-reactance model of six-phase synchronous machines considering stator mutual leakage inductance and main flux saturation. Electr. Power Syst. Res. 2016, 138, 155–164. [Google Scholar]
- Zhao, T.Y.; Li, G.B.; Pan, H.G.; Yuan, H.Q. Dynamic characteristics analysis for vehicle parts based on parallel optimization algorithm with CUDA. Eng. Comput. 2021, 38, 3622–3642. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, Z.F.; Zhao, T.Y.; Yang, J. Parameter Interval Uncertainty Analysis of Internal Resonance of Rotating Porous Shaft–Disk-Blade Assemblies Reinforced by Graphene Nanoplatelets. Materials 2021, 14, 5033. [Google Scholar] [CrossRef]
- Sun, H.T. Discussion on shafting torsional vibration of large turbo-generator sets. Therm. Power Gener. 2004, 1, 42–44; 54–88. [Google Scholar]
- Kimbark, E.W. Correction of IEEE Published Paper Suppression of Ground-Fault Arcs on Single-Pole-Switched EHV Lines bv Shunt Reactors. IEEE Power Eng. Rev. 1986, 6, 25. [Google Scholar] [CrossRef]
- Kimbark, E.W. Experimental analysis of double unbalances. Electr. Eng. 1935, 54, 205. [Google Scholar] [CrossRef]
- Kimbark, E.W. How to improve system stability without risking subsynchronous resonance. IEEE Trans. Energy Convers. 1977, 96, 1608–1619. [Google Scholar] [CrossRef]
- Kimbark, E.W. Power System Stability [Books and Reports]. IEEE Power Eng. Rev. 1995, 15, 40. [Google Scholar] [CrossRef]
- Dome, R.B. High-Efficiency Modulation System. Proc. IEEE 1938, 26, 963–982. [Google Scholar] [CrossRef]
- Ghasemi, S.; Allahbakhshi, M.; Behdani, B.; Tajdinian, M.; Popov, M. Probabilistic analysis of switching transients due to vacuum circuit breaker operation on wind turbine step-up transformers. Electr. Power Syst. Res. 2020. [Google Scholar] [CrossRef]
- Isidoro, G.; Gustavo, S.A. Delta-Wye Transformations and the Efficient Reduction of Almost-Planar Graphs. Electron. Notes Discret. Math. 2017, 62, 129–134. [Google Scholar]
- Isidoro, G.; Gustavo, S.A. An algorithm for delta–wye reduction of almost-planar graphs. Discret. Appl. Math. 2020, 285, 631–641. [Google Scholar]
- Juan, L.; Duarte, M.; Ospina, H.; González, Q. Dynamic Modeling and Simulation of an Underactuated System. J. Phys. Conf. Ser. 2017, 850, 012005. [Google Scholar]
- Duart, J.L.; Montero, B.; Ospina, P.A.; González, E. Dynamic Modeling and Simulation of a Rotational Inverted Pendulum. J. Phys. Conf. Ser. 2017, 792, 012081. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.F.; Lin, H. Application of MATLAB/SIMULINK in power system simulation. J. Xinjiang Univ. (Nat. Sci. Ed.) 2004, 2, 205–207. [Google Scholar]
- Rehman, A.U.; Chen, Y.; Wang, L. Simulation using MATLAB/SIMULINK on rotor winding inter-turn fault in DFIG/2016 IEEE International Conference on Dielectrics (ICD). IEEE 2016, 1, 506–509. [Google Scholar]
- Jiang, J.; Li, W.F.; Wang, X.J.; Sun, Q.; Wei, Q. Modal analysis of shaft system and spring foundation of turbine-generator unit model based on substructure method. Steam Turbine Technol. 2018, 60, 123–126. [Google Scholar]
- Liang, P.; Fan, L.L.; Long, X.F. The application of nonlinear model in vibration fault prediction of turbine generator sets. J. South China Univ. Technol. (Nat. Sci. Ed.) 2006, 6, 122–126. [Google Scholar]
- He, C.B.; Gu, Y.J.; Yang, K. Overview of torsional vibration model and algorithm of turbo-generator set. J. North China Electr. Power Univ. 2003, 2, 56–60. [Google Scholar]
- Wang, N.; Liang, Z.Q. The transfer matrix calculation method of natural frequency of rotor system and its MATLAB implementation. J. Sichuan Univ. Technol. (Nat. Sci. Ed.) 2006, 2, 55–59. [Google Scholar]
- Nazolin, A.L.; Polyakov, V.I.; Gnezdilov, S.G. Diagnostics of Shaft Trains of Large Turbine Sets for Integrity Using Torsional Vibration Measurements. Therm. Eng. 2020, 67, 25–35. [Google Scholar] [CrossRef]
- Briz, F.; Degner, M.W.; Lorenz, R.D. Analysis and design of current regulators using complex vectors. IEEE Trans. Ind. Appl. 2000, 36, 817–825. [Google Scholar] [CrossRef] [Green Version]
- Arumuga, T.; Muthukumar, D.; Saji, K.S. Matlab Simulation for Fault Analysis of Electrical Circuit on Hyperspectral Signal Processing. Int. J. Eng. Adv. Technol. (IJEAT) 2019, 9, 343–350. [Google Scholar]




| Order | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Frequency | 14.5 Hz | 22.3 Hz | 34.0 Hz | 61.9 Hz |
| Parameter | HP | IP | LP1 | LP2 |
|---|---|---|---|---|
| Volume time constant | 0.3 | 15 | 0.4 | 0.4 |
| Connection torque factor | 0.3 | 0.4 | 0.15 | 0.15 |
| Connection stiffness coefficient | 48.9 | 39.3 | 36 | 15.8 |
| Moment of inertia × 103(kg/m2) | 16.5 | 20.8 | 7.52 | 7.52 |
| Torsional rigidity × 108(Nm/rad) | 2.205 | 1.828 | 1.54 | 1.307 |
| Name | Parameter | Name | Parameter |
|---|---|---|---|
| Nominal power | 1112 MVA | Cross-axis ultra-transient reactance | 20.1% |
| Direct axis synchronous reactance | 261% | The transient time constant of straight axis short-circuit | 0.842% |
| Direct axis transient reactance | 23.8% | Subtransient time constant of straight-axis short-circuit | 0.030 s |
| Axial subtransient reactance | 18.2% | Transient time constant of cross-axis open circuit | 2.5 s |
| AC synchronous reactance | 248% | Subtransient time constant of open circuit | 0.2 s |
| AC transient reactance | 64.1% | Cross-axis stator resistance | 1.08 × 10−3 Ω/ph |
| Parameters | A-Phase Current | B-Phase Current | C-Phase Current | Current Torque | Power |
|---|---|---|---|---|---|
| Numerical value | 21192 A rms | 21192 A rms | 21192 A rms | 2.956 × 106 Nm | 9.9 × 108 W |
| Fault | Two-Phase Short-Circuit on the Grid Side | Three-Phase Short-Circuit on the Grid Side | Two-Phase Short-Circuit at Generator Terminals | Three-Phase Short-Circuit at Generator Terminals |
|---|---|---|---|---|
| Frequency of alternating electromagnetic force (Hz) | 51 | 49 | 49.5 | 48 |
| Fault | Two-Phase Short-Circuit on the Grid Side | Three-Phase Short-Circuit on the Grid Side | Two-Phase Short-Circuit at Generator Terminals | Three-Phase Short-Circuit at Generator Terminals |
|---|---|---|---|---|
| Maximum forward speed variable (rpm) | 20.1 | 74.8 | 31.2 | 41.7 |
| Maximum negative speed variable (rpm) | 22.3 | 87.0 | 46.2 | 37.6 |
| Extreme speed difference (rpm) | 22.2 | 90.3 | 47.9 | 48.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Wu, Y.; Pang, Z.; Fu, Y.; Zhao, T. Shafting Torsional Vibration Analysis of 1000 MW Unit under Electrical Short-Circuit Fault. Appl. Sci. 2021, 11, 9205. https://doi.org/10.3390/app11199205
Pan H, Wu Y, Pang Z, Fu Y, Zhao T. Shafting Torsional Vibration Analysis of 1000 MW Unit under Electrical Short-Circuit Fault. Applied Sciences. 2021; 11(19):9205. https://doi.org/10.3390/app11199205
Chicago/Turabian StylePan, Honggang, Yunshi Wu, Zhiyuan Pang, Yanming Fu, and Tianyu Zhao. 2021. "Shafting Torsional Vibration Analysis of 1000 MW Unit under Electrical Short-Circuit Fault" Applied Sciences 11, no. 19: 9205. https://doi.org/10.3390/app11199205
APA StylePan, H., Wu, Y., Pang, Z., Fu, Y., & Zhao, T. (2021). Shafting Torsional Vibration Analysis of 1000 MW Unit under Electrical Short-Circuit Fault. Applied Sciences, 11(19), 9205. https://doi.org/10.3390/app11199205








