How Insoluble Inclusions and Intersecting Layers Affect the Leaching Process within Potash Seams
Abstract
:1. Introduction
2. Materials and Methods
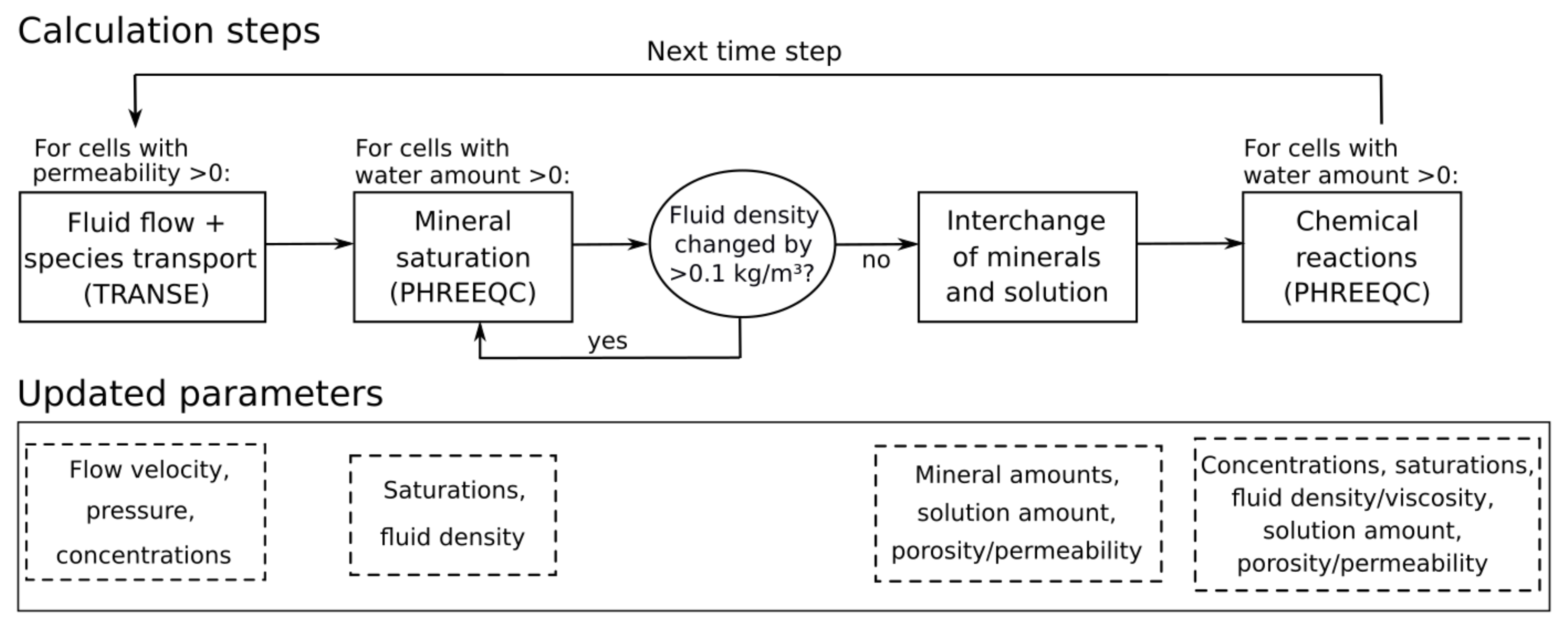
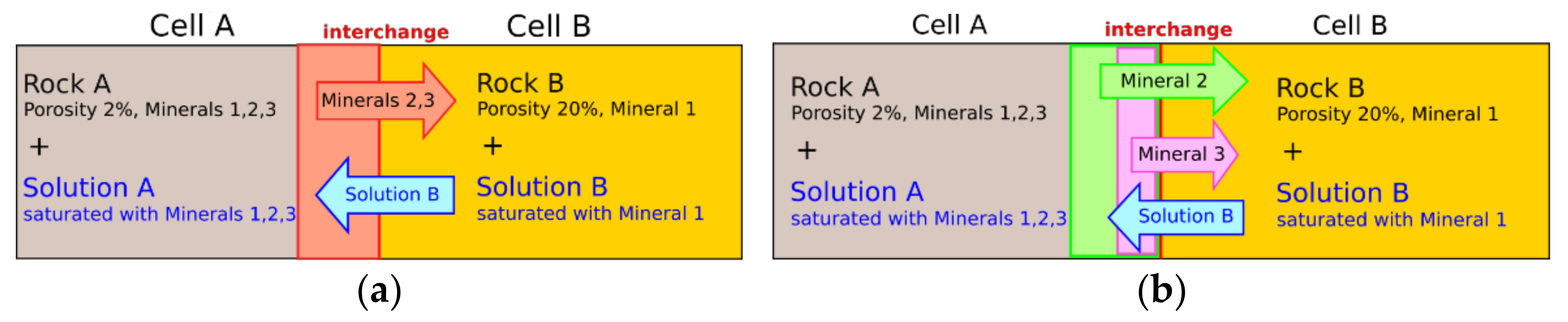
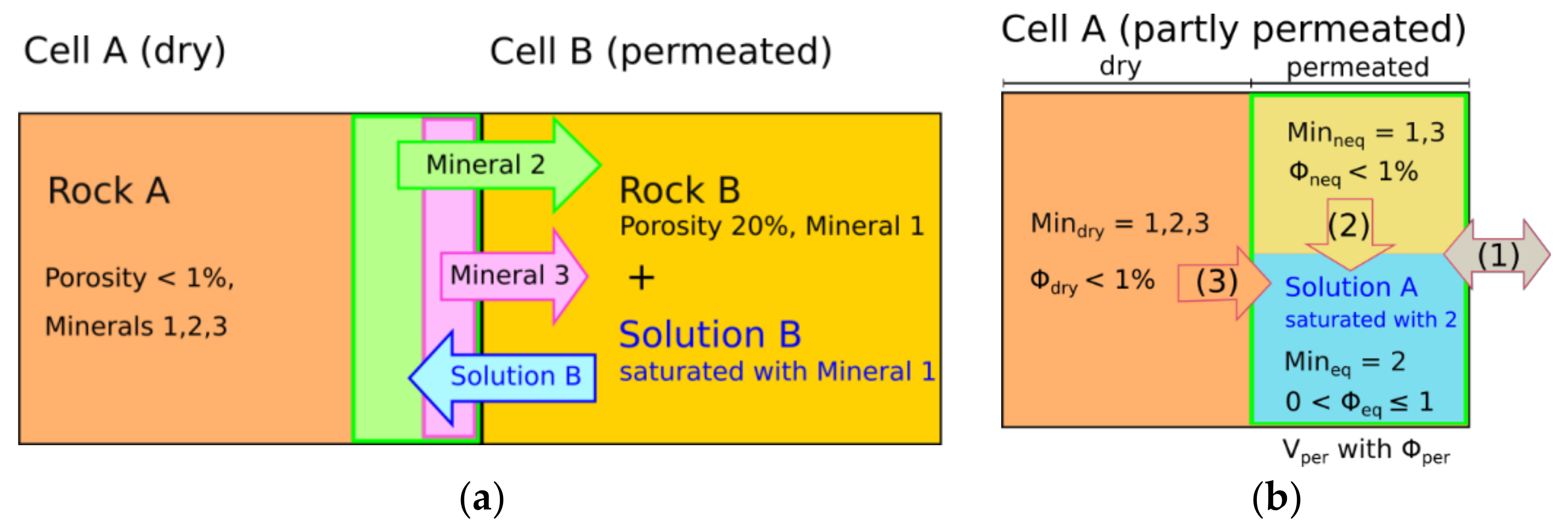
2.1. Extended Interchange Approach
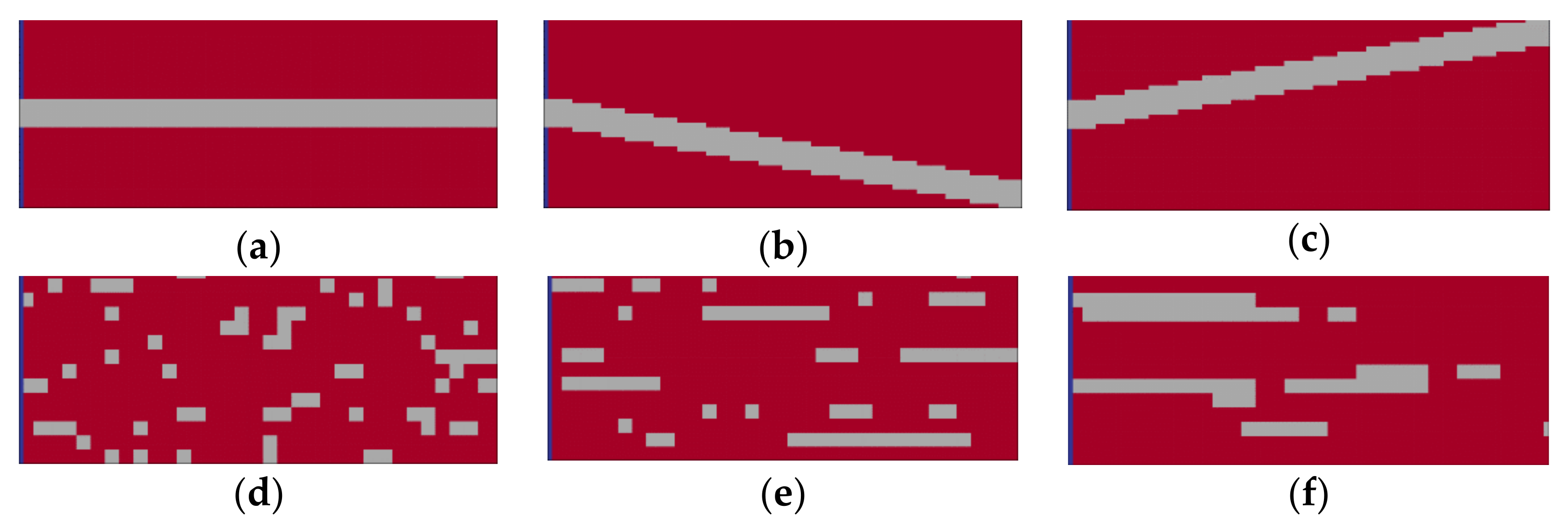
2.2. Scenario Analysis
3. Results
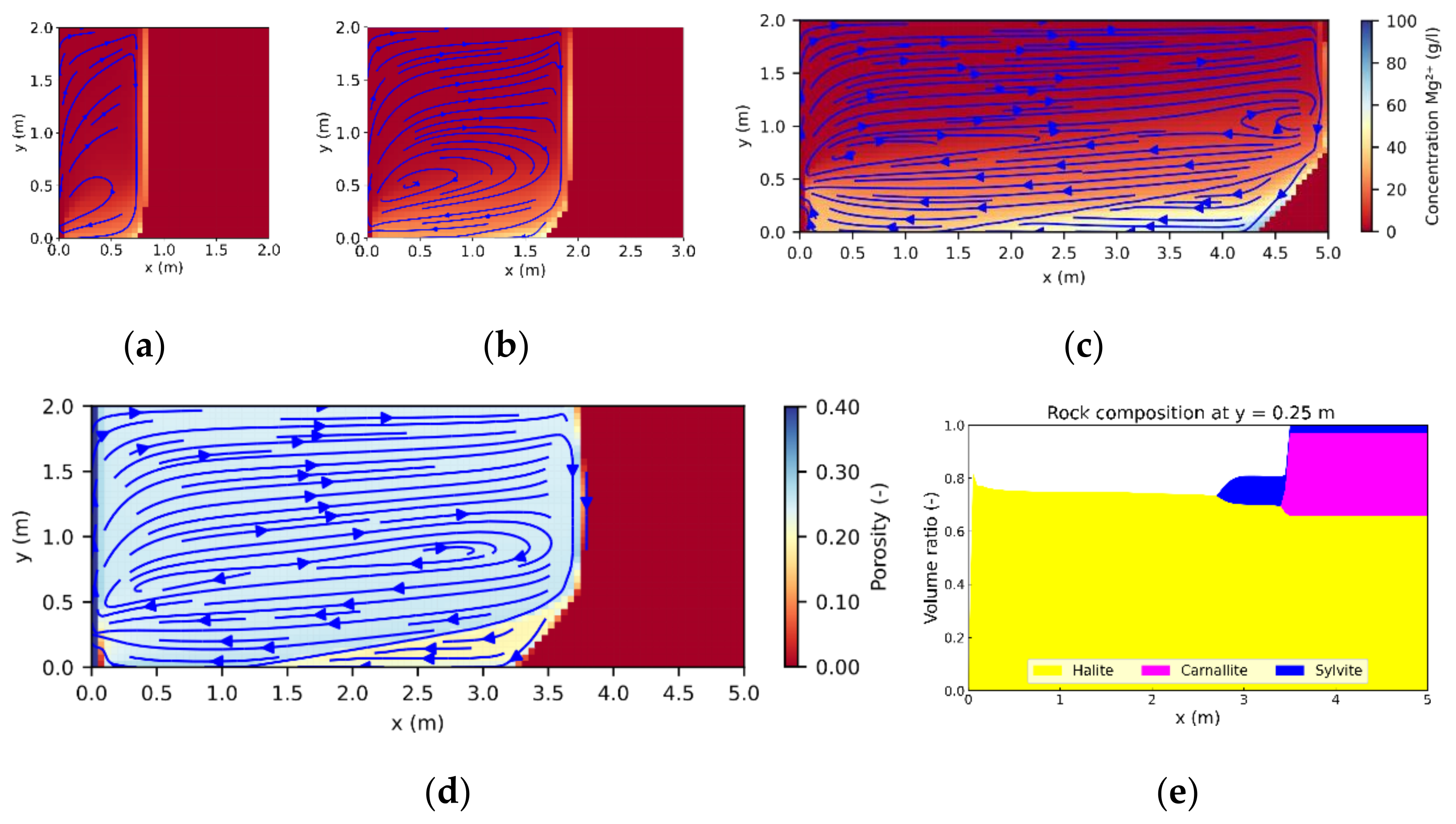
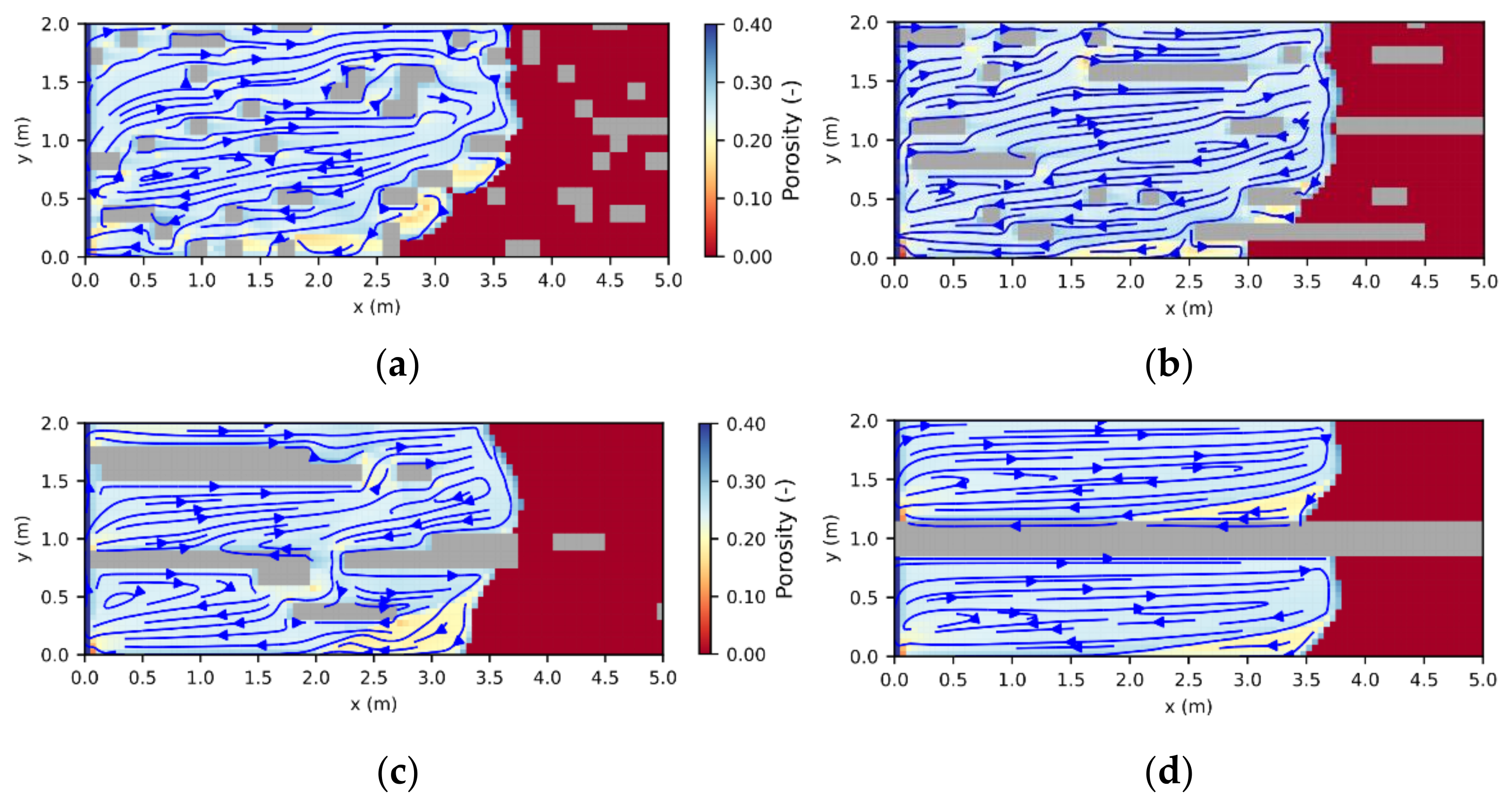
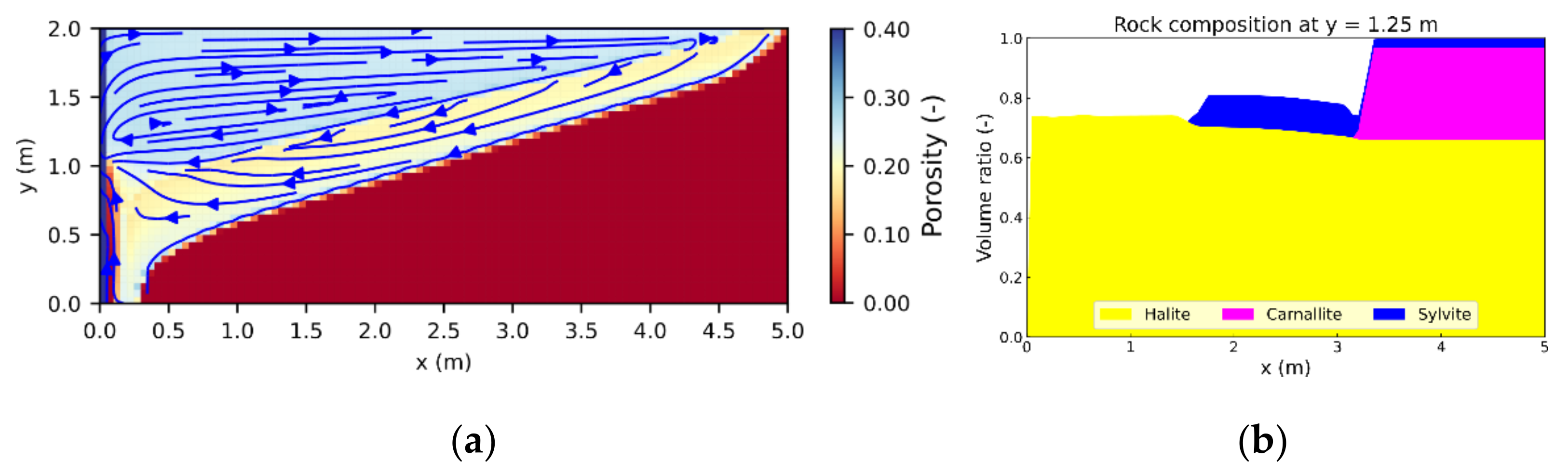
3.1. Leaching Zone Growth
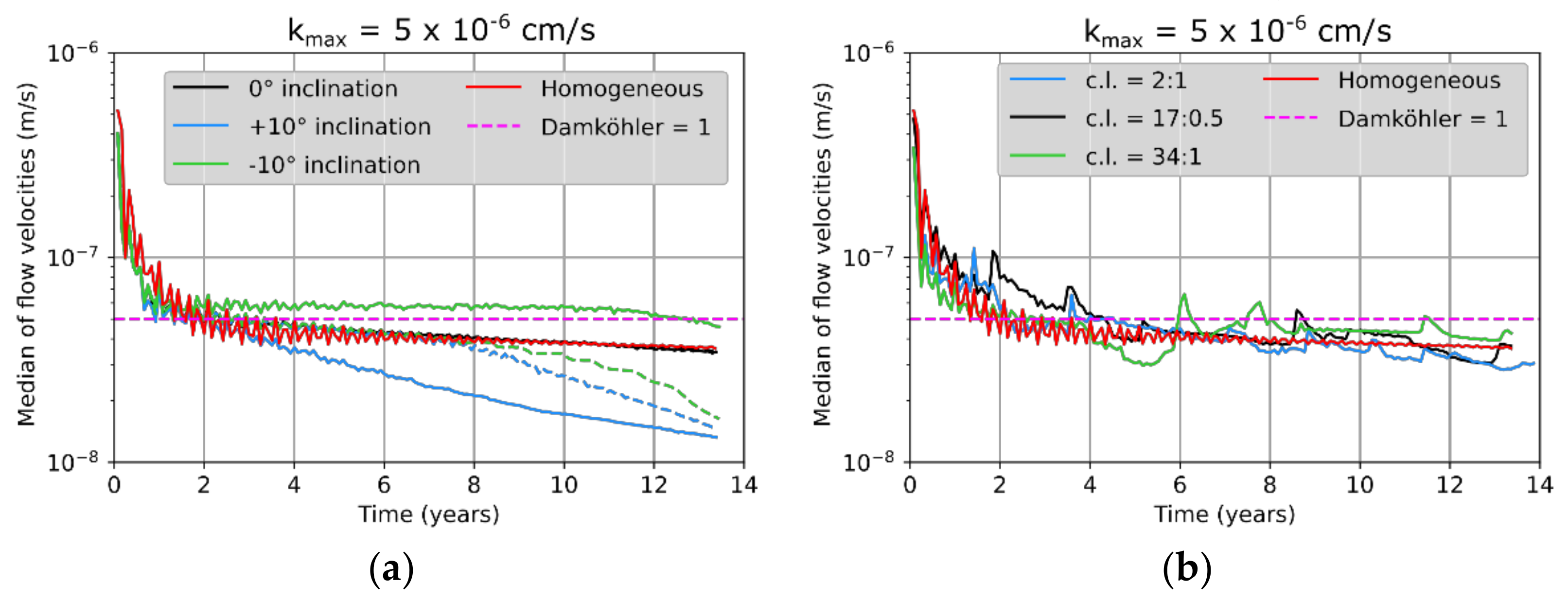
3.2. Péclet and Damköhler Numbers
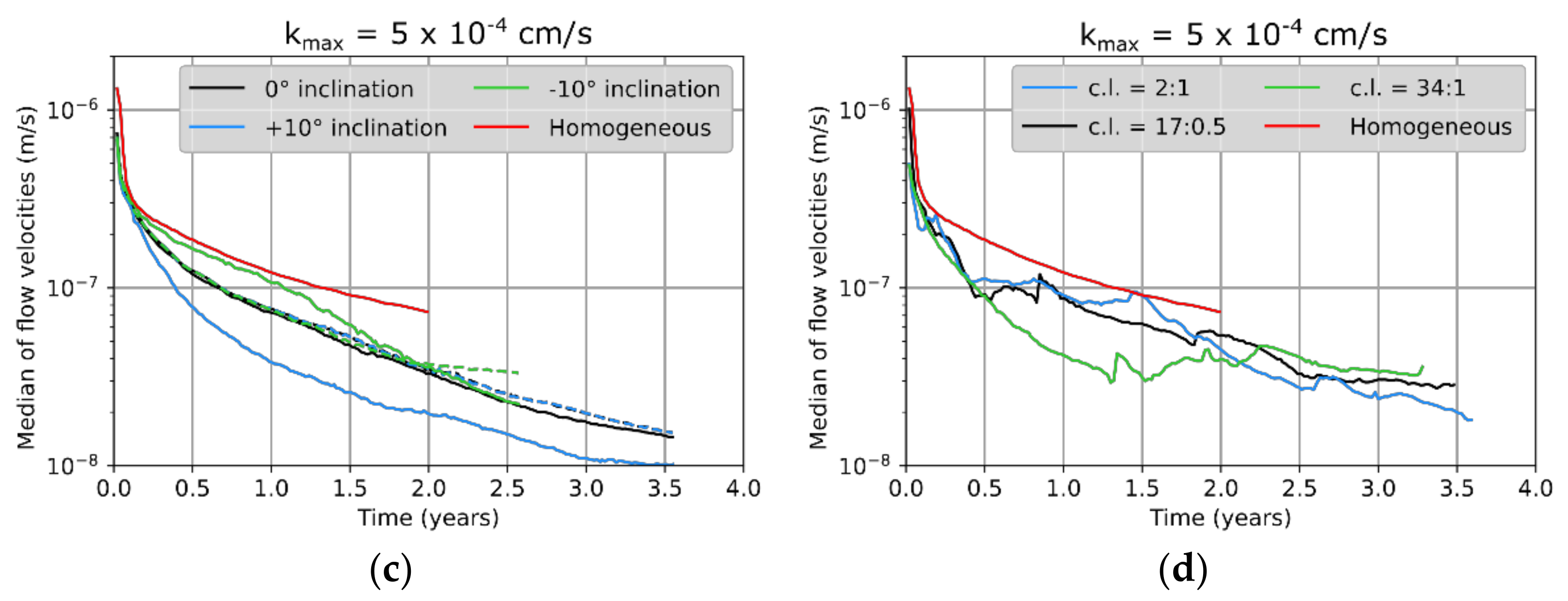
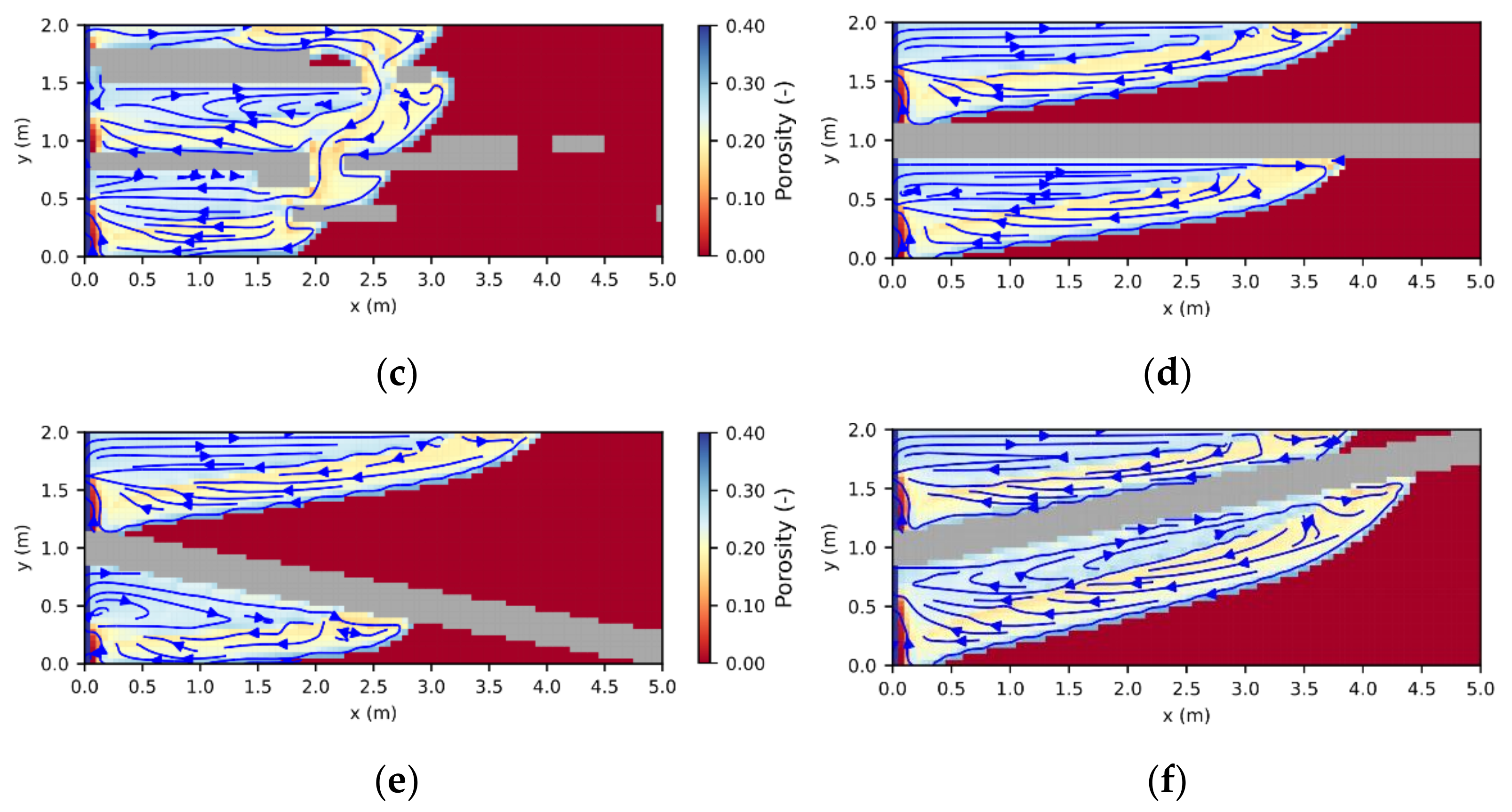
3.3. Leaching Zone Evolution for Low Dissolution Rates (Da ≈ 1)
3.4. Leaching Zone Evolution for High Dissolution Rates (Da > 1)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Warren, J.K. Salt usually seals, but sometimes leaks: Implications for mine and cavern stabilities in the short and long term. Earth Rev. 2017, 165, 302–341. [Google Scholar] [CrossRef]
- Prugger, F.F.; Prugger, A.F. Water problems in Saskatchewan potash mining—What can be learned from them? Undergr. Min. 1991, 84, 58–66. [Google Scholar]
- Boys, C. A Geological Approach to Potash Mining Problems in Saskatchewan, Canada. Explor. Min. Geol. 1993, 2, 129–138. [Google Scholar]
- Keime, M.; Charnavel, Y.; Lampe, G.; Theylich, H. Obstruction in a salt cavern: Solution is dissolution. In Proceedings of the 25th World Gas Conference, Kuala Lumpur, Malaysia, 4–8 June 2012. [Google Scholar]
- Mengel, K.; Röhlig, K.J.; Geckeis, H. Endlagerung radioaktiver Abfälle. Chemie Unserer Zeit 2012, 46, 208–217. [Google Scholar] [CrossRef]
- Steding, S.; Kempka, T.; Zirkler, A.; Kühn, M. Spatial and temporal evolution of leaching zones within potash seams reproduced by reactive transport simulations. Water 2021, 13, 168. [Google Scholar] [CrossRef]
- Thoms, R.L.; Gehle, R.M. Non-halites and fluids in salt formations, and effects on cavern storage operations. Geotech. Spec. Publ. 1999, 90, 780–796. [Google Scholar]
- Li, J.; Shi, X.; Yang, C.; Li, Y.; Wang, T.; Ma, H. Mathematical model of salt cavern leaching for gas storage in high-insoluble salt formations. Sci. Rep. Nat. 2018, 8, 372. [Google Scholar] [CrossRef] [PubMed]
- Jinlong, L.; Wenjie, X.; Jiangjing, Z.; Wei, L.; Xilin, S.; Chunhe, Y. Modeling the mining of energy storage salt caverns using a structural dynamic mesh. Energy 2020, 193, 116730. [Google Scholar] [CrossRef]
- Fokker, P.A. The behaviour of salt and salt caverns. Doctoral Dissertation, TU Delft, Delft, The Netherlands, 24 January 1995. Available online: http://resolver.tudelft.nl/uuid:6847f8e4-3b09-4787-be02-bcce9f0eed06 (accessed on 25 June 2021).
- Liu, M.; Shabaninejad, M.; Mostaghimi, P. Impact of mineralogical heterogeneity on reactive transport modelling. Comput. Geosci. 2017, 104, 12–19. [Google Scholar] [CrossRef]
- Wei, W.; Varavei, A.; Sanaei, A.; Sepehrnoori, K. Geochemical Modeling of Wormhole Propagation in Carbonate Acidizing Considering Mineralogy Heterogeneity. SPE J. 2019, 24, 2163–2181. [Google Scholar] [CrossRef]
- Kempka, T. Verification of a Python-based TRANsport Simulation Environment for density-driven fluid flow and coupled transport of heat and chemical species. Adv. Geosci. 2020, 54, 67–77. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-reaction, One-dimensional Transport, and Inverse Geochemical Calculations. In Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2013. [Google Scholar]
- Altmaier, M.; Brendler, V.; Bube, C.; Marquardt, C.; Moog, H.C.; Richter, A.; Scharge, T.; Voigt, W.; Wilhelm, S.; Wilms, T.; et al. THEREDA, Thermodynamische Referenz-Datenbasis; Report 265; Gesellschaft für Anlagen–Und Reaktorsicherheit (GRS): Braunschweig, Germany, 2011; 63p. [Google Scholar]
- Durie, R.; Jessen, F. Mechanism of the Dissolution of Salt in the Formation of Underground Salt Cavities. Soc. Pet. Eng. J. 1964, 4, 183–190. [Google Scholar] [CrossRef]
- Röhr, H.U. Lösungsgeschwindigkeiten von Salzmineralen beim Ausspülen von Hohlräumen im Salz. Kali Steinsalz 1981, 8, 103–111. [Google Scholar]
- Palandri, J.L.; Kharaka, Y.K. A Compilation of Rate Parameters of Water—Mineral Interaction Kinetics for Application to Geochemical Modeling; U.S. Geological Survey (USGS): Menlo Park, CA, USA, 2004; Available online: http://www.dtic.mil/cgi-bin/GetTRDoc?Location=U2&doc=GetTRDoc.pdf&AD=ADA440035 (accessed on 5 April 2021)Report 2004/1068.
- Alkattan, M.; Oelkers, E.; Dandurand, J.; Schott, J. Experimental studies of halite dissolution kinetics, 1 The effect of saturation state and the presence of trace metals. Chem. Geol. 1997, 137, 201–219. [Google Scholar] [CrossRef]
- Steding, S.; Zirkler, A.; Kühn, M. Geochemical reaction models quantify the composition of transition zones between brine occurrence and unaffected salt rock. Chem. Geol. 2020, 532, 119349. [Google Scholar] [CrossRef]
- Yang, X.; Liu, X.; Zang, W.; Lin, Z.; Wang, Q. A Study of Analytical Solution for the Special Dissolution Rate Model of Rock Salt. Adv. Mater. Sci. Eng. 2017, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Hoppe, H.; Winkler, F. Beitrag zur Lösekinetik von Mineralien der Kaliindustrie. Wiss. Z. Tech. Hochsch. Chem. Leuna-Mersebg. 1974, 16, 23–28. [Google Scholar]
- De Baere, B.; Molins, S.; Mayer, K.U.; François, R. Determination of mineral dissolution regimes using flow-through time-resolved analysis (FT-TRA) and numerical simulation. Chem. Geol. 2016, 430, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Dreybrodt, W.; Buhmann, D. A mass transfer model for dissolution and precipitation of calcite from solutions in turbulent motion. Chem. Geol. 1991, 90, 107–122. [Google Scholar] [CrossRef]
- Raines, M.A.; Dewers, T.A. Mixed transport/reaction control of gypsum dissolution kinetics in aqueous solutions and initiation of gypsum karst. Chem. Geol. 1997, 140, 29–48. [Google Scholar] [CrossRef]
- Ahoulou, A.W.A.; Tinet, A.J.; Oltéan, C.; Golfier, F. Experimental Insights into the Interplay Between Buoyancy, Convection, and Dissolution Reaction. J. Geophys. Res. Solid Earth 2020, 125, 1–18. [Google Scholar] [CrossRef]
- Dutka, F.; Starchenko, V.; Osselin, F.; Magni, S.; Szymczak, P.; Ladd, A.J.C. Time-dependent shapes of a dissolving mineral grain: Comparisons of simulations with microfluidic experiments. Chem. Geol. 2020, 540, 119459. [Google Scholar] [CrossRef]
- Höntzsch, S.; Zeibig, S. Geogenic caverns in rock salt formations—A key to the understanding of genetic processes and the awareness of hazard potential. In Earth System Dynamics, GeoFrankfurt 2014, Frankfurt a.M., Germany, Sept 2014; Schweizerbart Science Publishers: Stuttgart, Germany, 2014. [Google Scholar]
- Koch, K.; Vogel, J. Zu den Beziehungen von Tektonik, Sylvinitbildung und Basaltintrusionen im Werra-Kaligebiet. In Freiberger Forschungshefte; VEB Deutscher Verlag für Grundstoffindustrie: Leipzig, Germany, 1980; C 347; 104p. [Google Scholar]
- Müller, S.; Schüler, L. GeoStat-Framework/GSTools. Zenodo 2019. [Google Scholar] [CrossRef]
- Xie, M.; Kolditz, O.; Moog, H. A geochemical transport model for thermo-hydro-chemical (THC) coupled processes with saline water. Water Resour. Res. 2011, 47, W02545. [Google Scholar] [CrossRef]
- Yuan-Hui, L.; Gregory, S. Diffusion of ions in sea water and in deep-sea sediments. Geochim. Cosmochim. Acta 1974, 38, 703–714. [Google Scholar] [CrossRef]
- Field, L.; Milodowski, A.E.; Evans, D.; Palumbo-Roe, B.; Hall, M.R.; Marriott, A.L.; Barlow, T.; Devez, A. Determining constraints imposed by salt fabrics on the morphology of solution-mined energy storage cavities, through dissolution experiments using brine and seawater in halite. Q. J. Eng. Geol. Hydrogeol. 2019, 52, 240–254. [Google Scholar] [CrossRef]
- Weisbrod, N.; Alon-Mordish, C.; Konen, E.; Yechieli, Y. Dynamic dissolution of halite rock during flow of diluted saline solutions. Geophys. Res. Lett. 2012, 39, L09404. [Google Scholar] [CrossRef]
- Oltéan, C.; Golfier, F.; Buès, M.A. Numerical and experimental investigation of buoyancy-driven dissolution in vertical fracture. Journal of Geophysical Research: Solid Earth 2013, 118, 2038–2048. [Google Scholar] [CrossRef]
- Gechter, D.; Huggenberger, P.; Ackerer, P.; Niklaus Waber, H. Genesis and shape of natural solution cavities within salt deposits. Water Resour. Res. 2008, 44, W11409. [Google Scholar] [CrossRef] [Green Version]
- Molins, S.; Trebotich, D.; Steefel, C.I.; Shen, C. An investigation of the effect of pore scale flow on average geochemical reaction rates using direct numerical simulation. Water Resour. Res. 2012, 48, 1–11. [Google Scholar] [CrossRef]





| Mineral | Density (kg/m3) | Reaction Equation (Dissolution) | Log K |
|---|---|---|---|
| Carnallite | 1600 | KMgCl3∙6H2O → 3Cl− + 6 H2O + K+ + Mg2+ | 4.33 |
| Halite | 2170 | NaCl → Cl− + Na+ | 1.586 |
| Sylvite | 1990 | KCl → Cl− + K+ | 0.915 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steding, S.; Kempka, T.; Kühn, M. How Insoluble Inclusions and Intersecting Layers Affect the Leaching Process within Potash Seams. Appl. Sci. 2021, 11, 9314. https://doi.org/10.3390/app11199314
Steding S, Kempka T, Kühn M. How Insoluble Inclusions and Intersecting Layers Affect the Leaching Process within Potash Seams. Applied Sciences. 2021; 11(19):9314. https://doi.org/10.3390/app11199314
Chicago/Turabian StyleSteding, Svenja, Thomas Kempka, and Michael Kühn. 2021. "How Insoluble Inclusions and Intersecting Layers Affect the Leaching Process within Potash Seams" Applied Sciences 11, no. 19: 9314. https://doi.org/10.3390/app11199314
APA StyleSteding, S., Kempka, T., & Kühn, M. (2021). How Insoluble Inclusions and Intersecting Layers Affect the Leaching Process within Potash Seams. Applied Sciences, 11(19), 9314. https://doi.org/10.3390/app11199314






