Exciton-Photon Interactions in Semiconductor Nanocrystals: Radiative Transitions, Non-Radiative Processes and Environment Effects
Abstract
:1. Introduction
2. Light Emission in Nanocrystals
2.1. Spontaneous Emission Rate
2.2. Nanocrystals of Direct-Band-Gap Materials
2.3. Silicon Nanocrystals
3. Nonradiative Processes
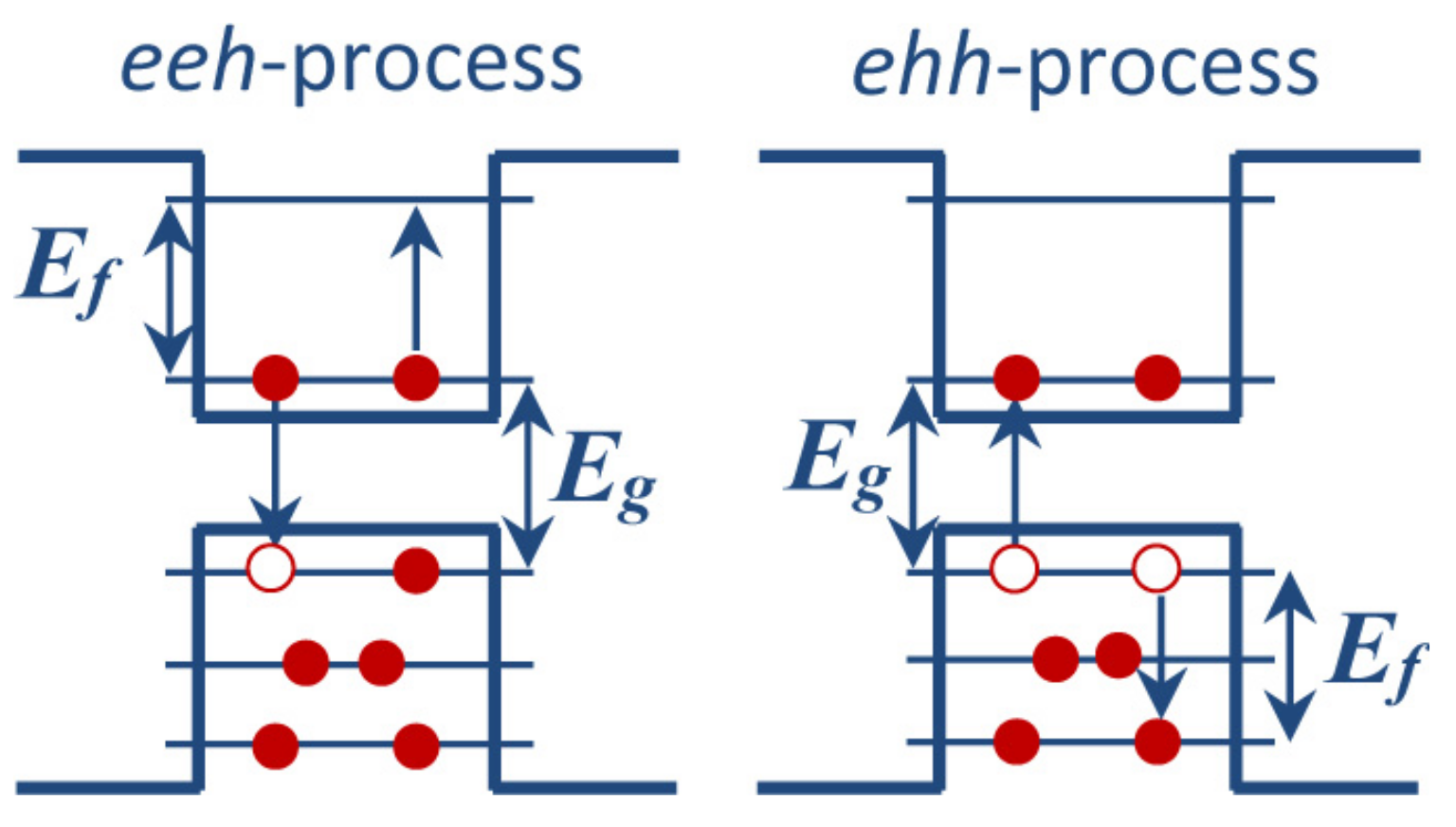
3.1. Auger Recombination
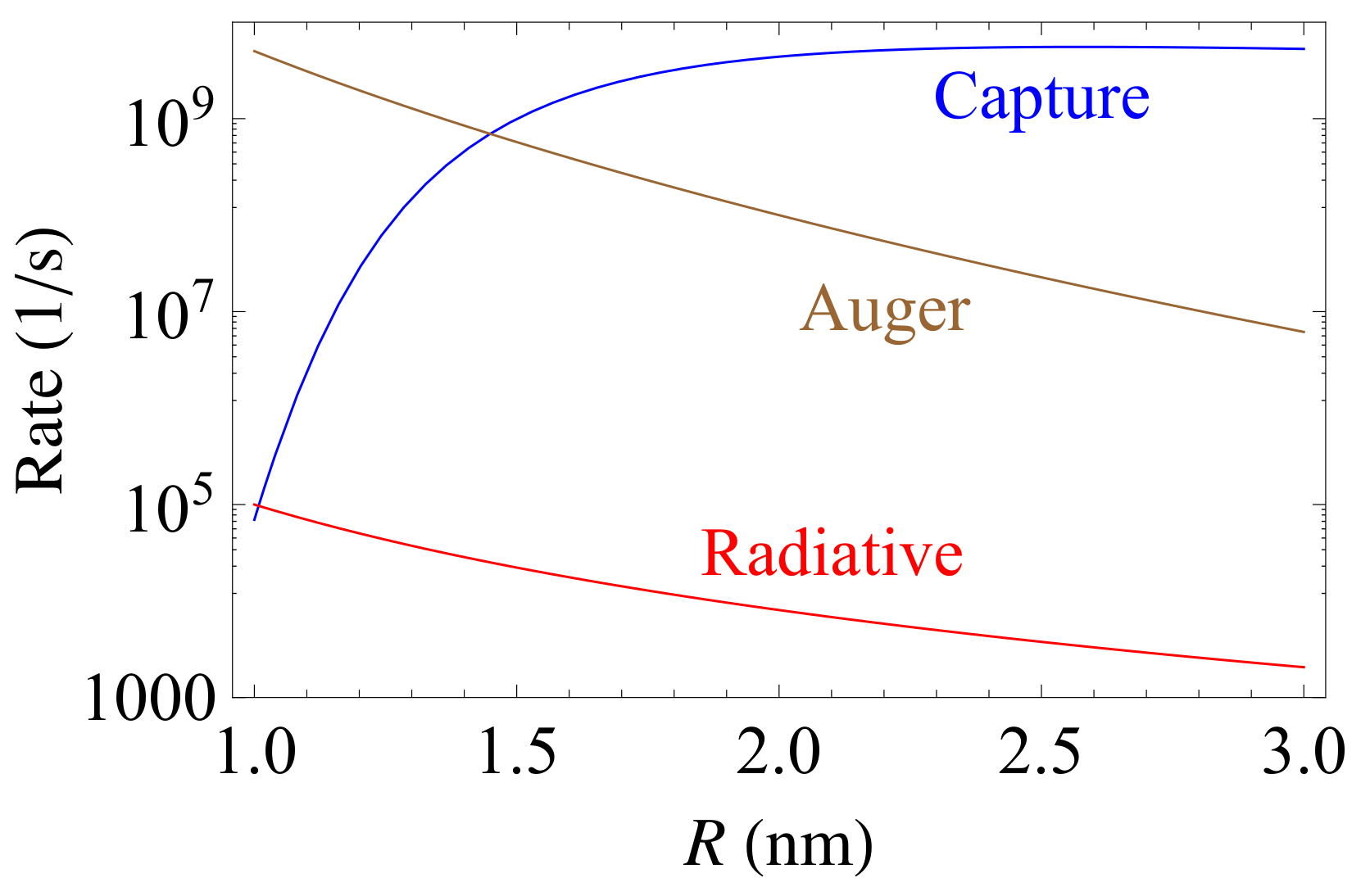
3.2. Capture on Dangling Bonds
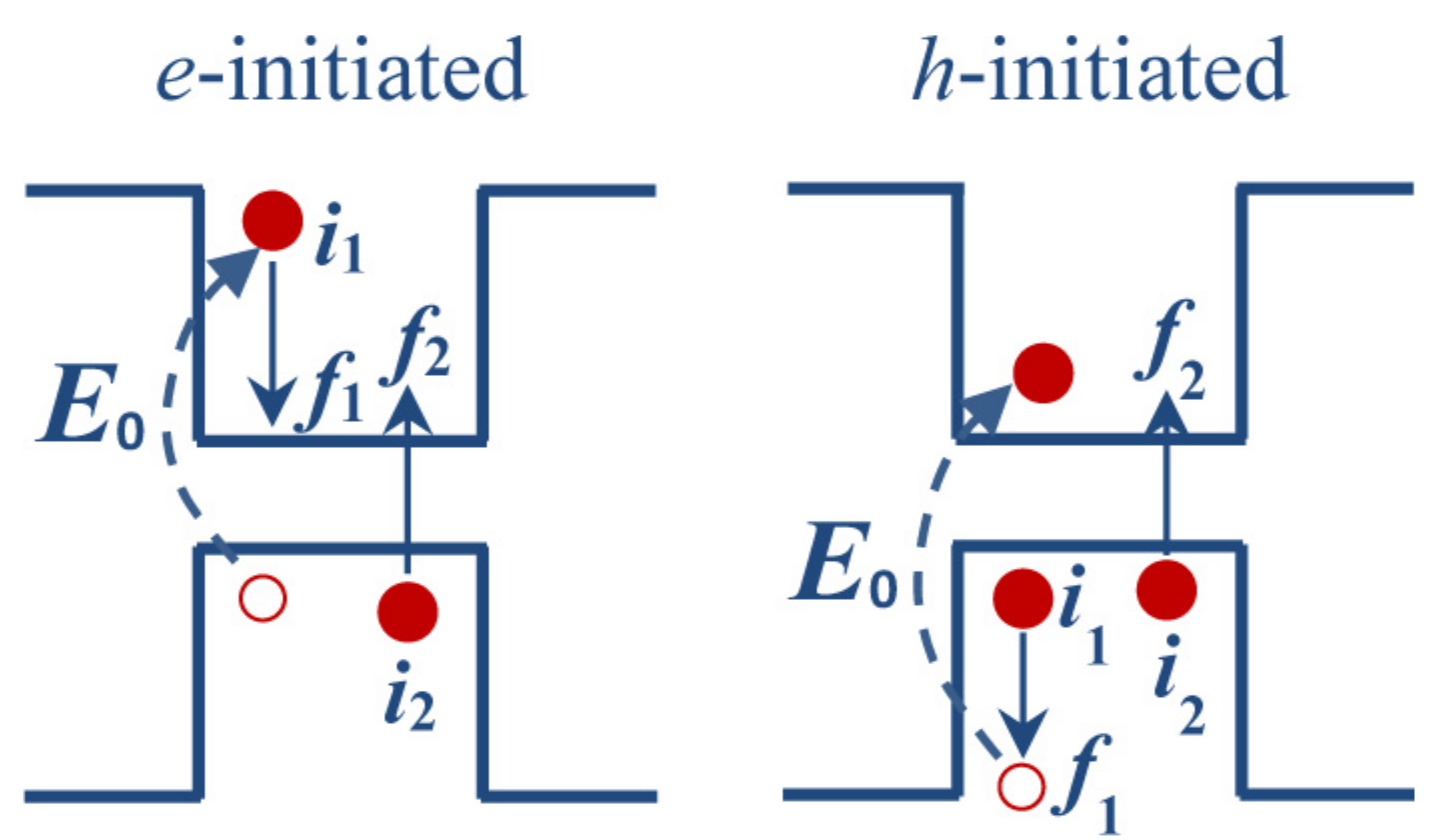
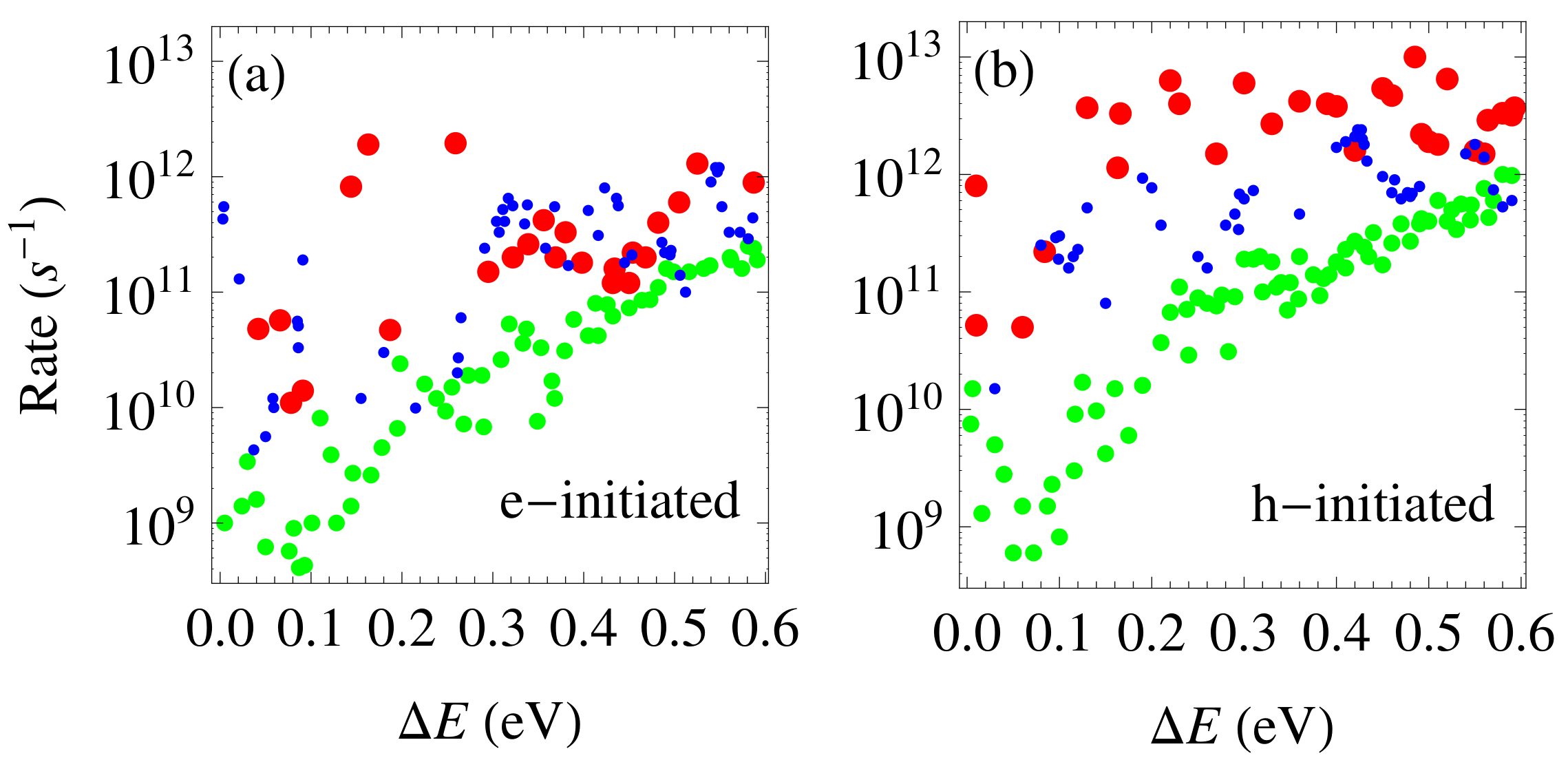
3.3. Phonon-Assisted Relaxation of Hot Carriers
- (i)
- The polaron has a rather short lifetime [162] because of the anharmonic effects that lead to a fast decay of nanocrystal’s optical phonons forming the polaron.
- (ii)
- Acoustic phonons can provide the possibility of transitions between different (exciton-) polaron states formed mostly by the interaction with optical phonons; the polaron spectrum is discrete but relatively dense owing to the non-adiabaticity of this interaction [148]. If the acoustic phonon spectrum is continuous, this additional interaction would drive the polaron dynamics towards equilibrium.
- (iii)
- In the strong confinement regime where the electron’s kinetic energy is larger than the electron–hole interaction, the electron (eventually dressed by phonons and forming the polaron) can relax by an Auger-type mechanism. The excess energy is first transferred from the electron to the hole through their Coulomb interaction and the subsequent hole’s cooling occurs via emission of acoustic phonons [163,164]. It can be feasible because the hole level spacings are relatively small in QDs and match the continuum of acoustic phonon energies.
4. Multiple Exciton Generation
5. FRET in Ensembles of Nanocrystals
6. QD Emitters Near a Flat Interface
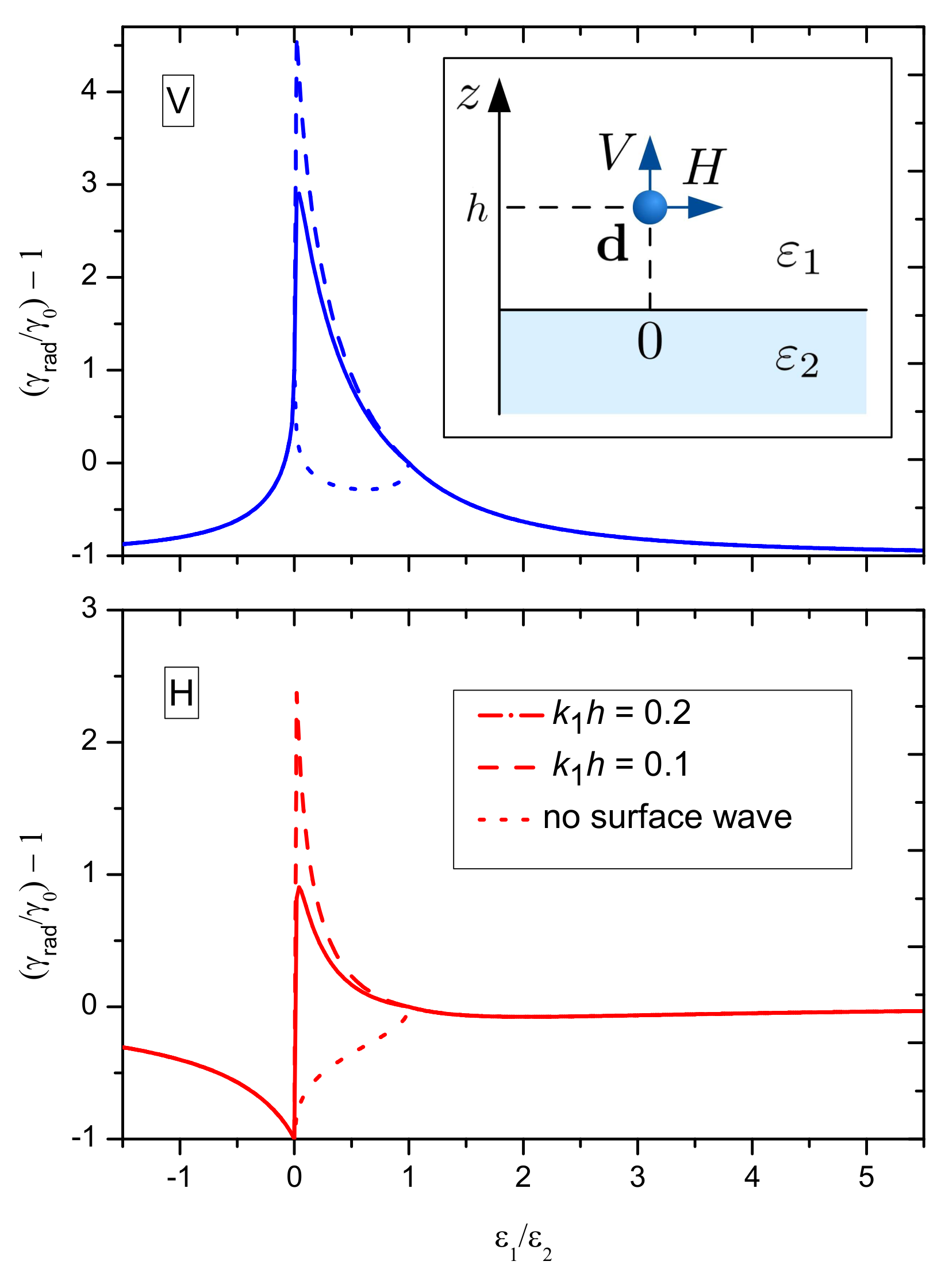
6.1. Radiative Lifetime Near Interface
6.2. Non-Radiative Losses to a Metal Substrate
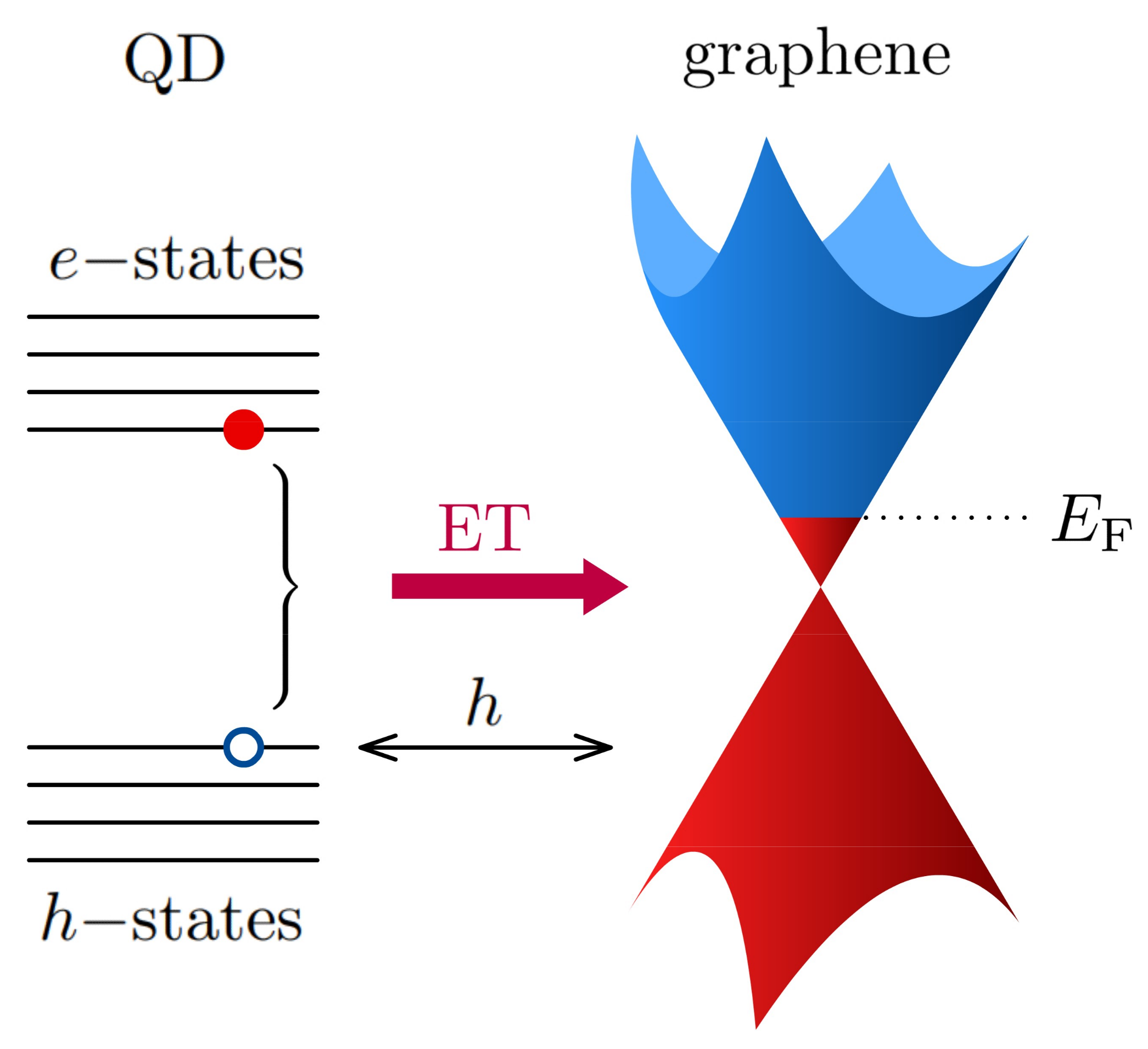
6.3. Energy Transfer to a 2D Material
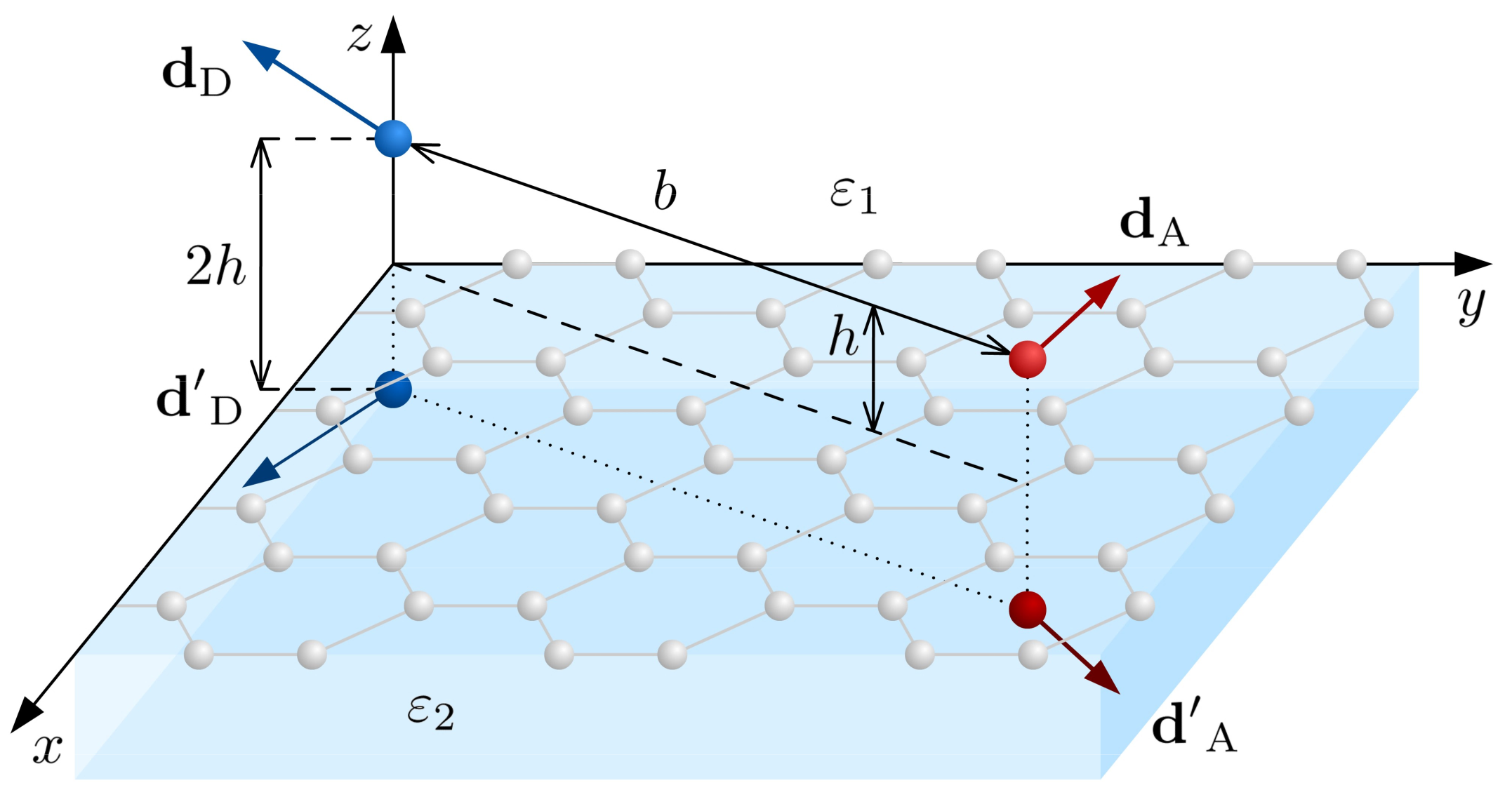
6.4. FRET between QDs Near Interface
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashoori, R.C. Electrons in artificial atoms. Nature 1996, 379, 413–419. [Google Scholar] [CrossRef]
- Efros, A.L.; Efros, A.L. Interband absorption of light in a semiconductor sphere. Sov. Phys. Semicond. 1982, 16, 772–775. [Google Scholar]
- Brus, L.E. A simple model for the ionization potential, electron affinity, and aqueous redox potentials of small semiconductor crystallites. J. Chem. Phys. 1983, 79, 5566–5571. [Google Scholar] [CrossRef]
- Kanemitsu, Y. Photoluminescence spectrum and dynamics in oxidized silicon nanocrystals: A nanoscopic disorder system. Phys. Rev. B 1996, 53, 13515–13520. [Google Scholar] [CrossRef] [PubMed]
- Zhuravlev, K.S.; Gilinsky, A.M.; Kobitsky, A.Y. Mechanism of photoluminescence of Si nanocrystals fabricated in a SiO2 matrix. Appl. Phys. Lett. 1998, 73, 2962–2964. [Google Scholar] [CrossRef]
- Tetelbaum, D.; Trushin, S.; Burdov, V.; Golovanov, A.; Revin, D.; Gaponova, D. The influence of phosphorus and hydrogen ion implantation on the photoluminescence of SiO2 with Si nanoinclusions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2001, 174, 123–129. [Google Scholar] [CrossRef]
- Negro, L.D.; Cazzanelli, M.; Pavesi, L.; Ossicini, S.; Pacifici, D.; Franzò, G.; Priolo, F.; Iacona, F. Dynamics of stimulated emission in silicon nanocrystals. Appl. Phys. Lett. 2003, 82, 4636–4638. [Google Scholar] [CrossRef]
- Tsybeskov, L.; Hirschman, K.D.; Duttagupta, S.P.; Zacharias, M.; Fauchet, P.M.; McCaffrey, J.P.; Lockwood, D.J. Nanocrystalline-silicon superlattice produced by controlled recrystallization. Appl. Phys. Lett. 1998, 72, 43–45. [Google Scholar] [CrossRef]
- Nayfeh, M.H.; Rao, S.; Barry, N.; Therrien, J.; Belomoin, G.; Smith, A.; Chaieb, S. Observation of laser oscillation in aggregates of ultrasmall silicon nanoparticles. Appl. Phys. Lett. 2002, 80, 121–123. [Google Scholar] [CrossRef]
- Meldrum, A.; Hryciw, A.; MacDonald, A.N.; Blois, C.; Marsh, K.; Wang, J.; Li, Q. Photoluminescence in the silicon-oxygen system. J. Vac. Sci. Technol. A Vac. Surf. Films 2006, 24, 713–717. [Google Scholar] [CrossRef]
- Murray, C.B.; Norris, D.J.; Bawendi, M.G. Synthesis and characterization of nearly monodisperse CdE (E = sulfur, selenium, tellurium) semiconductor nanocrystallites. J. Am. Chem. Soc. 1993, 115, 8706–8715. [Google Scholar] [CrossRef]
- Rogach, A.L. (Ed.) Semiconductor Nanocrystal Quantum Dots; Springer: Wien, Vienna, 2008. [Google Scholar]
- Bruchez, M.; Moronne, M.; Gin, P.; Weiss, S.; Alivisatos, A.P. Semiconductor Nanocrystals as Fluorescent Biological Labels. Science 1998, 281, 2013–2016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voznyy, O.; Levina, L.; Fan, F.; Walters, G.; Fan, J.Z.; Kiani, A.; Ip, A.H.; Thon, S.M.; Proppe, A.H.; Liu, M.; et al. Origins of Stokes Shift in PbS Nanocrystals. Nano Lett. 2017, 17, 7191–7195. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, W.; He, J.; Liu, Z.; Xu, K.; Chen, Z.; Yang, X.; Li, D.; Xia, Y.; Zhang, J.; Chen, C. Lead Selenide (PbSe) Colloidal Quantum Dot Solar Cells with >10% Efficiency. Adv. Mater. 2019, 31, 1900593. [Google Scholar] [CrossRef]
- Dohnalova, K.; Gregorkiewicz, T.; Kusova, K. Silicon quantum dots: Surface matters. J. Phys. Condens. Matter 2014, 26, 173201. [Google Scholar] [CrossRef]
- McVey, B.; Prabakar, S.; Gooding, J.; Tilley, R. Solution Synthesis, Surface Passivation, Optical Properties, Biomedical Applications, and Cytotoxicity of Silicon and Germanium Nanocrystals. ChemPlusChem 2017, 82, 60–70. [Google Scholar] [CrossRef]
- Memon, U.; Chatterjee, U.; Ganthi, M.; Tiwari, S.; Duttagupta, S. Synthesis of ZnSe Quantum Dots with Stoichiometric Ratio Difference and Study of its Optoelectronic Property. Procedia Mater. Sci. 2014, 5, 1027–1033. [Google Scholar] [CrossRef] [Green Version]
- Senthilkumar, K.; Kalaivani, T.; Kanagesan, S.; Balasubramanian, V. Synthesis and characterization studies of ZnSe quantum dots. J. Mater. Sci. Mater. Electron. 2012, 23, 2048–2052. [Google Scholar] [CrossRef]
- Baum, F.; da Silva, M.; Linden, G.; Feijo, D.; Rieder, E.; Santos, M. Growth dynamics of zinc selenide quantum dots: The role of oleic acid concentration and synthesis temperature on driving optical properties. J. Nanopart. Res. 2019, 21, 42. [Google Scholar] [CrossRef]
- Moura, I.; Filho, P.; Seabra, M.; Pereira, G.; Pereira, G.; Fontes, A.; Santos, B. Highly fluorescent positively charged ZnSe quantum dots for bioimaging. J. Lumin. 2018, 201, 284–289. [Google Scholar] [CrossRef]
- Talapin, D.V.; Rogach, A.L.; Kornowski, A.; Haase, M.; Weller, H. Highly Luminescent Monodisperse CdSe and CdSe/ZnS Nanocrystals Synthesized in a Hexadecylamine-Trioctylphosphine Oxide-Trioctylphospine Mixture. Nano Lett. 2001, 1, 207–211. [Google Scholar] [CrossRef]
- Maiti, S.; van der Laan, M.; Poonia, D.; Schall, P.; Kinge, S.; Siebbeles, L. Emergence of new materials for exploiting highly efficient carrier multiplication in photovoltaics. Chem. Phys. Rev. 2020, 1, 011302. [Google Scholar] [CrossRef]
- Ji, B.; Koley, S.; Slobodkin, V.; Remennik, S.; Banin, U. ZnSe/ZnS Core/Shell Quantum Dots with Superior Optical Properties through Thermodynamic Shell Growth. Nano Lett. 2020, 20, 2387–2395. [Google Scholar] [CrossRef]
- Silicon NanocrystalsPavesi, L.; Turan, R. (Eds.) Silicon NanocrystalsWiley VCH Verlag GmbH: Weinheim, Germany, 2010.
- Pereira, R.N.; Niesar, S.; Wiggers, H.; Brandt, M.S.; Stutzmann, M.S. Depassivation kinetics in crystalline silicon nanoparticles. Phys. Rev. B 2013, 88, 155430. [Google Scholar] [CrossRef]
- Otsuka, M.; Kurokawa, Y.; Ding, Y.; Juangsa, F.B.; Shibata, S.; Kato, T.; Nozaki, T. Silicon nanocrystal hybrid photovoltaic devices for indoor light energy harvesting. RSC Adv. 2020, 10, 12611–12618. [Google Scholar] [CrossRef]
- Holman, Z.C.; Liu, C.Y.; Kortshagen, U.R. Germanium and Silicon Nanocrystal Thin-Film Field-Effect Transistors from Solution. Nano Lett. 2010, 10, 2661–2666. [Google Scholar] [CrossRef] [PubMed]
- Bourzac, K. Quantum dots go on display. Nature 2013, 493, 283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qasim, K.; Lei, W.; Li, Q. Quantum dots for light emitting diodes. J. Nanosci. Nanotechnol. 2013, 13, 3173–3185. [Google Scholar] [CrossRef] [PubMed]
- Available online. Available online: https://www.samsung.com/us/televisions-home-theater/tvs/qled-tv/ (accessed on 20 December 2020).
- Available online. Available online: https://www.osram.com/os/technologies/quantum_dot_technology.jsp (accessed on 20 December 2020).
- Liu, Z.; Lin, C.H.; Hyun, B.R.; Sher, C.W.; Lv, Z.; Luo, B.; Jiang, F.; Wu, T.; Ho, C.H.; Kuo, H.C.; et al. Micro-light-emitting diodes with quantum dots in display technology. Light Sci. Appl. 2020, 9, 83. [Google Scholar] [CrossRef] [PubMed]
- Basko, D.M.; Agranovich, V.M.; Bassani, F.; Rocca, G.C.L. Colloidal metal films as a substrate for surface–enhanced spectroscopy. Eur. Phys. J. B 2000, 13, 653. [Google Scholar] [CrossRef]
- Achermann, M.; Petruska, M.A.; Kos, S.; Smith, D.L.; Koleska, D.D.; Klimov, V.I. Energy-transfer pumping of semiconductor nanocrystals using an epitaxial quantum well. Nature 2004, 429, 642–646. [Google Scholar] [CrossRef] [PubMed]
- Theuerholtz, T.S.; Carmele, A.; Richter, M.; Knorr, A. Influence of Förster interaction on light emission statistics in hybrid systems. Phys. Rev. B 2013, 87, 245313. [Google Scholar] [CrossRef] [Green Version]
- Lunz, M.; Zhang, X.; Gerard, V.A.; Gunko, Y.K.; Lesnyak, V.; Gaponik, N.; Susha, A.S.; Rogach, A.L.; Bradley, A.L. Effect of Metal Nanoparticle Concentration on Localized Surface Plasmon Mediated Foerster Resonant Energy Transfer. J. Phys. Chem. C 2012, 116, 26529–26534. [Google Scholar] [CrossRef]
- Pompa, P.P.; Martiradonna, L.; Torre, A.D.; Sala, F.D.; Manna, L.; Vittorio, M.D.; Calabi, F.; Cingolani, R.; Rinaldi, R. Metal-enhanced fluorescence of colloidal nanocrystals with nanoscale control. Nat. Nanotechnol. 2006, 1, 126–130. [Google Scholar] [CrossRef]
- Chen, Z.; Berciaud, S.; Nuckolls, C.; Heinz, T.F.; Brus, L.E. Energy transfer from individual semiconductor nanocrystals to graphene. ACS Nano 2010, 4, 2964–2968. [Google Scholar] [CrossRef] [Green Version]
- Biehs, S.A.; Agarwal, G.S. Large enhancement of Foerster resonance energy transfer on graphene platforms. Appl. Phys. Lett. 2013, 103, 243112. [Google Scholar] [CrossRef] [Green Version]
- Dovzhenko, D.S.; Ryabchuk, S.V.; Rakovich, Y.P.; Nabiev, I.R. Light-matter interaction in the strong coupling regime: Configurations, conditions and applications. Nanoscale 2018, 10, 3589–3605. [Google Scholar] [CrossRef]
- Klimov, V.I. Multicarrier Interactions in Semiconductor Nanocrystals in Relation to the Phenomena of Auger Recombination and Carrier Multiplication. Annu. Rev. Condens. Matter Phys. 2014, 5, 285–316. [Google Scholar] [CrossRef]
- Bruhn, B.; Limpens, R.; Chung, N.X.; Schall, P.; Gregorkiewicz, T. Spectroscopy of carrier multiplication in nanocrystals. Sci. Rep. 2016, 6, 20538. [Google Scholar] [CrossRef] [Green Version]
- Haverkort, J.E.M.; Garnett, E.C.; Bakkers, E.P.A.M. Fundamentals of the nanowire solar cell: Optimization of the open circuit voltage. Appl. Phys. Rev. 2018, 5, 031106. [Google Scholar] [CrossRef] [Green Version]
- Khriachtchev, L.; Ossicini, S.; Iacona, F.; Gourbilleau, F. Silicon Nanoscale Materials: From Theoretical Simulations to Photonic Applications. Int. J. Photoenergy 2012, 2012, 872576. [Google Scholar] [CrossRef]
- Ray, S.K.; Maikap, S.; Banerjee, W.; Das, S. Nanocrystals for silicon-based light-emitting and memory devices. J. Phys. D Appl. Phys. 2013, 46, 153001. [Google Scholar] [CrossRef]
- Barbagiovanni, E.G.; Lockwood, D.J.; Simpson, P.J.; Goncharova, L.V. Quantum confinement in Si and Ge nanostructures: Theory and experiment. Appl. Phys. Rev. 2014, 1, 011302. [Google Scholar] [CrossRef] [Green Version]
- Priolo, F.; Gregorkiewicz, T.; Galli, M.; Krauss, T.F. Silicon nanostructures for photonics and photovoltaics. Nat. Nanotechnol. 2014, 9, 19–32. [Google Scholar] [CrossRef]
- Förster, T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 1948, 437, 55–75. [Google Scholar] [CrossRef]
- Dexter, D.L. A theory of sensitized luminescence in solids. J. Chem. Phys. 1953, 21, 836–850. [Google Scholar] [CrossRef]
- Reich, K.V.; Shklovskii, B.I. Exciton Transfer in Array of Epitaxially Connected Nanocrystals. ACS Nano 2016, 10, 10267–10274. [Google Scholar] [CrossRef] [Green Version]
- Kagan, C.R.; Murray, C.B.; Nirmal, M.; Bawendi, M.G. Electronic Energy Transfer in CdSe Quantum Dot Solids. Phys. Rev. Lett. 1996, 76, 1517–1520. [Google Scholar] [CrossRef]
- Crooker, S.A.; Hollingsworth, J.A.; Tretiak, S.; Klimov, V.I. Spectrally Resolved Dynamics of Energy Transfer in Quantum-Dot Assemblies: Towards Engineered Energy Flows in Artificial Materials. Phys. Rev. Lett. 2002, 89, 186802. [Google Scholar] [CrossRef] [Green Version]
- Franzl, T.; Klar, T.A.; Scheitinger, S.; Rogach, A.L.; Feldmann, J. Exciton Recycling in Graded Gap Nanocrystal Structures. Nano Lett. 2004, 4, 1599. [Google Scholar] [CrossRef]
- Lunz, M.; Bradley, A.L.; Chen, W.Y.; Gerard, V.A.; Byrne, S.J.; Gun’ko, Y.K.; Lesnyak, V.; Gaponik, N. Influence of quantum dot concentration on Förster resonant energy transfer in monodispersed nanocrystal quantum dot monolayers. Phys. Rev. B 2010, 81, 205316. [Google Scholar] [CrossRef]
- Lunz, M.; Bradley, A.L.; Gerard, V.A.; Byrne, S.J.; Gun’ko, Y.K.; Lesnyak, V.; Gaponik, N. Concentration dependence of Förster resonant energy transfer between donor and acceptor nanocrystal quantum dot layers: Effect of donor-donor interactions. Phys. Rev. B 2011, 83, 115423. [Google Scholar] [CrossRef]
- Yu, D. n-Type Conducting CdSe Nanocrystal Solids. Science 2003, 300, 1277–1280. [Google Scholar] [CrossRef] [PubMed]
- Kawazoe, T.; Kobayashi, K.; Ohtsu, M. Optical nanofountain: A biomimetic device that concentrates optical energy in a nanometric region. Appl. Phys. Lett. 2005, 86, 103102. [Google Scholar] [CrossRef]
- Linnros, J.; Lalic, N.; Galeckas, A.; Grivickas, V. Analysis of the stretched exponential photoluminescence decay from nanometer-sized silicon crystals in SiO2. J. Appl. Phys. 1999, 86, 6128–6134. [Google Scholar] [CrossRef]
- Heitmann, J.; Müller, F.; Yi, L.; Zacharias, M.; Kovalev, D.; Eichhorn, F. Excitons in Si nanocrystals: Confinement and migration effects. Phys. Rev. B 2004, 69, 195309. [Google Scholar] [CrossRef] [Green Version]
- Glover, M.; Meldrum, A. Effect of “buffer layers” on the optical properties of silicon nanocrystal superlattices. Opt. Mater. 2005, 27, 977–982. [Google Scholar] [CrossRef]
- Ben-Chorin, M.; Möller, F.; Koch, F.; Schirmacher, W.; Eberhard, M. Hopping transport on a fractal: Ac conductivity of porous silicon. Phys. Rev. B 1995, 51, 2199–2213. [Google Scholar] [CrossRef]
- Priolo, F.; Franzò, G.; Pacifici, D.; Vinciguerra, V.; Iacona, F.; Irrera, A. Role of the energy transfer in the optical properties of undoped and Er-doped interacting Si nanocrystals. J. Appl. Phys. 2001, 89, 264–272. [Google Scholar] [CrossRef]
- Balberg, I.; Savir, E.; Jedrzejewski, J. The mutual exclusion of luminescence and transport in nanocrystalline silicon networks. J. Non-Cryst. Solids 2004, 338–340, 102–105. [Google Scholar] [CrossRef]
- Santos, J.R.; Vasilevskiy, M.I.; Filonovich, S.A. Energy transfer via exciton transport in quantum dot based self-assembled fractal structures. Phys. Rev. B 2008, 78, 245422. [Google Scholar] [CrossRef] [Green Version]
- Wargnier, R.; Baranov, A.V.; Maslov, V.G.; Stsiapura, V.; Artemyev, M.; Pluot, M.; Sukhanova, A.; Nabiev, I. Energy Transfer in Aqueous Solutions of Oppositely Charged CdSe/ZnS Core/Shell Quantum Dots and in Quantum Dot-Nanogold Assemblies. Nano Lett. 2004, 4, 451–457. [Google Scholar] [CrossRef]
- Sukhanova, A.; Baranov, A.V.; Perova, T.S.; Cohen, J.H.; Nabiev, I. Controlled Self-Assembly of Nanocrystals into Polycrystalline Fluorescent Dendrites with Energy-Transfer Properties. Angew. Chem. 2006, 45, 2048. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, C.; Moura, I.; Fernandez, Y.; Pereira, E.; Coutinho, P.; Garcia, A.; Schellenberg, P.; Belsley, M.; Costa, M.; Stauber, T.; et al. Energy transfer via exciton transport in quantum dot based self-assembled fractal structures. J. Phys. Chem. C 2014, 118, 4982–4990. [Google Scholar] [CrossRef]
- Rabouw, F.T.; den Hartog, S.A.; Senden, T.; Meijerink, A. Photonic effects on the Förster resonance energy transfer efficiency. Nat. Photonics 2014, 5, 3610. [Google Scholar] [CrossRef] [PubMed]
- Chance, R.P.; Prock, A.; Silbey, R. Molecular fluorescence and energy transfer near interfaces. Adv. Chem. Phys. 1978, 37, 1–65. [Google Scholar]
- Koppens, F.H.L.; Chang, D.E.; Garcia de Abajo, F.J. Graphene Plasmonics: A Platform for Strong Light–Matter Interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef] [Green Version]
- Purcell, E.M. Spontaneous emission probability at radio frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar]
- Gérard, J.M.; Sermage, B.; Gayral, B.; Legrand, B.; Costard, E.; Thierry-Mieg, V. Enhanced Spontaneous Emission by Quantum Boxes in a Monolithic Optical Microcavity. Phys. Rev. Lett. 1998, 81, 1110–1113. [Google Scholar] [CrossRef]
- Senden, T.; Rabouw, F.T.; Meijerink, A. Photonic Effects on the Radiative Decay Rate and Luminescence quantum Yield of Doped Nanocrystals. ACS Nano 2015, 9, 1801–1808. [Google Scholar] [CrossRef]
- Shimizu, K.T.; Woo, W.K.; Fisher, B.R.; Eisler, H.J.; Bawendi, M.G. Surface-Enhanced Emission from Single Semiconductor Nanocrystals. Phys. Rev. Lett. 2002, 89, 117401. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, R.; Do, J.; Roller, E.-M.; Zhang, T.; Schäler, V.J.; Nickels, P.C.; Feldmann, J.; Liedl, T. Hierarchical assembly of metal nanoparticles, quantum dots and organic dyes using DNA origami scaffolds. Nat. Nanotechnol. 2014, 9, 74. [Google Scholar] [CrossRef] [PubMed]
- Rakovich, A.; Albella, P.; Maier, S.A. Plasmonic control of radiative properties of semiconductor quantum dots coupled to plasmonic ring cavities. ACS Nano 2015, 9, 2648. [Google Scholar] [CrossRef] [Green Version]
- Novotny, L.; Hehct, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Thränhardt, A.; Ell, C.; Khitrova, G.; Gibbs, H.M. Relation between dipole moment and radiative lifetime in interface fluctuation quantum dots. Phys. Rev. B 2002, 65, 035327. [Google Scholar] [CrossRef]
- Efros, A.L.; Rosen, M.; Kuno, M.; Nirmal, M.; Norris, D.J.; Bawendi, M. Band-edge exciton in quantum dots of semiconductors with a degenerate valence band: Dark and bright exciton states. Phys. Rev. B 1996, 54, 4843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belyakov, V.A.; Burdov, V.A.; Gaponova, D.M.; Mikhaylov, A.N.; Tetelbaum, D.I.; Trushin, S.A. Phonon-assisted radiative electron-hole recombination in silicon quantum dots. Phys. Solid State 2004, 46, 27–31. [Google Scholar] [CrossRef]
- Tetelbaum, D.; Karpovich, I.; Stepikhova, M.; Shengurov, V.; Markov, K.; Gorshkov, O. Characteristics of photoluminescence in SiO2 with Si nanoinclusions produced by ion implantation. In Surface Investigation; OPA (Overseas Publishers Association) N.V.: New York, NY, USA, 1998; Volume 14, pp. 601–604. [Google Scholar]
- Fujii, M.; Mimura, A.; Hayashi, S.; Yamamoto, K. Photoluminescence from Si nanocrystals dispersed in phosphosilicate glass thin films: Improvement of photoluminescence efficiency. Appl. Phys. Lett. 1999, 75, 184–186. [Google Scholar] [CrossRef]
- Tetelbaum, D.I.; Gorshkov, O.N.; Burdov, V.A.; Trushin, S.A.; Mikhaylov, A.N.; Gaponova, D.M.; Morozov, S.V.; Kovalev, A.I. The influence of P+, B+, and N+ ion implantation on the luminescence properties of the SiO2: Nc-Si system. Phys. Solid State 2004, 46, 17–21. [Google Scholar] [CrossRef]
- Belov, A.I.; Belyakov, V.A.; Burdov, V.A.; Mikhailov, A.N.; Tetelbaum, D.I. Phosphorus doping as an efficient way to modify the radiative interband recombination in silicon nanocrystals. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2009, 3, 527–533. [Google Scholar] [CrossRef]
- Belyakov, V.; Belov, A.; Mikhaylov, A.; Tetelbaum, D.; Burdov, V. Improvement of the photon generation efficiency in phosphorus-doped silicon nanocrystals: Γ-X mixing of the confined electron states. J. Phys. Condens. Matter 2009, 21, 045803. [Google Scholar] [CrossRef]
- Nomoto, K.; Yang, T.C.J.; Ceguerra, A.V.; Zhang, T.; Lin, Z.; Breen, A.; Wu, L.; Puthen-Veettil, B.; Jia, X.; Conibeer, G.; et al. Microstructure analysis of silicon nanocrystals formed from silicon rich oxide with high excess silicon: Annealing and doping effects. J. Appl. Phys. 2017, 122, 025102. [Google Scholar] [CrossRef]
- Klimešová, E.; Kůsová, K.; Vacík, J.; Holý, V.; Pelant, I. Tuning luminescence properties of silicon nanocrystals by lithium doping. J. Appl. Phys. 2012, 112, 064322. [Google Scholar] [CrossRef]
- Kim, T.Y.; Park, N.M.; Kim, K.H.; Sung, G.Y.; Ok, Y.W.; Seong, T.Y.; Choi, C.J. Quantum confinement effect of silicon nanocrystals in situ grown in silicon nitride films. Appl. Phys. Lett. 2004, 85, 5355–5357. [Google Scholar] [CrossRef]
- Klangsin, J.; Marty, O.; Munguía, J.; Lysenko, V.; Vorobey, A.; Pitaval, M.; Céreyon, A.; Pillonnet, A.; Champagnon, B. Structural and luminescent properties of silicon nanoparticles incorporated into zirconia matrix. Phys. Lett. A 2008, 372, 1508–1511. [Google Scholar] [CrossRef]
- Nozaki, T.; Sasaki, K.; Ogino, T.; Asahi, D.; Okazaki, K. Microplasma synthesis of tunable photoluminescent silicon nanocrystals. Nanotechnology 2007, 18, 235603. [Google Scholar] [CrossRef]
- Zhou, S.; Ding, Y.; Pi, X.; Nozaki, T. Doped silicon nanocrystals from organic dopant precursor by a SiCl4-based high frequency nonthermal plasma. Appl. Phys. Lett. 2014, 105, 183110. [Google Scholar] [CrossRef]
- Baldwin, R.K.; Pettigrew, K.A.; Garno, J.C.; Power, P.P.; yu Liu, G.; Kauzlarich, S.M. Room Temperature Solution Synthesis of Alkyl-Capped Tetrahedral Shaped Silicon Nanocrystals. J. Am. Chem. Soc. 2002, 124, 1150–1151. [Google Scholar] [CrossRef]
- Wolf, O.; Dasog, M.; Yang, Z.; Balberg, I.; Veinot, J.G.C.; Millo, O. Doping and Quantum Confinement Effects in Single Si Nanocrystals Observed by Scanning Tunneling Spectroscopy. Nano Lett. 2013, 13, 2516–2521. [Google Scholar] [CrossRef]
- Bell, J.P.; Cloud, J.E.; Cheng, J.; Ngo, C.; Kodambaka, S.; Sellinger, A.; Williams, S.K.R.; Yang, Y. N-Bromosuccinimide-based bromination and subsequent functionalization of hydrogen-terminated silicon quantum dots. RSC Adv. 2014, 4, 51105–51110. [Google Scholar] [CrossRef]
- Zhou, T.; Anderson, R.T.; Li, H.; Bell, J.; Yang, Y.; Gorman, B.P.; Pylypenko, S.; Lusk, M.T.; Sellinger, A. Bandgap Tuning of Silicon Quantum Dots by Surface Functionalization with Conjugated Organic Groups. Nano Lett. 2015, 15, 3657–3663. [Google Scholar] [CrossRef]
- Carroll, G.M.; Limpens, R.; Neale, N.R. Tuning Confinement in Colloidal Silicon Nanocrystals with Saturated Surface Ligands. Nano Lett. 2018, 18, 3118–3124. [Google Scholar] [CrossRef] [PubMed]
- Belyakov, V.; Burdov, V. Γ-X mixing in phosphorus-doped silicon nanocrystals: Improvement of photon generation efficiency. Phys. Rev. B 2009, 79, 35302. [Google Scholar] [CrossRef]
- Kůsová, K.; Cibulka, O.; Dohnalová, K.; Pelant, I.; Valenta, J.; Fučíková, A.; Žídek, K.; Lang, J.; Englich, J.; Matějka, P.; et al. Brightly Luminescent Organically Capped Silicon Nanocrystals Fabricated at Room Temperature and Atmospheric Pressure. ACS Nano 2010, 4, 4495–4504. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Chen, X.; Pi, X.; Yang, D. Theoretical Study of Chlorine for Silicon Nanocrystals. J. Phys. Chem. C 2011, 115, 12822–12825. [Google Scholar] [CrossRef]
- Ma, Y.; Pi, X.; Yang, D. Fluorine-Passivated Silicon Nanocrystals: Surface Chemistry versus Quantum Confinement. J. Phys. Chem. C 2012, 116, 5401–5406. [Google Scholar] [CrossRef]
- Wang, R.; Pi, X.; Yang, D. Surface modification of chlorine-passivated silicon nanocrystals. Phys. Chem. Chem. Phys. 2013, 15, 1815. [Google Scholar] [CrossRef]
- Dohnalová, K.; Poddubny, A.N.; Prokofiev, A.A.; de Boer, W.D.; Umesh, C.P.; Paulusse, J.M.; Zuilhof, H.; Gregorkiewicz, T. Surface brightens up Si quantum dots: Direct bandgap-like size-tunable emission. Light Sci. Appl. 2013, 2, e47. [Google Scholar] [CrossRef]
- Poddubny, A.N.; Dohnalová, K. Direct band gap silicon quantum dots achieved via electronegative capping. Phys. Rev. B 2014, 90, 245439. [Google Scholar] [CrossRef] [Green Version]
- Derbenyova, N.V.; Burdov, V.A. Effect of Doping with Shallow Donors on Radiative and Nonradiative Relaxation in Silicon Nanocrystals: Ab Initio Study. J. Phys. Chem. C 2017, 122, 850–858. [Google Scholar] [CrossRef]
- Derbenyova, N.V.; Burdov, V.A. Radiative decay rates in Si crystallites with a donor ion. J. Appl. Phys. 2018, 123, 161598. [Google Scholar] [CrossRef]
- Sangghaleh, F.; Sychugov, I.; Yang, Z.; Veinot, J.G.C.; Linnros, J. Near-Unity Internal Quantum Efficiency of Luminescent Silicon Nanocrystals with Ligand Passivation. ACS Nano 2015, 9, 7097–7104. [Google Scholar] [CrossRef] [PubMed]
- Belyakov, V.A.; Burdov, V.A. Chemical-shift enhancement for strongly confined electrons in silicon nanocrystals. Phys. Lett. A 2007, 367, 128–134. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Burdov, V.A. Fine Splitting of Electron States in Silicon Nanocrystal with a Hydrogen-like Shallow Donor. Nanoscale Res. Lett. 2007, 2, 569–575. [Google Scholar] [CrossRef] [Green Version]
- Belyakov, V.A.; Burdov, V.A. Anomalous splitting of the hole states in silicon quantum dots with shallow acceptors. J. Phys. Condens. Matter 2007, 20, 025213. [Google Scholar] [CrossRef]
- Chelikowsky, J.R.; Alemany, M.M.G.; Chan, T.L.; Dalpian, G.M. Computational studies of doped nanostructures. Rep. Prog. Phys. 2011, 74, 046501. [Google Scholar] [CrossRef]
- Oliva-Chatelain, B.L.; Ticich, T.M.; Barron, A.R. Doping silicon nanocrystals and quantum dots. Nanoscale 2016, 8, 1733–1745. [Google Scholar] [CrossRef]
- Arduca, E.; Perego, M. Doping of silicon nanocrystals. Mater. Sci. Semicond. Process. 2017, 62, 156–170. [Google Scholar] [CrossRef]
- Nomoto, K.; Sugimoto, H.; Breen, A.; Ceguerra, A.V.; Kanno, T.; Ringer, S.P.; Wurfl, I.P.; Conibeer, G.; Fujii, M. Atom Probe Tomography Analysis of Boron and/or Phosphorus Distribution in Doped Silicon Nanocrystals. J. Phys. Chem. C 2016, 120, 17845–17852. [Google Scholar] [CrossRef]
- Marri, I.; Degoli, E.; Ossicini, S. First Principle Studies of B and P Doped Si Nanocrystals. Phys. Status Solidi A 2017, 215, 1700414. [Google Scholar] [CrossRef]
- Hiller, D.; Lopez-Vidrier, J.; Gutsch, S.; Zacharias, M.; Nomoto, K.; Konig, D. Defect-Induced luminescence quenching vs. Charge carrier generation of phosphorus incorporated in silicon nanocrystals as function of size. Sci. Rep. 2017, 7, 863. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.C.J.; Nomoto, K.; Puthen-Veettil, B.; Lin, Z.; Wu, L.; Zhang, T.; Jia, X.; Conibeer, G.; Perez-Wurfl, I. Properties of silicon nanocrystals with boron and phosphorus doping fabricated via silicon rich oxide and silicon dioxide bilayers. Mater. Res. Express 2017, 4, 075004. [Google Scholar] [CrossRef]
- Hybertsen, M.S. Absorption and emission of light in nanoscale silicon structures. Phys. Rev. Lett. 1994, 72, 1514–1517. [Google Scholar] [CrossRef] [PubMed]
- Moskalenko, A.S.; Berakdar, J.; Prokofiev, A.A.; Yassievich, I.N. Single-particle states in spherical Si/SiO2 quantum dots. Phys. Rev. B 2007, 76, 085427. [Google Scholar] [CrossRef] [Green Version]
- Belyakov, V.A.; Burdov, V.A.; Lockwood, R.; Meldrum, A. Silicon Nanocrystals: Fundamental Theory and Implications for Stimulated Emission. Adv. Opt. Technol. 2008, 2008, 279502. [Google Scholar] [CrossRef]
- Delerue, C.; Allan, G.; Lannoo, M. Electron-phonon coupling and optical transitions for indirect-gap semiconductor nanocrystals. Phys. Rev. B 2001, 64, 193402. [Google Scholar] [CrossRef]
- Casida, M. Recent Developments and Applications of Modern Density Functional Theory (Volume 4) (Theoretical and Computational Chemistry (Volume 4)); Time–Dependent Density Functional Response Theory of Molecular Systems: Theory, Computational Methods and Functionals; Elsevier Science: Amsterdam, The Netherlands, 1996; Chapter 11. [Google Scholar]
- Li, Q.; Jin, R. Photoluminescence from colloidal silicon nanoparticles: Significant effect of surface. Nanotechnol. Rev. 2017, 6, 601–602. [Google Scholar] [CrossRef]
- Heuer-Jungemann, A.; Feliu, N.; Bakaimi, I.; Hamaly, M.; Alkilany, A.; Chakraborty, I.; Masood, A.; Casula, M.; Kostopoulou, A.; Oh, E.; et al. The Role of Ligands in the Chemical Synthesis and Applications of Inorganic Nanoparticles. Chem. Rev. 2019, 119, 4819–4880. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, L.; Anderson, N.; Palomaki, P.; Blackburn, J.; Johnson, J.; Neale, N. Silyl radical abstraction in the functionalization of plasma-synthesized silicon nanocrystals. Chem. Mater. 2015, 27, 6869–6878. [Google Scholar] [CrossRef]
- Purkait, T.; Iqbal, M.; Islam, M.; Mobarok, H.; Gonzalez, C.; Hadidi, L.; Veinot, J. Alkoxy-Terminated Si Surfaces: A New Reactive Platform for the Functionalization and Derivatization of Silicon Quantum Dots. J. Am. Chem. Soc. 2016, 138, 7114–7120. [Google Scholar] [CrossRef]
- De los Reyes, G.; Dasog, M.; Na, M.; Titova, L.; Veinot, J.; Hegmann, F. Charge transfer state emission dynamics in blue-emitting functionalized silicon nanocrystals. Phys. Chem. Chem. Phys. 2015, 17, 30125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sinelnikov, R.; Dasog, M.; Beamish, J.; Meldrum, A.; Veinot, J. Revisiting an Ongoing Debate: What Role Do Surface Groups Play in Silicon Nanocrystal Photoluminescence? ACS Photonics 2017, 4, 1920. [Google Scholar] [CrossRef]
- Derbenyova, N.V.; Konakov, A.A.; Shvetsov, A.E.; Burdov, V.A. Electronic structure and absorption spectra of silicon nanocrystals with a halogen (Br, Cl) coating. JETP Lett. 2017, 106, 247–251. [Google Scholar] [CrossRef]
- Derbenyova, N.V.; Shvetsov, A.E.; Konakov, A.A.; Burdov, V.A. Effects of surface halogenation on exciton relaxation in Si crystallites: Prospects for photovoltaics. Phys. Chem. Chem. Phys. 2019, 21, 20693–20705. [Google Scholar] [CrossRef] [PubMed]
- Derbeneva, N.V.; Konakov, A.A.; Burdov, V.A. Effect of Halogen Passivation of a Surface on Radiative and Nonradiative Transitions in Silicon Nanocrystals. J. Exp. Theor. Phys. 2019, 129, 234–240. [Google Scholar] [CrossRef]
- Stolle, C.J.; Lu, X.; Yu, Y.; Schaller, R.D.; Korgel, B.A. Efficient Carrier Multiplication in Colloidal Silicon Nanorods. Nano Lett. 2017, 17, 5580–5586. [Google Scholar] [CrossRef]
- Pevere, F.; Sychugov, I.; Sangghaleh, F.; Fucikova, A.; Linnros, J. Biexciton Emission as a Probe of Auger Recombination in Individual Silicon Nanocrystals. J. Phys. Chem. C 2015, 119, 7499–7505. [Google Scholar] [CrossRef]
- Sevik, C.; Bulutay, C. Auger recombination and carrier multiplication in embedded silicon and germanium nanocrystals. Phys. Rev. B 2008, 77, 125414. [Google Scholar] [CrossRef] [Green Version]
- Delerue, C.; Lannoo, M.; Allan, G.; Martin, E.; Mihalcescu, I.; Vial, J.C.; Romestain, R.; Muller, F.; Bsiesy, A. Auger and Coulomb Charging Effects in Semiconductor Nanocrystallites. Phys. Rev. Lett. 1995, 75, 2228–2231. [Google Scholar] [CrossRef]
- Mahdouani, M.; Bourguiga, R.; Jaziri, S.; Gardelis, S.; Nassiopoulou, A. Investigation of Auger recombination in Ge and Si nanocrystals embedded in SiO2 matrix. Phys. E Low-Dimens. Syst. Nanostructures 2009, 42, 57–62. [Google Scholar] [CrossRef]
- Kurova, N.V.; Burdov, V.A. Resonance structure of the rate of Auger recombination in silicon nanocrystals. Semiconductors 2010, 44, 1414–1417. [Google Scholar] [CrossRef]
- Califano, M. Suppression of Auger Recombination in Nanocrystals via Ligand-Assisted Wave Function Engineering in Reciprocal Space. J. Phys. Chem. Lett. 2018, 9, 2098–2104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delerue, C.J.; Lannoo, M. Nanostructures: Theory and Modeling (NanoScience and Technology); Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Blacha, A.; Presting, R.; Cardona, M. Deformation potentials of k = 0 states of tetrahedral semiconductors. Phys. Stat. Sol. B 1984, 126, 11–35. [Google Scholar] [CrossRef]
- Rolo, A.G.; Vasilevskiy, M.I.; Hamma, M.; Trallero-Giner, C. Anomalous first-order Raman scattering in III-V quantum dots: Optical deformation potential interaction. Phys. Rev. B 2008, 78, 081304. [Google Scholar] [CrossRef]
- Glembocki, O.J.; Pollak, F.H. Calculation of the Γ-Δ electron-phonon and hole-phonon scattering matrix elements in silicon. Phys. Rev. Lett. 1982, 48, 413–416. [Google Scholar] [CrossRef]
- Inoshita, T.; Sakaki, H. Electron relaxation in a quantum dot: Significance of multiphonon processes. Phys. Rev. B 1992, 46, 7260–7263. [Google Scholar] [CrossRef] [PubMed]
- Bockelmann, U.; Bastard, G. Phonon scattering and energy relaxation in two-, one-, and zero-dimensional electron gases. Phys. Rev. B 1990, 42, 8947–8951. [Google Scholar] [CrossRef]
- Stauber, T.; Zimmermann, R.; Castella, H. Electron-phonon interaction in quantum dots: A solvable model. Phys. Rev. B 2000, 62, 7336–7343. [Google Scholar] [CrossRef] [Green Version]
- Jacak, L.; Machnikowski, P.; Krasnyj, J.; Zoller, P. Coherent and incoherent phonon processes in artificial atoms. Eur. Phys. J. D-Atomic Mol. Opt. Plasma Phys. 2003, 22, 319–331. [Google Scholar] [CrossRef]
- Vasilevskiy, M.I.; Anda, E.V.; Makler, S.S. Electron-phonon interaction effects in semiconductor quantum dots: A nonperturabative approach. Phys. Rev. B 2004, 70, 035318. [Google Scholar] [CrossRef] [Green Version]
- Sauvage, S.; Boucaud, P.; Lobo, R.P.S.M.; Bras, F.; Fishman, G.; Prazeres, R.; Glotin, F.; Ortega, J.M.; Gérard, J.M. Long Polaron Lifetime in InAs/GaAs Self-Assembled Quantum Dots. Phys. Rev. Lett. 2002, 88, 177402. [Google Scholar] [CrossRef] [Green Version]
- Miranda, R.P.; Vasilevskiy, M.I.; Trallero-Giner, C. Nonperturbative approach to the calculation of multiphonon Raman scattering in semiconductor quantum dots: Polaron effect. Phys. Rev. B 2006, 74, 115317. [Google Scholar] [CrossRef]
- Sarkar, D.; van der Meulen, H.P.; Calleja, J.M.; Becker, J.M.; Haug, R.J.; Pierz, K. Quantum dots observed by optical emission. Phys. Rev. B 2005, 71, 081302. [Google Scholar] [CrossRef]
- Stauber, T.; Vasilevskiy, M.I. Polaron relaxation in a quantum dot due to anharmonic coupling within a mean-field approach. Phys. Rev. B 2009, 79, 113301. [Google Scholar] [CrossRef]
- Marcinkevičius, S.; Gaarder, A.; Leon, R. Rapid carrier relaxation by phonon emission in In0.6Ga0.4As/GaAs quantum dots. Phys. Rev. B 2001, 64, 115307. [Google Scholar] [CrossRef]
- Sun, K.W.; Kechiantz, A.; Lee, B.C.; Lee, C.P. Ultrafast carrier capture and relaxation in modulation-doped InAs quantum dots. Appl. Phys. Lett. 2006, 88, 163117. [Google Scholar] [CrossRef] [Green Version]
- Müller, T.; Schrey, F.F.; Strasser, G.; Unterrainer, K. Ultrafast intraband spectroscopy of electron capture and relaxation in InAs/GaAs quantum dots. Appl. Phys. Lett. 2003, 83, 3572–3574. [Google Scholar] [CrossRef]
- Schaller, R.D.; Pietryga, J.M.; Goupalov, S.V.; Petruska, M.A.; Ivanov, S.A.; Klimov, V.I. Breaking the Phonon Bottleneck in Semiconductor Nanocrystals via Multiphonon Emission Induced by Intrinsic Nonadiabatic Interactions. Phys. Rev. Lett. 2005, 95, 196401. [Google Scholar] [CrossRef]
- Hendry, E.; Koeberg, M.; Wang, F.; Zhang, H.; de Mello Donegá, C.; Vanmaekelbergh, D.; Bonn, M. Direct Observation of Electron-to-Hole Energy Transfer in CdSe Quantum Dots. Phys. Rev. Lett. 2006, 96, 057408. [Google Scholar] [CrossRef] [Green Version]
- Heitz, R.; Born, H.; Guffarth, F.; Stier, O.; Schliwa, A.; Hoffmann, A.; Bimberg, D. Existence of a phonon bottleneck for excitons in quantum dots. Phys. Rev. B 2001, 64, 241305. [Google Scholar] [CrossRef] [Green Version]
- Urayama, J.; Norris, T.B.; Singh, J.; Bhattacharya, P. Observation of Phonon Bottleneck in Quantum Dot Electronic Relaxation. Phys. Rev. Lett. 2001, 86, 4930–4933. [Google Scholar] [CrossRef]
- Guyot-Sionnest, P.; Wehrenberg, B.; Yu, D. Intraband relaxation in CdSe nanocrystals and the strong influence of the surface ligands. J. Chem. Phys. 2005, 123, 074709. [Google Scholar] [CrossRef] [PubMed]
- Nozik, A.J. Spectroscopy and hot electron relaxation dynamics in semiconductor quantum wells and quantum dots. Annu. Rev. Phys. Chem. 2001, 52, 193–231. [Google Scholar] [CrossRef] [PubMed]
- Li, X.Q.; Nakayama, H.; Arakawa, Y. Phonon bottleneck in quantum dots: Role of lifetime of the confined optical phonons. Phys. Rev. B 1999, 59, 5069–5073. [Google Scholar] [CrossRef]
- Efros, A.L.; Kharchenko, V.; Rosen, M. Breaking the phonon bottleneck in nanometer quantum dots: Role of Auger-like processes. Solid State Commun. 1995, 93, 281–284. [Google Scholar] [CrossRef]
- Narvaez, G.A.; Bester, G.; Zunger, A. Carrier relaxation mechanisms in self-assembled (In,Ga)As/GaAs quantum dots: Efficient P–S Auger relaxation of electrons. Phys. Rev. B 2006, 74, 075403. [Google Scholar] [CrossRef] [Green Version]
- Prokofiev, A.A.; Poddubny, A.N.; Yassievich, I.N. Phonon decay in silicon nanocrystals: Fast phonon recycling. Phys. Rev. B 2014, 89, 125409. [Google Scholar] [CrossRef]
- Poddubny, A.N.; Prokofiev, A.A.; Yassievich, I.N. Optical transitions and energy relaxation of hot carriers in Si nanocrystals. Appl. Phys. Lett. 2010, 97, 231116. [Google Scholar] [CrossRef] [Green Version]
- Prokofiev, A.A.; Goupalov, S.V.; Moskalenko, A.S.; Poddubny, A.N.; Yassievich, I.N. Carrier relaxation in quantum dots. Phys. E Low-Dimens. Syst. Nanostructures 2009, 41, 969–971. [Google Scholar] [CrossRef] [Green Version]
- Moskalenko, A.S.; Berakdar, J.; Poddubny, A.N.; Prokofiev, A.A.; Yassievich, I.N.; Goupalov, S.V. Multiphonon relaxation of moderately excited carriers in Si/SiO2 nanocrystals. Phys. Rev. B 2012, 85, 085432. [Google Scholar] [CrossRef] [Green Version]
- Ohnesorge, B.; Albrecht, M.; Oshinowo, J.; Forchel, A.; Arakawa, Y. Rapid carrier relaxation in self-assembledInxGa1-xAs/GaAs quantum dots. Phys. Rev. B 1996, 54, 11532–11538. [Google Scholar] [CrossRef]
- Beard, M.C.; Knutsen, K.P.; Yu, P.; Luther, J.M.; Song, Q.; Metzger, W.K.; Ellingson, R.J.; Nozik, A.J. Multiple Exciton Generation in Colloidal Silicon Nanocrystals. Nano Lett. 2007, 7, 2506–2512. [Google Scholar] [CrossRef] [PubMed]
- Nozik, A.J. Nanoscience and Nanostructures for Photovoltaics and Solar Fuels. Nano Lett. 2010, 10, 2735–2741. [Google Scholar] [CrossRef] [PubMed]
- de Boer, W.D.A.M.; Trinh, M.T.; Timmerman, D.; Schins, J.M.; Siebbeles, L.D.A.; Gregorkiewicz, T. Increased carrier generation rate in Si nanocrystals in SiO2 investigated by induced absorption. Appl. Phys. Lett. 2011, 99, 053126. [Google Scholar] [CrossRef]
- Trinh, M.T.; Limpens, R.; de Boer, W.D.A.M.; Schins, J.M.; Siebbeles, L.D.A.; Gregorkiewicz, T. Direct generation of multiple excitons in adjacent silicon nanocrystals revealed by induced absorption. Nat. Photonics 2012, 6, 316–321. [Google Scholar] [CrossRef]
- Schaller, R.D.; Klimov, V.I. High Efficiency Carrier Multiplication in PbSe Nanocrystals: Implications for Solar Energy Conversion. Phys. Rev. Lett. 2004, 92, 186601. [Google Scholar] [CrossRef] [Green Version]
- Nair, G.; Bawendi, M.G. Carrier multiplication yields ofCdSeandCdTenanocrystals by transient photoluminescence spectroscopy. Phys. Rev. B 2007, 76, 081304. [Google Scholar] [CrossRef] [Green Version]
- Davis, N.J.L.K.; Böhm, M.L.; Tabachnyk, M.; Wisnivesky-Rocca-Rivarola, F.; Jellicoe, T.C.; Ducati, C.; Ehrler, B.; Greenham, N.C. Multiple-exciton generation in lead selenide nanorod solar cells with external quantum efficiencies exceeding 120%. Nat. Commun. 2015, 6, 8259. [Google Scholar] [CrossRef] [Green Version]
- Hu, F.; Lv, B.; Yin, C.; Zhang, C.; Wang, X.; Lounis, B.; Xiao, M. Carrier Multiplication in a Single Semiconductor Nanocrystal. Phys. Rev. Lett. 2016, 116, 106404. [Google Scholar] [CrossRef]
- Smith, C.T.; Leontiadou, M.A.; Clark, P.C.J.; Lydon, C.; Savjani, N.; Spencer, B.F.; Flavell, W.R.; O’Brien, P.; Binks, D.J. Multiple Exciton Generation and Dynamics in InP/CdS Colloidal Quantum Dots. J. Phys. Chem. C 2017, 121, 2099–2107. [Google Scholar] [CrossRef] [Green Version]
- Meldrum, A.; Lockwood, R.; Belyakov, V.; Burdov, V. Computational simulations for ensembles of luminescent silicon nanocrystals: Implications for optical gain and stimulated emission. Phys. E Low-Dimens. Syst. Nanostructures 2009, 41, 955–958. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Sidorenko, K.V.; Konakov, A.A.; Ershov, A.V.; Chugrov, I.A.; Grachev, D.A.; Pavlov, D.A.; Bobrov, A.I.; Burdov, V.A. Quenching the photoluminescence from Si nanocrystals of smaller sizes in dense ensembles due to migration processes. J. Lumin. 2014, 155, 1–6. [Google Scholar] [CrossRef]
- Derbenyova, N.V.; Konakov, A.A.; Burdov, V.A. Resonant tunneling of carriers in silicon nanocrystals. J. Appl. Phys. 2016, 120, 134302. [Google Scholar] [CrossRef]
- Curutchet, C.; Franceschetti, A.; Zunger, A.; Scholes, G.D. Examining Förster energy transfer for semiconductor nanocrystalline quantum dot donors and acceptorsl study. J. Phys. Chem. C Lett. 2008, 112, 13336–13341. [Google Scholar] [CrossRef]
- Andrews, D.L.; Sherborne, B.S. Resonant excitation transfer: A quantum electrodynamical study. J. Chem. Phys. 1987, 86, 4011–4017. [Google Scholar] [CrossRef] [Green Version]
- Allan, G.; Delerue, C. Energy transfer between semiconductor nanocrystals: Validity of Förster’s theory. Phys. Rev. B 2007, 75, 195311. [Google Scholar] [CrossRef]
- Stavola, M.; Dexter, D.L.; Knox, R.S. Electron-hole pair excitation in semiconductors via energy transfer from an external sensitizer. Phys. Rev. B 1985, 31, 2277–2289. [Google Scholar] [CrossRef]
- Lyo, S.K. Spectral and spatial transfer and diffusion of excitons in multiple quantum dot structures. Phys. Rev. B 2009, 79, 125328. [Google Scholar] [CrossRef]
- Jang, S.; Hossein-Nejad, H.; Scholes, G.D. Generalized Förster resonance energy transfer. In Quantum Effects in Biology; Mohseni, M., Omar, Y., Engel, G.S., Plenio, M.B., Eds.; Cambridge University Press: Cambridge, UK, 2014; pp. 53–90, Chapter 3. [Google Scholar]
- Scholes, G.D.; Andrews, D.L. Resonance energy transfer and quantum dots. Phys. Rev. B 2005, 72, 125331. [Google Scholar] [CrossRef]
- Shafiei, F.; Ziama, S.P.; Curtis, E.D.; Decca, R.S. Measurement of the separation dependence of resonant energy transfer between CdSe/ZnS core/shell nanocrystallite quantum dots. Phys. Rev. B 2011, 84, 075301. [Google Scholar] [CrossRef] [Green Version]
- Mork, A.; Weidman, M.; Prins, F.; Tisdale, W. Magnitude of the Förster Radius in Colloidal Quantum Dot Solids. J. Phys. Chem. C 2014, 118, 13920–13928. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Burdov, V.A. Radiative Recombination and Migration Effects in Ensembles of Si Nanocrystals: Towards Controllable Nonradiative Energy Transfer. J. Comput. Theor. Nanosci. 2011, 8, 365–374. [Google Scholar] [CrossRef]
- Gusev, O.B.; Prokofiev, A.A.; Maslova, O.A.; Terukov, E.I.; Yassievich, I.N. Energy transfer between silicon nanocrystals. JETP Lett. 2011, 93, 147–150. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Burdov, V.A. Intensification of Förster transitions between Si crystallites due to their doping with phosphorus. Phys. Rev. B 2013, 88, 045439. [Google Scholar] [CrossRef]
- Aharoni, A.; Oron, D.; Banin, U.; Rabani, E.; Jortner, J. Long-Range Electronic-to-Vibrational Energy Transfer from Nanocrystals to Their Surrounding Matrix Environment. Phys. Rev. Lett. 2008, 100, 057404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, Q.; Kershaw, S.V.; Kalytchuk, S.; Zhovtiuk, O.; Reckmeier, C.; Vasilevskiy, M.I.; Rogach, A.L. Impact of D2O/H2O Solvent Exchange on the Emission of HgTe and CdTe Quantum Dots: Polaron and Energy Transfer Effects. ACS Nano 2016, 10, 4301–4311. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.E.; Vasilevskiy, M.I.; Peres, N.M.R.; Smirnov, G.; Bludov, Y.V. Renormalization of nanoparticle polarizability in the vicinity of a graphene-covered interface. Phys. Rev. B 2014, 90, 235420. [Google Scholar] [CrossRef] [Green Version]
- Amorim, B.; Gonçalves, P.A.D.; Vasilevskiy, M.I.; Peres, N.M.R. Impact of Graphene on the Polarizability of a Neighbour Nanoparticle: A Dyadic Green’s Function Study. Appl. Sci. 2017, 7, 1158–1188. [Google Scholar] [CrossRef] [Green Version]
- Lukosz, W.; Kunz, R.E. Light emission by magnetic and electric dipoles close to a plane interface. J. Opt. Soc. Am. 1977, 67, 1607–1615. [Google Scholar] [CrossRef]
- Drexhage, K. Influence of a Dielectric Interface on Fluorescence Decay Time. J. Luminescence 1970, 1–2, 693–701. [Google Scholar] [CrossRef]
- Ford, G.W.; Weber, W.H. Electromagnetic Interactions of Molecules with Metal Surfaces. Phys. Rep. 1984, 113, 195–287. [Google Scholar] [CrossRef] [Green Version]
- Gordon, J.M.; Cartstein, Y.N. Local field effects for spherical quantum dot emitters in the proximity of a planar dielectric interface. J. Opt. Soc. Am. B 2014, 31, 2029–2035. [Google Scholar] [CrossRef]
- Benner, R.E.; Barber, P.W.; Owen, J.F.; Chang, R.K. Observation of Structure Resonances in the Fluorescence Spectra from Microspheres. Phys. Rev. Lett. 1980, 44, 475–478. [Google Scholar] [CrossRef]
- Scheneipp, H.; Sandoghbar, V. Spontaneous Emission of Europium Ions Embedded in Dielectric Nanospheres. Phys. Rev. Lett. 2002, 89, 257403. [Google Scholar] [CrossRef] [PubMed]
- Giannini, V.; Fernández-Domíngueez, A.I.; Heck, S.C.; Maier, S.A. Plasmonic Nanoantennas: Fundamentals and Their Use in Controlling the Radiative Properties of Nanoemitters. Chem. Rev. 2011, 111, 3888–3912. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.Q.; Henriksen, E.A.; Jiang, Z.; Hao, Z.; Martin, M.C.; Kim, P.; Stormer, H.L.; Basov, D.N. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 2008, 4, 532–535. [Google Scholar] [CrossRef] [Green Version]
- Bludov, Y.V.; Ferreira, A.; Peres, N.M.R.; Vasilevskiy, M. A Primer on Surface Plasmon-Polaritons in Graphene. Int. J. Mod. Phys. B 2013, 27, 1341001. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Galera, A.J.; Brihuega, I.; Gutiérrez-Rubio, A.; Stauber, T.; Gómez-Rodríguez, J.M. Towards scalable nano-engineering of graphene. Sci. Rep. 2014, 4, 7314. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez-Rubio, A.; Stauber, T. Mass-profile quantum dots in graphene and artificial periodic structures. Phys. Rev. B 2015, 91, 165415. [Google Scholar] [CrossRef] [Green Version]
- Gaudreau, L.; Tielrooij, K.J.; Prawiroatmodjo, C.E.D.K.; Osmond, J.; de Abajo, F.J.G.; Koppens, F.H.L. Universal distance-scaling of non-radiative energy transfer to graphene. Nano Lett. 2013, 13, 2030. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Federspiel, F.; Froehlicher, G.; Nasilowski, M.; Pedetti, S.; Mahmood, A.; Doudin, B.; Park, S.; Lee, J.O.; Halley, D.; Dubertret, B.; et al. Distance Dependence of the Energy Transfer Rate from a Single Semiconductor Nanostructure to Graphene. Nano Lett. 2015, 15, 1252–1258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gonçalves, H.; Bernardo, C.; Moura, C.; Ferreira, R.A.S.; André, P.S.; Stauber, T.; Belsley, M.; Schellenberg, P. Long range energy transfer in graphene hybrid structures. J. Phys. D Appl. Phys. 2016, 49, 315102. [Google Scholar] [CrossRef]
- Raja, A.; Montoya-Castillo, A.; Zultak, J.; Zhang, X.X.; Ye, Z.; Roquelet, C.; Chenet, D.A.; van der Zande, A.M.; Huang, P.; Jockusch, S.; et al. Energy Transfer from Quantum Dots to Graphene and MoS2: The Role of Absorption and Screening in Two-Dimensional Materials. Nano Lett. 2016, 16, 2328–2333. [Google Scholar] [CrossRef]
- Gómez-Santos, G.; Stauber, T. Fluorescence quenching in graphene: A fundamental ruler and evidence for transverse plasmons. Phys. Rev. B 2011, 84, 165438. [Google Scholar] [CrossRef] [Green Version]
- Konstantatos, G.; Badioli, M.; Osmond, J.; Gaudreau, L.; de Arquer, F.P.G.; Gatti, F.; Koppens, F.H.L. Hybrid graphene-quantum dot phototransistors with ultrahigh gain. Nat. Nanotechnol. 2012, 7, 363–368. [Google Scholar] [CrossRef]
- Sun, S.; Gao, L.; Liu, Y.; Sun, J. Assembly of CdSe nanoparticles on graphene for low-temperature fabrication of quantum dot sensitized solar cell. Appl. Phys. Lett. 2011, 98, 093112. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Bao, W.; Ju, L.; Schuck, P.J.; Wang, F.; Weber-Bargioni, A. Switching Individual Quantum Dot Emission through Electrically Controlling Resonant Energy Transfer to Graphene. Nano Lett. 2014, 14, 7115–7119. [Google Scholar] [CrossRef] [Green Version]
- Salihoglu, O.; Kakenov, N.; Balci, O.; Balci, S.; Kocabas, C. Graphene as a Reversible and Spectrally Selective Fluorescence Quencher. Sci. Rep. 2016, 6, 33911. [Google Scholar] [CrossRef]
- Prasai, D.; Klots, A.R.; Newaz, A.; Niezgoda, J.S.; Orfield, N.J.; Escobar, C.A.; Wynn, A.; Efimov, A.; Jennings, G.K.; Rosenthal, S.J.; et al. Electrical Control of near-Field Energy Transfer between Quantum Dots and Two-Dimensional Semiconductors. Nano Lett. 2015, 15, 4374–4380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prins, F.; Goodman, A.J.; Tisdale, W.A. Reduced Dielectric Screening and Enhanced Energy Transfer in Single- and Few-Layer MoS2. Nano Lett. 2014, 14, 6087–6091. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zang, H.; Routh, P.K.; Huang, Y.; Chen, J.S.; Sutter, E.; Sutter, P.; Cotlet, M. Nonradiative Energy Transfer from Individual CdSe/ZnS Quantum Dots to Single-Layer and Few-Layer Tin Disulfide. ACS Nano 2016, 10, 4790–4796. [Google Scholar] [CrossRef]
- Karanikolas, V.D.; Marocico, C.A.; Eastham, P.R.; Bradley, A.L. Near-field relaxation of a quantum emitter to two-dimensional semiconductors: Surface dissipation and exciton polaritons. Phys. Rev. B 2016, 94, 195418. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Chernikov, A.; Glazov, M.M.; Heinz, T.F.; Marie, X.; Amand, T.; Urbaszek, B. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 2018, 90, 021001. [Google Scholar] [CrossRef] [Green Version]
- Gomes, J.N.S.; Trallero-Giner, C.; Peres, N.M.R.; Vasilevskiy, M.I. Exciton–polaritons of a 2D semiconductor layer in a cylindrical microcavity. J. Appl. Phys. 2020, 127, 133101. [Google Scholar] [CrossRef] [Green Version]
- Komarala, V.K.; Bradley, A.L.; Rakovich, Y.P.; Byrne, S.J.; Gun’ko, Y.K.; Rogach, A.L. Surface plasmon enhanced Förster resonance energy transfer between the CdTe quantum dots. Appl. Phys. Lett. 2008, 93, 123102. [Google Scholar] [CrossRef] [Green Version]
- Huidobro, P.A.; Nikitin, A.Y.; González-Ballestero, C.; Martin-Moreno, L.; García-Vidal, F.J. Superradiance mediated by graphene surface plasmons. Phys. Rev. B 2012, 85, 155438. [Google Scholar] [CrossRef] [Green Version]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Scheibner, M.; Schmidt, T.; Worschech, L.; Forchel, A.; Bacher, G.; Passow, T.; Hommel, D. Superradiance of quantum dots. Nat. Phys. 2007, 3, 106–110. [Google Scholar] [CrossRef]
- Klar, T.A.; Franzl, T.; Rogach, A.L.; Feldmann, J. Super-Efficient Exciton Funneling in Layer-by-Layer Semiconductor Nanocrystal Structures. Adv. Mater. 2005, 17, 769–773. [Google Scholar] [CrossRef]
- Rakovich, Y.P.; Donegan, J.F.; Vasilevskiy, M.I.; Rogach, A.L. Anti-Stokes cooling in semiconductor nanocrystal quantum dots: A feasibility study. Phys. Status Solidi A 2009, 206, 2497–2509. [Google Scholar] [CrossRef] [Green Version]
- Mirkovic, T.; Ostroumov, E.E.; Anna, J.M.; van Grondelle, R.G.; Scholes, G.D. Light Absorption and Energy Transfer in the Antenna Complexes of Photosynthetic Organisms. Chem. Rev. 2016, 117, 249–293. [Google Scholar] [CrossRef] [PubMed]
- Sambur, J.B.; Novet, T.; Parkinson, B.A. Multiple Exciton Collection in a Sensitized Photovoltaic System. Science 2010, 330, 63–66. [Google Scholar] [CrossRef] [Green Version]
- Coles, D.M.; Somaschi, N.; Michetti, P.; Clark, C.; Lagoudakis, P.G.; Savvidis, P.G.; Lidzey, D.G. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 2014, 13, 712–719. [Google Scholar] [CrossRef]
- Schachenmayer, J.; Genes, C.; Tignone, E.; Pupillo, G. Cavity-Enhanced Transport of Excitons. Phys. Rev. Lett. 2015, 114, 196403. [Google Scholar] [CrossRef] [Green Version]
- Törmä, P.; Barnes, W.L. Strong coupling between surface plasmon polaritons and emitters: A review. Rep. Prog. Phys. 2014, 78, 013901. [Google Scholar] [CrossRef]


| X = H | X = Cl | X = Br | |
|---|---|---|---|
| SiX | 3.3 | 2.7 | |
| SiX | |||
| SiX | 36 | ||
| SiX | |||
| SiX | 15 | ||
| SiX | |||
| SiX | |||
| SiX | 63 |
| X = H | X = Cl | X = Br | X = H | X = Cl | X = Br | |
|---|---|---|---|---|---|---|
| () | () | () | () | () | () | |
| SiX | 390 | 3 | 4 | 40 | 163 | 10 |
| SiX | 78 | 0.3 | 7 | 5 | 27 | 19 |
| SiX | 120 | 4 | 2 | 1780 | 59 | 11 |
| SiX | 8 | 3 | 280 | 108 | 25 | 24 |
| SiX | 59 | 84 | 2 | 474 | 20 | 65 |
| SiX | 120 | 21 | 100 | 47 | 9 | 19 |
| SiX | 270 | 2 | 2 | 161 | 90 | 0.8 |
| SiX | 0.3 | 0.4 | 0.02 | 5 | 3 | 78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burdov, V.A.; Vasilevskiy, M.I. Exciton-Photon Interactions in Semiconductor Nanocrystals: Radiative Transitions, Non-Radiative Processes and Environment Effects. Appl. Sci. 2021, 11, 497. https://doi.org/10.3390/app11020497
Burdov VA, Vasilevskiy MI. Exciton-Photon Interactions in Semiconductor Nanocrystals: Radiative Transitions, Non-Radiative Processes and Environment Effects. Applied Sciences. 2021; 11(2):497. https://doi.org/10.3390/app11020497
Chicago/Turabian StyleBurdov, Vladimir A., and Mikhail I. Vasilevskiy. 2021. "Exciton-Photon Interactions in Semiconductor Nanocrystals: Radiative Transitions, Non-Radiative Processes and Environment Effects" Applied Sciences 11, no. 2: 497. https://doi.org/10.3390/app11020497
APA StyleBurdov, V. A., & Vasilevskiy, M. I. (2021). Exciton-Photon Interactions in Semiconductor Nanocrystals: Radiative Transitions, Non-Radiative Processes and Environment Effects. Applied Sciences, 11(2), 497. https://doi.org/10.3390/app11020497






