Electronic Structure Correspondence of Singlet-Triplet Scale Separation in Strained Sr₂RuO₄

Abstract

At a temperature of roughly 1 K, ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ undergoes a transition from a normal Fermi liquid to a superconducting phase. Even while the former is relatively simple and well understood, the superconducting state has not even been understood after 25 years of study. More recently, it has been found that critical temperatures can be enhanced by the application of uniaxial strain, up to a critical strain, after which it falls off. In this work, we take an “instability” approach and seek divergences in susceptibilities. This provides an unbiased way to distinguish tendencies to competing ground states. We show that in the unstrained compound, the singlet and triplet instabilities of the normal Fermi liquid phase are closely spaced. Under uniaxial strain, electrons residing on all orbitals contributing to the Fermiology become more coherent, while the electrons of the Ru-$d_{xy}$ character become heavier, and the electrons of the Ru-$d_{xz,yz}$ characters become lighter. In the process, Im $\chi (\mathbf{q},\omega )$ increases rapidly around $\mathbf{q} = (0.3,0.3,0)2\pi /a$ and $\mathbf{q} = (0.5,0.25,0)2\pi /a$, while it gets suppressed at all other commensurate vectors, in particular at $\mathbf{q} = 0$, which is essential for spin-triplet superconductivity. We observe that the magnetic anisotropy under strain drops smoothly, which is concomitant with the increment in singlet instability. Thus, the triplet superconducting instability remains the lagging instability of the system, and the singlet instability enhances under strain, leading to a large energy-scale separation between these competing instabilities. However, since this happens even without spin-orbit coupling, we believe it is primarily the enhancement in the spin fluctuation glue around quasi-anti-ferromagnetic vectors that drives the Cooper pairing instead of the magnetic anisotropy. At large strain, an instability to a spin density wave overtakes the superconducting one. The analysis relies on a high-fidelity, ab initio description of the one-particle properties and two-particle susceptibilities, based on the quasiparticle self-consistent GW approximation augmented by dynamical mean field theory. This approach is described and its high fidelity confirmed by comparing to observed one- and two-particle properties.

1. Introduction

The origin of superconducting pairing in ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ (SRO) has been one of the most debated topics in materials research over the last two decades [1]. Until recently, the superconductivity was believed to be of a spin-triplet character. A series of recent experimental findings, including strain dependent enhancement in the critical temperature T${}_c$ [2,3] and the pronounced drop in O${}^{17}$ NMR [4] measurements, the observation of momentum-resolved superconducting energy gaps of ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ from quasiparticle interference imaging [5], the direct observation of Lifshitz transition [6], the jump in the c${}_{66}$ shear modulus [7], the high resolution $\mu$-SRstudies [8] and magnetic order at large strains [9], have challenged the existing beliefs and demand a fresh look into the enigmatic problem of superconductivity in SRO.

Strongly correlated electronic systems have a multiplicity of closely packed phases, owing to the small energy scale of the different kinds of correlations. Strain is an effective tool to tune correlations in bulk crystalline systems, as it makes small, but significant changes to the one-particle spectrum, which in turn modifies two-particle properties such as superconductivity. It can lift degeneracies and separate out energy scales of competing phases, which sheds light on the underlying mechanisms that lead to different orders. ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ is a particularly salient example: as noted, a recent study showed that uniaxial strain induces a two-fold enhancement T${}_c$ up to a critical strain, after which it falls off rapidly [2,3]. This study generated huge interest in the community, and it was followed by a series of careful experimental and theoretical works, including the work by Steppke et al. [3], which attributed the increase to a van Hove singularity inducing a Lifshitz transition just around the critical point. In the unstrained case, Sr${}_2$RuO${}_4$ has tetragonal symmetry, with three bands present at the Fermi level. These bands are composed predominantly of three Ru d orbitals: the $d_{xy}$ and the symmetry-equivalent $d_{xz}$ and $d_{yz}$ pair. Under strain, the $d_{xz}$ and $d_{yz}$ equivalence is broken, and the Fermi surface undergoes a topological transition at a critical strain ${ϵ}_x$∼ 0.6%.

A series of theoretical studies [10,11,12,13,14] followed to explain the observations related to the enhancement and later suppression of T${}_c$ under strain. Some studies rely on a starting electronic band structure from density functional theory (DFT); more often, they are phenomenological and based on low energy minimal model Hamiltonians. The latter typically employ model parameters for the Hubbard U and J and often rely on DFT eigenvalues to parameterise the one-body part. Such approaches are justified by the observation that superconductivity is a low energy phenomena and should be well described if starting from a good underlying one-body part. Nevertheless, Kivelson et al. [15] recently argued that while much is known about the normal phases of Sr${}_2$RuO${}_4$, understanding the nature of superconductivity in ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ continues to be one of the most enigmatic problems in unconventional superconductivity even after 25 years [16]. This is indeed a remarkable observation considering that the normal phase of ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ is a relatively simple normal Fermi liquid, which is one of the better understood phases of correlated electronic materials.

In a recent work [17], we performed a thorough analysis of ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ with and without uniaxial strain, using a new high-fidelity ab initio approach [18]. It uses an instability analysis: we monitor two-particle instabilities (points where a susceptibility diverges) in all particle-hole and particle-particle channels, starting from a high temperature and decreasing it. This is a significant departure from the ground state low energy model Hamiltonian approach noted above, but we believe it is key to addressing the right questions for unconventional superconductivity, namely “can we reliably compute all finite temperature instabilities in the normal phase that upon lowering of temperature would become unstable to a certain order?” As Kivelson et al. noted [15], we believe one key reason why superconductivity in ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ seems so difficult to explain stems from the inability of theoretical schemes to calculate all possible two-particle instabilities in the normal phase. This is particularly difficult to accomplish in a parameter-free fashion. The instability analysis we use allows for possible competing phases in an unbiased manner. Further, because the theory is both ab initio and has very high fidelity, it has unprecedented predictive power [17,19,20,21,22]. In this way, we are able to circumvent the difficulties Kivelson et al. noted.

Our ab initio approach starts from a one-particle Hamiltonian calculated from the quasiparticle self-consistent GW(QSGW) approximation [23]. It plays the role of DFT as a bath for the many-body problem to be embedded in, but its fidelity is vastly superior. The one-particle Green’s function is generated from dynamical mean field theory (DMFT) [24], using QSGW as a bath. This is accomplished with a continuous-time quantum Monte Carlo (CTQMC) solver [25,26]. This framework [20,27] is extended by computing the local vertex from the two-particle Green’s function by DMFT [28,29], which is combined with nonlocal bubble diagrams to construct a Bethe–Salpeter equation [17,21]. The latter is solved to yield the essential two-particle spin and charge susceptibilities ${\chi }^d$ and ${\chi }^m$—physical observables that provide an important benchmark. Moreover, they supply the ingredients needed for the Eliashberg equation, which yields eigenvalues and eigenfunctions that describe instabilities to superconductivity in both singlet and triplet channels. We will denote QSGW⁺⁺ as the shorthand for the four-tier QSGW+DMFT+Bethe–Salpeter equation (BSE)+Eliashberg theory. The numerical implementation was discussed by Pashov et al. [18], and codes are available on the open source electron structure suite Questaal [30].

QSGW⁺⁺ has high fidelity because QSGW captures non-local dynamic correlation particularly well in the charge channel [18,31], but it cannot adequately capture the effects of spin fluctuations. DMFT does an excellent job at the latter, which are strong, but mostly controlled by a local effective interaction given by U and J. For ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ in particular, the QSGW Fermi surface is practically indistinguishable from a recent high-resolution ARPESmeasurement [32], and the spin susceptibility is in excellent agreement with inelastic neutron scattering (INS) measurements [17] (measured only for the unstrained case when this work was published).

The present work reviews this prior study [17], which was our first attempt to use instability analysis with the full machinery of QSGW⁺⁺. It computed spin, charge and superconducting susceptibilities resolved in both energy and momenta and both in the singlet and triplet channels. We showed how the singlet instability increases under strain, while the triplet one does not, and explained why T${}_c$ increases. Here, we extend that initial work to include wider excursion in strain to emphasize the trends and provide a more detailed description of the connection between the single-particle and two-particle properties. In particular, we establish the following:

• the benchmark QSGW and QSGW⁺⁺ with a detailed comparison to the laser ARPES measurement [32]
• we show how strain modifies both one- and two-particle properties in a markedly orbital-dependent manner: strain enhances the role of the $d_{xy}$ orbital relative to the $d_{xz+yz}$ orbitals
• we show how the system becomes a better Fermi liquid with decreasing temperature; at low temperature, J becomes the dominant factor, and the increase in coherence is orbital specific, on account of the van Hove singularity
• we show how the system becomes a better Fermi liquid with increasing strain, while at the same time, $d_{xy}$ becomes heavier and $d_{xz}$ and $d_{yz}$ lighter; strain enhances the role of the $d_{xy}$ orbital relative to the $d_{xz+yz}$ orbitals and enhances spin singlet superconductivity
• we use instability analysis to clarify how the relative strength of competing phases evolves with strain and compare against a spin density wave (SDW) (the latter eventually overtakes the instability towards superconductivity at a strain larger than the critical one)
• we show how spin-orbit coupling affects superconductivity.

In our original work, we took U and J from constrained RPA [33] calculations obtained from DFT [34], which yielded U = 4.5 eV and J = 1.0 eV, and $J/U = 0.22$. We recently discovered from a recent implementation of C-RPA [30] that U and J computed from DFT are too large to be used in a QSGW framework: in Hund’s metals, U and J decrease in proportion to the bandwidth renormalisation, while $J/U$ remains fixed. For ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ in particular, QSGW renormalises the DFT bandwidth by about 0.6. Thus, for the present study, we use U = 3.0 eV and J = 0.67 eV; $J/U = 0.22$. This reduction does not change anything qualitatively, but important details change, the most important being that with the DFT-C-RPA estimates U and J, the leading triplet eigenvalue was found to be slightly larger than the singlet eigenvalue in unstrained ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$, inconsistent with recent experimental findings [5,7,8]. In the present study, we use the newer parameterisation of U and J.

Before turning to the results, we note that our original work emphasised the interplay between charge and spin susceptibility. Those conclusions remain unchanged in the present work. As we have nothing new to report on this aspect, we focus on analysis spin susceptibility, which we denote as $\chi (\mathbf{q},\omega )$, and label spin and charge susceptibilities as ${\chi }^m$ and ${\chi }^d$ only where a description of both is needed. The superconducting instabilities we present here include both spin and charge susceptibilities.

2. Results

2.1. Single-Particle Properties Near the Fermi Surface

In addition to an ARPES measurements of the Fermi surface in 2014 [35], a new high-resolution laser ARPES measurement was reported [32], which provides an excellent benchmark of the theory. In [17], we compared the Fermi surface; here, we present a more detailed benchmark.

• In the unstrained case, DFT yields a good Fermi surface [32], but QSGW performs a little better. QSGW and QSGW⁺⁺ are very similar (left panel, Figure 1). In the vicinity of the $\theta$ = 45 degree line connecting $\mathrm{\Gamma }$ and X, the inner ($\beta$) pocket makes a smooth transition from xz (green) to xy (red) at the 45 degree mark, to the yz (blue) character (middle panel, Figure 1). Thus, xy and xz,yz exchange roles on this line. The nesting vector along this line give rise to peaks in ${\chi }^m$ at $q=(\pm 0.3,\pm 0.3)$, which mainly drive superconductivity.
• The tendency for QSGW to yield smaller v_F than DFT is typical [31]; and so is further renormalisation from spin fluctuations, computed via DMFT. It is noteworthy that v_F computed in QSGW⁺⁺ (hexagons) is in very good agreement with ARPES data (blue circles), including the variation with $\theta$.
• Under strain, the xy symmetry is broken: the two points MGin the middle panel of Figure 1 become different. One point contracts, and the other widens, touching the boundary at a critical strain and causing a topological (Lifshitz) transition. QSGW and DMT capture this transition, but QSGW accurately captures the critical strain (${ϵ}_x = 0.6$%), whereas DFT gets it severely wrong [17].
• Spin-orbit modification of the band structure is poorly described in DFT; Reference [32] referred to “correlation enhancements” to it. QSGW, however, describes the splitting very well (∼90 meV), in good agreement with an estimate of 100 meV [32], revised downward from the 2014 estimate of 130 ± 30 meV [35].

Figure 1. Dynamical mean field theory (DMFT) spectral function in Sr₂RuO₄ at 145 K (left). Yellow lines are QSGW bands; green lines extract the peak in the QSGW⁺⁺ spectral functions near the Fermi level. The middle panel shows the QSGW Fermi surface, showing the inner ($\beta$), middle ($\gamma$), and outer ($\alpha$) pockets resolved by the orbital character (red = xy, green = xz, blue = yz). Point MGis midway between the M and $\mathrm{\Gamma }$ points. QSGW, QSGW⁺⁺, and ARPESFermi surfaces are all very similar, with QSGW⁺⁺ being slightly closer to the ARPES measurement. The right figure shows the Fermi velocities v_F (10⁵ m/s) of the $\beta$ and ($\gamma$) pockets, on a line connecting q = 0 to a zone boundary point, whose direction is given by $(cos(\theta ),sin(\theta \left)\right)$.

Figure 1. Dynamical mean field theory (DMFT) spectral function in Sr₂RuO₄ at 145 K (left). Yellow lines are QSGW bands; green lines extract the peak in the QSGW⁺⁺ spectral functions near the Fermi level. The middle panel shows the QSGW Fermi surface, showing the inner ($\beta$), middle ($\gamma$), and outer ($\alpha$) pockets resolved by the orbital character (red = xy, green = xz, blue = yz). Point MGis midway between the M and $\mathrm{\Gamma }$ points. QSGW, QSGW⁺⁺, and ARPESFermi surfaces are all very similar, with QSGW⁺⁺ being slightly closer to the ARPES measurement. The right figure shows the Fermi velocities v_F (10⁵ m/s) of the $\beta$ and ($\gamma$) pockets, on a line connecting q = 0 to a zone boundary point, whose direction is given by $(cos(\theta ),sin(\theta \left)\right)$.

Figure 2a shows how the orbitally resolved electronic masses and single-particle scattering rates evolve with strain ${ϵ}_x$. The single-site DMFT Im $\mathrm{\Sigma }\left(i\omega \right)$ is fit to a fourth order polynomial in $i\omega$ for low energies (first six Matsubara points at $\beta = 40 {\mathrm{eV}}^{-1} = 290$ K) [36]. The mass enhancement, related to the coefficient $s_1$ of the linear term in the expansion $m_{\mathrm{DMFT}}/m_{\mathrm{QS}GW} = 1 + \left|s_1\right|$ [37] and the intercept $|s_0|$ = $\mathrm{\Gamma }{m}_{\mathrm{DMFT}}/m_{\mathrm{QS}GW}$ with $m_{\mathrm{DMFT}}$/$m_{\mathrm{QS}GW}$ = $Z^{-1}$, is resolved in different intra-orbital channels. Both the masses and $\mathrm{\Gamma }$ are orbital-dependent, and this differentiation is a signature of a Hund’s metal [21]. Electrons in the $d_{xy}$ orbital become heavier, while the $d_{xz,yz}$ electrons become lighter with ${ϵ}_x$. Beyond a critical ${ϵ}_x$∼ 0.6%, $m_{xy,\mathrm{DMFT}}$/$m_{xy,\mathrm{QS}GW}$ becomes heavier than $m_{xz,\mathrm{DMFT}}$/$m_{xz,\mathrm{QS}GW}$ (see Figure 2b). The trend is similar at lower temperatures: the $d_{xy}$ mass increases under strain while decreasing on $d_{xz}$ and $d_{yz}$. On the other hand, all orbitals become more coherent under strain, as seen in the reduction of the scattering rate $\mathrm{\Gamma }$ (see Figure 2c).

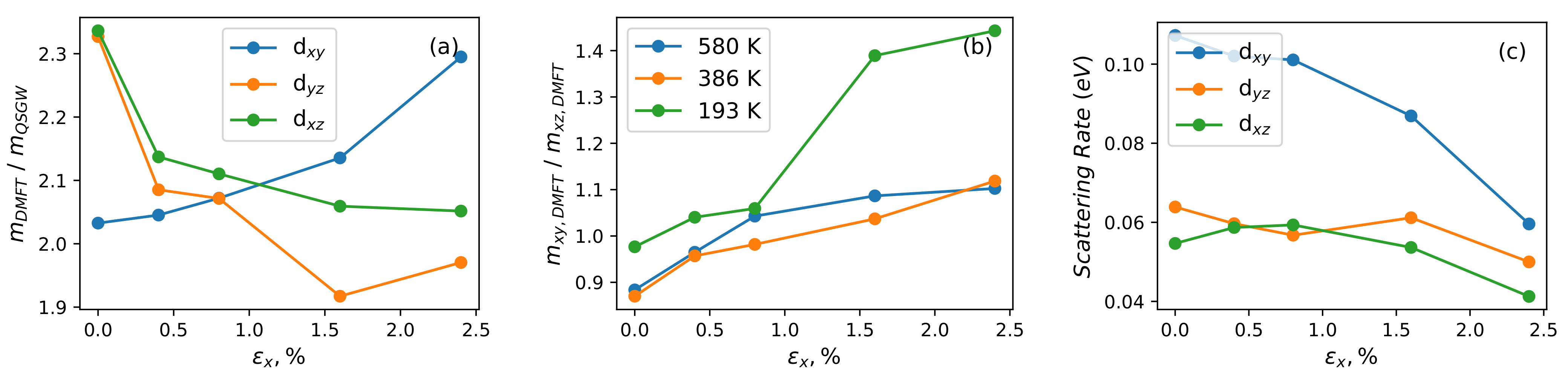
2.2. Spin Fluctuations: Incommensurability and Coherence

$\chi (\mathbf{q},\omega )$ is computed from the momentum-dependent Bethe–Salpeter Equation (1) in the magnetic channel.

$${\chi }_{\genfrac{}{}{0pt}{}{{\alpha }_1,{\alpha }_2}{{\alpha }_3,{\alpha }_4}}^m{(i\nu ,i{\nu }^{\prime })}_{\mathbf{q},i\omega }={[{\left({\chi }^0\right)}_{\mathbf{q},i\omega }^{-1}-{\mathrm{\Gamma }}_{loc}^{irr,m}]}_{\genfrac{}{}{0pt}{}{{\alpha }_1,{\alpha }_2}{{\alpha }_3,{\alpha }_4}}^{-1}{(i\nu ,i{\nu }^{\prime })}_{\mathbf{q},i\omega }.$$

(1)

${\chi }^0$ is the non-local (k-dependent) polarisation bubble computed from single-particle QSGW Green’s functions dressed by the local DMFT self-energy, and $\mathrm{\Gamma }$ is the local irreducible two-particle vertex function computed in the magnetic channel. $\mathrm{\Gamma }$ is a function of two fermionic frequencies $\nu$ and ${\nu }^{\prime }$ and the bosonic frequency $\omega$. $\chi (\mathbf{q},i\omega )$ is computed by closing ${\chi }_{\genfrac{}{}{0pt}{}{{\alpha }_1,{\alpha }_2}{{\alpha }_1,{\alpha }_2}}^{m\left(d\right)}{(i\nu ,i{\nu }^{\prime })}_{\mathbf{q},i\omega }$ with spin bare vertex $\gamma$ and summing over frequencies ($i\nu$,$i{\nu }^{\prime }$) and orbitals (${\alpha }_{1,2}$).

We compute the real part of the static susceptibility Re$\chi (\mathbf{q},i\omega = 0)$ and resolve it in different inter- and intra-orbital channels to develop a systematic understanding of which orbitals dominate the spin susceptibilities at different q-vectors. In the vicinity of the ferromagnetic (FM) vector ${\mathbf{q}}^{FM} = (0,0,0)$, $\chi$ is dominated by the intra-orbital fluctuations in the $d_{xy}$ channel (Figure 3a), while at the incommensurate (IC) vector ${\mathbf{q}}^{IC} = (0.3,0.3,0)$ (we use units $2\pi /a$ throughout), the three orbitals contribute almost equally. The antiferromagnetic (AFM) vector ${\mathbf{q}}^{\mathrm{A}FM} = (0.5,0.5,0)$ is fully gapped.

When strain is applied, we find that the IC peak rapidly increases, and $d_{xy}$ emerges as the leading component of total spin susceptibilities along all high symmetry directions (see Figure 3b–e). This is consistent with the fact that under strain, $d_{xy}$ becomes the most strongly correlated orbital. Nevertheless, the AFM vector remains fully gapped for strains up to ${ϵ}_x$ = 2.4%. We compute both the real and imaginary parts of spin and charge susceptibilities by solving the BSE in the respective channels. These equations are solved in the Matsubara representation with local dynamic vertex functions (which are functions of three Matsubara frequencies) and the non-local polarisation bubble, which also has the Matsubara frequencies. After summing over all internal Fermionic Matsubara frequencies and orbital indices, we are left with $\chi (\mathbf{q},i\omega )$. Further, it needs to be analytically continued to real bosonic frequencies. One way is to analytically continue $\chi \left(i\omega \right)$ at each momentum, which is tremendously expensive. To understand the precise nature of the spin fluctuations at finite energies, it is imperative in this work that we extract Im $\chi (\mathbf{q},\omega )$ for finite $\omega$. For low energies, which is the focus here, the vertex ${\mathrm{\Gamma }}_{loc}^{irr}$ is analytically continued by a quasiparticle-like approximation. We replace the frequency-dependent vertex with a constant, i.e., ${\mathrm{\Gamma }}_{loc}^{irr}{(i\nu ,i{\nu }^{\prime },i\omega )}_{\genfrac{}{}{0pt}{}{{\alpha }_2{\sigma }_2,{\alpha }_4{\sigma }_4}{{\alpha }_1{\sigma }_1,{\alpha }_3{\sigma }_3}}\sim U_{\genfrac{}{}{0pt}{}{{\alpha }_2{\sigma }_2,{\alpha }_4{\sigma }_4}{{\alpha }_1{\sigma }_1,{\alpha }_3{\sigma }_3}}^{\mathrm{eff}}$, which satisfies the constraint that $\chi (\mathbf{q},i\omega =0)=\chi (\mathbf{q},\omega =0)$.

This “quasiparticlized” vertex $U^{\mathrm{eff}}$ contains all the important spin, orbital dependence. This approximation for analytic continuation works remarkably well for spin susceptibilities at low energy as shown in previous works [17,21,28,29]. We compute the dynamic susceptibility Im $\chi (\mathbf{q},\omega )$ and observe that the intensity drops at ${\mathbf{q}}^{FM} = (0,0,0)$ under strain (see Figure 4a). The energy dispersion of Im $\chi (\mathbf{q},\omega )$ at ${\mathbf{q}}^{FM} = (0,0,0)$ remains almost invariant up to ${ϵ}_x$ = 1.6%, but for much larger strains, the branch loses both intensity and dispersion simultaneously. The reverse happens at ${\mathbf{q}}^{IC} = (0.3,0.3,0)$ where under strain, both the intensity and dispersion of the branch increase (see Figure 4b). For all strains, ${\mathbf{q}}^{\mathrm{A}FM} = (0.5,0.5,0)$ remains fully gapped (see Figure 4c), while the peaks at $\mathbf{q} = (0.25,0,0)$ and $\mathbf{q} = (0,0.25,0)$ lose intensity, but in a very anisotropic manner (see Figure 4d–e). Interestingly enough, we observe the emergence of slightly weaker nesting (compared to the one at ${\mathbf{q}}^{IC} = (0.3,0.3,0)$) and therefore enhancement in Im $\chi (\mathbf{q},\omega )$ at $\mathbf{q} = (0.5,0.25,0)$ (see Figure 4d). A similar observation was reported in a recent theoretical work [11]. The coherent low energy part of the susceptibility peak at $\mathbf{q} = (0.5,0.25,0)$ increases in intensity by roughly 50% going from ${ϵ}_x$ = 0 to 2.4%. Simultaneously, the position of the peak gets red shifted by ∼20 meV from 65 meV (at ${ϵ}_x$ = 0) to 45 meV (at ${ϵ}_x$ = 2.4%). For larger strains, one additional broad and incoherent high energy branch of Im $\chi (\mathbf{q},\omega )$ becomes prominent at ∼200 meV. However, the peak at $\mathbf{q} = (0.25,0.5,0)$ loses intensity under strain. We also show in Figure 4f how the IC peak starts diverging with lowering temperatures at ${ϵ}_x$ = 0.8%, signalling an instability towards an SDW order. However, whether the Fermi liquid phase will become unstable to an SDW phase or a superconducting phase can only be confirmed from further investigation of superconducting pairing instabilities.

2.3. Superconducting Pairing: Nodal Character and Dimensionality

The superconducting pairing susceptibility ${\chi }^{p-p}$ is computed by dressing the non-local pairing polarisation bubble ${\chi }^{0,p-p}(k,i\nu )$ with the pairing vertex ${\mathrm{\Gamma }}^{irr,p-p}$ using the Bethe-Salpeter equation in the particle-particle channel.

$$\begin{array}{c}\hfill {\chi }^{p-p}={\chi }^{0,p-p}·{[\mathbf{1}+{\mathrm{\Gamma }}^{irr,p-p}·{\chi }^{0,p-p}]}^{-1}\end{array}$$

(2)

${\mathrm{\Gamma }}^{irr,p-p}$ in the singlet (s) and triplet (t) channels are obtained from the magnetic (spin) and density (charge) particle-hole reducible vertices by:

$$\begin{array}{cc}& {\mathrm{\Gamma }}_{\genfrac{}{}{0pt}{}{{\alpha }_2,{\alpha }_4}{{\alpha }_1,{\alpha }_3}}^{irr,p-p,s}(\mathbf{k},i\nu ,{\mathbf{k}}^{\prime },i{\nu }^{\prime })={\mathrm{\Gamma }}_{\genfrac{}{}{0pt}{}{{\alpha }_2,{\alpha }_4}{{\alpha }_1,{\alpha }_3}}^{f-irr}(i\nu ,i{\nu }^{\prime })\\ & +\frac{1}{2}[\frac{3}{2}{\tilde{\mathrm{\Gamma }}}^{p-h,\left(m\right)}\\ & -\frac{1}{2}{\tilde{\mathrm{\Gamma }}}^{p-h,\left(d\right)}{]}_{\genfrac{}{}{0pt}{}{{\alpha }_2,{\alpha }_3}{{\alpha }_1,{\alpha }_4}}{(i\nu ,-i{\nu }^{\prime })}_{{\mathbf{k}}^{\prime }-\mathbf{k},i{\nu }^{\prime }-i\nu }\\ & +\frac{1}{2}[\frac{3}{2}{\tilde{\mathrm{\Gamma }}}^{p-h,\left(m\right)}\\ & -\frac{1}{2}{\tilde{\mathrm{\Gamma }}}^{p-h,\left(d\right)}{]}_{\genfrac{}{}{0pt}{}{{\alpha }_4,{\alpha }_3}{{\alpha }_1,{\alpha }_2}}{(i\nu ,i{\nu }^{\prime })}_{-{\mathbf{k}}^{\prime }-\mathbf{k},-i{\nu }^{\prime }-i\nu }\end{array}$$

(3)

$$\begin{array}{cc}& {\mathrm{\Gamma }}_{\genfrac{}{}{0pt}{}{{\alpha }_2,{\alpha }_4}{{\alpha }_1,{\alpha }_3}}^{irr,p-p,t}(\mathbf{k},i\nu ,{\mathbf{k}}^{\prime },i{\nu }^{\prime })={\mathrm{\Gamma }}_{\genfrac{}{}{0pt}{}{{\alpha }_2,{\alpha }_4}{{\alpha }_1,{\alpha }_3}}^{f-irr}(i\nu ,i{\nu }^{\prime })\\ & -\frac{1}{2}[\frac{1}{2}{\tilde{\mathrm{\Gamma }}}^{p-h,\left(m\right)}\\ & +\frac{1}{2}{\tilde{\mathrm{\Gamma }}}^{p-h,\left(d\right)}{]}_{\genfrac{}{}{0pt}{}{{\alpha }_2,{\alpha }_3}{{\alpha }_1,{\alpha }_4}}{(i\nu ,-i{\nu }^{\prime })}_{{\mathbf{k}}^{\prime }-\mathbf{k},i{\nu }^{\prime }-i\nu }\\ & +\frac{1}{2}[\frac{1}{2}{\tilde{\mathrm{\Gamma }}}^{p-h,\left(m\right)}\\ & +\frac{1}{2}{\tilde{\mathrm{\Gamma }}}^{p-h,\left(d\right)}{]}_{\genfrac{}{}{0pt}{}{{\alpha }_4,{\alpha }_3}{{\alpha }_1,{\alpha }_2}}{(i\nu ,i{\nu }^{\prime })}_{-{\mathbf{k}}^{\prime }-\mathbf{k},-i{\nu }^{\prime }-i\nu }\end{array}$$

(4)

Finally, ${\chi }^{p-p}$ can be represented in terms of the eigenvalues $\lambda$ and eigenfunctions ${\varphi }^{\lambda }$ of the Hermitian particle-particle pairing matrix.

$$\begin{array}{ccc}\hfill {\chi }^{p-p}(\mathbf{k},{\mathbf{k}}^{\prime })& =& \sum _{\lambda }\frac{1}{1-\lambda }·(\sqrt{{\chi }^{0,p-p}\left(\mathbf{k}\right)}·{\varphi }^{\lambda }\left(\mathbf{k}\right))\hfill \\ & ·(& \sqrt{{\chi }^{0,p-p}\left({\mathbf{k}}^{\prime }\right)}·{\varphi }^{\lambda }\left({\mathbf{k}}^{\prime }\right))\hfill \end{array}$$

(5)

The pairing susceptibility diverges when the leading eigenvalue $\lambda$ becomes unity. The corresponding eigenfunction represents the momentum structure of ${\chi }^{p-p}$. Unconventional superconductivity in SRO is multi-orbital in nature with multiple competing instabilities. In our previous work [17], we performed a thorough analysis of all possible singlet and triplet instabilities in SRO and associated with a particular symmetry group. We showed that the leading eigenvalue in the singlet channel had a $d_{x^2-y^2}$ instability (B${}_{1g}$ symmetry), while the leading eigenvalue in the triplet channel was of an extended nodeless s-wave 2${\delta }_0+cos{k}_x+cos{k}_y$ gap structure with A${}_{1g}$ irreducible representation in the $d_{xz,yz}$ basis.

A subsequent Bogoliubov quasiparticle scattering interference visualization of the gap structure at milli-Kelvin temperatures was measured to be of a B${}_{1g}$-$d_{x^2-y^2}$ nature [5]. We observe that for all strains (and without strain), the eigenvalue corresponding to the singlet instability remains the leading one, and the relative strength of the singlet to triplet eigenvalues (${\lambda }_s/{\lambda }_t$) keeps increasing under strain. The enhancement in ${\lambda }_s/{\lambda }_t$ under strain becomes more apparent at lower temperatures (see Figure 5a). This is concomitant with the mass becoming heavier in the $d_{xy}$ channel, while the masses relax on other orbitals. Further, this is a direct consequence of the spin fluctuations getting suppressed at ${\mathbf{q}}^{FM} = (0,0,0)$ and rising steeply at ${\mathbf{q}}^{IC} = (0.3,0.3,0)$ and $\mathbf{q} = (0.5,0.25,0)$. It is understandable that the system can undergo a spin density wave (SDW) order mediated primarily via the fluctuations at and around these quasi-antiferromagnetic vectors. Once the spin susceptibility diverges, at lower temperatures, under large strains, the system will encounter the density wave phase, and the superconducting channel will be suppressed. To check that we extract the leading eigenvalue (${\lambda }_{SDW}$) in the density wave channel, we diagonalise the susceptibility matrix. We observe that while for ${ϵ}_x$ = 0.0, ${\lambda }_{SDW}$ and ${\lambda }_s$ show a very similar temperature dependence (${\lambda }_s$ is slightly more steeper than ${\lambda }_{SDW}$), for finite and large strains (${ϵ}_x > 0.6\%$), ${\lambda }_{SDW}$ acquires a steeper temperature dependence than ${\lambda }_s$ (see Figure 5b). This suggests that although ${\lambda }_s/{\lambda }_t$ continues to enhance under large strains, the superconducting phase will be suppressed by an SDW phase: the normal Fermi liquid phase will make a transition to the SDW phase before it becomes superconducting [3,9,13].

We observe that all our essential conclusions for both spin and superconducting instabilities remain qualitatively invariant once the spin-orbit coupling (SOC) is included in the calculations. We observe that under strain, with SOC, the singlet and triplet eigenvalues get further removed from each other, making the scale separation clearer for all strains. The FM spin fluctuations go down under strain, in the presence of SOC, and the IC becomes steeper, making an SDW instability likely for larger strains.

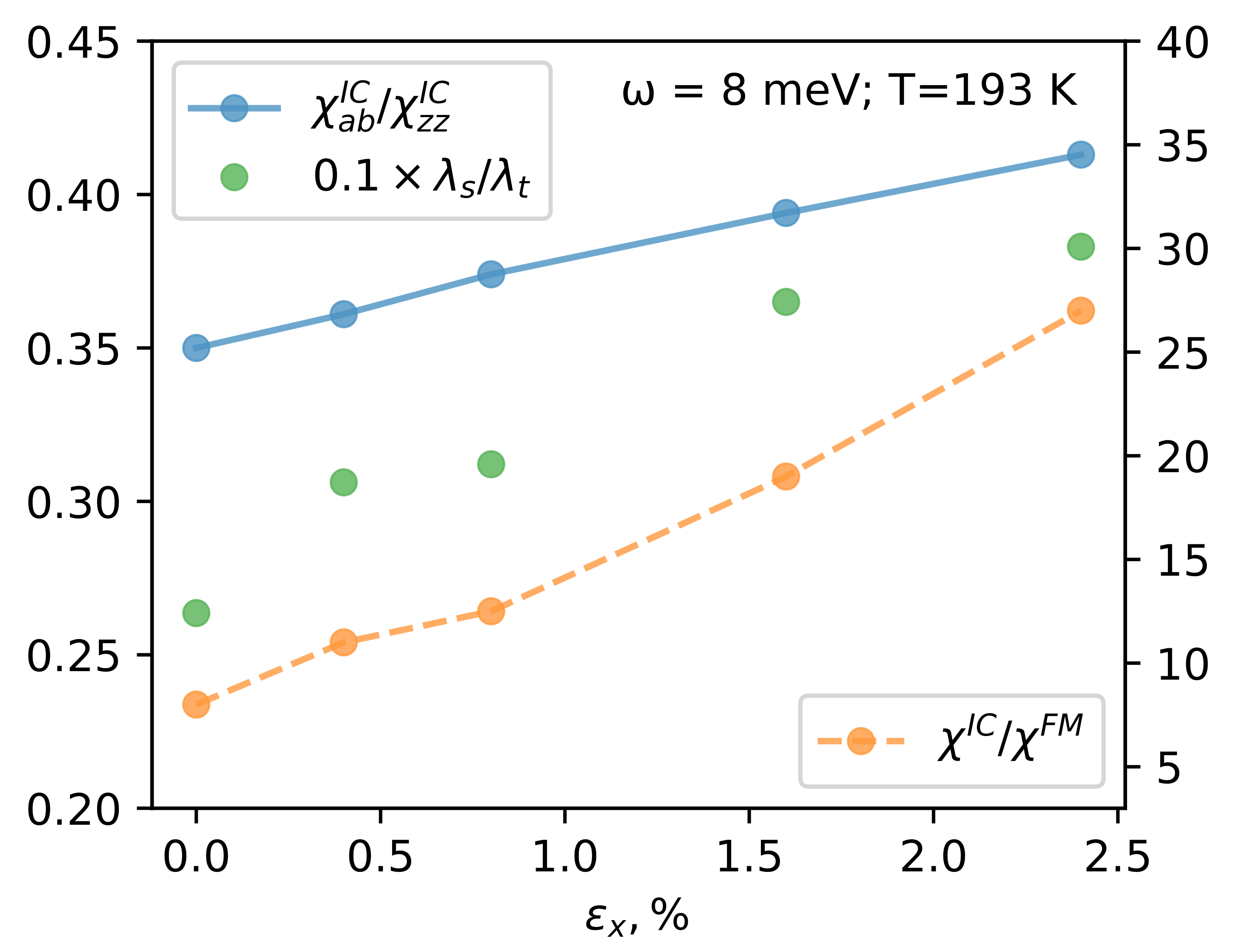
2.4. Magnetic Incommensurability, Anisotropy, and Their Role in Cooper Pairing

One of the long debated questions for Sr${}_2$RuO${}_4$ has been the strength of magnetic anisotropy at the IC vector and its implications for superconductivity. In the early part of the century, several INS [38,39,40,41,42] and NMR [43] measurements were performed to probe the anisotropy (${\chi }_{zz}^{IC}/{\chi }_{ab}^{IC}$) of the physical magnetic susceptibility. Barring some initial ambiguities related to the usage of un-polarised neutrons for measurements of magnetic anisotropy (a nice discussion can be found in Nagata et al. [38]), over the years, a consensus built that the anisotropy ${\chi }_{zz}^{IC}/{\chi }_{ab}^{IC}$ is ∼2.5. A series of theoretical studies [44,45,46,47,48,49,50] followed to argue that this anisotropy is the key factor that can drive the triplet superconductivity in Sr${}_2$RuO${}_4$. These calculations and the inferences therefrom also strongly contrasted the theoretical results from Mazin and Singh [51,52]. Mazin and Singh did not include the magnetic anisotropy in their theoretical calculations, and they showed that in Sr${}_2$RuO${}_4$ a singlet d-wave Cooper pairing should be favoured due to the spin fluctuations at the IC vector.

However, until late 2018, the superconductivity in Sr${}_2$RuO${}_4$ was believed to be primarily of spin triplet origin, unless the situation dramatically changed with the careful NMR measurements performed recently by Pustogow et al. [4]. Furthermore, during this period, almost all neutron studies failed to pick up any magnetic susceptibility at the FM vector from INS measurements. In view of this persisting experimental situation between 1994 and 2018, non-observing of FM spin fluctuations in INS and NMR results suggesting a triplet pairing scenario, the theoretical studies argued in favour of a triplet pairing scenario mediated primarily by the magnetic anisotropy at the IC vector. An opposing view was presented in a recent INS study by Steffens et al. [53]. They observed a significant amount of spin susceptibility near the FM vector, but concluded that the fluctuations were too weak to form enough glue for purely triplet superconductivity.

We built our theoretical ability recently [27], and in our previous work [17] on Sr${}_2$RuO${}_4$, we showed that it is primarily the relative strengths of the spin fluctuations at the IC and FM vectors and their coherence that determine ${\lambda }_s/{\lambda }_t$. However, we also showed that the charge susceptibility has an intricate momentum-dependent structure, and the superconductivity is a product of the interplay of both the spin and charge fluctuations. However, on a more fundamental level of electronic interactions, the rotationally invariant quantum Hamiltonian that we solve also includes important spin-flip scattering and pair-hopping terms. These interaction terms are crucial to incorporate the relevant spin dynamics in Sr${}_2$RuO${}_4$ that is neither fully itinerant nor fully localised. The self-energies and two-particle vertex functions computed in the presence of such interactions include the resulting energy dynamics. An exact estimation of how our approach differs from the older theoretical studies both qualitatively and quantitatively is beyond the scope of the present work. Nevertheless, we solve the many-body interacting Hamiltonian in the presence of spin-orbit (SO) coupling and observe that in the presence of the relevant vertex functions, ${\chi }_{zz}^{IC}/{\chi }_{ab}^{IC}$ is ∼2.85. This is in excellent agreement with what was observed in experiments [38,39,41,43]. We also find that ${\chi }_{zz}^{FM}/{\chi }_{ab}^{FM}$ is ∼2.12 (which drops weakly under strain before increasing slightly for larger strains), and we do not know whether there exists any experimental results for the same. We find that under strain, $\frac{{\chi }_{ab}^{IC}}{{\chi }_{zz}^{IC}}$ increases smoothly, resulting in a reduced anisotropy (see Figure 6). ${\lambda }_s/{\lambda }_t$ increases simultaneously, and so does ${\chi }^{IC}/{\chi }^{FM}$. What is intriguing is that we find ${\chi }_{zz}^{IC}/{\chi }_{ab}^{IC}$ to be much larger than the critical estimate of 1.14 for triplet instability from the work of Kuwabara and Ogata [47], and yet, we find singlet instability to be the dominant one (${\lambda }_s/{\lambda }_t$ = 2.63) in unstrained Sr${}_2$RuO${}_4$. Most importantly, we observe that under strain, ${\lambda }_s/{\lambda }_t$ increases as ${\chi }^{IC}/{\chi }^{FM}$ increases even without SO coupling. We believe this is a crucial point for determining the fact that in unstrained SRO, it is most likely ${\chi }^{IC}/{\chi }^{FM}$ that determines the nature of the Cooper pairing instead of the anisotropy ${\chi }_{zz}^{IC}/{\chi }_{ab}^{IC}$. A thorough analysis of the temperature and doping (magnetic) dependence of the anisotropy is needed to resolve this question satisfactorily, which is beyond the scope of the present work.

2.5. Summary

We performed a detailed analysis of the single-particle and two-particle response of ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ under large strains. The instability approach allows us to compare different kinds of instabilities of the normal phase. By performing excursions in temperature or external parameters such as strain, we can identify which ground states are the preferred instabilities of the normal phase, distinguishing among multiple closely-spaced many-body ordered phases. Key to the success of this approach is the ab initio QSGW⁺⁺ machinery, whose high fidelity (which is essential) is confirmed by the excellent agreement with observed one- and two-particle properties, as we showed.

We find that while the singlet and triplet instabilities are similar in the unstrained ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$, the ratio of eigenvalues ${\lambda }_s/{\lambda }_t$ under uniaxial strain ${ϵ}_x$ keeps increasing at all temperatures, leading to a clear separation between the singlet and the triplet superconducting pairing instabilities. Its emergence can be traced to the orbital-selective evolution in single-particle properties under strain: in particular, $d_{xy}$ acquires a heavy mass, while $d_{xz}$ and $d_{yz}$ become lighter. This directly modifies the two-particle susceptibilities; the spin susceptibility at ${\mathbf{q}}^{FM}$ is suppressed under strain, and at quasi-anti-ferromagnetic vectors, it diverges, leading to the relative suppression of the triplet instability. Finally, the rapid divergence of $\chi$ temperature at ${\mathbf{q}}^{IC}$ leads to enhancement in both ${\lambda }_s$ and ${\lambda }_{SDW}$. The latter has a steeper temperature dependence, and thereby, for large strains, the superconducting phase is suppressed by an emergent SDW phase.

3. Methods

We used a recently developed quasi-particle self-consistent GW + dynamical mean field theory (QSGW + DMFT) [18,19,27], as implemented in the all-electron Questaal package [30]. Paramagnetic DMFT was combined with non-magnetic QSGW via local projectors of the Ru 4d states on the Ru augmentation spheres to form the correlated subspace. We carried out the QSGW calculations in the tetragonal and strained phases of ${\mathrm{Sr}}_2{\mathrm{RuO}}_4$ with space group 139/I4mmm. DMFT provides a non-perturbative treatment of the local spin and charge fluctuations. We used an exact hybridisation expansion solver, namely the continuous-time Monte Carlo (CTQMC) [54], to solve the Anderson impurity problem.

The one-body part of QSGW was performed on a $16\times 16\times 16$ k-mesh, and the charge was converged up to ${10}^{-6}$ accuracy, while the (relatively smooth) many-body static self-energy ${\mathrm{\Sigma }}^0\left(\mathbf{k}\right)$ was constructed on a $8\times 8\times 8$ k-mesh from the dynamical $GW$$\mathrm{\Sigma }(\mathbf{k},\omega )$. ${\mathrm{\Sigma }}^0\left(\mathbf{k}\right)$ was iterated until convergence (RMS change in ${\mathrm{\Sigma }}^0 < {10}^{-5}$ Ry). U = 3.0 eV and J = 0.67 eV were used as correlation parameters for DMFT. The DMFT for the dynamical self-energy was iterated and converged in ≈20 iterations. Calculations of the single particle response functions were performed with ${10}^9$ QMC steps per core, and the statistics were averaged over 64 cores. The two particle Green’s functions were sampled over a larger number of cores (10,000–20,000) to improve the statistical error bars. We sampled the local two-particle Green’s functions with CTQMC for all the correlated orbitals and computed the local polarisation bubble to solve the inverse Bethe–Salpeter equation (BSE) for the local irreducible vertex. Finally, we computed the non-local polarisation bubble $G(\mathbf{k},\omega )G(\mathbf{k}-\mathbf{q},\omega -\mathrm{\Omega })$, and combined with the local irreducible vertex [55], we obtained the full non-local spin and charge susceptibilities ${\chi }^{m,d}(\mathbf{q},\omega )$. The susceptibilities were computed on a $16\times 16\times 16$ $\mathbf{Q}$-mesh. BSE equations in the particle-particle pairing channels were solved [17,21] on the same k-mesh to extract the susceptibilities, and the Eliashberg eigenvalue equations were solved to extract the eigenvalue spectrum and corresponding pairing symmetries.