Prediction of Swelling Index Using Advanced Machine Learning Techniques for Cohesive Soils
Abstract
:1. Introduction
2. Materials and Methods
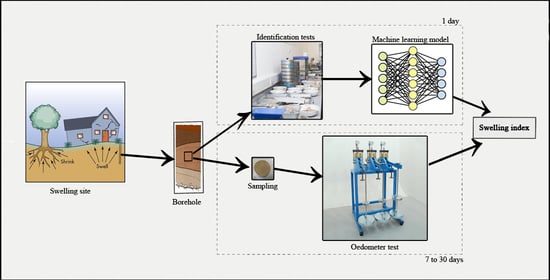
2.1. Overview of the Methodology
2.2. Oedometer Test
2.3. Case Study
2.4. Optimal Input Selections
2.4.1. Overview of Principal Component Analysis (PCA)
2.4.2. Overview of Gamma Test (GT)
2.4.3. Overview of Forward Selection (FS)
2.5. Machine Learning Methods
2.6. Statistical Performance Indicators
- Mean absolute error (MAE):
- Root mean square error (RMSE):
- Index of scattering (IOS):
- Nash–Sutcliffe efficiency (NSE):
- Pearson correlation coefficient (R):
- Index of agreement (IOA):where , , , and present the target, output, mean of target, and mean of output swelling index values for N data samples, respectively. Furthermore, the proposed machine learning model having the lowest value of RMSE, IOS, and MAE and the highest value of IOA, NSE, and R presents the better one and the closest to the experimental data.
2.7. Methodology
- Creation of a geotechnical database of Algerian soil, collected from different laboratories around the geotechnical constructions projects in progress or completed before.
- Selecting the optimal input variables using Principal component analysis (OSA), Gamma Test (GT), and Forward selection (FS) has been used.
- Analyzing selected optimal inputs using several machine learning methods. The ELM, DNN, SVR, RF, LASSO, PLS, Ridge, KRidge, Stepwise, and PG methods have been used in this step for proposing 30 models.
- Determine the most appropriate model for predicting the Cs value between the thirty proposed models using important statistical performance indicators as MAE, RMSE, IOS, NSE, R, and IOA.
- Assessing the predictive capacity of the best model to overcome under-fitting and over-fitting problem by using the K-fold cross validation approach with K = 10.
- Doing a sensitivity analysis by utilizing the step-by-step method to know the most or less influenced input on Cs through the proposed model.
3. Results
3.1. Database Compilation
3.2. Correlation between Cs and Geotechnical Parameters
3.3. Optimal Input Selection
3.3.1. Optimal Input Selection Using Principal Component Analysis
3.3.2. Optimal Input Selection Using the Gamma Test
3.3.3. Optimal Input Selection Using Forward Selection
3.4. Swelling Index Prediction through AI Models
3.5. Evaluating the Best Fitted Model Using the K-fold Cross Validation Approach
3.6. Comparison between the Proposed Models and Empirical Formulae
3.7. Sensitivity Analysis
4. Discussion
4.1. Significance of the Findings and Cross-Validation of the Results
4.2. Scientific Importance of the Findings and Novelty of the Research
4.3. Limitations of the Study and Future Research Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A






























References
- Hunt, R. Geotechnical Investigation Methods: A Field Guide for Geotechnical Engineers; CRC Press: Boca Raton, FL, USA, 2006; ISBN 978-1-4200-4274-0. [Google Scholar]
- Benbouras, M.A.; Kettab, R.M.; Debiche, F.; Lagaguine, M.; Mechaala, A.; Bourezak, C.; Petrişor, A.-I. Use of Geotechnical and Geographical Information Systems to Analyze Seismic Risk in Algiers Area. Rev. Şcolii Dr. de Urban 2018, 3, 11. [Google Scholar]
- Yuan, S.; Liu, X.; Sloan, S.W.; Buzzi, O.P. Multi-Scale Characterization of Swelling Behaviour of Compacted Maryland Clay. Acta Geotech. 2016, 11, 789–804. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, H.; Li, L. Use of Oedometer Equipped with High-Suction Tensiometer to Characterize Unsaturated Soils. Transp. Res. Rec. 2016, 2578, 58–71. [Google Scholar] [CrossRef]
- Teerachaikulpanich, N.; Okumura, S.; Matsunaga, K.; Ohta, H. Estimation of Coefficient of Earth Pressure at Rest Using Modified Oedometer Test. Soils Found. 2007, 47, 349–360. [Google Scholar] [CrossRef] [Green Version]
- Benbouras, M.A.; Kettab, R.; Zedira, H.; Petrisor, A.; Mezouer, N.; Debiche, F. A new approach to predict the Compression Index using Artificial Intelligence Methods. Mar. Georesour. Geotechnol. 2018, 6, 704–720. [Google Scholar] [CrossRef]
- Shahin, M.A. Artificial intelligence in geotechnical engineering: Applications, modeling aspects, and future directions. In Metaheuristics in Water, Geotechnical and Transport Engineering; Elsevier: Amsterdam, The Netherlands, 2013; pp. 169–204. [Google Scholar]
- Nagaraj, H.; Munnas, M.; Sridharan, A. Swelling Behavior of Expansive Soils. Int. J. Geotech. Eng. 2010, 4, 99–110. [Google Scholar] [CrossRef]
- Ameratunga, J.; Sivakugan, N.; Das, B.M. Correlations of Soil and Rock Properties in Geotechnical Engineering; Developments in Geotechnical Engineering; Springer India: New Delhi, India, 2016; ISBN 978-81-322-2627-7. [Google Scholar]
- Samui, P.; Hoang, N.-D.; Nhu, V.-H.; Nguyen, M.-L.; Ngo, P.T.T.; Bui, D.T. A New Approach of Hybrid Bee Colony Optimized Neural Computing to Estimate the Soil Compression Coefficient for a Housing Construction Project. Appl. Sci. 2019, 9, 4912. [Google Scholar] [CrossRef] [Green Version]
- Moayedi, H.; Tien Bui, D.; Dounis, A.; Ngo, P.T.T. A Novel Application of League Championship Optimization (LCA): Hybridizing Fuzzy Logic for Soil Compression Coefficient Analysis. Appl. Sci. 2020, 10, 67. [Google Scholar] [CrossRef] [Green Version]
- Onyejekwe, S.; Kang, X.; Ge, L. Assessment of Empirical Equations for the Compression Index of Fine-Grained Soils in Missouri. Bull. Eng. Geol. Environ. 2015, 74, 705–716. [Google Scholar] [CrossRef]
- Onyejekwe, S.; Kang, X.; Ge, L. Evaluation of the Scale of Fluctuation of Geotechnical Parameters by Autocorrelation Function and Semivariogram Function. Eng. Geol. 2016, 214, 43–49. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Recent Advances and Future Challenges for Artificial Neural Systems in Geotechnical Engineering Applications. Adv. Artif. Neural Syst. 2009, 2009, 1–9. [Google Scholar] [CrossRef]
- Hossein Alavi, A.; Hossein Gandomi, A. A Robust Data Mining Approach for Formulation of Geotechnical Engineering Systems. Eng. Comput. 2011, 28, 242–274. [Google Scholar] [CrossRef]
- Park, H.I.; Lee, S.R. Evaluation of the Compression Index of Soils Using an Artificial Neural Network. Comput. Geotech. 2011, 38, 472–481. [Google Scholar] [CrossRef]
- Cai, G.; Liu, S.; Puppala, A.J.; Tong, L. Identification of Soil Strata Based on General Regression Neural Network Model from CPTU Data. Mar. Georesour. Geotechnol. 2015, 33, 229–238. [Google Scholar] [CrossRef]
- Nagaraj, T.S.; Srinivasa Murthy, B.R. A Critical Reappraisal of Compression Index Equations. Geotechnique 1986, 36, 27–32. [Google Scholar] [CrossRef]
- Cozzolino, V.M. Statistical Forecasting of Compression Index. In Proceedings of the Proceedings of the fifth international conference on soil mechanics and foundation engineering, Paris, France, 17–22 July 1961; Volume 1, pp. 51–53. [Google Scholar]
- Işık, N.S. Estimation of Swell Index of Fine Grained Soils Using Regression Equations and Artificial Neural Networks. Sci. Res. Essays 2009, 4, 1047–1056. [Google Scholar]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. State of the Art of Artificial Neural Networks in Geotechnical Engineering. Electron. J. Geotech. Eng. 2008, 8, 1–26. [Google Scholar]
- Das, S.K.; Samui, P.; Sabat, A.K.; Sitharam, T.G. Prediction of Swelling Pressure of Soil Using Artificial Intelligence Techniques. Environ. Earth Sci. 2010, 61, 393–403. [Google Scholar] [CrossRef]
- Kumar, V.P.; Rani, C.S. Prediction of Compression Index of Soils Using Artificial Neural Networks (ANNs). Int. J. Eng. Res. Appl. 2011, 1, 1554–1558. [Google Scholar]
- Kurnaz, T.F.; Dagdeviren, U.; Yildiz, M.; Ozkan, O. Prediction of Compressibility Parameters of the Soils Using Artificial Neural Network. SpringerPlus 2016, 5, 1801. [Google Scholar] [CrossRef] [Green Version]
- Alavi, A.H.; Gandomi, A.H.; Mollahasani, A.; Bazaz, J.B. Linear and Tree-Based Genetic Programming for Solving Geotechnical Engineering Problems. In Metaheuristics in Water, Geotechnical and Transport Engineering; Elsevier: Amsterdam, The Netherlands, 2013; pp. 289–310. ISBN 978-0-12-398296-4. [Google Scholar]
- Narendra, B.S.; Sivapullaiah, P.V.; Suresh, S.; Omkar, S.N. Prediction of Unconfined Compressive Strength of Soft Grounds Using Computational Intelligence Techniques: A Comparative Study. Comput. Geotech. 2006, 33, 196–208. [Google Scholar] [CrossRef]
- Rezania, M.; Javadi, A.A. A New Genetic Programming Model for Predicting Settlement of Shallow Foundations. Can. Geotech. J. 2007, 44, 1462–1473. [Google Scholar] [CrossRef]
- Yin, Z.-Y.; Zhu, Q.-Y.; Zhang, D.-M. Comparison of Two Creep Degradation Modeling Approaches for Soft Structured Soils. Acta Geotech. 2017, 12, 1395–1413. [Google Scholar] [CrossRef]
- Stoica, I.-V.; Tulla, A.F.; Zamfir, D.; Petrișor, A.-I. Exploring the Urban Strength of Small Towns in Romania. Soc. Indic. Res. 2020, 152, 843–875. [Google Scholar] [CrossRef]
- Petrişor, A.-I.; Ianoş, I.; Iurea, D.; Văidianu, M.-N. Applications of Principal Component Analysis Integrated with GIS. Procedia Environ. Sci. 2012, 14, 247–256. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.Z.; Wang, W.J.; Wang, X.K.; Xu, Z.B.; Leung, A.Y.T. Using Improved Neural Network Model to Analyze RSP, NO x and NO 2 Levels in Urban Air in Mong Kok, Hong Kong. Environ. Monit. Assess. 2003, 87, 235–254. [Google Scholar] [CrossRef]
- Çamdevýren, H.; Demýr, N.; Kanik, A.; Keskýn, S. Use of Principal Component Scores in Multiple Linear Regression Models for Prediction of Chlorophyll-a in Reservoirs. Ecol. Model. 2005, 181, 581–589. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-662-05294-5. [Google Scholar]
- Tabachnick, B.G.; Fidell, L.S.; Ullman, J.B. Using Multivariate Statistics, 7th ed.; Pearson: New York, NY, USA, 2019; ISBN 978-0-13-479054-1. [Google Scholar]
- Noori, R.; Karbassi, A.; Salman Sabahi, M. Evaluation of PCA and Gamma Test Techniques on ANN Operation for Weekly Solid Waste Prediction. J. Environ. Manag. 2010, 91, 767–771. [Google Scholar] [CrossRef]
- Noori, R.; Karbassi, A.R.; Moghaddamnia, A.; Han, D.; Zokaei-Ashtiani, M.H.; Farokhnia, A.; Gousheh, M.G. Assessment of Input Variables Determination on the SVM Model Performance Using PCA, Gamma Test, and Forward Selection Techniques for Monthly Stream Flow Prediction. J. Hydrol. 2011, 401, 177–189. [Google Scholar] [CrossRef]
- Koncar, N. Optimisation Methodologies for Direct Inverse Neurocontrol. Ph.D. Thesis, University of London, London, UK, 1997. [Google Scholar]
- Stefánsson, A.; Končar, N.; Jones, A.J. A Note on the Gamma Test. Neural Comput. Appl. 1997, 5, 131–133. [Google Scholar] [CrossRef]
- Kemp, S.; Wilson, I.; Ware, J. A Tutorial on the Gamma Test. Int. J. Simul. Syst. Sci. Technol. 2004, 6, 67–75. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Benbouras, M.A.; Kettab, R.M.; Zedira, H.; Debiche, F.; Zaidi, N. Comparing nonlinear regression analysis and artificial neural networks to predict geotechnical parameters from standard penetration test. Urban. Archit. Constr. 2018, 1, 275–288. [Google Scholar]
- Awad, M.; Khanna, R. Support Vector Regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Awad, M., Khanna, R., Eds.; Apress: Berkeley, CA, USA, 2015; pp. 67–80. ISBN 978-1-4302-5990-9. [Google Scholar]
- Biau, G.; Scornet, E. A Random Forest Guided Tour. TEST 2016, 25, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Hebiri, M.; Lederer, J. How Correlations Influence Lasso Prediction. IEEE Trans. Inf. Theory 2013, 59, 1846–1854. [Google Scholar] [CrossRef] [Green Version]
- Vinzi, V.E.; Chin, W.W.; Henseler, J.; Wang, H. Editorial: Perspectives on Partial Least Squares. In Handbook of Partial Least Squares: Concepts, Methods and Applications; Esposito Vinzi, V., Chin, W.W., Henseler, J., Wang, H., Eds.; Springer Handbooks of Computational Statistics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–20. ISBN 978-3-540-32827-8. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression—1980: Advances, Algorithms, and Applications. Am. J. Math. Manag. Sci. 1981, 1, 5–83. [Google Scholar] [CrossRef]
- Douak, F.; Melgani, F.; Benoudjit, N. Kernel Ridge Regression with Active Learning for Wind Speed Prediction. Appl. Energy 2013, 103, 328–340. [Google Scholar] [CrossRef]
- Jennrich, R.I.; Sampson, P.F. Application of Stepwise Regression to Non-Linear Estimation. Technometrics 1968, 10, 63–72. [Google Scholar] [CrossRef]
- Wagner, S.; Kronberger, G.; Beham, A.; Kommenda, M.; Scheibenpflug, A.; Pitzer, E.; Vonolfen, S.; Kofler, M.; Winkler, S.; Dorfer, V.; et al. Architecture and Design of the HeuristicLab Optimization Environment. In Advanced Methods and Applications in Computational Intelligence; Klempous, R., Nikodem, J., Jacak, W., Chaczko, Z., Eds.; Topics in Intelligent Engineering and Informatics; Springer International Publishing: Heidelberg, Germany, 2014; pp. 197–261. ISBN 978-3-319-01436-4. [Google Scholar]
- Tikhamarine, Y.; Malik, A.; Pandey, K.; Sammen, S.S.; Souag-Gamane, D.; Heddam, S.; Kisi, O. Monthly Evapotranspiration Estimation Using Optimal Climatic Parameters: Efficacy of Hybrid Support Vector Regression Integrated with Whale Optimization Algorithm. Environ. Monit. Assess. 2020, 192, 696. [Google Scholar] [CrossRef]
- Breiman, L.; Spector, P. Submodel Selection and Evaluation in Regression. The X-Random Case. Int. Stat. Rev. 1992, 60, 291–319. [Google Scholar] [CrossRef]
- Oommen, T.; Baise, L.G. Model Development and Validation for Intelligent Data Collection for Lateral Spread Displacements. J. Comput. Civ. Eng. 2010, 24, 467–477. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating Machine Learning and Statistical Prediction Techniques for Landslide Susceptibility Modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Benbouras, M.A.; Kettab, R.M.; Zedira, H.; Petrisor, A.-I.; Debiche, F. Dry Density in Relation to Other Geotechnical Proprieties of Algiers Clay. Rev. Şcolii Dr. Urban 2017, 2, 5–14. [Google Scholar]
- Debiche, F.; Kettab, R.M.; Benbouras, M.A.; Benbellil, B.; Djerbal, L.; Petrisor, A.-I. Use of GIS systems to analyze soil compressibility, swelling and bearing capacity under superficial foundations in Algiers region, Algeria. Urban. Arhit. Constr. 2018, 9, 357–370. [Google Scholar]
- Abba, S.I.; Pham, Q.B.; Usman, A.G.; Linh, N.T.T.; Aliyu, D.S.; Nguyen, Q.; Bach, Q.-V. Emerging Evolutionary Algorithm Integrated with Kernel Principal Component Analysis for Modeling the Performance of a Water Treatment Plant. J. Water Process. Eng. 2020, 33, 101081. [Google Scholar] [CrossRef]
- Kanellopoulos, I.; Wilkinson, G.G. Strategies and Best Practice for Neural Network Image Classification. Int. J. Remote Sens. 1997, 18, 711–725. [Google Scholar] [CrossRef]
- Liong, S.-Y.; Lim, W.-H.; Paudyal, G.N. River Stage Forecasting in Bangladesh: Neural Network Approach. J. Comput. Civ. Eng. 2000, 14, 1–8. [Google Scholar] [CrossRef]
- Mawlood, Y.I.; Hummadi, R.A. Large-Scale Model Swelling Potential of Expansive Soils in Comparison with Oedometer Swelling Methods. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 1283–1293. [Google Scholar] [CrossRef]
- Ly, H.-B.; Le, T.-T.; Le, L.M.; Tran, V.Q.; Le, V.M.; Vu, H.-L.T.; Nguyen, Q.H.; Pham, B.T. Development of Hybrid Machine Learning Models for Predicting the Critical Buckling Load of I-Shaped Cellular Beams. Appl. Sci. 2019, 9, 5458. [Google Scholar] [CrossRef] [Green Version]
- Asteris, P.G.; Nikoo, M. Artificial Bee Colony-Based Neural Network for the Prediction of the Fundamental Period of Infilled Frame Structures. Neural Comput. Appl. 2019, 31, 4837–4847. [Google Scholar] [CrossRef]
- Sarir, P.; Chen, J.; Asteris, P.G.; Armaghani, D.J.; Tahir, M.M. Developing GEP Tree-Based, Neuro-Swarm, and Whale Optimization Models for Evaluation of Bearing Capacity of Concrete-Filled Steel Tube Columns. Eng. Comput. 2019. [Google Scholar] [CrossRef]








| Variables | Correlations | Comments | References | |
|---|---|---|---|---|
| () | (1) | fine-grained soils | [18] | |
| () | (2) | fine-grained soils | [19] | |
| () | (3) | fine-grained soils | Isik 1 [20] | |
| () | (4) | fine-grained soils | Isik 2 [20] | |
| (Yh) | (5) | fine grained soils | Isik 3 [20] | |
| Authors | Inputs | Targets | Architecture (Inputs–Nodes–Outputs) | Database | References |
|---|---|---|---|---|---|
| Işık (2009) | e0 and W | Cs | 2-8-1 | 42 | [20] |
| Das et al. (2010) | W, Yd, WL, PI, and FC | Cs | 5-3-1 | 230 | [22] |
| Kumar and Rani (2011) | FC, WL, PI, Yopt, and Wopt | Cs and Cc | 5-8-2 | 68 | [23] |
| Kurnaz et al. (2016) | W, e0, WL, and PI | Cs and Cc | 4-6-2 | 246 | [24] |
| Algorithms | Algorithm Parameters | Value |
|---|---|---|
| ELM | Hidden layers | H = 1 |
| hidden neurons | N = 12 | |
| activation function | ‘linear’ | |
| regulation parameter | C = 0.02 | |
| DNN | Hidden layers | H = 2 |
| hidden neurons in the first layer | N1 = (1–20) | |
| hidden neurons in the second layer | N2 = (1–20) | |
| activation function in the first layer | ‘Tansg’ | |
| activation function in the second layer | ‘Tansg’ | |
| SVR | regulation parameter C | Series of C |
| regulation parameter lambda | Series of lambda | |
| kernel function | ‘rbf’ | |
| RF | nTrees | nTrees = 100 |
| mTrees | mTrees = 26 | |
| LASSO | lambda | series of lambda |
| PLS | PLS components | NumComp = 3 for PSO NumComp = 4 for GT and FS |
| Ridge | regularization parameter lambda | lambda = 1 |
| KRidge | regularization parameter lambda | lambda = 1 |
| kernel function | ‘linear’ | |
| parameter for kernel | sigma = 2 × 10−7 | |
| PG | Function set | +, −, ×, ÷, power, ln, sqrt, sin, cos, tan |
| Population size | 100 up to 500 | |
| Number of generations | 1000 | |
| Genetic operators | Reproduction, crossover, mutation |
| Sr | Yh | Yd | W | e0 | FC | WL | PI | Cs | ||
|---|---|---|---|---|---|---|---|---|---|---|
| N | Valid | 875 | 875 | 875 | 875 | 875 | 875 | 875 | 875 | 875 |
| Missing | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Mean | 89.45 | 2.01 | 1.67 | 20.61 | 0.63 | 86.55 | 50.11 | 26.09 | 0.0443 | |
| Std. Error of Mean | 0.397 | 0.003 | 0.004 | 0.164 | 0.005 | 0.572 | 0.338 | 0.233 | 0.00072 | |
| Median | 94.00 | 2.01 | 1.67 | 20.00 | 0.62 | 94.00 | 50.00 | 26.00 | 0.0399 | |
| Mode | 100.00 | 2.04 | 1.69 | 20.00 | 0.61 | 98.00 | 58.00 | 29.00 | 0.04 | |
| Std. Deviation | 11.77 | 0.09 | 0.13 | 4.86 | 0.13 | 16.92 | 10.00 | 6.89 | 0.01910 | |
| Variance | 138.54 | 0.01 | 0.02 | 23.64 | 0.02 | 286.23 | 100.09 | 47.43 | 0.000 | |
| Skewness | −1.32 | 0.10 | 0.29 | 0.36 | 0.21 | −1.75 | −0.08 | −0.12 | 0.686 | |
| Std. Error of Skewness | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.092 | |
| Kurtosis | 1.09 | −0.20 | −0.09 | −0.08 | −0.29 | 2.41 | −0.28 | −0.43 | 0.073 | |
| Std. Error of Kurtosis | 0.165 | 0.165 | 0.165 | 0.165 | 0.165 | 0.165 | 0.165 | 0.165 | 0.183 | |
| Range | 64.45 | 0.57 | 0.73 | 26.00 | 0.79 | 78.00 | 64.31 | 38.00 | 0.10 | |
| Minimum | 41.00 | 1.70 | 1.34 | 8.00 | 0.23 | 22.00 | 19.00 | 7.00 | 0.01 | |
| Maximum | 100.00 | 2.27 | 2.07 | 34.00 | 1.02 | 100.00 | 83.31 | 45.00 | 0.11 | |
| Percentiles | 25 | 84 | 1.95 | 1.58 | 17.10 | 0.53 | 81.82 | 42.81 | 21.50 | 0.03 |
| 50 | 94 | 2.01 | 1.67 | 20.00 | 0.62 | 94.00 | 50.00 | 26.00 | 0.041 | |
| 75 | 99 | 2.075 | 1.75 | 23.85 | 0.71 | 98.00 | 58.00 | 31.38 | 0.057 | |
| Sr | Z | Yh | Yd | W | e0 | FC | WL | PI | Cs | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sr | R | 1 | 0.199 ** | 0.170 ** | −0.197 ** | 0.582 ** | −0.06 | 0.194 ** | 0.082 * | −0.01 | 0.138 ** |
| Sig. (2-tailed) | 0 | 0 | 0 | 0 | 0.06 | 0 | 0.02 | 0.78 | 0 | ||
| Z | R | 0.199 ** | 1 | 0.281 ** | 0.164 ** | 0.03 | 0.02 | 0.127 ** | 0 | −0.06 | 0.02 |
| Sig. (2-tailed) | 0 | 0 | 0 | 0.33 | 0.54 | 0 | 1 | 0.07 | 0.58 | ||
| Yh | R | 0.170 ** | 0.281 ** | 1 | 0.877 ** | −0.481 ** | −0.579 ** | −0.317 ** | −0.275 ** | −0.267 ** | −0.230 ** |
| Sig. (2-tailed) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Yd | R | −0.197 ** | 0.164 ** | 0.877 ** | 1 | −0.803 ** | −0.659 ** | −0.384 ** | −0.348 ** | −0.292 ** | −0.324 ** |
| Sig. (2-tailed) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| W | R | 0.582 ** | 0.03 | −0.481 ** | −0.803 ** | 1 | 0.633 ** | 0.385 ** | 0.372 ** | 0.264 ** | 0.349 ** |
| Sig. (2-tailed) | 0 | 0.33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| e0 | R | −0.06 | 0.02 | −0.579 ** | −0.659 ** | 0.633 ** | 1 | 0.227 ** | 0.321 ** | 0.260 ** | 0.216 ** |
| Sig. (2-tailed) | 0.06 | 0.54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| FC | R | 0.194 ** | 0.127 ** | −0.317 ** | −0.384 ** | 0.385 ** | 0.227 ** | 1 | 0.429 ** | 0.412 ** | 0.387 ** |
| Sig. (2-tailed) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| WL | R | 0.082 * | 0 | −0.275 ** | −0.348 ** | 0.372 ** | 0.321 ** | 0.429 ** | 1 | 0.914 ** | 0.553 ** |
| Sig. (2-tailed) | 0.02 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| PI | R | −0.01 | −0.06 | −0.267 ** | −0.292 ** | 0.264 ** | 0.260 ** | 0.412 ** | 0.914 ** | 1 | 0.512 ** |
| Sig. (2-tailed) | 0.78 | 0.07 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Cs | R | 0.138 ** | 0.02 | −0.230 ** | −0.324 ** | 0.349 ** | 0.216 ** | 0.387 ** | 0.553 ** | 0.552 ** | 1 |
| Sig. (2-tailed) | 0 | 0.58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Number | Eigenvalue | % Variance | % Cumulative Variance |
|---|---|---|---|
| 1 | 3.81 | 42.34 | 42.34 |
| 2 | 1.61 | 17.85 | 60.19 |
| 3 | 1.48 | 16.44 | 76.63 |
| 4 | 0.92 | 10.21 | 86.84 |
| 5 | 0.65 | 7.23 | 94.07 |
| 6 | 0.42 | 4.64 | 98.71 |
| 7 | 0.08 | 0.91 | 99.62 |
| 8 | 0.03 | 0.29 | 99.91 |
| 9 | 0.01 | 0.09 | 100.00 |
| Input Parameters | Gamma Test Statistics | ||
|---|---|---|---|
| Γ | Vratio | Mask | |
| All | 0.00014759 | 0.4054 | 111111111 |
| All-Sr | 0.00014653 | 0.4025 | 011111111 |
| All-Z | 0.00015130 | 0.4156 | 101111111 |
| All-Yh | 0.00014672 | 0.4030 | 110111111 |
| All-Yd | 0.00014689 | 0.4034 | 111011111 |
| All-W | 0.00017471 | 0.4798 | 111101111 |
| All-e0 | 0.00014712 | 0.4041 | 111110111 |
| All-FC | 0.00019292 | 0.5299 | 111111011 |
| All-WL | 0.00017584 | 0.4829 | 111111101 |
| All-PI | 0.00016223 | 0.4456 | 111111110 |
| Input Parameters | Gamma Test Statistics | ||
|---|---|---|---|
| Γ | Vratio | Mask | |
| WL | 0.00020688 | 0.5944 | 1000 |
| WL, PI | 0.00018845 | 0.5176 | 1100 |
| WL, PI, FC | 0.00017979 | 0.4938 | 1110 |
| WL, PI, FC, W | 0.00013524 | 0.3714 | 1111 |
| Input Subset | ANN Architecture | R2 | Decision |
|---|---|---|---|
| WL | 1-2-1 | 0.327 | WL selected |
| WL, Sr | 2-4-1 | 0.332 | Sr rejected |
| WL, Z | 2-4-1 | 0.328 | Z rejected |
| WL, Yd | 2-4-1 | 0.38 | Yd selected |
| WL, Yd, Yh | 3-6-1 | 0.41 | Yh rejected |
| WL, Yd, W | 3-6-1 | 0.444 | W selected |
| WL, Yd, W, e0 | 4-8-1 | 0.47 | e0 rejected |
| WL, Yd, W, FC | 4-8-1 | 0.46 | FC rejected |
| WL, Yd, W, PI | 4-8-1 | 0.498 | PI selected. |
| PSO | GT | FS | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE × 10−3 | RMSE | IOS | NSE | R | IOA | MAE × 10−3 | RMSE | IOS | NSE | R | IOA | MAE × 10−3 | RMSE | IOS | NSE | R | IOA | |
| Training | ||||||||||||||||||
| DNN | 9.5 | 0.013 | 0.283 | 0.56 | 0.75 | 0.85 | 8.3 | 0.0113 | 0.251 | 0.64 | 0.80 | 0.88 | 8.4 | 0.011 | 0.245 | 0.67 | 0.82 | 0.89 |
| ELM | 12 | 0.015 | 0.355 | −0.67 | 0.61 | 0.72 | 12 | 0.0153 | 0.340 | −1.33 | 0.61 | 0.69 | 12,2 | 0.015 | 0.34 | −0.88 | 0.61 | 0.72 |
| Lasso | 12.2 | 0.0154 | 0.344 | −0.76 | 0.60 | 0.72 | 12.1 | 0.0151 | 0.335 | −0.65 | 0.61 | 0.73 | 12.1 | 0.015 | 0.34 | −0.84 | 0.59 | 0.71 |
| PLS | 11.9 | 0.015 | 0.338 | −0.81 | 0.6 | 0.71 | 12.1 | 0.0152 | 0.339 | −0.66 | 0.61 | 0.73 | 12 | 0.015 | 0.34 | −0.69 | 0.61 | 0.73 |
| RF | 5.8 | 0.0075 | 0.168 | 0.72 | 0.94 | 0.95 | 5.7 | 0.0075 | 0.167 | 0.72 | 0.94 | 0.95 | 5.6 | 0.007 | 0.165 | 0.75 | 0.94 | 0.95 |
| Kridge | 12 | 0.015 | 0.342 | −0.73 | 0.61 | 0.72 | 12 | 0.015 | 0.343 | −0.71 | 0.61 | 0.73 | 12 | 0.015 | 0.334 | −0.67 | 0.61 | 0.73 |
| Ridge | 12.2 | 0.015 | 0.341 | −0.77 | 0.60 | 0.72 | 11.9 | 0.015 | 0.337 | −0.71 | 0.61 | 0.72 | 11.9 | 0.015 | 0.343 | −0.74 | 0.60 | 0.72 |
| LS | 12 | 0.0152 | 0.343 | −0.63 | 0.62 | 0.73 | 12.1 | 0.015 | 0.34 | −0.64 | 0.61 | 0.73 | 12 | 0.015 | 0.341 | −0.74 | 0.60 | 0.72 |
| Step | 12.1 | 0.0153 | 0.346 | −0.86 | 0.59 | 0.71 | 11.9 | 0.015 | 0.33 | −0.61 | 0.62 | 0.74 | 12.4 | 0.015 | 0.343 | −0.76 | 0.60 | 0.72 |
| SVR | 10.3 | 0.014 | 0.32 | 0.12 | 0.7 | 0.8 | 11.8 | 0.015 | 0.33 | −0.57 | 0.64 | 0.75 | 11.8 | 0.015 | 0.331 | −0.63 | 0.63 | 0.74 |
| GP | 11.3 | 0.014 | 0.305 | −0.22 | 0.67 | 0.78 | 11.1 | 0.014 | 0.302 | 0.46 | 0.68 | 0.79 | 11 | 0.014 | 0.299 | 0.47 | 0.69 | 0.8 |
| Validation | ||||||||||||||||||
| DNN | 10.8 | 0.0135 | 0.304 | 0.47 | 0.69 | 0.82 | 11.2 | 0.0149 | 0.347 | 0.41 | 0.66 | 0.80 | 10,3 | 0.014 | 0.312 | 0.47 | 0.70 | 0.82 |
| ELM | 11.4 | 0.014 | 0.346 | −0.53 | 0.6 | 0.73 | 12.5 | 0.015 | 0.35 | −1.68 | 0.64 | 0.69 | 11.7 | 0.015 | 0.331 | −0.93 | 0.62 | 0.72 |
| Lasso | 11.5 | 0.014 | 0.318 | −0.65 | 0.64 | 0.74 | 12 | 0.015 | 0.325 | −0.55 | 0.64 | 0.75 | 11.6 | 0.015 | 0.346 | −0.85 | 0.67 | 0.74 |
| PLS | 12.3 | 0.016 | 0.354 | −0.66 | 0.65 | 0.74 | 11.7 | 0.0146 | 0.312 | −0.59 | 0.64 | 0.74 | 12.2 | 0.015 | 0.339 | −0.59 | 0.61 | 0.73 |
| RF | 11 | 0.0138 | 0.308 | −0.29 | 0.70 | 0.79 | 11.1 | 0.0143 | 0.32 | −0.17 | 0.70 | 0.8 | 10.6 | 0.013 | 0.298 | 0.13 | 0.71 | 0.82 |
| Kridge | 12 | 0.0156 | 0.335 | −1.14 | 0.61 | 0.7 | 11.7 | 0.015 | 0.316 | −0.86 | 0.65 | 0.73 | 12.4 | 0.015 | 0.34 | −0.93 | 0.60 | 0.71 |
| Ridge | 11.8 | 0.0144 | 0.322 | −0.37 | 0.63 | 0.753 | 12 | 0.015 | 0.34 | −0.75 | 0.66 | 0.74 | 12.1 | 0.014 | 0.333 | −0.79 | 0.63 | 0.73 |
| LS | 12 | 0.015 | 0.334 | −0.49 | 0.57 | 0.72 | 12 | 0.015 | 0.33 | −0.49 | 0.62 | 0.75 | 12.2 | 0.015 | 0.33 | −0.55 | 0.63 | 0.75 |
| Step | 11.8 | 0.0145 | 0.315 | −0.47 | 0.67 | 0.76 | 12.3 | 0.015 | 0.34 | −0.67 | 0.61 | 0.73 | 11 | 0.014 | 0.31 | −0.54 | 0.64 | 0.75 |
| SVR | 12.1 | 0.016 | 0.34 | −0.76 | 0.53 | 0.69 | 12.6 | 0.015 | 0.34 | −0.51 | 0.59 | 0.71 | 12.6 | 0.015 | 0.344 | −0.49 | 0.58 | 0.71 |
| GP | 12.8 | 0.016 | 0.36 | −0.95 | 0.53 | 0.62 | 13.6 | 0.0162 | 0.357 | −1.14 | 0.55 | 0.60 | 13.5 | 0.017 | 0.363 | −0.72 | 0.55 | 0.62 |
| Equations No. | Study | Average | Standard Deviation |
|---|---|---|---|
| FS-RF (in the current study) | 1.07 | 0.25 | |
| FS-DNN (in the current study) | 1.08 | 0.34 | |
| (2) | Cozzolino 1961 | 1.096 | 0.761 |
| (1) | Nagaraj and Srinivasa 1986 | 1.695 | 0.989 |
| (3) | Işık1 2009 | 0.81 | 0.497 |
| (4) | Işık2 2009 | 0.766 | 0.461 |
| (5) | Işık3 2009 | 0.446 | 0.259 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin Benbouras, M.; Petrisor, A.-I. Prediction of Swelling Index Using Advanced Machine Learning Techniques for Cohesive Soils. Appl. Sci. 2021, 11, 536. https://doi.org/10.3390/app11020536
Amin Benbouras M, Petrisor A-I. Prediction of Swelling Index Using Advanced Machine Learning Techniques for Cohesive Soils. Applied Sciences. 2021; 11(2):536. https://doi.org/10.3390/app11020536
Chicago/Turabian StyleAmin Benbouras, Mohammed, and Alexandru-Ionut Petrisor. 2021. "Prediction of Swelling Index Using Advanced Machine Learning Techniques for Cohesive Soils" Applied Sciences 11, no. 2: 536. https://doi.org/10.3390/app11020536
APA StyleAmin Benbouras, M., & Petrisor, A.-I. (2021). Prediction of Swelling Index Using Advanced Machine Learning Techniques for Cohesive Soils. Applied Sciences, 11(2), 536. https://doi.org/10.3390/app11020536