Position Control Based on Add-on-Type Iterative Learning Control with Nonlinear Controller for Permanent-Magnet Stepper Motors
Abstract
1. Introduction
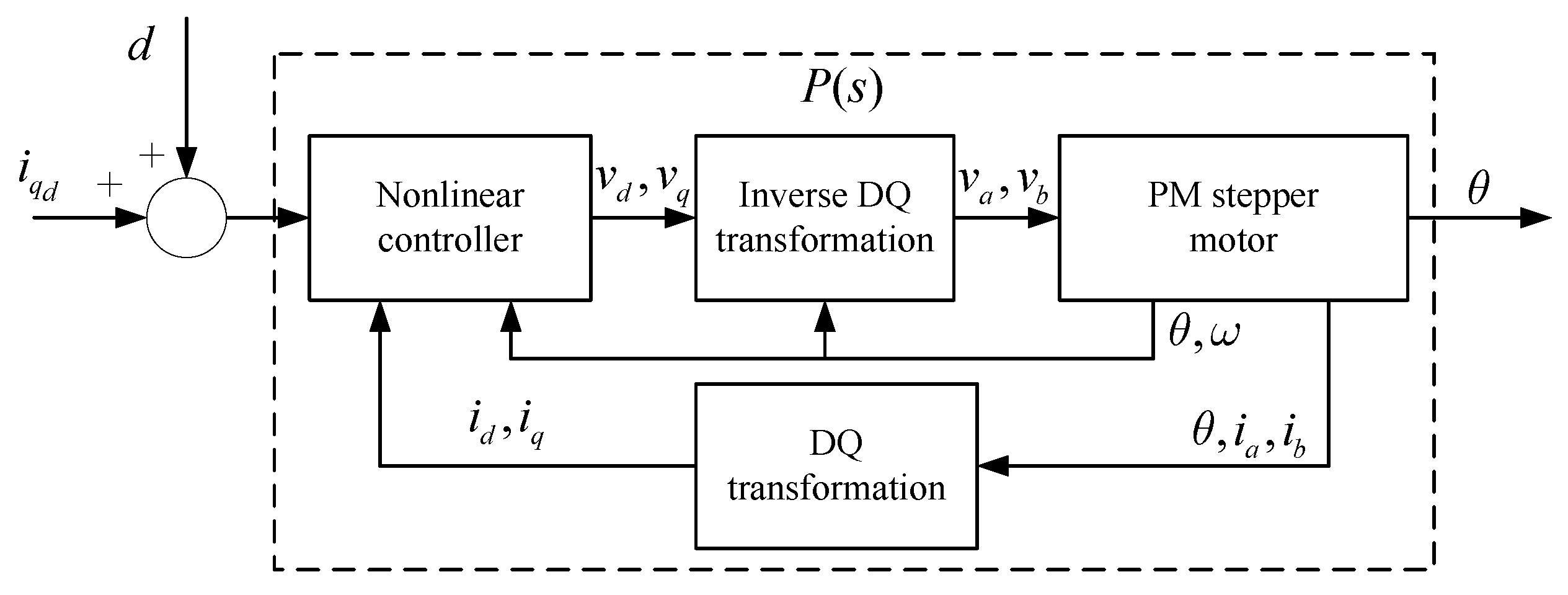
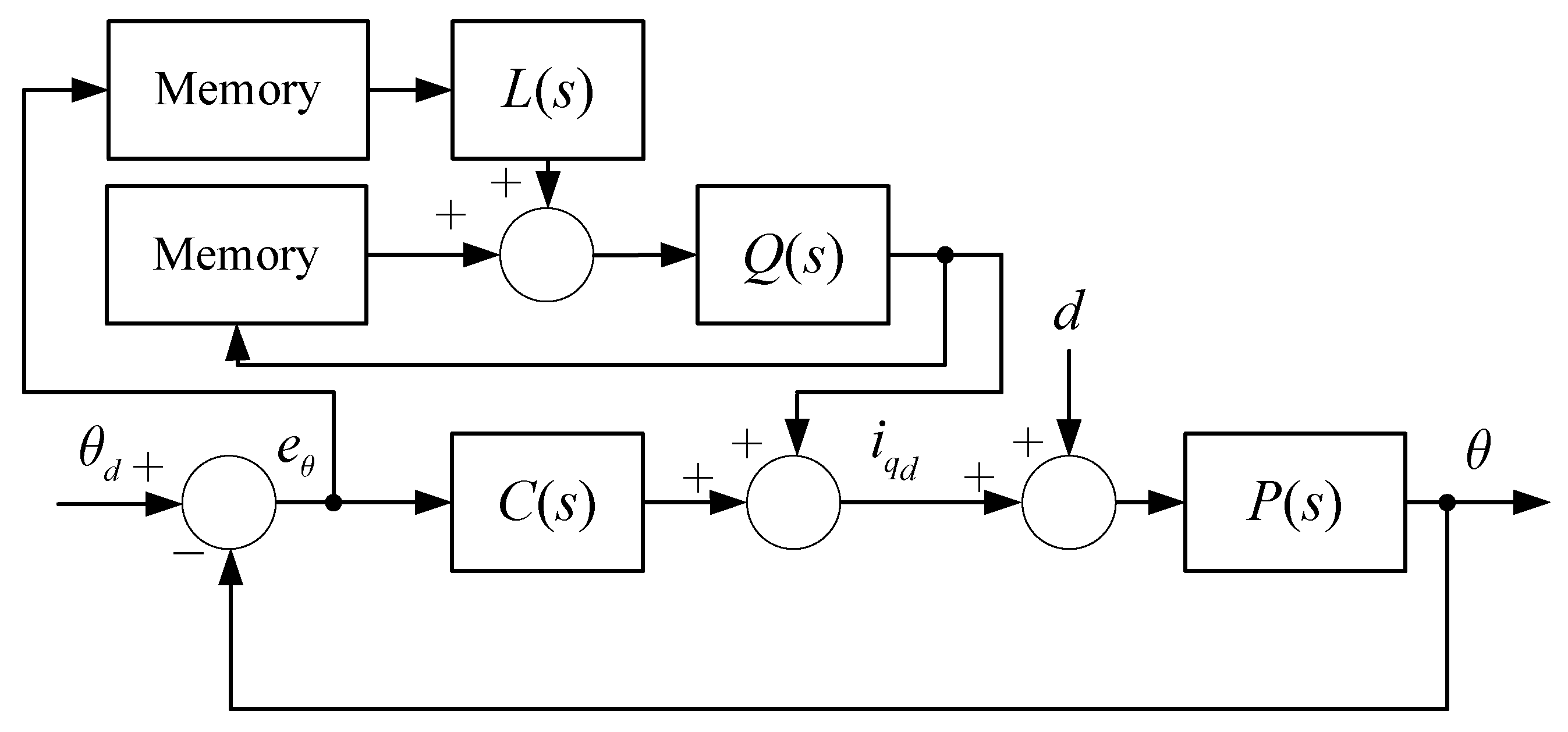
2. Controller Design
2.1. Nonlinear Controller for Current Dynamics
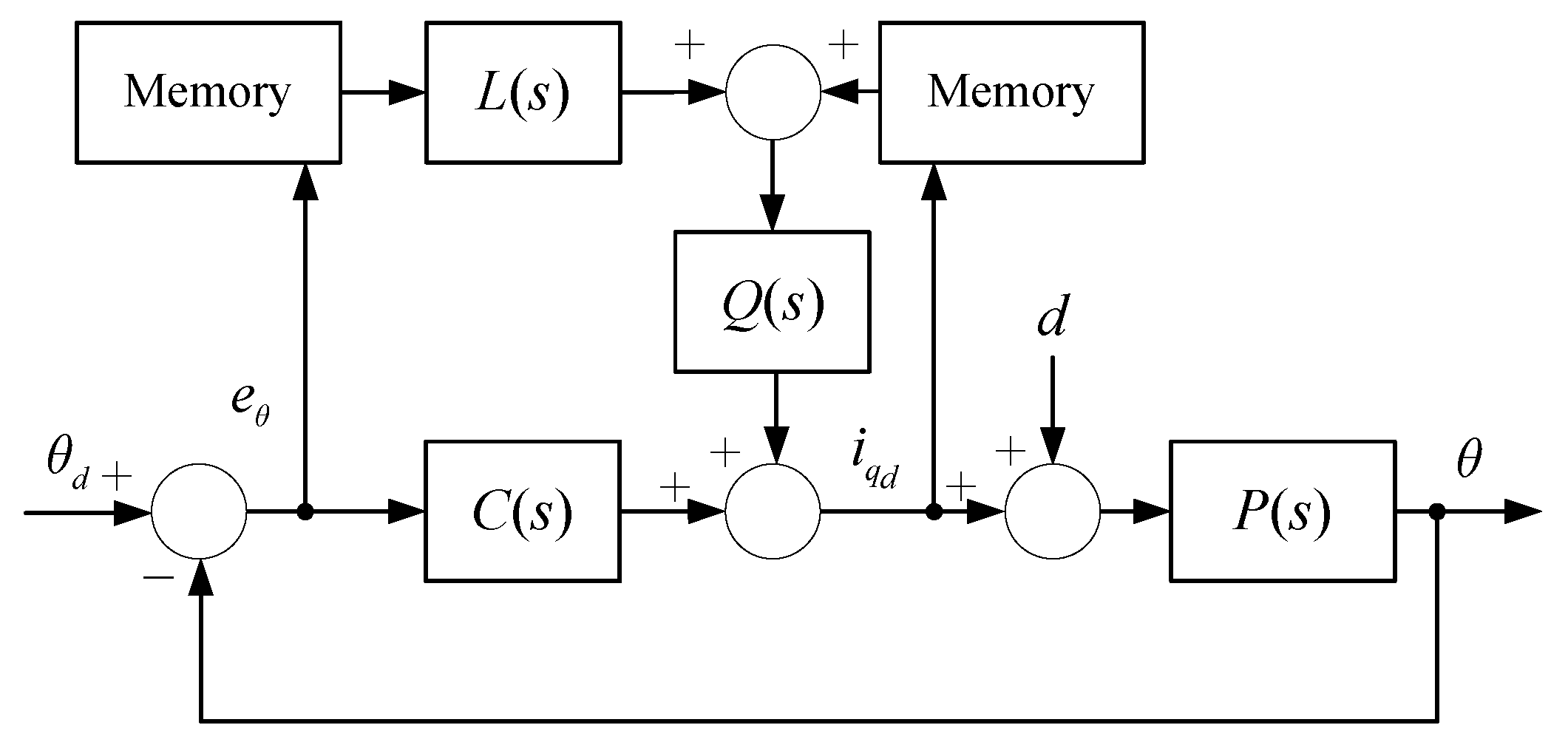
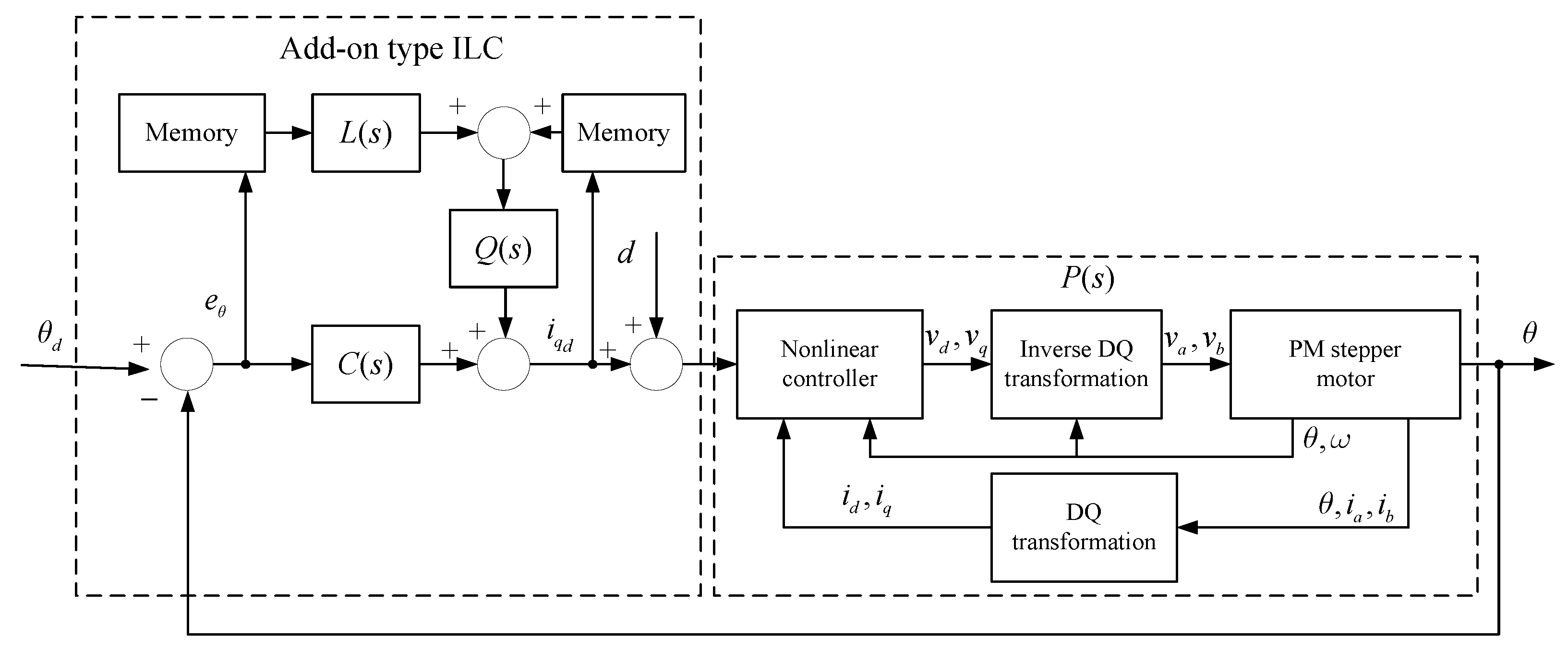
2.2. Add-on-Type ILC for Mechanical Dynamics
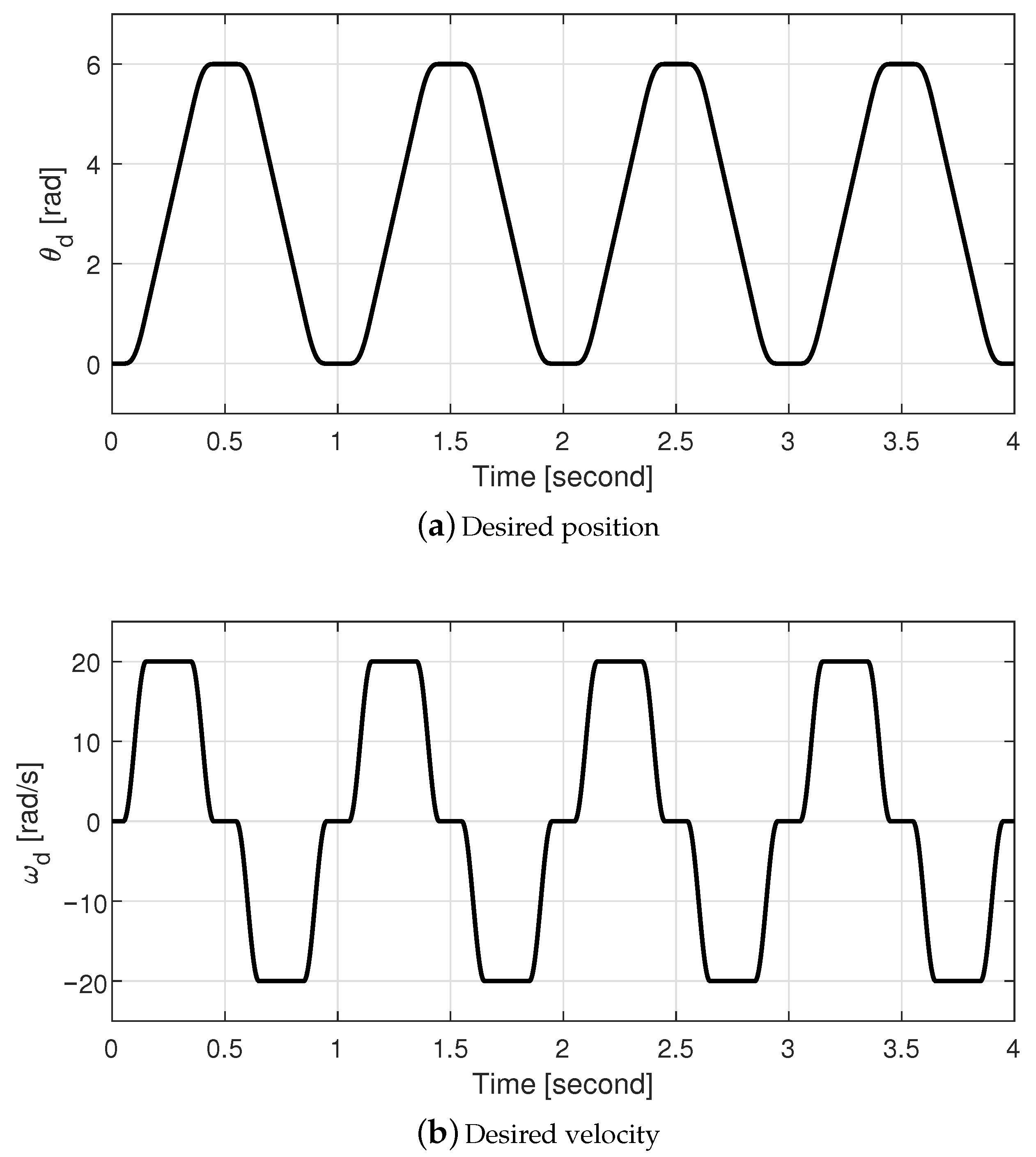
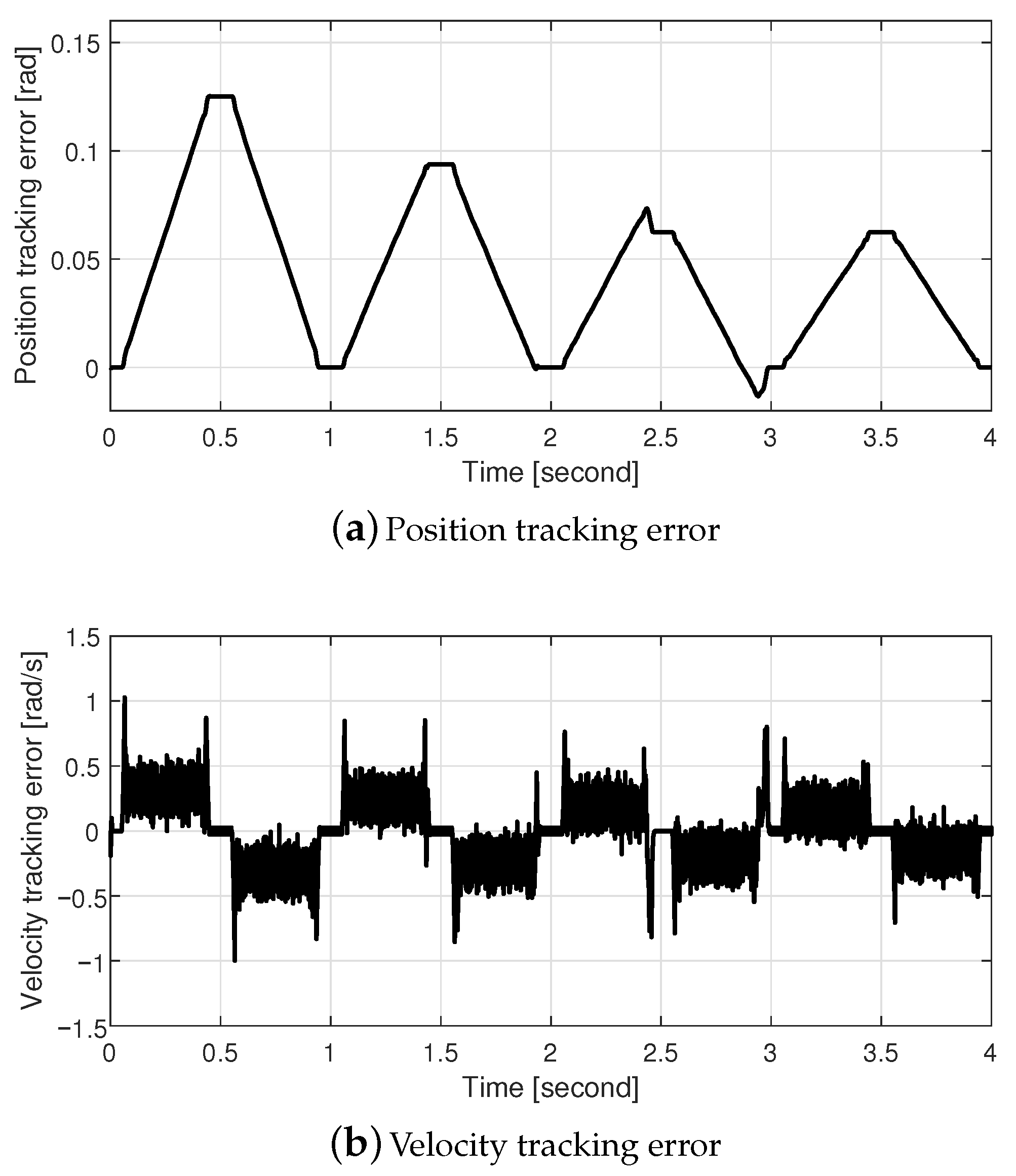
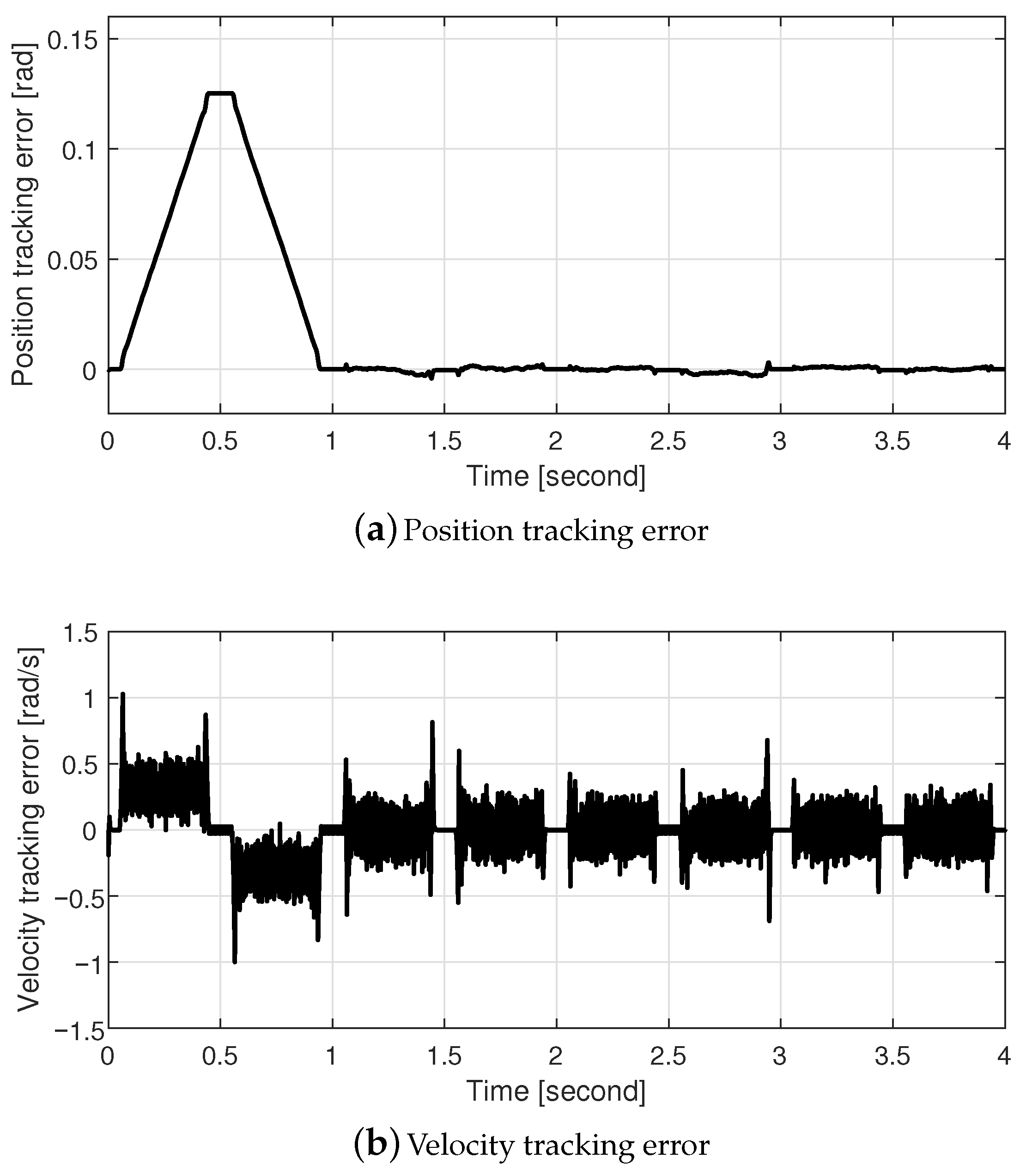
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuo, B.C. Theory and Applications of the Step Motors; West Publishing Co.: New York, NY, USA, 1974. [Google Scholar]
- Kenjo, T. Stepping Motors and Their Microprocessor Control; Clarendon: Oxford, UK, 1994. [Google Scholar]
- Ariasa, A.; Caum, J.; Griñóa, R. Moving towards the maximum speed in stepping motors by means of enlarging the bandwidth of the current controller. Mechatronics 2016, 40, 51–62. [Google Scholar] [CrossRef]
- Shin, D.; Kim, W.; Lee, Y.; Chung, C.C. Phase compensated microstepping for permanent magnet stepper motors. IEEE Trans. Ind. Electron. 2013, 60, 5773–5780. [Google Scholar] [CrossRef]
- Bodson, M.; Chiasson, J.; Novotnak, R.; Rekowski, R. High-performance nonlinear feedback control of a permanent magnet stepper motor. IEEE Trans. Control Syst. Technol. 1993, 1, 5–14. [Google Scholar] [CrossRef]
- Chen, J.-J.; Chin, K.-P. Automatic flux-weakening control of permanent magnet synchronous motors using a reduced-order controller. IEEE Trans. Power Electron. 2000, 15, 881–890. [Google Scholar] [CrossRef]
- Lee, J.; Hong, J.; Nam, K.; Ortega, R.; Praly, L.; Astolfi, A. Sensorless control of surface-mount permanent-magnet synchronous motors based on a nonlinear observer. IEEE Trans. Power Electron. 2010, 25, 290–297. [Google Scholar]
- Kim, W.; Shin, D.; Chung, C.C. Microstepping with nonlinear torque modulation for permanent magnet stepper motors. IEEE Trans. Control Syst. Technol. 2013, 21, 1971–1979. [Google Scholar]
- Shin, D.; Kim, W.; Lee, Y.; Chung, C.C. Nonlinear control with state-dependent reset integrator for a class of singularly perturbed interconnected nonlinear systems. IEEE Trans. Control Syst. Technol. 2017, 25, 1193–1203. [Google Scholar] [CrossRef]
- Shin, D.; Kim, W.; Lee, Y.; Chung, C.C. Enhanced nonlinear damping for a class of singularly perturbed interconnected nonlinear systems. Automatica 2016, 65, 36–42. [Google Scholar] [CrossRef]
- Lee, Y.; Shin, D.; Kim, W.; Chung, C.C. Nonlinear H2 control for LPV system with nonlinear varying parameters: Application to PM stepper motors. IEEE/ASME Trans. Mechatr. 2017, 22, 1349–1359. [Google Scholar] [CrossRef]
- Le, K.M.; Hoang, H.V.; Jeon, J.W. An advanced closed-loop control to improve the performance of hybrid stepper motors. IEEE Trans. Power Electron. 2017, 32, 7244–7255. [Google Scholar] [CrossRef]
- Zhou, Z.; Xia, C.; Yan, Y.; Wang, Z.; Shi, T. Disturbances attenuation of permanent magnet synchronous motor drives using cascaded predictive-integral-resonant controllers. IEEE Trans. Power Electron. 2017, 33, 1514–1527. [Google Scholar] [CrossRef]
- Mendoza-Mondragón, F.; Hernández-Guzmán, V.M.; Rodríguez-Reséndiz, J. Robust speed control of permanent magnet synchronous motors using two-degrees-of-freedom control. IEEE Trans. Ind. Electron. 2018, 65, 6099–6108. [Google Scholar]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lü, J. Discrete-time fast terminal sliding mode control for permanent magnet linear motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Du, H.; Wen, G.; Cheng, Y.; Lu, J. Design and implementation of bounded finite-time control algorithm for speed regulation of permanent magnet synchronous motor. IEEE Trans. Ind. Electron. 2020, 68, 2417–2426. [Google Scholar] [CrossRef]
- Lee, Y.; Gil, J.; Kim, W. Velocity control for sideband harmonics compensation in permanent magnet synchronous motors with low switching frequency inverter. IEEE Trans. Ind. Electron. 2021, 68, 3434–3444. [Google Scholar] [CrossRef]
- Moore, K.L.; YangQuan, C.; Ahn, H. Iterative learning control: A tutorial and big picture view. In Proceedings of the IEEE Conference on Decision Control, San Diego, CA, USA, 13–15 December 2006; pp. 2352–2357. [Google Scholar]
- Graham, M.R.; de Callafon, R.A.; Shrinkle, L. An iterative learning controller for reduction of repeatable runout in hard disk drives. In Proceedings of the IEEE American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 566–571. [Google Scholar]
- Mishra, S.; Coaplen, J.; Tomizuka, M. Precision positioning of wafer scanners segmented iterative learning control for nonrepetitive disturbances [Applications of control]. IEEE Control Syst. Mag. 2007, 27, 20–25. [Google Scholar]
- Sahoo, S.K.; Panda, S.K.; Xu, J.X. Iterative learning-based high-performance current controller for switched reluctance motors. IEEE Trans. Energy Conv. 2004, 19, 491–498. [Google Scholar] [CrossRef]
- Mandra, S.; Galkowski, K.; Rogers, E.; Rauh, A.; Aschemann, H. Performance-enhanced robust iterative learning control with experimental application to PMSM position tracking. IEEE Trans. Control Syst. Technol. 2018, 27, 1813–1819. [Google Scholar] [CrossRef]
- Fei, Q.; Deng, Y.; Li, H.; Liu, J.; Shao, M. Speed ripple minimization of permanent magnet synchronous motor based on model predictive and iterative learning controls. IEEE Access. 2019, 7, 31791–31800. [Google Scholar] [CrossRef]
- Deltoro, V. Machines and Power Systems; Prentice-Hall: Englwood Cliffs, NJ, USA, 1985. [Google Scholar]
- Acarnley, P.P. Stepping Motors: A Guide to Modern Theory and Practice; Peregrinus: New York, NY, USA, 1982. [Google Scholar]
- 2-Phase Stepping Motors, PK Series, Oriental Motor. Available online: https://www.orientalmotor.eu/media/files/pk2-catalogue-2013-en.pdf?dwnl=1 (accessed on 18 December 2020).


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| L | 40 mH | R | |
| J | kg·m2 | N·m/A | |
| 50 | B | N·m·s/rad |
| Control Gain | Value | Control Gain | Value |
|---|---|---|---|
| 200 | 200 | ||
| 0.1 | 0.1 | ||
| 20 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suh, S.; Kim, W. Position Control Based on Add-on-Type Iterative Learning Control with Nonlinear Controller for Permanent-Magnet Stepper Motors. Appl. Sci. 2021, 11, 587. https://doi.org/10.3390/app11020587
Suh S, Kim W. Position Control Based on Add-on-Type Iterative Learning Control with Nonlinear Controller for Permanent-Magnet Stepper Motors. Applied Sciences. 2021; 11(2):587. https://doi.org/10.3390/app11020587
Chicago/Turabian StyleSuh, Sangmin, and Wonhee Kim. 2021. "Position Control Based on Add-on-Type Iterative Learning Control with Nonlinear Controller for Permanent-Magnet Stepper Motors" Applied Sciences 11, no. 2: 587. https://doi.org/10.3390/app11020587
APA StyleSuh, S., & Kim, W. (2021). Position Control Based on Add-on-Type Iterative Learning Control with Nonlinear Controller for Permanent-Magnet Stepper Motors. Applied Sciences, 11(2), 587. https://doi.org/10.3390/app11020587






