A Thermomechanical Coupling Constitutive Model of Concrete Including Elastoplastic Damage
Abstract
:1. Introduction
2. Model Development
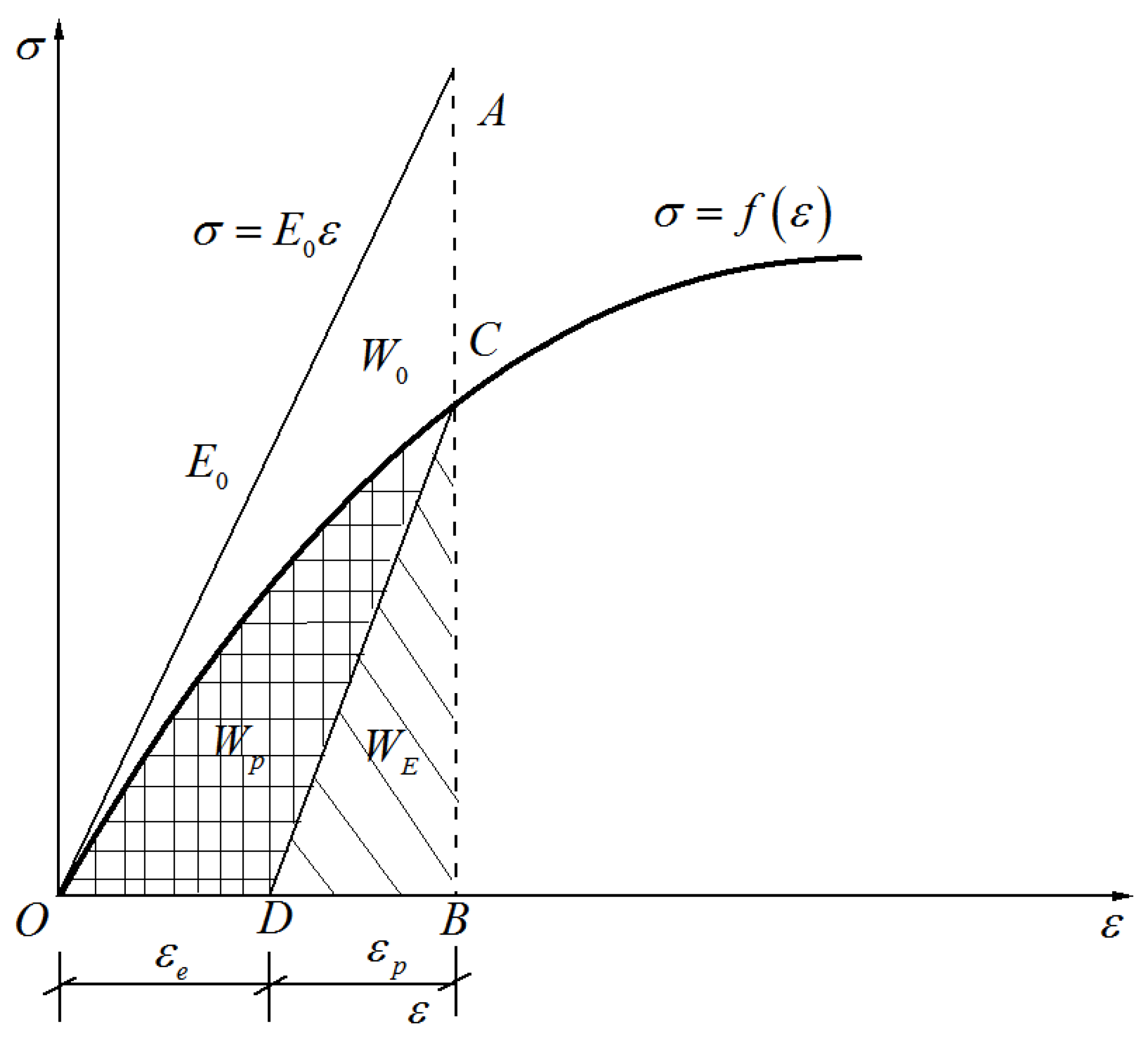
2.1. Elastic Stress–Strain Model
2.2. Plastic Stress–Strain Model
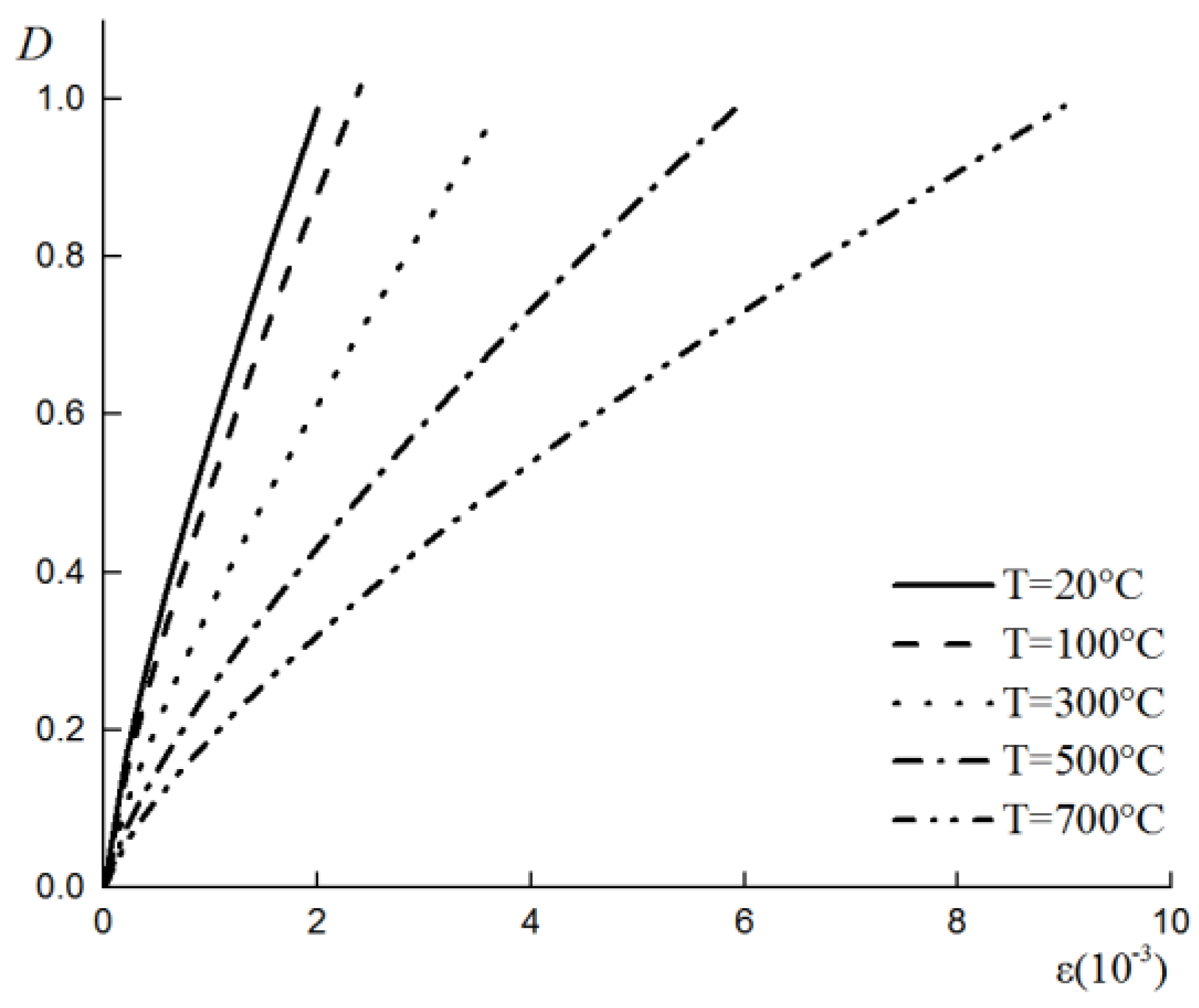
2.3. Damage Evolution Model
2.4. Formulation of Developed Constitutive Model
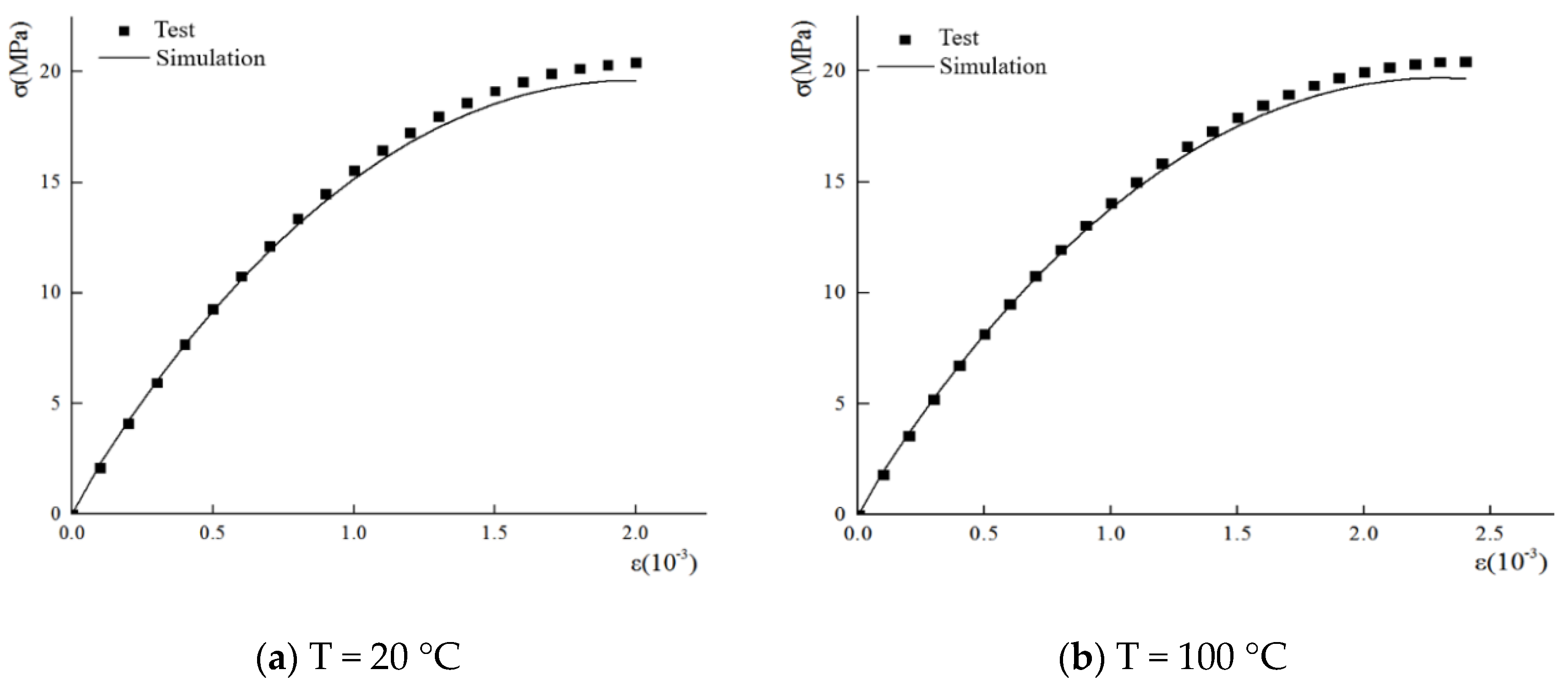
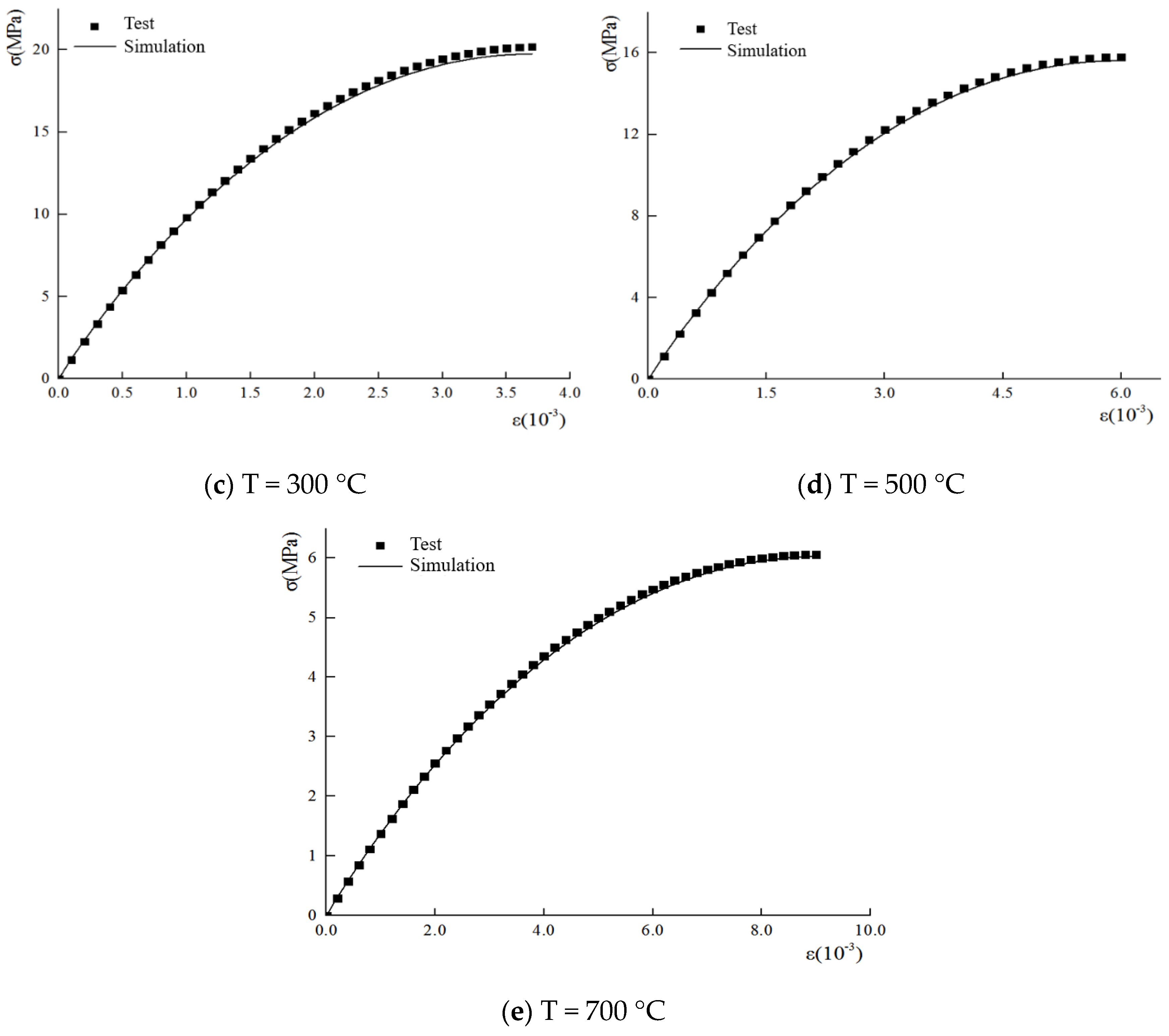
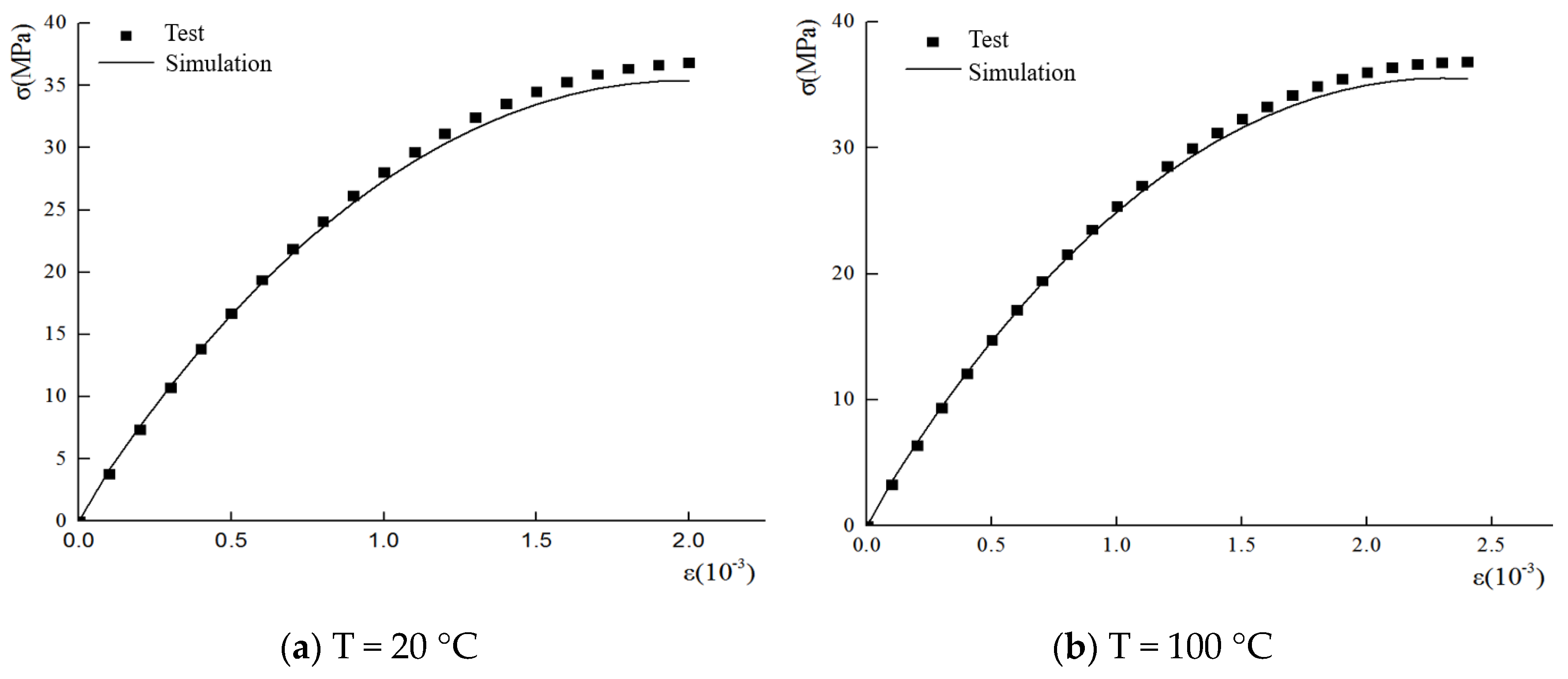
3. Model Validation
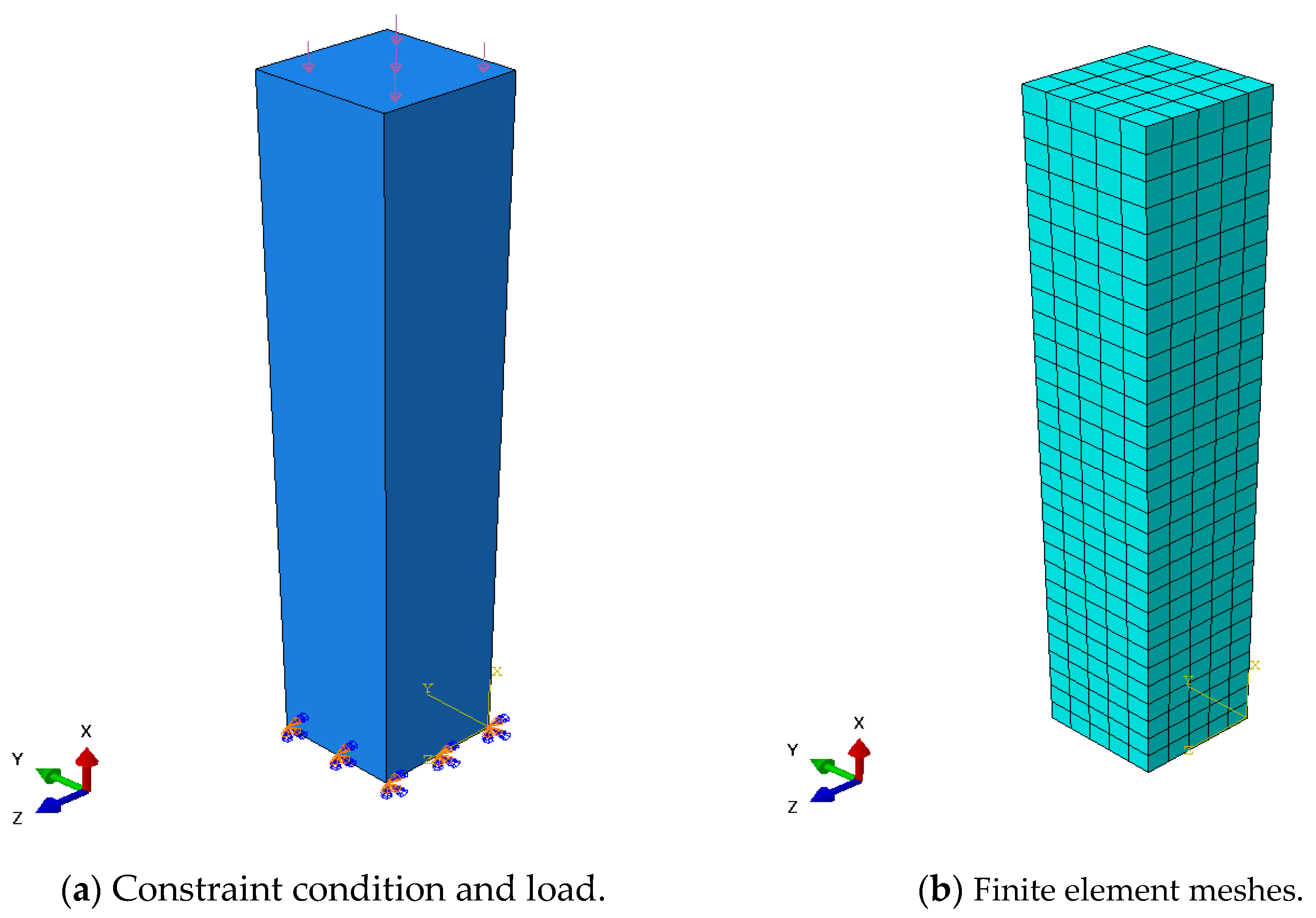
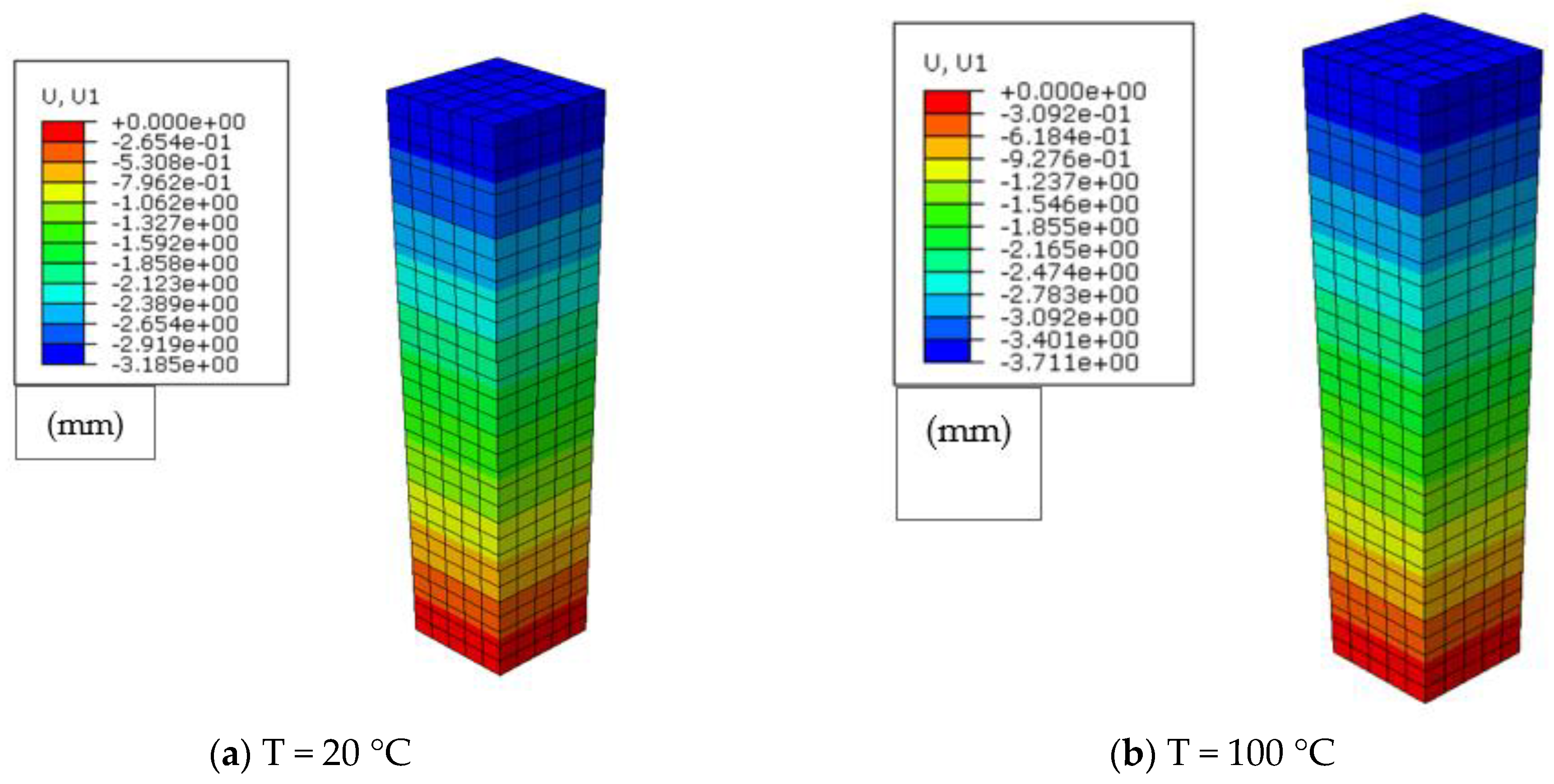
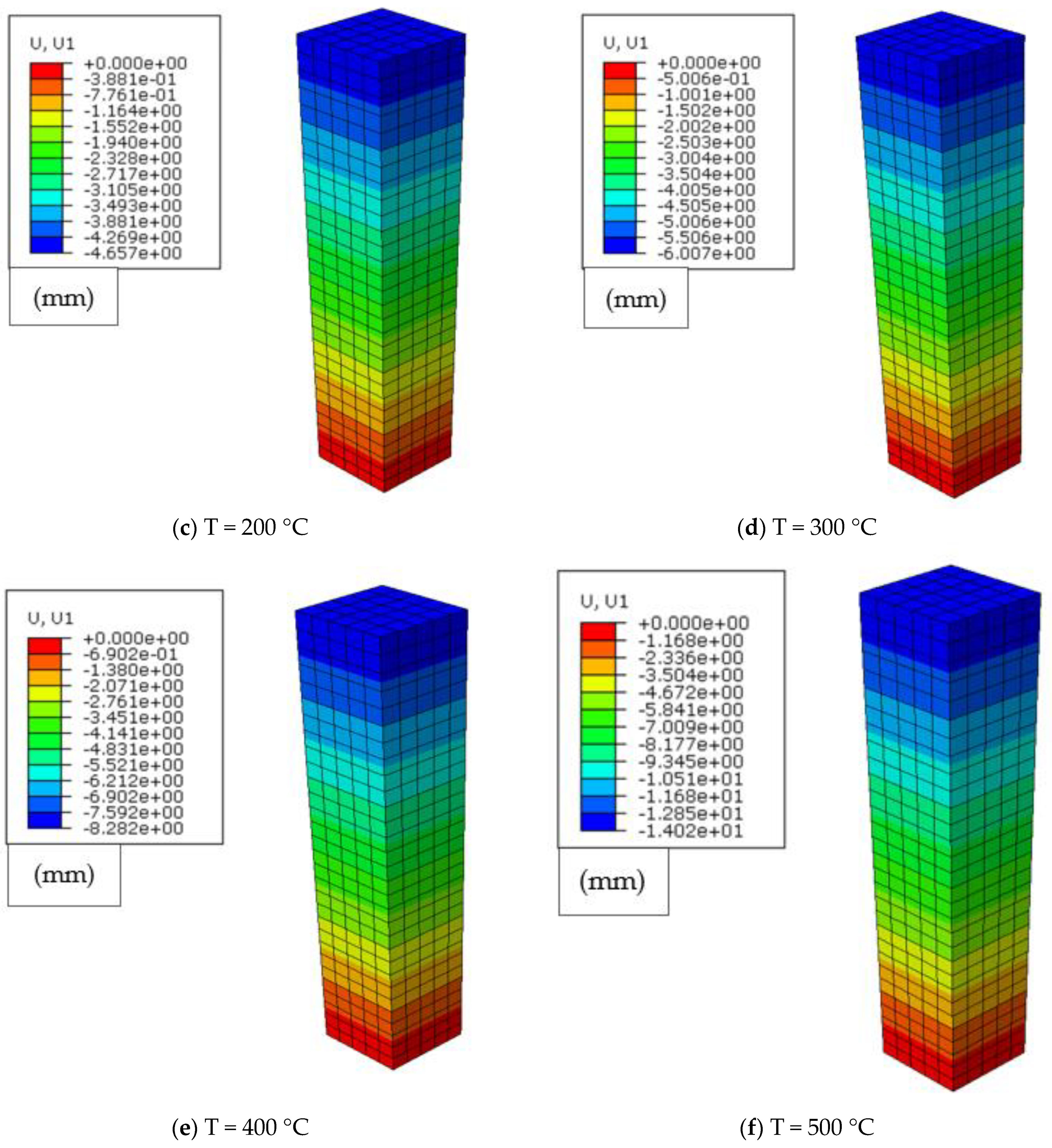
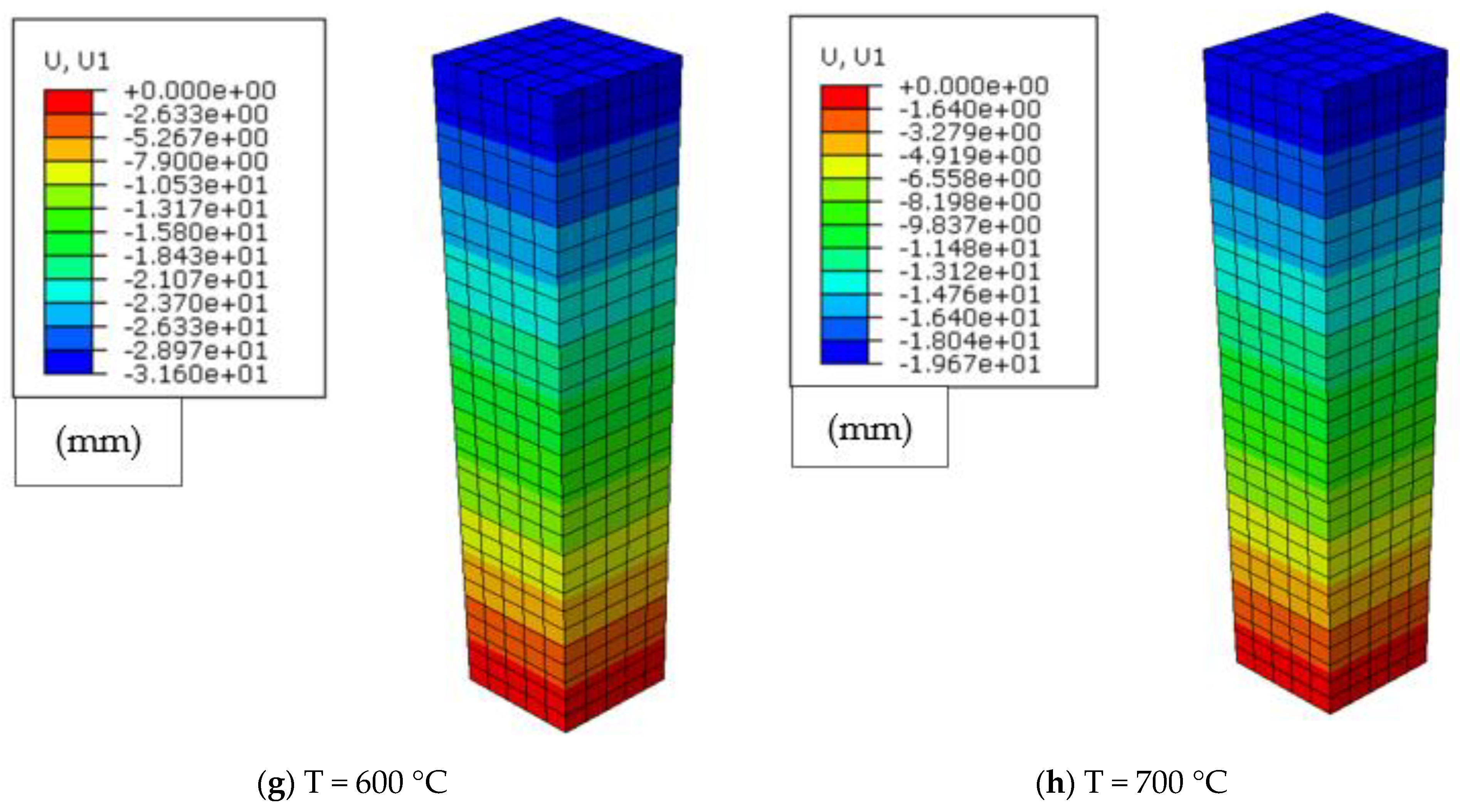
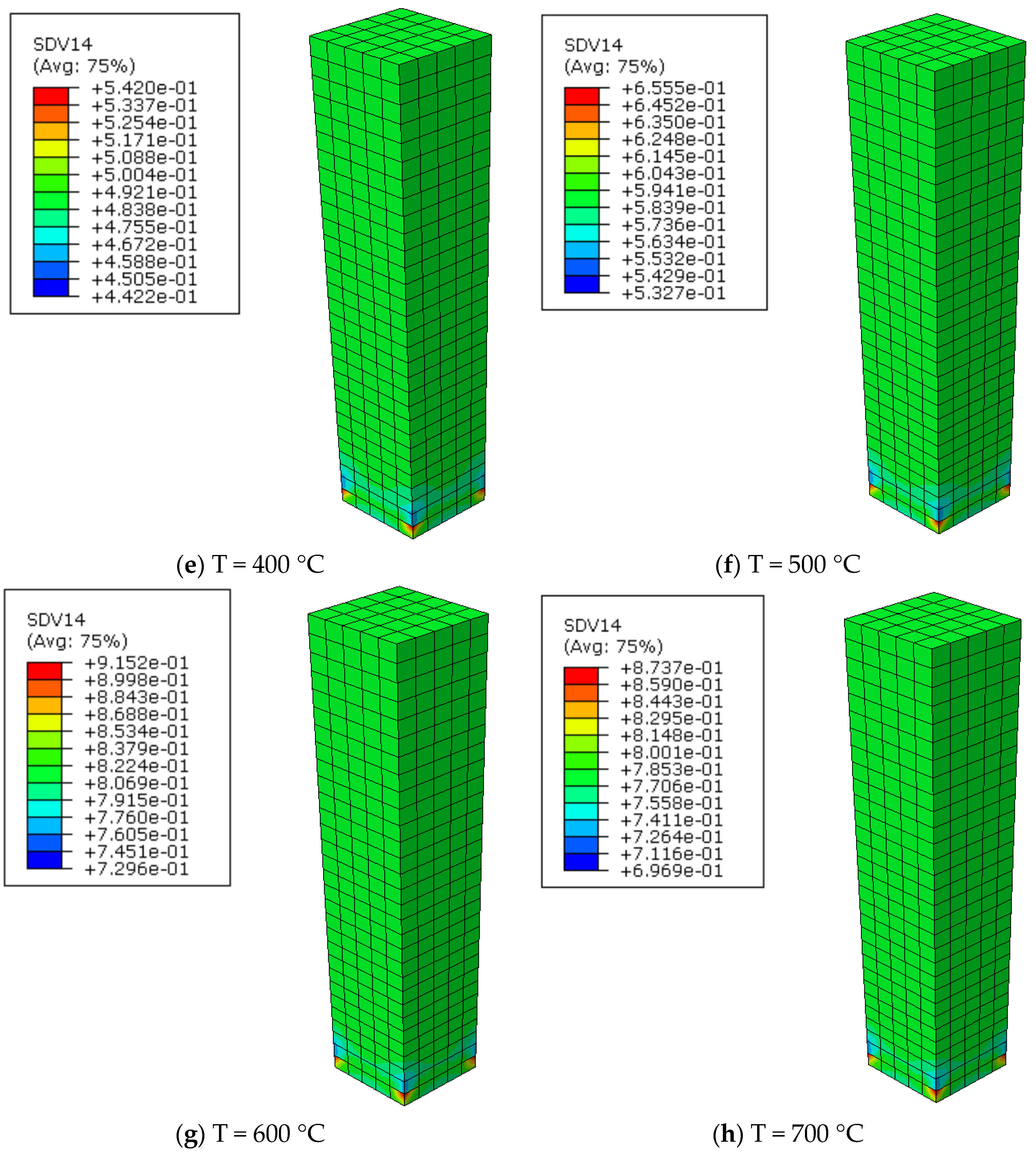
4. Model Application
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kapsalis, P.; El Kadi, M.; Vervloet, J.; De Munck, M.; Wastiels, J.; Triantafillou, T.; Tysmans, T. Thermomechanical Behavior of Textile Reinforced Cementitious Composites Subjected to Fire. Appl. Sci. 2019, 9, 747. [Google Scholar] [CrossRef] [Green Version]
- Pires, D.; Barros, R.C.; Silveira, R.A.M.; Lemes, I.J.M.; Rocha, P.A.S. An Efficient Inelastic Approach Using SCM/RPHM Coupling to Study Reinforced Concrete Beams, Columns and Frames under Fire Conditions. Eng. Struct. 2020, 219, 110852. [Google Scholar] [CrossRef]
- Albuquerque, G.L.; Silva, A.B.; Rodrigues, J.P.C.; Silva, V.P. Behavior of Thermally Restrained RC Beams in Case of Fire. Eng. Struct. 2018, 174, 407–417. [Google Scholar] [CrossRef]
- Akca, A.H.; Özyurt, N. Post-Fire Mechanical Behavior and Recovery of Structural Reinforced Concrete Beams. Constr. Build. Mater. 2020, 253, 119188. [Google Scholar] [CrossRef]
- Thanaraj, D.P.; Anand, N.; Arulraj, P.; Al-Jabrib, K. Investigation on Structural and Thermal Performance of Reinforced Concrete Beams Exposed to Standard Fire. J. Build. Eng. 2020, 32, 101764. [Google Scholar] [CrossRef]
- Guo, Z.; Li, W. Deformation Testing and Constitutive Relationship of Concrete under Different Stress-Temperature Paths. Chin. Civ. Eng. 1993, 26, 58–69. [Google Scholar]
- Qin, L.; Song, Y.; Chen, H.; Zhang, Z.; Yu, C. Experimental Study of Strength and Deformation of Concrete under Biaxial Tension-Compression Stress after High Temperature. Eng. Mech. 2006, 23, 112–116. [Google Scholar]
- Zhang, Z.; Song, Y.; Shi, J. Mechanical Behavior of Normal Concrete under Triaxial Compression after High Temperature. Eng. Mech. 2009, 26, 159–164. [Google Scholar]
- Liang, A.; Zhang, Q.; Yuan, G.; Dong, Y. Study on The Influencing Factors of Concrete Compressive Strength after Elevated Temperature. J. Chin. Coal. Soc. 2010, 35, 2049–2052. [Google Scholar]
- Jia, F.; Wang, Y.; Qu, Y.; Cheng, Y.; Cao, B. Influences of Various Cooling Methods and Standing Time on Residual Strength of Concrete after Elevated Temperature Exposure. J. Build. Mater. 2011, 14, 400–405. [Google Scholar]
- Xing, W.; Shi, X.; Ni, J. Short-Term Thermal Creep Model of Concrete Based on Experiments. Eng. Mech. 2011, 28, 158–163. [Google Scholar]
- Yu, Z.; Zi, W.; Kuang, Y.; Zhang, L. Influences of Temperature and Time on Concrete Cubic Compressive Strength. Fire Sci. Tech. 2012, 31, 111–114. [Google Scholar]
- Shao, W.; Chen, Y.; Zhou, Y. Experimental Study on Mechanical Properties of Concrete after Different Temperature and Different Heating Time. J. Dis. Prev. MIT Eng. 2012, 32, 248–252. [Google Scholar]
- Kizilkanat, A.B.; Yuezer, N.; Kabay, N. Thermo-Physical Properties of Concrete Exposed to High Temperature. Constr. Build. Mater. 2013, 45, 157–161. [Google Scholar] [CrossRef]
- Ergün, A.; Kürklü, G.; Baspinar, M.S.; Mansour, M.Y. The Effect of Cement Dosage on Mechanical Properties of Concrete Exposed to High Temperatures. Fire Saf. J. 2013, 55, 160–167. [Google Scholar] [CrossRef]
- Zhai, Y.; Deng, Z.; Li, N.; Xu, R. Study on Compressive Mechanical Capabilities of Concrete after High Temperature Exposure and Thermo-Damage Constitutive Model. Constr. Build. Mater. 2014, 68, 777–782. [Google Scholar] [CrossRef]
- Tang, C.W. Residual Mechanical Properties of Fiber-Reinforced Lightweight Aggregate Concrete after Exposure to Elevated Temperatures. Appl. Sci. 2020, 10, 3519. [Google Scholar] [CrossRef]
- Gowacki, M.; Kowalski, R. An Experimental Approach to the Estimation of Stiffness Changes in RC Elements Exposed to Bending and High Temperature. Eng. Struct. 2020, 217, 110720. [Google Scholar] [CrossRef]
- Ma, Q.; Guo, R.; Zhao, Z.; Lin, Z.; He, K. Mechanical Properties of Concrete at High Temperature—A Review. Constr. Build. Mater. 2015, 93, 371–383. [Google Scholar] [CrossRef]
- Zhang, P.; Kang, L.; Wang, J.; Guo, J.; Hu, S.; Ling, Y. Mechanical Properties and Explosive Spalling Behavior of Steel-Fiber-Reinforced Concrete Exposed to High Temperatur—A Review. Appl. Sci. 2020, 10, 2324. [Google Scholar] [CrossRef] [Green Version]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Laterza, M.; D’Amato, M.; Thanthirige, L.P.; Braga, F.; Gigliotti, R. Comparisons of Codal Detailing Rules for Curvature Ductility and Numerical Investigations. Open Constr. Build. Technol. J. 2014, 8, 132–141. [Google Scholar] [CrossRef] [Green Version]
- Gernay, T.; Millard, A.; Franssen, J.M. A Multiaxial Constitutive Model for Concrete in the Fire Situation: Theoretical Formulation. Int. J. Solids Struct. 2013, 50, 3659–3673. [Google Scholar] [CrossRef] [Green Version]
- Gernay, T.; Franssen, J.M. A Plastic-Damage Model for Concrete in Fire: Applications in Structural Fire Engineering. Fire Saf. J. 2015, 71, 268–278. [Google Scholar] [CrossRef]
- Yu, X.; Chen, L.; Fang, Q.; Ruan, Z.; Hong, J.; Xiang, H. A Concrete Constitutive Model Considering Coupled Effects of High Temperature and High Strain Rate. Int. J. Impact Eng. 2016, 101, 66–77. [Google Scholar] [CrossRef]
- Bouras, Y.; Dušan, Z.; Teodor, M.A.; Zora, V. A Non-Linear Thermo-Viscoelastic Rheological Model Based on Fractional Derivatives for High Temperature Creep in Concrete. Appl. Math. Model. 2018, 55, 551–568. [Google Scholar] [CrossRef]
- Liang, W.; Zhao, J.; Li, Y.; Zhai, Y.; Wang, Z.; Yang, Y. Research on Dynamic Mechanical Properties and Constitutive Model of Basalt Fiber Reinforced Concrete after Exposure to Elevated Temperatures under Impact Loading. Appl. Sci. 2020, 10, 7684. [Google Scholar] [CrossRef]
- Heinfling, G.; Reynouard, J.; Merabet, O.; Duval, C. A Thermo-Elastic-Plastic Model for Concrete at Elevated Temperatures Including Cracking and Thermo-Mechanical Interaction Strains. In Computational Plasticity, Fundamentals and Applications, Proceedings of the 5th International Conference on Computational Plasticity, Barcelona, Spain, 17–20 March 1997; Owen, D., Onate, E., Hinton, E., Eds.; International Center for Numerical Methods in Engineering: Barcelona, Spain, 1997. [Google Scholar]
- Ju, J.W.; Zhang, Y. Advanced Thermomechanical Constitutive Models for Airfield Concrete Pavement under High Temperatures. In Damage Mechanics in Engineering Materials; Voyiadjis, G.Z., Ju, J.W., Chaboche, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Gawin, D.; Majorana, C.; Schrefler, B. Numerical Analysis of Hygro-Thermal Behaviour and Damage of Concrete at High Temperature. Mech. Cohes Frict. Mater. 1999, 4, 37–74. [Google Scholar] [CrossRef]
- Nechnech, D.; Meftah, F.; Reynouard, J. An Elasto-Plastic Damage Model for Plain Concrete Subjected to High Temperature. Eng. Struct. 2002, 24, 597–611. [Google Scholar] [CrossRef]
- Wu, J.; Li, J. Unified Elasto-Plastic Damage Constitutive Relations Model for Concrete. J. Archit. Civ. Eng. 2005, 22, 15–21. [Google Scholar]
- Pont, S.; Durand, S.; Schrefler, B.A. A Multiphase Thermo-Hydro-Mechanical Model for Concrete at High Temperatures-Finite Element Implementation and Validation under LOCA Load. Nucl. Eng. Des. 2007, 237, 2137–2150. [Google Scholar] [CrossRef]
- Krairi, A.; Doghri, I. A Thermodynamically-Based Constitutive Model for Thermoplastic Polymers Coupling Viscoelasticity, Viscoplasticity and Ductile Damage. Int. J. Plast. 2014, 60, 163–181. [Google Scholar] [CrossRef]
- Torelli, G.; Mandal, P.; Gillie, M.; Tran, V.X. A Confinement-Dependent Load-Induced Thermal Strain Constitutive Model for Concrete Subjected to Temperatures up to 500 °C. Int. J. Mech. Sci. 2018, 144, 887–896. [Google Scholar] [CrossRef]
- Chen, X.D.; Bu, J.W.; Zhou, W.; Wang, Q. Effect of Pre-Cyclic Damage and High Temperature on Residual Tensile Behavior of Concrete. Fire Saf. J. 2019, 108, 102853. [Google Scholar] [CrossRef]
- Pečenko, R.; Hozjan, T.; Planinc, I.; Bratina, S. A Computational Model for Prestressed Concrete Hollow-Core Slab Under Natural Fire. Int. J. Concr. Struct. Mater. 2019, 13, 60–76. [Google Scholar] [CrossRef]
- Yao, Y.; Guo, H.; Tan, K. An Elastoplastic Damage Constitutive Model of Concrete Considering the Effects of Dehydration and Pore Pressure at High Temperatures. Mater. Struct. 2020, 53, 19–36. [Google Scholar] [CrossRef]
- Torelli, G.; Gillie, M.; Mandal, P.; Draup, J.; Tran, V.X. A Moisture-Dependent Thermomechanical Constitutive Model for Concrete Subjected to Transient High Temperatures. Eng. Struct. 2020, 210, 110170. [Google Scholar] [CrossRef]
- Stabler, J.; Baker, G. On the Form of Free Energy and Specific Heat in Coupled Thermo-Elasticity with Isotropic Damage. Int. J. Solids Struct. 2000, 37, 4691–4713. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil Mechanics and Plastic Analysis or Limit Design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Krajcinovi, D.; Lemaitre, J. Continuum Damage Mechanics Theory and Applications; Springer: New York, NY, USA, 1987; pp. 233–294. ISBN 978-3-211-82011-7. [Google Scholar]




(GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (MPa) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 21.781 | 18.732 | 11.696 | 5.793 | 1.481 | 0.15 | 0.01 | 0.002 | 20.435 | 0.0189 | 0.9102 | 0.0296 | 0.6225 |
(GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (MPa) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 39.278 | 33.779 | 21.090 | 10.446 | 2.671 | 0.15 | 0.01 | 0.002 | 36.85 | 0.0189 | 0.9102 | 0.0296 | 0.6225 |
(GPa) | (MPa) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 39.278 | 0.15 | 0.01 | 0.002 | 36.85 | 0.0189 | 0.9102 | 0.0296 | 0.6225 | |
| 33.779 | |||||||||
| 27.001 | |||||||||
| 21.090 | |||||||||
| 15.751 | |||||||||
| 10.446 | |||||||||
| 5.725 | |||||||||
| 2.671 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Wang, H.; Wu, J.; Jiang, W. A Thermomechanical Coupling Constitutive Model of Concrete Including Elastoplastic Damage. Appl. Sci. 2021, 11, 604. https://doi.org/10.3390/app11020604
Li L, Wang H, Wu J, Jiang W. A Thermomechanical Coupling Constitutive Model of Concrete Including Elastoplastic Damage. Applied Sciences. 2021; 11(2):604. https://doi.org/10.3390/app11020604
Chicago/Turabian StyleLi, Liang, Hongwei Wang, Jun Wu, and Wenhua Jiang. 2021. "A Thermomechanical Coupling Constitutive Model of Concrete Including Elastoplastic Damage" Applied Sciences 11, no. 2: 604. https://doi.org/10.3390/app11020604
APA StyleLi, L., Wang, H., Wu, J., & Jiang, W. (2021). A Thermomechanical Coupling Constitutive Model of Concrete Including Elastoplastic Damage. Applied Sciences, 11(2), 604. https://doi.org/10.3390/app11020604





