The Design and FPGA-Based Implementation of a Stream Cipher Based on a Secure Chaotic Generator

Abstract

In this study, with an FPGA-board using VHDL, we designed a secure chaos-based stream cipher (SCbSC), and we evaluated its hardware implementation performance in terms of computational complexity and its security. The fundamental element of the system is the proposed secure pseudo-chaotic number generator (SPCNG). The architecture of the proposed SPCNG includes three first-order recursive filters, each containing a discrete chaotic map and a mixing technique using an internal pseudo-random number (PRN). The three discrete chaotic maps, namely, the 3D Chebyshev map (3D Ch), the 1D logistic map (L), and the 1D skew-tent map (S), are weakly coupled by a predefined coupling matrix M. The mixing technique combined with the weak coupling technique of the three chaotic maps allows preserving the system against side-channel attacks (SCAs). The proposed system was implemented on a Xilinx XC7Z020 PYNQ-Z2 FPGA platform. Logic resources, throughput, and cryptanalytic and statistical tests showed a good tradeoff between efficiency and security. Thus, the proposed SCbSC can be used as a secure stream cipher.

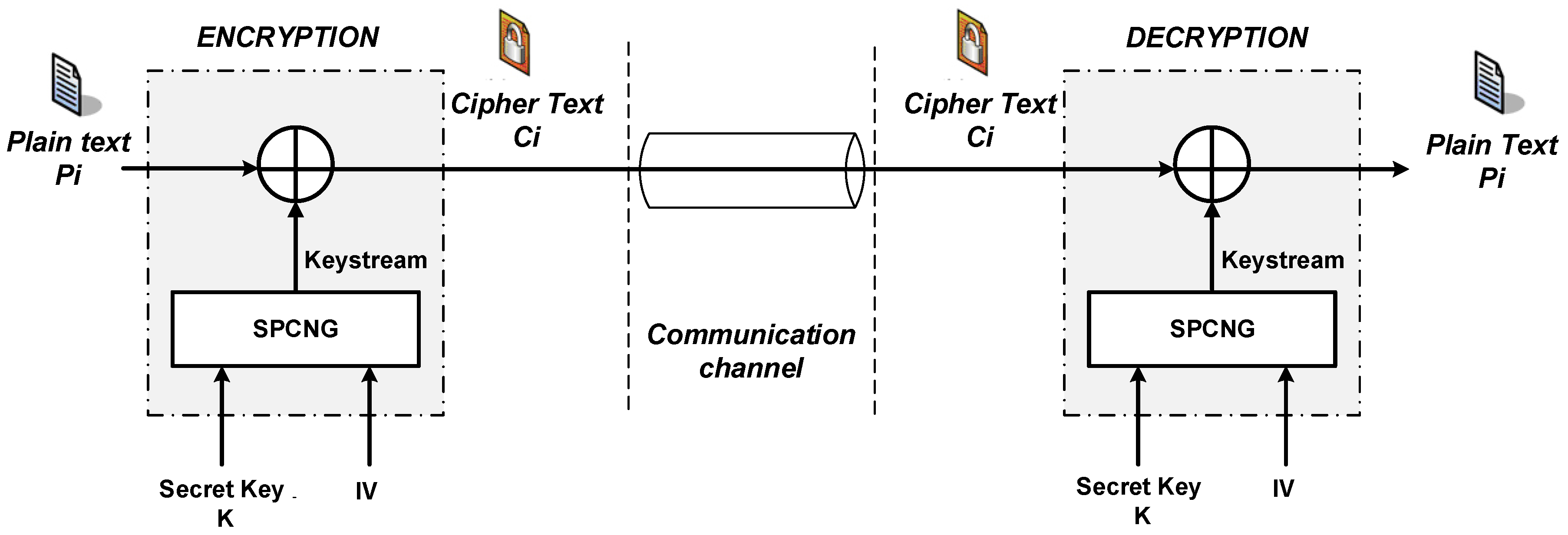
1. Introduction

The protection of information against unauthorized eavesdropping and exchanges is essential, in particular for military, medical, and industrial applications. Nowadays, cryptographic attacks are more and more numerous and sophisticated; consequently, new effective and fast techniques of information protection have appeared or are under development. In this context, recent works have focused on designing new chaos-based algorithms, which provide reliable security while minimizing the cost of hardware and computing time. Chaos theory was first discovered in the computer system by Edward Lorenz in 1963 [1]. A chaotic system, although deterministic and not truly random, has unpredictable behavior, due to its high sensitivity to initial conditions and control parameters which constitute the secret key. It can generate an aperiodic analog signal whenever its phase space is continuous (i.e., with an infinity of values). However, when its phase state is discrete (with a finite set of values), its orbits must be periodic, even with a very long period.

In the field of chaos-based digital communication systems, the chaotic signal has been one of the main concerns in recent decades and is widely used to secure communication. In chaos-based cryptography, discrete chaotic maps are used in most chaotic systems (encryption, steganography, watermark, hash functions) to generate pseudo-random chaotic sequences with robust cryptographic properties [2,3,4,5,6,7,8,9,10]. In a stream cipher, the pseudo-random number generator (PRNG) is the most important component since all the security of the system depends on it. For this, a new category of pseudo-chaotic number generator (PCNG) has been recently built to secure stream-data [11,12,13,14]. These PCNGs use combined chaotic maps because single chaotic maps are not secure for use in stream ciphers.

In 2017, M. Abu Taha et al. [15] designed a novel stream cipher based on an efficient chaotic generator; the results obtained from the cryptographic analysis and of common statistical tests indicate the robustness of the proposed stream cipher. In 2018, Ons et al. [16] developed two new stream ciphers based on pseudo-chaotic number generators (PCNGs) that integrate discrete chaotic maps and use the weak coupling and switching technique introduced by Lozi [17]. Indeed, the obtained results show that the proposed stream ciphers can be used in practical applications, including secure network communication.

In 2019, Ding et al. [18] proposed a new lightweight stream cipher system based on chaos—a chaotic system—and two nonlinear feedback shift registers (NFSRs) are used. The results show that the stream cipher has good cryptographic characteristics. In 2020, Abdelfatah et al. [19] proposed several efficient multimedia encryption techniques based on four combined chaotic maps (Arnold Map, Lorenz Map, Chebyshev Map, and logistic Map) using serial or parallel connections. With the rapid growth of Internet of Things (IoT) technology that connects devices with low power consumption and low computing resources, the hardware implementation of chaotic and non-chaotic ciphers is more suitable than a software implementation. Note that few chaotic encryption systems are realized in the hardware [20,21,22].

In this study, we designed an efficient chaos-based stream cipher (SCbSC) using a proposed secure PCNG. Then, we addressed the hardware implementation and evaluated the performance in terms of resilience against cryptanalytic attacks and in terms of hardware metrics (areas, throughput, and efficiency). The proposed system uses three weakly coupled chaotic maps (3D Chebyshev, logistic, and skew-tent) and integrates a masking technique in the recursive cells to resist side-channel attacks (SCAs). Its implementation on a Xilinx XC7Z020 PYNQ-Z2 FPGA hardware platform achieves a throughput of 1.1 Gbps at an operating frequency of 37.25 MHZ.

The main contributions of the proposed chaotic system are: First all, the introduction of some countermeasures to fix side channel attacks (SCAs) which is done using the masking technique on the recursive cells, and to fix division and conquer attacks on the initial vector (IV), using a weakly coupling matrix. Second, its hardware implementation on a Xilinx XC7Z020 PYNQ-Z2 FPGA platform and evaluation of its performance in terms of computational complexity and security.

The remainder of this paper is organized as follows. The next Section 2 presents the architecture of the proposed secure chaos-based stream cipher. Section 3 presents the hardware implementation on the Xilinx XC7Z020 PYNQ-Z2 FPGA platform of the proposed secure pseudo-chaotic number generator (SPCNG) and analyzes its performance. Section 4, investigates the performance of the proposed SCbSC in terms of hardware metrics and cryptanalytic analysis. Finally, Section 5 summarizes the whole paper.

2. The Proposed SCbSC-Based Architecture

The block diagram of a stream encryption/decryption system is presented in Figure 1. As we can see, the stream encryption/decryption algorithm comes down to an XOR operation between the plaintext and the keystream for encryption; the ciphertext and the keystream for decryption. The security of such a system depends entirely on the keystream delivered by the keystream generator. If the keystream is perfectly random and the period tends to infinity, then the encryption/decryption system becomes unconditionally secure (called a one-time pad). The keystream generator takes as input a secret key and an initial value (IV) used to overcome known plain text attacks. The IV is changed with each new session and must be used only once. Thus, the sequences generated in the different sessions with the same secret key are different. Recall that stream ciphers are used to encrypt data (bits or samples) continuously, such as network communications or selective video encryption. In the following, we will describe in detail the proposed SPCNG as a secure keystream generator.

Description of the Architecture of the Proposed SPCNG

The architecture of the proposed SPCNG is on the one hand, partly based on one of our previous PCNG [16,17], and on the other hand, it takes into account the vulnerabilities detected by SCAs [23,24] in one of our other PCNGs [15]. This new architecture makes it possible to resist SCAs. The proposed system comprises three one-delay recursive cells, shown in blue, containing weakly coupled chaotic maps, namely: the logistic map (L), the skew-tent (S), and the 3D Chebyshev map (3D Ch) in parallel with a linear feedback shift register (LFSR), and a mixing technique on each recursive cell, depicted in red, as shown in Figure 2.

The M-matrix weak coupling technique creates an interdependence between the three chaotic maps that avoids an attacker using the divide and conquer approach on the first 128-bit IV. Indeed, for each new sample calculation, an attacker must take into account the three chaotic maps together. Besides, the use of the logistic map and especially the 3D Chebyshev map (which we have discretized) adds robustness to the system against algebraic attacks. Finally, the three recursive one-delay cells are protected against SCAs by using a mixing technique based on three internal pseudo-random numbers: PRNL, PRNS, and PRNT respectively, shown in red.

The proposed SPCNG takes as input an initial vector (IV) and a secret key (K). The IV of the system provides the initial vectors of the three chaotic maps, $IVL$, $IVS$, and $IVT$; the initial condition $XS0$ of the skew-tent map; and the initial seeds $X0\_L$, $X0\_S$, and $X0\_T$ (of 128 bits each) of the three pseudo-random numbers PRNL, PRNS, and PRNT. The output of each PRN is of size N = 32 bits. The secret key K provides the initial conditions and parameters of the SPCNG listed in

Table 1. Composition of the secret key K.

Symbol	Definition
XL0 and XT0	The initial conditions of the chaotic maps: logistic and 3D Chebyshev respectively, ranging from 1 to $2^N-1$.
XLC1, XSC1, and XTIC1	The initial conditions of the delayed values in recursive cells: logistic, skew-tent, and 3D Chebyshev respectively, in the range $[1,2^N-1]$.
Q0	The initial value Q0 of the Linear Feedback Shift Register (LFSR) defined by: $$Q\left(n\right)=x^{32}+x^{22}+x^2+x+1.$$
KL, KS, and KT	The coefficients of the recursive cells: logistic, skew-tent, and 3D Chebyshev respectively, ranging from 1 to $2^N-1$.
$P_s$	The control parameter of the skew-tent map, in the range $[1,2^N-1]$.
${ϵ}_{ij}$	The parameters of the coupling matrix M, in the interval $[1,2^k]$ with $k\le 5$.
$T_r$	The transient phase of 10 bits.

.

Note that $XLC1$, $XSC1$, and $XTIC1$ mean $XLC(-1)$, $XSC(-1)$, and $XTIC(-1)$.

The models of the discrete logistic, skew-tent, and 3D Chebyshev maps are respectively given by:

• The discrete logistic map [25]:

  $$XL\left(n\right)=\left\{\begin{array}{cc}⌊\frac{XL(n-1)\left[2^N-XL(n-1)\right]}{2^{N-2}}⌋& ifXL(n-1)\ne \left[3\times 2^{N-2},2^N\right]\\ 2^N-1& otherwise\end{array}\right.$$

  (1)
  This is the discretized equation of the standard logistic map:

  $$x\left(n\right)=\mu x(n-1)(1-x(n-1\left)\right)$$

  (2)

  with here $\mu =4$ and $x\left(n\right)\in \left[0,1\right]$.
• The discrete skew-tent map [26]:

  $$XS\left(n\right)=\left\{\begin{array}{cc}⌊\frac{2^N\times XS(n-1)}{P_s}⌋& if0<XS(n-1)<P_s\\ ⌊2^N\times \frac{\left[2^N-XS(n-1)\right]}{2^N-P_s}⌋& if{P}_s<XS(n-1)<2^N\\ 2^N-1& otherwise\end{array}\right.$$

  (3)
  This is the discretized equation of the standard skew-tent map:

  $$x\left(n\right)=\left\{\begin{array}{cc}\frac{x(n-1)}{p}& if0\le x(n-1)\le p\\ \frac{1-x(n-1)}{1-p}& ifp\le x(n-1)\le 1\end{array}\right.$$

  (4)

  with $x\left(n\right)\in \left[0,1\right];0<p<1$.
• The discrete 3D Chebyshev map [27]:

  $$XT\left(n\right)=⌊2^{\left(-2N+2\right)}\times \left(\begin{array}{c}4\times {\left(XT-2^{\left(N-1\right)}\right)}^3-3\hfill \\ \times 2^{\left(2N-2\right)}\times \left(XT-2^{\left(N-1\right)}\right)\hfill \end{array}\right)+2^{\left(N-1\right)}⌋$$

  (5)
  This is the discretized equation of the standrd 3D Chebyshev map:

  $$x\left(n\right)=4{\left[x\left(n-1\right)\right]}^3-3x\left(n-1\right).$$

  (6)

  with $x\left(n\right)\in \left[-1,1\right]$.

$\lfloor Z\rfloor$ (floor function) is the greatest integer less than or equal to Z and $X\left(n\right)$ takes integer values $\in [1,2^N-1]$ and $N=32$ is the precision used.

In Figure 3a,b, we show the mapping and attractor of the 3D Chebyshev map respectively.

Further, in Figure 4a,b, we give the histogram of a sequence produced by the 3D Chebyshev map alone and the histogram of a sequence generated by the 3D Chebyshev map in parallel with an LFSR, respectively. As we can see, the histogram of Figure 4b becomes uniform (confirmed by the chi-square test) compared to that of Figure 4a. The histograms of the skew-tent and logistic maps are known, and an example of their shape is given in [28].

The first sample is calculated by:

$$XL\left(1\right)=Logistic\left\{mod\left(XL\left(0\right){,2}^N\right)\right\}$$

(7)

$$XS\left(1\right)=SkewT\left\{mod\left(XS\left(0\right){,2}^N\right),P_s\right\}$$

(8)

$$XT\left(1\right)=3DCh\left\{mod\left(XT\left(0\right){,2}^N\right)\right\}$$

(9)

where $XL\left(0\right)$, $XS\left(0\right)$ and $XT\left(0\right)$ are the initial values (inputs) of the three chaotic maps defined as follows:

$$\begin{array}{c}XL\left(0\right)=\left(IVL+XL0+KL\times XLC1\right)\\ XS\left(0\right)=\left(IVS+XS0+KS\times XSC1\right)\\ XT\left(0\right)=\left(IVT+XT0+KT\times XTIC1\right)\end{array}$$

(10)

Afterward, for $n\ge 2$ and $n\le N_s$, we calculate the samples by the following relations:

$$XL\left(n\right)=Logistic\left\{mod\left(KL\times XLC(n-1),2^N\right)\right\}$$

(11)

$$XS\left(n\right)=SkewT\left\{mod\left(KS\times XSC(n-1),2^N\right),P_s\right\}$$

(12)

$$XT\left(n\right)=3DCh\left\{mod\left(KT\times XTIC(n-1),2^N\right)\right\}$$

(13)

where $N_s$ is the number of the desired samples, and $XLC(n-1)$, $XSC(n-1)$, and $XTIC(n-1)$ are the unmasked inputs of the three chaotic maps.

The coupling system is defined by the following relation:

$$\left[\begin{array}{c}XLC\left(n\right)\\ XSC\left(n\right)\\ XTIC\left(n\right)\end{array}\right] =M\times \left[\begin{array}{c}XL\left(n\right)\\ XS\left(n\right)\\ XTI\left(n\right)\end{array}\right],$$

(14)

where:

$$M=\left[\begin{array}{ccc}{M}_{11}& {\epsilon }_{12}& {\epsilon }_{13}\\ {\epsilon }_{21}& M_{22}& {\epsilon }_{23}\\ {\epsilon }_{31}& {\epsilon }_{32}& M_{33}\end{array}\right],$$

(15)

with $M_{11}=(2^N-{\epsilon }_{12}-{\epsilon }_{13})$, $M_{22}=(2^N-{\epsilon }_{21}-{\epsilon }_{23})$, and $M_{33}=(2^N-{\epsilon }_{31}-{\epsilon }_{32})$.

$XL\left(n\right)$, $XS\left(n\right)$, and $XT\left(n\right)$ are the outputs of the chaotic maps: logistic, skew-tent, and 3D Chebyshev respectively, and

$$XTI\left(n\right)=XT\left(n\right)\oplus Q\left(n\right)$$

(16)

where $Q\left(n\right)$ is the output of the LFSR.

The masking operations aim to randomize the intermediate results, and they are carried out by adding a random value to the outputs of the weak coupling samples $XLC\left(n\right)$, $XSC\left(n\right)$, and $XTIC\left(n\right)$.

$$\begin{array}{c}XLCM\left(n\right)=XLC\left(n\right)\oplus PRNL\left(n\right)\\ XSCM\left(n\right)=XSC\left(n\right)\oplus PRNS\left(n\right)\\ XTICM\left(n\right)=XTIC\left(n\right)\oplus PRNT\left(n\right)\end{array}$$

(17)

where $XLCM\left(n\right)$, $XSCM\left(n\right)$, and $XTICM\left(n\right)$ represent the masked outputs of the recursive cells: logistic, skew-tent, and 3D Chebyshev, respectively, and $PRNL\left(n\right)$, $PRNS\left(n\right)$, and $PRNT\left(n\right)$ are random integer values generated by the Xorshift pseudo-random number generator of random integer values, in the range $[1,2^N-1]$. To get the same output X(n) for the same secret key and the same IV, the masking operations are reversed at the inputs of the chaotic maps.

$$\begin{array}{c}XLC(n-1)\times KL=XLCM(n-1)\times KL\oplus PRNL(n-1)\times KL\\ XSC(n-1)\times KS=XSCM(n-1)\times KS\oplus PRNS(n-1)\times KS\\ XTIC(n-1)\times KT=XTICM(n-1)\times KT\oplus PRNT(n-1)\times KT\end{array}$$

(18)

Note that PRNs are based on Xoshiro’s RNG, which was developed by David Blackman and Sebastiano Vigna [29] in 2019, which serves as a parameter module for PRNs. The Xoshiro construction itself is based on the Xorshift concept invented by George Marsaglia [30]. Therefore, the masking operation is an effective countermeasure to protect the implementation against power analysis-based side-channel attacks (SCAs) [31,32]. Note that the VHDL implementation of these PRNs produce 32 bits at each clock cycle.

Algorithm 1 summarizes the full operation of the proposed SPCNG.

Algorithm 1: Generation of the pseudo-chaotic sequence X(n).

3. Hardware Implementation of the Proposed SCbSC and Evaluation of Its Performance

The implementation of the secure chaos-based stream cipher was realized on the PYNQ Z-2 FPGA prototyping board from Xilinx. For implementation, the SCbSC’s code was written in VHDL with 32-bit fixed-point data formats, then synthesized, and implemented using the Xilinx Vivado design suite (V.2017.2). Vivado design tools essentially made it possible to carry out the various steps from design to implementation on the target FPGA board. It allows, among other things, description, synthesis, simulation, and implementation of a design, then programming it on a chip from one of the different families of Xilinx FPGAs. In Figure 5, we summarize the different steps of the design flow that were performed under Vivado for the performance evaluation of the proposed SPCNG.

First, we describe the proposed SPCNG using a hierarchical description containing several modules described in VHDL. Second, the synthesis step checks the VHDL description of the SPCNG, converts it into a gate-level representation, and creates a netlist. Third, we perform a behavioral simulation of the SPCNG to check its validity and make sure that the results obtained X(n) are consistent with those gotten by MATLAB. The simulation was invoked directly by the Xsim simulator integrated into the Vivado tools and the results obtained are displayed in a chronogram (see Figure 6 (Behavioral simulation)). At this step we can assess the statistical performance of the SPCNG. Fourth, the design implementation performs: First, Translate merges the netlists resulting from the design synthesis and the specified constraints file (Xilinx Design Constraint XDC file); then Map fits the design with the available resources of the target FPGA. After that, the Place and Route process places the components and routes them, respecting the constraints specified during the translation, to obtain a configuration file. At this step, we get the maximum frequency and hardware resources summarized in the implementation reports. After the design implementation, we performed the post-implementation timing simulation to get the true timing delay information of the SPCNG as shown in the chronogram of Figure 6 (Post-implementation timing simulation).

Finally, we generated a programming file (BIT) to program the Xilinx device PYNQ-Z2 FPGA.

3.1. Hardware Cost of the Proposed Secure PCNG

In this section, we analyze the performance of the proposed SPCNG implementation in terms of resources used (area, DSP), speed (maximum frequency—Max. Freq., throughput), and efficiency. Four SPNG versions were realized to choose the best among them in terms of hardware resources, throughput, and statistical resilience (NIST test) for use in the SCbSC system (see

Table 2. Comparison of the proposed SPCNG design versions on ZYNQ PYNQ Z2 FPGA.

			Versions
			Chaotic Multiplexing		XOR Operation
			Without LFSR	With LFSR	Without LFSR	With LFSR
Resources used	Area	LUTs	3744/7.04%	3763/7.07%	3586/6.74%	3599/6.77%
		FFS	1066/1%	1130/1.06%	1064/1%	1128/1.06%
		Slices *	1079/8.11%	1087/8.17%	1031/7.75%	1029/7.74%
	DSPs		25/11.36%	25/11.36%	22/10%	22/10%
Speed	WNS [ns]		−18.968	−19.062	−19.632	−18.018
	Max. Freq. [Mhz]		37.08	36.95	36.18	38.43
	Throughput [Mbps]		1186.59	1182.46	1158.07	1229.91
Efficiency [Mbps/Slices]			1.09	1.08	1.12	1.19
NIST			Successful	Successful	Successful	Successful

* Note: Each slice contains four LUTs with 6 inputs and eight FFs.

). Furthermore, we give the efficiency (in terms of throughput/slices) of all versions. The efficiency parameter gives us an overall idea of the hardware metrics performance of the implementation.

$$Max.Freq.=\frac{1}{T-WNS}\left[\mathrm{Mhz}\right].$$

(19)

where $T=8$ ns is the target clock period ($F=1/T=125$ Mhz) and WNS is the worst negative slack of the clock signal in the intra-clock paths section.

$$Throughput=N\times Max.Freq.\left[\mathrm{Mbps}\right].$$

(20)

$$Efficiency=\frac{Throughput}{Slices}\left[\mathrm{Mbps}/\mathrm{Slices}\right].$$

(21)

The proposed SPCNG versions were implemented on a Xilinx XC7Z020 PYNQ-Z2 FPGA hardware platform.

The four SPCNG versions have the same general structure but are completely different in their output function and slightly different in their internal state. The differences between the versions of columns 1 and 2 on the one hand, and the versions of columns 3 and 4 on the other hand, are in the output function used, as shown in Table 2. Indeed, versions 1 and 2 use a chaotic multiplexing technique as output function, where the sequence X(n) is controlled by a chaotic sample $X_{th}\left(n\right)$ and a threshold $T_{th}$ is defined as follows:

$$X\left(n\right)= \left\{\begin{array}{cc}XSC\left(n\right)& if0<X_{th}<T_{th}\\ XTIC\left(n\right)& otherwise\end{array}\right.$$

(22)

with $X_{th}\left(n\right)=XLC\left(n\right)\oplus XSC\left(n\right)$ and $T_{th}=0.8\times 2^N$.

Version 2, compared to version 1, contains a LFSR in parallel with the 3D Chebyshev map. Version 4 is the one shown in Figure 2, and version 3 is the same as version 4, but without the LFSR. Moreover, all SPCNG versions successfully passed the 15 NIST tests. However, versions without LFSR did not pass certain sub-tests. For the chaotic multiplexing technique, we found only one failed sub-test out of 148 non-overlapping template sub-tests, and for the XOR operation, we found three failed sub-tests out of 148 non-overlapping template sub-tests. Therefore, based on all results in Table 2, we chose version 4, which is the best (in terms of resources used, throughput, and efficiency) compared to other versions, to be used in the SCbSC system.

3.2. SPCNG Resilience against Statistical Attacks

To quantify the cryptographic properties of the pseudo-chaotic sequences generated by the proposed SPCNG, a series of tests must be applied. Each test measures a particular characteristic, such as the correlation between generated sequences or their uniformity, and the overall results of these tests give an idea of the degree of randomness of the sequences produced. The pseudo-chaotic behavior of the generated sequences is closely linked to the statistical characteristics of these sequences. The National Institute of Standards and Technology (NIST) tests [33] serve, among other things, as a reference to quantify and compare the statistical properties of binary pseudo-chaotic sequences.

Note that the Lyapunov exponents of the three chaotic maps used are positive; however, it is not obvious to compute the Lyapunov exponents of the new stream cipher we propose here. Nevertheless, its chaotic nature is due mainly to the weak coupling of the three chaotic maps. The weak coupling mechanism of chaotic maps has been thoroughly studied [17]; it leads generally to high quality pseudo-random generators. The chaotic nature of it is highlighted by the histogram and figures of the uniform and uncorrelated distribution of its iterates (Figure 7 and Figure 8).

3.2.1. Phase Space Test

We draw in Figure 7a the phase space or mapping of a sequence X(n) generated by the proposed SPCNG formed by 3,125,000 samples out of the 3,125,100 samples generated to deviate from the transitional regime $T_r=100$, and in Figure 7b, we show the mapping of 1000 samples taken randomly from $X\left(n\right)$.

Already, from Figure 7b, the region looks like a totally disordered region, indicating the lack of correlation between adjacent sample values.

3.2.2. Histogram and Chi-Square Tests

An important key property of a secure pseudo-chaotic number generator is that the sequences generated should have a uniform distribution. The histogram of a sequence X (n) produced is given in Figure 8, the uniformity of which is observed visually.

The visual uniformity result should be confirmed by the chi-square test formulated as follows:

$${\chi }_{ex}^2=\sum _{i=0}^{N_c-1}\frac{{\left(O_i-E_i\right)}^2}{E_i}$$

(23)

where:

• $N_c=1000$: number of classes.
• $O_i$: number of calculated samples in the ith class $E_i$.
• $E_i=N_s/N_c$: expected number of samples of a uniform distribution.
• Ns: the number of samples produced—here, Ns = 3,125,000

After that step, we obtain: ${\chi }_{ex}^2=909.46<{\chi }_{th}^2(N_c-1;\alpha )=1073.64$ (for $N_c=1000$ and $\alpha =0.05$). The experimental value of the chi-square test is less than the theoretical one, asserting the histogram’s uniformity. This test was performed on 100 different sequences using 100 different secret keys, and all sequences were uniform.

3.2.3. NIST Test

Another important key property of a secure pseudo-chaotic number generator is that the sequences generated should pass the statistical NIST test, which is a package of 188 tests and sub-tests used to evaluate the randomness of long binary sequences. NIST test was applied to 100 pseudo-chaotic sequences of size ${10}^8$ bits, generated from the initial conditions and the parameters of the chaotic system. For each test, a set of 100 p-values was calculated to indicate the result of the test. A p-value larger than $\alpha =0.01$ (the level of significance of the test) indicates that the sequence would be random and a p-value less than $0.01$ means that the sequence is nonrandom. The proportion of 100 sequences passing a test is equal to the number of p-values $\ge \alpha$ divided by 100. The results obtained, given in

Table 3. P-values and proportion results of NIST test.

Test	p-Value	Proportion %
Frequency test	0.616	100
Block-frequency test	0.182	97
Cumulative-sums test (2)	0.825	99.5
Runs test	0.956	100
Longest-run test	0.868	100
Rank test	0.182	99
FFT test	0.868	99
Nonperiodic-templates (148)	0.507	98.912
Overlapping-templates	0.956	99
Universal	0.575	98
Approximate Entropie	0.658	99
Random-excursions (8)	0.511	99.432
Random-excursion-variant(18)	0.376	99.832
Serial test (2)	0.290	98
Linear-complexity	0.834	100

, indicate that the sequences generated passed all 15 statistical tests.

This means that the proposed SPCNG produces indistinguishable sequences of integer random sequences.

4. Performance Analysis of the Proposed SCbSC

In this section, we first give the hardware metrics obtained by the proposed SCbSC system and compare them with those of some published systems. Then, and we assess its security against a known cryptanalytic analysis.

4.1. SCbSC Hardware Metrics

The hardware metrics of the SCbSC system are shown in

Table 4. Hardware metrics of the proposed SCbSC.

Resources used	Area	LUTs	3631/6.83%
		FFS	1225/1.15%
		Slices	1081/8.13%
	DSPs		22/10%
Speed	WNS [ns]		−18.845
	Max. Freq. [Mhz]		37.25
	Throughput [Mbps]		1192.02
Efficiency [Mbps/Slices]			1.1

, and as expected, they are similar to those of SPCNG.

The comparison of the hardware metrics of several chaotic and non-chaotic systems (from eSTREAM project phase-2 focus hardware profile) is summarized in

Table 5. Hardware metrics usage comparison of several chaotic and non-chaotic systems.

Cipher	Device	Frequency [Mhz]		Slices	Throughput	Efficiency
		Clock Frequency	Max. Freq.		[Mbps]	[Mbps/slices]
SCbSC	Pynq Z2	125	37.25	1081	1119.02	1.1
LWCB SC [20]	Zynq7000	-	18.5	2363 LUTs	565	-
Lorenz’s chaotic System [21]	Virtex-II	50	15.598	1926	124	0.06
Chaos-ring [22]	Virtex-6	125	464.688	1050	464.688	0.44
Trivium [36]	Spartan 3	50	190	388	12,160	31.34
Grain-128 [37]	Virtex- II	50	181	48	181	3.77
Mickey-128 [37]	Virtex- II	50	200	190	200	1.05

. This comparison is difficult to interpret due to the differences in characteristics of the FPGAs tested—particularly for the clock rate parameter. However, considering the clock rate of the FPGA board and the efficiency achieved, we can make this comparison. Thus, the SCbSc system presents competitive hardware metrics compared to those obtained from most other chaotic and non-chaotic systems, except the Trivium cipher. However, since 2007, different types of attacks have been applied to eSTREAM ciphers, thereby revealing some weaknesses, in particular on Trivium cipher [34,35]. Indeed, in Trivium AND gates are the only nonlinear elements to prevent attacks that exploit, among other things, the linearity of linear feedback shift registers.

4.2. Cryptanalytic Analysis

In order to assess the security of the proposed SCbSC system against the most common attacks, we performed the following the key space analysis and assessed its sensitivity; then we used statistical analysis.

4.2.1. Key Size and Sensitivity Analysis

For a secure image encryption system, the key space should be large enough to resist a brute-force attack [38]. The secret key is produced here by Xorshif generator [30] and its size is given by:

$$\begin{array}{c}\left|K\right|=\left|XL0\right|+\left|XT0\right|+\left|Q0\right|+\left|XLC1\right|+\left|XSC1\right|+\left|XTIC1\right|+\left|P_s\right|\\ +\left|KL\right|+\left|KS\right|+\left|KT\right|+\left|T_r\right|+(6\times \left|{\epsilon }_{ij}\right|)=360\mathrm{bits}\end{array}$$

(24)

where $\left|XL0\right|=\left|XT0\right|=\left|Q0\right|=\left|XLC1\right|=\left|XSC1\right|=\left|XTIC1\right|=\left|P_s\right|=\left|KL\right|=\left|KS\right|=\left|KT\right|=32\mathrm{bits}$, $\left|T_r\right|=10\mathrm{bits}$, and $\left|{\epsilon }_{ij}\right|=5\mathrm{bits}$

Thus, the key space contains $2^{360}$ different combinations of the secret key, which is large enough to make brute force attack impracticable.

A robust cryptosystem should also be sensitive to the secret key; that is, changing a one bit in the secret key must produce a completely different encrypted image. This sensitivity is conventionally measured by two parameters which are the NPCR (number of pixel change rate) and the UACI (unified average changing intensity) [39]. Besides, instead of those two parameters which operate on the bytes, we use the Hamming distance $H_D$ which operates on the bits (in our opinion $H_D$ is more precise than NPCR and UACI parameters). The expressions of these parameters are given below, with $C_1$ and $C_2$ being the two ciphered images of the same plain image P.

$$NPCR=\frac{1}{M\times N}\sum _{i,j}D\left(i,j\right)\times 100\%$$

(25)

$$D\left(i,j\right)=\left\{\begin{array}{cc}1& if{C}_1\left(i,j\right) \ne C_2\left(i,j\right)\\ 0& if{C}_1\left(i,j\right) =C_2\left(i,j\right)\end{array}\right.$$

(26)

where M and N are the width and height of $C_1$ and $C_2$. The NPCR measures the percentage of different pixel numbers between two ciphered images.

$$UACI=\frac{1}{M\times N\times 255}\sum _{i,j}\left|C_1\left(i,j\right)-C_2\left(i,j\right)\right|\times 100\%$$

(27)

which measures the average intensity of differences between the two images.

$$H_D\left(C_1,C_2\right)=\frac{1}{Nb}\sum _{i=1}^{Nb}(C_1\left(i\right)\oplus C_2\left(i\right))$$

(28)

with $Nb$ being the number of bits in an encrypted image.

For a random image, the expected values of NPCR, UACI, and $H_D$ are $99.609\%$, $33.4635\%$, and $50\%$ respectively.

Table 6. Number of pixel change rate (NPCR), unified average changing intensity (UACI), and $H_D$ values.

Test	Lena	Pepper	Baboon	Barbara	Boats
NPCR %	99.5483	99.5452	99.5788	99.5513	99.5529
UACI %	33.7768	33.6530	33.5595	33.7723	33.6886
$H_D$	0.5015	0.4991	0.4996	0.5009	0.4996

shows the results obtained of NPCR, UACI, and $H_D$ for the plain images Lena, Pepper, Baboon, Barbara, and Boats of the same size—$256\times 256$ grayscale images. As we can see from these results, the NPCR, UACI, and $H_D$ values obtained are very close to the optimal values. These values indicate that the proposed SCbSC system is very sensitive to slight modifications of the secret key.

4.2.2. Statistical Analysis

In order to analyze the resilience of the proposed SCbSC system against most statistical attacks, we use histogram, chi-square, entropy, and correlation analysis.

Histogram and Chi-Square Analysis

The histogram of an encrypted image is an important feature in evaluating the performance of the encryption process. It illustrates how the gray levels of the pixels in an image are distributed and should be very close to a uniform distribution. In Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, we give the results obtained for Lena, Peppers, Baboon, Barbara, and Boats of size 256 × 256, in (a) and (c) the plain/cipher images and in (b) and (d) their histograms respectively.

It was observed that the histograms of the ciphered images are very close to the uniform distribution and are completely different from the plain images. We applied the chi-square test, using Equation (23), on ciphered images to statistically confirm their uniformity. $N_c=2^8=256$ is the number of levels, $O_i$ is the calculated occurrence frequency of each gray level $i\in [0,255]$ in the histogram of the ciphered image, and $E_i$ is the expected occurrence frequency of the uniform distribution, calculated by $E_i=imagesizeinbytes/N_c$. The distribution of the histogram tested is uniform if it satisfies the following condition: ${\chi }_{ex}^2<{\chi }_{th}^2(N_c-1,\alpha )=293.24$ (for $N_c=256$ and $\alpha =0.05$). The results obtained for the chi-square test, given in

Table 7. Chi-square results on the histograms tested.

Chi-Square Test	Lena	Pepper	Baboon	Barbara	Boats
${\chi }_{ex}^2$	216.10	231.84	244.05	233.62	265.47
${\chi }_{th}^2$ (255, 0.05)	293.24	293.24	293.24	293.24	293.24

, indicate that the histograms of the ciphered images tested are uniform because their experimental values are smaller than the theoretical values.

Entropy Analysis

The random behavior of the ciphered image can be quantitatively measured by entropy information given by Shannon [40]:

$$H\left(C\right)=-\sum _{i=0}^{N_c-1}P\left(c_i\right)\times lo{g}_2\left(P\left(c_i\right)\right)$$

(29)

where $H\left(C\right)$ is the entropy of the encrypted image, and $P\left(c_i\right)$ is the probability of each gray level appearance ($c_i=0,1,\dots ,255$). In the case of equal probability levels, the entropy is maximum (=8). The closer the experimental entropy value is to the maximum value, the more robust the encryption algorithm. We give in

Table 8. Entropy results obtained.

Entropy	Lena	Pepper	Baboon	Barbara	Boats
Plain image	7.4504	7.5939	7.3102	7.5199	7.2392
Cipher image	7.9571	7.9550	7.9545	7.9570	7.9567

, the results obtained from the entropy test on the plain and encrypted images. It is clear that the obtained entropies of ciphered images are close to the optimal value. Then, from these results, the proposed stream cipher has a high degree level of resilience.

Correlation Analysis

In an original image, each pixel is highly-correlated with adjacent pixels in a horizontal, vertical, and diagonal directions. A good encryption algorithm should produce encrypted images with correlation and redundancy as low as possible (close to zero) between adjacent pixels. To assess the correlation, we performed the following: first, we randomly selected 8000 pairs of two adjacent pixels from the image; then we calculated the correlation coefficients by using the following equation:

$${\rho }_{xy}=\frac{Cov\left(x,y\right)}{\sqrt{D\left(x\right)}\sqrt{D\left(y\right)}}$$

(30)

where:

$$Cov\left(x,y\right)=\frac{1}{N}\sum _{i=1}^N\left[x_i-E\left(x\right)\right]\left[y_i-E\left(y\right)\right]$$

(31)

$$E\left(x\right)=\frac{1}{N}\sum _{i=1}^N{x}_i$$

(32)

$$D\left(x\right)=\frac{1}{N}\sum _{i=1}^N{\left[x_i-E\left(x\right)\right]}^2$$

(33)

where x and y are the grayscale values of two adjacent pixels in the image. The obtained results are shown in

Table 9. Correlation coefficients of two adjacent pixels in the plain and ciphered images.

Image	Horizontal	Vertical	Diagonal
Lena	0.939403	0.971060	0.931085
Lena encrypted	−0.003684	−0.009015	0.002278
Peppers	0.959869	0.967869	0.940375
Peppers encrypted	−0.005938	−0.004665	−0.001154
Baboon	0.877794	0.834230	0.788141
Baboon encrypted	−0.006750	−0.005998	−0.002088
Barbara	0.907829	0.946119	0.883508
Barbara encrypted	−0.008293	−0.010526	0.004815
Boats	0.940837	0.953357	0.904555
Boats encrypted	−0.002802	−0.009909	0.002302

.

It appears from Table 9 that the correlation coefficients for the plain images are close to 1, which shows that the pixels are highly correlated, whereas for the encrypted images, the correlation coefficients are close to 0, which proves that there is no correlation between the plain and ciphered images. Therefore, there is no similarity between plain and encrypted images, proving the very good achieved confusion by the proposed SCbSC.

According to all these results of the histogram, entropy, and correlation, the proposed stream cipher presents a good ability to resist statistical attacks.

5. Conclusions

In this paper, we studied and implemented on a Xilinx PYNQ-Z2 FPGA hardware platform using VHDL a novel chaos-based stream cipher (SCbSC) using a proposed secure pseudo-chaotic number generator (SPCNG). The proposed chaotic system includes some countermeasures against side channel attacks (SCAs) and uses a weekly coupling matrix, which prevents division and conquers attacks on the initial vector (IV). Next, we analyzed the cryptographic properties of the proposed SPCNG and evaluated the performances of its hardware metrics. The results obtained demonstrate, on the one hand, the high degree of security, and on the other hand, the good hardware metrics achieved by the SCPNG. After that, we realized the SCbSC system and asserted its resilience against cryptanalytic attacks. Further, we evaluated its hardware metrics and compared them to those of some chaotic and non-chaotic systems. All the results obtained indicate that the proposed SCbSC is a good candidate for encrypting private data. Our future work will focus on designing a chaos-based block cipher to secure IoT data and to check hardware implementations when using non-volatile FPGA technology, which reduces the side attack possibilities in real-field applications.