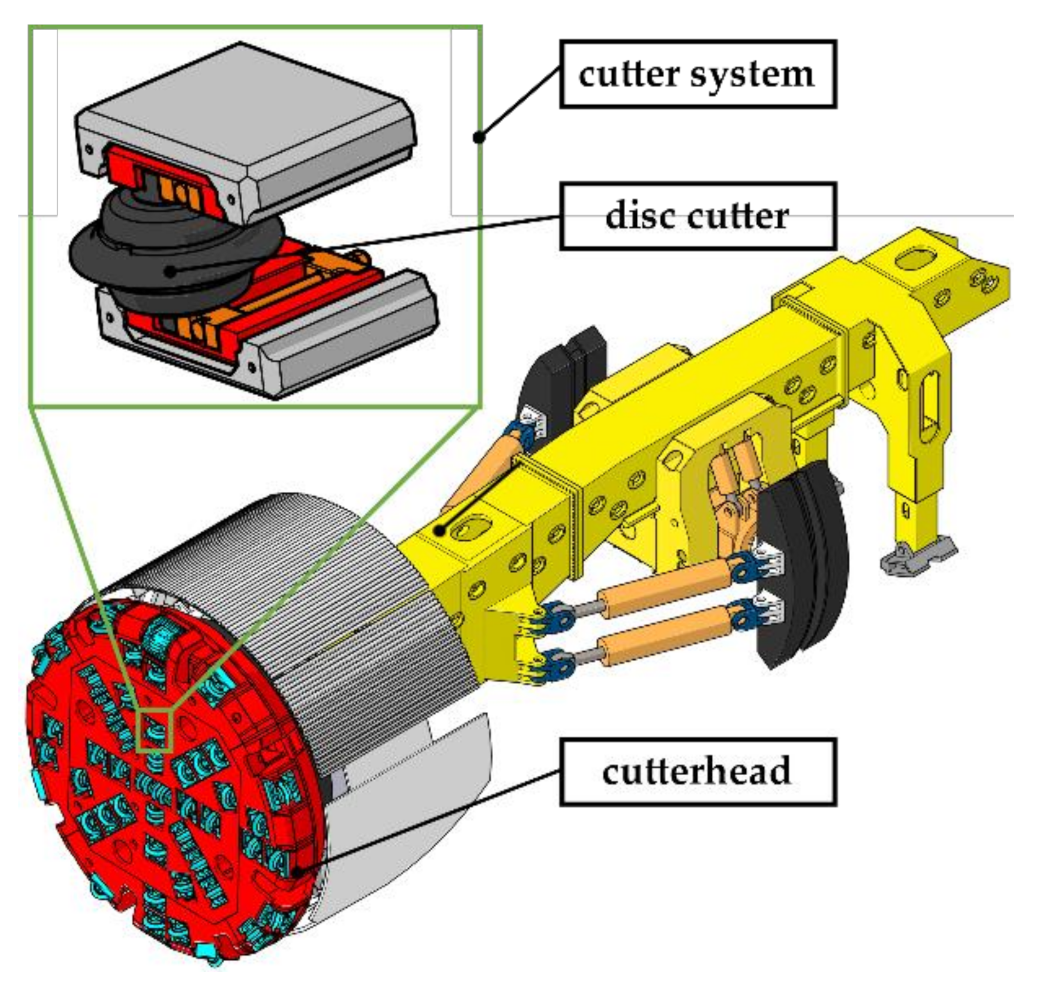
Development and Performance Evaluation of an Integrated Disc Cutter System for TBMs
Abstract
:1. Introduction
- A design method of the ICS configuration based on topology theory is presented, which can obtain all schemes under this configuration.
- Combined with engineering experience and the AHP, the evaluation system of the ICS is established.
- A simple experiment suitable for verifying the tightening performance of the ICS is innovatively designed.
2. Scheme Design of Integrated Cutter Systems
2.1. Design Objectives
- The removal and installation of the ICS should be as simple as possible to reduce the action of the end effector of the cutter changing robot and improve the efficiency of the cutter replacement process.
- The ICS must have good mechanical properties to ensure that it can work in a dangerous, high stress, and alternating load environment for a long time.
- Severe vibration during TBM operation will loosen the ICS, which can lead to a sharp decline in the lifespan of a cutter. Consequently, it is vital to improve the fastening performance of the ICS.
2.2. Mechanism Type Synthesis Based on Mechanism Topology Theory
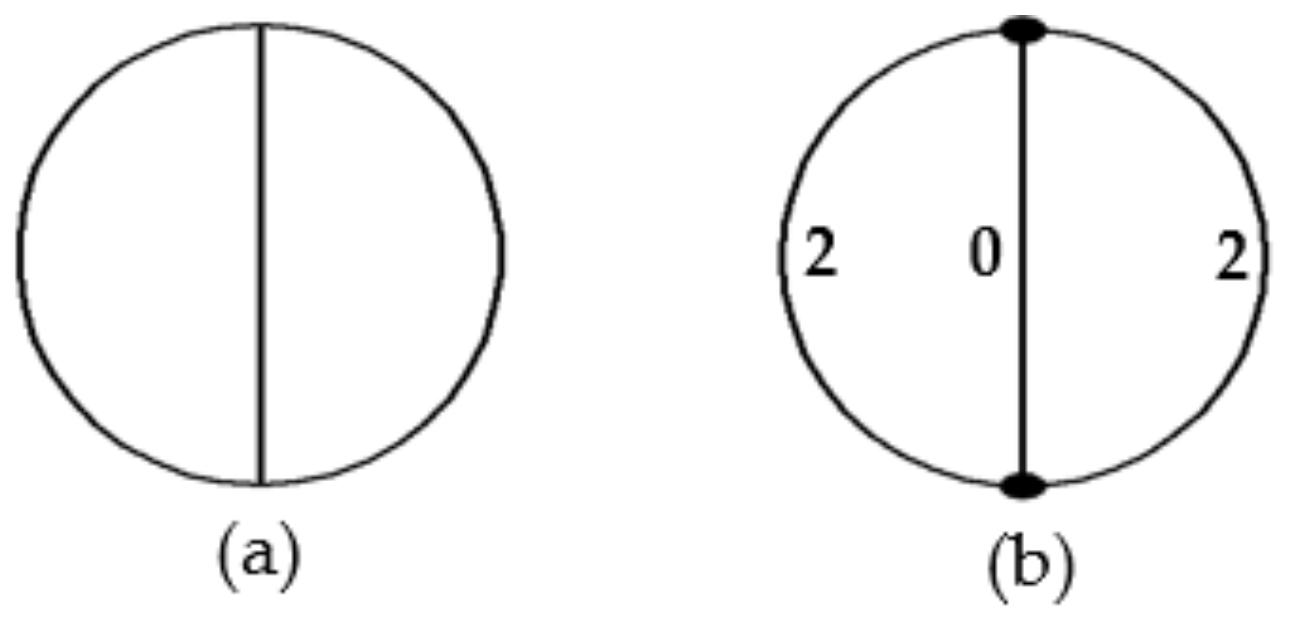
2.2.1. Solution for the Kinematic Chain and Mechanism Diagram
2.2.2. Determination of the ICS Structure
3. Performance Evaluation of the ICS
3.1. Selection and Analysis of the Evaluation Parameters of the ICS
3.1.1. Number of Disassembly Actions
3.1.2. Dimensions for Drawing out Cutters
3.1.3. Overall Dimensions of the ICS
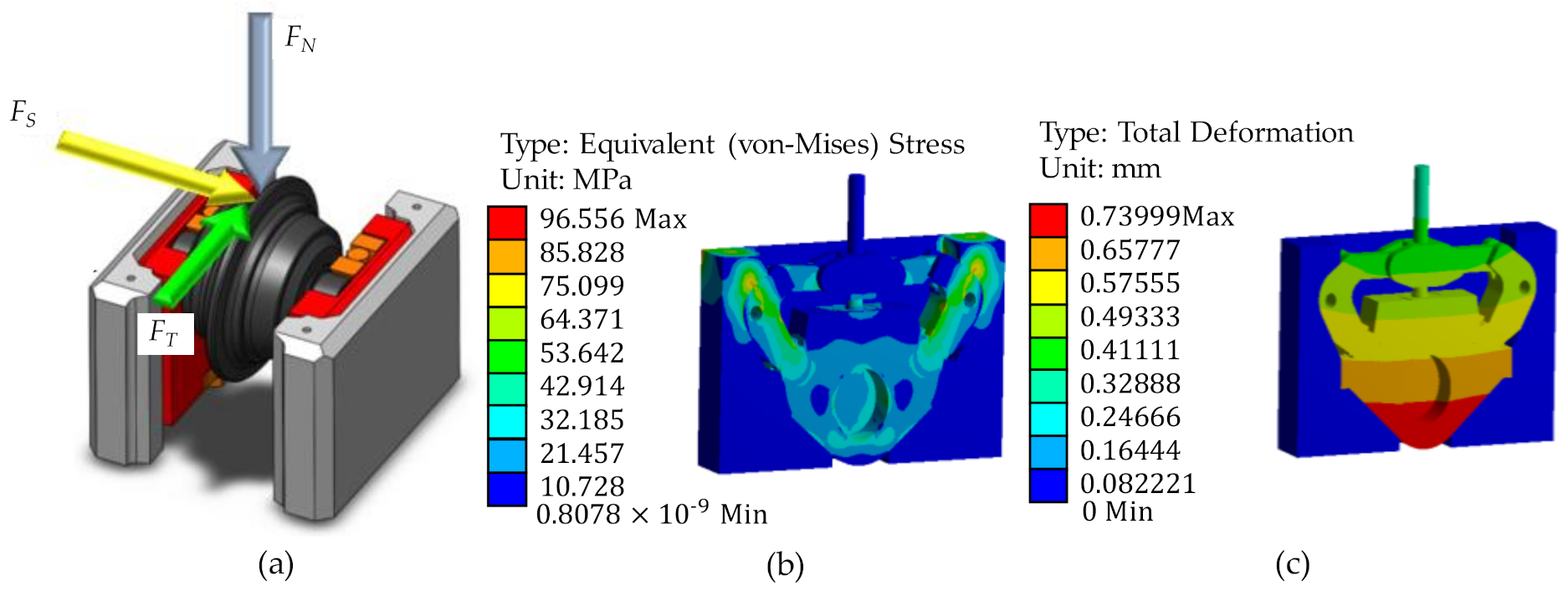
3.1.4. Static Strength
3.1.5. Mass of the ICS
3.1.6. Preload Provided by the ICS
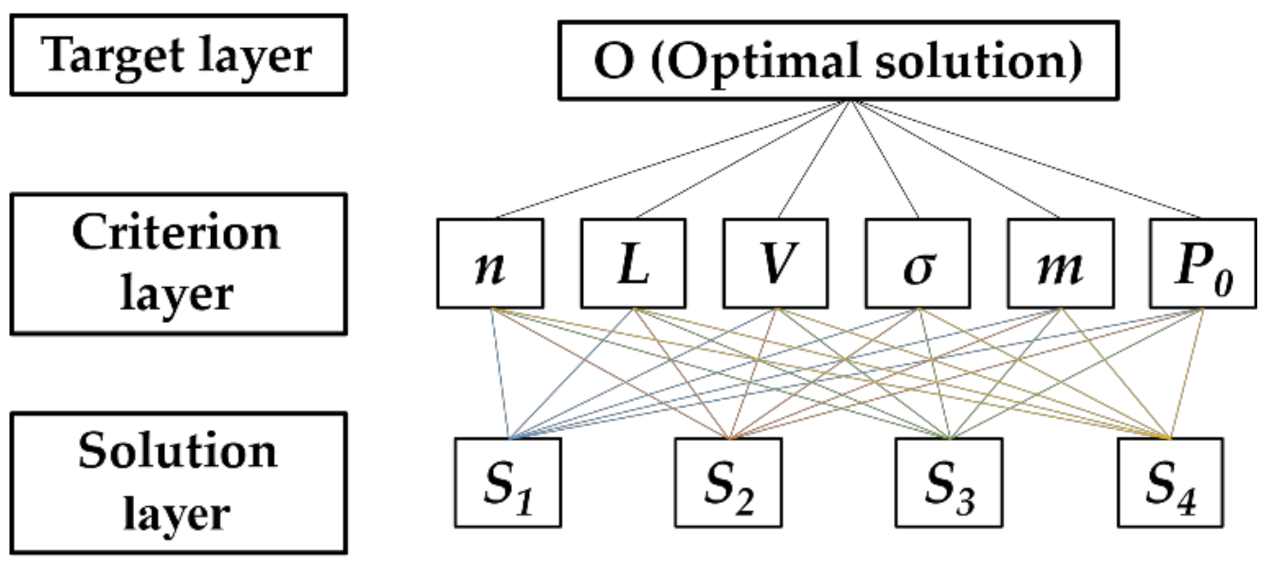
3.2. Establishment of the Evaluation Indicator of the ICS
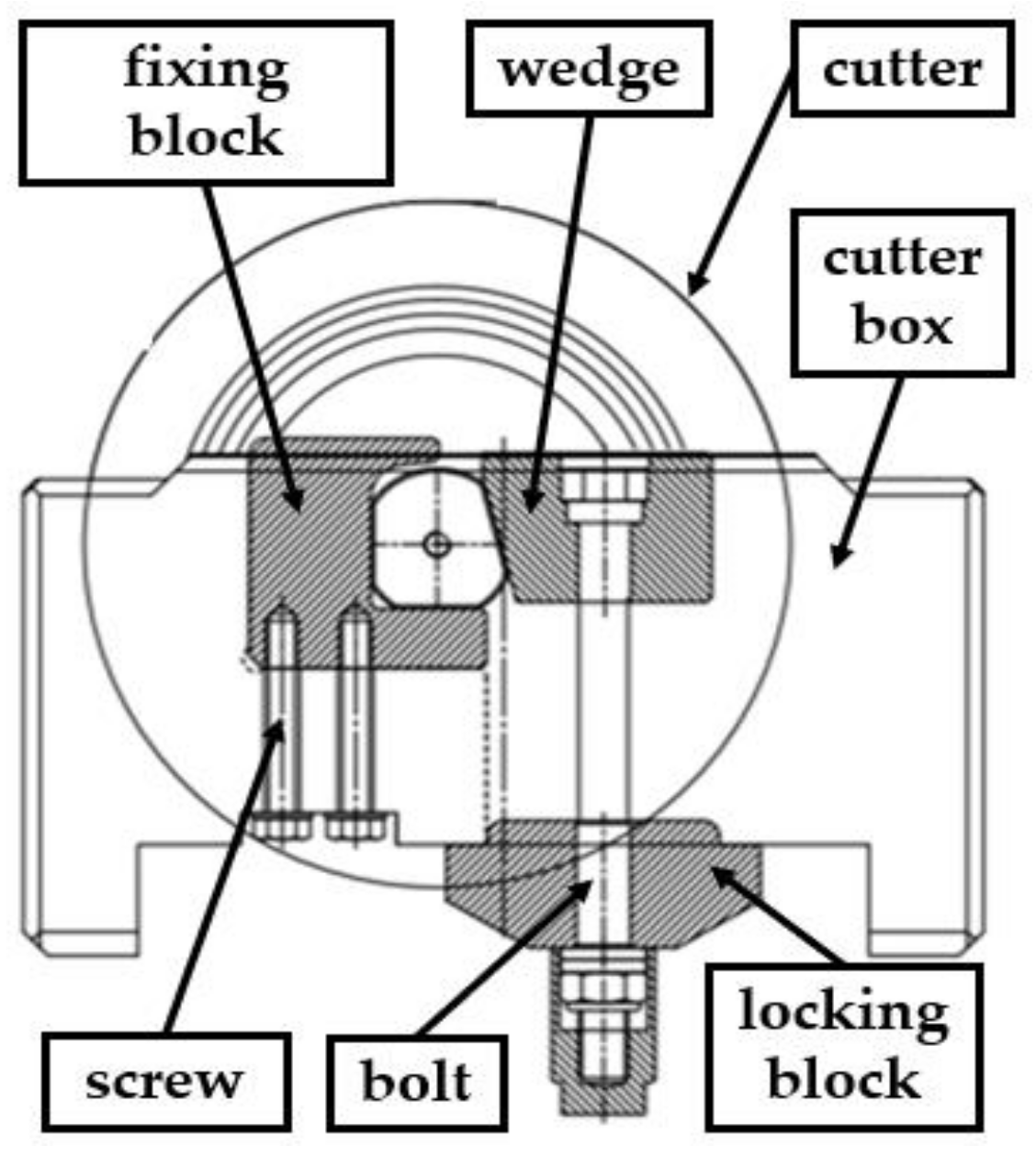
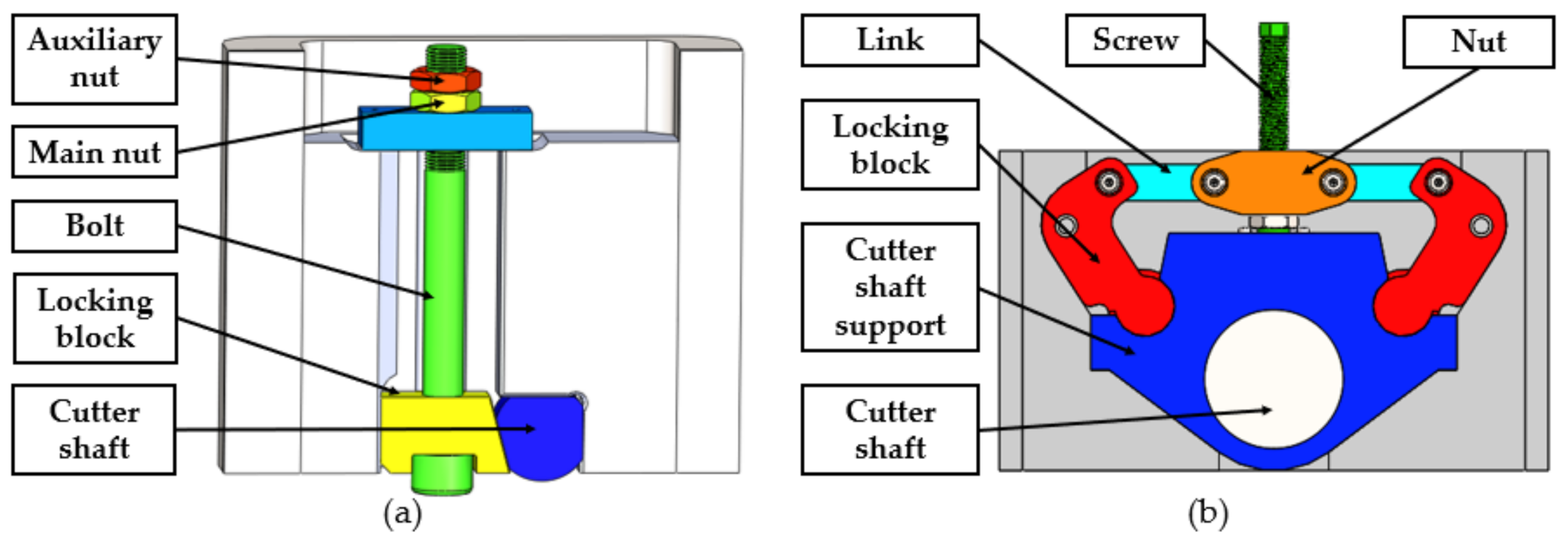
4. Design of the Anti-Looseness Structure of the ICS
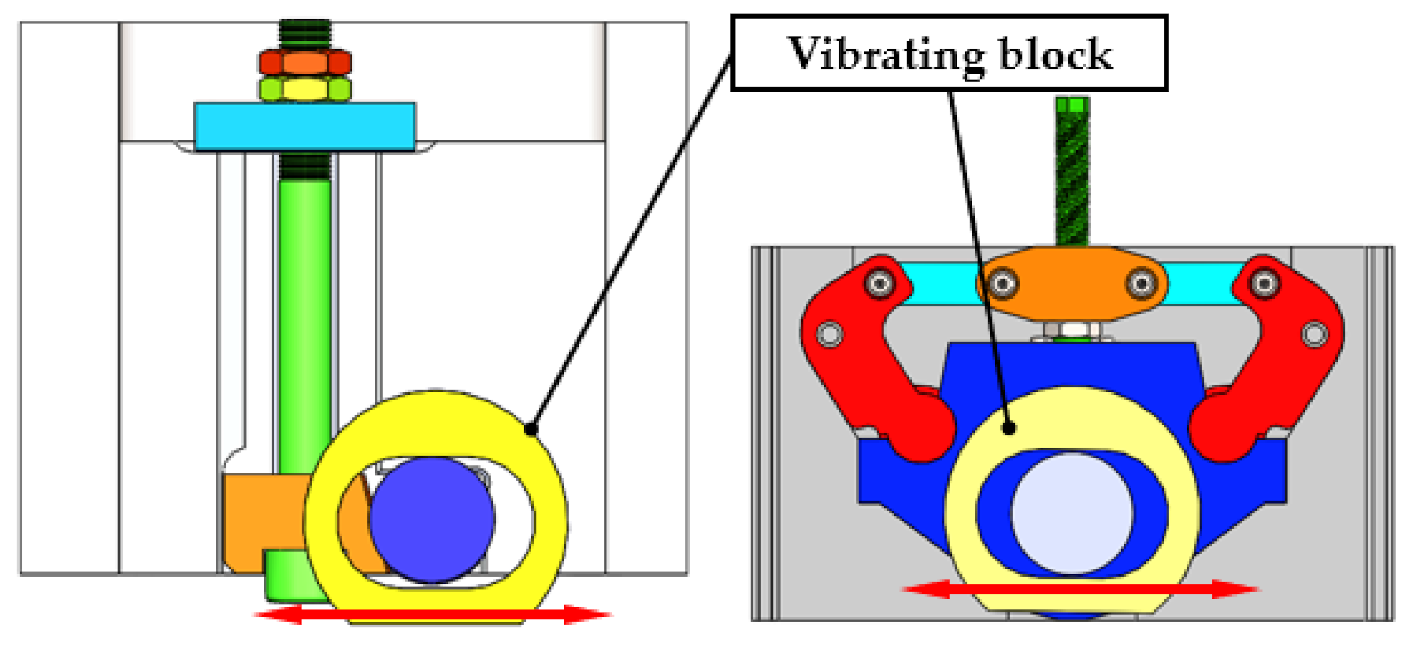
4.1. Anti-Loosening Principle of the TCS
4.2. Anti-Loosening Principle of the ICS
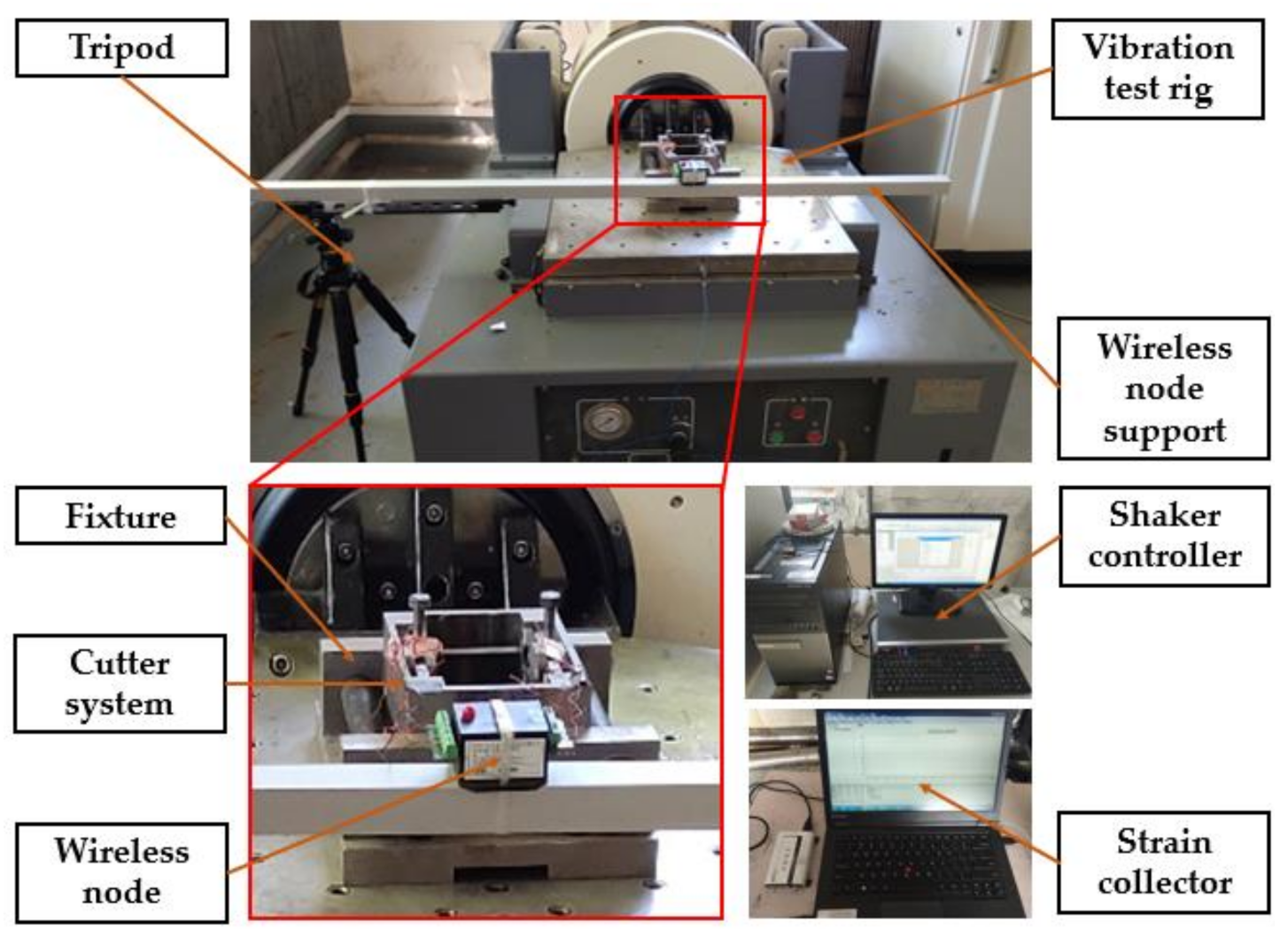
5. Experimental Verification
5.1. Experimental Principle
5.2. Experimental Program
5.3. Analysis of the Experimental Results
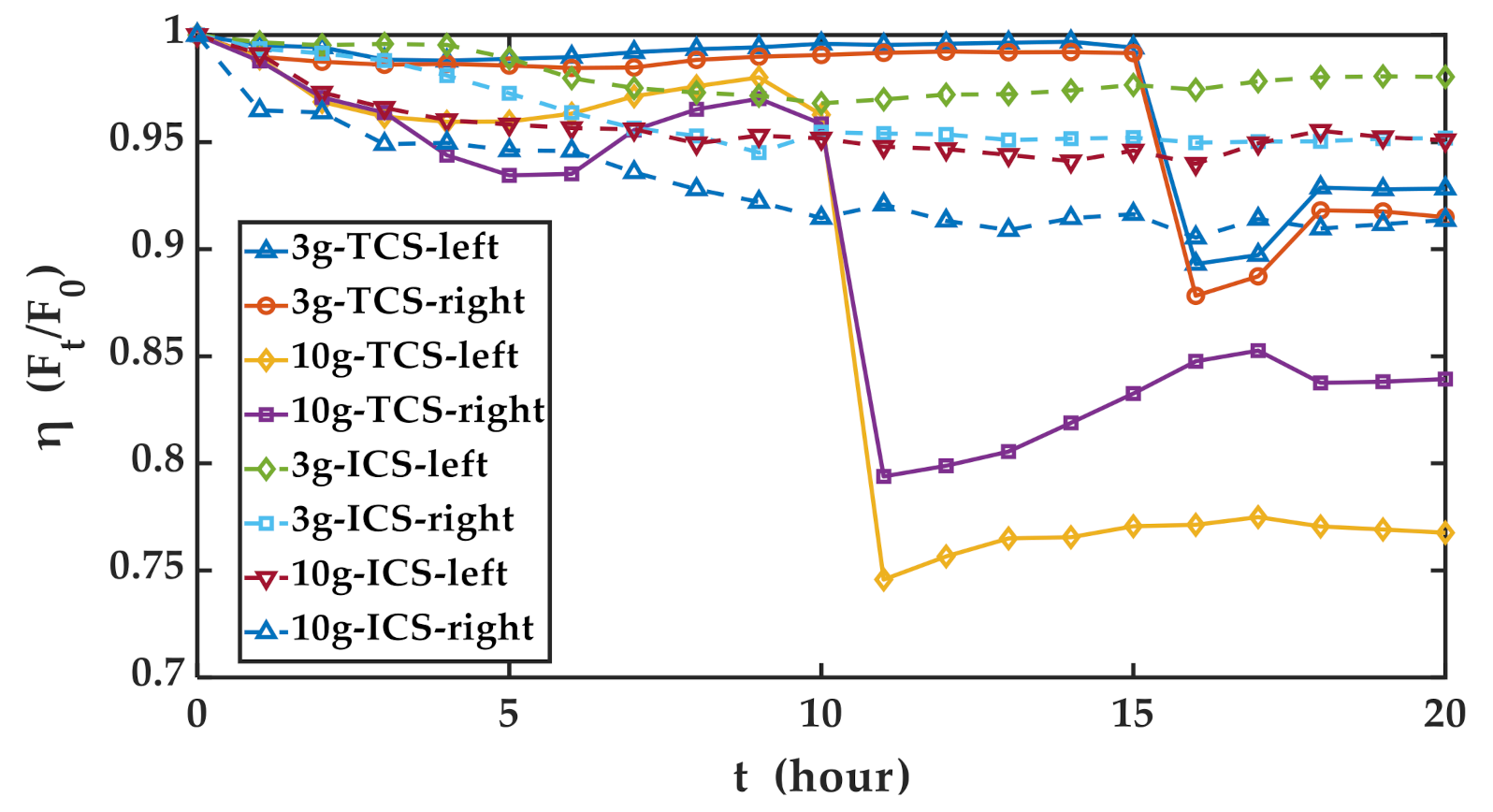
- Under the experimental condition of 3 g, the changes in the preload on the left and right sides of the two cutter systems were synchronous. After basically remaining stable during the first 15 h, the preload of the TCS suddenly dropped sharply at the 15th hour before rising slightly to reach stability. At the end of the 20th hour, the preload on the left and right sides of the TCS decreased by 7.18% and 8.51%, respectively. The preload of the TBM ICS slowly decreased between 0–10 h, and then it was stable in the following 10 h. Finally, at the 20th hour, the pretension on the left and right sides of the ICS decreased by 1.96% and 4.82%, respectively.
- In the 10 g experimental condition, the changes in the pretension of the left and right sides of the two cutter systems were also synchronous. After slowly decreasing in the first 6 h, the preload of the TCS increased slightly in the following 4 h, then plummeted at the 10th hour. Then, it climbed gradually to reach stability. Finally, the pretension force on the left side decreased by 23.25%, and that on the right side decreased by 16.07%. After falling mildly between 0–10 h, the preload of the TBM ICS reached a substantially stable state in the following 10 h. In the end, the pretension force on the left side decreased by 4.92%, and that on the right side decreased by 8.64%.
6. Conclusions
- The development of the existing TBM ICSs relies too much on the engineering experience of the designer. The design scheme is relatively simple, and the contrast is not strong. The topological structure theory of planar mechanisms was applied for the first time to the design of a new TBM ICS in this paper.
- To evaluate the performance of TBM ICSs to obtain the optimal design, this paper established a TBM ICS evaluation index based on the AHP. The evaluation method considers six factors that affect the performance of the TBM ICS, including the number of disassembly actions, dimensions of the drawing out cutters, overall dimensions, static strength, mass, and preload. By evaluating the four ICSs proposed, an ICS with the best performance was selected.
- To improve the anti-loosening performance of the ICS, this article proposed a dead-point anti-loosening structure for the ICS and conducted related experimental research. The experimental results show that after a 20 h vibration experiment, the preload reduction of the TCS was 1.76 times and 2.69 times that of the ICS under the experimental conditions of 3 g and 10 g, respectively. That is, under the same vibration conditions, the ICS had better anti-loosening performance than did the TCS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Armaghani, D.J.; Koopialipoor, M.; Marto, A.; Yagiz, S. Application of several optimization techniques for estimating TBM advance rate in granitic rocks. J. Rock Mech. Geotech. Eng. 2019, 11, 779–789. [Google Scholar] [CrossRef]
- Delisio, A.; Zhao, J. A new model for TBM performance prediction in blocky rock conditions. Tunn. Undergr. Space Technol. 2014, 43, 440–452. [Google Scholar] [CrossRef]
- Wang, L.H.; Kang, Y.L.; Zhao, X.J.; Zhang, Q. Disc cutter wear prediction for a hard rock TBM cutterhead based on energy analysis. Tunn. Undergr. Space Technol. 2015, 50, 324–333. [Google Scholar] [CrossRef]
- Ren, D.J.; Shen, S.L.; Arulrajah, A.; Cheng, W.C. Prediction Model of TBM Disc Cutter Wear during Tunnelling in Heterogeneous Ground. Rock Mech. Rock Eng. 2018, 51, 3599–3611. [Google Scholar] [CrossRef]
- Hassanpour, J.; Rostami, J.; Azali, S.T.; Zhao, J. Introduction of an empirical TBM cutter wear prediction model for pyroclastic and mafic igneous rocks; a case history of Karaj water conveyance tunnel, Iran. Tunn. Undergr. Space Technol. 2014, 43, 222–231. [Google Scholar] [CrossRef]
- Liu, Q.S.; Liu, J.P.; Pan, Y.C.; Zhang, X.P.; Peng, X.X.; Gong, Q.M.; Du, L.J. A Wear Rule and Cutter Life Prediction Model of a 20-in. TBM Cutter for Granite: A Case Study of a Water Conveyance Tunnel in China. Rock Mech. Rock Eng. 2017, 50, 1303–1320. [Google Scholar] [CrossRef]
- Copur, H.; Cinar, M.; Okten, G.; Bilgin, N. A case study on the methane explosion in the excavation chamber of an EPB-TBM and lessons learnt including some recent accidents. Tunn. Undergr. Space Technol. 2012, 27, 159–167. [Google Scholar] [CrossRef]
- Su, F.; Wang, W.; Huo, J.; Li, Z. Optimal layout design of cutters on tunnel boring machine. J. Northeast. Univ. (Nat. Sci.) 2010, 31, 877–881. [Google Scholar]
- Gallo, J.; Perez-Acebo, H. Performance model for Micro Tunnelling Boring Machines (MTBM). Inf. Constr. 2017, 69, e203. [Google Scholar] [CrossRef] [Green Version]
- Hegab, M.Y.; Smith, G.R. Delay time analysis in microtunneling projects. J. Constr. Eng. Manag. ASCE 2007, 133, 191–195. [Google Scholar] [CrossRef]
- Jianjun, Y.; Renming, G.; Du, J. Design and implementation of disc cutter changing robot for tunnel boring machine (TBM). In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 2402–2407. [Google Scholar]
- Moubarak, S. Maintenance Robotics in TBM Tunnelling. In Proceedings of the 32nd International Symposium on Automation and Robotics in Construction and Mining (ISARC 2015), Oulu, Finland, 15–18 June 2015; International Association for Automation and Robotics in Construction (IAARC): London, UK, 2015; pp. 1–8. [Google Scholar]
- Chen, G. Design and Test of Intelligent Inspection and Replacement System of TBM Excavation Tools. In Proceedings of the 2019 International Conference on Virtual Reality and Intelligent Systems, Jishou, China, 14–15 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 219–222, ISBN 978-1-7281-5050-5. [Google Scholar]
- Simi, A.; Manacorda, G. The NeTTUN Project: Design of a GPR Antenna for a TBM. In Proceedings of the 2016 16th International Conference on Ground Penetrating Radar, Hong Kong, China, 13–16 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6, ISBN 978-1-5090-5181-6. [Google Scholar]
- Bogue, R. Snake robots A review of research, products and applications. Ind. Robot 2014, 41, 253–258. [Google Scholar] [CrossRef]
- David, O.; Russotto, F.X.; Simoes, M.D.; Measson, Y. Collision avoidance, virtual guides and advanced supervisory control teleoperation techniques for high-tech construction: Framework design. Autom. Constr. 2014, 44, 63–72. [Google Scholar] [CrossRef]
- Rubrecht, S.; Singla, E.; Padois, V.; Bidaud, P.; de Broissia, M. Evolutionary Design of a Robotic Manipulator for a Highly Constrained Environment. In New Horizons in Evolutionary Robotics: Extended Contributions from the 2009 Evoderob Workshop; Doncieux, S., Bredeche, N., Mouret, J.B., Eds.; Springer Science & Business Media: Berlin, Germany, 2011; pp. 109–121. ISBN 978-3-642-18271-6. [Google Scholar]
- Satoh, J.; Hanaoka, Y.; Okada, T. Development of cutter bit replacement system. Hitachi Zosen Tech. Rev. 2008, 68, 26–35. [Google Scholar]
- Chao, Y. Design and experimental verification of motion mechanism for automatic laser welding robot. Electr. Weld. Mach. 2014, 44, 69–71, 75. [Google Scholar] [CrossRef]
- Huo, J.Z.; Xu, Z.H.; Meng, Z.C.; Li, J.B.; Dong, J.H.; Wang, L.P. Coupled modeling and dynamic characteristics of TBM cutterhead system under uncertain factors. Mech. Syst. Signal Proc. 2020, 140, 106664. [Google Scholar] [CrossRef]
- Cay, T.; Uyan, M. Evaluation of reallocation criteria in land consolidation studies using the Analytic Hierarchy Process (AHP). Land Use Pol. 2013, 30, 541–548. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Tateishi, R. Urban Flood Vulnerability and Risk Mapping Using Integrated Multi-Parametric AHP and GIS: Methodological Overview and Case Study Assessment. Water 2014, 6, 1515–1545. [Google Scholar] [CrossRef]
- Huo, J.; Yang, J.; Sun, W.; Zhang, X. Structure design and static/dynamic analysis of TBM cutterhead supporting ribs. J. Harbin Eng. Univ. 2014, 35, 883–888. [Google Scholar]
- Huo, J.Z.; Wu, H.Y.; Yang, J.; Sun, W.; Li, G.Q.; Sun, X.L. Multi-directional coupling dynamic characteristics analysis of TBM cutterhead system based on tunnelling field test. J. Mech. Sci. Technol. 2015, 29, 3043–3058. [Google Scholar] [CrossRef]
- Zhang, J.; Du, M.; Shao, Y.; Chen, J. Simulation on Loosening Behavior of Threaded Fastener under Transverse Vibration. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation, Beijing, China, 2–5 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1886–1890, ISBN 978-1-4799-7098-8. [Google Scholar]
- Panja, B.; Das, S. Development of an anti-loosening fastener and comparing its performance with different other threaded fasteners. Sadhana Acad. Proc. Eng. Sci. 2017, 42, 1793–1801. [Google Scholar] [CrossRef]
- Yang, G.; Xie, J.; Xie, Y. Study on mechanism of anti-loosening of a new type of nut based on fem. Eng. Mech. 2010, 27, 224–228. [Google Scholar]
- Jing, X.; Pan, F.; Shen, Z. Development of transverse vibration test-bed for fasteners. J. Mach. Design 2005, 22, 59–61. [Google Scholar]
- Liu, C.; Sun, J.; Mo, Y. A study of effects on anti-loosening performance of threaded fasteners. Mod. Manuf. Eng. 2018, 451, 138. [Google Scholar]
- Bhattacharya, A.; Sen, A.; Das, S. An investigation on the anti-loosening characteristics of threaded fasteners under vibratory conditions. Mech. Mach. Theory 2010, 45, 1215–1225. [Google Scholar] [CrossRef]




| The Motion Chain Diagram | The Schematic Diagram of the ICS Mechanism | |||
|---|---|---|---|---|
| Bar 1 as the ICS Frame | Bar 2 as the ICS Frame | |||
| Locking Block Position | Locking Block Position | |||
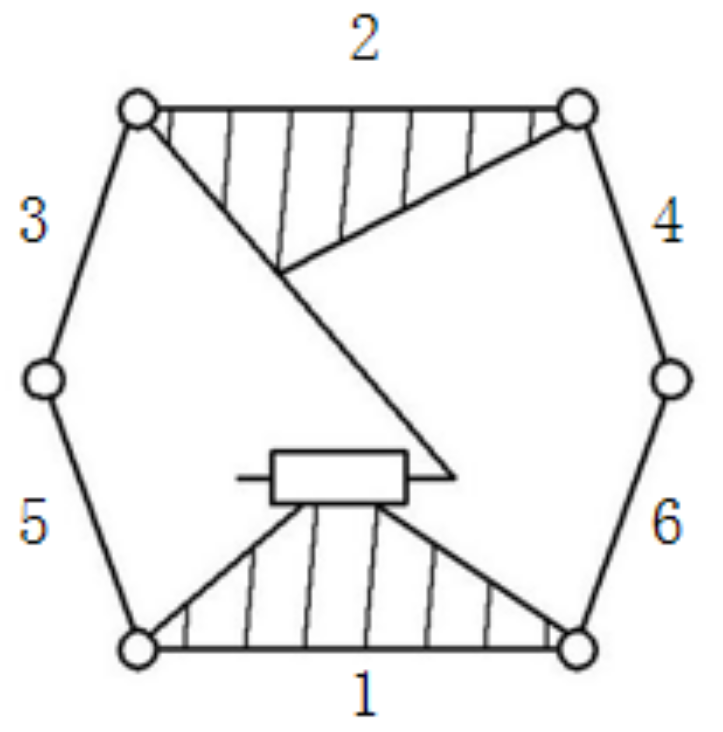 | Bars 5 and 6 | 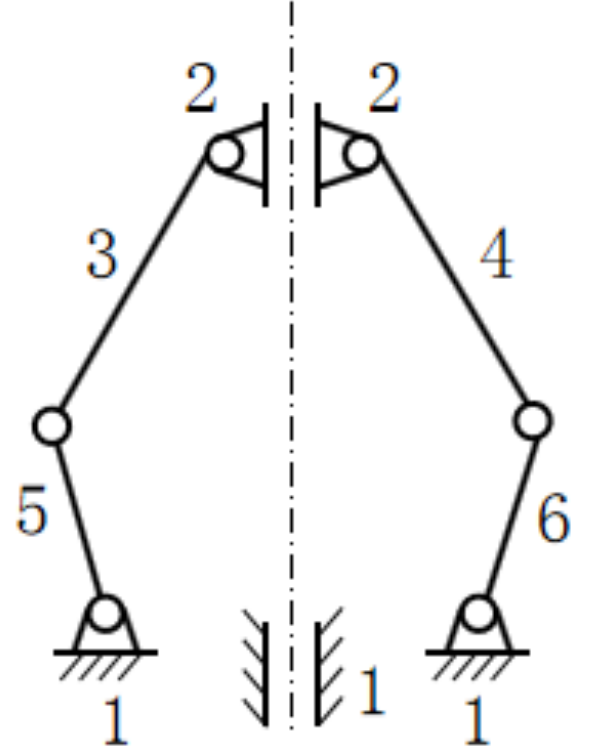 | Bars 3 and 4 | The mechanism with bar 1 is the same as the frame, and bars 5 and 6 are the same as the locking block |
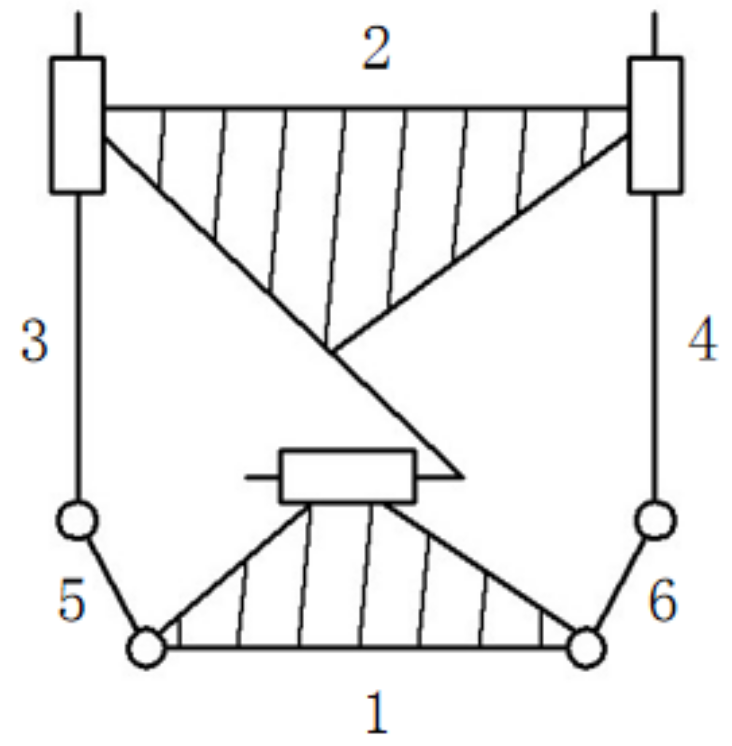 | Bars 5 and 6 |  | Bars 3 and 4 | 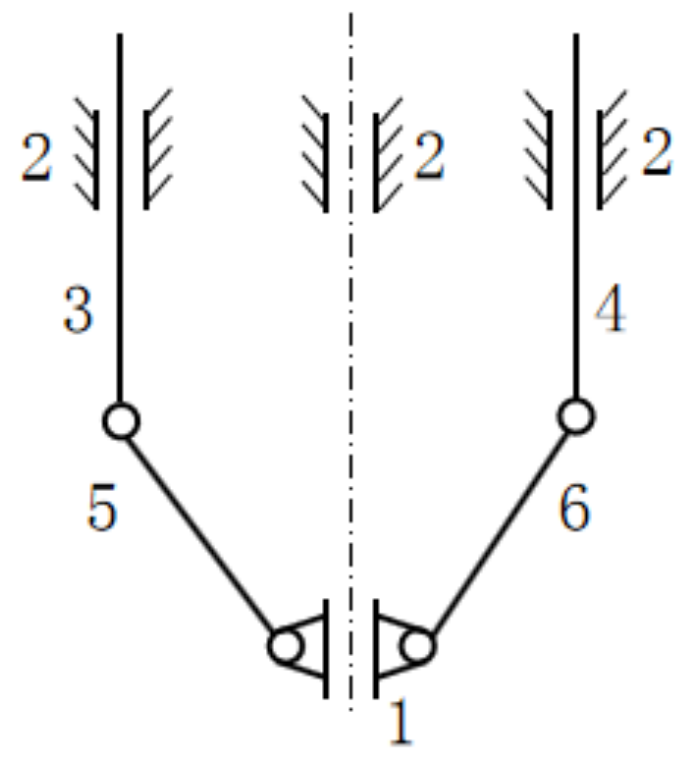 |
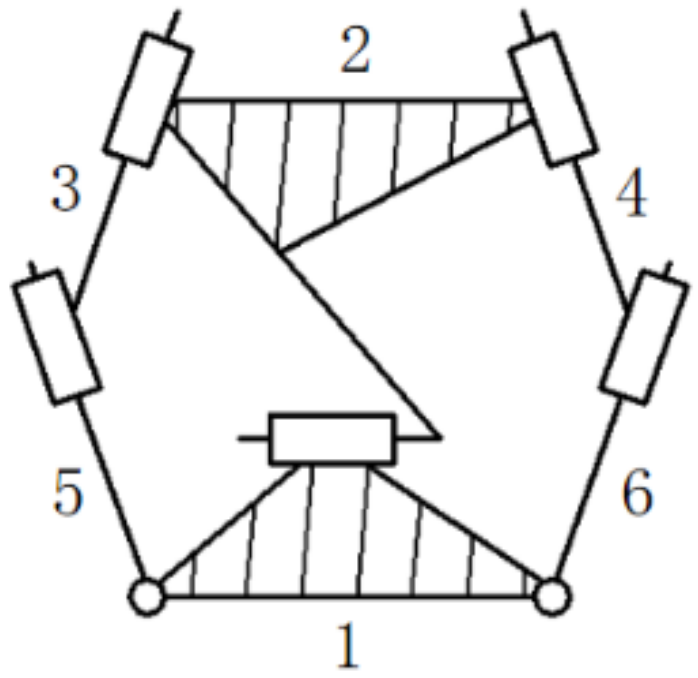 | Bars 5 and 6 | 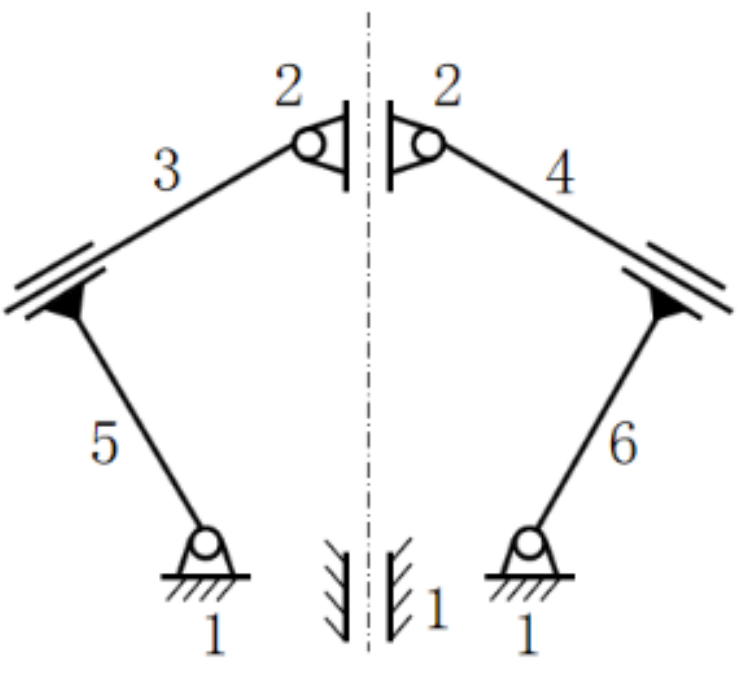 | Bars 3 and 4 | The mechanism with bar 1 is the same as the frame, and bars 5 and 6 are the same as the locking block |
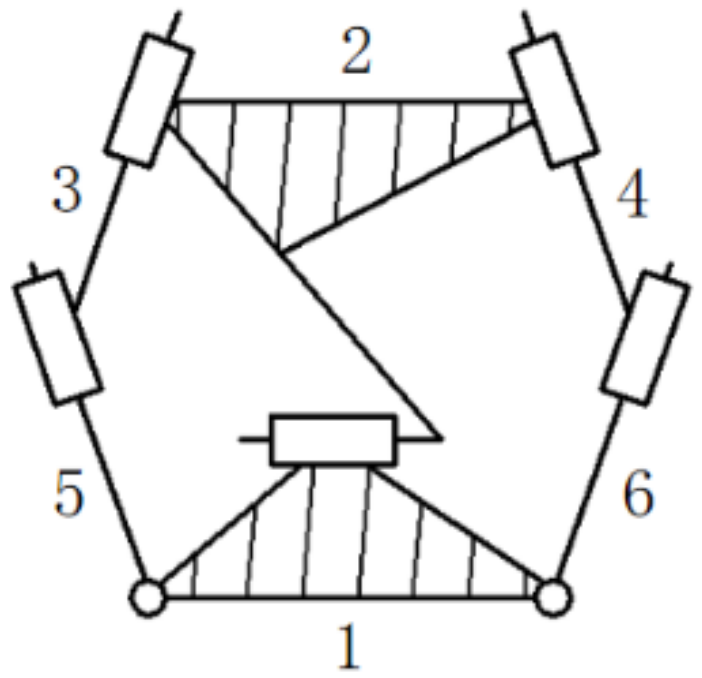 | Bars 5 and 6: it is equivalent to a 4-bar mechanism | |||
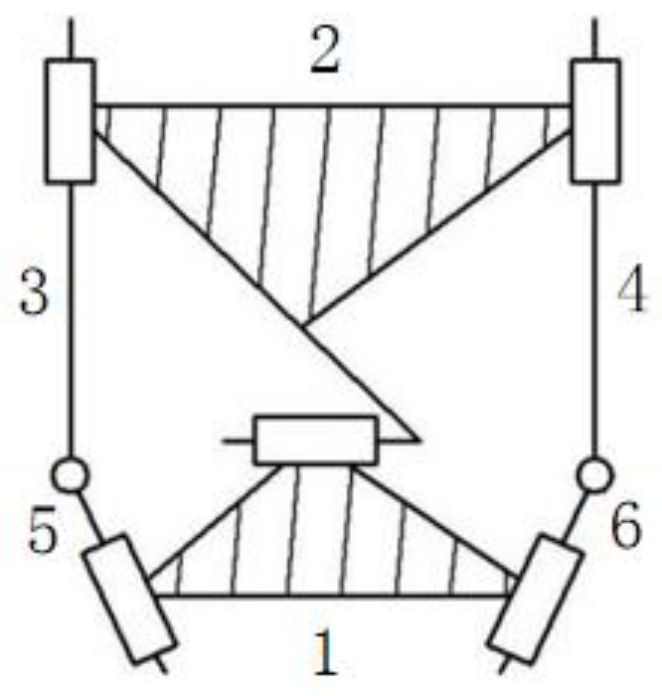 | Bars 5 and 6: it is equivalent to a 4-bar mechanism | |||
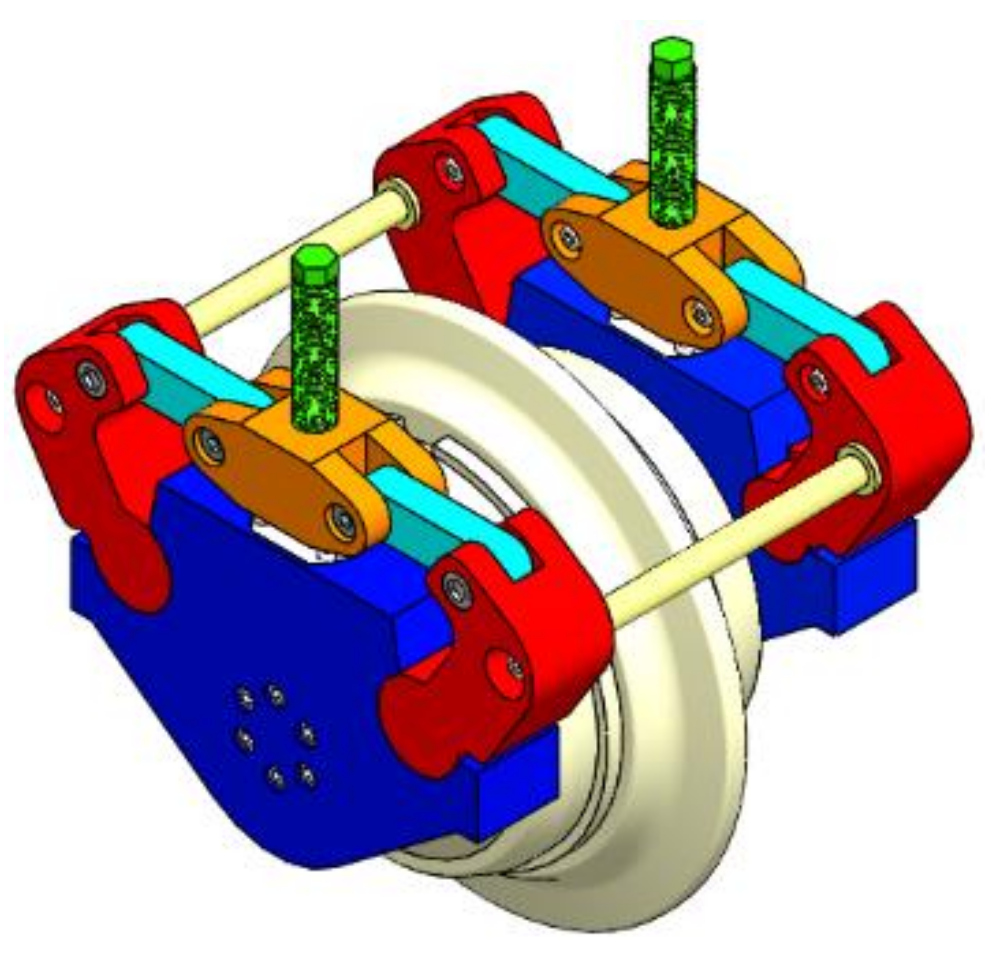
| Solution | Schematic Diagram | Structure Diagram | 3D Axonometric Diagram |
|---|---|---|---|
| Solution 1 | 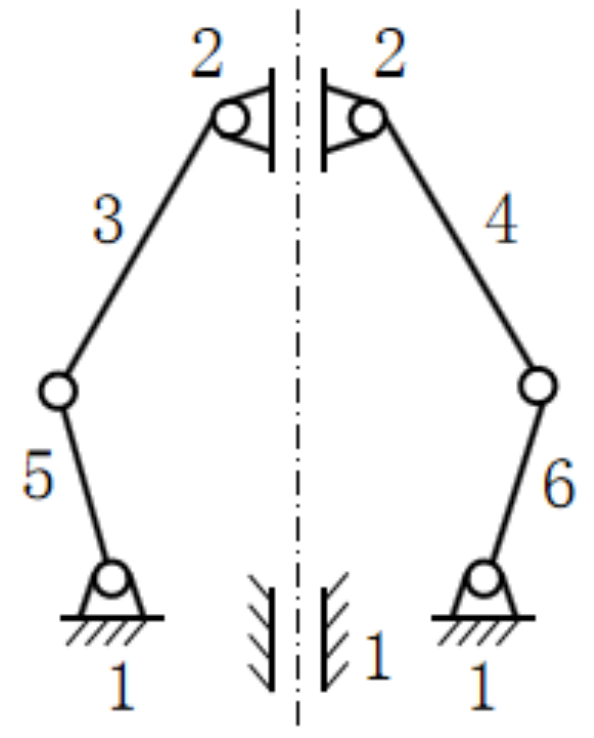 |  | 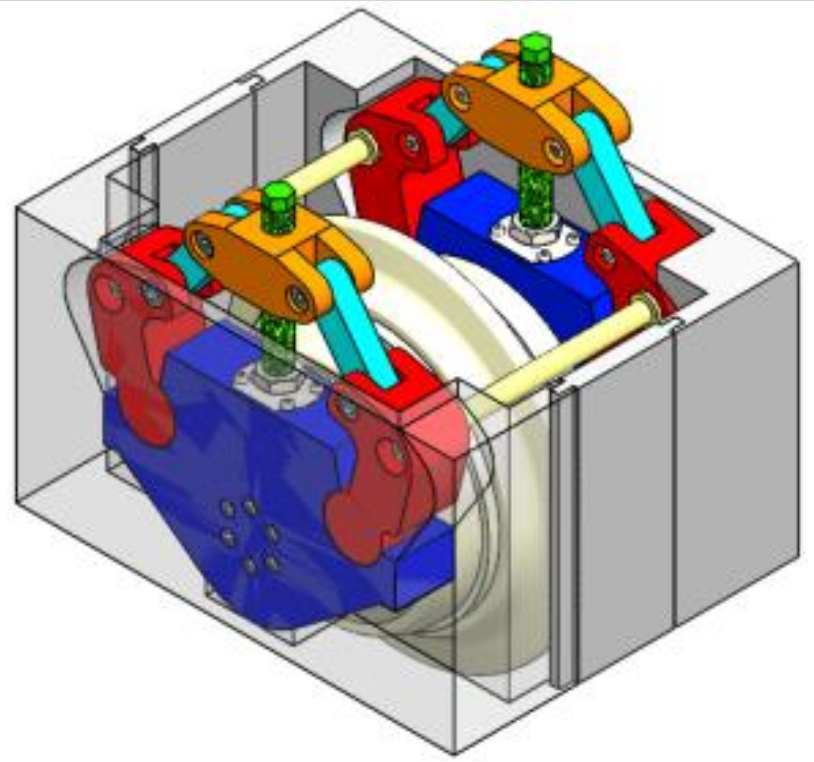 |
| Solution 2 | 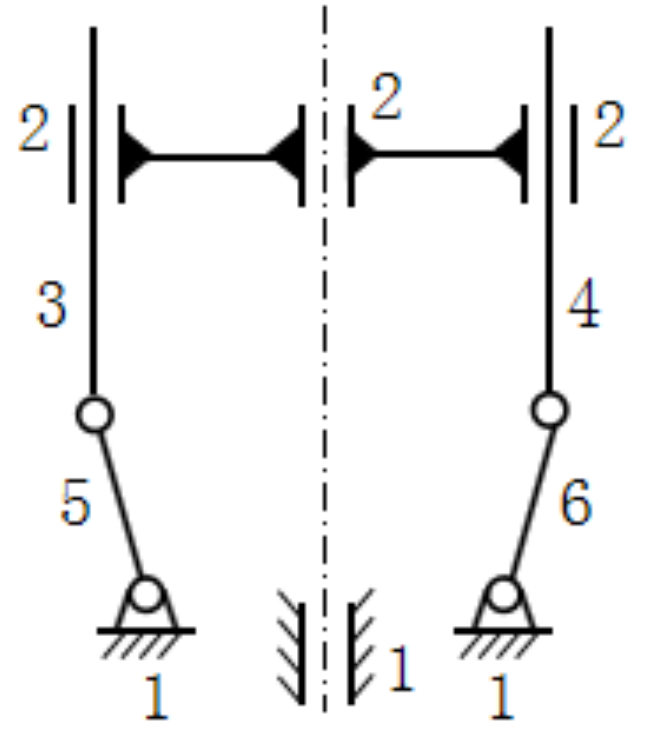 | 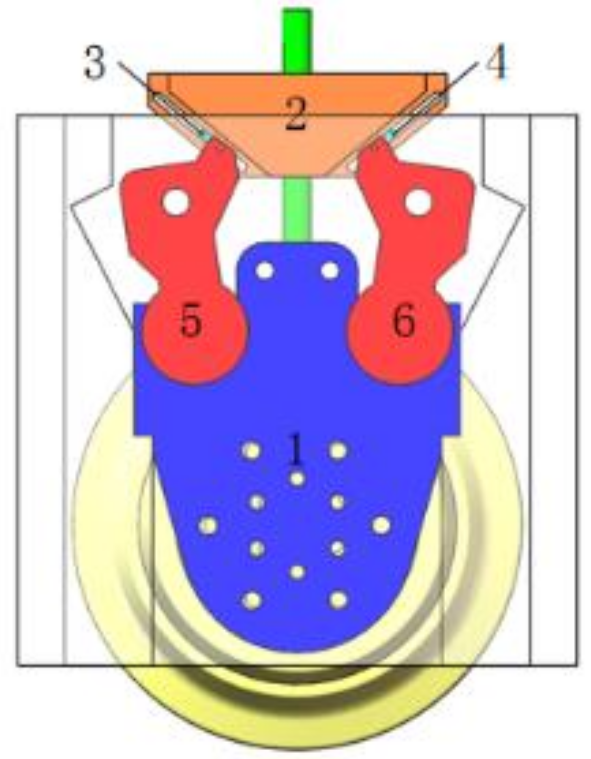 | 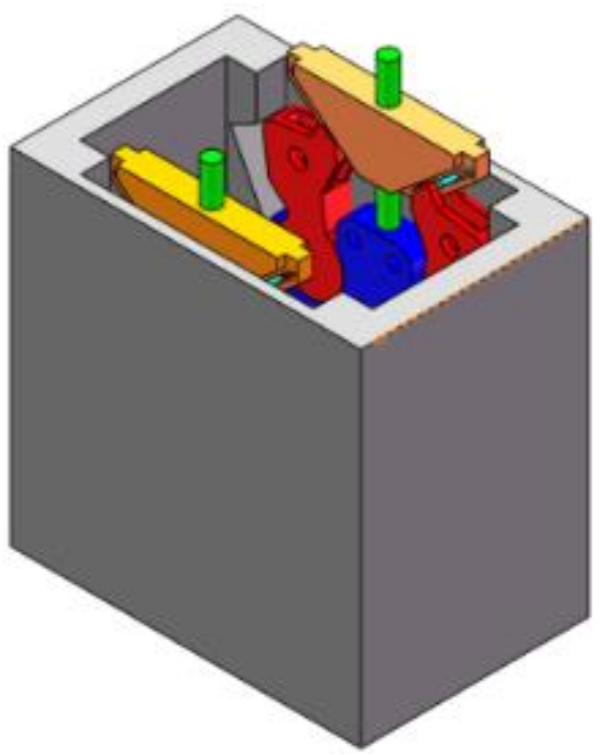 |
| Solution 3 | 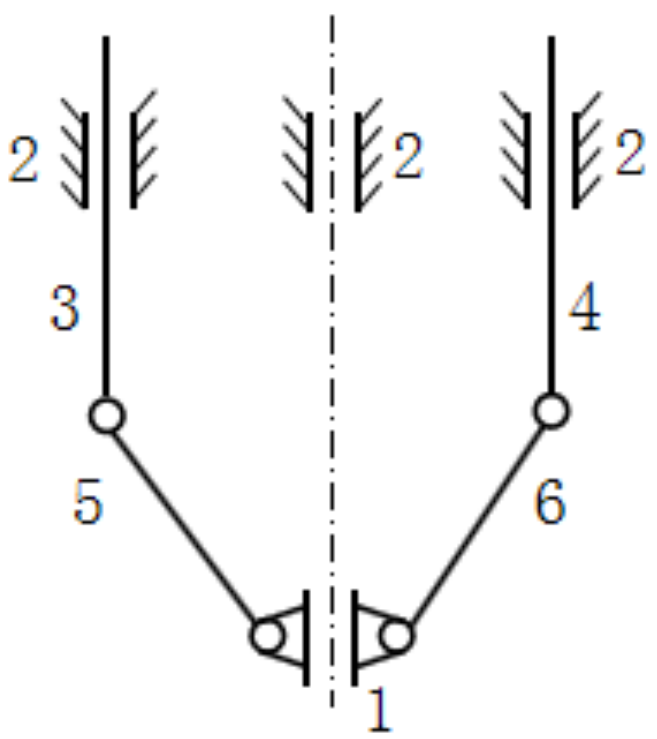 |  | 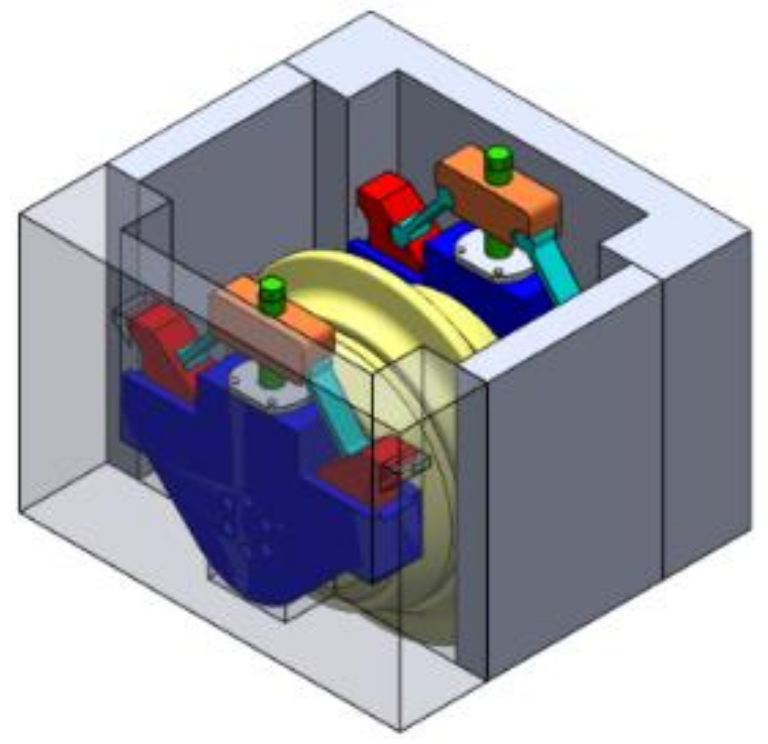 |
| Solution 4 |  | 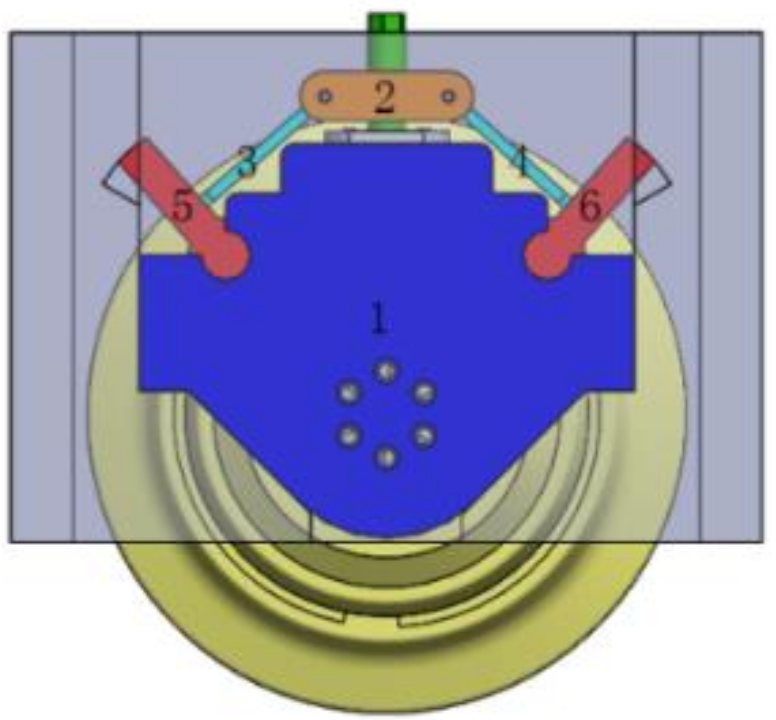 | 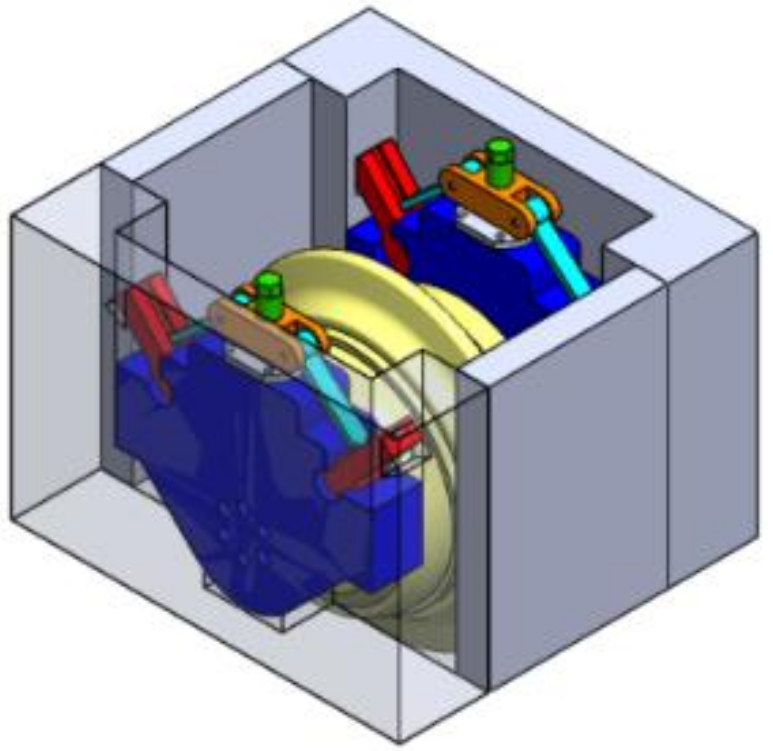 |
| Solutions | n | L/mm | V/mm3 | σ/MPa | M/kg | P0/kN |
|---|---|---|---|---|---|---|
| TCS | 9 | 650 | 606×530×650 | 95.37 | 197 | 916 |
| Solution 1 | 3 | 490 | 472×600×620 | 95.56 | 319 | 916 |
| Solution 2 | 3 | 690 | 390×600×720 | 347.42 | 318 | 916 |
| Solution 3 | 3 | 520 | 563×624×635 | 114.40 | 445 | 916 |
| Solution 4 | 3 | 546 | 584×624×648 | 168.37 | 432 | 916 |
| Solutions | n | L | V | σ | m | P0 |
|---|---|---|---|---|---|---|
| TCS | 0.33 | 0.75 | 0.81 | 1.00 | 1.00 | 1.00 |
| Solution 1 | 1.00 | 1.00 | 0.96 | 1.00 | 0.62 | 1.00 |
| Solution 2 | 1.00 | 0.71 | 1.00 | 0.27 | 0.62 | 1.00 |
| Solution 3 | 1.00 | 0.94 | 0.76 | 0.83 | 0.44 | 1.00 |
| Solution 4 | 1.00 | 0.90 | 0.71 | 0.57 | 0.46 | 1.00 |
| Acceleration | Cutter Type | Decrease Range of Left Bolt Preload | Decrease Range of Right Bolt Preload |
|---|---|---|---|
| 3 g | TCS | 7.18% | 8.51% |
| ICS | 1.96% | 4.82% | |
| 10 g | TCS | 23.25% | 16.07% |
| ICS | 4.92% | 8.64% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Z.; Yang, D.; Huo, J.; Zhuo, P.; Bao, Y. Development and Performance Evaluation of an Integrated Disc Cutter System for TBMs. Appl. Sci. 2021, 11, 644. https://doi.org/10.3390/app11020644
Meng Z, Yang D, Huo J, Zhuo P, Bao Y. Development and Performance Evaluation of an Integrated Disc Cutter System for TBMs. Applied Sciences. 2021; 11(2):644. https://doi.org/10.3390/app11020644
Chicago/Turabian StyleMeng, Zhichao, Dongjian Yang, Junzhou Huo, Puzhou Zhuo, and Youneng Bao. 2021. "Development and Performance Evaluation of an Integrated Disc Cutter System for TBMs" Applied Sciences 11, no. 2: 644. https://doi.org/10.3390/app11020644
APA StyleMeng, Z., Yang, D., Huo, J., Zhuo, P., & Bao, Y. (2021). Development and Performance Evaluation of an Integrated Disc Cutter System for TBMs. Applied Sciences, 11(2), 644. https://doi.org/10.3390/app11020644





