Analysis of Eddy-Current Probe Signals in Steam Generator U-Bend Tubes Using the Finite Element Method
Abstract
:1. Introduction
2. Theoretical Background
Eddy-Current Field Equations
3. Experimental Methods
3.1. Computed Tomography (CT) Analysis
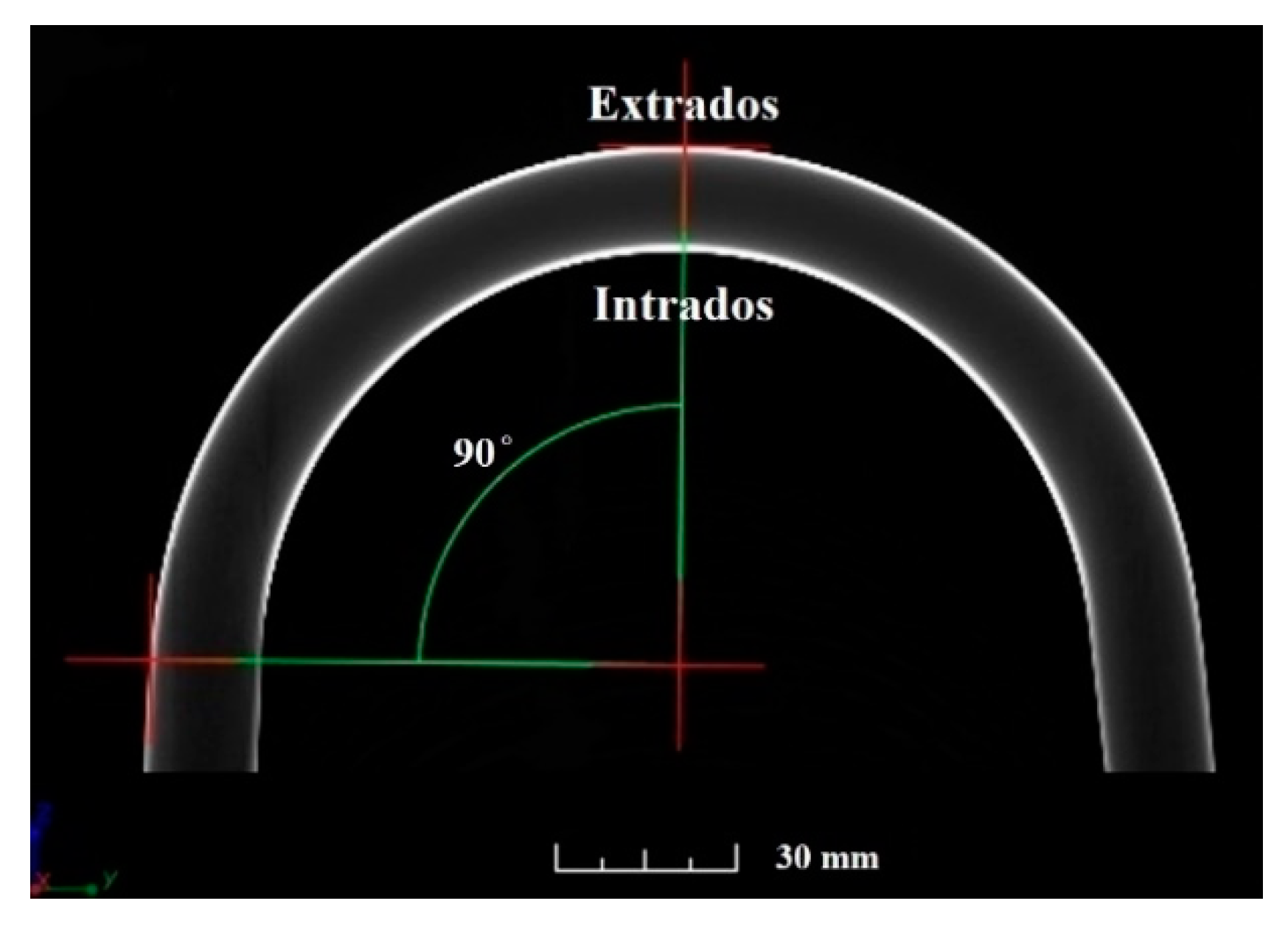
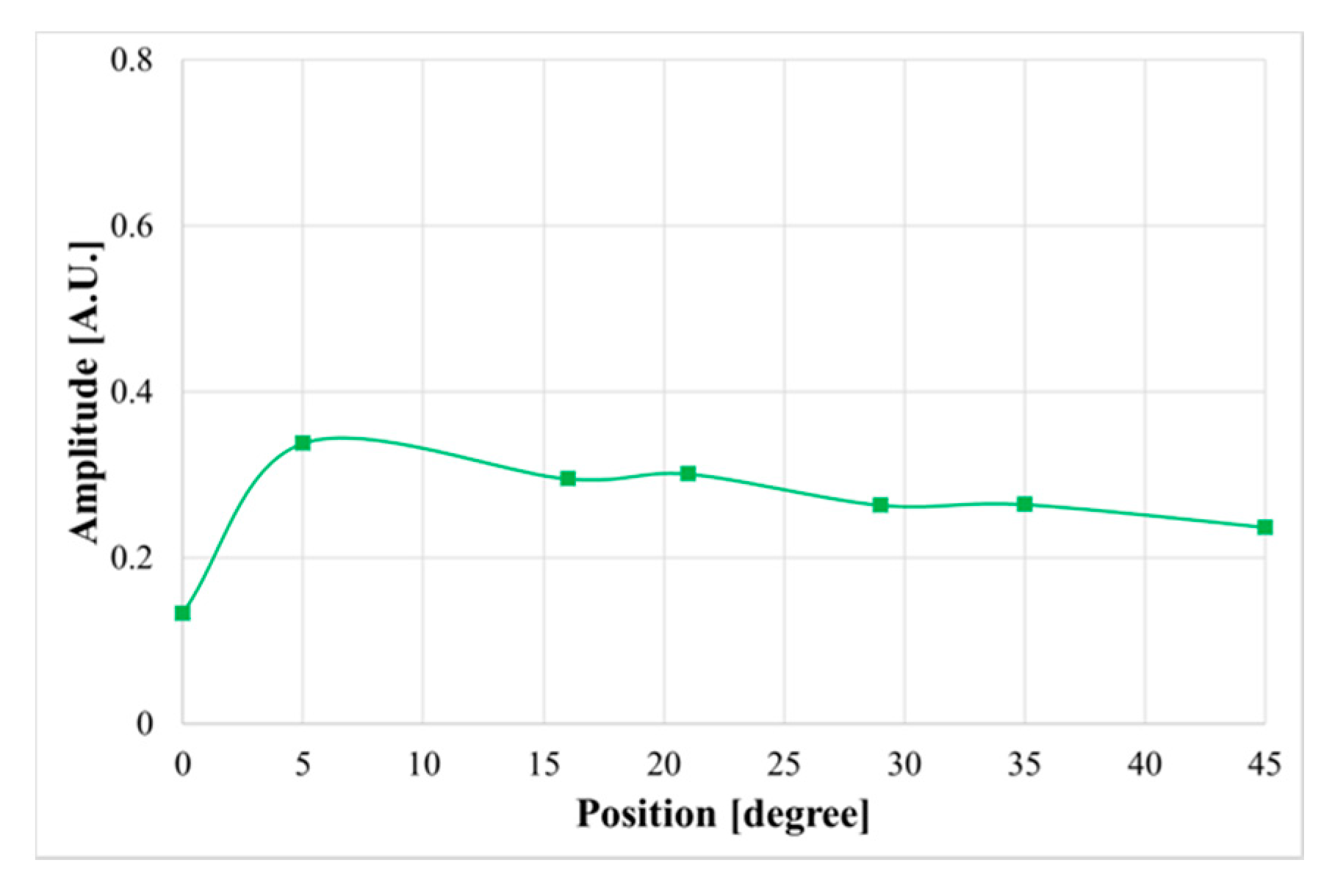
3.2. Tube Curvature Analysis
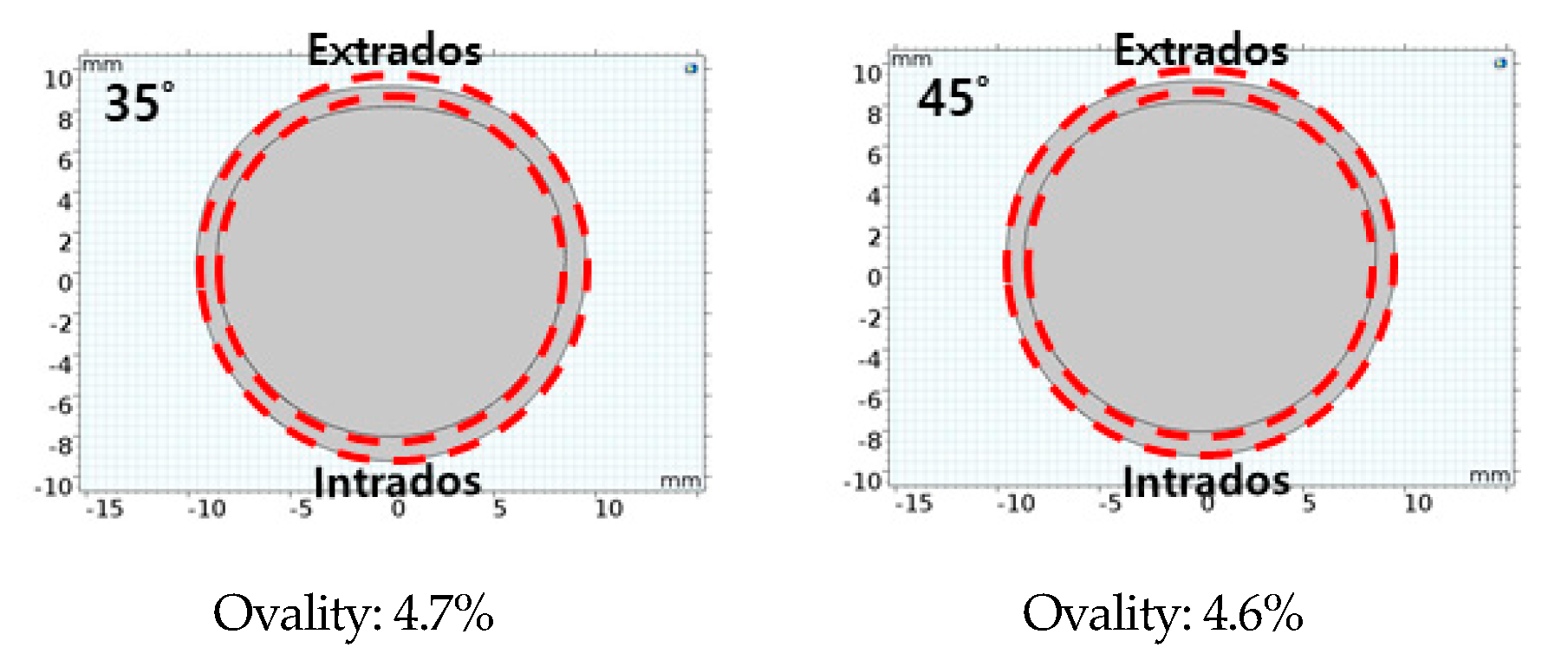
3.3. Geometry Conditions
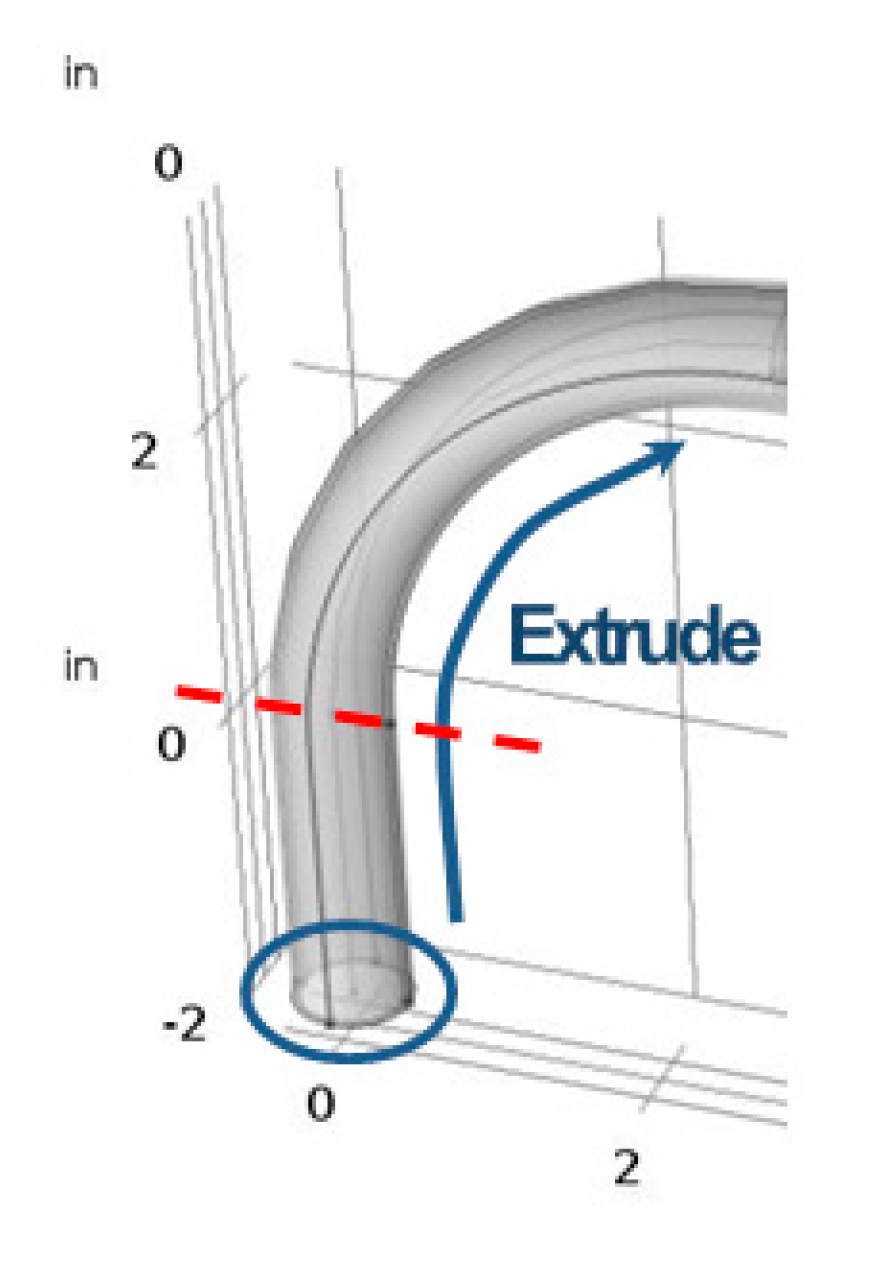
3.4. Curvature Cross-Sectional Area Modeling
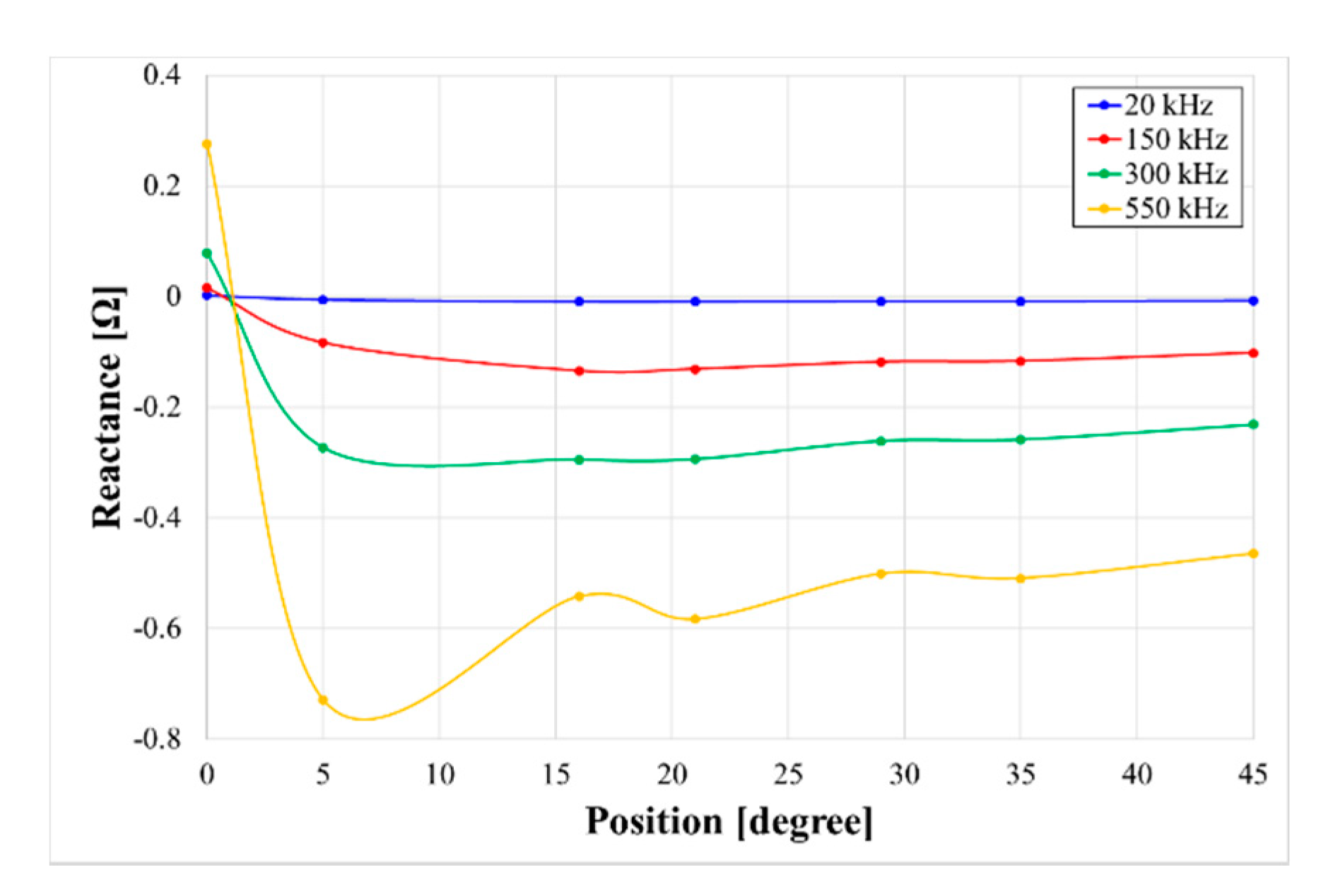
4. Finite Elements Method (FEM) Analysis Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rao, B.P.C. Practical Eddy Current testing, Indian Society for Nondestructive Testing–National Certification Board Series; Alpha Sci. Int. Ltd.: Oxford, UK, 2007; pp. 1–25. [Google Scholar]
- Terry, H.; Mike, W. Eddy Current Testing Technology; Eclipse Scientific Products Inc.: Oshawa, ON, Canada, 2012; pp. 1–6. [Google Scholar]
- Einav, I. Non-destructive Testing for Plant Life Assessment; International Atomic Energy Agency: Vienna, Austria, 2005; pp. 1–61. [Google Scholar]
- Zhang, Y.H.; Luo, F.L.; Sun, H.X. Impedance Evaluation of a Probe-Coil’s Lift-off and Tilt Effect in Eddy-Current Nondestructive Inspection by 3D Finite Element Modeling. In Proceedings of the 17th World Conference on Nondestructive Testing, Shanghai, China, 25–28 October 2008. [Google Scholar]
- Bakhtiari, S.; Kupperman, D.S. Modeling of eddy current probe response for steam generator tubes. Nucl. Eng. Des. 1999, 194, 57–71. [Google Scholar] [CrossRef] [Green Version]
- Johnston, D.P.; Buck, J.A.; Underhill, P.R.; Morelli, J.E.; Krause, T.W. Pulsed eddy-current detection of loose parts in steam generators. IEEE Sens. J. 2018, 18, 2506–2512. [Google Scholar] [CrossRef]
- Jung, H.S.; Kweon, Y.H.; Lee, D.H.; Shin, W.J.; Yim, C.K. Detection of Foreign Objects using Bobbin Probe in Eddy Current Test. J. Korean Soc. Nondestruct. Test. 2016, 36, 295–299. [Google Scholar] [CrossRef] [Green Version]
- Buck, J.A.; Underhill, P.R.; Morelli, J.; Krause, T.W. Simultaneous multi-parameter measurement in pulsed eddy current steam generator data using artificial neural networks. IEEE Trans. Instrum. Meas. 2016, 65, 672–679. [Google Scholar] [CrossRef]
- Sophian, A.; Tian, G.Y.; Taylor, D.; Rudlin, J. A feature extraction technique based on principal component analysis for pulsed eddy current NDT. NDT E Int. 2003, 36, 37–41. [Google Scholar] [CrossRef]
- Xin, J.J. Design and Analysis of Rotating Field Eddy Current Probe for Tube Inspection. Ph. D. Thesis, Department of Electronic Engineering, Michigan State University, East Lansing, MI, USA, 2014; pp. 46–63. [Google Scholar]
- Sadiku, M.N.O. Elements of Electromagnetics; Oxford Univ. Press, Inc.: New York, NY, USA, 2001; pp. 261–392. [Google Scholar]
- Palanisamy, R. Finite Element Modeling of Eddy Current Nondestructive Testing Phenomena. Ph. D. Thesis, Department of Electronic Engineering, Colorado State University, Fort Collins, CO, USA, 1980; pp. 23–90. [Google Scholar]
- Ida, N.; Betzold, K.; Lord, W. Finite Element Modeling of Absolute Eddy Current Probe Signals. J. Nondestr. Eval. 1982, 3, 147–154. [Google Scholar] [CrossRef]
- Bennoud, S.; Zergoug, M. Modeling and Simulation for 3D Eddy Current Testing in Conduction Materials. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2014, 8, 754–757. [Google Scholar]
- Song, S.J.; Shin, Y.K. Eddy Current Flaw Characterization in Tubes by Neural Networks and Finite Element Modeling. J. NDT E Int. 2000, 33, 233–243. [Google Scholar] [CrossRef]
- Shin, Y.K.; Song, S.C.; Jung, H.S.; Lee, Y.T. Prediction and Analysis of ECT Signals due to Tube Defects near Support Plate in Steam Generator. J. Key Eng. Mater. 2006, 321–323, 420–425. [Google Scholar] [CrossRef]
- Rosell, A. Finite Element Modelling of Eddy Current Nondestructive Evaluation in Probability of Detection Studies; Department Applied Mechanics, Chalmers University: Göteborg, Sweden, 2012; pp. 13–28. [Google Scholar]
- Thompson, A.; Maskery, I.; Leach, R.K. X-ray Computed Tomography for Additive Manufacturing: A review. Meas. Sci. Technol. 2016, 27, 072001. [Google Scholar] [CrossRef]
- De Chiffre, L.; Carmignato, S.; Kruth, J.-P.; Schmitt, R.; Weckenmann, A. Industrial Applications of Computed Tomography. CIRP Ann. Manuf. Technol. 2014, 63, 655–677. [Google Scholar] [CrossRef]






| Relative Permeability | Relative Permittivity | Electrical Conductivity (S/m) | |
|---|---|---|---|
| Air | 1.00000037 | 1.000536 | 310−15 |
| Coil (Copper) | 0.999994 | 0.9999996 | 5.96107 |
| Tube (Inconel 690) | 1.01 | 1 | 6.7567106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, S.; Choi, G.; Lee, D.; Choi, M.; Kim, K. Analysis of Eddy-Current Probe Signals in Steam Generator U-Bend Tubes Using the Finite Element Method. Appl. Sci. 2021, 11, 696. https://doi.org/10.3390/app11020696
Oh S, Choi G, Lee D, Choi M, Kim K. Analysis of Eddy-Current Probe Signals in Steam Generator U-Bend Tubes Using the Finite Element Method. Applied Sciences. 2021; 11(2):696. https://doi.org/10.3390/app11020696
Chicago/Turabian StyleOh, Sebeom, Gahyun Choi, Deokhyun Lee, Myungsik Choi, and Kyungmo Kim. 2021. "Analysis of Eddy-Current Probe Signals in Steam Generator U-Bend Tubes Using the Finite Element Method" Applied Sciences 11, no. 2: 696. https://doi.org/10.3390/app11020696
APA StyleOh, S., Choi, G., Lee, D., Choi, M., & Kim, K. (2021). Analysis of Eddy-Current Probe Signals in Steam Generator U-Bend Tubes Using the Finite Element Method. Applied Sciences, 11(2), 696. https://doi.org/10.3390/app11020696




