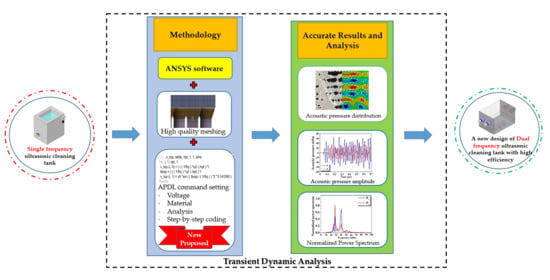
A Dual Frequency Ultrasonic Cleaning Tank Developed by Transient Dynamic Analysis
Abstract
1. Introduction
2. Theoretical Background
2.1. Transient Dynamic Analysis (TDA)
2.2. Harmonic Response Analysis (HRA)
3. Methodology
3.1. Ultrasonic Cleaning Tank (UCT)
3.2. Mesh Model
3.3. Software Setting
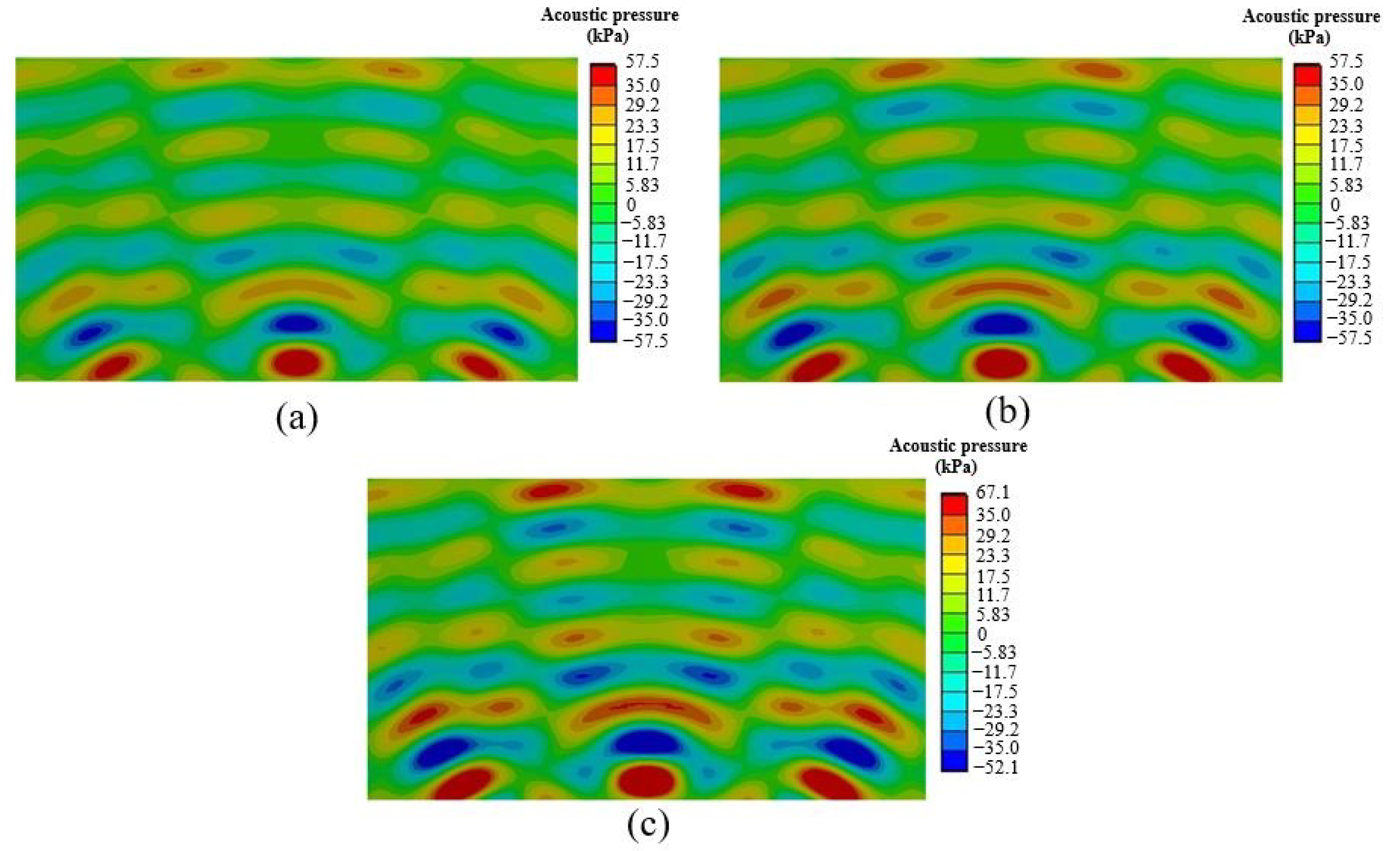
4. Result and Discussion
4.1. Validation
4.2. Scheme to Develop Dual Frequency UCT
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| i, j | 1, 2, 3 correspond to the components of x, y, and z, respectively |
| {},{} | 1st and 2nd derivatives of nodal acoustic pressure vector. |
| {}, {} | 1st and 2nd derivatives of nodal voltage vector. |
| [CF] | acoustic damping matrix (N s/Pa) |
| [KF] | acoustic fluid stiffness matrices (N/Pa) |
| {fF} | acoustic load (N) |
| p | acoustic pressure (Pa) |
| [R]T | acoustic fluid boundary matrices (m3) |
| c | acoustic velocity (m/s) |
| ω | angular frequency (rad/s) |
| [Muu] | coupling mass matrix (kg) |
| [C] | damping matrix (N s/m) |
| [Cvv] | dielectric dissipation matrices |
| [Kvv] | dielectric permittivity matrices |
| {Q} | electrical load |
| {ρf} | fluid density (kg/m3) |
| [MF] | fluid mass matrix (N s2/Pa) |
| HRA | harmonic response analysis |
| [M] | mass matrix (kg) |
| +max | maximum positive acoustic pressure (Pa) |
| −max | maximum negative acoustic pressure (Pa) |
| {p} | nodal acoustic pressure vector (Pa) |
| {u} | nodal displacement vector (m) |
| {V} | nodal voltage vector (V) |
| NPS | normalized power spectrum |
| [Kuv] | piezoelectric coupling element matrix |
| [MS] | solid mass matrix (N s2/m) |
| [CS], [Cuu] | structural damping matrices (N s/m) |
| {F}, {fS} | structural load (N) |
| [K], [Kuu], [KS] | structural stiffness matrices (N/m) |
| f | transducer frequency (Hz) |
| TDA | transient dynamic analysis |
| t | time (s) |
| UCT | ultrasonic cleaning tank |
References
- Zheng, J.; Li, Q.; Hu, A.; Yang, L.; Lu, J.; Zhang, X.; Lin, Q. Dual-frequency ultrasound effect on structure and properties of sweet potato starch. Starch Stärke 2013, 65, 621–627. [Google Scholar] [CrossRef]
- Zhu, F.; Li, H. Modification of quinoa flour functionality using ultrasound. Ultrason. Sonochem. 2019, 52, 305–310. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, G.; Liu, M.; Mei, X.; Yu, Q.; Kan, J. Effects of multi-frequency ultrasound on physicochemical properties, structural characteristics of gluten protein and the quality of noodle. Ultrason. Sonochem. 2020, 67, 105135. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Molares, A.; Dickson, S.; Hobson, P.; Howard, C.; Zander, A.; Burch, M. Quantification of the ultrasound induced sedimentation of Microcystis aeruginosa. Ultrason. Sonochem. 2014, 21, 1299–1304. [Google Scholar] [CrossRef] [PubMed]
- Leclercq, D.J.J.; Howard, C.; Hobson, P.; Dickson, S.; Zander, A.C.; Burch, M. Controlling cyanobacteria with ultrasound. In Proceedings of the INTERNOISE 2014—43rd International Congress on Noise Control Engineering: Improving the World Through Noise Control, Melbourne, Australia, 16–19 November 2014. [Google Scholar]
- Salta, M.; Goodes, L.R.; Maas, B.J.; Dennington, S.P.; Secker, T.J.; Leighton, T.G. Bubbles versus biofilms: A novel method for the removal of marine biofilms attached on antifouling coatings using an ultrasonically activated water stream. Surf. Topogr. Metrol. Prop. 2016, 4, 034009. [Google Scholar] [CrossRef]
- Lais, H.; Lowe, P.S.; Gan, T.H.; Wrobel, L.C. Numerical modelling of acoustic pressure fields to optimize the ultrasonic cleaning technique for cylinders. Ultrason. Sonochem. 2018, 45, 7–16. [Google Scholar] [CrossRef]
- Lais, H.; Lowe, P.S.; Gan, T.H.; Wrobel, L.C. Numerical investigation of design parameters for optimization of the in-situ ultrasonic fouling removal technique for pipelines. Ultrason. Sonochem. 2019, 56, 94–104. [Google Scholar] [CrossRef]
- Felver, B.; King, D.C.; Lea, S.C.; Price, G.J.; Damien Walmsley, A. Cavitation occurrence around ultrasonic dental scalers. Ultrason. Sonochem. 2009, 16, 692–697. [Google Scholar] [CrossRef]
- Manmi, K.M.A.; Wu, W.B.; Vyas, N.; Smith, W.R.; Wang, Q.X.; Walmsley, A.D. Numerical investigation of cavitation generated by an ultrasonic dental scaler tip vibrating in a compressible liquid. Ultrason. Sonochem. 2020, 63, 104963. [Google Scholar] [CrossRef]
- Vetrimurugan, R. Optimization of Hard Disk Drive Heads Cleaning by Using Ultrasonics and Prevention of Its Damage. Apcbee Procedia 2012, 3, 222–230. [Google Scholar] [CrossRef]
- Vetrimurugan; Goodson, J.; Lim, T. Ultrasonic and megasonic cleaning to remove nano-dimensional contaminants from various disk drive components. Int. J. Innov. Res. Sci. Eng. Technol. 2013, 2, 5971–5977. [Google Scholar]
- Mason, T.J. Ultrasonic cleaning: An historical perspective. Ultrason. Sonochem. 2016, 29, 519–523. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Zhu, X.; Liu, Y. Numerical study on dual-frequency ultrasonic enhancing cavitation effect based on bubble dynamic evolution. Ultrason. Sonochem. 2019, 59, 104744. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K. A new formulation of bubble dynamics for sonoluminescence. Electron. Commun. Jpn. (Part II Electron.) 1998, 81, 39–45. [Google Scholar] [CrossRef]
- Lee, M.; Oh, J. Synergistic effect of hydrogen peroxide production and sonochemiluminescence under dual frequency ultrasound irradiation. Ultrason. Sonochem. 2011, 18, 781–788. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Du, X.; Xian, H.; Wu, Y. Instability of interfaces of gas bubbles in liquids under acoustic excitation with dual frequency. Ultrason. Sonochem. 2015, 23, 16–20. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Li, S. Combination and simultaneous resonances of gas bubbles oscillating in liquids under dual-frequency acoustic excitation. Ultrason. Sonochem. 2017, 35, 431–439. [Google Scholar] [CrossRef]
- Suo, D.; Govind, B.; Zhang, S.; Jing, Y. Numerical investigation of the inertial cavitation threshold under multi-frequency ultrasound. Ultrason. Sonochem. 2018, 41, 419–426. [Google Scholar] [CrossRef]
- Hegedus, F.; Klapcsik, K.; Lauterborn, W.; Parlitz, U.; Mettin, R. GPU accelerated study of a dual-frequency driven single bubble in a 6-dimensional parameter space: The active cavitation threshold. Ultrason. Sonochem. 2020, 67, 105067. [Google Scholar] [CrossRef]
- Lee, J.; Hallez, L.; Touyeras, F.; Ashokkumar, M.; Hihn, J.Y. Influence of frequency sweep on sonochemiluminescence and sonoluminescence. Ultrason. Sonochem. 2020, 64, 105047. [Google Scholar] [CrossRef]
- Moholkar, V.S.; Rekveld, S.; Warmoeskerken, M.M.C.G. Modeling of the acoustic pressure fields and the distribution of the cavitation phenomena in a dual frequency sonic processor. Ultrasonics 2000, 38, 666–670. [Google Scholar] [CrossRef]
- Tudela, I.; Saez, V.; Esclapez, M.D.; Diez-Garcia, M.I.; Bonete, P.; Gonzalez-Garcia, J. Simulation of the spatial distribution of the acoustic pressure in sonochemical reactors with numerical methods: A review. Ultrason. Sonochem. 2014, 21, 909–919. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Weavers, L.K. Combining COMSOL modeling with acoustic pressure maps to design sono-reactors. Ultrason. Sonochem. 2016, 31, 490–498. [Google Scholar] [CrossRef] [PubMed]
- Rashwan, S.S.; Dincer, I.; Mohany, A. Investigation of acoustic and geometric effects on the sonoreactor performance. Ultrason. Sonochem. 2020, 68, 105174. [Google Scholar] [CrossRef]
- Henneberg, J.; Gerlach, A.; Cebulla, H.; Marburg, S. The potential of stop band material in multi-frequency ultrasonic transducers. J. Sound Vib. 2019, 452, 132–146. [Google Scholar] [CrossRef]
- Perincek, S.; Uzgur, A.E.; Duran, K.; Dogan, A.; Korlu, A.E.; Bahtiyari, I.M. Design parameter investigation of industrial size ultrasound textile treatment bath. Ultrason. Sonochem. 2009, 16, 184–189. [Google Scholar] [CrossRef]
- Tangsopha, W.; Thongsri, J.; Busayaporn, W. Simulation of ultrasonic cleaning and ways to improve the efficiency. In Proceedings of the 2017 International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 8–10 March 2017; pp. 1–4. [Google Scholar]
- Tangsopa, W.; Keawklan, T.; Kesngam, K.; Ngaochai, S.; Thongsri, J. Improved Design of Ultrasonic Cleaning Tank Using Harmonic Response Analysis in ANSYS. IOP Conf. Ser. Earth Environ. Sci. 2018, 159, 012042. [Google Scholar] [CrossRef]
- Tangsopa, W.; Thongsri, J. Development of an industrial ultrasonic cleaning tank based on harmonic response analysis. Ultrasonics 2019, 91, 68–76. [Google Scholar] [CrossRef]
- Tangsopa, W.; Thongsri, J. A Novel Ultrasonic Cleaning Tank Developed by Harmonic Response Analysis and Computational Fluid Dynamics. Metals 2020, 10, 335. [Google Scholar] [CrossRef]
- Zhang, T. Valveless Piezoelectric Micropump for Fuel Delivery in Direct Methanol Fuel Cell (DMFC) Devices; University of Pittsburgh: Pittsburgh, PA, USA, 2005. [Google Scholar]
- Boonkaew, P.; Thongsri, J. The optimum design of micro gripper for lifetime improvement based on fatigue analysis and six sigma analysis. Int. J. Appl. Eng. Res. 2017, 12, 10233–10241. [Google Scholar]
- Thongsri, J. Transient Thermal-Electric Simulation and Experiment of Heat Transfer in Welding Tip for Reflow Soldering Process. Math. Probl. Eng. 2018, 2018, 4539054. [Google Scholar] [CrossRef]
- Ansys Inc. Introduction to Acoustics; ANSYS Europe Ltd.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Ansys Inc. Piezo and MEMS ACTx R180; ANSYS Europe Ltd.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Ansys Inc. ANSYS 2020 R1. In ANSYS Mechanical APDL Theory Reference; ANSYS Europe Ltd.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Niazi, S.; Hashemabadi, S.H.; Razi, M.M. CFD simulation of acoustic cavitation in a crude oil upgrading sonoreactor and prediction of collapse temperature and pressure of a cavitation bubble. Chem. Eng. Res. Des. 2014, 92, 166–173. [Google Scholar] [CrossRef]
- Li, F.; Ge, S.; Qin, S.; Hao, Q. Simulation of Ultrasonic Cleaning and Experimental Study of the Liquid Level Adjusting Method. In Proceedings of the Re-Engineering Manufacturing for Sustainability, Singapore, 17–19 April 2013; pp. 275–278. [Google Scholar]
- John, F. Ultrasonic Intensity Measurement Techniques. JASA 1965, 38, 817–823. [Google Scholar]













| Domain | Type | Value |
|---|---|---|
| Water (45 °C) | Water density | 990.15 kg/m3 |
| Acoustic velocity | 1533.5 m/s | |
| Dynamic viscosity | 5.7977 × 10−4 kg/ms | |
| Aluminum alloy | Density | 2770 kg/m3 |
| Young’s modulus | 7.1 × 1010 Pa | |
| Poisson’s ratio | 0.33 | |
| Bulk modulus | 6.9608 × 1010 Pa | |
| Shear modulus | 2.6692 × 1010 Pa | |
| Stainless steel | Density | 7750 kg/m3 |
| Young’s modulus | 1.93 × 1011 Pa | |
| Poisson’s ratio | 0.31 | |
| Bulk modulus | 1.693 × 1010 Pa | |
| Shear modulus | 7.3664 × 1010 Pa | |
| Lead Zirconate Titanate (PZT4) | Density | 7500 kg/m3 |
| Permittivity constant () | 8.854 × 10−12 F/m | |
| Stiffness matrix [CE] | C11 = C22 = 1.39 × 1011, C21 = 7.78 × 1010, C31 = C32 = 7.43 × 1010, C44 = 3.06 × 1010, C55 = C66 = 2.56 × 1010 Pa | |
| Piezoelectric stress matrix [e] | e31 = 5.2 c/m2, e33 = 15.1 c/m2, e15 = 12.7 | |
| Relative permittivity | K11 = 1475, K33 = 1300 |
| Model | Position | NPS | |
|---|---|---|---|
| 28 kHz | 40 kHz | ||
| A | P1 | 0.48 | 0.70 |
| P2 | 0.82 | 0.26 | |
| B | P1 | 0.53 | 0.32 |
| P2 | 0.35 | 0.39 | |
| 28 kHz (in Figure 2b) | P1 | 1.00 | - |
| P2 | 0.40 | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tangsopa, W.; Thongsri, J. A Dual Frequency Ultrasonic Cleaning Tank Developed by Transient Dynamic Analysis. Appl. Sci. 2021, 11, 699. https://doi.org/10.3390/app11020699
Tangsopa W, Thongsri J. A Dual Frequency Ultrasonic Cleaning Tank Developed by Transient Dynamic Analysis. Applied Sciences. 2021; 11(2):699. https://doi.org/10.3390/app11020699
Chicago/Turabian StyleTangsopa, Worapol, and Jatuporn Thongsri. 2021. "A Dual Frequency Ultrasonic Cleaning Tank Developed by Transient Dynamic Analysis" Applied Sciences 11, no. 2: 699. https://doi.org/10.3390/app11020699
APA StyleTangsopa, W., & Thongsri, J. (2021). A Dual Frequency Ultrasonic Cleaning Tank Developed by Transient Dynamic Analysis. Applied Sciences, 11(2), 699. https://doi.org/10.3390/app11020699