Electron Pumping and Spectral Density Dynamics in Energy-Gapped Topological Chains

Abstract

Electron pumping through energy-gapped systems is restricted for vanishing local density of states at the Fermi level. In this paper, we propose a topological Su–Schrieffer–Heeger (SSH) chain between unbiased leads as an effective electron pump. We analyze the electron transport properties of topologically trivial and nontrivial systems in the presence of external time-dependent forces in the form of one-Gaussian or two-Gaussian perturbations (train impulses). We have found that the topologically trivial chain stands for much better charge pump than other normal or nontrivial chains. It is important that, during the perturbation, electrons are pumped through the mid-gap temporary states or through the induced sidebands states outside the energy gap. We also analyze the local density of states dynamics during the quench transition between different topological phases of the SSH chain. It turns out that after the quench, the edge topological states migrate through other sites and can temporarily exist in a topologically trivial part of the system. The tight-binding Hamiltonian and the evolution operator technique are used in our calculations.

1. Introduction

Atomic wires are the thinnest electrical conductors, and they can be used in plenty of applications [1,2,3,4]. Many new quantum effects were observed in such systems as spin-charge separation [5], charge-density waves [6] or Majorana topological states [7,8]. Non-equilibrium one-dimensional (1D) systems reveal much richer physics and in the presence of time-dependent perturbations the turnstile effect, photon-assisted tunneling, or coherent destruction of tunneling [9,10,11,12,13,14] can appear. Dynamical phenomena in 1D structures can also lead to novel solid-state phases such as the Floquet topological insulators [15], time crystals [16,17,18] or transient crystals [19].

For a quantum system between unbiased leads the electron current does not flow in the stationary case. However, in the presence of non-equilibrium phenomena (e.g., time-dependent forces or perturbations) electrons can be transferred between leads even without the source-drain voltage which leads to the electron pumping effect. This effect has been the subject of many theoretical and experimental works [18,20,21,22,23,24,25]—it was observed in single and double quantum dot (QD) systems for periodical changes of two or more device-control parameters [20,26] which were responsible for the left-right spatial symmetry breaking of the whole system. Please note that in the presence of the spatial symmetry the probability of electron tunneling from the central system to the left or to the right lead is exactly the same. The pumping current can be also generated for breaking the time-reversal symmetry in the system e.g., by adding the second harmonic to the driving potential or in the presence of time-dependent dipole-like forces [25]. In particular, single-parametric pumping or train-impulse pumps are especially interesting due to their potential applications in nanoelectronics [27,28,29]. For larger one-dimensional systems electron pumping effects were studied for different time-periodic perturbations (delta-like, harmonic or pulsed) [30,31,32,33,34], where the net electron current flows between unbiased leads. From the local electronic properties point of view this current can appear if the system is characterized by finite spectral density function (Local Density of States, LDOS) near the Fermi energy. In such a case an electron can flow from the lead to the unoccupied LDOS state of the central system and then pass to the second lead. On the other hand, the presence of an energy gap in the structure of the central system strongly restricts the pumping effect. However, this conclusion can be invalid for the new state of matter i.e., for topological insulators where energy gaps appear inside the system. These structures are also characterized by collective edge states (topological states) at the system boundaries. Please note that the quantization of particle transport in such structures were studied for Thouless pumping [35], Moire pumping [36], for quantum spin-Hall insulator [37], for twisted bilayer graphene [38], coupled fermionic chains [39], nonadiabatic Floquet structures [40] or others. Topological phases in one-dimensional chains can be obtained within a Su–Schrieffer–Heeger (SSH) model [41,42,43]. The model due its $\mathcal{CT}$ symmetry possesses two different topological phases: the trivial phase with an energy gap along the whole system, and the nontrivial one for which there exist spectrally isolated mid-gap states localized at the system boundaries which are protected against local perturbations [41,42,44].

In this paper, we explore the possibility of electron pumping in the SSH chain under a time-periodic driving in the form of external one-Gaussian or two-Gaussian perturbations moving along the system (so called the train impulse) which in the nonadiabatic regime can generate the pumping current between unbiased leads. Although plenty of studies in the topic of electron pumping have been performed for single or double parameter time-dependent potentials there is a lack of information in the literature about the electron pumping through topological systems affected by the train-impulse perturbations. Such a train-like impulse can drug electrons between unbiased electrodes in the same or also in the opposite direction in comparison with the impulse propagation way which makes these structures especially interesting. Thus, in this paper we consider trivial and nontrivial SSH chains and concentrate on the time dynamics of the site occupancies and the electron currents under the influence of external train perturbations. It allows us to find the net electron charge which is transferred between unbiased leads. In our studies we also analyze the spectral density dynamics during the external perturbation spreading along the system and observe time evolution of the system quasiparticles. From these studies we can find how electrons are transfer through various energy-gapped 1D systems. Moreover, we consider dynamical transition processes (sudden quenches) between two different topological phases of the SSH chain [45,46,47] and observe mid-gap topological states migration between the system sites. We expect that topological states do not disappear immediately after the quench, but they survive in nontopological systems for a longer time and can penetrate even middle sites of the normal or trivial chain.

It is worth noting that new experimental techniques allow one to investigate quench dynamics and different geometric configurations of such atomic systems within the scanning tunneling microscope methods. Moreover, train-like perturbations can be realized experimentally in many one-dimensional systems e.g., for a linear series of QDs with fully controlled external electrodes, for atomic chains in the mechanically controlled break junction geometry with periodical changes of the electrode position. Alternatively, one can use fully controlled 1D optical lattices or atomic chains epitaxially grown on a surface and change the atom-atom couplings using a piezoelectric substrate or laser impulses.

The paper is organized as follows. The theoretical model and the calculation methods are described in Section 2. In Section 3, the main results of the paper are discussed for electron pumping through the SSH chain. In Section 4 the spectral density dynamics for train impulses and quenches is analyzed. The last Section 5 gives a short summary.

2. Theoretical Description

The physical model consists of the SSH chain composed of N sites that may be coupled to the electron reservoir (substrate electrode) underneath or to the left and right leads via the edge sites as shown in Figure 1. This model corresponds to atomic chains on vicinal surfaces (with the insulating or conducting substrate below the chain) or to the linear series of QDs with fully controlled system parameters.

The SSH chain is characterized by the two-site primitive cell with two different couplings between sites inside each cell and between cells—V and W parameters, respectively. The chain for $V=W$ represents nontopological normal chain without an energy gap. For the intracell couplings greater than intercell couplings we get a topological SSH chain in the nontrivial phase i.e., with topological mid-gap states at both chain ends (SSH${}_1$), otherwise we obtain a chain in the trivial topological phase with an energy gap but without the edge states (SSH${}_0$).

The Hamiltonian describing the SSH chain composed of N sites coupled with the electrodes can be written in terms of the second quantization notation as follows:

$$\begin{array}{ccc}\hfill H& =& \sum _{i=1}^N{\epsilon }_i{a}_i^{†}{a}_i+\sum _{i=1}^N\sum _{{\overrightarrow{k}}_i}({\epsilon }_{{\overrightarrow{k}}_i}{a}_{{\overrightarrow{k}}_i}^{†}{a}_{{\overrightarrow{k}}_i}+V_{\overrightarrow{k_i},i}{a}_{\overrightarrow{k_i}}^{†}{a}_i)+\sum _{i,j}^N{V}_{i,j}\left(t\right)a_i^{†}{a}_j+H.c.\hfill \end{array}$$

(1)

Here $a_i^{†},a_i$ are creation/annihilation operators respectively at i-th site, ${\epsilon }_i$ is the on-site energy level and ${\epsilon }_{\overrightarrow{k}}$ corresponds to possible electron energies in the leads. $V_{\overrightarrow{k},i}$ stands for the coupling between electrodes and corresponding chain atom and $V_{i,j}$ is responsible for the couplings between chain sites (note that $V_{i,j}=V$ within the primitive cell and $V_{i,j}=W$ between the neighboring cells). These couplings can vary in time during the train-impulse propagation or sudden quenches. For $V_{\overrightarrow{k},i}=0$ except for $i=1$ and $i=N$ (i.e., for nonzero $V_{\overrightarrow{k},L}$ and $V_{\overrightarrow{k},R}$ elements) the model corresponds to that from Figure 1.

In our paper time dynamics of the system is calculated within the interaction picture using the evolution operator method for which the following equation of motion can be written ($ħ=1$):

$$i\frac{\partial }{\partial t}U(t,t_0)=\widehat{V}\left(t\right)U(t,t_0),$$

(2)

where $\widehat{V}\left(t\right)=U_0(t,t_0)V\left(t\right)U^{†}(t,t_0)$, $U_0(t,t_0)=\mathcal{T}exp\left(i{\int }_{t_0}^{t}d{t}^{\prime }{H}_0\left(t^{\prime }\right)\right)$ and $\mathcal{T}$ is the time ordering operator. Here $V\left(t\right)$ is the coupling part of the total Hamiltonian and $H_0\left(t\right)$ represents the on-site energy part, $H_0={\sum }_{\alpha }{\epsilon }_{\alpha }{a}_{\alpha }^{†}{a}_{\alpha }$. The physical properties of the system are expressed by the evolution operator matrix elements obtained from Equation (2). The local time-dependent charge occupancies, $n_i\left(t\right)$, can be found from the relation [48,49]:

$$\begin{array}{c}\hfill n_i\left(t\right)=\sum _{j=1}^N{n}_j\left(t_0\right)|U_{i,j}(t,t_0){|}^2+\sum _{j,{\overrightarrow{k}}_j}{n}_{{\overrightarrow{k}}_j}\left(t_0\right){|U_{i,{\overrightarrow{k}}_j}(t,t_0)|}^2,\end{array}$$

(3)

where $n_i\left(t_0\right)$ represents the initial filling of the corresponding single-particle state. As we are not interested in the transient effects, which appear only for small t ($t\ge t_0$), we assume empty initial occupancies of all chain sites. The evolution operator elements, which are necessary to obtain the occupancies, satisfy the following set of integro-differential equations ($t_0=0$ is assumed):

$$\begin{array}{ccc}\hfill i\frac{\partial U_{i,{\overrightarrow{k}}_j}\left(t\right)}{\partial t}& =& \sum _{i^{\prime }}{V}_{i{i}^{\prime }}\left(t\right)e^{i({\epsilon }_{i^{\prime }}-{\epsilon }_i)t}{U}_{i^{\prime },{\overrightarrow{k}}_j}\left(t\right)-V_{i{\overrightarrow{k}}_j}\left(t\right)e^{i({\epsilon }_i-{\epsilon }_{{\overrightarrow{k}}_j})t}\hfill \\ & -& |V_{i{\overrightarrow{k}}_j}{\left(t\right)|}^2{\int }_0^{t}d{t}^{\prime }\int d\epsilon D_j\left(\epsilon \right)e^{i\epsilon (t-t^{\prime })}{e}^{i{\epsilon }_i(t-t^{\prime })}{U}_{i,{\overrightarrow{k}}_j}\left(t^{\prime }\right),\hfill \end{array}$$

(4)

where $D_j\left(\epsilon \right)$ is the j-th lead’s spectral density function.

Assuming the wide-band approximation which is justified for flat leads DOS or in the case when the lead’s DOS varies slowly in the vicinity of the central system electron energies, the effective chain-electrode coupling can be expressed by ${\Gamma }_i\left(\epsilon \right)=2\pi {\sum }_{\overrightarrow{k}}{\left|V_{i\overrightarrow{k}}\right|}^2\delta (\epsilon -{\epsilon }_{\overrightarrow{k}})={\Gamma }_i$, which is energy independent. Within this approach Equation (4) for the left electrode takes the form:

$$\begin{array}{ccc}\hfill \frac{d{U}_{i,kL}\left(t\right)}{dt}& =& -i\sum _{i^{\prime }}{V}_{i{i}^{\prime }}\left(t\right)e^{i({\epsilon }_{i^{\prime }}-{\epsilon }_i)t}{U}_{i^{\prime },{\overrightarrow{k}}_L}\left(t\right)-i{V}_{1,\overrightarrow{k}L}\left(t\right)e^{i({\epsilon }_1-{\epsilon }_{\overrightarrow{k}L})t}-\frac{{\Gamma }_L}{2}{U}_{i,\overrightarrow{k}L}\left(t\right),\hfill \end{array}$$

(5)

and similar for the right lead.

The current flowing from the left electrode is obtained from the time derivative of the total number of electrons in this reservoir:

$$\begin{array}{c}\hfill j_L\left(t\right)=-e\frac{d}{dt}\sum _{{\overrightarrow{k}}_L}{n}_{{\overrightarrow{k}}_L}\left(t\right),\end{array}$$

(6)

where the occupancies $n_{{\overrightarrow{k}}_L}\left(t\right)$ can be expressed similarly to Equation (3) by the corresponding evolution operator matrix elements. In this case, the spectral density function at each chain site for the zero temperature satisfies the relation:

$$\begin{array}{c}\hfill {\rho }_i(\epsilon ,t)=\sum _{\alpha }{D}_{\alpha }\left(E\right){\left|U_{i,\alpha }(\epsilon ,t)\right|}^2,\end{array}$$

(7)

where $U_{i,\alpha }$ elements are calculated numerically from Equation (4) or Equation (5).

In this manuscript we use the unit of energy ${\Gamma }_L=\Gamma \equiv 1$, the time unit is $ħ/\Gamma$, and the current is expressed in the units of $e\Gamma /ħ$. Thus, for $\Gamma =1$ meV the units of time and current are $0.66$ ps and $0.25$ μA, respectively. Please note that the reference energy point is the left electrode Fermi energy, $E_F=0$.

3. Electron Pumping through SSH Chains

Topological chains seem to be very poor candidates for an effective quantum pump due to their electronic structure i.e., energy gap at the Fermi level. However, for quantum systems which are suddenly quenched the spectral density function at each site changes/evolves and it takes some time for the system to obtain its new equilibrium state. For a system with strong asymmetry in its LDOS this non-equilibrium processes can lead to the pumping effect between unbiased leads. Here we propose a 1D topological chain as an electron pump where the electron current direction can be controlled by means of the gate voltage potential. In such systems a gate electrode can be provided by external auxiliary electrodes or the substrate underneath the atomic chain. To avoid the electron leakage to the substrate we consider the chain on the insulating surface with two electron reservoirs at both chain ends (${\overrightarrow{k}}_1=\overrightarrow{k}L$ and ${\overrightarrow{k}}_N=\overrightarrow{k}R$). It is assumed that the external perturbation applied to the chain does not change the couplings homogeneously but there is a kind of the wire inertia which introduces the phase shift between the couplings (depending on the site position in the chain). In our investigations we consider the one-Gaussian or two-Gaussian perturbations in the form of a train-impulse spreading through the chain, see Figure 2, upper panels, where we show time-dependent perturbations, $f_0$, $f_i$ and $f_N$ which are related to the couplings, $V_{\overrightarrow{k}L}$, $V_i$ and $V_{\overrightarrow{k}R}$, respectively and $V_i\left(t\right)=V_i{f}_i\left(t\right)$. The analytical relations for these perturbations can be written in the following form $f_j\left(t\right)=1+exp\left(\frac{{\tilde{t}}^2}{\sigma }\right)$ for the one-Gaussian pulse and $f_j\left(t\right)=1+exp\left(\frac{{\tilde{t}}^2}{\sigma }\right)-exp\left(\frac{{[\tilde{t}-t_1]}^2}{\sigma }\right)$ for the two-Gaussian perturbation, where $\tilde{t}=t-(t_{00}+j{t}_x)$ and $j=0,1,2,\cdots ,N$. Here $t_{00}$ stands for the time for the first Gaussian maximum, $t_x$ is responsible for the time shift of the external perturbation between the nearest-neighbor couplings (for $t_x=0$ all couplings change simultaneously in time in the same way), $t_1$ stands for the time shift between the Gaussian functions, and $\sigma$ corresponds to the half-width of the Gaussian signal. Such train pulses locally modify the site-site couplings and can change the system topology (depending on the coupling differences between chain sites). This perturbation concerns only small part of the whole chain, but it has a huge impact on the electron current flowing through the system.

The time-dependent occupancies are obtained from Equation (3) and the current flowing through the system from Equation (6), which in the wide-band approximation we calculate from the relation:

$$\begin{array}{ccc}\hfill j_L\left(t\right)& =& -{\Gamma }^L{f}_0^2\left(t\right)n_1\left(t\right)-2\mathrm{Im}\left\{\sum _{\overrightarrow{k}L}{n}_{\overrightarrow{k}L}\left(0\right)V_{\overrightarrow{k}L}{f}_0\left(t\right)e^{i({\epsilon }_{\overrightarrow{k}L}-{\epsilon }_0)t}{U}_{1,\overrightarrow{k}L}\left(t\right)\right\},\hfill \end{array}$$

(8)

where the evolution operator matrix elements $U_{1,\overrightarrow{k}L}$ are obtained from Equation (5).

In the beginning in Figure 2 we analyze the time-dependent electron occupations (middle panels) and the currents flowing from the left electrode (bottom panels) for the SSH topological chain in the trivial phase (SSH${}_0$, $V=4,W=1$, yellow curves) and nontrivial phase (SSH${}_1$, $V=1,W=4$, violet curves) for ${\epsilon }_0=3$. Before the train impulse starts (at $t\simeq 390$) the system is in its equilibrium state – the occupancies do not change in time and the currents do not flow between electrodes. The structure of LDOS is symmetrical with respect to ${\epsilon }_0$ and in the first case (SSH${}_0$ chain) there is an energy gap around the Fermi energy, thus the electron occupancy is almost 0.5 (middle panels) even for ${\epsilon }_0=3$. For the one-Gaussian perturbation, in the first stage, the chain-lead coupling strength increases and some charge from the chain leaks to the lead and the chain occupation locally decreases. This is also the reason why in this case the current is negative (it flows from the chain to the left electrode). In the second stage of this train perturbation the couplings between atomic sites inside the chain increase and the lower sideband LDOS states move deeper below the Fermi energy, thus the occupancy locally increases, and the current is positive. On the other hand, in the presence of this perturbation, for the chain with topological states at both edges (nontrivial phase) the empty LDOS states spread below the Fermi level and the occupancy of the chain site increases rapidly (the current flows from the left electrode to the chain). Please note that the perturbation (train impulse) goes through the chain up to $t=420$ units of time but the occupancies and the currents tend very fast to their equilibrium values.

The situation changes for the two-Gaussian perturbation (right panels). In this case, charge oscillations do not vanish rapidly, but they are visible also for larger t, i.e., even for times for which the perturbation has passed through the system. The reason for such long-time oscillations is very low value of the two-Gaussian perturbation for a short period of time, $f\left(t\right)$, which leads to almost vanishing site-site couplings in the system. Thus, the chain sites are almost decoupled for a moment (like in the atomic limit) and then the system needs much more time to reach the equilibrium state. Please note that after and before the perturbation, the occupancies are exactly the same and from the careful inspection of the currents flowing from the left electrode one can find the total charge pumped through the chain. For the SSH${}_1$ chain and two-Gaussian impulse it is evident that most of the violet curve is negative, thus one expects the net pumping charge in the system. For the one-Gaussian impulse (left bottom panel) the currents for SSH${}_0$ and SSH${}_1$ chains oscillate around the zero value, but they are asymmetrical and more detailed study is required to classify these systems as electron pumps.

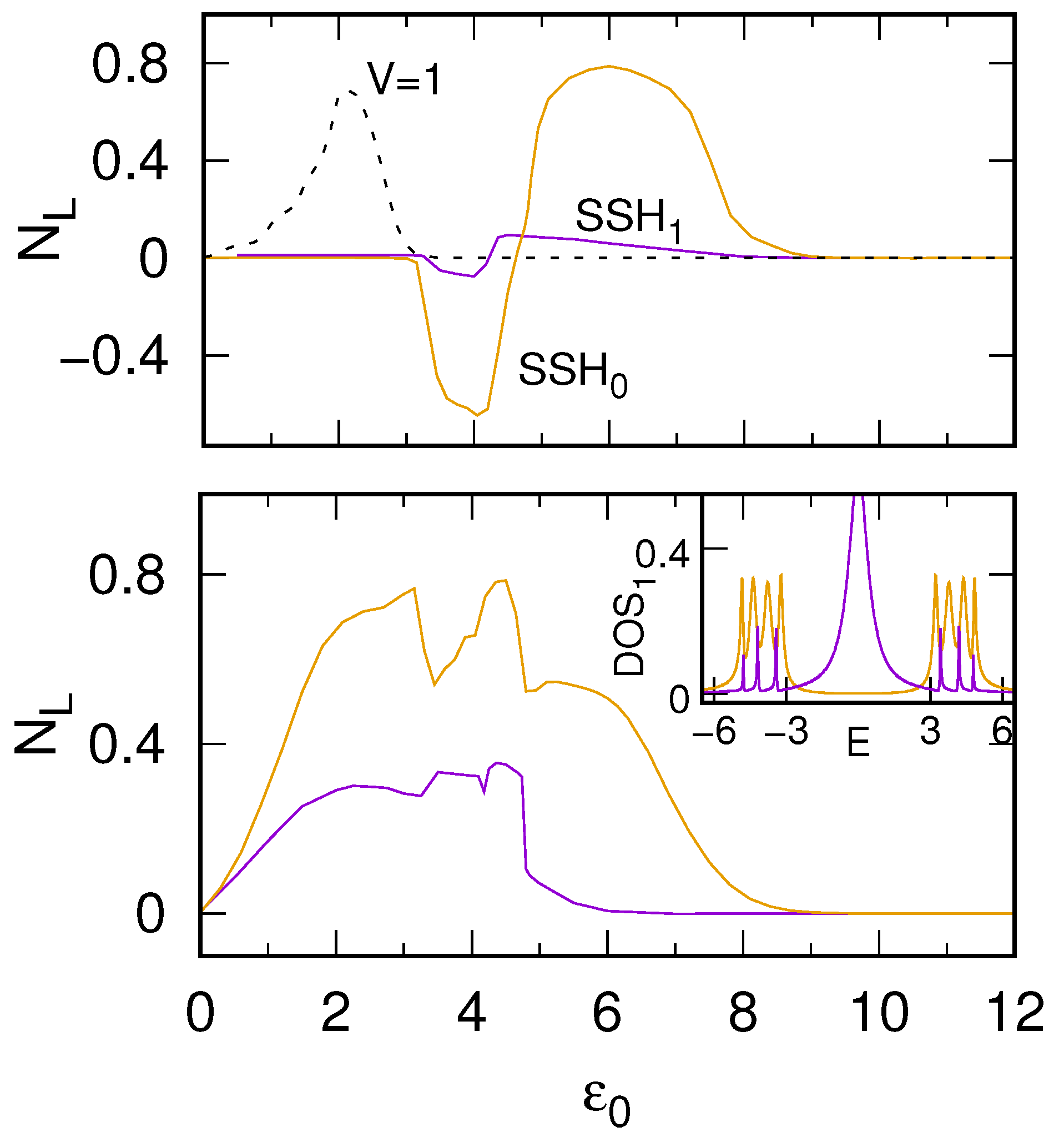
The total charge pumped through the chain is obtained by integrating the time-dependent currents, $N_{L/R}=\int j_{L/R}\left(t\right)dt$, where in our system the condition $N_L=-N_R$ is always satisfied. Here, positive values of $N_{L/R}$ correspond to electrons flowing from the electrode to the chain. In Figure 3 the pumped charge from the left lead is analyzed as a function of ${\epsilon }_0$ (which corresponds to the gate voltage) for the one-Gaussian (upper panel) and two-Gaussian perturbations (bottom panel) for both SSH${}_0$ (yellow curves) and SSH${}_1$ (violet curves) chains. As one can see for symmetrical LDOS with respect to the Fermi energy (${\epsilon }_0=0$) the charge does not flow through the chain, independently on the perturbation shape and topological phase of the chain. For ${\epsilon }_0\ne 0$ the shape of the train impulse spreading through the chain plays a crucial role in the electron pumping effect in topological systems. For the one-Gaussian perturbation the couplings between sites locally increase leading to smaller difference between $V_i$ parameters. In this case, the energy gap is not closed. It is the reason that electrons do not flow through the SSH${}_0$ chain for ${\epsilon }_0$ smaller than the energy gap width (here the gap appears for $|\epsilon -{\epsilon }_0|\le 3$, cf. the inset in Figure 3, bottom panel). Note that also for the chain in the nontrivial phase the pumping effect does not occur for these values of ${\epsilon }_0$ although there is a topological state at the first chain site (nonzero LDOS at the Fermi level, see the inset, violet curve). In this case, electrons which flow out from the electrode cannot be transferred through the middle part of the chain due to the energy gap at these middle sites. It means that the zero-energy edge states do not play a main role in the electron pumping through 1D systems—this problem will be discussed in more details in the next section.

For larger ${\epsilon }_0$ (beyond the energy gap) electrons are pumped in the system. In our case for ${\epsilon }_0>3$ the bottom sideband peaks which are below the Fermi level (they are occupied) change their positions in the presence of the one-Gaussian perturbation, and thus the electron charge leaks out of the chain (the current is negative). Next, for larger ${\epsilon }_0$ (${\epsilon }_0\simeq 4.7$) the bottom LDOS sideband is symmetrical with respect to the Fermi energy and the current does not flow through the system (similarly as for ${\epsilon }_0=0$). The second upper LDOS sideband lies too far from the Fermi level and does not influence the current. For ${\epsilon }_0>4.5$ there are more LDOS peaks above the Fermi level and in the presence of the perturbation they move below the Fermi energy. In that case electrons from the electrode occupy these empty LDOS states and the current is positive. For larger and larger ${\epsilon }_0$ there are no electron states near the Fermi level and the net charge cannot be pumped through the system. Note that for the nontrivial chain (SSH${}_1$, violet curve upper panel) and the one-Gaussian impulse the pumping current almost does not flow through the system which is a consequence of relatively low LDOS in the upper and lower sidebands (cf. the violet curve in the inset), and because the sidebands are responsible for the pumping current this effect is marginal in the SSH${}_1$ chain. Thus, the shape of the pumping current as a function of the gate voltage allows us to distinguish between the trivial and nontrivial phases of the topological system.

In Figure 3 the results obtained for the SSH${}_0$ and SSH${}_1$ chains are compared also with the normal chain of the same length (black broken curve, upper panel). There are crucial differences between topological and normal systems. First, for the normal chain the pumping current starts to flow for ${\epsilon }_0>0$ as there is no energy gap in the system and even small asymmetry in its energetic structure leads to the electron pumping. The maximal pumping current is observed for such ${\epsilon }_0$ for which the bottom of chain energy band corresponds to the Fermi energy (here it is for ${\epsilon }_0=2$). For larger ${\epsilon }_0$ the pumping current vanishes due to the lack of states at the Fermi level. It is also important that for the normal chain the pumping current is always positive (for ${\epsilon }_0>0$) whereas in the topological chains one can control the direction of the current slightly tuning the gate voltage of the system.

The situation changes for the two-Gaussian perturbation (bottom panel) which modulates the coupling strengths along the chain in such a way that in the first stage the couplings increase but then they decrease below their initial values. It leads to smaller difference between the neighboring couplings in the chain which almost closes the energy gap at the Fermi level. Thus, electrons can flow from the electrode to the chain (like in the normal chain) even for small ${\epsilon }_0$. However, in the second stage of the perturbation the couplings tend to zero and these electrons cannot back to the previous sites (they are pushed toward the second electrode). In this case, the pumping current is always positive and for larger and larger ${\epsilon }_0$ it vanishes. Moreover, the system in the trivial phase, SSH${}_0$, more effectively pumps electrons through the chain due to its unique energetic structure which will be analyzed in the next section. Please note that the pumping current curves are not very smooth because they reflect the peaked structure of the sidebands (see the inset figure) which for smaller couplings in the two-Gaussian mode tends to atomic limit and the peaks are much more evident.

4. Spectral Density Dynamics

To explain the nature of the pumping process in topological chains in more details we must study time-dependent LDOS along the chain during the perturbations. Please note that within the evolution operator method which we use in our calculations one can analyze simultaneously the occupancies, currents and time-dependent LDOS structures. Detailed analysis of the spectral density dynamics during the pumping process or sudden quenches allows one to observe time evolution of the system quasiparticles at a given site as well as their time-migration along the system or between chain sites.

4.1. Train Impulses

Here, we are going to explain more precisely the electron transfer process through the energy-gapped structure between unbiased leads. Thus, in Figure 4 we show the spectral density functions related to four sites of the SSH${}_0$ chain during the propagation of the train impulse (one-Gaussian perturbation, panel a, or two-Gaussian impulse, panel b). As one can see the chain is characterized by the energy gap at the Fermi level, independent on the site number (the total chain length is $N=8$). The perturbation starts at $t=400$ and it leads to wider LDOS - the sidebands are shoved outside the Fermi energy due to larger values of the coupling parameters. After some time, all LDOS peaks return to their initial positions and the induced sideband structure follows the perturbation. When the train impulse reaches the edge site the system evolves to its previous equilibrium state. In this case, electrons are transferred through the LDOS sidebands which are outside the energy gap of the chain.

The situation changes for the two-Gaussian perturbation (panel b) as now some site-site couplings decrease in time and at the same time some of them increase. It leads to the induced sidebands outside the energy gap (like in the one-Gaussian impulse) but also dynamical nonzero LDOS structure in the energy gap region is observed. Thus, for this perturbation electrons can be pumped through these temporary mid-gap states. For the nontrivial topological chain, SSH${}_1$, the LDOS dynamics during the two-Gaussian impulse is analyzed in panel c. In this case, the sidebands outside the energy gap are slightly visible and the main pumping process is realized only inside the energy gap region. Thus, one expects lower values of the net pumping current in comparison with the trivial chain, as one can see in Figure 3. The inside structure of LDOS during the perturbation is formed from the mid-gap topological state localized at the first site—this state oscillates in time and we observe a periodic emission of this state to other chain sites. These induced states also follow the train-impulse propagation along the chain. Please note that sudden local change of the site-site couplings disturbs both topological states related to the first and the last chain sites for a moment (the difference between the nearest-neighbor couplings decreases rapidly which influences the chain periodicity) but after some time the mid-gap states are rebuilt again. It is also interesting that for the two-Gaussian pulse both topological states have very high intensity for short period of time. This results from the fact that for a moment the coupling between the first (last) chain site and its neighboring site decreases and the energetic structure of LDOS tends to the atomic limit in this case.

From the detailed studies of time-dependent LDOS characteristics we have found that electrons are transferred through the mid-gap temporary states in nontrivial topological chains or through the induced sidebands outside the energy gap region in trivial chains. The pumped current direction depends only on the relative position of the LDOS peaks and the leads Fermi energy, cf. Figure 3. We have also checked that the spectral density dynamics of the SSH chain coupled with a noninsulating surface underneath does not reveal significant differences. In that case the chain-substrate coupling is responsible for the half-width of the spectral density peaks and for larger couplings these LDOS peaks are wider and smoother. It is important from the practical point of view, because it opens more perspectives for experimental studies of such structures.

4.2. Quench Dynamics in SSH Chains

Topological chains which are characterized by an energy gap along the system can transfer electrons through the induced mid-gap states as shown in the previous section. This effect can be observed only for non-equilibrium processes such as in the presence of a train impulse moving along the chain. Alternatively, after a sudden change of the system parameters (so called the quantum quench) the system needs some time to reach its steady state which opens a new possibility for coexistence of both trivial and nontrivial phases simultaneously in the system. Thus, it is desirable to analyze the mid-gap topological states dynamics between SSH${}_1$ and SSH${}_0$ (or normal) chains, which takes place not just for a while (as during the train impulse) but which lasts for a long time after the quench.

Thus, in Figure 5 we analyze a segment of energy-dependent LDOS near the Fermi energy (at sites from $i=1$ to $i=10$) as a function of time for topological chain of the length $N=20$. At a given time ($t=400$) the quantum quench switches topological phase from nontrivial to the trivial one (panel a) or to the normal chain (panel b) and we can analyze the mid-gap state dynamics along the chain. As one can see before the transition the system is characterized by wide topological states at the edge sites ($i=1$, and the same at $i=20$) and the energy gap in all middle sites (panels a and b). For very large time after the quench, we can notice that the system reaches its steady state i.e., trivial topological state with energy-gapped LDOS (panel a) or normal nontopological chain with no energy gap (panel b).

The most interesting physics happens just after the quench. Surprisingly, topological state does not disappear immediately but rather moves into middle parts of the chain. However, in the upper panel this state survives only on the first few boundary sites and then it is blurred in time, but it is visible that at $t\simeq 410$ it reaches the middle site of the chain. The same signal moves from the last chain site and they pass each other. Thus, the X-shaped LDOS is observed and as time evolves these states balance between the edges with vanishing intensities. This process is more evident in the bottom panel where both topological states migrate after the quench through the normal chain and they also form a V-shaped LDOS dynamical structure. Note that in the normal chain the edge states travel much faster and they reach the middle chain site just at $t\simeq 403$, i.e., only 3 time units after the quench. It means that the travel speed of the mid-gap state strongly depends on the energy-gapped structure in the spectral density function and for nonzero LDOS it moves much faster along the chain. Please note that similar time evolution was observed for the absolute value of the spinor component related to the Majorana mode in 1D topological systems [50].

5. Conclusions

In this work we have studied electron transfer through the 1D topological systems which are characterized by an energy gap and are expected to be poor electron pumps. Using the evolution operator technique and the tight-binding Hamiltonian we have analyzed the occupancies, currents and time-dependent LDOS along the SSH trivial and nontrivial chains affected by external train impulses in the form of the one-Gaussian and two-Gaussian perturbations. It turns out that such systems can work as effective electron pumps and surprisingly, topological trivial chains can transfer more charge during one cycle of such external perturbation than nontrivial SSH chains. This effect is explained by strong asymmetry in the structure of LDOS for the edge sites (due to the absence of topological states) and is crucial for the pumping effect. It is also important that for the normal chain the pumping current is always positive (for positive on-site energies) whereas in topological chains one can control the direction of the pumping current slightly tuning the gate voltage of the system.

We have also analyzed how electrons are transferred through the energy-gapped topological materials and we have found that during the train perturbation electrons are pumped through the mid-gap temporary states in the nontrivial topological chains and through the induced LDOS sidebands outside the energy gap region in the trivial chains. This conclusion stands for the main result of the paper and can be useful for potential applications of such topological materials in nanoelectronics.

Additionally, we have investigated LDOS time dynamics along the chain after a sudden quench which changes topological phase of the system (from the nontrivial to the normal or to the trivial one). We have found that during this change topological states do not disappear at once, but they balance between the edges of the chain with vanishing intensities. Even more importantly, the travel speed of topological states strongly depends on the chain energetic structure such that for gapped materials the states move relatively slow and for normal materials they move much faster along the chain.