Study on the Method of Moving Load Identification Based on Strain Influence Line
Abstract
:1. Introduction
2. Theoretical Background
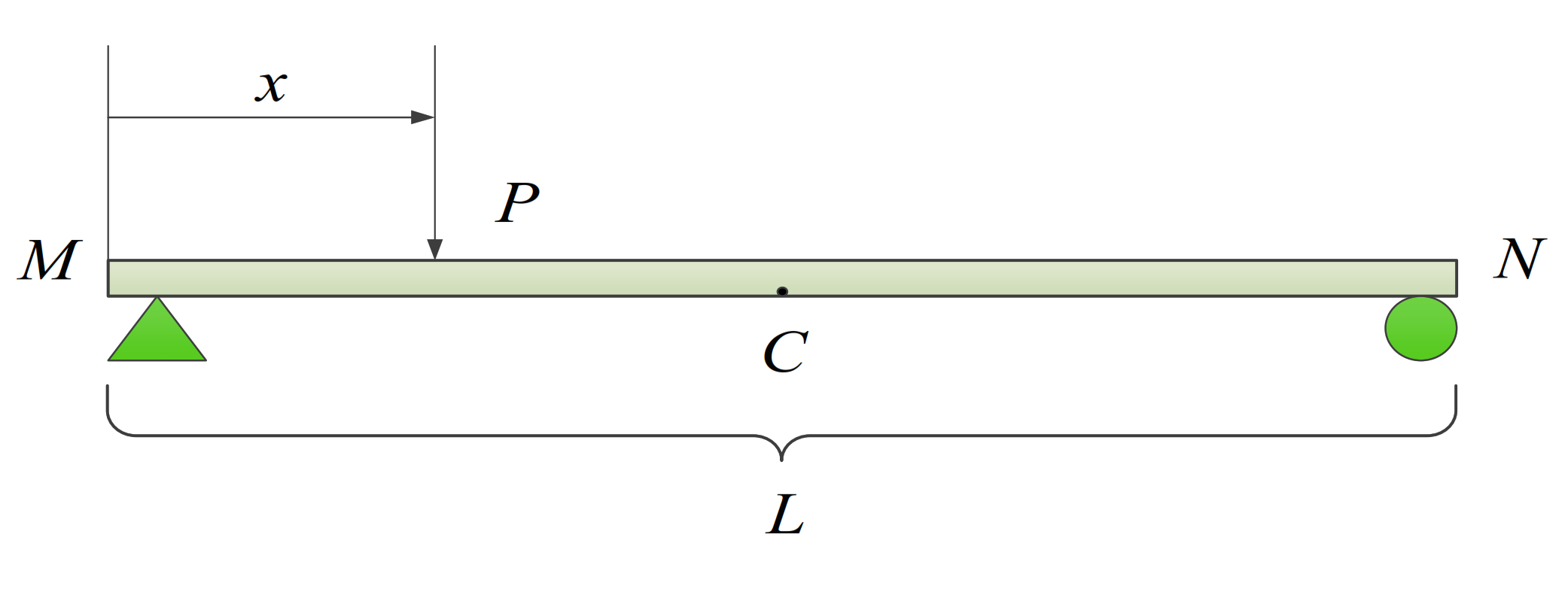
2.1. Identification Theory of Influence Lines
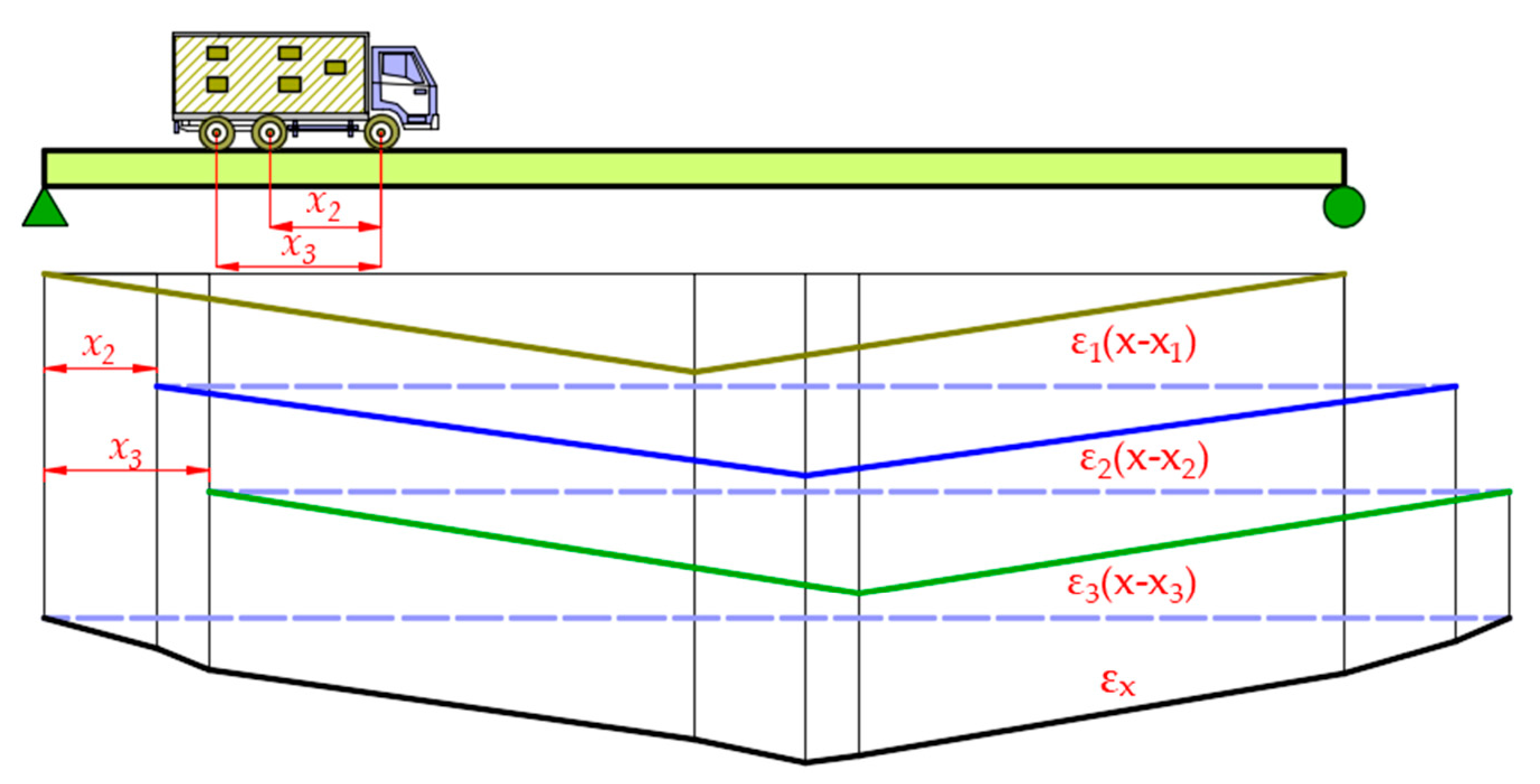
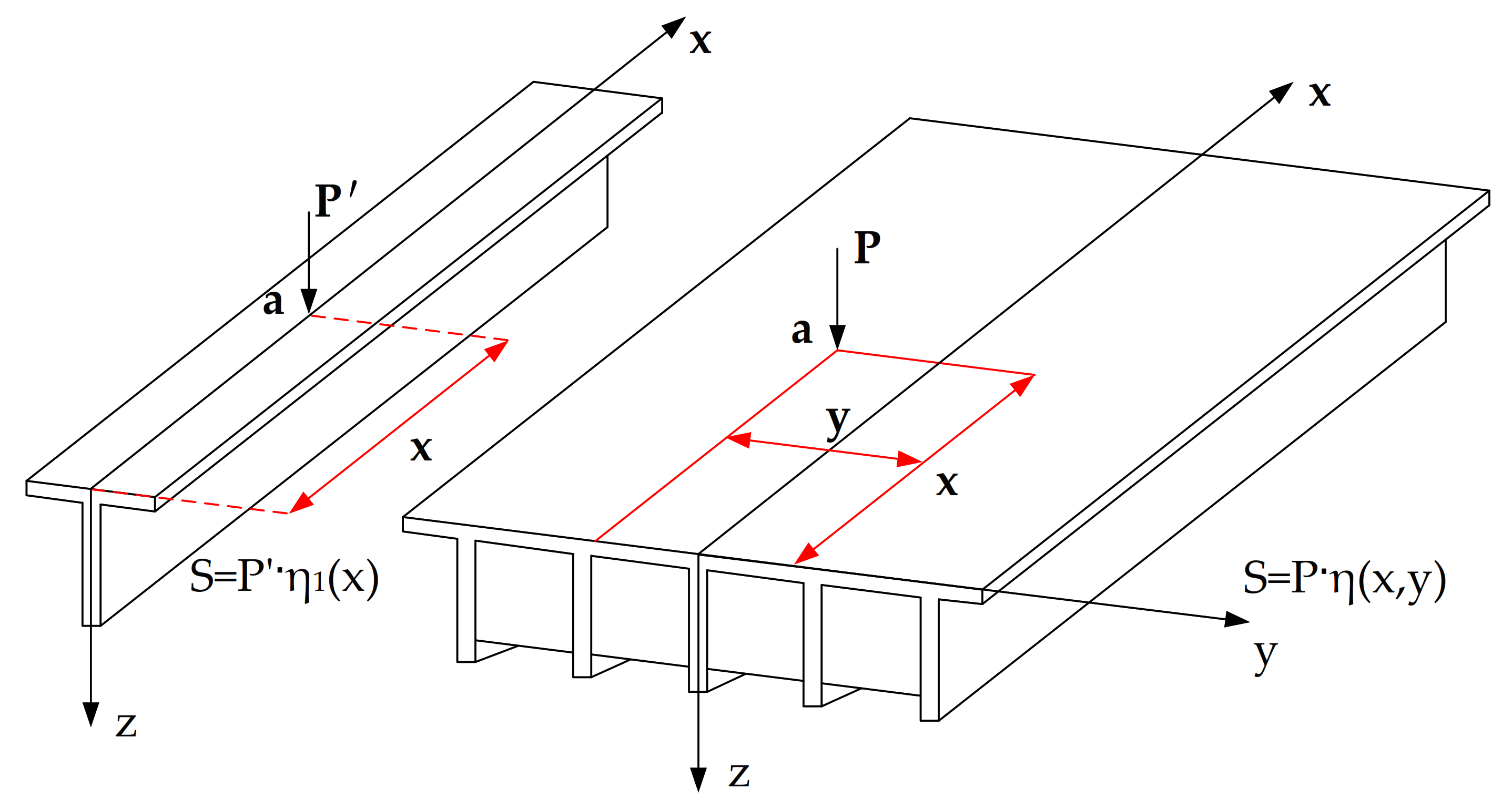
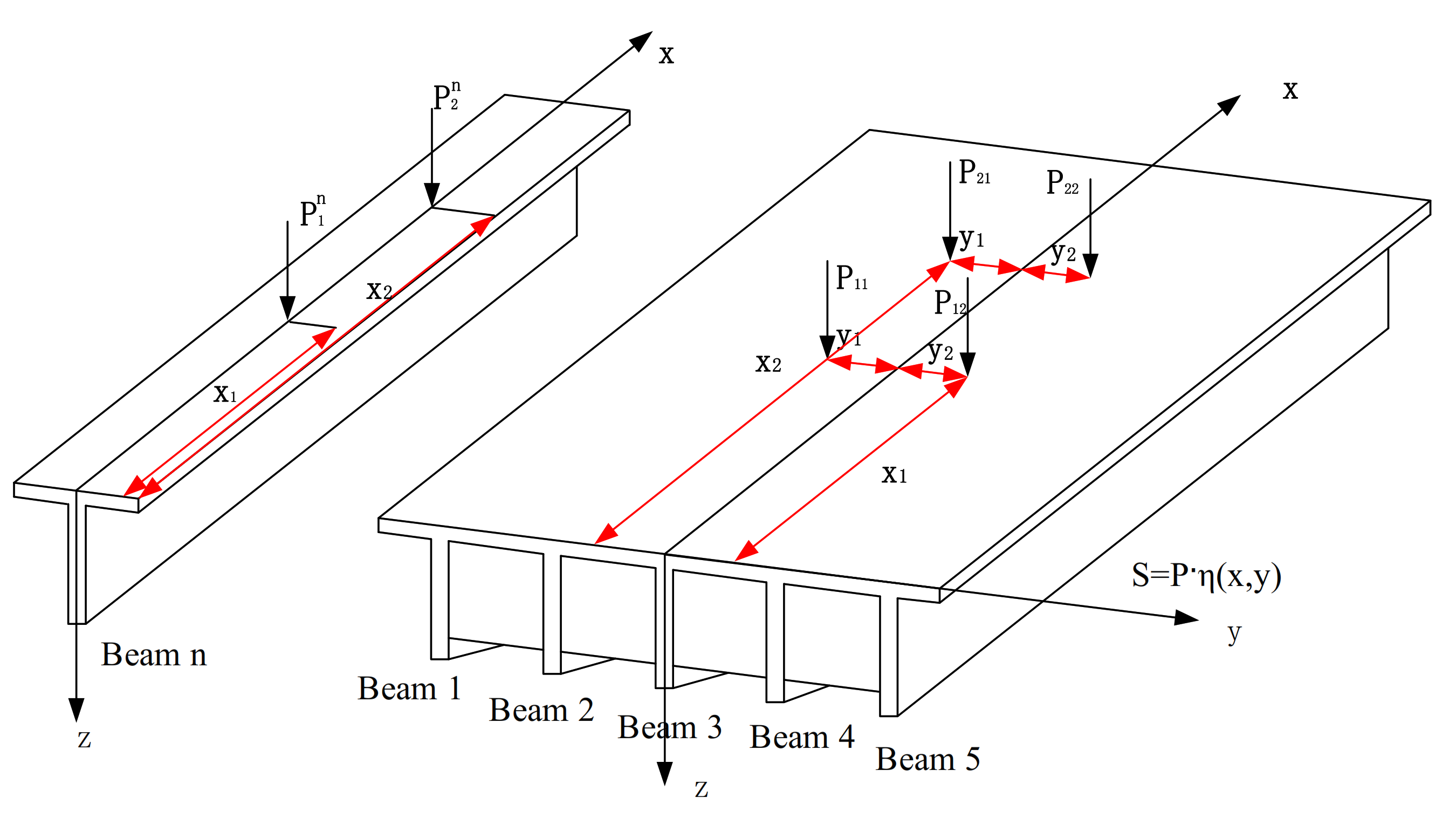
2.2. Moving Load Identification Method Considering the Load Transverse Distribution
3. Numerical Simulation
3.1. Model Building
3.2. Simulation Results Analysis
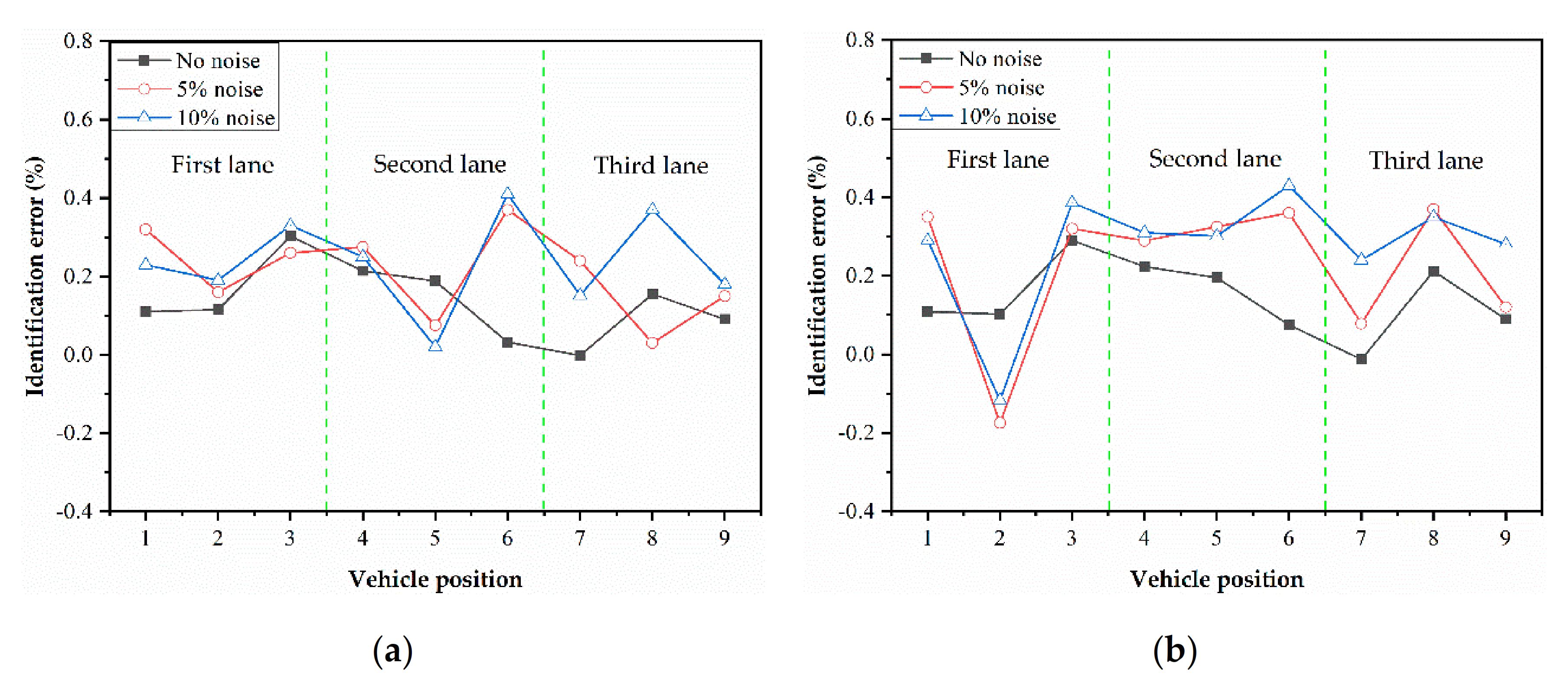
3.2.1. Analysis of the Identification Results without Considering the Load Transverse Distribution
3.2.2. Analysis of the Identification Results Considering the Load Transverse Distribution
3.2.3. Analysis of the Anti-Noise Performance
4. Verification by Experiment
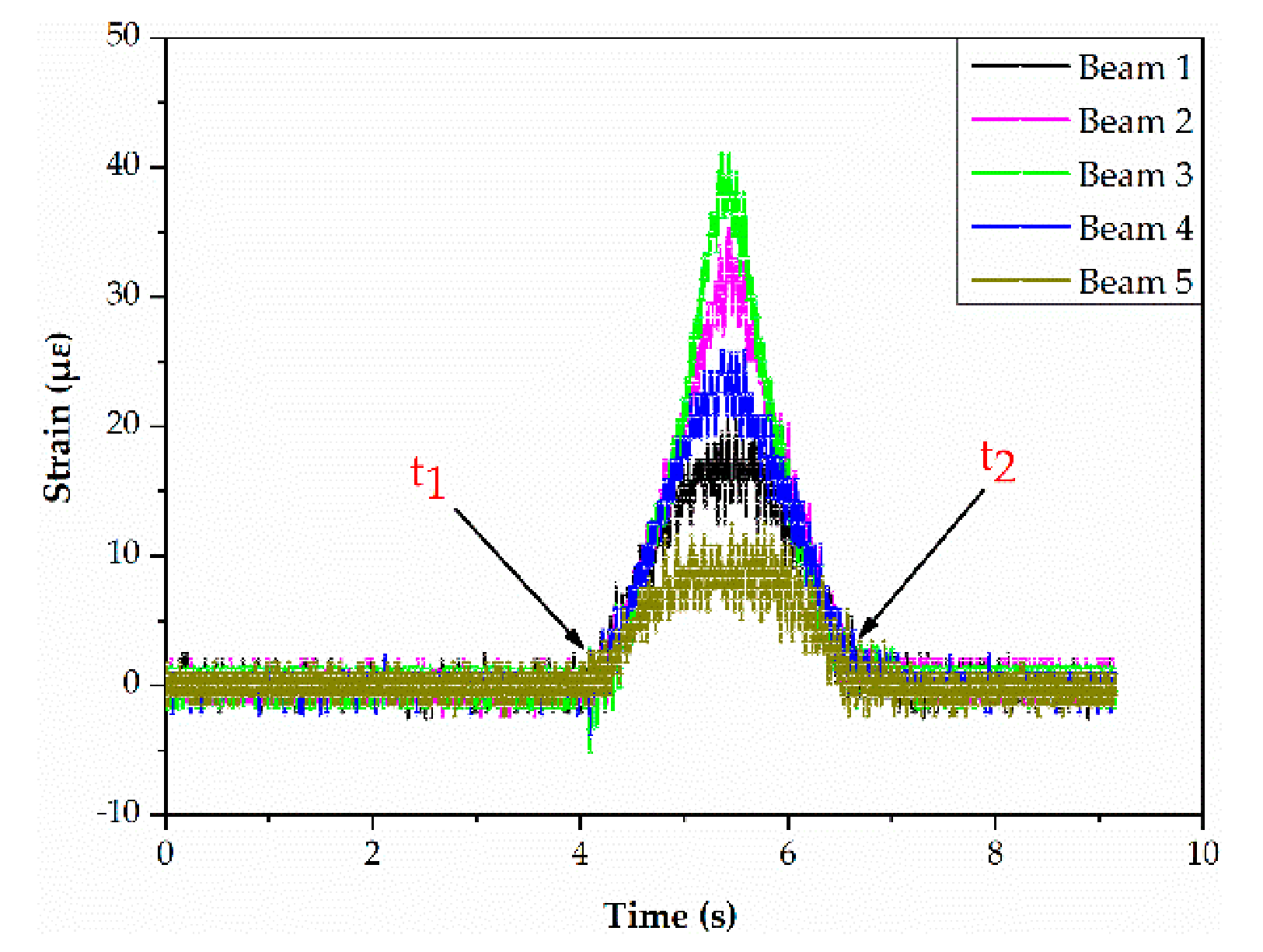
4.1. Experimental Setup
4.2. Analysis of Experiment Results
4.2.1. Speed Identification
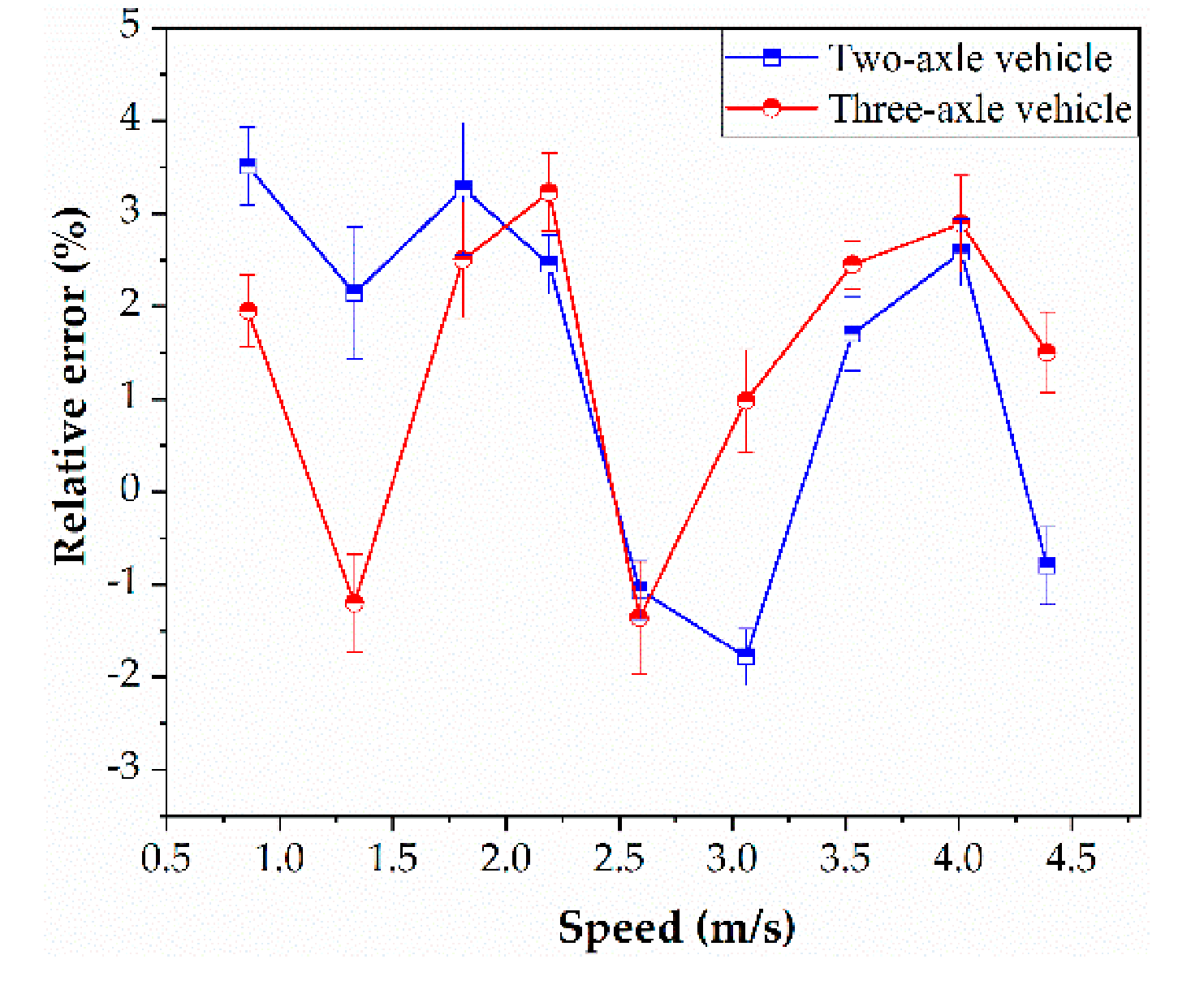
4.2.2. Influence of Speed on Load Identification
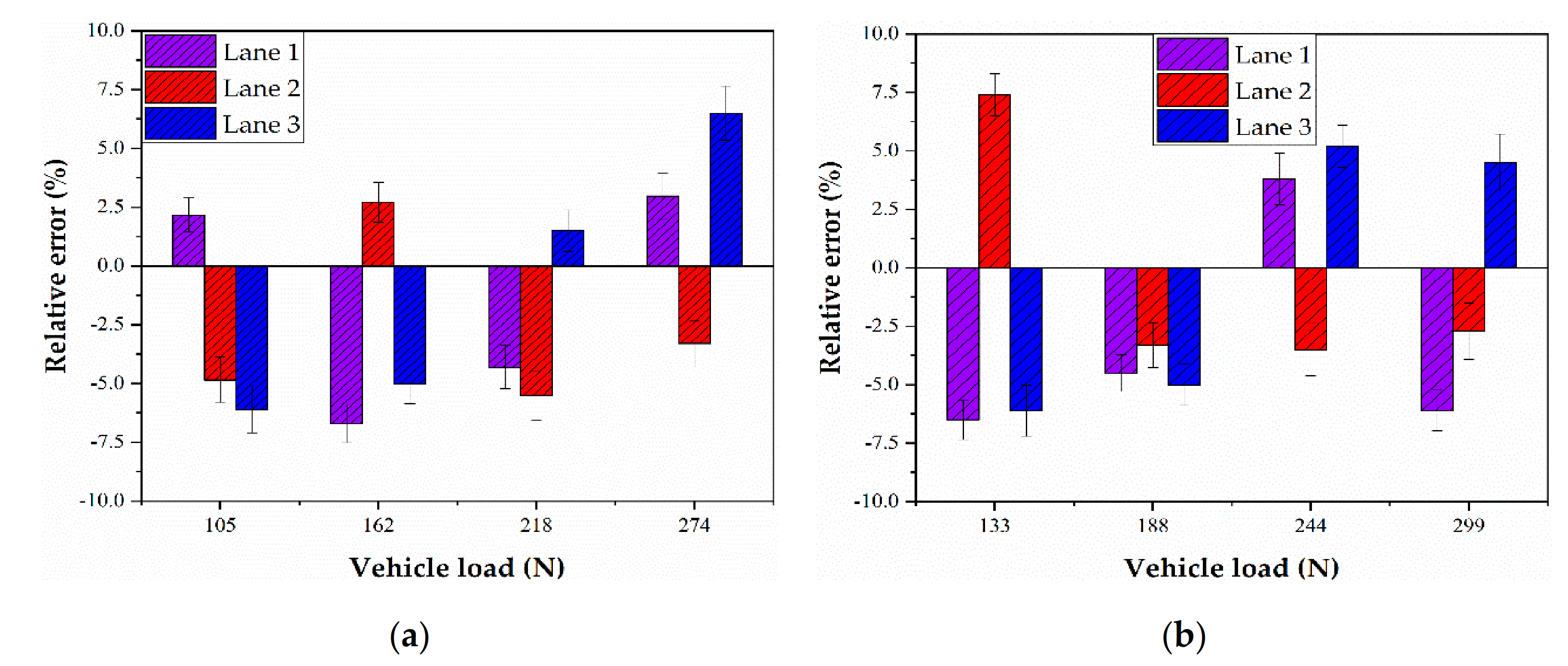
4.2.3. The Identification Results of Vehicle Weight
5. Conclusions
- Through the verification of numerical simulation, the method without considering the load transverse distribution was not suitable for solving the space problem, and the method considering the load transverse distribution has a high identification accuracy and excellent performance of anti-noise performance.
- The results of the model test showed that the average relative error of the speed identification was smaller than ±4%, which shows the great performance of the method.
- The speed has no obvious influence on the vehicle weight identification, and the average identification error was smaller than ±5%. In addition, it should be noted that the results obtained by using the actual speed to calculate the vehicle weight were more accurate than those obtained by using the inversion speed.
- The relative error of the vehicle weight identification was smaller than ±10%, and the error of more than 90% of samples was smaller than ±5%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.Z.; Wu, Z.S. Development of distributed long-gage fiber optic sensing system for structural health monitoring. Struct. Health Monit. 2007, 6, 133–143. [Google Scholar] [CrossRef]
- Cardini, A.J.; DeWolf, J.T. Long-term structural health monitoring of a multi-girder steel composite bridge using strain data. Struct. Health Monit. 2009, 8, 47–58. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W. Structural health monitoring of civil infrastructure. Philos. Trans. R. Soc. Lond. Ser. A 2007, 365, 589–622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wong, K.Y. Instrumentation and health monitoring of cable-supported bridges. Struct. Control Health Monit. 2004, 11, 91–124. [Google Scholar] [CrossRef]
- Li, H.N.; Li, D.S.; Song, G.B. Recent applications of fiber optic sensors to health monitoring in civil engineering. Eng. Struct. 2004, 26, 1647–1657. [Google Scholar] [CrossRef]
- Karoumi, R.; Wiberg, J.; Liljencrantz, A. Monitoring traffic loads and dynamic effects using an instrumented railway bridge. Eng. Struct. 2005, 27, 1813–1819. [Google Scholar] [CrossRef]
- Sekuła, K.; Kołakowski, P. Piezo-based weigh-in-motion system for the railway transport. Struct. Control Health Monit. 2012, 19, 199–215. [Google Scholar] [CrossRef]
- Kim, S.H.; Heo, W.H.; You, D. Vehicle loads for assessing the required load capacity considering the traffic environment. Appl. Sci. 2017, 7, 365. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.H.; Choi, J.G.; Ham, S.M. Reliability evaluation of a PSC highway bridge based on resistance capacity degradation due to a corrosive environment. Appl. Sci. 2016, 6, 423. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, J.; Caprani, C.C.; Padgett, J.E. Influence of traffic loading on the seismic reliability assessment of highway bridge structures. J. Bridge. Eng. 2014, 19, 04013009. [Google Scholar] [CrossRef]
- Pinkaew, T. Identification of vehicle axle loads from bridge responses using updated static component technique. Eng. Struct. 2006, 28, 1599–1608. [Google Scholar] [CrossRef]
- Han, L.D.; Ko, S.S.; Gu, Z.; Jeong, M.K. Adaptive weigh-inmotion algorithms for truck weight enforcement. Transp. Res. 2012, 24, 256–269. [Google Scholar]
- Richardson, J.; Jones, S.; Brown, A.; O’Brien, E.; Hajialzadeh, D. On the use of bridge weigh-in-motion for overweight truck enforcement. Int. J. Heavy Veh. Syst. 2014, 21, 83–104. [Google Scholar] [CrossRef]
- Yu, Y.; Cai, C.S.; Deng, L. State-of-the-art review on bridge weigh-in-motion technology. Adv. Struct. Eng. 2016, 19, 1514–1530. [Google Scholar] [CrossRef]
- Bajwa, R.; Coleri, E.; Rajagopal, R.; Varaiya, P.; Flores, C. Development of a cost-effective wireless vibration weigh-in-motion system to estimate axle weights of trucks. Comput. Aided Civ. Inf. Eng. 2017, 32, 443–457. [Google Scholar] [CrossRef]
- Zolghadri, N.; Halling, M.; Johnson, N.; Barr, P. Field verification of simplified bridge weigh-in-motion techniques. J. Bridge. Eng. 2016, 21, 04016063. [Google Scholar] [CrossRef]
- Ojio, T.; Carey, C.; Obrien, E.; Doherty, C.; Taylor, S.E. Contactless bridge weigh-in-motion. J. Bridge. Eng. 2016, 21, 04016032. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Uddin, N.; O’Brien, E.; Hao, X.S.; Zhu, P. Identification of vehicular axle weights with a bridge weigh-in-motion system considering transverse distribution of wheel loads. J. Bridge. Eng. 2014, 19, 04013008. [Google Scholar] [CrossRef] [Green Version]
- Helmi, K.; Taylor, T.; Ansari, F. Shear force based method and application for real-time monitoring of moving vehicle weights on bridges. J. Intell. Mater. Syst. Struct. 2015, 26, 505–516. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Law, S.S. Practical aspects in moving load identification. J. Sound Vib. 2002, 258, 123–146. [Google Scholar] [CrossRef]
- Yang, H.; Yan, W.; He, H. Parameters Identification of Moving Load Using ANN and Dynamic Strain. Shock Vib. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Wang, Y.; Qu, W.L. Moving train loads identification on a continuous steel truss girder by using dynamic displacement influence line method. Int. J. Steel Struct. 2011, 11, 109–115. [Google Scholar] [CrossRef]
- Chen, S.Z.; Wu, G.; Feng, D.C.; Zhang, L. Development of a bridge weigh-in-motion system based on long-gauge fiber Bragg grating sensors. J. Bridge. Eng. 2018, 23, 04018063. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, G.; Li, H.; Chen, S. Synchronous Identification of Damage and Vehicle Load on Simply Supported Bridges Based on Long-Gauge Fiber Bragg Grating Sensors. J. Perform. Constr. Fac. 2020, 34, 04019097. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Q.; Li, J.; Mao, J.; Hu, S.; Zhao, X. Identification of moving train loads on railway bridge based on strain monitoring. Smart Struct. Syst. 2019, 23, 263–278. [Google Scholar]
- Yang, C.Q.; Yang, D.; He, Y.; Wu, Z.S.; Xia, Y.F.; Zhang, Y.F. Moving load identification of small and medium-sized bridges based on distributed optical fiber sensing. Int. J. Struct. Stab. Dyn. 2016, 16, 1640021. [Google Scholar] [CrossRef]
- Zuo, X.H.; He, W.Y.; Ren, W.X. Vehicle weight identification for a bridge with multi-T-girders based on load transverse distribution coefficient. Adv. Struct. Eng. 2019, 22, 3435–3443. [Google Scholar] [CrossRef]
- Ojio, T.; Yamada, K. Bridge weigh-in-motion systems using stringers of plate girder bridges. In Proceedings of the Third International Conference on Weigh-in-Motion (ICWIM3) Iowa State University, Ames, Orlando, FL, USA, 13–15 May 2002. [Google Scholar]
- O’Connor, C.; Chan, T.H.T. Dynamic wheel loads from bridge strains. J. Struct. Eng. 1988, 114, 1703–1723. [Google Scholar] [CrossRef]

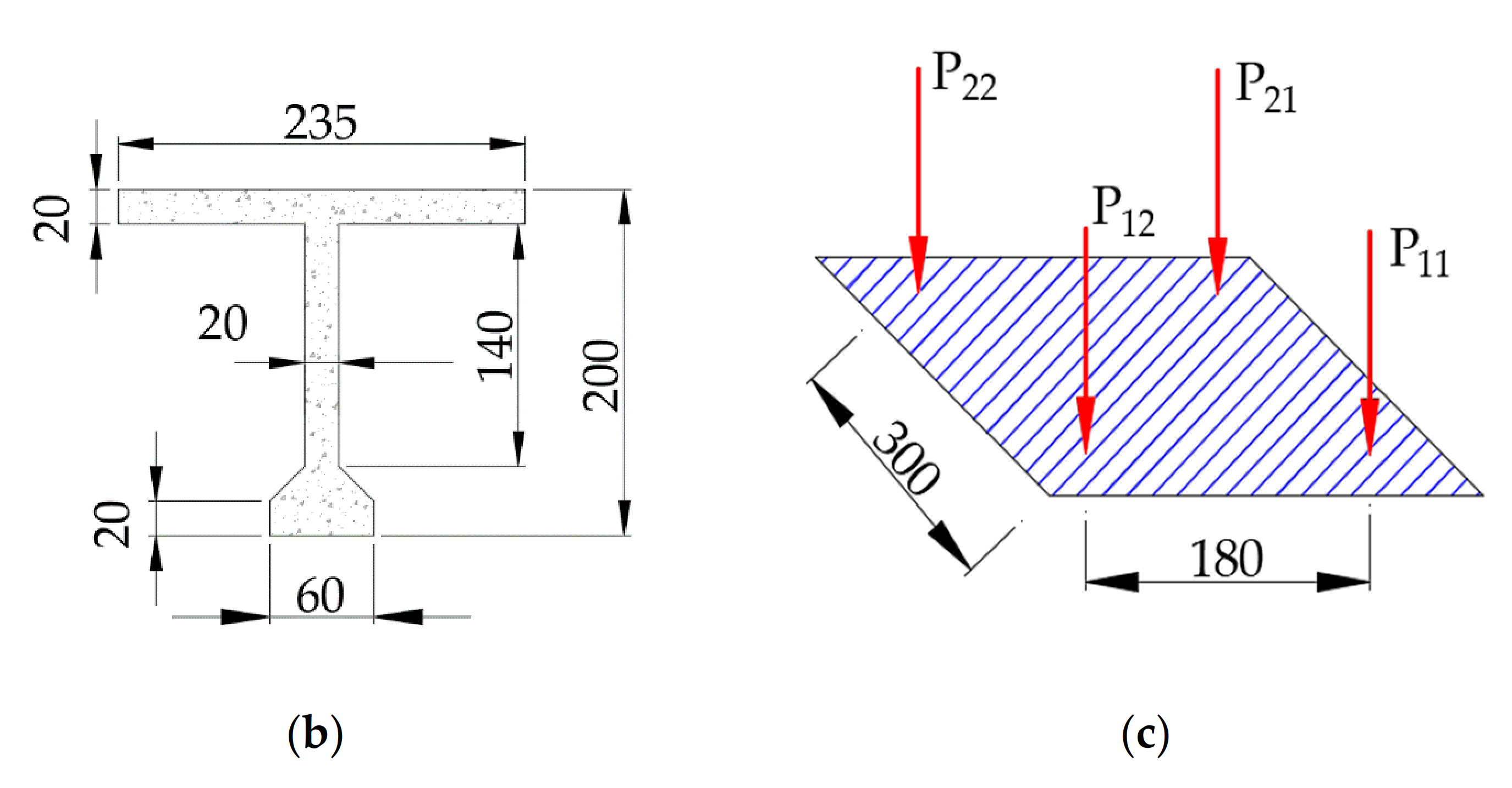
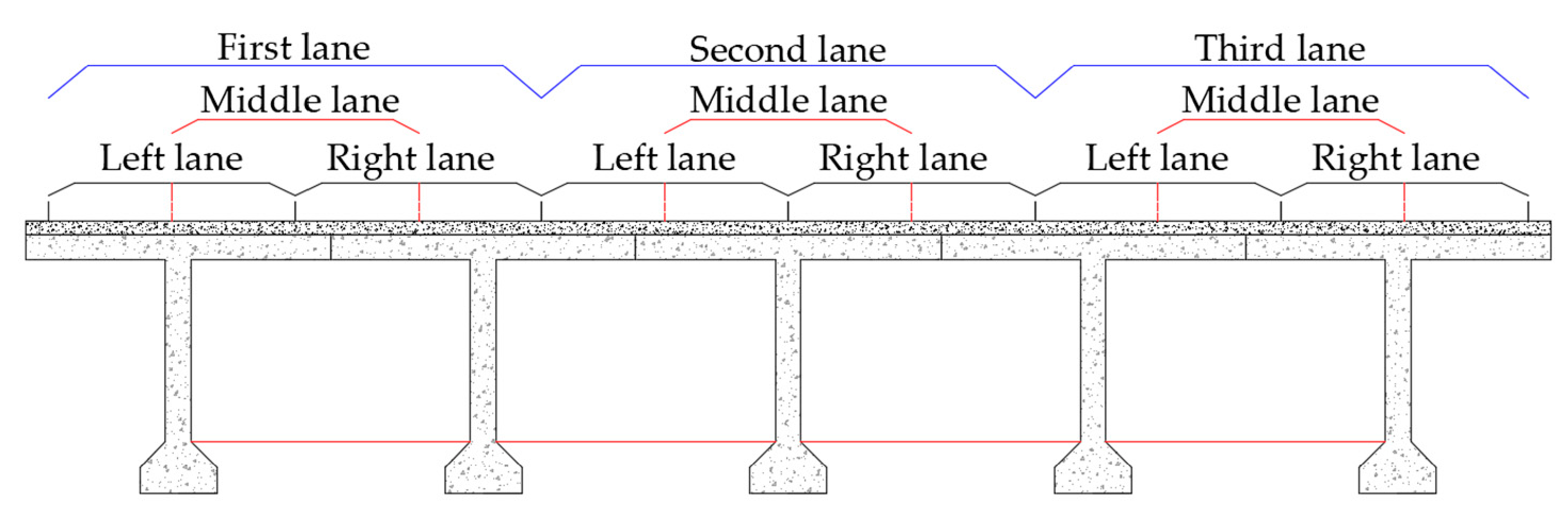


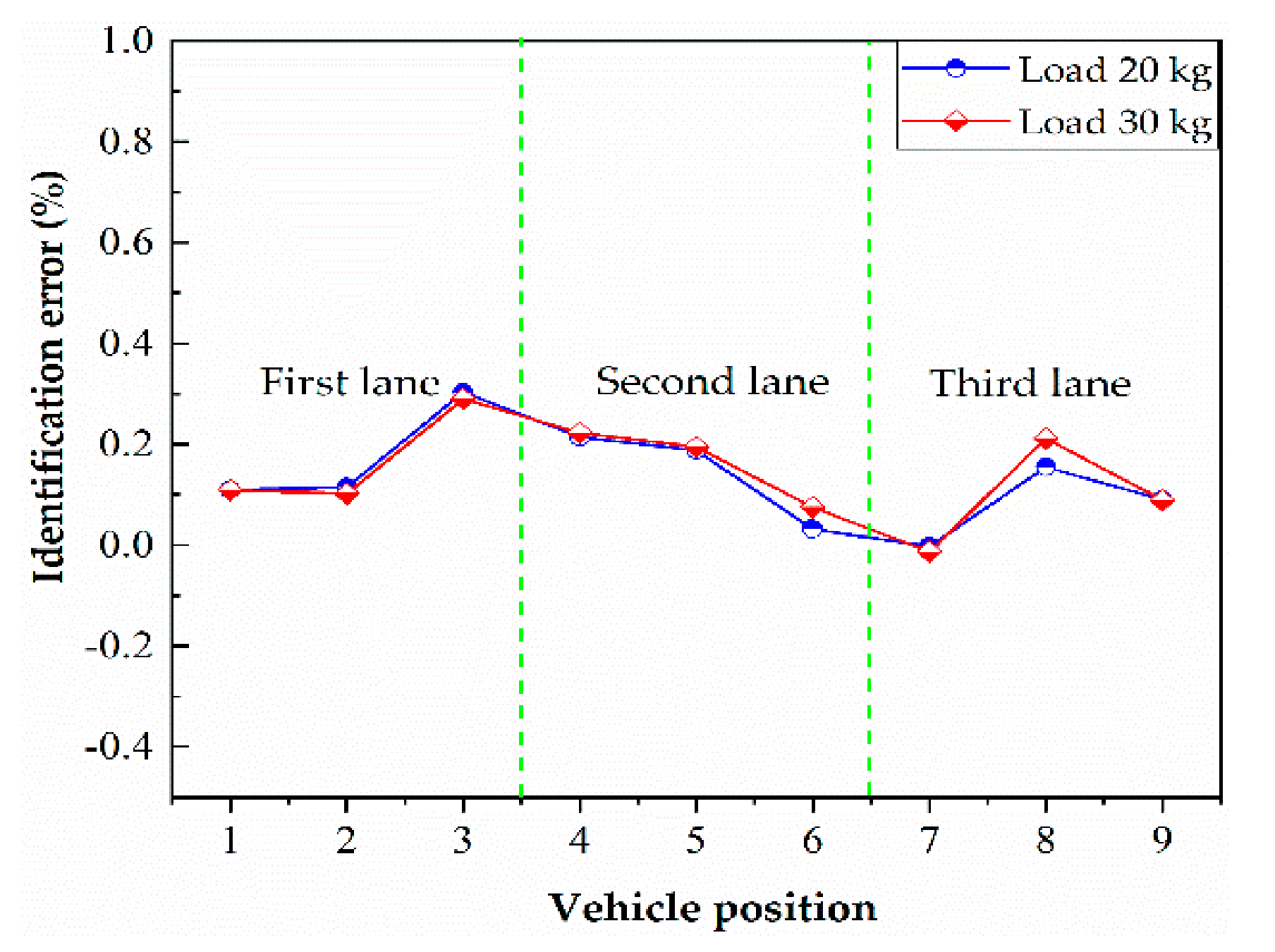
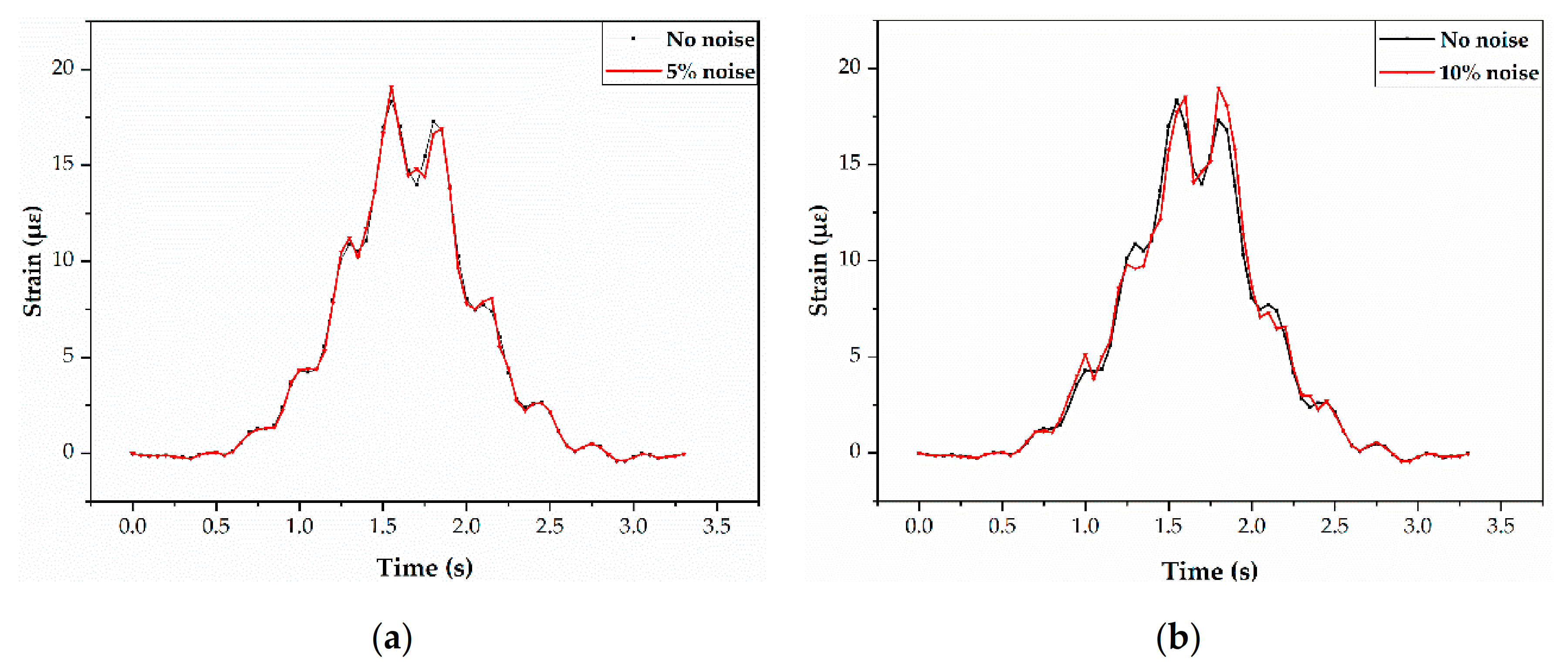



| Vehicle Driving Position | The Middle of the First Lane | The Middle of the Second Lane | The Middle of the Third Lane |
|---|---|---|---|
| Beam number | 1# | 3# | 5# |
| Total weight (kg) | 10 | 10 | 10 |
| The integral value of strain influence line (10−6 m) | 14.46 | 7.57 | 13.48 |
| Strain integral coefficient (10−8) | 14.75 | 7.73 | 13.75 |
| 1# Beam | 2# Beam | 3# Beam | 4# Beam | 5# Beam | |
|---|---|---|---|---|---|
| Strain integral coefficient (10−8) | 29.17 | 28.84 | 27.93 | 27.70 | 26.61 |
| Ratio to integral coefficient of 1# beam | 1 | 0.989 | 0.957 | 0.949 | 0.912 |
| Ratio to reciprocal 1# beam stiffness | 1 | 0.980 | 0.952 | 0.936 | 0.910 |
| Vehicle Speed (m/s) | 0.86 | 1.33 | 1.81 | 2.19 | 2.59 | 3.06 | 3.53 | 4.01 | 4.39 |
| 1# Beam | 2# Beam | 3# Beam | 4# Beam | 5# Beam | |
|---|---|---|---|---|---|
| The strain integral coefficient (10−7) | 8.11 | 8.33 | 8.04 | 7.23 | 7.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Hou, P.; Yang, C.; Zhang, Y. Study on the Method of Moving Load Identification Based on Strain Influence Line. Appl. Sci. 2021, 11, 853. https://doi.org/10.3390/app11020853
Yang J, Hou P, Yang C, Zhang Y. Study on the Method of Moving Load Identification Based on Strain Influence Line. Applied Sciences. 2021; 11(2):853. https://doi.org/10.3390/app11020853
Chicago/Turabian StyleYang, Jing, Peng Hou, Caiqian Yang, and Yang Zhang. 2021. "Study on the Method of Moving Load Identification Based on Strain Influence Line" Applied Sciences 11, no. 2: 853. https://doi.org/10.3390/app11020853





