Separation of Two-Dimensional Mixed Circular Fringe Patterns Based on Spectral Projection Property in Fractional Fourier Transform Domain
Abstract
:1. Introduction
2. Circular Fringe Pattern and Their Applications
3. Proposed Method
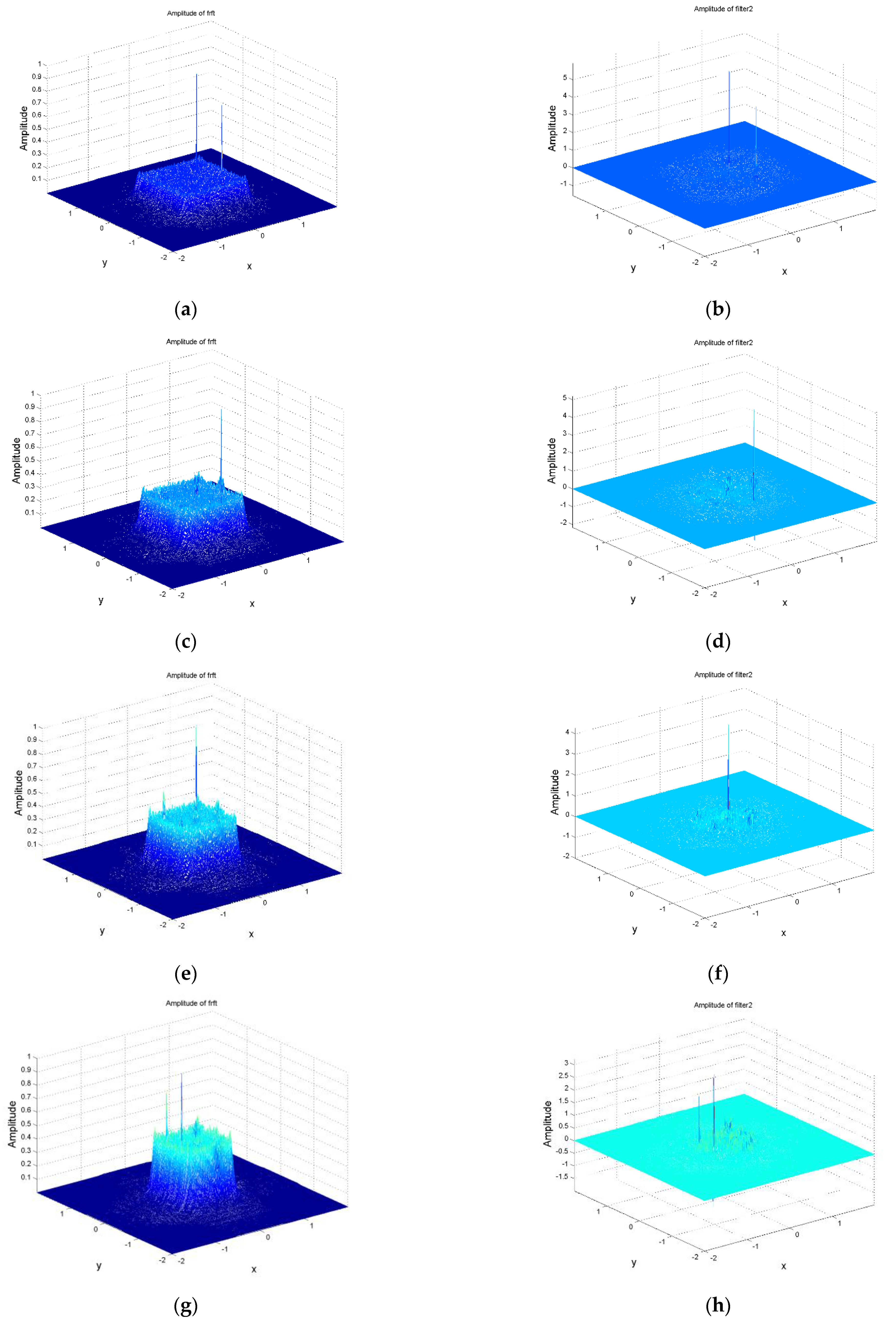
- First, given an image of size N by N, which consists of mixed multiple 2-D fringe patterns, we apply the 2-D FrFTs to the whole image with the fractional orders of the range within [0.1] with the increment step 0.01 in either the x or y direction. When we perform the FrFTs in the x-direction, the order in the y-direction is fixed as 1;
- The orders with the maximum projection in the x-direction of the signal are calculated and recorded;
- Then, we perform the FrFTs in the y-direction and, similarly, the order in the x-direction is fixed as 1;
- The orders with the maximum projection in the y-direction of the signal are calculated and recorded as well;
- We calculate the orders of maximum projection, αx and αy, from the local maximum values of fractional Fourier spectra through a differential operation. Then, the set of best orders, αbest, and the number of the paired orders in the set, M, can be determined by finding the intersections of the maximum projection orders and . Equations (8) and (9) show the definitions of the maximal projection orders for the x and y directions, respectively.Here, we have assumed that the fractional orders of and should be identical in the FrFT. Therefore, the maximum width of for each fringe pattern, a, can be determined based on the best order αbest by using Equation (6).
- By enumerating their absolute values and normalizing the transformed results Fr(u,v), we deal with it by using a filter mask and searching the peak-value position in the filtered results. The filter mask is of size 3 × 3 and its weighting coefficients are [−1 −1 −1; −1 8 −1; −1 −1 −1]. The filtered image result is denoted as G(u,v) and its maximum gmax is then determined. Through setting up a threshold value T between 0 and 1, we can get a binary map gbw from the filtered transformed result by using the criterion shown in Equation (10)In this binary map, we consider the neighboring area near the pixel value 1 as the same fringe pattern by searching the 8-connected positions.
- The original signal is FrFTed with the best order, αbest, to calculate the center position of a specific circular fringe pattern. If the positions (um, vm) of the kf maximal values in the binary map derived from the filtered fractional Fourier spectra G(u,v) are detected, it means that we can separate kf fringe patterns from the original mixture signal;
- The center points (x0, y0) in each corresponding circular fringe pattern can be determined according to Equation (11)
- After calculating the center points and maximum widths of the kf fringe patterns, we can reconstruct kf fringe patterns separately. For the cases of the fringe patterns with only 180° phase difference, the reconstructed signals, sk1, and sk2 (from the signal sk1) are generated by using Equation (3) with and , respectively;
- The correlation coefficients (CCs) between the original and reconstructed signals, sk1, and sk2, are denoted as cork1 and cork2 for all the kf reconstructed fringe patterns, respectively. The CC value r between the two 2-D fringe patterns X(i, j) and Y(i, j) of size N by N is defined in Equation (12), which is used to measure the similarity between the reconstructed and original signals.Note that and represent the average values of X(i, j) and Y(i, j), respectively.
- By comparing the CC values of cork1 and cork2, we can determine the constant phase shift denoted in Equation (3). That is, we select the reconstructed signal that has a larger CC value than the other one;
- Finally, all the kf separated fringe patterns can be solely reconstructed and the accuracy of each reconstructed fringe pattern can be evaluated by using the CC values.
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pei, S.-C.; Yeh, M.-H. Two dimensional discrete fractional Fourier transform. Signal Process. 1998, 67, 99–108. [Google Scholar] [CrossRef]
- Sejdić, E.; Djurović, I.; Stanković, L. Fractional Fourier transform as a signal processing tool: An overview of recent developments. Signal Process. 2011, 91, 1351–1369. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.-C. Study on Multiple Signal Separation by Using Fractional Fourier Transform. Master’s Thesis, National Yunlin University of Science and Technology, Yunlin, Taiwan, June 2012. [Google Scholar]
- Cowell, D.M.J.; Freear, S. Separation of overlapping linear frequency modulated (LFM) signals using the fractional Fourier transform. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2324–2333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roshen, J.; Tessamma, T.; Unnikrishnan, A. Applications of fractional Fourier transform in sonar signal processing. IETE J. Res. 2009, 55, 16–27. [Google Scholar] [CrossRef]
- Capus, C.; Brown, K. Fractional Fourier transform of the Gaussian and fractional domain signal support. IEEE Proc. Vis. Image Signal Process. 2003, 150, 99–106. [Google Scholar] [CrossRef]
- Kutay, A.M.; Ozaktas, H.M. Optimal image restoration with the fractional Fourier transform. J. Opt. Soc. Am. A 1998, 15, 825–833. [Google Scholar] [CrossRef]
- Sahin, A.; Ozaktas, H.M.; Mendlovic, D. Optical implementation of the two-dimensional fractional Fourier transform with different orders in the two dimensions. Opt. Commun. 1995, 120, 134–138. [Google Scholar] [CrossRef]
- Chang, H.T.; Peng, H.-W.; Lai, H.-L. 2-D Linear frequency modulation signal separation using fractional Fourier transform. In Proceedings of the IEEE Third International Symposium on Computer, Consumer and Control (IS3C), Xi’an, China, 4–6 July 2016; pp. 755–758. [Google Scholar] [CrossRef]
- Qian, K. Two-dimensional windowed Fourier transform for fringe pattern analysis: Principles, applications and implementations. Opt. Lasers Eng. 2007, 45, 304–317. [Google Scholar] [CrossRef]
- Trusiak, M.; Patorski, K.; Wielgus, M. Hilbert-Huang processing and analysis of complex fringe patterns. In Proceedings of the Interferometry XVII: Techniques and Analysis, San Diego, CA, USA, 18 August 2014; Volume 9203. [Google Scholar] [CrossRef]
- Pokorski, K.; Patorski, K. Separation of complex fringe patterns using 2-D continuous wavelet transform. Appl. Opt. 2012, 51, 8433–8439. [Google Scholar] [CrossRef] [PubMed]
- Lai, X.-L. Mixed Signal Separation by Using Fractional Fourier Transform and Short-Time Fourier Transform. Master’s Thesis, National Yunlin University of Science and Technology, Yunlin, Taiwan, June 2014. [Google Scholar]
- Trusiak, M.; Wielgus, M.; Patorski, K. Advanced processing of optical fringe patterns by automated selective reconstruction and enhanced fast empirical mode decomposition. Opt. Lasers Eng. 2014, 52, 230–240. [Google Scholar] [CrossRef]
- Lu, M.-F.; Zhang, F.; Tao, R.; Ni, G.-Q.; Bai, T.-Z.; Yang, W.-M. Parameter estimation of optical fringes with quadratic phase using the fractional Fourier transform. Opt. Lasers Eng. 2015, 74, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Sciammarella, C.A.; Lamberti, L. Mathematical models utilized in the retrieval of displacement information encoded in fringe patterns. Opt. Lasers Eng. 2016, 77, 100–111. [Google Scholar] [CrossRef]
- Wu, J.-M.; Lu, M.-F.; Tao, R.; Zhang, F.; Li, Y. Improved FRFT-based method for estimating the physical parameters from Newton’s rings. Opt. Lasers Eng. 2017, 91, 178–186. [Google Scholar] [CrossRef]
- Dong, Z.; Chen, Z. Advanced Fourier transform analysis method for phase retrieval from a single-shot spatial carrier fringe pattern. Opt. Lasers Eng. 2018, 107, 149–160. [Google Scholar] [CrossRef]
- Ratnam, M.; Saxena, M.; Gorthi, S.S. Circular fringe projection technique for out-of-plane deformation measurements. Opt. Lasers Eng. 2019, 121, 369–376. [Google Scholar] [CrossRef]
- Muñoz-Maciel, J.; Duran-Ramírez, V.M.; Mora-Gonzalez, M.; Casillas-Rodriguez, F.J.; Peña-Lecona, F.G. Demodulation of a single closed-fringe interferogram with symmetric wavefront and tilt. Opt. Commun. 2019, 436, 168–173. [Google Scholar] [CrossRef]
- Sciammarella, C.A.; Lamberti, L.; Sciammarella, F.M. The optical signal analysis (OSA) method to process fringe patterns containing displacement information. Opt. Lasers Eng. 2019, 115, 225–237. [Google Scholar] [CrossRef]
- Moré, I.; Cuevas, F.J.; Jiménez, J. Parallel Demodulation Algorithm for processing independent windows of a fringe patterns using Simulating Annealing. Opt. Commun. 2020, 463, 125403. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, L.-D. Chirp-Fourier transform for quadratic phase interference fringe analysis: Principles, method and application. Opt. Lasers Eng. 2020, 133, 106145. [Google Scholar] [CrossRef]
- Pokorski, K.; Patorski, K. Wavelet transform in fringe separation. In Proceedings of the 19th Polish-Slovak-Czech Optical Conference on Wave and Quantum Aspects of Contemporary Optics, Jelenia Gora, Poland, 5 December 2014; Volume 9441. [Google Scholar] [CrossRef]
- Trusiak, M.; Patorski, K. Two-shot fringe pattern phase-amplitude demodulation using Gram-Schmidt orthonormalization with Hilbert-Huang pre-filtering. Opt. Express 2015, 23, 4672–4690. [Google Scholar] [CrossRef] [PubMed]
- Patorski, K.; Trusiak, M. Chapter 12 Interferometric Methods in NDE. In Handbook of Advanced Nondestructive Evaluation; Ida, N., Meyendorf, N., Eds.; Springer Nature Switzerland AG: Basel, Switzerland, 2019. [Google Scholar] [CrossRef]










| Parameter | Result |
|---|---|
| αx | (0.14, 0.16, 0.18, 0.20, 0.22, 0.25, 0.37, 0.44, 0.51, 0.53, 0.73, 0.76, 0.76, 0.81) |
| αy | (0.73, 0.76, 0.79, 0.82) |
| αbest | (0.73, 0.76, 0.79, 0.82) |
| a | (45.39, 39.80, 34.42, 29.21) |
| Signal | Position of Original Signals | Position of Reconstructed Signals | Difference |
|---|---|---|---|
| (a) | (0.1, −0.2) | (0.095, −0.209) | (0.005, 0.009) |
| (b) | (1.6, −0.2) | (1.595, −0.209) | (0.005, 0.009) |
| (c) | (0.6, −1.6) | (0.594, −1.613) | (0.006, 0.013) |
| (d) | (1.2,1.2) | (1.206, 1.206) | (0.006, 0.006) |
| (e) | (−1.5, −0.8) | (−1.512, −0.812) | (0.012, 0.012) |
| (f) | (−1.3,1.0) | (−1.344, 1.008) | (0.044, 0.008) |
| Signal | Width of Original Signals | Width of Reconstructed Signals | Difference/Percentage | CC Value |
|---|---|---|---|---|
| (a) | 45 | 45.392 | 0.392/0.87% | 0.746 |
| (b) | 45 | 45.392 | 0.392/0.87% | 0.828 |
| (c) | 40 | 39.803 | 0.197/0.49% | 0.849 |
| (d) | 35 | 34.419 | 0.581/1.66% | 0.910 |
| (e) | 30 | 29.207 | 0.793/2.64% | 0.813 |
| (f) | 30 | 29.207 | 0.793/2.64% | 0.431 |
| Signal | Position of Original Signals | Position of Reconstructed Signals | Difference |
|---|---|---|---|
| (a) | (−0.7, −0.5) | (−0.710, −0.515) | (0.010, 0.015) |
| (b) | (0.1, −0.2) | (0.095, −0.209) | (0.005, 0.009) |
| (c) | (1.6, −0.2) | (1.595, −0.209) | (0.005, 0.006) |
| (d) | (−0.3, 1.5) | (−0.297, 1.486) | (0.003, 0.014) |
| (e) | (0.6, −1.6) | (0.594, −1.613) | (0.006, 0.013) |
| (f) | (1.2, 1.2) | (1.206, 1.206) | (0.006, 0.006) |
| (g) | (−1.5, −0.8) | (−1.540, −0.812) | (0.040, 0.012) |
| (h) | (−1.3, 1.0) | (−1.344, 1.008) | (0.044, 0.008) |
| Signal | Width of Original Signals | Width of Reconstructed Signals | Difference/Percentage | CC Value |
|---|---|---|---|---|
| (a) | 50 | 49.250 | 0.750/1.50% | 0.497 |
| (b) | 45 | 45.392 | 0.392/0.87% | 0.746 |
| (c) | 45 | 45.392 | 0.392/0.87% | 0.828 |
| (d) | 40 | 39.803 | 0.197/0.49% | 0.705 |
| (e) | 40 | 39.803 | 0.197/0.49% | 0.849 |
| (f) | 35 | 34.419 | 0.581/1.66% | 0.910 |
| (g) | 30 | 29.207 | 0.793/2.64% | 0.571 |
| (h) | 30 | 29.207 | 0.793/2.64% | 0.431 |
| SNR (dB) | Number of Detected Fringe Patterns | CC Values of Separated Fringe Patterns | |||||
|---|---|---|---|---|---|---|---|
| No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No. 6 | ||
| 1 | 4 | 0.746 | 0.828 | 0.849 | 0.910 | NA | NA |
| 2 | 3 | 0.746 | 0.828 | 0.849 | NA | NA | NA |
| 3 | 3 | 0.746 | 0.828 | NA | 0.910 | NA | NA |
| 4 | 7 | 0.746 | 0.828 | 0.849 | 0.910 | 0.813 | 0.430 |
| 5 | 6 | 0.746 | 0.828 | 0.849 | 0.910 | −0.009 | 0.004 |
| 6 | 5 | 0.746 | 0.828 | 0.849 | 0.910 | NA | 0.430 |
| 7 | 6 | 0.746 | 0.828 | 0.849 | 0.910 | 0.813 | 0.430 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.-T.; Lin, T.-Y.; Chuang, C.-H.; Chen, C.-Y.; Ho, C.C.; Chang, C.-Y. Separation of Two-Dimensional Mixed Circular Fringe Patterns Based on Spectral Projection Property in Fractional Fourier Transform Domain. Appl. Sci. 2021, 11, 859. https://doi.org/10.3390/app11020859
Chang H-T, Lin T-Y, Chuang C-H, Chen C-Y, Ho CC, Chang C-Y. Separation of Two-Dimensional Mixed Circular Fringe Patterns Based on Spectral Projection Property in Fractional Fourier Transform Domain. Applied Sciences. 2021; 11(2):859. https://doi.org/10.3390/app11020859
Chicago/Turabian StyleChang, Hsuan-Ting, Tzu-Yao Lin, Chih-Hao Chuang, Chien-Yu Chen, Chian C. Ho, and Chuan-Yu Chang. 2021. "Separation of Two-Dimensional Mixed Circular Fringe Patterns Based on Spectral Projection Property in Fractional Fourier Transform Domain" Applied Sciences 11, no. 2: 859. https://doi.org/10.3390/app11020859
APA StyleChang, H.-T., Lin, T.-Y., Chuang, C.-H., Chen, C.-Y., Ho, C. C., & Chang, C.-Y. (2021). Separation of Two-Dimensional Mixed Circular Fringe Patterns Based on Spectral Projection Property in Fractional Fourier Transform Domain. Applied Sciences, 11(2), 859. https://doi.org/10.3390/app11020859







