Fundamental Investigations on the Performance of Micro Steel Fibres in Ultra-High-Performance Concrete under Monotonic and Cyclic Tensile Loading

Abstract

Ultra-high-performance fibre-reinforced concrete (UHPFRC) can preferably be used for lean and thin-walled structures due to its very high compressive strength. Based on the adverse relation between the increased load bearing capacities and the condensed dead weight of UHPFRC-structures, the impact of live loads in the design gets bigger and, in case of traffic loads, the effects of a cyclic loading have to be considered in more detail. In this context, this study investigated the material behaviour of UHPFRC, especially the tensile fatigue behaviour of high-strength micro steel fibres and the bond behaviour between those fibres and plain UHPC. The test programme included once tensile tests of high-strength micro steel fibres under monotonic and cyclic loading. Based on the test results, an S/N-curve was set up with the characteristic values. Furthermore, the test programme included pullout tests of fibre groups with different embedded lengths and orientations under monotonic and cyclic loading. It was observed that some fibres rupture under certain test configurations like the angle of orientation and the load amplitude.

1. Introduction

Ultra-high-performance concrete (UHPC) offers enormous possibilities in relation to thin-walled, light, and filigree concrete constructions. Thus, UHPFRC concrete constructions have substantial advantages over conventional reinforced concrete constructions when considering important ecological aspects like saving of material, resource efficiency, and sustainability, as well as the load bearing capacities.

Due to the very brittle failure of plain UHPC under tensile and compressive loading, recent research projects (e.g., [1,2]) as well as several European standards (Swiss SIA [3], French national additions to Eurocode 2 [4]) recommend a fibre reinforcement in UHPC-components, leading to ultra-high-performance fibre-reinforced concrete (UHPFRC). UHPFRC usually requires high steel fibre contents (up to 250 kg/m³) to provide a ductile failure mechanism. Besides the pure addition of steel fibres and in regard to the aforementioned ecological aspects, the design and the performance of micro steel fibres in UHPFRC under monotonic and cyclic tensile loading is of great importance.

The fatigue behaviour of a material is quite complex. High-strength micro steel fibres embedded in UHPC provide a ductile failure mode under monotonic loading. However, the effect of cyclic loading might be rupture, which leads to sudden failure of the components.

Fahrat [5] ran tests on UHPFRC beams under bending with an almost fibre-free tension zone. He found that the fatigue strength under cyclic loading decreases considerably after only a few load cycles and is clearly below the “static” strength.

Graybeal [6] investigated the flexural fatigue behaviour of un-cracked UHPFRC-specimens under cyclic loading and ascertained that the fatigue strength of the concrete matrix is in the lower scatter range of the “static” strength. In contrast, Behloul [7] observed a positive fatigue behaviour of cracked UHPFRC influenced by steel fibres.

Graybeal [6], Abrahimsof [8], Cao [9], McSwain [10], and Wille [11] investigated the pullout behaviour of embedded fibres in UHPC more fundamentally. The test programmes consisted of fibre pullout tests of embedded UHPC under monotonic loading with varying steel fibre geometries, UHPC-properties, and number of fibres. All tests showed a continuous fibre pullout. Makita [12], Graybeal [6], Lappa [13], and Bornemann [14] also observed continuous fibre pullout but under cyclic tensile loading. However, these observations rest upon UHPFRC-specimens with a 3-D fibre orientation and not upon pullout tests.

Beyond this, Graybeal [6] also recognised fibre rupture under cyclic loading during the test’s execution. Actually, the geometric design of steel fibres and the high tensile strength always provide continuous fibre pullout. The bond stress between the fibre and UHPC must have been so high that fatigue failure of the steel fibre material occurred un-der the cyclic loading.

As part of a tandem research project funded by the German Research Foundation under the Priority Program 2020 (Ger. SPP 2020), various damage processes in UHPFRC under monotonic and cyclic tensile loading were investigated at the iBMB, Division of Concrete Construction of TU Braunschweig. The following article reports the experimental and theoretical investigations.

2. Fibre Design Philosophy

Under compressive loading, concrete usually fails and is quite brittle. Besides conventional reinforcing, which leads to a more ductile failure mode, fibre reinforcement might also be an option to prevent concrete components from sudden failure. Steel fibres are the most common material in terms of fibre reinforcement. The design of steel fibres rests upon the material properties of the concrete (i.e., the bond behaviour) and the fibre material (i.e., the tensile strength) itself. Besides the better compressive behaviour of fibre-reinforced concrete, fibre reinforcement leads to a post-cracking tensile strength that might be considered in terms of tensile loading.

Ultra-high-performance concrete with a compressive strength of more than 150 N/mm² usually requires very high fibre contents, leading to a relatively high post-cracking tensile strength. The design of UHPC-suited high-strength micro steel fibres, i.e., the geometry and the tensile strength, should lead to fibre pullout instead of fibre rupture under tensile loading. Therefore, the fibre material’s tensile strength has to be higher than the bond strength between the micro steel fibre and UHPC.

Under short-term static loading, in most UHPFRC components under bending, shear, and torsion, the desired fibre pullout always occurs [6,15,16].

As weight-reduced UHPFRC structures are more susceptible to fatigue, the performance of micro steel fibres under cyclic loading has to be considered additionally. Here, the occurrence of the desired fibre pullout is not entirely clear yet. Makita [12] assumed that cyclic loading causes fibre pullout under the top load and slips back into the concrete channel by elastic rebound under the bottom load. The cyclic pulling out and slipping back abrades the fibre’s surface. After a certain number of load cycles, the abrasion progresses so far, and there is no longer any “bond”; thus, the fibres pull out of the concrete matrix. Furthermore, it might also be possible that a so-called “tribocorrosion” (the combination of wear and corrosion) of fibres in the crack area occurs. This combination might lead to a faster decreasing cross-sectional area of the fibre, and an unexpected material failure might happen.

3. Investigation Strategy

The experimental program was consecutively structured with fundamental investigations of all components of UHPFRC, i.e.,

• Micro steel fibre (“bare”)—part 1.
• Plain UHPC—part 2.
• UHPC–fibre interaction of single fibres and fibre groups—parts 3 and 4.
• Tensile tests on small UHPFRC samples—part 5.

Figure 1 shows the chronological order of the test programme.

The investigations aimed to extend the understanding of the monotonic and fatigue behaviour of UHPFRC by isolated observations of its components. The study of [15] contains the investigations of the plain UHPC (part 2) as well as the UHPC–fibre interaction of single fibres (part 3). The tensile tests on small UHPFRC samples (part 5) will be the topic of a later article.

4. Experimental Program

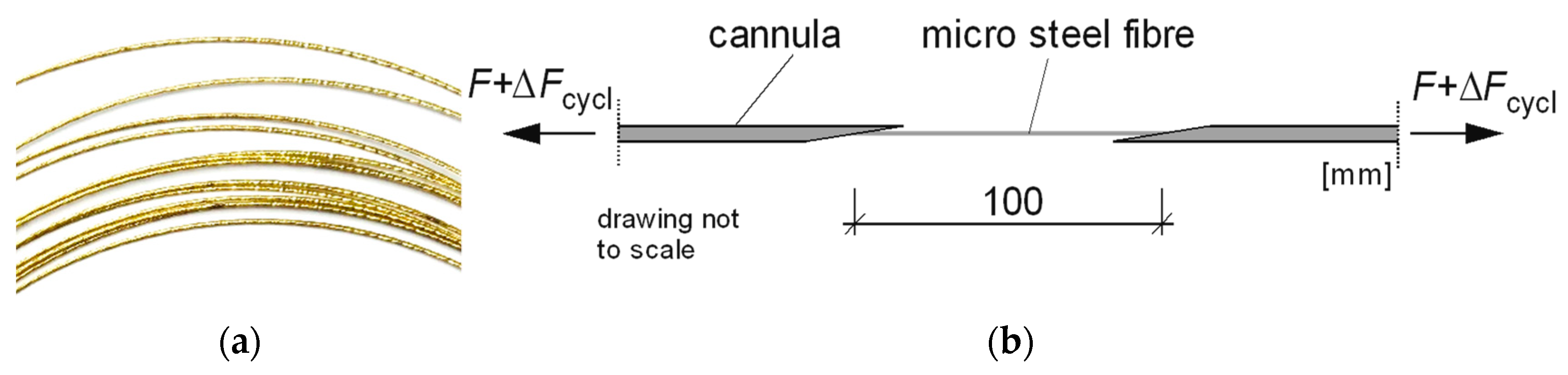
4.1. Test Specimen and Test Configuration

The experimental investigations in this research part (“bare” steel fibre, Figure 1) included monotonic and cyclic loaded tensile tests of high-strength micro steel fibres suitable for UHPFRC. Two types of micro steel fibres were investigated under monotonic loading: one with a diameter of 0.19 mm (VFS-A) and another with a diameter of 0.13 mm (VFS-B).

According to the manufacturer’s specifications, both fibres show similar properties like a brass coating, a young’s modulus of 200,000 N/mm², and a tensile strength of more than 2200 N/mm². The only mechanical difference between the fibres is the diameter. The authors of [15] give further detailed information regarding the high-strength micro steel fibre.

Due to the steel’s fibre filigree character (0.19 mm and 0.13 mm) and the short length (13 mm and 6 mm), it was challenging to perform the tensile tests, especially for cyclic loading. In terms of pilot tests, clamping the bare steel fibre directly into the jaws of a testing machine led to high transverse pressure on the fibre’s surface. The clamping jaws damaged the fibre considerably, and a following examination of the surface near the crack area was no longer possible. Therefore, gluing the uncut (raw) material of the steel fibre with a length of 300 mm into the (medical) cannulas at both ends was performed. Figure 2 shows the raw material of the steel fibre (a) and the test specimen for the monotonic and cyclic loaded tensile tests (b). The length between the cannulas (test length) was 100 mm. A precision testing machine with a 500 N load cell ran the test execution of all tests and its transducer measured the displacement of the fibre.

4.2. Monotonic Loading

Nine (VFS-A) and six (VFS-B) specimens were subjected to monotonically increasing tensile loading. The loading rate was 0.01 mm/s for each test. The measured loads of the testing machine were converted into the tensile stress of the fibre by ${\sigma }_{\mathrm{st}}^{\mathrm{f}}=F/A$. The diameter of the fibres was assumed to be in good order to 0.19 and 0.13 mm. Figure 3 shows the tensile stress–strain curves for VFS-A and VFS-B (black lines) and the mean curves (red lines) of the test series.

The curves of VFS-A $\left({\varnothing }_{\mathrm{f}}=0.19 \mathrm{mm}\right)$ in Figure 3a show an approximately linear elastic behaviour up to 90% of the failure load. After that, the curves are slightly curved until fibre rupture occurs abruptly. The failure occurs at an elongation of about 22 to 27‰ and an average ultimate tensile strength of approximately 3576 N/mm².

The curves of VFS-B $\left({\varnothing }_{\mathrm{f}}=0.13 \mathrm{mm}\right)$ show slightly uneven characteristics. The curves increase nonlinearly, and the curve’s curvature does not change upon failure load. The failure also occurs without preannouncement. The strain at the failure point of about 22 to 27‰ is nearly equal to the micro steel fibres of test series VFS-A. However, the ultimate tensile strength of VFS-B is approximately 15% higher.

Table 1. Mechanical properties of steel fibres under monotonic tensile loading.

Name	Number	Diameter ${\mathsf{\varnothing }}_{\mathbf{f}}$	Ultimate Tensile Strength ${\mathit{f}}_{\mathrm{st}}^{\mathbf{f}}$	Ultimate Strain ${\mathsf{\epsilon }}_{\mathrm{st}}^{\mathbf{f}}$
[-]	[Num.]	[mm]	[N/mm2]	[‰]
VFS-A	9	0.19	3575.8±80.2	22.8±0.7
VFS-B	6	0.13	4250.4±95.2	24.6±2.3

lists the detailed results of the tensile tests of the high-strength micro steel fibres under monotonic loading. The value’s exponent is its standard deviation.

Due to the unexpected high deviation of the tensile strengths between the manufacturer’s specification and the test results in Table 1, scanning electron microscopy (SEM) images were obtained in order to confirm the “true” diameter of the fibre. In this connection, removal of the brass coating from the steel surface of the fibre was inevitable. No chemical removal was possible because it might have affected the steel of the fibre. Removing the brass coating with sandpaper was also unrewarding because it also damaged the steel’s material.

The third possibility was an embedment of the steel fibre in UHPC and a careful pullout with a precision testing machine. The embedment in concrete seemed to be a good solution, which is why the pulled out fibre was prepared for SEM images. Figure 4 shows the steel fibre’s surface with brass coating (a) and without brass coating (b) in SEM.

The steel fibre’s surface (VFS-A) with brass coating in Figure 4a is quite smooth. Only some faults are noticeable on the surface with a very slight depth. In contrast to that, the fibre’s surface without brass coating in Figure 4b shows many gouges located mostly in the longitudinal direction of the fibre. The production process might have caused these gouges and the brass coating hides them underneath.

As the cross-sectional area is very important for the calculation of the tensile strength of the micro steel fibre, accurate determination of the gouge’s depth was attempted in additional SEM investigations. Instead of the micro steel fibre’s surface, the cross-sectional area should reveal the depth of the gouges. The fibre had to be located parallel to the electron beam for visualization. Nevertheless, a steel fibre located in the electron beam’s direction works like an antenna. The detector might not collect all electrons and provide blurry pictures. This is why the steel fibre was orientated at an angle of approximately 45° to the electron beam. Figure 5 shows the image of the SEM with the cross-section of the fibre.

The SEM image shows quite a high resolution of the cross-sectional area of the fibre. The image shows a slight shadow, starting at the top edge of the fibre and moving towards its centre. The electron beam might have caused the shadow because of the (nearly) parallel location of the fibre. The gouges of the surface (Figure 4) are not visible in the cross-section, so that it is assumed that they are probably not deeper than 1.0 μm. Thus, the calculation of the tensile strength with the “bare” diameter of approximately 0.19 and 0.13 mm is feasible.

Based on this finding, the theoretical tensile stress–strain values for high-strength micro steel fibres were calculated with a diameter of 0.19 (VFS-A) and 0.13 mm (VFS-B). Besides the theoretical relationship, the characteristic material values are also required. Characteristic values are usually 5% quantiles of mean values assuming that the measured data is normally distributed.

Table 2. Characteristic values for the theoretical stress–strain relationship of high-strength micro steel fibres.

Name	${\varnothing }_{\mathbf{f}}$	Tensile Strength ${\mathit{f}}_{\mathrm{st},\mathbf{m}}^{\mathbf{f}}$	Standard Deviation	5%-Quantile of ${\mathit{f}}_{\mathrm{st},\mathbf{m}}^{\mathbf{f}}$
[-]	[mm]	[N/mm2]	[N/mm2]	[N/mm2]
VFS-A	0.19	3575.8	80.2	3462.4
VFS-B	0.13	4250.4	95.2	4080.7

gives the parameters for the statistical evaluation of the theoretical tensile stress–stain curve.

4.3. Cyclic Loading

The test configuration for cyclic loading was the same compared to monotonic loading. Each test series contained three test specimens for gathering possible scatter. The load amplitudes $\Delta {\sigma }_{\mathrm{st}}^{\mathrm{f}}$ varied between 5% and 80% of the reference tensile strength $f_{\mathrm{st}}$, according to Table 1. The testing machine’s electromechanical drive limited the frequency to approximately 0.85 Hz.

Table 3. Experimental programme of tensile tests subjected to cyclic loading.

Name	Quantity	Upper Stress Level $\mathbf{\Delta }{\mathbf{\sigma }}_{\mathbf{st},\mathbf{o}}^{\mathbf{f}}$	Lower Stress Level $\mathbf{\Delta }{\mathbf{\sigma }}_{\mathbf{st},\mathbf{u}}^{\mathbf{f}}$	Load Amplitude $\mathbf{\Delta }{\mathbf{\sigma }}_{\mathbf{st}}^{\mathbf{f}}$	Load Amplitude $\mathbf{\Delta }{\mathbf{\sigma }}_{\mathbf{st}}^{\mathbf{f}}$	Load Cycles ${\mathit{N}}_{\mathbf{um}}$
[-]	[num.]	[-]	[-]	[-]	[N/mm2]	[num.]
VFZ-1	3	0.90	0.10	0.80	2860.7	962±5
VFZ-2	3	0.80	0.10	0.70	2503.1	1008±46
VFZ-3	3	0.70	0.10	0.60	2145.5	1593±344
VFZ-4	3	0.60	0.10	0.50	1787.9	2382±260
VFZ-5	3	0.50	0.10	0.40	1430.3	4240±580
VFZ-6	3	0.40	0.10	0.30	1072.7	3364±40
VFZ-7	3	0.30	0.10	0.20	715.2	7986±1963
VFZ-8	3	0.20	0.10	0.10	357.6	57,375±10,073
VFZ-9	3	0.15	0.10	0.05	178.8	1,000,000±0

lists the most critical parameters of the experimental program for cyclic tensile loading. Besides general test parameters, Table 3 also contains basic results (load cycles leading to failure $N_{\mathrm{um}}$) of the cyclic loaded fibre tests.

Except for the test series VFZ-7 and VFZ-8, all fibres fractured within the test area, i.e., between the cannulas. However, in one test of VFZ-7 and VFZ-8, the fibre crack occurred in the cannulas. This crack location could indicate higher scatter of ultimate load cycles $N_{\mathrm{um}}$. The specimen’s manufacturing process might have caused additional damage while pressing and gluing the filigree steel fibre into the cannulas. The additional damage might be responsible for the lesser fatigue resistance of the steel fibres. Nevertheless, the test results and the number of load cycles lie within the usual scatter range for fatigue tests [17,18].

The load cycles $N_{\mathrm{um}}$ and load amplitudes $\Delta {\sigma }_{\mathrm{st}}^{\mathrm{f}}$ were plotted on an S/N-diagram, and the corresponding regression curve was determined. Equation (1) gives the formulae of the regression curve:

$$\Delta {\sigma }_{\mathrm{st}}^{\mathrm{f}}=5·{10}^4·N^{-0.44}$$

(1)

where $\Delta {\sigma }_{\mathrm{st}}^{\mathrm{f}}$ is the load amplitude and $N$ is the number of load cycles. Figure 6 shows the S/N curve of the high-strength micro steel fibre and the plotted test results. For load amplitudes smaller than $\Delta {\sigma }_{\mathrm{st}}^{\mathrm{f}}<3500 \mathrm{N}/{\mathrm{mm}}^2$, the regression curve (red dashed line) equals the short-term strength. The red arrows pointing to the right Figure 6 mark so-called “run-outs”.

Furthermore, Figure 6 shows the S/N curve for prestressing steel according to Model Code 2010 [19] (dashed black line). In comparison, prestressing steel shows no good agreement with the fatigue behaviour of high-strength micro steel fibres in “low-cycle fatigue” $\left(N\le {10}^4 \mathrm{LW}\right)$ and “high-cycle fatigue” $(N>{10}^4 \mathrm{LW})$. The non-agreement could be the reason for comparing the characteristic values (for prestressing steel) and mean values (high-strength steel fibre) with each other. This is why modification of the steel fibre S/N curve (conversion of the mean values into characteristic values) is necessary.

Additionally, the typical ranges of the fatigue life in S/N curves for conventional reinforcing bars and prestressing steel are not transferable to high-strength micro steel fibres and need adjustment. While fatigue loads in reinforcing bars and prestressing steel strands are precisely calculable, the stresses in randomly distributed fibres of UHPFRC components might differ vastly from each other. Some fibres in UHPFRC components obtain higher stresses than others, although they lie right next to each other. Therefore, the beginning of the fatigue endurance limit starts earlier at $N={10}^5 \mathrm{LW}$ load cycles (instead of ${10}^6$). The other limits of the S/N curve remain equal to conventional reinforcing bars and prestressing steel (

Table 4. Modified ranges of fatigue life for high-strength micro steel fibres.

	Reinforcing Steel Bars:	High-Strength Micro Steel Fibre:
Low cycle fatigue	$N\le {10}^3$	$N\le {10}^3$
Finite-life fatigue strength	${10}^3<N<{10}^6$	${10}^3<N<{10}^5$
Fatigue endurance limit	$N\ge {10}^6$	$N\ge {10}^5$

).

The calculation goal is a bilinear S/N curve for the high-strength steel fibre under consideration of the 5% quantile values. Therefore, the S/N curve of finite-life fatigue strength between ${10}^3$ and ${10}^5$ load cycles needs a conversion of the mean values into the characteristic values. This conversion requires the test series results with the highest scattering in terms of ultimate load cycles. All the other test series remain disregarded for the calculation at first. The 5% quantile of the test series with the highest scattering (VFZ-7) is:

$$N_{0.05;\mathrm{VFZ}-7}=5615$$

(2)

The 5% quantile $N_{0.05;\mathrm{VFZ}-7}$ of the test series VFZ-7 belongs to a load amplitude of 715.2 N/mm². Two points ($P_1$ and $P_2$) are added to the S/N diagram: Point $P_1$ (7986/715.2) is equal to the load cycles and load amplitude of the mean S/N curve. Point $P_2$ (5615/715.2) corresponds to the 5% quantile of the test series VFZ-7.

If the mean S/N curve (red line) is moved parallel until it intersects point $P_2$ (5615/715.2), the characteristic S/N-curve is formed and is shown in Figure 6 by the blue line. Equation (3) expresses the characteristic S/N curve determined by regression with:

$$\Delta {\sigma }_{\mathrm{st}}^{\mathrm{f}}=2.69·{10}^4·N^{-0.425} \mathrm{for} N<{10}^5$$

(3)

Equation (3) is consequently only valid for ultimate load cycles between ${10}^3$ and ${10}^5$, i.e., the finite-life fatigue strength. For higher ultimate load cycles, Equation (3) shows no good accordance, and modification would be useful.

The test series VFZ-9 has not been included in the calculation so far. It shows three run-outs at a load amplitude of ${\sigma }_{\mathrm{st}}^{\mathrm{f}}=178.8 \mathrm{N}/{\mathrm{mm}}^2$ (cf. Table 3). Thus, the characteristic S/N curve (blue line in Figure 6) changes its direction and obtaines a reduced inclination and crosses the “run-outs”. The redirection of the S/N curve requires another regression to assign an equation. Equation (4) gives the formulae of the carried on S/N-curve for $N\ge {10}^5$:

$$\Delta {\sigma }_{\mathrm{st}}^{\mathrm{f}}=350·N^{-0.05} \mathrm{for} N\ge {10}^5$$

(4)

Comparing the 5% quantile values, Equation (4) shows very good accordance with the behaviour of prestressing steel strands. Only at higher load cycles ($N>{10}^7$), high-strength steel fibres may have a slightly better fatigue resistance. However, Equation (4) is not applicable for global data because it only rests upon one type of high-strength micro steel fibre. A general validated S/N cure for steel fibre requires more fatigue of other fibre types, especially in terms of high cycle fatigue.

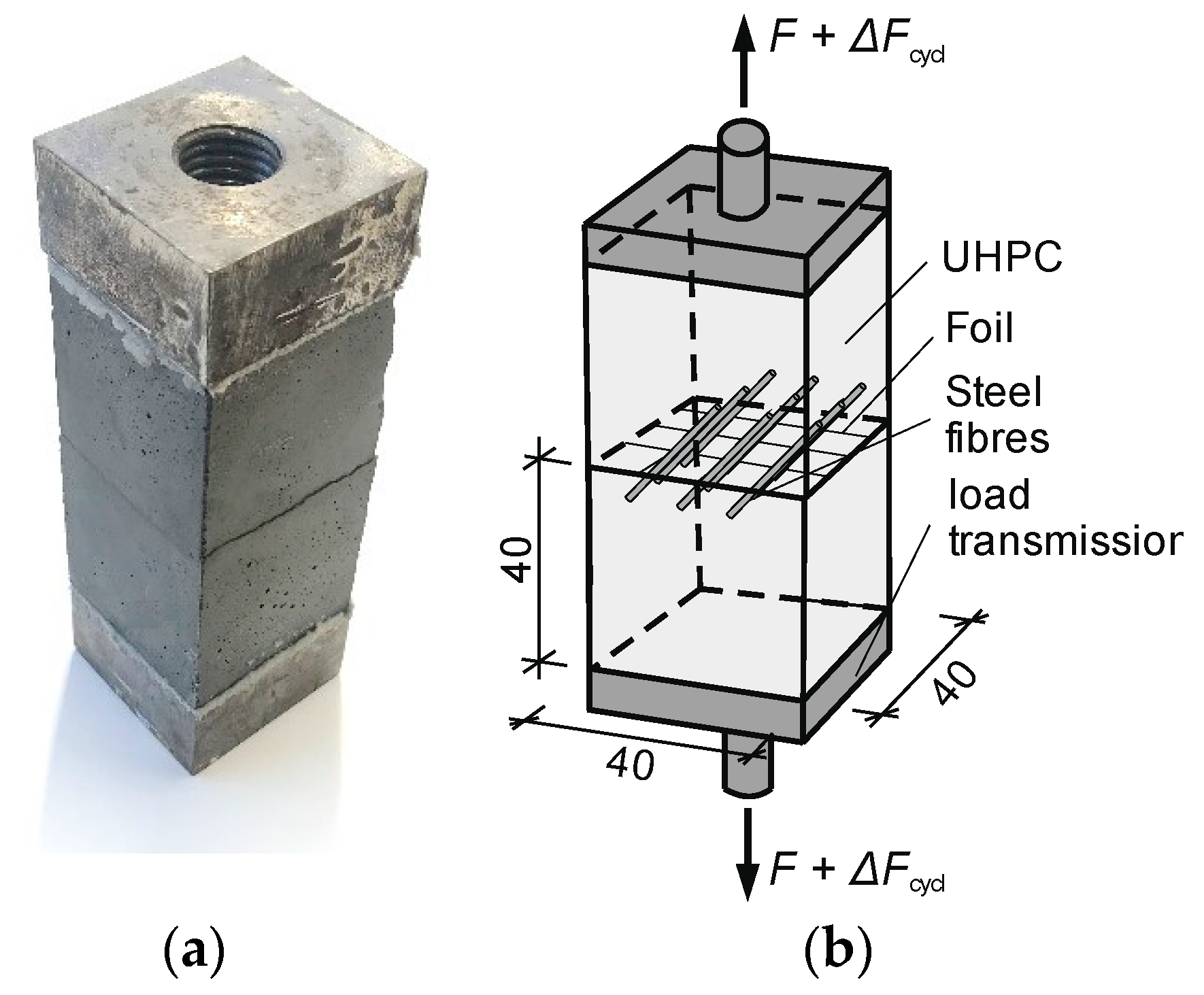
5. Fibre Groups Embedded in UHPC

5.1. Test Specimen and Test Programme

The test specimens VM (fibre-group-pullout-tests, Figure 7) consisted of two plain UHPC cubes with nine oriented fibres located in between [15–17]. The concrete age of all tests was at least 28 days and the cylinder compressive strength reached more than 150 N/mm². The components of the used UHPC are listed in

Table 5. Mix proportions of the used plain UHPC-1017.

Components	UHPC-1017
[-]	[kg/m3]
Cement CEM I	795.0
Silica fume	168.6
Superplasticiser	24.1
Quartz powder	198.4
Quartz sand 0.125/0.5 mm	971.0
Water	189.9

.

The production of the test specimens needed two casting steps. First, nine steel fibres with a diameter of ${\varnothing }_{\mathrm{f}}=0.19 \mathrm{mm}$ and a length of $l_{\mathrm{f}}=13.0 \mathrm{mm}$ were put with a 1 cm × 1 cm grid in a polystyrene cube, so that half (or $3/4$) of the fibre was in the cube and the other half (resp. 1/4) was “on the air”. A template ensured the desired orientation $\alpha$ and embedded length $l_{\mathrm{e}}$ of the fibres. Afterwards, the polystyrene cube with the aligned steel fibres was placed in a formwork. Then, the concreting of the first half of the test specimen followed. After one day of hardening, the polystyrene cube was removed. Subsequently, the second concreting was carried out. A foil between the UHPC cubes prevented transmission of tensile forces between the concrete. Bonded steel plates with threaded holes ensured load transmission between the testing machine and the specimen.

The experimental programme of the pullout tests contained a variation of the fibre orientation between $\alpha \approx 30°, 60°, \mathrm{and} 90$° as well as different embedded lengths of $l_{\mathrm{e}}\approx 6.50 \mathrm{mm} \left(\stackrel{\wedge}{=}{l}_{\mathrm{f}}/2\right) \mathrm{and} l_{\mathrm{e}}\approx 3.25 \mathrm{mm} \left(\stackrel{\wedge}{=}{l}_{\mathrm{f}}/4\right)$. The displacement transducer of the testing machine measured the displacement of the two UHPC cubes and the so-called “crack mouth opening displacement”. A comparative measurement between the transducer and an optical laser in preliminary tests confirmed its accuracy.

The loading velocity was 0.01 mm/s (cf. Section 4.2) for the monotonic tests. The load amplitude of the cyclic tests oscillated between 10% and 70% of the maximum pullout resistance of the monotonic tests. The test frequency of the cyclic tests varied between 0.5 and 1 Hz.

Table 6. Experimental programme and test results of the monotonic and cyclic loaded pullout tests.

Name	Number	Orientation $\mathbf{\alpha }$	Length ${\mathit{l}}_{\mathbf{e}}$	Max. Pullout Resistance ${\mathbf{\sigma }}_{\mathbf{st},\mathbf{max}}^{\mathbf{f}}$	Displacement $\mathbf{\delta }$ at Max. ${\mathbf{\sigma }}_{\mathbf{st},\mathbf{max}}^{\mathbf{f}}$	Load Changes Num	Failure Mode
[-]	[No.]	[°]	[mm]	[N/mm2]	[mm]	[No.]	[-]
VMS30-1	3	30°	3.25	376.9±41.2	1.46	-	Pullout
VMS30-2	3		6.50	993.6±66.6	2.28	-	Pullout
VMS60-1	3	60°	3.25	480.7±71.0	0,63	-	Pullout
VMS60-2	3		6.50	1176.3±26.7	0.60	-	Pullout
VMS90-1	3	90°	3.25	568.7±42.4	0.45	-	Pullout
VMS90-2	3		6.50	1159.1±53.3	0.50	-	Pullout
VMZ30-1	3	30°	3.25	-	-	158±116	Pullout
VMZ30-2	3		6.50	-	-	250±42	Pullout
VMZ60-1	3	60°	3.25	-	-	88±19	Pullout
VMZ60-2	3		6.50	-	-	848±442	Pullout/Rupture
VMZ90-1	3	90°	3.25	-	-	455±399	Pullout
VMZ90-2	3		6.50	-	-	373±12	Pullout
	∑ 36

shows the test programme including typical results.

5.2. Monotonic Tensile Loading

As part of the evaluation, the general relationship $\sigma =F/\left(n·A\right)$ coverts the measured loads $F$ into tensile stresses ${\sigma }_{\mathrm{st}}^{\mathrm{f}}$, with $n$ being the number of fibres (here nine). The calculation of the cross-sectional area $A$ considers a fibre diameter of ${\varnothing }_{\mathrm{f}}=0.19 \mathrm{mm}$ (see Section 4.2). Each test series comprises at least three individual tests to gather possible scatter.

Figure 8 shows the pullout curves of fibre groups with an orientation of 30°, 60°, and 90° under monotonic loading (mean values = mv). The highest pullout resistance for an embedded length of 6.50 mm ($l_{\mathrm{f}}/2$) is approximately 1175 N/mm², which equals to nearly one-third of the tensile strength. All other pullout resistances show lower values. Additionally, the pullout resistance for an embedded length of 3.25 mm ($l_{\mathrm{f}}/4$) does not correspond proportionally to 50% of the pullout resistance for an embedded length of 6.50 mm; the relation is approximately 40%. Due to the low utilization of the tensile strength of the fibre, there was always a systematic fibre pullout, i.e., no steel fibre broke.

The pullout tests of the steel fibres orientated at 60° and 90° with an embedded length of 6.50 mm showed the typical course of a standardized bond test of conventional reinforcement, i.e., they reached the maximum pullout resistance relatively quickly and then dropped almost linearly. Many contributions ([11,16,20,21]) observed similar phenomena but only for 90°-orientated fibres.

The pullout curve of steel fibres with an orientation of 30° shows a different course of the curve than the standardized bond tests. The maximum pullout resistance occurs at a higher relative displacement between the fibre and the UHPC (black dashed lines in Figure 8). The fibre bending effects might control the relation of the highest pullout resistance and relative displacement. These bending effects occur at the exit point of the concrete canal and need some relative displacement for activation.

Low fibre orientation angles (e.g., 30°) result in higher bending effects than high angles of orientation (dashed line in Figure 8). Figure 9 visualizes the context of the bending effects at the exit point of the inclined fibres.

Besides the bending effects of the fibre, a concrete breakout occurred at the exit of the UHPC canal. A visual investigation showed that the concrete breakout area got bigger with lower fibre orientation angles. The combination of the fibre inclination and uniaxial load caused a constriction of the fibre into the concrete canal. Compression stresses emerged between the fibre and the concrete, and caused concrete spalling at the exit point. This phenomenon refers to “snubbing” [22] and has been observed on the fractured surfaces of uniaxial UHPFRC tensile tests [12,23].

The snubbing effect was visualised by digital microscopy images, as shown in Figure 10, and the concrete breakout areas were measured with MountainsMap. MountainsMap is a software used to quantity the roughness and the surface textures of materials. Figure 10 shows the digitally microscopy images and scales in MountainsMap of the breakout cones at 30° and 60°. The concrete breakout area equals 5.76 mm² for 30°- and 2.80 mm² for 60°-orientated micro steel fibres. This means that an inverse relation occurred after halving the size of the breakout area by doubling the angle of orientation.

No breakout occurred at fibre orientations of 90°. The uniaxial load of the pullout specimen tried to drag the angled fibres straight out of the concrete.

The damage of the concrete surface due to the inclination of the fibres is very important to understanding the bond behaviour and damage mechanism of steel fibres. While 90°-orientated steel fibres only cause one damage mechanism (pullout), inclined fibres (30° and 60°) cause two and three types of damage mechanisms: fibre pullout and concrete spalling as well as consequent fibre bending. The additional damage mechanism is quite important for the load bearing behaviour of UHPFRC components with high fibre contents. Every fibre located in the direct surroundings of these inclined fibres, i.e., in the breakout cone, might lose their load bearing effect.

5.3. Cyclic Tensile Loading

Each test series contained at least three individual tests in terms of cyclic loading. The upper load level was fixed to 70% and the lower load level to 10% of the maximum pullout resistance obtained in the monotonic tests, leading to a relative stress oscillation width of $\Delta {\sigma }_{\mathrm{st}}^{\mathrm{f}}=0.6$ [-].

In the VMZ90 series, the test execution stopped unexpectedly after 1000 load cycles due to a defect of the test machine. For the VMZ60 series with an embedded length of $l_{\mathrm{e}}=6.50 \mathrm{mm}$ and a fibre angle inclination of $\alpha =60°$, Figure 11 shows the measured pullout displacement δ as a function of the applied load cycles $N$. It can be concluded that the three typical phases of fatigue of concrete also apply to the pullout tests of embedded high-strength micro steel fibres in UHPC:

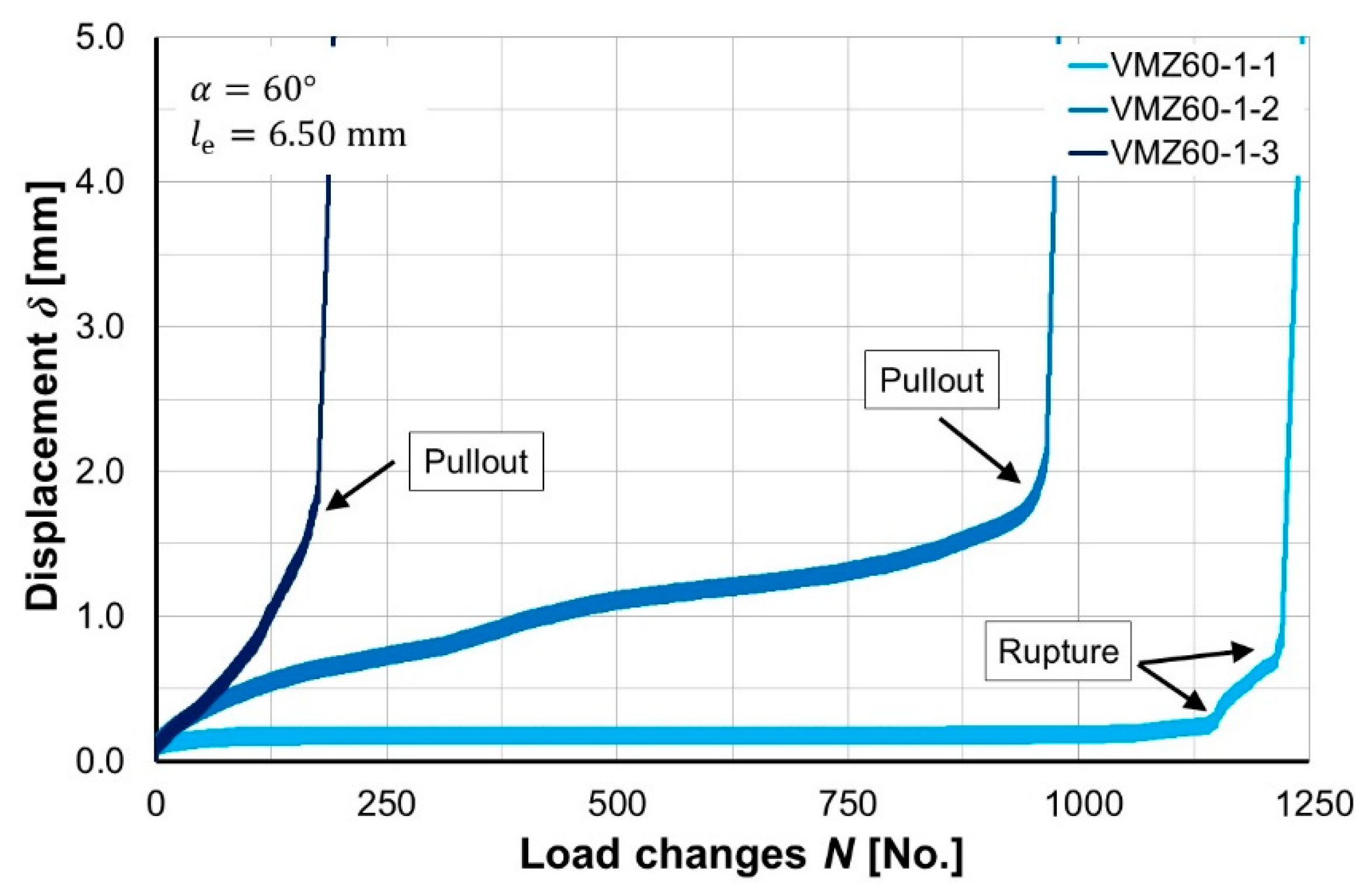
• Phase I marks the initial non-linear increase in strain.
• Phase II begins between 5% and 10% of the ultimate load cycle number $N$ with the transition to a constant, small increase in deformation.
• Phase III is reached at around 95% of the breaking load cycle number $N$. The total deformations increase rapidly, disproportionately, leading to failure of the concrete.

High-strength steel fibres should—as described in Section 2—be designed by their geometry and tensile strength to be pulled out under load, i.e., to fail in the bond and thus have a certain deformation capacity. While all test results under monotonic loading show this mechanical behaviour (Table 6), another type of failure could be detected under cyclic loading in VMZ60-2: fibre breakage.

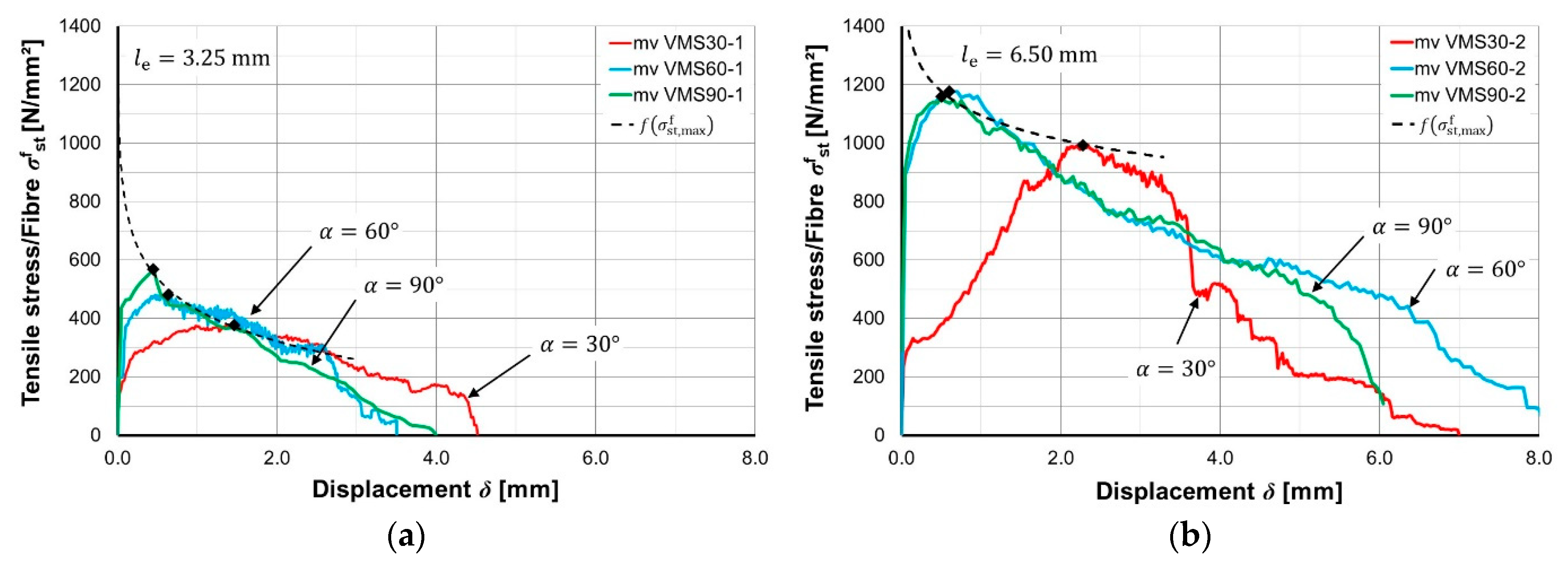
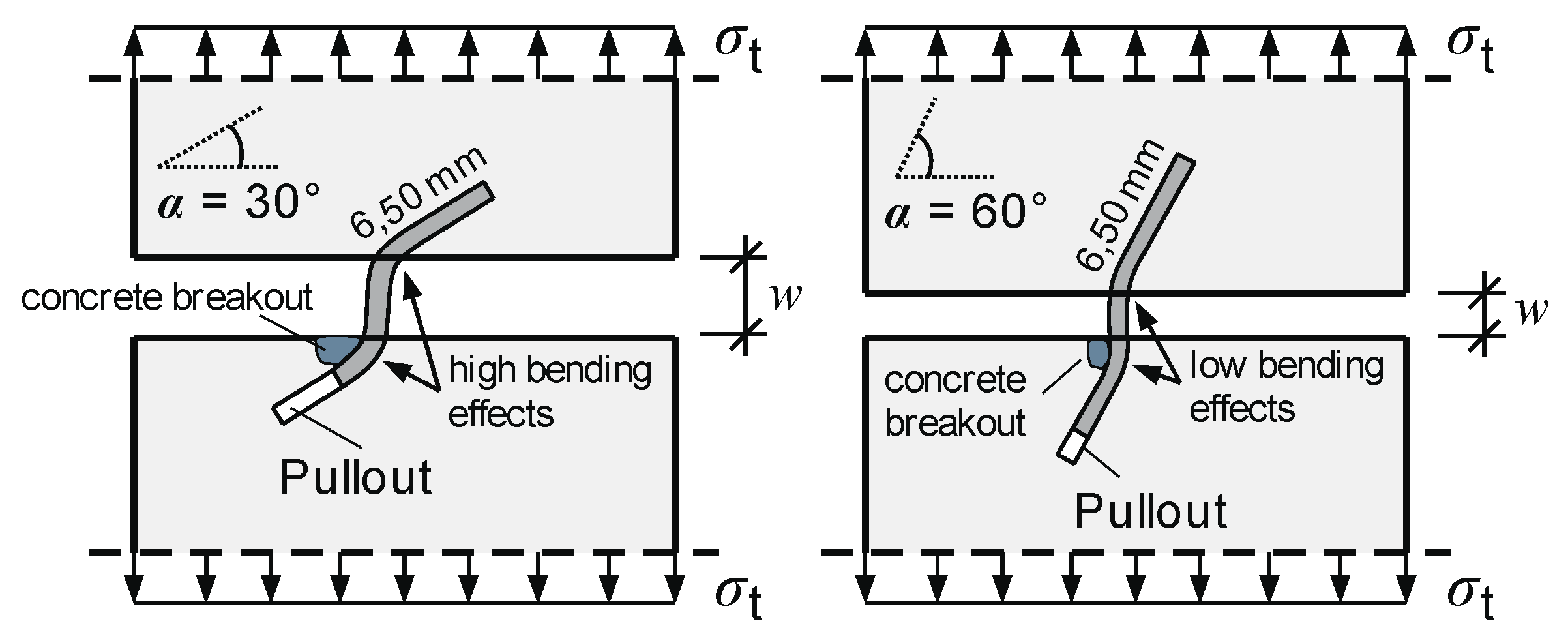
• This type of failure would actually have been expected with a fibre orientation of 30°, because greater bending stresses occur in the steel fibre compared to an orientation of 60° (cf. Figure 9). The following explanation can be given for this:
• With a fibre orientation of 30°, no fibre breakage occurs because the “snubbing effect” causes a larger concrete breakout, which in turn considerably shortens the bond length. This reduces the bending stresses on the one hand and increases the bond stresses on the other. The latter causes the fatigue damage of the bond zone to progress faster than the material damage. This eventually leads to fibre pullout.
• With 60°-inclined fibres, on the other hand, the “snubbing effect” leads to less concrete breakout and the bond length is reduced less (in comparison to a fibre orientation of 30°). The relationship between the damage of the bond zone and the fibre material (bending effects) is in an indifferent state, where both fibre pullout (VMZ60-1) and fibre breakage (VMZ60-2) can occur. Both failure modes can also be seen in Figure 12.

For embedded fibres with an orientation of 90°, neither bending effects nor snubbing occur. Damage takes place in the bond zone and progresses until the bond stresses can no longer be transferred between the fibre and the concrete; the fibre pulls out of the concrete matrix.

6. Conclusions and Outlook

The experimental investigations presented in this paper were carried out within the framework of the DFG-SPP 2020. They included uniaxial tensile tests on high-strength micro steel fibres as well as pullout tests of embedded fibre groups, each under monotonic and cyclic loading. In addition, extensive efforts were made to further localise the damage mechanisms on the fibre surface and in the fibre cross-section with the help of SEM images.

The experimental investigations and the evaluations of the imaging methods provided the following findings:

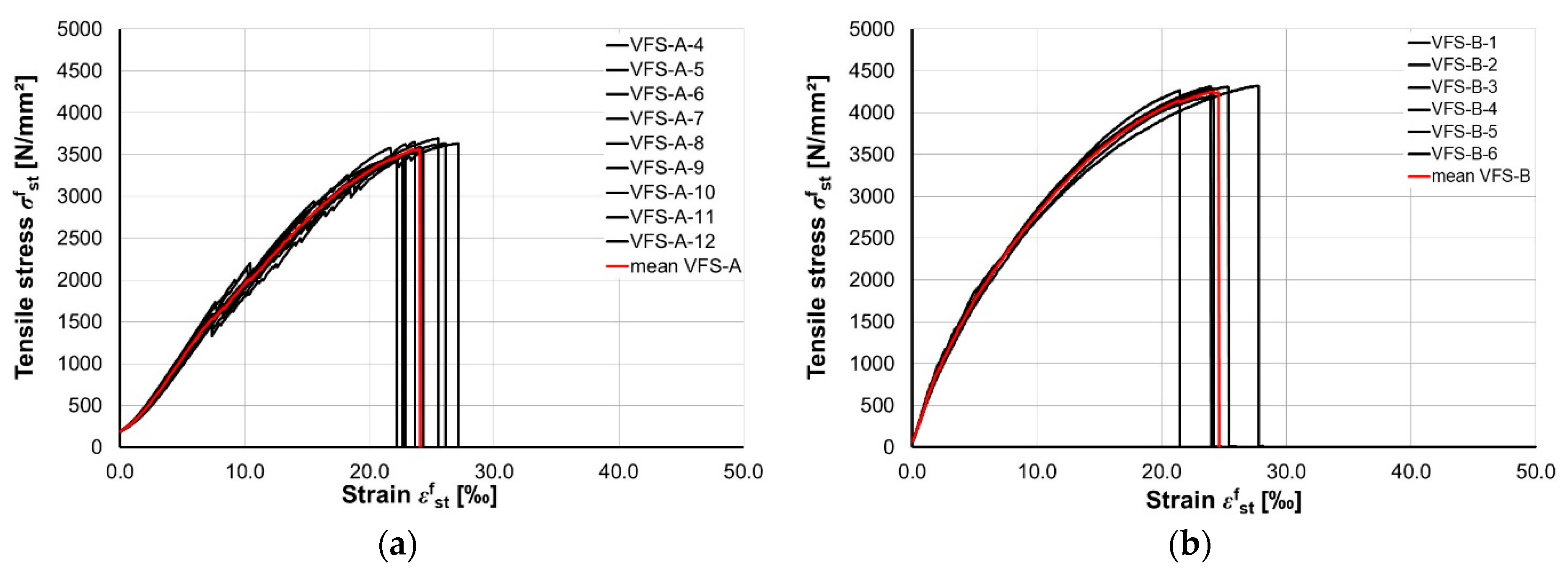
• The stress–strain relationship of the high-strength micro steel fibres showed no considerable ductility like conventional steel. The failure is brittle.
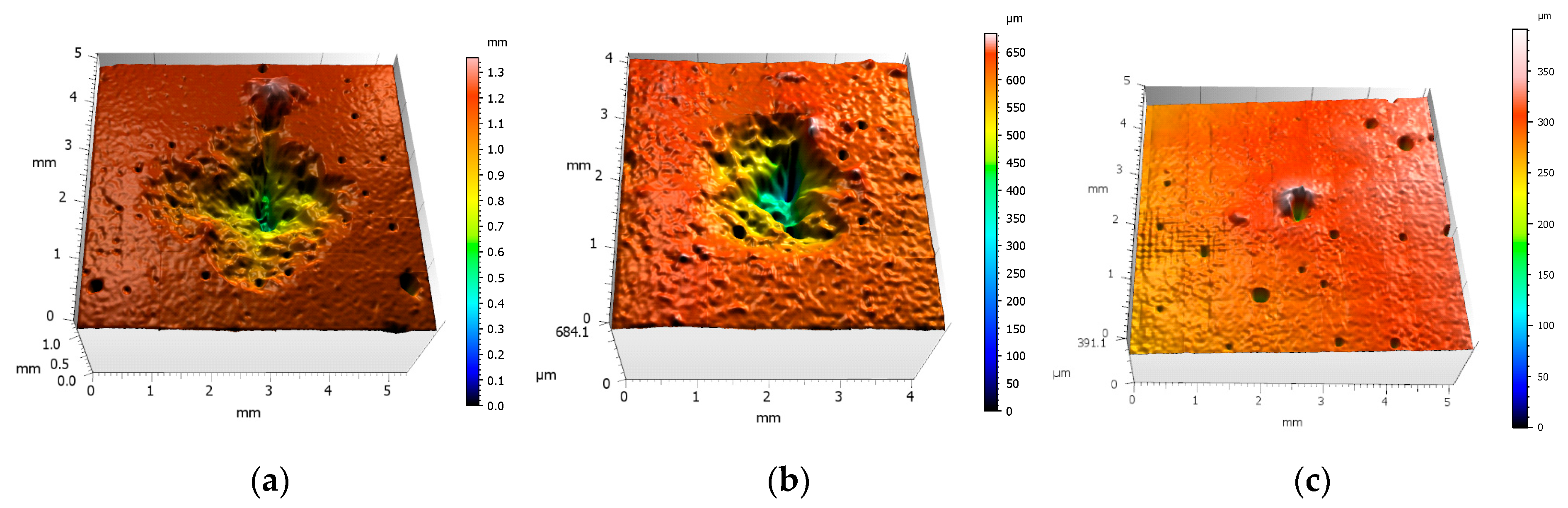
• The brass coating of the high-strength micro steel fibre hides gouges located in the longitudinal direction of the fibre underneath. The gouges reduce the cross-sectional insignificantly and do not affect the tensile strength in a considerable manner.
• The mean S/N curve of the high-strength micro steel fibre showed in the first instance no good agreement with prestressing steel. After converting the mean S/N curve into characteristic values, a comparison with prestressing steel was possible and provided relatively good agreement for the high-cycle fatigue. Equation (4) provides a recommendation for a mathematical formulation of the S/N curve.
• The used high-strength steel fibres always pulled out of the concrete matrix under monotonic loading, i.e., no fibre rupture occurred. The maximal pullout resistance in the test program was approximately one-third of the fibre’s tensile strength. After the peak load, the pullout curves show an almost linear decreasing course of curves.
• Under cyclic loading, fibre rupture occurred partly at orientations of 60° but not for 30° and 90°. The fatigue curves of the un-cracked micro steel fibres showed the typical course of curves like fatigue of concrete: strain stabilisation, linear strain increase, and exponential strain increase.

Since the experimental investigations showed that fibre breakage might occur for some embedded lengths and orientations, the current design (slenderness) of the fibres $l_{\mathrm{f}}⁄{\varnothing }_{\mathrm{f}}=13.0⁄0.19\approx 68$ might not be suited for cyclic loading. Damaging bending effects might have large impacts in thin fibres so that the slenderness should be considered to be below 68 [-] for fibres subjected to cyclic loading. However, an accurate determination of the fibre design (geometry and tensile strength) that is suitable for cyclic loading requires further fundamental investigation in terms of pullout tests with varying fibre slenderness.