Study of the Error Caused by Camera Movement for the Stereo-Vision System

Abstract

The stereo-vision system plays an increasingly important role in various fields of research and applications. However, inevitable slight movements of cameras under harsh working conditions can significantly influence the 3D measurement accuracy. This paper focuses on the effect of camera movements on the stereo-vision 3D measurement. The camera movements are divided into four categories, viz., identical translations and rotations, relative translation and rotation. The error models of 3D coordinate and distance measurement are established. Experiments were performed to validate the mathematical models. The results show that the 3D coordinate error caused by identical translations increases linearly with the change in the positions of both cameras, but the distance measurement is not affected. For identical rotations, the 3D coordinate error introduced only in the rotating plane is proportional to the rotation angle within 10° while the distance error is zero. For relative translation, both coordinate and distance errors keep linearly increasing with the change in the relative positions. For relative rotation, the relationship between 3D coordinate error and rotation angle can be described as the nonlinear trend similar to a sine-cosine curve. The impact of the relative rotation angle on distance measurement accuracy does not increase monotonically. The relative rotation is the main factor compared to other cases. Even for the occurrence of a rotation angle of 10°, the resultant maximum coordinate error is up to 2000 mm, and the distance error reaches 220%. The results presented are recommended as practice guidelines to reduce the measurement errors.

1. Introduction

In recent years, the stereo-vision system has been used widely in many fields, e.g., industrial manufacturing and inspection [1,2,3,4], experimental mechanics [5,6,7,8], structural health monitoring [9,10,11], medical diagnosis [12] and aerospace engineering [13,14,15]. To obtain accurate 3D information, the two cameras in the stereo-vision system should remain stationary during the whole test period. This is because most stereo-vision systems calibrate the camera parameters at the beginning of the measurement [16,17,18]. Any slight camera movements during the tests can cause the extrinsic parameters (positions and orientations of the cameras) to vary and then decrease measurement accuracy.

However, it is often impractical for the two cameras in a stereoscopic system to stay stationary in harsh working conditions, particularly in an outdoor environment. For example, when performing deflection measurement by digital image correlation in the outdoors for the inspection of bridge structures [19], the changes in the position and orientation of the stereo cameras often occur owing to various factors like wind, oscillations, and the lack of stability of the ground. When the stereo-vision systems are employed in autonomous land navigation [20], the road roughness can cause unpredictable camera movements. A strong vibration induced by a heavy steam hammer at high-speed is an unavoidable factor to compromise the measurement accuracy while using the stereo vision to measure the ram speed in forming workpieces [21]. Furthermore, a stereoscopic camera system has already been demonstrated for wing deformation measurements. Nevertheless, they have to cope with the problems of camera movements induced by the high aerodynamic loads and mechanical vibration during a measurement. Particularly, it is difficult to avoid these movements for in-flight applications [22], since the high vibration level occurs during the dynamic flight maneuvers.

In all of the above cases, one common issue is camera movement, which adversely affects the applicability and versatility of the vision method. Sohn and Kehtarnavaz [20] used mini-max and minimum-mean-square estimators to analyze the error caused by camera movements in a monocular vision-based tracking system while the effects of camera movement on 3D measurement of stereo-vision systems were not involved. Many researchers used monocular camera systems to measure the structural displacements that are parallel to the imaging plane in an outdoor environment [23,24,25,26]. They found that it is difficult to keep the monitoring camera stationary during the entire process, which affected the accuracy of displacement measurements. Several compensation methods [26,27] have been developed to compensate for the camera movements. For instance, to address this challenge of camera movement, Yoon et al. [28] calculated and removed the nonstationary motion of the camera by tracking the background feature points to obtain the accurate absolute displacement. However, the out-of-plane displacement of the structure is neglected. These methods consider structural displacements to be in-plane translations. Zhang et al. [29] presented a hybrid inertial vision-based system that can measure three-dimensional structural displacements by using a monocular camera. This system does not require the camera to remain stationary during the measurements, but the camera movements, i.e., rotations and translations during the measurement process are compensated by using a stationary calibration target in the field of view and an attached tilt sensor.

Kirmse [30] performed an in-flight wing deformation measurement on a Cobra VUT100 airplane using the stereo image pattern correlation technique. They found that relative camera movement led to a decalibration of the stereo system and then affected the precision of the measured 3D position significantly. Xu et al. [31] developed a semi-physical simulation system to investigate the effect of camera parameter error on 3D reconstruction accuracy in a stereo-vision system. They pointed out that extrinsic parameter error has a relatively large impact on system reconstruction accuracy by affecting baseline distance and the angle between cameras. In their works, only the relative movement between the cameras was studied without considering the movement of the two cameras together (identical movement). Yang et al. [32] analyzed the impact of system structure parameters and camera calibration parameters on location accuracy in binocular stereo vision system. However, it also did not include the error caused by identical movement. Satoru and Hiroki [19] performed bridge deflection measurement outside using digital image correlation with a single camera where the effect of camera movement is corrected by perspective transformation. However, the 2D DIC setup requires a perpendicular alignment of the camera towards the planar specimen, which limits the applicability. Kim et al. [33] developed marker-based displacement measurement models for correcting the systematic errors caused by camera movements. However, an assumption made is that the structural displacement occurs on a two-dimensional plane. Bier and Luchowski [34] investigated the influence of input data errors on the quality of reconstructed 3D points in the stereo-vision process while they only considered those particular camera calibration and 3D reconstruction algorithms which employ singular value decomposition (SVD) methods. Reu [35] presented a study of the influence of calibration errors on the uncertainty in 3D position and object motion for the stereo-DIC system using the Monte Carlo approach. However, this “black-box” method lacks the support of an analytically derived model. Wang et al. [36] analyzed the depth measurement error of binocular stereo vision and proposed some strategies to reduce the errors. They had not given the error models of 3D coordinates and distance. Su et al. [37] proposed a new method to calibrate the stereo-DIC system automatically with feature correspondences in an unconstrained scene, but the performance with respect to the feature matching errors rather than the camera movement error was evaluated.

The aforementioned studies primarily focus on analyzing the errors of the camera movements in the monocular vision system, or investigating the camera movement errors using either simulated or numerically altered images. The works attempting to quantify the effect of both identical and relative camera movement in a stereo-vision system on 3D measurement by both analytical and experimental approaches are insufficient. The contributions are that the calculation models of 3D coordinates and distance measurement error are derived by considering the identical and relative movement. The effect characteristic of each case was verified and analyzed, and the main factor was determined as relative rotation. Some strategies are proposed to reduce the measurement errors caused by camera movement.

The rest of this paper is organized as follows. In Section 2, the principle of stereo-vision 3D measurement is introduced. In Section 3, the measurement error models for different types of camera movements are established. In Section 4, four groups of experiments are performed to validate our analysis. Finally, the conclusions of this study are given in Section 5.

2. Principle

As shown in Figure 1, the stereo-vision system consists of two cameras, which are used to capture the images of the same object from different positions at the same time. For any spatial point, the 3D world coordinate is denoted by $P\left(X_w,Y_w, Z_w\right)$, and the pixel coordinates are $p_l\left(u_l,v_l\right)$ in the left camera and $p_r\left(u_r,v_r\right)$ in the right camera. The left camera and right camera coordinate systems are defined as $C_l-X_{cl}{Y}_{cl}{Z}_{cl}$ and $C_r-X_{cr}{Y}_{cr}{Z}_{cr}$, respectively, and their origins $C_l$ and $C_r$ are located at the optical centers.

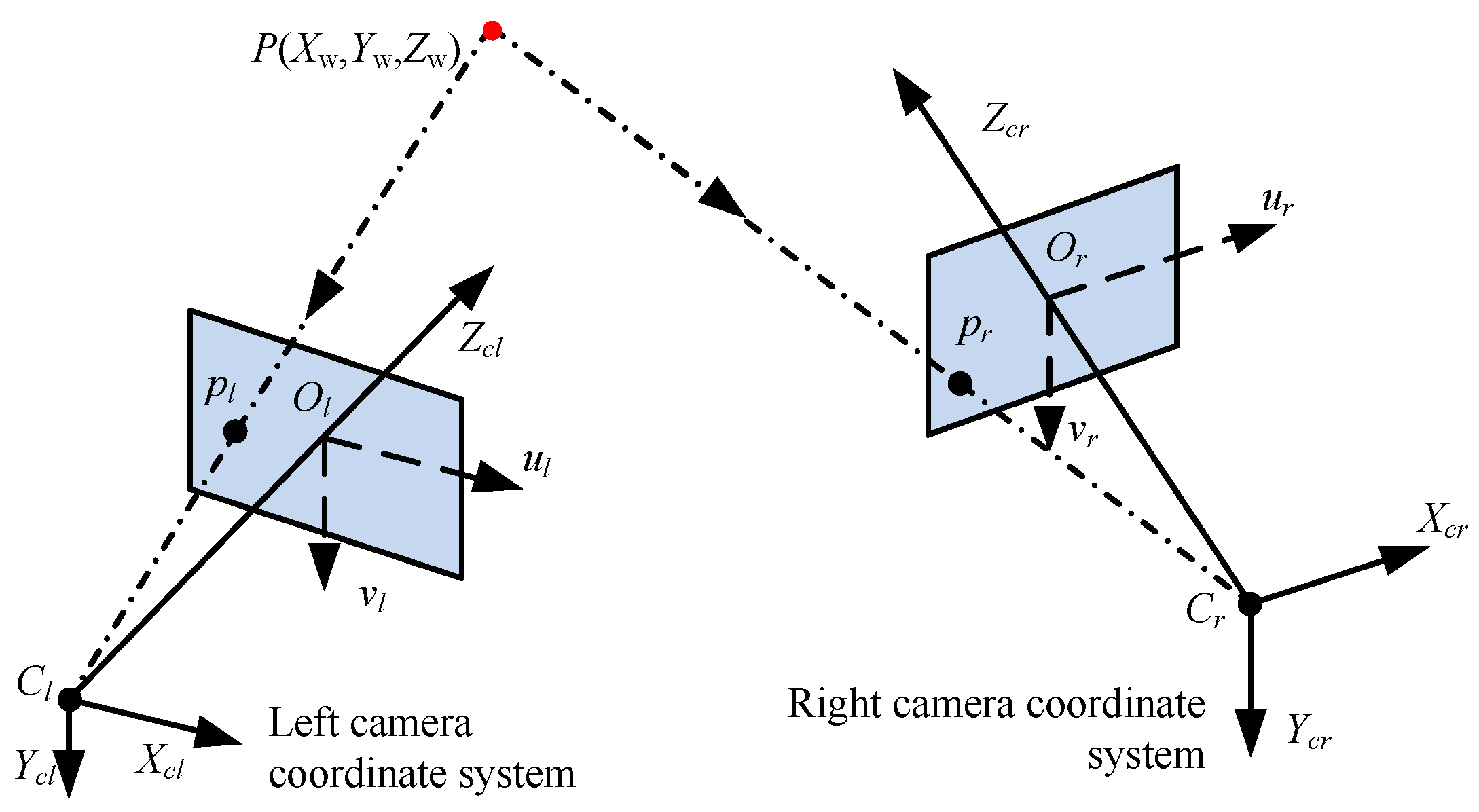
According to the pinhole imaging principle [38], we have

$$\{\begin{array}{c}\left[\begin{array}{c}{X}_{cl}/Z_{cl}\\ Y_{cl}/Z_{cl}\\ 1\end{array}\right]=\left[\begin{array}{c}{x}_{nl}\\ y_{nl}\\ 1\end{array}\right]={\mathit{A}}_l^{-1}\left[\begin{array}{c}{u}_l\\ v_l\\ 1\end{array}\right]\\ \left[\begin{array}{c}{X}_{cr}/Z_{cr}\\ Y_{cr}/Z_{cr}\\ 1\end{array}\right]=\left[\begin{array}{c}{x}_{nr}\\ y_{nr}\\ 1\end{array}\right]={\mathit{A}}_r^{-1}\left[\begin{array}{c}{u}_r\\ v_r\\ 1\end{array}\right]\end{array},$$

(1)

where $\left(x_{nl},y_{nl}\right)=\left(X_{cl}/Z_{cl},Y_{cl}/Z_{cl}\right)$ and $\left(x_{nr},y_{nr}\right)=\left(X_{cr}/Z_{cr},Y_{cr}/Z_{cr}\right)$ are denoted as the image coordinates after focal length normalization, ${\mathit{A}}_l$ and ${\mathit{A}}_r$ are the intrinsic matrices.

Without loss of generality, the world coordinate system coincides with the left camera coordinate system. Thus, the imaging model of the stereo-vision system can be described as

$$\{\begin{array}{l}{Z}_w\left[\begin{array}{c}{x}_{nl}\\ y_{nl}\\ 1\end{array}\right]=\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]\hfill \\ Z_{cr}\left[\begin{array}{c}{x}_{nr}\\ y_{nr}\\ 1\end{array}\right]=\left[{\mathit{R}}_{lr}|{\mathit{T}}_{lr}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\hfill \end{array}, \mathrm{with} {\mathit{R}}_{lr}=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right] \mathrm{and} {\mathit{T}}_{lr}=\left[\begin{array}{c}{T}_x\\ T_y\\ T_z\end{array}\right],$$

(2)

where ${\mathit{R}}_{lr }$ and ${\mathit{T}}_{lr}$ denotes the rotation matrix and translation vector from the left camera coordinate system to the right camera coordinate system. From Equation (2), P$\left(X_w,Y_w, Z_w\right)$ in the world coordinate system can be derived as.

$$\{\begin{array}{l}{X}_w=x_{nl}{Z}_w\hfill \\ Y_w=y_{nl}{Z}_w\hfill \\ Z_w=\frac{T_x-x_{nr}{T}_z}{x_{nr}\left(r_{31}{x}_{nl}+r_{32}{y}_{nl}+r_{33}\right)-\left(r_{11}{x}_{nl}+r_{12}{y}_{nl}+r_{13}\right)}\hfill \\ =\frac{T_y-y_{nr}{T}_z}{y_{nr}\left(r_{31}{x}_{nl}+r_{32}{y}_{nl}+r_{33}\right)-\left(r_{21}{x}_{nl}+r_{22}{y}_{nl}+r_{23}\right)}\hfill \end{array},$$

(3)

3. Camera Movement Errors

In the stereo-vision system, ${\mathit{A}}_l$, ${\mathit{A}}_r$,${\mathit{R}}_{lr }$ and ${\mathit{T}}_{lr}$ have been calibrated before measurement. It is generally assumed that the intrinsic parameters (${\mathit{A}}_l$, ${\mathit{A}}_r$) are unaffected during slight camera movements. However, the extrinsic parameters (${\mathit{R}}_{lr}, {\mathit{T}}_{lr}$) and the global world coordinate system coinciding with the left camera coordinate system have been altered. The movement of a camera is composed of both translation and rotation, which correspond to the change of position and orientation. To clarify how the 3D coordinate error is varied with the changes of the positions and orientations of two cameras, we have divided the camera movements into four categories as below.

(1)

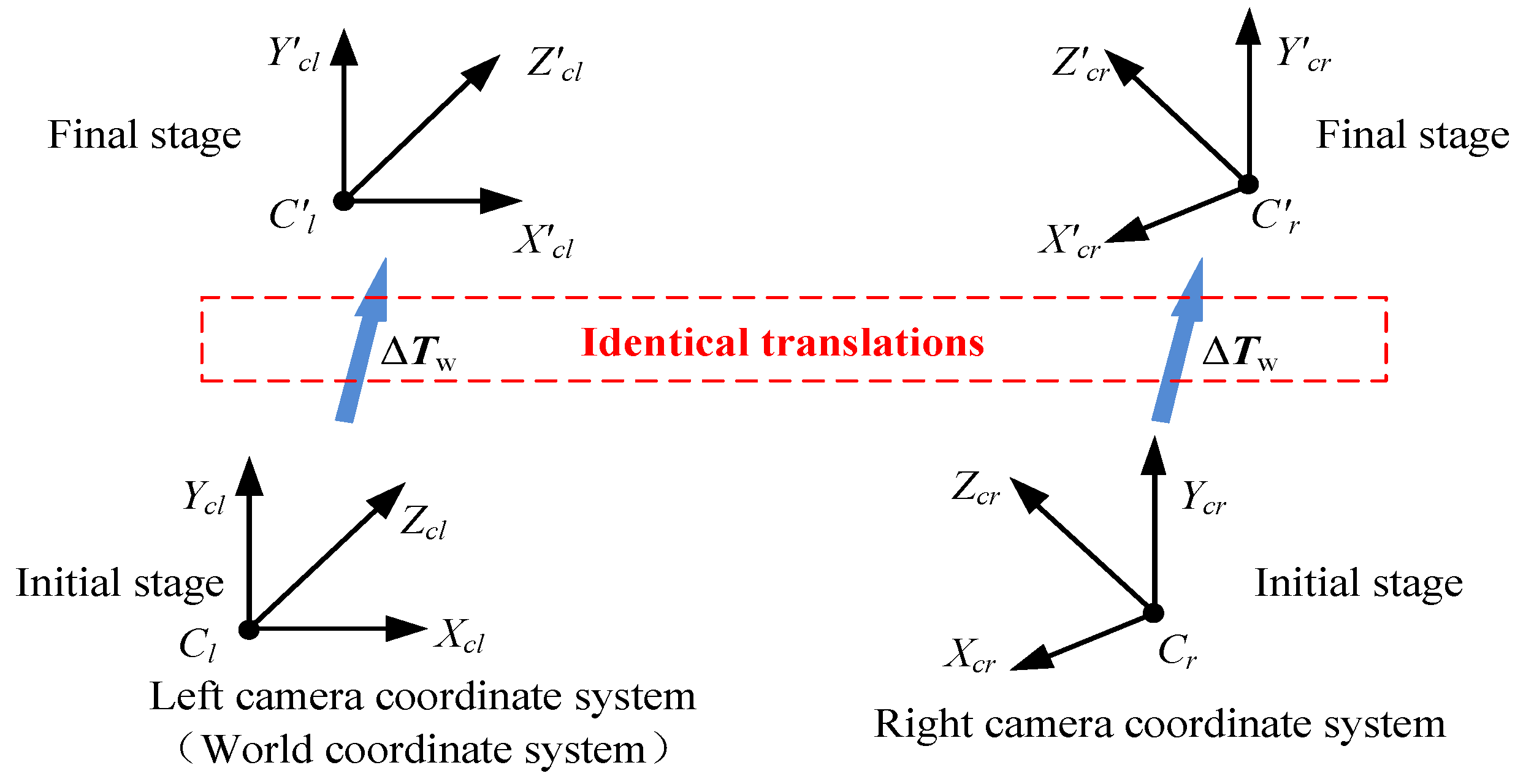
Identical translations of the left and right cameras when the positions and orientations of their optical centers have the same changes.

(2)

Identical rotations of the two cameras when the orientations of two cameras have the same changes.

(3)

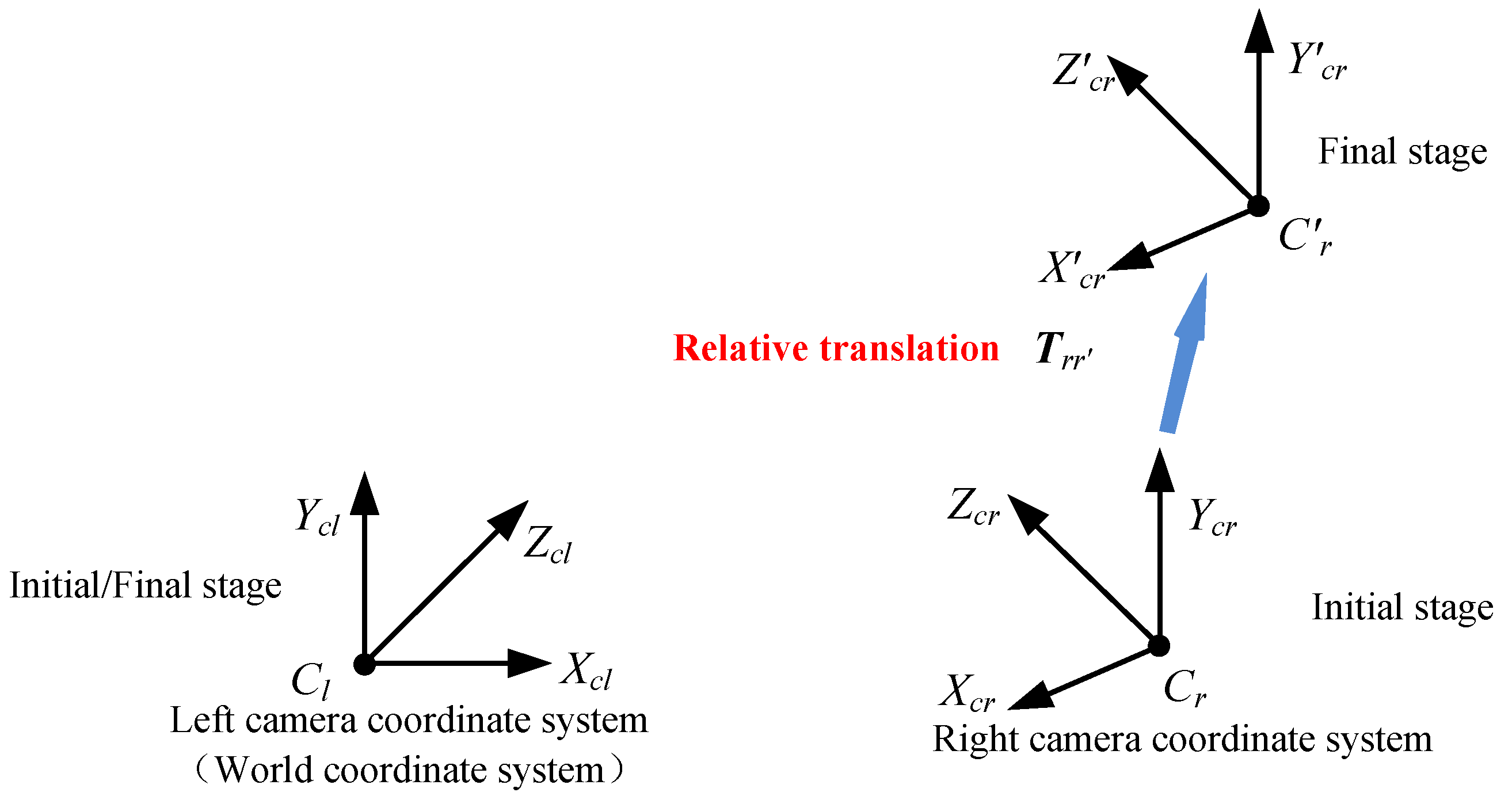
Relative translation when the position of the left camera relative to that of the right camera is changed.

(4)

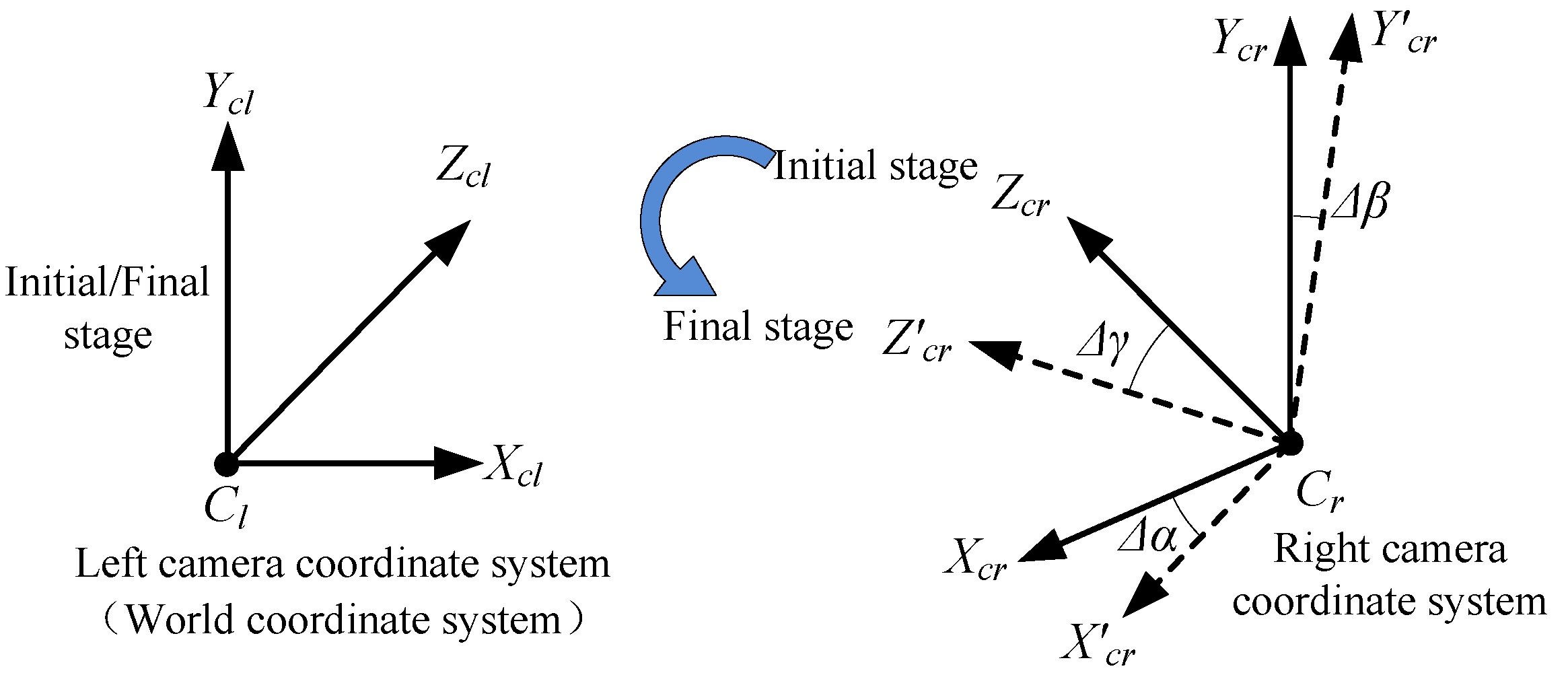
Relative rotation when the orientation of the left camera relative to that of the right camera is changed.

3.1. Identical Translations

Figure 2 shows the relationship between a pair of camera coordinate systems before and after identical translations. In this case, the global world coordinate system experiences rigid body translations. The translation amount is denoted by $\mathrm{∆}{\mathit{T}}_w={\left[\mathrm{∆}{T}_{wx}, \mathrm{∆}{T}_{wy}, \mathrm{∆}{T}_{wz}\right]}^T$. Let the world coordinate of any point, before and after identical translations, be ${\mathit{X}}_w\left(X_w,Y_w, Z_w\right)$ and ${\mathit{}}_w^{\prime }\left(X_w^{\prime },Y_w^{\prime }, Z_w^{\prime }\right)$, respectively. $\mathrm{∆}{\mathit{T}}_w$ is considered to be the error introduced in the initial 3D coordinate ${\mathit{X}}_w$. Then, the 3D coordinate error $\mathrm{∆}{\mathit{X}}_w$ is described as follows.

$$\mathrm{\Delta }{\mathit{X}}_w=\left[\begin{array}{c}{X}_w^{\prime }\\ Y_w^{\prime }\\ Z_w^{\prime }\end{array}\right]-\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]=\left[\begin{array}{c}\mathrm{\Delta }{T}_{wx}\\ \mathrm{\Delta }{T}_{wy}\\ \mathrm{\Delta }{T}_{wz}\end{array}\right],$$

(4)

From Equation (4), the 3D coordinate error $\mathrm{∆}{\mathit{X}}_{w }$ is equal to the identical translation $\mathrm{∆}{\mathit{T}}_w$.

Suppose that any two points on the measured object are defined as ${\mathit{X}}_{w1}\left(X_{w1},Y_{w1}, Z_{w1}\right)$ and ${\mathit{X}}_{w2}\left(X_{w2},Y_{w2}, Z_{w2}\right)$ in the initial world coordinate system. After camera movements, ${\mathit{X}}_{w1}^{\prime }\left(X_{w1}^{\prime },Y_{w1}^{\prime }, Z_{w1}^{\prime }\right)$ and ${\mathit{X}}_{w2}^{\prime }\left(X_{w2}^{\prime },Y_{w2}^{\prime }, Z_{w2}^{\prime }\right)$ are the corresponding points in the new world coordinate system. The distances between the two selected points before and after the identical translations are expressed as

$$\{\begin{array}{l}{L}_w=\sqrt{{\left(X_{w1}-X_{w2}\right)}^2+{\left(Y_{w1}-Y_{w2}\right)}^2+{\left(Z_{w1}-Z_{w2}\right)}^2}\hfill \\ L_w^{\prime }=\sqrt{{\left(X_{w1}^{\prime }-X_{w2}^{\prime }\right)}^2+{\left(Y_{w1}^{\prime }-Y_{w2}^{\prime }\right)}^2+{\left(Z_{w1}^{\prime }-Z_{w2}^{\prime }\right)}^2}\hfill \end{array},$$

(5)

For the two pairs of points, viz., ${\mathit{X}}_{w1}$ and ${\mathit{X}}_{w1}^{\prime }$, ${\mathit{X}}_{w2}$ and ${\mathit{X}}_{w2}^{\prime }$, the following relations from Equation (4) can be obtained as

$$\{\begin{array}{l}{X}_{w1}^{\prime }=X_{w1}+\mathrm{\Delta }{T}_{wx}\hfill \\ Y_{w1}^{\prime }=Y_{w1}+\mathrm{\Delta }{T}_{wy}\hfill \\ Z_{w1}^{\prime }=Z_{w1}+\mathrm{\Delta }{T}_{wz}\hfill \end{array},\{\begin{array}{l}{X}_{w2}^{\prime }=X_{w2}+\mathrm{\Delta }{T}_{wx}\hfill \\ Y_{w2}^{\prime }=Y_{w2}+\mathrm{\Delta }{T}_{wy}\hfill \\ Z_{w2}^{\prime }=Z_{w2}+\mathrm{\Delta }{T}_{wz}\hfill \end{array}$$

(6)

Combining Equations (5) and (6) yields the following expression

$$L_w=L_w^{\prime }$$

(7)

It was concluded that the distance between any two points remains unchanged after identical translations.

Displacement and strain form an important group of parameters concerning the deformation measurement. Displacement represents the change of position of an object in a certain period of time. Strain refers to the ratio of the change in length of a small line segment to the original length. From Equations (4) and (7), the error in measuring the displacement should be equal to the amount of identical translations, while the strain measurement is not affected.

3.2. Identical Rotations

The identical rotations of two cameras in a stereo-vision system imply that the global world coordinate system experiences a rigid body rotation, as shown in Figure 3. The 3D coordinate error $\mathrm{∆}{\mathit{X}}_w$ can be expressed as

$$\left[\begin{array}{c}\mathrm{\Delta }{X}_w\\ \mathrm{\Delta }{Y}_w\\ \mathrm{\Delta }{Z}_w\end{array}\right]=\left[\begin{array}{c}{X}_w^{\prime }\\ Y_w^{\prime }\\ Z_w^{\prime }\end{array}\right]-\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]=\mathrm{\Delta }{\mathit{R}}_w\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]-\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]$$

(8)

where $\mathrm{∆}{\mathit{R}}_w$ denotes the transformation from the initial world coordinate system to the final world coordinate system owing to the identical rotations of both cameras.

The rotation matrix $\mathrm{∆}{\mathit{R}}_w$ is a 3 × 3-unit orthogonal matrix, and depends only on three independent variables. Therefore, $\mathrm{∆}{\mathit{R}}_w$ can be represented as

$$\mathrm{\Delta }{\mathit{R}}_w=\left[\begin{array}{ccc}\cos \tilde{\gamma }& -\sin \tilde{\gamma }& 0\\ \sin \tilde{\gamma }& \cos \tilde{\gamma }& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \tilde{\alpha }& -\sin \tilde{\alpha }\\ 0& \sin \tilde{\alpha }& \cos \tilde{\alpha }\end{array}\right]\left[\begin{array}{ccc}\cos \tilde{\beta }& 0& -\sin \tilde{\beta }\\ 0& 1& 0\\ \sin \tilde{\beta }& 0& \cos \tilde{\beta }\end{array}\right]$$

(9)

where $\left(\tilde{\alpha },\tilde{\beta }, \tilde{\gamma }\right)$ are defined as the rotation angles that the initial world coordinate system is transformed to the orientation that coincides with the final world coordinate system.

The unavoidable camera movements are often slight, and then the rotation angles $\left(\tilde{\alpha },\tilde{\beta }, \tilde{\gamma }\right)$ can be set to a small value. By taking the small angle approximation, i.e., $\sin \tilde{\alpha }\approx \tilde{\alpha }, \cos \tilde{\alpha }\approx 1, \sin \tilde{\beta }\approx \tilde{\beta }, \cos \tilde{\beta }\approx 1, \sin \tilde{\gamma }\approx \tilde{\gamma }, \cos \tilde{\gamma }\approx 1$, we have

$$\{\begin{array}{l}\mathrm{\Delta }{X}_w\approx \tilde{\beta }\tilde{\alpha }\tilde{\gamma }{X}_w-\tilde{\gamma }{Y}_w+\left(-\tilde{\beta }+\tilde{\alpha }\tilde{\gamma }\right)Z_w\hfill \\ \mathrm{\Delta }{Y}_w\approx \left(\tilde{\gamma }-\tilde{\beta }\tilde{\alpha }\right)X_w+\left(-\tilde{\beta }\tilde{\gamma }-\tilde{\alpha }\right)Z_w\hfill \\ \mathrm{\Delta }{Z}_w\approx \tilde{\beta }{X}_w+\tilde{\alpha }{Y}_w\hfill \end{array}$$

(10)

From Equation (10), the 3D coordinate error $\mathrm{∆}{\mathit{X}}_w$ has a linear relationship with the identical rotation angle of the two cameras.

According to Equation (8), the distance between the two measured points after camera movement can be described as

$$L_w^{\prime }=\Vert {\mathit{X}}_{w1}^{\prime }-{\mathit{X}}_{w2}^{\prime }\Vert =\Vert \mathrm{\Delta }{\mathit{R}}_w\left({\mathit{X}}_{w1}-{\mathit{X}}_{w2}\right)\Vert$$

(11)

Since $\parallel \mathrm{∆}{\mathit{R}}_w\parallel =1$, we have $L_w=L_w^{\prime }$. It indicates that the distance between any two points is unaffected by the identical rotations of two cameras.

3.3. Relative Translations

As shown in Figure 4, the relative translation can be regarded as the case in which the left camera is fixed and only the translation of the right camera causes the position between the two cameras to change. The translation vector between the right camera coordinate systems before and after camera movement is expressed by ${\mathit{T}}_{r{r}^{\prime }}={\left[\mathrm{∆}{T}_x, \mathrm{∆}{T}_y, \mathrm{∆}{T}_z\right]}^T$. According to Equation (3), the 3D coordinate error $\mathrm{∆}{\mathit{X}}_w$ can be described as

$$\{\begin{array}{l}\mathrm{\Delta }{X}_w=x_{nl}\mathrm{\Delta }{Z}_w\hfill \\ \mathrm{\Delta }{Y}_w=y_{nl}\mathrm{\Delta }{Z}_w\hfill \\ \mathrm{\Delta }{Z}_w=\frac{\mathrm{\Delta }{T}_x-x_{nr}\mathrm{\Delta }{T}_z}{x_{nr}\left(r_{31}{x}_{nl}+r_{32}{y}_{nl}+r_{33}\right)-\left(r_{11}{x}_{nl}+r_{12}{y}_{nl}+r_{13}\right)}\hfill \\ \hspace{1em}\hspace{1em}=\frac{\mathrm{\Delta }{T}_y-y_{nr}\mathrm{\Delta }{T}_z}{y_{nr}\left(r_{31}{x}_{nl}+r_{32}{y}_{nl}+r_{33}\right)-\left(r_{21}{x}_{nl}+r_{22}{y}_{nl}+r_{23}\right)}\hfill \end{array}$$

(12)

According to Equation (12), $\mathrm{∆}{\mathit{X}}_w$ is linear with the change of relative translation vector, and the coefficient depends on the normalized image coordinates $\left(x_{nl},y_{nl}\right)$ and $\left(x_{nr},y_{nr}\right)$, and the relative rotation matrix ${\mathit{R}}_{lr}$. Since each point in the field of view of both cameras has a specific image coordinate, $\mathrm{∆}{\mathit{X}}_w$ varies with different measuring points. Therefore, the 3D coordinate errors of any two points owing to the relative translation are described as

$$\{\begin{array}{l}\mathrm{\Delta }{X}_{w1}=X_{w1}^{\prime }-X_{w1}\hfill \\ \mathrm{\Delta }{Y}_{w1}=Y_{w1}^{\prime }-Y_{w1}\hfill \\ \mathrm{\Delta }{Z}_{w1}=Z_{w1}^{\prime }-Z_{w1}\hfill \end{array},\{\begin{array}{l}\mathrm{\Delta }{X}_{w2}=X_{w2}^{\prime }-X_{w2}\hfill \\ \mathrm{\Delta }{Y}_{w2}=Y_{w2}^{\prime }-Y_{w2}\hfill \\ \mathrm{\Delta }{Z}_{w2}=Z_{w2}^{\prime }-Z_{w2}\hfill \end{array}$$

(13)

Based on Equation (13), the distance between two selected points after camera movement can be expanded with Taylor’s formula [39]. Ignoring the second-order term, the linearized equation of distance error is expressed as follows.

$$\begin{array}{l}\mathrm{\Delta }{L}_w=L_w^{\prime }-L_w\\ =\mathrm{\Delta }{X}_{w1}\frac{X_{w1}^0-X_{w2}^0}{L_w}+\mathrm{\Delta }{Y}_{w1}\frac{Y_{w1}^0-Y_{w2}^0}{L_w}+\mathrm{\Delta }{Z}_{w1}\frac{Z_{w2}^0-Z_{w1}^0}{L_w}-\mathrm{\Delta }{X}_{w2}\frac{X_{w1}^0-X_{w2}^0}{L_w}-\mathrm{\Delta }{Y}_{w2}\frac{Y_{w1}^0-Y_{w2}^0}{L_w}-\mathrm{\Delta }{Z}_{w2}\frac{Z_{w2}^0-Z_{w1}^0}{L_w}\end{array}$$

(14)

Combining Equations (12) to (14), we find that the distance measurement error varies linearly with the change in the relative translation vector.

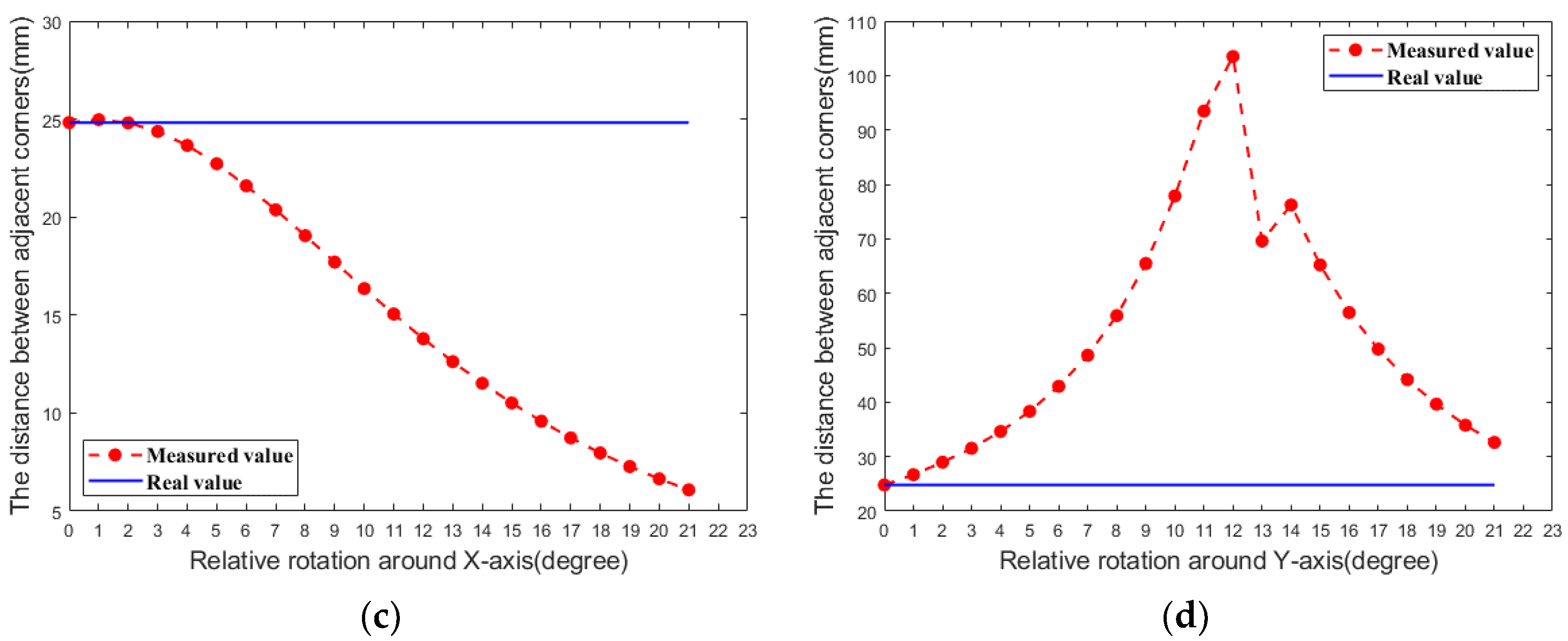
3.4. Relative Rotation

As shown in Figure 5, the relative rotation between two cameras can be treated as a process in which the left camera coordinate system is fixed while the right camera coordinate system is rotated. The rotation matrix ${\mathit{R}}_{lr}^{\prime }$ between the two camera coordinate systems after the camera movement can be expressed as

$${{\mathit{R}}^{\prime }}_{lr}={\mathit{R}}_{lr}{\mathit{R}}_{r{r}^{\prime }}, \mathrm{with} {\mathit{R}}_{r{r}^{\prime }}=\left[\begin{array}{ccc}\mathrm{\Delta }{r}_{11}& \mathrm{\Delta }{r}_{12}& \mathrm{\Delta }{r}_{13}\\ \mathrm{\Delta }{r}_{21}& \mathrm{\Delta }{r}_{22}& \mathrm{\Delta }{r}_{23}\\ \mathrm{\Delta }{r}_{31}& \mathrm{\Delta }{r}_{32}& \mathrm{\Delta }{r}_{33}\end{array}\right]$$

(15)

where ${\mathit{R}}_{lr}$ denotes the initial rotation matrix, ${\mathit{R}}_{r{r}^{\prime }}$ represents the transformation matrix between right camera coordinate systems before and after camera movement.

According to Equation (3), the 3D coordinate error $\mathrm{∆}{\mathit{X}}_w$ introduced by relative rotation can be expressed as

$$\{\begin{array}{l}\mathrm{\Delta }{X}_w=x_{nl}\mathrm{\Delta }{Z}_w\\ \mathrm{\Delta }{Y}_w=y_{nl}\mathrm{\Delta }{Z}_w\\ \mathrm{\Delta }{Z}_w=\frac{T_x-x_{nr}{T}_z}{x_{nr}\left(x_{nl}{\displaystyle \sum _{i=1}^3{r}_{3i}\mathrm{\Delta }{r}_{i1}}+y_{nl}{\displaystyle \sum _{i=1}^3{r}_{3i}\mathrm{\Delta }{r}_{i2}}+{\displaystyle \sum _{i=1}^3{r}_{3i}\mathrm{\Delta }{r}_{i3}}\right)-\left(x_{nl}{\displaystyle \sum _{i=1}^3{r}_{1i}\mathrm{\Delta }{r}_{i1}}+y_{nl}{\displaystyle \sum _{i=1}^3{r}_{1i}\mathrm{\Delta }{r}_{i2}}+{\displaystyle \sum _{i=1}^3{r}_{1i}\mathrm{\Delta }{r}_{i3}}\right)}\\ \hspace{1em}\hspace{1em}-\frac{T_x-x_{nr}{T}_z}{x_{nr}\left(x_{nl}{r}_{31}+y_{nl}{r}_{32}+r_{33}\right)-\left(x_{nl}{r}_{11}+y_{nl}{r}_{12}+r_{13}\right)}\end{array}$$

(16)

Similar to Equation (9), ${\mathit{R}}_{r{r}^{\prime }}$ can be expressed by three rotation angles $\mathrm{∆}\alpha$, $\mathrm{∆}\beta$, and $\mathrm{∆}\gamma$. If the right camera is only subjected to one rotation angle movement, for instance, $\mathrm{∆}\alpha$ ≠ 0, $\mathrm{∆}\beta$ = 0 and $\mathrm{∆}\gamma$ = 0, Equation (16) becomes

$$\{\begin{array}{l}\mathrm{\Delta }{X}_w=x_{nl}\mathrm{\Delta }{Z}_w\hfill \\ \mathrm{\Delta }{Y}_w=y_{nl}\mathrm{\Delta }{Z}_w\hfill \\ \mathrm{\Delta }{Z}_w=\frac{T_x-x_{nr}{T}_z}{\left(x_{nr}{y}_{nl}{r}_{32}+x_{nr}{r}_{33}-y_{nl}{r}_{12}-r_{13}\right)\cos \mathrm{\Delta }\alpha +\left(x_{nr}{y}_{nl}{r}_{33}-x_{nr}{r}_{32}-y_{nl}{r}_{13}+r_{12}\right)\sin \mathrm{\Delta }\alpha +x_{nr}{x}_{nl}{r}_{31}-x_{nl}{r}_{11}}\hfill \\ \hspace{1em}\hspace{1em}-\frac{T_x-x_{nr}{T}_z}{x_{nr}\left(r_{31}{x}_{nl}+r_{32}{y}_{nl}+r_{33}\right)-\left(r_{11}{x}_{nl}+r_{12}{y}_{nl}+r_{13}\right)}\hfill \end{array}$$

(17)

Based on the auxiliary angle formula of the trigonometric function, the denominator of $\mathrm{∆}{Z}_w$ in Equation (17) varies with $\mathrm{∆}\alpha$ according to the shape of a sine-cosine curve, hence, the changes of 3D coordinate measurement error should have a sine-cosine trend. Furthermore, there will be a non-linear variation in the measured distance when the relative rotation occurs in the stereo cameras.

4. Experiments and Results

To verify the analysis and model described in the previous section, four groups of experiments have been performed.

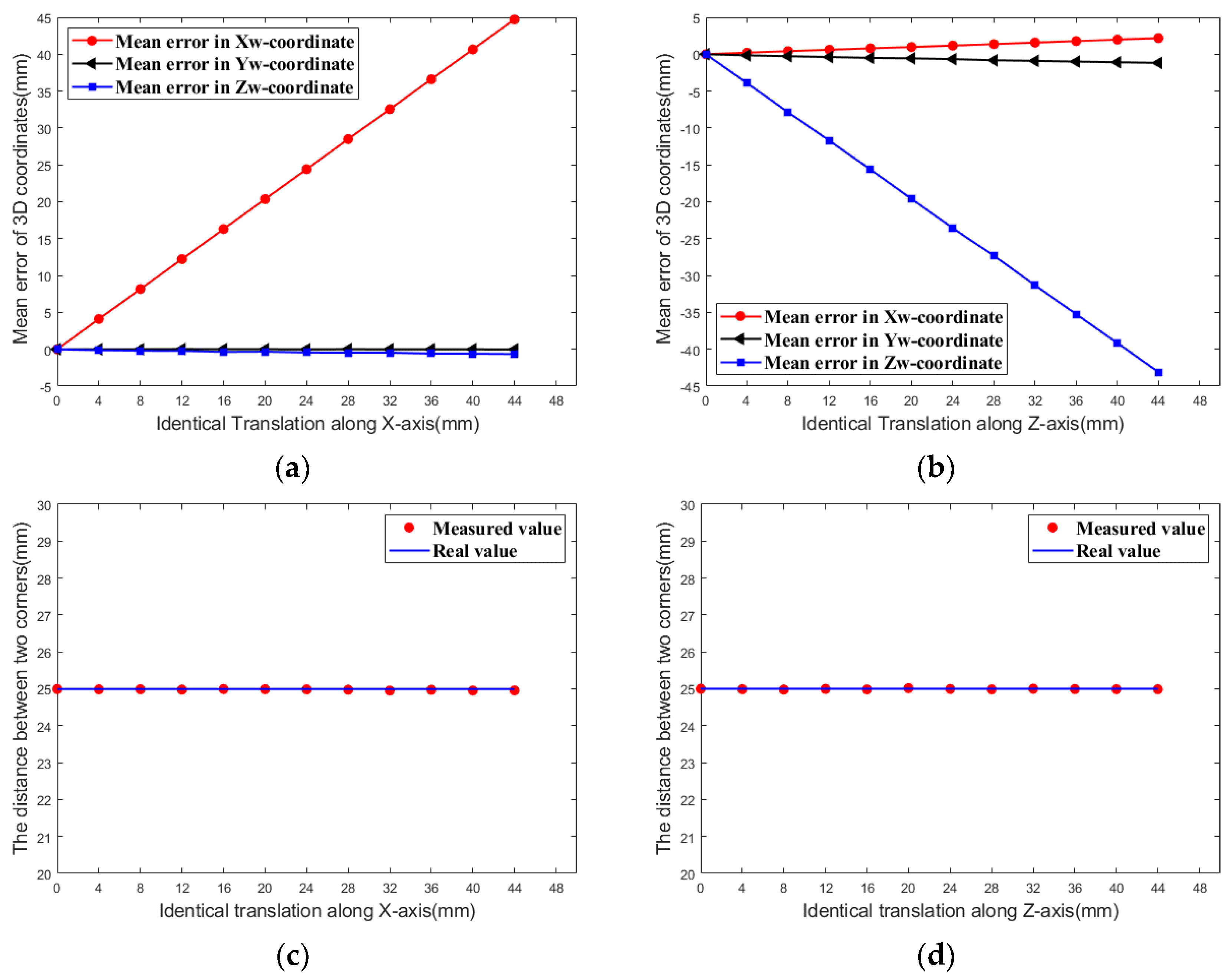
4.1. Identical Translation Experiment

As shown in Figure 6a, the stereo-vision system in this experiment consisted of two MER-1070-14U3x cameras with image resolutions of 3840 × 2748 pixels and lens focal lengths of 8 mm. The left and right cameras are all mounted directly onto an electronic control platform, which consists of a two-dimensional translation stage and a two-axis rotation stage. The accuracy of the translation motion is 0.03 mm, and the rotation accuracy is 0.05°. A flat checkerboard placed at the opposite side of the stereo-vision system is the measured object. The size of each square is 25 mm × 25 mm. Figure 6b shows the high-precision motion controller to achieve the independent translational and rotational movement by the electrical step motors. Figure 6c shows the definition of the coordinate system of the rotational stage. The Z-axis of rotational stage is parallel to the optical axes (i.e., $C_l{Z}_{cl}$ axis and $C_r{Z}_{cr}$ in Figure 1) of the two cameras, and the X and Y-axes are parallel to the camera’s CCD imaging plane.

Before performing translational movement of two cameras, we employ Zhang’s method [39] to calibrate the initial camera parameters (${\mathit{A}}_l$, ${\mathit{A}}_r$,${\mathit{R}}_{lr }$ and ${\mathit{T}}_{lr}$) and the lens distortion parameters (κ1, κ2, κ3, p1, p2). Thereafter, a pair of reference images of the checkerboard is acquired by the left and right cameras simultaneously, as shown in Figure 7a. Subsequently, both the cameras are translated together with the movement of the electronic control platform along the X and Z-axes, respectively. The two cameras are moved by 44 mm with an increment of 4 mm, and 11 image pairs are taken at 11 different positions by the stereo-vision system. Figure 7a also shows the stereo image pair captured in the state of identical translations of 44 mm along the X-axis. The five distortion parameters are used to calculate an ideal distortion-free image. After removing the distortions, we adopt the corner detection algorithm to extract the image coordinates of the corner points in each pair of undistorted images. The world coordinates of the corner points in all the pairs of images can be calculated through the triangulation algorithm. The difference between the 3D world coordinate ${\mathit{X}}_w^{\prime }$ from the image pair at each translational position, and ${\mathit{X}}_w$ from initial reference image pair, is the 3D coordinate error.

Figure 8a,b shows the average ${\mathit{X}}_w^{\prime }-{\mathit{X}}_w$ of all corner points at each translational position while the two cameras are translated along the X and Z-axes, respectively. It can be seen that the 3D coordinate measure ment errors in the three directions increase linearly with the increasing translation. Particularly, the error in $X_w$ direction is higher than that of the other two directions when translating the two cameras along the X-axis. In contrast, the error in $Z_w$ direction is higher than that of the other two directions when translating the two cameras along the Z-axis. In this experiment, the X and Z-axes of the translation stage are parallel to the $X_w$ and $Z_w$ directions of the world coordinate system, respectively. Therefore, the component of 3D coordinates is more greatly affected in the direction along which the two cameras are translated.

Figure 8c,d shows the comparison between the measured and real distance between the adjacent corner points at each translational position. The results show that the impact of identical translation on the distance measurement can be neglected, which is consistent with the theoretical analysis in Section 3.1.

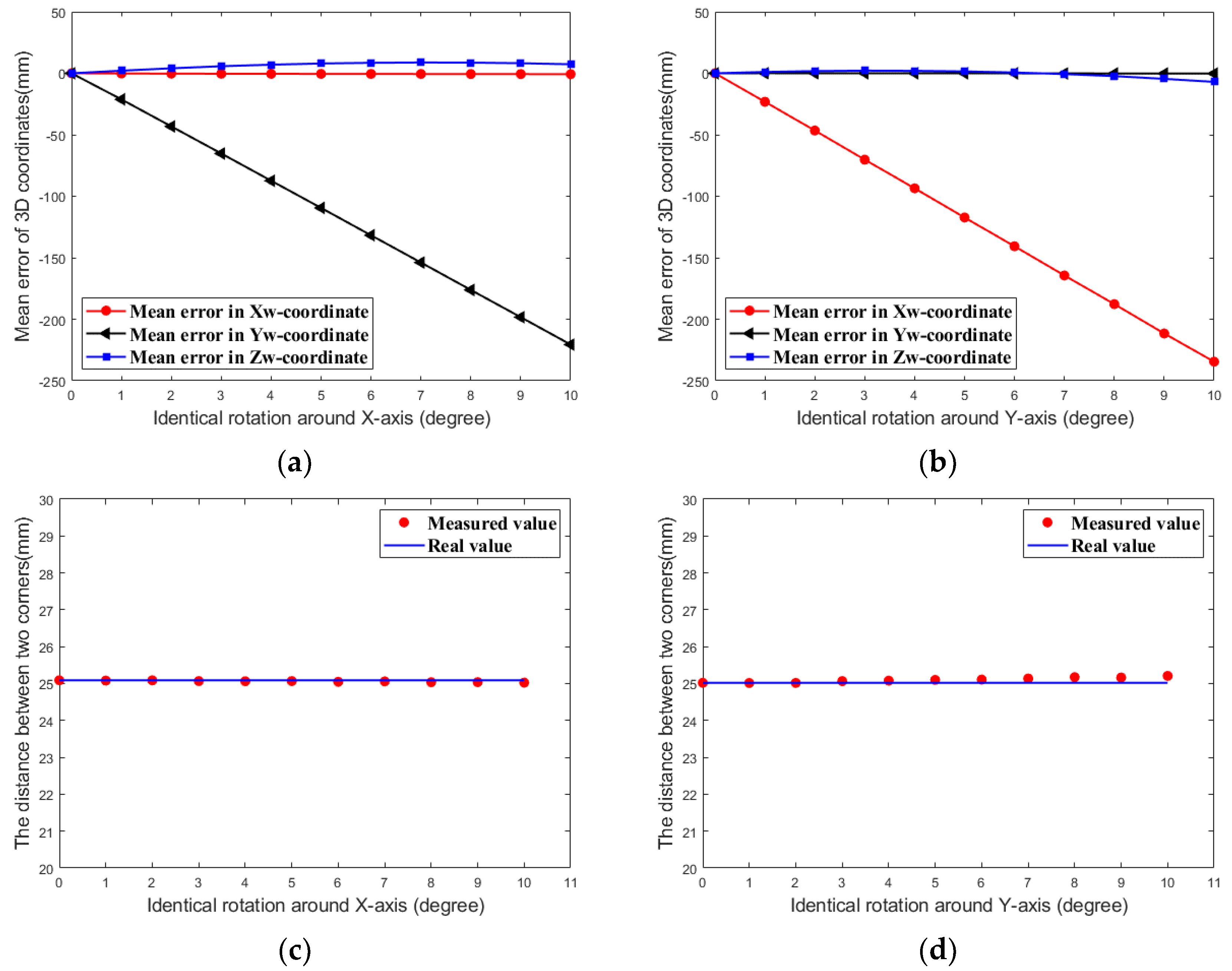
4.2. Identical Rotation Experiment

The experimental setup for identical rotation of the two cameras is the same as that shown in Figure 6. First, a pair of images of the checkerboard are acquired without camera rotation, as shown in Figure 7b. Then both cameras are rotated together from 0° to 10° in an angular step of 1° around the X-axis and Y-axis, respectively. In each rotation pose, a pair of checkerboard images are taken by the left and right cameras, simultaneously. Figure 7b also shows the stereo image pair captured in the state of identical rotations of 10° around the Y-axis.

Figure 9a shows the mean value of the 3D coordinate errors of all the corner points in each rotation pose, while the two cameras are rotated around the X-axis. The 3D coordinate error in $Y_w$ direction is significantly proportional to the rotation angle, and the error coefficient is −22.1 mm/degree. The error in the $Z_w$ direction experiences minuscule change, whereas the error in the $X_w$ direction is always zero. This result can be explained based on the analysis given in Section 3.2. The rotation of both cameras around the X-axis implies that $\tilde{\beta }=0, \tilde{\gamma }=0$. Using Equation (10), we can obtain that $\mathrm{∆}{X}_w\approx 0, \mathrm{∆}{Y}_w\approx -\tilde{\alpha }{Z}_{w0}, \mathrm{∆}{Z}_w\approx \tilde{\alpha }{Y}_{w0}$. Initially, the mean $Z_{w0}$ of all the corner points is 1174 mm. Therefore, the mean error of all corner points in the $Y_w$ direction can be approximated as $\mathrm{∆}{\overline{Y}}_w\approx$ 20.49$\tilde{\alpha }$. Considering the small deviation between the Z-axis of the rotational stage and the $Z_w$ direction of the world coordinate system, the present experimental results succeed in verifying the theoretical model. When the two cameras are rotated around the Y-axis, similar trends have been observed in Figure 9b. We can conclude that the identical rotation of the two cameras in a stereo-vision system produces errors in coordinates only in the rotating plane.

Figure 9c,d shows the measured distance between the adjacent corner points compared to the real distance of 25 mm. The maximum difference is less than 0.08 mm. Therefore, the effect of the identical rotation on the distance measurement can be negligible. This result agrees with the theoretical prediction from Section 3.2 that the angle of identical rotation should have produced zero distance error.

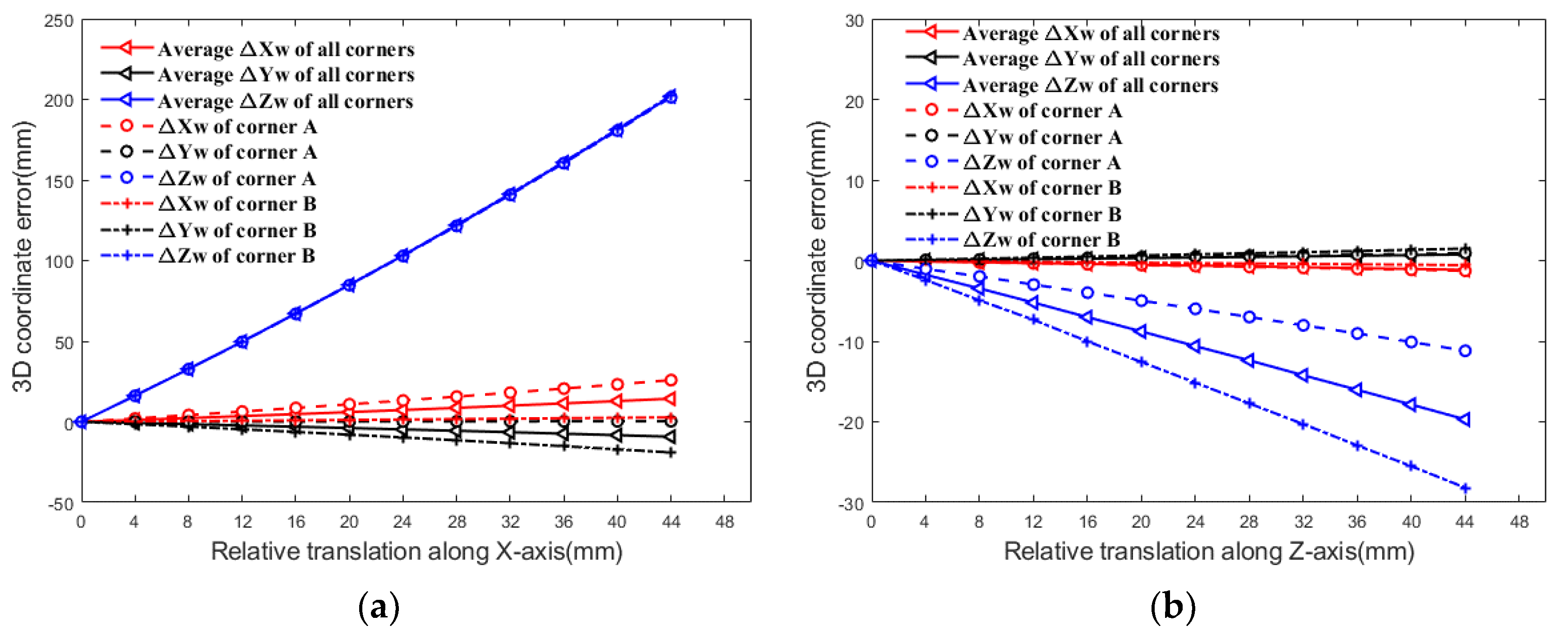
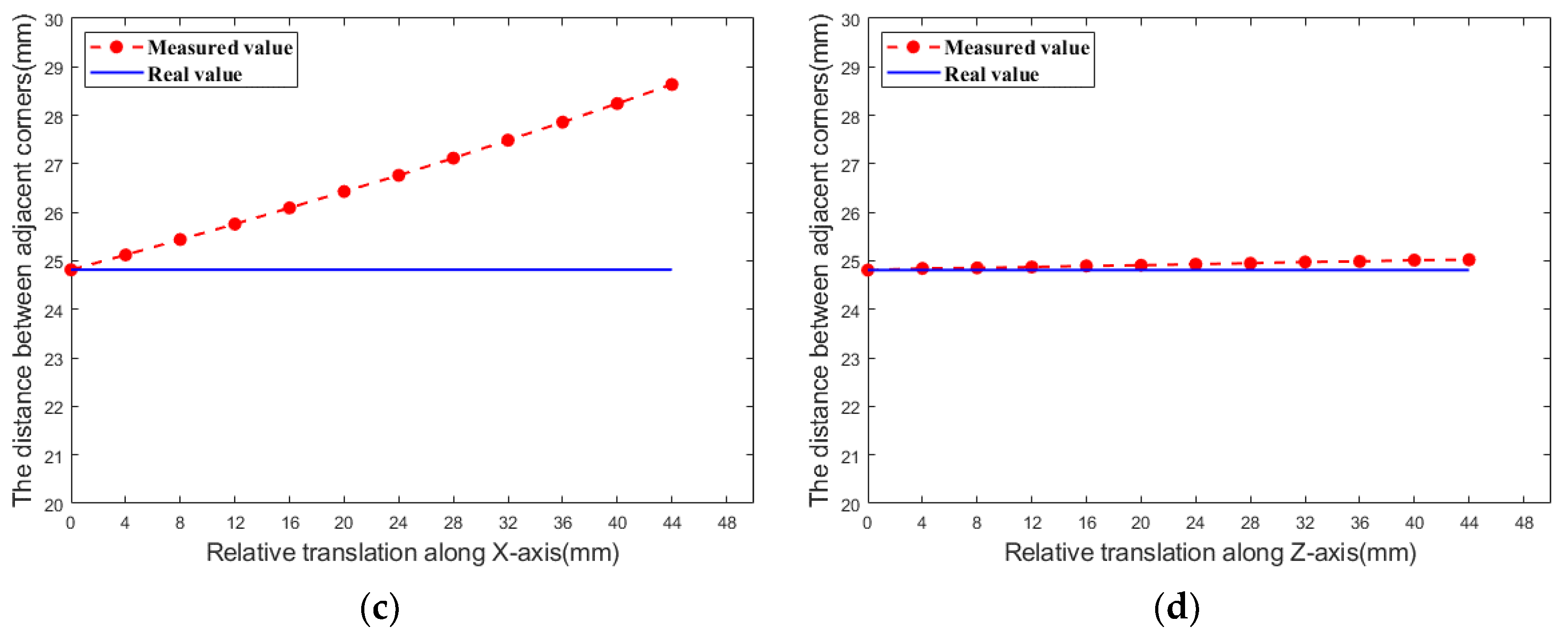
4.3. Relative Translation Experiment

Figure 10 shows the experimental setup for the relative movement between the two cameras. The left camera is fixed directly onto the optical isolation table while the right camera is mounted onto the electronic control platform. The position or orientation of the right camera is changed by controlling the translational or rotational stage.

In the experiment for relative translation, the right camera is translated in 4 mm increments along the X and Z-axes, respectively. Eleven image pairs are captured at 11 different positions by the two cameras. Figure 7c shows the stereo image pairs captured in the initial state and the state of relative translation (44 mm) along X-axis.

Figure 11a,b shows the 3D coordinate error introduced by the relative translation. Two points from the checkerboard (Corner A and B in Figure 9) are selected to analyze the error variation trend. It can be seen that the 3D coordinate error of any point and the mean error of all the corner points in three directions keep linearly increasing with the increasing translation. Specifically, the 3D coordinate errors vary for different measured points on the object. These results effectively verify the theoretical analysis given in Section 3.3.

Figure 11c,d shows the comparisons of the measured distance between the two adjacent points and the real value of 25 mm. It can be seen that the distance error varies linearly with the increasing translation. This trend shows a good agreement with the prediction using Taylor’s formula. In Figure 10, the 3D coordinate and distance error caused by the translation along the X-axis are larger than those along the Z-axis (its optical axis).

4.4. Relative Rotation Experiment

The experimental setup for the relative rotation is the same as that shown in Figure 10. First, a pair of images of the checkerboard is acquired before rotating the right camera, as shown in Figure 7d. Thereafter, the left and right cameras simultaneously take a pair of checkerboard images every time the rotation stage is rotated in an angular step of 1° around the X and Y-axes, respectively. Figure 7d shows the stereo image pair captured in the state of relative rotation (21°) around the X-axis.

Figure 12a,b shows the 3D coordinate error introduced by the relative rotation around X and Y-axes, respectively. It can be observed that the coordinate error of any point (A or B) and the mean error of all corner points in three directions, keep the nonlinear changes of the sine-cosine curve with the increasing rotation angle. These results effectively verify the theoretical analysis given in Section 3.4. Figure 12c,d shows the comparative results of the measured distance between the two adjacent points and the real value of 25 mm. The distance error is not monotonically increasing with the rotation angle.

Furthermore, it is evident from Figure 12 that the 3D coordinate and distance errors caused by the relative rotation are much higher than those caused by the identical translation and rotation, and the relative translation. Even for the occurrence of a rotation angle of 10° during images acquisition, the resultant maximum coordinate error is up to 2000 mm, and the distance error reaches 220%. Therefore, the stereo-vision system is highly sensitive to the relative rotation between the two cameras.

5. Conclusions

Under harsh working conditions, the perfect stability of the two cameras in a stereo-vision system cannot be realized, especially in an outdoor environment. Any slight movements of the cameras can significantly influence the 3D measurement accuracy. In this paper, we have investigated the impact of the camera movement on 3D measurements in detail. The camera movements are divided into four categories, viz., identical translation and rotation, and relative translation and rotation. For each case, the calculation model of the 3D coordinate and distance measurement error was derived. Experimental verification was performed with high-precision translation and rotation stages. The theoretical analysis and experiments have brought some valuable conclusions as follows.

For identical translations, the 3D coordinate measurement error increases linearly with the increasing change in both cameras’ positions while the measurement of the distance between two points remains unaffected.

For identical rotations, the 3D coordinate error is introduced only in the rotating plane, and it is proportional to the rotation angle within 10°. The identical rotation angle of both cameras has no impact on the distance measurement.

For the relative translation, the coordinate error of any measured point in three directions keeps linearly increasing with the increasing translation. Particularly, the coordinate error varies among different points on the object. The distance measurement error is proportional to the change in positions between the two cameras. Furthermore, the errors of the 3D coordinate and distance, caused by the right camera translation along its own optical axis, are less than for those along other directions.

For the relative rotation, the relationship between the 3D coordinate error of a point and the rotation angle can be described as the nonlinear trend of a sine-cosine curve. The distance measurement error does not increase monotonically with the relative rotation angle. Furthermore, the errors of the 3D coordinate and distance measurement, caused by the relative rotation, are significantly larger than those caused by other cases of the camera movement. Even for the occurrence of a rotation angle of 10° during images acquisition, the resultant maximum coordinate error is up to 2000 mm, and the distance error reaches 220%. The stereo-vision system is highly sensitive to the relative rotation between the two cameras.

In brief, we have meticulously analyzed the effect of the unavoidable slight movements of the two cameras on the 3D measurement of an object. The ensuing results are recommended as a guideline to correct the effect of the camera movement, while using a stereo-vision system in a noisy or outdoor environment.