On the Improved Mechanical Properties of Ball-Milled GNPs Reinforced Short Chain Branched-Polyethylene Nanocomposite: Micromechanical Modeling and Fractography Study
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. SCB-PE Nanocomposites Preparation
2.3. Characterization Techniques
3. Results and Discussion
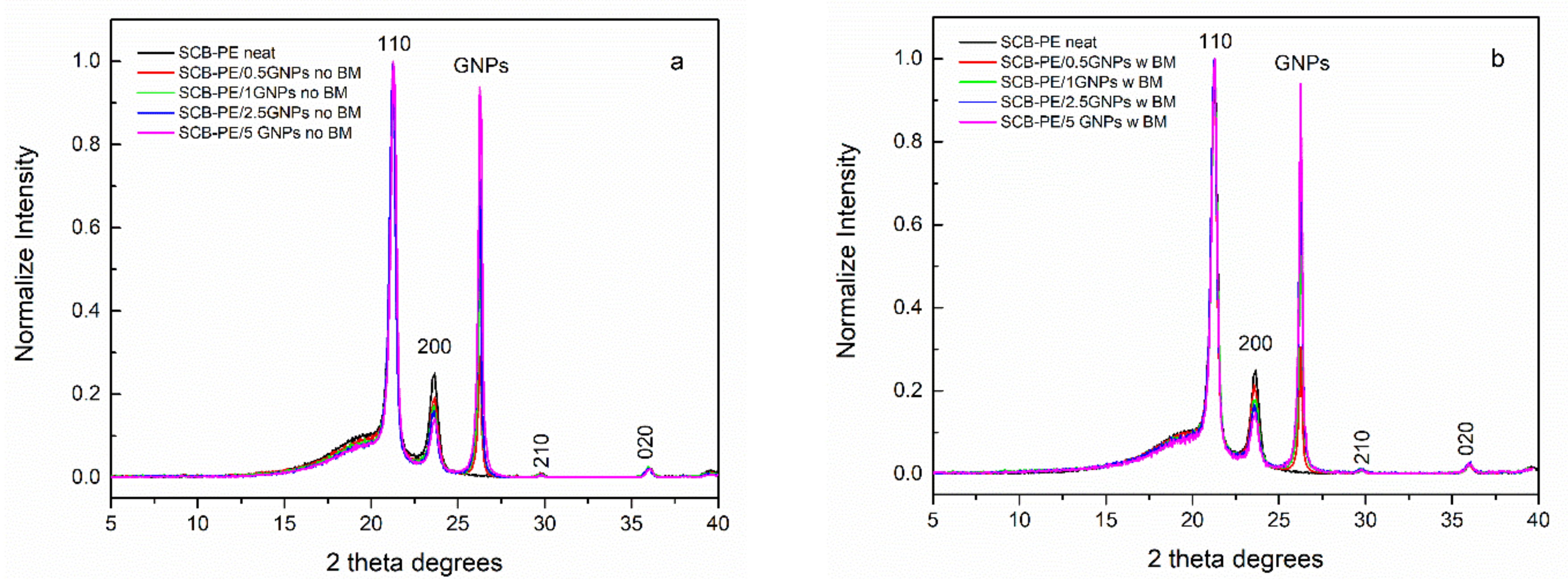
3.1. Structural Investigation
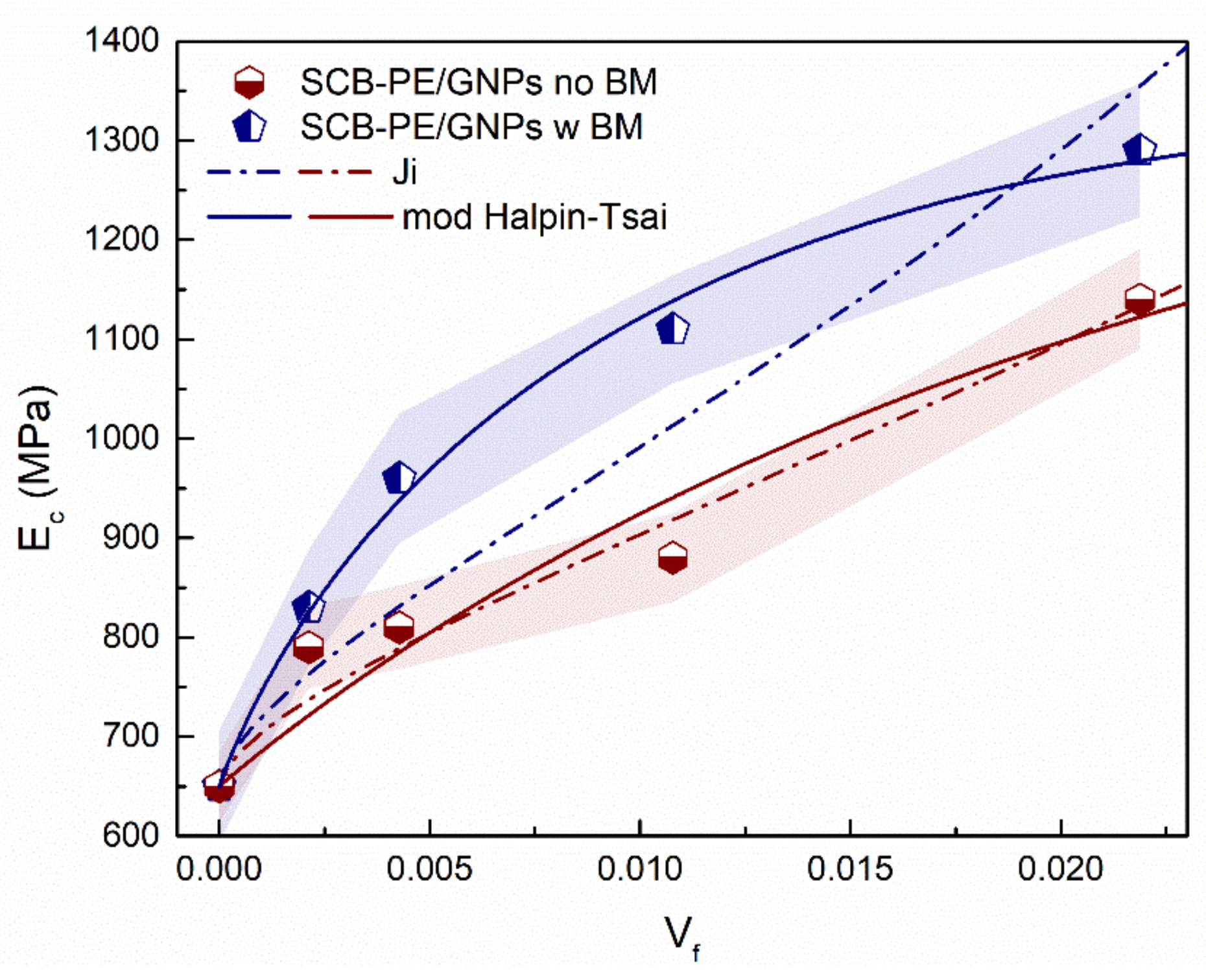
3.2. Tensile Properties
3.3. Scanning Electron Microscopy-Fractography Study
3.4. Shear Test Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gedde, U.W.; Viebke, J.; Leijström, H.; Ifwarson, M. Long-term properties of hot-water polyolefin pipes—A review. Polym. Eng. Sci. 1994, 34, 1773–1787. [Google Scholar] [CrossRef]
- Schramm, D. Polyethylene Used in Industrial Applications at Eleveated Temperatures; Holger Bruening Basell Polyolefine GmbH Industriepark Hoechst: Frankfurt, Germany; Detlef Schramm: Rotterdam, The Netherlands, 2017. [Google Scholar]
- Schramm, D.; Service, T.; Dow, D.; Gmbh, E.; Plastic, E.; Conference, P. Pe-Rt, a New Class of Polyethylene for Pipe. In Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006. [Google Scholar]
- Mendrinos, D.; Katsantonis, S.; Karytsas, C. Pipe materials for borehole heat exchangers. In Proceedings of the European Geothermal Congress, Strasbourg, France, 19–24 September 2016; pp. 19–24. [Google Scholar]
- Šupová, M.; Martynková, G.S.; Barabaszová, K. Effect of nanofillers dispersion in polymer matrices: A review. Sci. Adv. Mater. 2011, 3, 1–25. [Google Scholar] [CrossRef]
- Balasubramanian, K.B.N.; Ramesh, T. Role, effect, and influences of micro and nano-fillers on various properties of polymer matrix composites for microelectronics: A review. Polym. Adv. Technol. 2018, 29, 1568–1585. [Google Scholar] [CrossRef]
- Jankong, S.; Srikulkit, K. Preparation of Polypropylene/Hydrophobic Silica Nanocomposites. J. Met. Mater. Miner. 2008, 18, 143–146. [Google Scholar]
- Chae, D.W.; Kim, B.C. Characterization on polystyrene/zinc oxide nanocomposites prepared from solution mixing. Polym. Adv. Technol. 2005, 16, 846–850. [Google Scholar] [CrossRef]
- Pan, W.; Zou, H. Characterization of PAN/ATO nanocomposites prepared by solution blending. Bull. Mater. Sci. 2008, 31, 807–811. [Google Scholar] [CrossRef]
- Motaung, T.E.; Mochane, M.J.; Linganiso, Z.L.; Mashigo, A.P. In-situ Polymerization of Nylon-Cellulose Nano composite. Polym. Sci. 2017, 3, 1. [Google Scholar] [CrossRef]
- Ambrosio-Martín, J.; Gorrasi, G.; Lopez-Rubio, A.; Fabra, M.J.; Mas, L.C.; Lõpez-Manchado, M.A.; Lagaron, J.M. On the use of ball milling to develop poly(3-hydroxybutyrate-co-3-hydroxyvalerate)-graphene nanocomposites (II)—Mechanical, barrier, and electrical properties. J. Appl. Polym. Sci. 2015, 132, 42217. [Google Scholar] [CrossRef] [Green Version]
- Ambrosio-Martin, J.; Fabra, M.J.; López-Rubio, A.; Gorrasi, G.; Sorrentino, A.; Lagaron, J.M. Assessment of Ball Milling as a Compounding Technique to Develop Nanocomposites of Poly(3-Hydroxybutyrate-co-3-Hydroxyvalerate) and Bacterial Cellulose Nanowhiskers. J. Polym. Environ. 2016, 24, 241–254. [Google Scholar] [CrossRef] [Green Version]
- Delogu, F.; Gorrasi, G.; Sorrentino, A. Fabrication of polymer nanocomposites via ball milling: Present status and future perspectives. Prog. Mater. Sci. 2017, 86, 75–126. [Google Scholar] [CrossRef]
- Burmeister, C.F.; Kwade, A. Process engineering with planetary ball millss. Chem. Soc. Rev. 2013, 42, 7660–7667. [Google Scholar] [CrossRef] [PubMed]
- Taylor, P.; Shao, W.; Wang, Q.; Chen, Y.; Gu, Y. Preparation and Properties of Polypropylene/Vermiculite Nanocomposite Through Solid-State Shear Compounding (S3C) Method Using Pan-Mill Equipment. Mater. Manuf. Process. 2013, 6914, 37–41. [Google Scholar] [CrossRef]
- Xia, H.; Wang, Q.; Li, K.; Hu, G.H. Preparation of polypropylene/carbon nanotube composite powder with a solid-state mechanochemical pulverization process. J. Appl. Polym. Sci. 2004, 93, 378–386. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Realff, M.L.; Kumar, S.; Schiraldi, D.A. Processing, structure, and properties of fibers from polyester/carbon nanofiber composites. Compos. Sci. Technol. 2003, 63, 1617–1628. [Google Scholar] [CrossRef]
- Chen, T.; Liu, H.; Wang, X.; Zhang, H.; Zhang, X. Properties and fabrication of PA66/surface-modified multi-walled nanotubes composite fibers by ball milling and melt-spinning. Polymers 2018, 10, 547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, W.; Xu, J.; Niu, L.; Kang, C.; Ma, B. Effects of high energy ball milling on mechanical and interfacial properties of PBT/nano-Sb2O3 composites. J. Adhes. Sci. Technol. 2018, 32, 291–301. [Google Scholar] [CrossRef]
- Zhang, G.; Schlarb, A.K.; Tria, S.; Elkedim, O. Tensile and tribological behaviors of PEEK/nano-SiO2 composites compounded using a ball milling technique. Compos. Sci. Technol. 2008, 68, 3073–3080. [Google Scholar] [CrossRef]
- Uemura, S.; Takayanagi, M. Application of the theory of elasticity and viscosity of two-phase systems to polymer blends. J. Appl. Polym. Sci. 1966, 10, 113–125. [Google Scholar] [CrossRef]
- Kourtidou, D.; Symeou, E.; Terzopoulou, Z.; Vasileiadis, I.; Kehagias, T.; Pavlidou, E.; Kyratsi, T.; Bikiaris, D.N.; Chrissafis, K. Graphite reinforced silane crosslinked high density polyethylene: The effect of filler loading on the thermal and mechanical properties. Polym. Compos. 2021, 42, 1181–1197. [Google Scholar] [CrossRef]
- Tarani, E.; Chrysafi, I.; Kállay-Menyhárd, A.; Pavlidou, E.; Kehagias, T.; Bikiaris, D.N.; Vourlias, G.; Chrissafis, K. Influence of graphene platelet aspect ratio on the mechanical properties of HDPE nanocomposites: Microscopic observation and micromechanical modeling. Polymers 2020, 12, 1719. [Google Scholar] [CrossRef]
- Ji, X.L.; Jing, J.K.; Jiang, W.; Jiang, B.Z. Tensile modulus of polymer nanocomposites. Polym. Eng. Sci. 2002, 42, 983–993. [Google Scholar] [CrossRef]
- Affdl, J.C.H.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Ouali, N.; Cavaille, J.Y.; Perez, J. Elastic, viscoelastic and plastic behavior of multiphase polymer blends. Plast. Rubber Compos. Process. Appl. 1991, 16, 55–60. [Google Scholar]
- Kourtidou, D.; Grigora, M.E.; Tsongas, K.; Terzopoulou, Z.; Tzetzis, D.; Bikiaris, D.N.; Chrissafis, K. Effect of ball milling on the mechanical properties and crystallization of graphene nanoplatelets reinforced short chain branched-polyethylene. J. Appl. Polym. Sci. 2021, 138, 50874. [Google Scholar] [CrossRef]
- Roumeli, E.; Paraskevopoulos, K.M.; Bikiaris, D.; Chrissafis, K. Effect of high energy ball milling on the structure and mechanical properties of cross-linked high density polyethylene. J. Mater. Sci. 2013, 48, 6753–6761. [Google Scholar] [CrossRef]
- Balani, K.; Verma, V.; Agarwal, A.; Narayan, R. Physical, Thermal, and Mechanical Properties of Polymers. In Biosurfaces; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015; pp. 329–344. [Google Scholar] [CrossRef]
- Amjadi, M.; Fatemi, A. Tensile behavior of high-density polyethylene including the effects of processing technique, thickness, temperature, and strain rate. Polymers 2020, 12, 1857. [Google Scholar] [CrossRef]
- Tarani, E.; Papageorgiou, D.G.; Valles, C.; Wurm, A.; Terzopoulou, Z.; Bikiaris, D.N.; Schick, C.; Chrissafis, K.; Vourlias, G. Insights into crystallization and melting of high density polyethylene/graphene nanocomposites studied by fast scanning calorimetry. Polym. Test. 2018, 67, 349–358. [Google Scholar] [CrossRef] [Green Version]
- Matthews, J.L.; Peiser, H.S.; Richards, R.B. The X-ray measurement of the amorphous content of polythene samples. Acta Crystallogr. 1949, 2, 85–90. [Google Scholar] [CrossRef]
- Zheng, Y.; Fu, Z.; Li, D.; Wu, M. Effects of ball milling processes on the microstructure and rheological properties of microcrystalline cellulose as a sustainable polymer additive. Materials 2018, 11, 1057. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, J.; Li, J.; Chen, S.; Zhu, S.; Li, H.; Cao, Y.; Yang, F.; Xiang, M. Hydrogenated petroleum resin effect on the crystallization of isotactic polypropylene. J. Appl. Polym. Sci. 2013, 130, 25–38. [Google Scholar] [CrossRef]
- Khanam, P.N.; Almaadeed, M.A.; Ouederni, M.; Mayoral, B.; Hamilton, A.; Sun, D. Effect of two types of graphene nanoplatelets on the physico-mechanical properties of linear low-density polyethylene composites. Adv. Manuf. Polym. Compos. Sci. 2016, 2, 67–73. [Google Scholar] [CrossRef] [Green Version]
- Rao, N.; O’Brien, K.; Rao, N.; O’Brien, K. Mechanical Properties of Solid Polymers; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1998; ISBN 9781444319507. [Google Scholar]
- Chatterjee, A.P. A model for the elastic moduli of three-dimensional fiber networks and nanocomposites. J. Appl. Phys. 2006, 100, 054302. [Google Scholar] [CrossRef]
- Halpin, J.C.; Kardos, J.L. Moduli of crystalline polymers employing composite theory. J. Appl. Phys. 1972, 43, 2235–2241. [Google Scholar] [CrossRef]
- Hassanzadeh-Aghdam, M.K.; Jamali, J. A new form of a Halpin-Tsai micromechanical model for characterizing the mechanical properties of carbon nanotube-reinforced polymer nanocomposites. Bull. Mater. Sci. 2019, 42, 117. [Google Scholar] [CrossRef] [Green Version]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Hayward, M.R.; Johnston, J.H.; Dougherty, T.; De Silva, K. Interfacial adhesion: Improving the mechanical properties of silicon nitride fibre-epoxy polymer composites. Compos. Interfaces 2019, 26, 263–273. [Google Scholar] [CrossRef]
- Radebaugh, G.W.; Murtha, J.L.; Julian, T.N.; Bondi, J.N. Methods for evaluating the puncture and shear properties of pharmaceutical polymeric films. Int. J. Pharm. 1988, 45, 39–46. [Google Scholar] [CrossRef]
- Namdev, A.; Telang, A.; Purohit, R. Effect of Graphene Nano Platelets on Mechanical and Physical Properties of Carbon Fibre/Epoxy Hybrid Composites. Adv. Mater. Process. Technol. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Bellemare, S.C.; Bureau, M.N.; Denault, J.; Dickson, J.I. Fatigue crack initiation and propagation in polyamide-6 and in polyamide-6 nanocomposites. Polym. Compos. 2004, 25, 433–441. [Google Scholar] [CrossRef] [Green Version]
- El Aboudi, I.; Mdarhri, A.; Brosseau, C.; Montagne, A.; Elhaouzi, F.; Bouyahia, Z.; Iost, A. Investigating carbon-black-filled polymer composites’ brittleness. Polym. Bull. 2020, 77, 4959–4969. [Google Scholar] [CrossRef]




| Sample | L110 (Å) | L200 (Å) | L110/L200 | Xc% |
|---|---|---|---|---|
| neat SCB-PE | 97.2 | 32.8 | 3 | 53.5 |
| SCB-PE/0.5 GNPs no BM | 100.3 | 33.7 | 3 | 56.3 |
| SCB-PE/1 GNPs no BM | 102.9 | 33.1 | 3.1 | 62.4 |
| SCB-PE/2.5 GNPs no BM | 101.4 | 34.6 | 2.9 | 66.4 |
| SCB-PE/5 GNPs no BM | 99.8 | 33.3 | 3 | 69.4 |
| SCB-PE/0.5 GNPs w BM | 103.5 | 34 | 3 | 53.6 |
| SCB-PE/1 GNPs w BM | 101.8 | 34.4 | 3 | 56.2 |
| SCB-PE/2.5 GNPs w BM | 100.8 | 33.8 | 3 | 57.9 |
| SCB-PE/5 GNPs w BM | 103.8 | 34.2 | 3 | 60.7 |
| Sample | Elastic Modulus (MPa) | Tensile Strength at Yield (MPa) | Tensile Strength at Break (MPa) | Elongation at Break (%) |
|---|---|---|---|---|
| neat SCB-PE | 650 ± 37 | 15 ± 1.3 | 21.3 ± 5.2 | 623 ± 126 |
| SCB-PE/0.5 GNPs no BM | 790 ± 42 | 19.6 ± 0.6 | 29.6 ± 6.3 | 710 ± 152 |
| SCB-PE/1 GNPs no BM | 810 ± 42 | 19.5 ± 1 | 21.9 ± 3.1 | 590 ± 91 |
| SCB-PE/2.5 GNPs no BM | 880 ± 45 | 20.1 ± 1 | 22.3 ± 2.2 | 589 ± 88 |
| SCB-PE/5 GNPs no BM | 1140 ± 51 | 22.6 ± 0.8 | 21.8 ± 3.2 | 421 ± 123 |
| SCB-PE/0.5 GNPs w BM | 830 ± 58 | 20.8 ± 0.6 | 26.4 ± 3.7 | 646 ± 110 |
| SCB-PE/1 GNPs w BM | 960 ± 65 | 21.8 ± 1 | 27.2 ± 3.6 | 583 ± 87 |
| SCB-PE/2.5 GNPs w BM | 1110 ± 55 | 23.1 ± 0.4 | 28.7 ± 2.5 | 424 ± 103 |
| SCB-PE/5 GNPs w BM | 1290 ± 68 | 25.3 ± 1.2 | 28.3 ± 1.3 | 342 ± 121 |
| Model | A/A | Sample | |
|---|---|---|---|
| SCB-PE/GNPs no BM | SCB-PE/GNPs w BM | ||
| Ji | Ei(0) (GPa) | 74.54 | 98.67 |
| τ (nm) | 29.45 | 43.9 | |
| R2 | 0.964 | 0.859 | |
| Modified Halpin-Tsai | fW | 0.23 | 0.94 |
| α | 9.74 | 9.88 | |
| β | 0.76 | 0.47 | |
| R2 | 0.928 | 0.992 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kourtidou, D.; Tsongas, K.; Grigora, M.-E.; Tzetzis, D.; Bikiaris, D.N.; Chrissafis, K. On the Improved Mechanical Properties of Ball-Milled GNPs Reinforced Short Chain Branched-Polyethylene Nanocomposite: Micromechanical Modeling and Fractography Study. Appl. Sci. 2021, 11, 9420. https://doi.org/10.3390/app11209420
Kourtidou D, Tsongas K, Grigora M-E, Tzetzis D, Bikiaris DN, Chrissafis K. On the Improved Mechanical Properties of Ball-Milled GNPs Reinforced Short Chain Branched-Polyethylene Nanocomposite: Micromechanical Modeling and Fractography Study. Applied Sciences. 2021; 11(20):9420. https://doi.org/10.3390/app11209420
Chicago/Turabian StyleKourtidou, Dimitra, Konstantinos Tsongas, Maria-Eirini Grigora, Dimitrios Tzetzis, Dimitrios N. Bikiaris, and Konstantinos Chrissafis. 2021. "On the Improved Mechanical Properties of Ball-Milled GNPs Reinforced Short Chain Branched-Polyethylene Nanocomposite: Micromechanical Modeling and Fractography Study" Applied Sciences 11, no. 20: 9420. https://doi.org/10.3390/app11209420
APA StyleKourtidou, D., Tsongas, K., Grigora, M.-E., Tzetzis, D., Bikiaris, D. N., & Chrissafis, K. (2021). On the Improved Mechanical Properties of Ball-Milled GNPs Reinforced Short Chain Branched-Polyethylene Nanocomposite: Micromechanical Modeling and Fractography Study. Applied Sciences, 11(20), 9420. https://doi.org/10.3390/app11209420