Cardiac Arrhythmia Classification Based on One-Dimensional Morphological Features
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset and Preprocessing
2.2. Proposed One-Dimensional Feature Extraction Method
2.2.1. First-Order Features
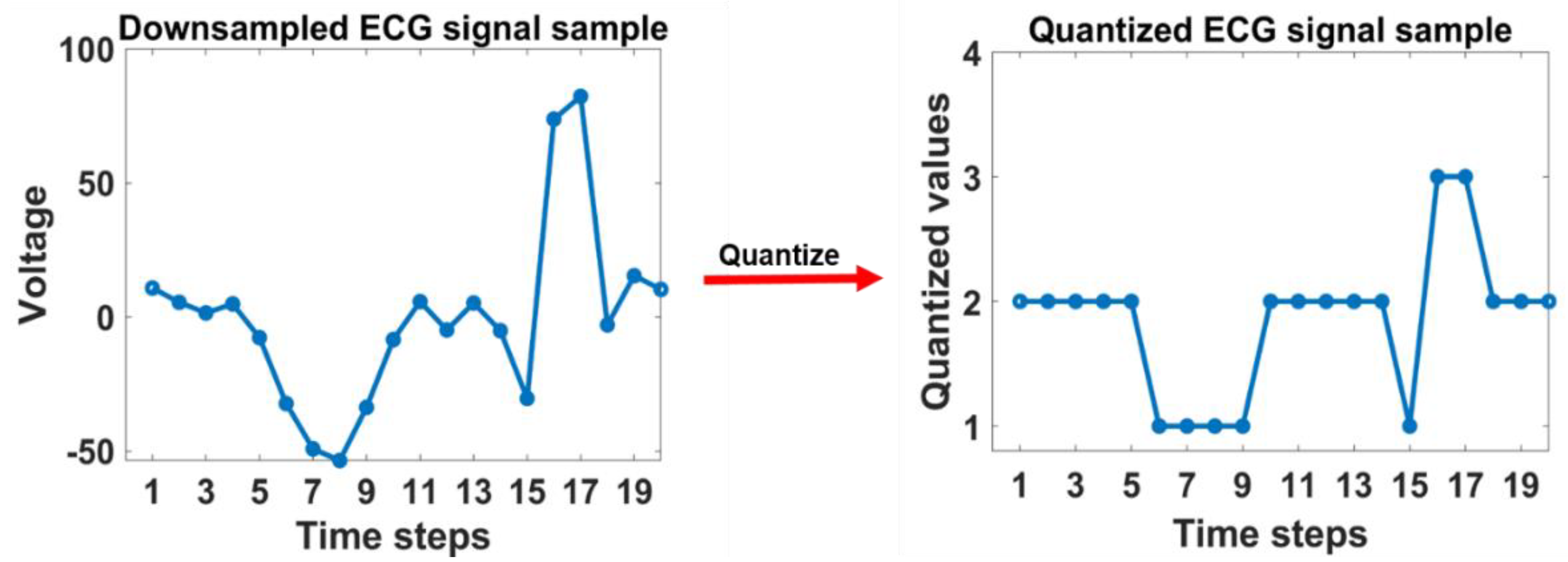
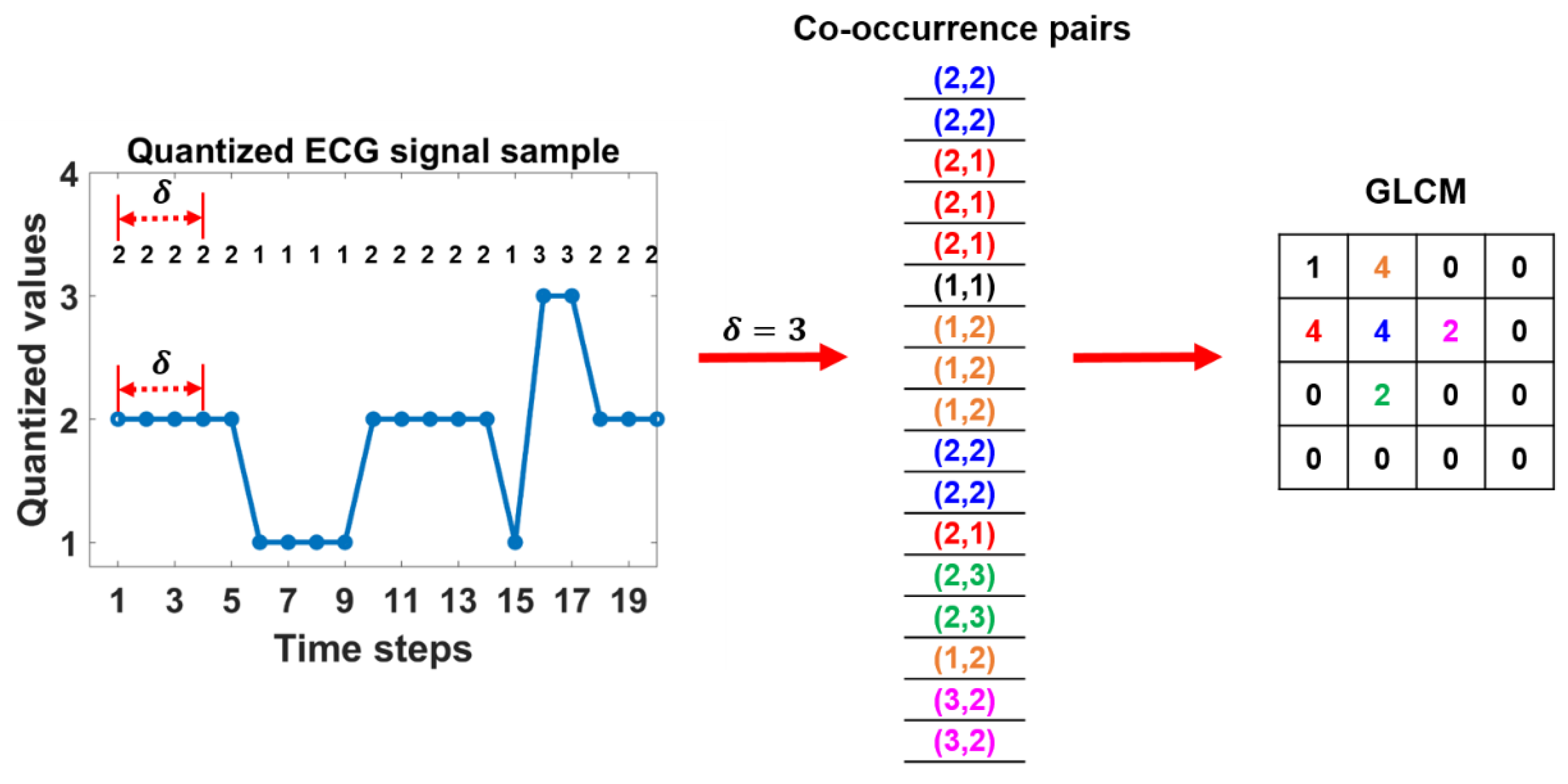
2.2.2. GLCM features
2.2.3. GLRLM Features
2.3. Wavelet Features
2.4. Machine Learning
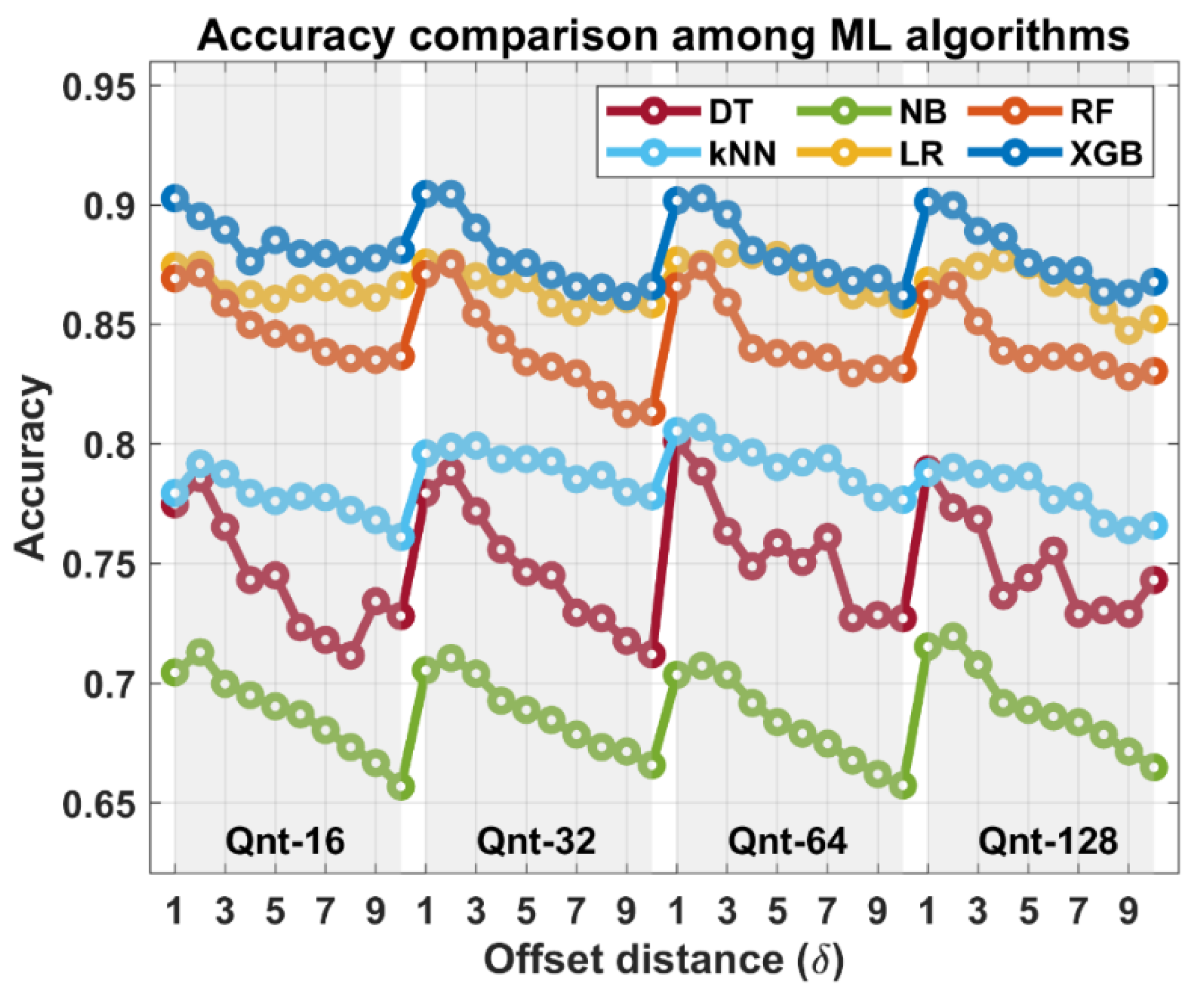
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Cardiovascular Disease (CVDs). 2021. Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 2 September 2021).
- Ribeiro, A.H.; Ribeiro, M.H.; Paixão, G.M.M.; Oliveira, D.M.; Gomes, P.R.; Canazart, J.A.; Ferreira, M.P.S.; Andersson, C.R.; Macfarlane, P.W.; Meira, W., Jr.; et al. Automatic diagnosis of the 12-lead ECG using a deep neural network. Nat. Commun. 2020, 11, 1760. [Google Scholar] [CrossRef] [Green Version]
- Salerno, S.M.; Alguire, P.C.; Waxman, H.S. Competency in interpretation of 12-lead electrocardiograms: A summary and appraisal of published evidence. Ann. Intern. Med. 2003, 138, 751–760. [Google Scholar] [CrossRef] [PubMed]
- Murat, F.; Yildirim, O.; Talo, M.; Baloglu, U.B.; Demir, Y.; Acharya, U.R. Application of deep learning techniques for heartbeats detection using ECG signals-analysis and review. Comput. Biol. Med. 2020, 120, 103726. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Shin, M. Learning Explainable Time-Morphology Patterns for Automatic Arrhythmia Classification from Short Single-Lead ECGs. Sensors 2021, 21, 4331. [Google Scholar] [CrossRef]
- Sahoo, S.; Dash, M.; Behera, S.; Sabut, S. Machine Learning Approach to Detect Cardiac Arrhythmias in ECG Signals: A Survey. IRBM 2020, 41, 185–194. [Google Scholar] [CrossRef]
- de Chazal, P.; Dwyer, M.O.; Reilly, R.B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 2004, 51, 1196–1206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharma, L.D.; Sunkaria, R.K. Inferior myocardial infarction detection using stationary wavelet transform and machine learning approach. Signal. Image Video Process. 2018, 12, 199–206. [Google Scholar] [CrossRef]
- Guo, L.; Sim, G.; Matuszewski, B. Inter-patient ECG classification with convolutional and recurrent neural networks. Biocybern. Biomed. Eng. 2019, 39, 868–879. [Google Scholar] [CrossRef] [Green Version]
- Porumb, M.; Iadanza, E.; Massaro, S.; Pecchia, L. A convolutional neural network approach to detect congestive heart failure. Biomed. Signal Process. Control 2020, 55, 101597. [Google Scholar] [CrossRef]
- Xia, Y.; Wulan, N.; Wang, K.; Zhang, H. Detecting atrial fibrillation by deep convolutional neural networks. Comput. Biol. Med. 2018, 93, 84–92. [Google Scholar] [CrossRef]
- Faust, O.; Shenfield, A.; Kareem, M.; San, T.R.; Fujita, H.; Acharya, U.R. Automated detection of atrial fibrillation using long short-term memory network with RR interval signals. Comput. Biol. Med. 2018, 102, 327–335. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Zhang, H.; Lu, P.; Wang, Z. An Effective LSTM Recurrent Network to Detect Arrhythmia on Imbalanced ECG Dataset. J. Healthc. Eng. 2019, 2019, 6320651. [Google Scholar] [CrossRef] [Green Version]
- Hasan, N.I.; Bhattacharjee, A. Deep Learning Approach to Cardiovascular Disease Classification Employing Modified ECG Signal from Empirical Mode Decomposition. Biomed. Signal Process. Control 2019, 52, 128–140. [Google Scholar] [CrossRef]
- Tanoh, I.-C.; Napoletano, P. A Novel 1-D CCANet for ECG Classification. Appl. Sci. 2021, 11, 2758. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, J.; Danioko, S.; Yao, H.; Guo, H.; Rakovski, C. A 12-lead electrocardiogram database for arrhythmia research covering more than 10,000 patients. Sci. Data 2020, 7, 48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Butterworth, S. On the Theory of Filter Amplifiers. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J. A Review of Image Denoising Algorithms, with a New One. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Galloway, M.M. Texture analysis using gray level run lengths. Comput. Graph. Image Process. 1975, 4, 172–179. [Google Scholar] [CrossRef]
- Vallières, M.; Freeman, C.R.; Skamene, S.R.; El Naqa, I. A radiomics model from joint FDG-PET and MRI texture features for the prediction of lung metastases in soft-tissue sarcomas of the extremities. Phys. Med. Biol. 2015, 60, 5471–5496. [Google Scholar] [CrossRef]
- Parmar, C.; Grossmann, P.; Bussink, J.; Lambin, P.; Aerts, H.J.W.L. Machine Learning methods for Quantitative Radiomic Biomarkers. Sci. Rep. 2015, 5, 13087. [Google Scholar] [CrossRef]
- van Griethuysen, J.J.M.; Fedorov, A.; Parmar, C.; Hosny, A.; Aucoin, N.; Narayan, V.; Beets-Tan, R.G.H.; Fillion-Robin, J.-C.; Pieper, S.; Aerts, H.J.W.L. Computational Radiomics System to Decode the Radiographic Phenotype. Cancer Res. 2017, 77, e104–e107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, G.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Strodthoff, N.; Wagner, P.; Schaeffter, T.; Samek, W. Deep Learning for ECG Analysis: Benchmarks and Insights from PTB-XL. IEEE J. Biomed. Health Inform. 2021, 25, 1519–1528. [Google Scholar] [CrossRef]
- Kang, D.; Park, J.E.; Kim, Y.-H.; Kim, J.H.; Oh, J.Y.; Kim, J.; Kim, Y.; Kim, S.T.; Kim, H.S. Diffusion radiomics as a diagnostic model for atypical manifestation of primary central nervous system lymphoma: Development and multicenter external validation. Neuro-Oncology 2018, 20, 1251–1261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Zhao, X.; Li, Q.; Xia, W.; Peng, Z.; Zhang, R.; Li, Q.; Jian, J.; Wang, W.; Tang, Y.; et al. Can peritumoral radiomics increase the efficiency of the prediction for lymph node metastasis in clinical stage T1 lung adenocarcinoma on CT? Eur. Radiol. 2019, 29, 6049–6058. [Google Scholar] [CrossRef]
- Golden, D.I.; Lipson, J.A.; Telli, M.L.; Ford, J.M.; Rubin, D.L. Dynamic contrast-enhanced MRI-based biomarkers of therapeutic response in triple-negative breast cancer. J. Am. Med. Inf. Assoc. 2013, 20, 1059–1066. [Google Scholar] [CrossRef] [Green Version]


| ECG Rhythm Names | Number of Subjects | Merged Group Names | Number of Subjects |
|---|---|---|---|
| Atrial Fibrillation (AFIB) | 1780 | AFIB | 2218 |
| Atrial Flutter (AF) | 438 | ||
| Atrial Tachycardia (AT) | 121 | GSVT | 2260 |
| Atrioventricular Node Reentrant Tachycardia (AVNRT) | 16 | ||
| Atrioventricular Reentrant Tachycardia (AVRT) | 8 | ||
| Sinus Atrium to Atrial Wandering Rhythm (SAAWR) | 7 | ||
| Sinus Tachycardia (ST) | 1564 | ||
| Supraventricular Tachycardia (SVT) | 544 | ||
| Sinus Bradycardia (SB) | 3888 | SB | 3888 |
| Sinus Rhythm (SR) | 1825 | SR | 2222 |
| Sinus Irregularity (SI) | 397 |
| GLCM Feature Names | Definition | Measure |
|---|---|---|
| Energy | homogeneous patterns | |
| Contrast | local variation, favoring values away from the diagonal () | |
| Entropy | the randomness and variability in neighborhood values | |
| Homogeneity | with more uniform levels; the denominator will remain low, resulting in a higher overall value | |
| Correlation | linear dependency of quantized values on their respective signals in the GLCM | |
| Dissimilarity | local intensity variation defined as the mean absolute difference between the neighboring pairs | |
| Autocorrelation | magnitude of the fineness and coarseness of the texture | |
| Sum average | relationship between occurrences of pairs with lower values and occurrences of pairs with higher values | |
| Variance | groupings of signals with similar quantized values |
| GLRLM Feature Names | Definition | Measure |
|---|---|---|
| Short Run Emphasis | distribution of short run lengths | |
| Long Run Emphasis | distribution of long run lengths | |
| Gray-Level Nonuniformity | similarity of quantized values in the signal | |
| Run-Length Nonuniformity | similarity of run lengths throughout the signal | |
| Run Percentage | coarseness of the signal | |
| Low Gray-Level Run Emphasis | distribution of the lower quantized values | |
| High Gray-Level Run Emphasis | distribution of the higher quantized values | |
| Short Run Low Gray-Level Emphasis | joint distribution of shorter run lengths with lower quantized values | |
| Short Run High Gray-Level Emphasis | joint distribution of shorter run lengths with higher quantized values | |
| Long Run Low Gray-Level Emphasis | joint distribution of long run lengths with lower quantized values | |
| Long Run High Gray-Level Emphasis | joint distribution of long run lengths with higher quantized values | |
| Gray-Level Variance | variance in gray level intensity for the runs | |
| Run-Length Variance | variance in runs for the run lengths |
| Classifier | Hyperparameters in Scikit-Learn | Hyperparameter Grid |
|---|---|---|
| DT | max_depth | 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, None |
| kNN | n_neighbors | 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31 |
| NB | - | - |
| RF | n_estimators | 100, 200, 300, 500, 1000, 2000, 3000, 5000 |
| LR | C | 1 × 10−4, 1 × 10−3, 1 × 10−2, 0.1, 1, 10, 100, 1000, 10,000 |
| XGB | n_estimators | 100, 500 |
| max_depth | 3, 5, 7, 9 | |
| learning_rate | 0.05, 0.01 |
| Classifier | Morphological Feature | Wavelet Feature | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ACC | AUC | SENS | PREC | F1 | ACC | AUC | SENS | PREC | F1 | |
| DT | 80.12 | 0.923 | 0.774 | 0.787 | 0.779 | 79.11 | 0.912 | 0.761 | 0.773 | 0.767 |
| kNN | 80.69 | 0.943 | 0.782 | 0.800 | 0.788 | 76.98 | 0.930 | 0.730 | 0.770 | 0.743 |
| NB | 71.95 | 0.900 | 0.707 | 0.708 | 0.698 | 64.32 | 0.854 | 0.594 | 0.616 | 0.592 |
| RF | 87.54 | 0.971 | 0.858 | 0.870 | 0.863 | 85.87 | 0.970 | 0.836 | 0.851 | 0.841 |
| LR | 88.00 | 0.973 | 0.867 | 0.872 | 0.870 | 88.00 | 0.975 | 0.865 | 0.873 | 0.868 |
| XGB | 90.46 | 0.982 | 0.892 | 0.900 | 0.895 | 90.26 | 0.984 | 0.888 | 0.898 | 0.892 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Yoon, T.; Yeo, C.; Oh, H.; Ji, Y.; Sim, S.; Kang, D. Cardiac Arrhythmia Classification Based on One-Dimensional Morphological Features. Appl. Sci. 2021, 11, 9460. https://doi.org/10.3390/app11209460
Lee H, Yoon T, Yeo C, Oh H, Ji Y, Sim S, Kang D. Cardiac Arrhythmia Classification Based on One-Dimensional Morphological Features. Applied Sciences. 2021; 11(20):9460. https://doi.org/10.3390/app11209460
Chicago/Turabian StyleLee, Heechang, Taeyoung Yoon, Chaeyun Yeo, HyeonYoung Oh, Yebin Ji, Seongwoo Sim, and Daesung Kang. 2021. "Cardiac Arrhythmia Classification Based on One-Dimensional Morphological Features" Applied Sciences 11, no. 20: 9460. https://doi.org/10.3390/app11209460
APA StyleLee, H., Yoon, T., Yeo, C., Oh, H., Ji, Y., Sim, S., & Kang, D. (2021). Cardiac Arrhythmia Classification Based on One-Dimensional Morphological Features. Applied Sciences, 11(20), 9460. https://doi.org/10.3390/app11209460





