Mirau-Based CSI with Oscillating Reference Mirror for Vibration Compensation in In-Process Applications
Abstract
:1. Introduction
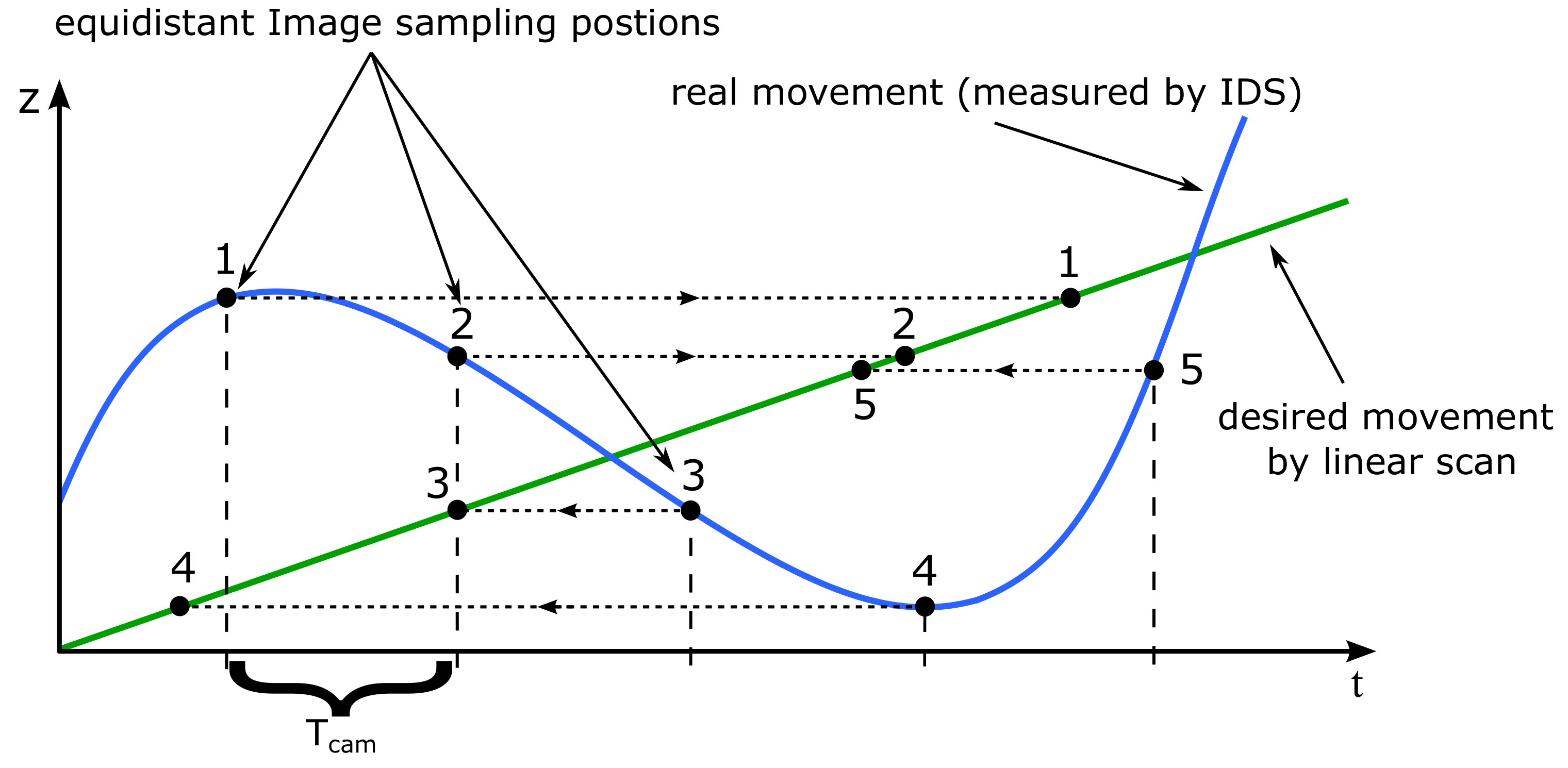
2. Sensor Configuration
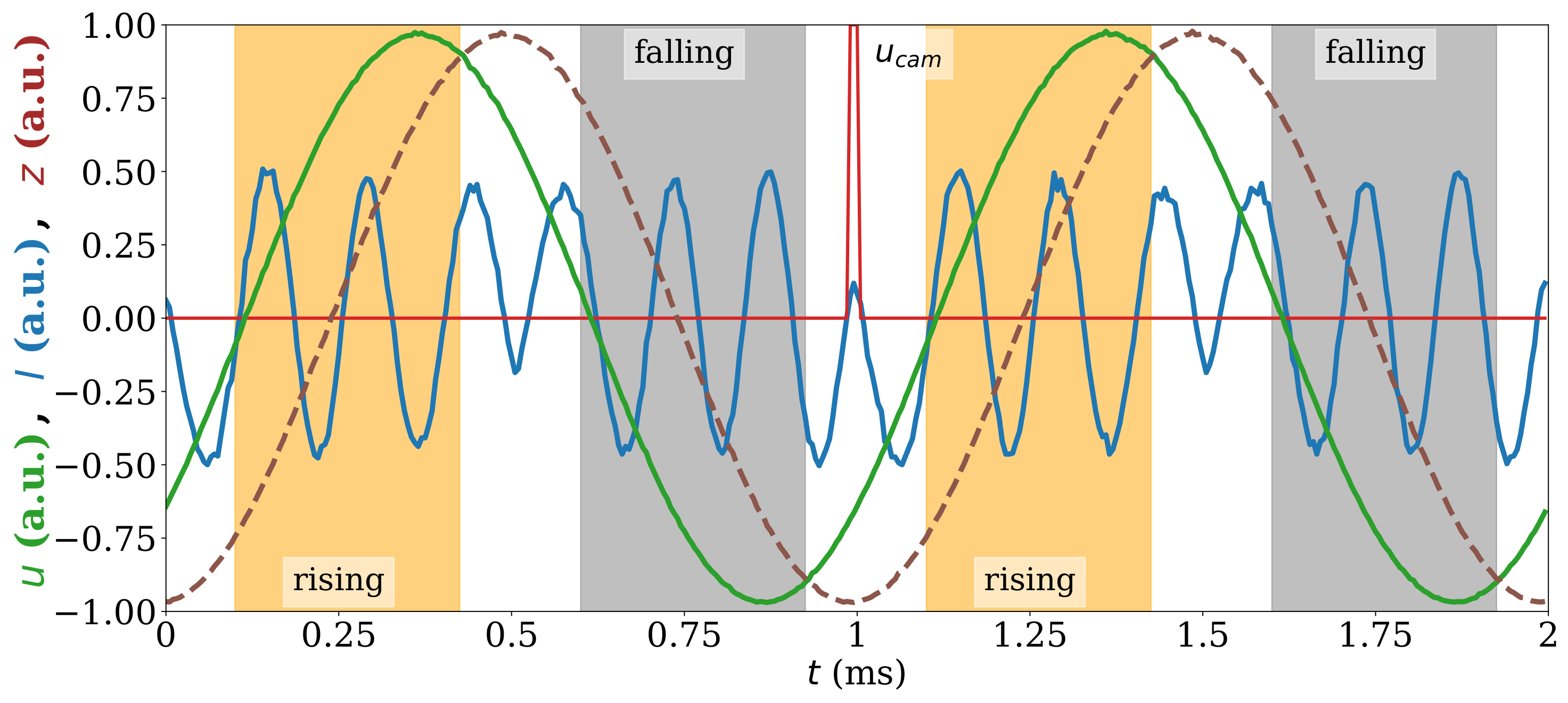
3. Signal Processing
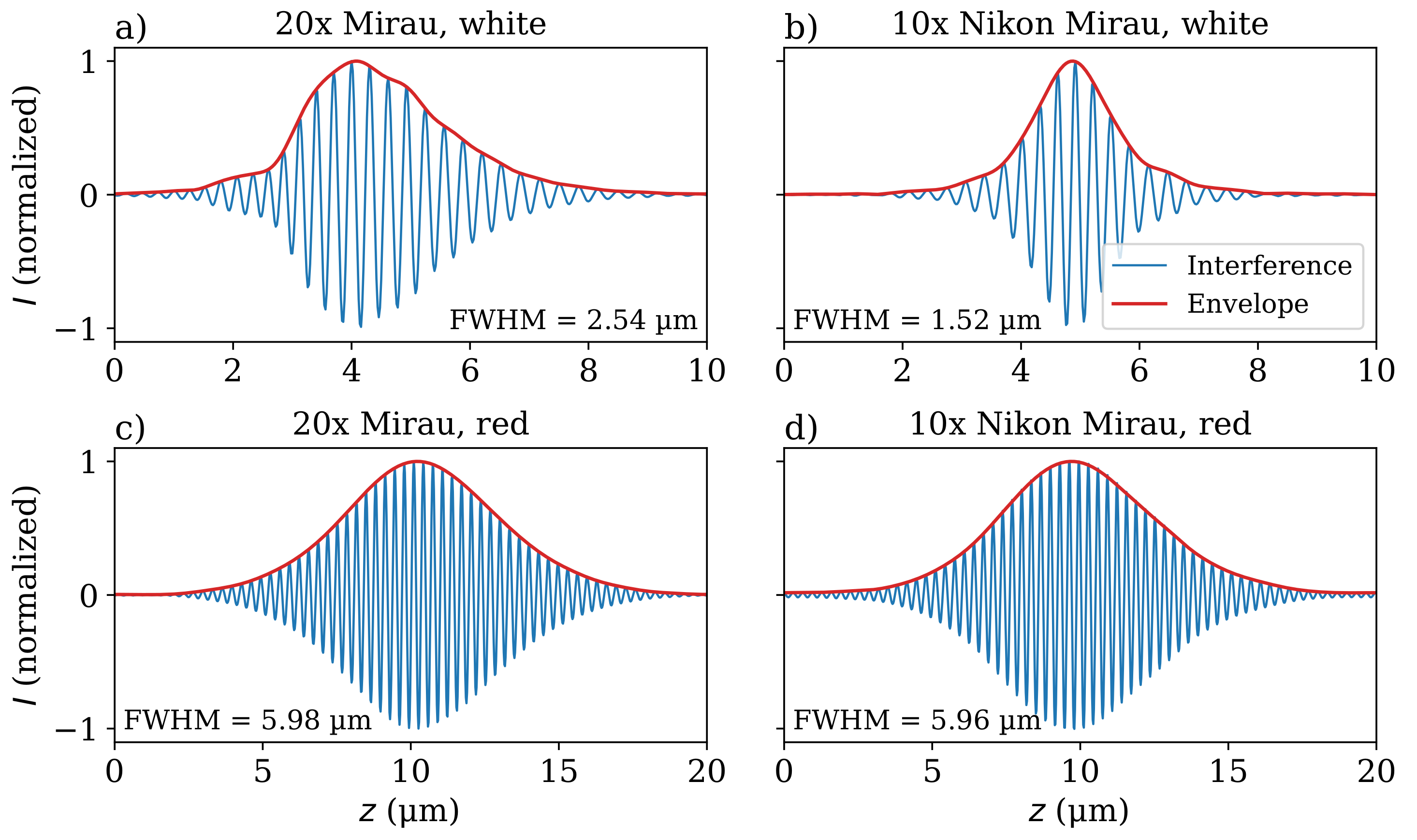
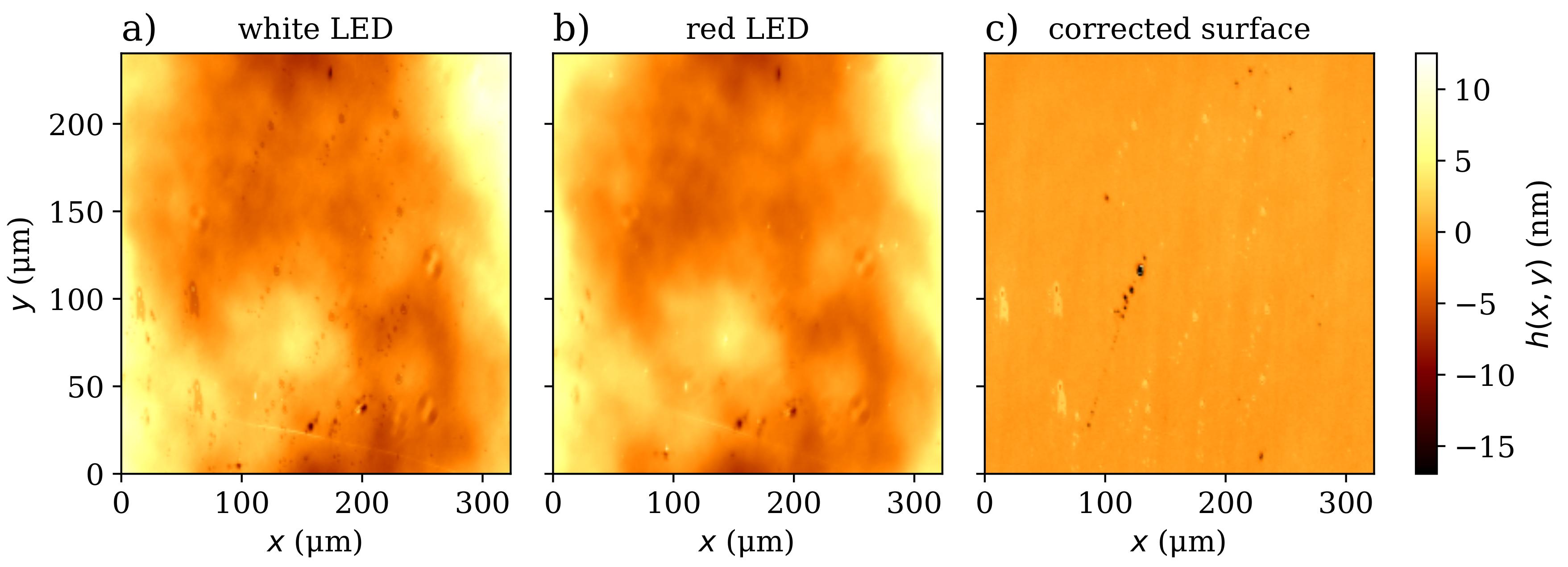
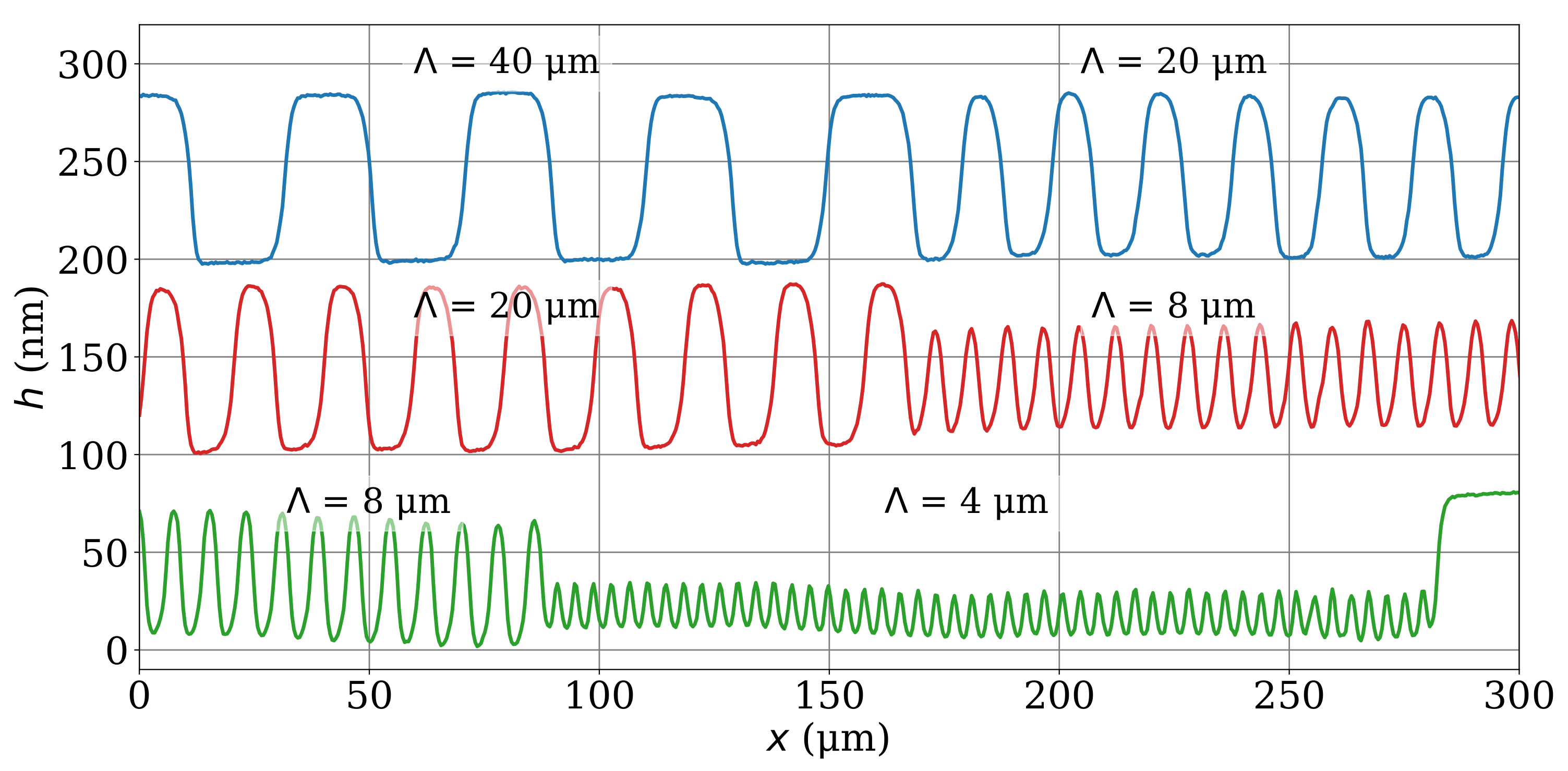
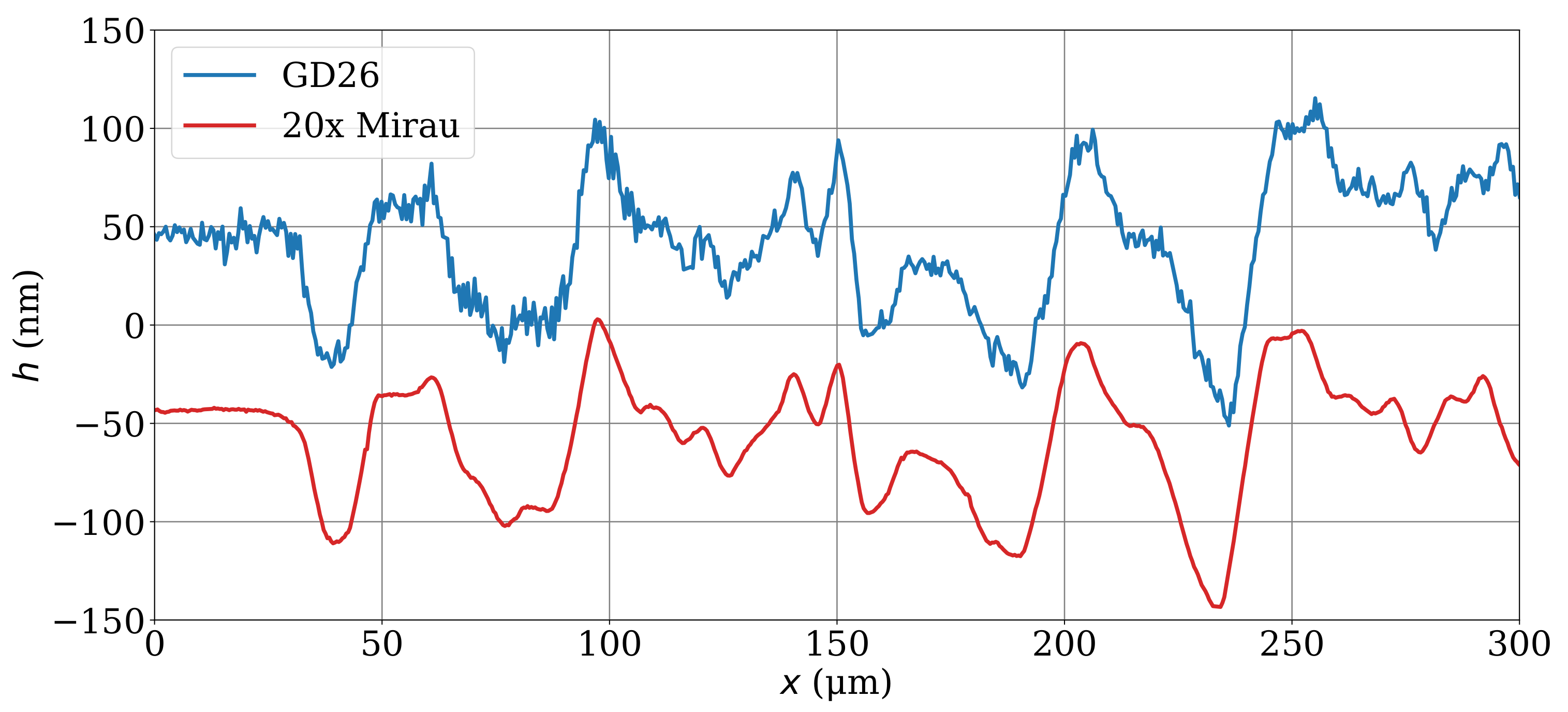
4. Results and Discussion
4.1. Functioning of the Mirau Configuration
4.2. Validation of Vibration Compensation Capabilities of the MA
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kino, G.S.; Corle, T.R. Confocal Scanning Optical Microscopy and Related Imaging Systems; Academic Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Lehmann, P.; Tereschenko, S.; Xie, W. Fundamental aspects of resolution and precision in vertical scanning white-light interferometry. Surf. Topogr. Metrol. Prop. 2016, 4, 024004. [Google Scholar] [CrossRef] [Green Version]
- De Groot, P. Principles of interference microscopy for the measurement of surface topography. Adv. Opt. Photonics 2015, 7, 1–65. [Google Scholar] [CrossRef]
- Schake, M.; Lehmann, P. Quadrature-based interferometry using pulsed RGB illumination. Opt. Express 2019, 27, 16329–16343. [Google Scholar] [CrossRef] [PubMed]
- Gollor, P.; Schake, M.; Tereschenko, S.; Roetmann, K.; Mann, K.; Schäfer, B.; Uhlrich, G.; Haberland, M.; Lehmann, P. Kombination eines neuartigen Doppelpuls-RGB-Interferometers mit einem Hartmann-Shack-Wellenfrontsensor zur dynamischen flächenhaften Topographieerfassung. Tm-Tech. Mess. 2020, 87, 523–534. [Google Scholar] [CrossRef]
- Kühn, J.; Colomb, T.; Montfort, F.; Charrière, F.; Emery, Y.; Cuche, E.; Marquet, P.; Depeursinge, C. Real-time dual-wavelength digital holographic microscopy with a single hologram acquisition. Opt. Express 2007, 15, 7231–7242. [Google Scholar] [CrossRef]
- Wu, D.; Zhu, R.H.; Chen, L.; Li, J.Y. Transverse spatial phase-shifting method used in vibration-compensated interferometer. Optik 2004, 115, 343–346. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, K.; Gao, F.; Muhamedsalih, H. Fast surface measurement using wavelength scanning interferometry with compensation of environmental noise. Appl. Opt. 2010, 49, 2903–2909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schäfer, P.; Broschart, D.; Seewig, J. Aktive Schwingungsdämpfung eines Weißlichtinterferometers. Tm-Tech. Mess. 2013, 80, 16–20. [Google Scholar] [CrossRef]
- Teale, C.; Barbastathis, G.; Schmidt, M.A. Vibration compensated, scanning white light interferometer for in situ depth measurements in a deep reactive ion etcher. J. Microelectromech. Syst. 2019, 28, 441–446. [Google Scholar] [CrossRef]
- Deck, L.L. Suppressing phase errors from vibration in phase-shifting interferometry. Appl. Opt. 2009, 48, 3948–3960. [Google Scholar] [CrossRef]
- Kiselev, I.; Kiselev, E.I.; Drexel, M.; Hauptmannl, M. Noise robustness of interferometric surface topography evaluation methods. Correlogram correlation. Surf. Topogr. Metrol. Prop. 2017, 5, 045008. [Google Scholar] [CrossRef] [Green Version]
- Tereschenko, S.; Lehmann, P.; Gollor, P.; Kuehnhold, P. Robust vertical scanning white-light interferometry in close-to-machine applications. In Optical Measurement Systems for Industrial Inspection IX; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9525, p. 95250Q. [Google Scholar]
- Tereschenko, S.; Lehmann, P.; Zellmer, L.; Brueckner-Foit, A. Passive vibration compensation in scanning white-light interferometry. Appl. Opt. 2016, 55, 6172–6182. [Google Scholar] [CrossRef]
- Tereschenko, S.; Lehmann, P.; Gollor, P.; Kuehnhold, P. Vibration compensated high-resolution scanning white-light Linnik-interferometer. In Optical Measurement Systems for Industrial Inspection X; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10329, p. 1032940. [Google Scholar]
- Hagemeier, S.; Tereschenko, S.; Lehmann, P. High-speed laser interferometric distance sensor with reference mirror oscillating at ultrasonic frequencies. Tm-Tech. Mess. 2019, 86, 164–174. [Google Scholar] [CrossRef]
- Sasaki, O.; Okazaki, H. Sinusoidal phase modulating interferometry for surface profile measurement. Appl. Opt. 1986, 25, 3137–3140. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Pan, W.; Cross, L.E. Laser interferometer for the study of piezoelectric and electrostrictive strains. J. Appl. Phys. 1988, 63, 2492–2496. [Google Scholar] [CrossRef]
- Martini, G. Analysis of a single-mode optical fibre piezoceramic phase modulator. Opt. Quantum Electron. 1987, 19, 179–190. [Google Scholar] [CrossRef]
- De Groot, P. Design of error-compensating algorithms for sinusoidal phase shifting interferometry. Appl. Opt. 2009, 48, 6788–6796. [Google Scholar] [CrossRef]
- Schulz, M.; Lehmann, P. Measurement of distance changes using a fibre-coupled common-path interferometer with mechanical path length modulation. Meas. Sci. Technol. 2013, 24, 065202. [Google Scholar] [CrossRef]
- Knell, H.; Laubach, S.; Ehret, G.; Lehmann, P. Continuous measurement of optical surfaces using a line-scan interferometer with sinusoidal path length modulation. Opt. Express 2014, 22, 29787–29798. [Google Scholar] [CrossRef] [PubMed]
- Kino, G.S.; Chim, S.S. Mirau correlation microscope. Appl. Opt. 1990, 29, 3775–3783. [Google Scholar] [CrossRef] [PubMed]
- Tereschenko, S. Digitale Analyse Periodischer und Transienter Messsignale Anhand von Beispielen aus der Optischen Präzisionsmesstechnik. Ph.D. Thesis, University of Kassel, Kassel, Germany, 2018. [Google Scholar]
- Mitutoyo Corporation. Microscope Units and Objectives (UV, NUV, Visible and NIR Region). 2019. Available online: https://www.mitutoyo.com/wp-content/uploads/2020/12/E14020.pdf (accessed on 11 October 2021).
- CDGM Glass Company Ltd. Datasheet H-K9L. 2021. Available online: http://cdgmglass.com/Portals/0/CDGMSearch2/pdf/H-K9L.pdf (accessed on 11 October 2021).
- PI Ceramic GmbH. Datasheet PICMA Chip Actuator PL0xx. 2017. Available online: https://static.piceramic.com/fileadmin/user_upload/physik_instrumente/files/datasheets/PL0xx_Datasheet.pdf (accessed on 11 October 2021).
- Reichel, L.; Ammar, G.; Gragg, W. Discrete least squares approximation by trigonometric polynomials. Math. Comput. 1991, 57, 273–289. [Google Scholar] [CrossRef]
- De Groot, P.; Deck, L. Surface profiling by analysis of white-light interferograms in the spatial frequency domain. J. Mod. Opt. 1995, 42, 389–401. [Google Scholar] [CrossRef]
- Larkin, K.G. Efficient nonlinear algorithm for envelope detection in white light interferometry. JOSA A 1996, 13, 832–843. [Google Scholar] [CrossRef] [Green Version]
- Harasaki, A.; Schmit, J.; Wyant, J.C. Improved vertical-scanning interferometry. Appl. Opt. 2000, 39, 2107–2115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fleischer, M.; Windecker, R.; Tiziani, H.J. Fast algorithms for data reduction in modern optical three-dimensional profile measurement systems with MMX technology. Appl. Opt. 2000, 39, 1290–1297. [Google Scholar] [CrossRef]
- De Groot, P.; Colonna de Lega, X. Signal modeling for low-coherence height-scanning interference microscopy. Appl. Opt. 2004, 43, 4821–4830. [Google Scholar] [CrossRef]
- Hagemeier, S.; Lehmann, P. High resolution topography sensors in a multisenor measuring setup. In Optical Measurement Systems for Industrial Inspection XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11056, p. 110563I. [Google Scholar]
- De Groot, P.; DiSciacca, J. Surface-height measurement noise in interference microscopy. In Interferometry XIX; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10749, p. 107490Q. [Google Scholar]
- Giusca, C.L.; Leach, R.K.; Helary, F.; Gutauskas, T.; Nimishakavi, L. Calibration of the scales of areal surface topography-measuring instruments: Part 1. Measurement noise and residual flatness. Meas. Sci. Technol. 2012, 23, 035008. [Google Scholar] [CrossRef]
- Krüger-Sehm, R.; Frühauf, J.; Dziomba, T. Determination of the short wavelength cutoff of interferential and confocal microscopes. Wear 2008, 264, 439–443. [Google Scholar] [CrossRef]
- Halle GmbH. Calibration Standards for Contact Stylus Instruments, Line of Products KNT 4070/03. 2009. Available online: http://www.halle-normale.de/pdf/Prospektseiten/englisch/17%20Ps-KNT4070_03_Bl_6-6_GB.pdf (accessed on 11 October 2021).
- Hagemeier, S.; Schake, M.; Lehmann, P. Sensor characterization by comparative measurements using a multi-sensor measuring system. J. Sens. Sens. Syst. 2019, 8, 111–121. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serbes, H.; Gollor, P.; Hagemeier, S.; Lehmann, P. Mirau-Based CSI with Oscillating Reference Mirror for Vibration Compensation in In-Process Applications. Appl. Sci. 2021, 11, 9642. https://doi.org/10.3390/app11209642
Serbes H, Gollor P, Hagemeier S, Lehmann P. Mirau-Based CSI with Oscillating Reference Mirror for Vibration Compensation in In-Process Applications. Applied Sciences. 2021; 11(20):9642. https://doi.org/10.3390/app11209642
Chicago/Turabian StyleSerbes, Hüseyin, Pascal Gollor, Sebastian Hagemeier, and Peter Lehmann. 2021. "Mirau-Based CSI with Oscillating Reference Mirror for Vibration Compensation in In-Process Applications" Applied Sciences 11, no. 20: 9642. https://doi.org/10.3390/app11209642





