Robust Static Structural System Identification Using Rotations
Abstract
:1. Introduction
1.1. Existing Structural System Identification Method
1.2. Application of Inclinometers in Civil Engineering
1.3. Research Objective
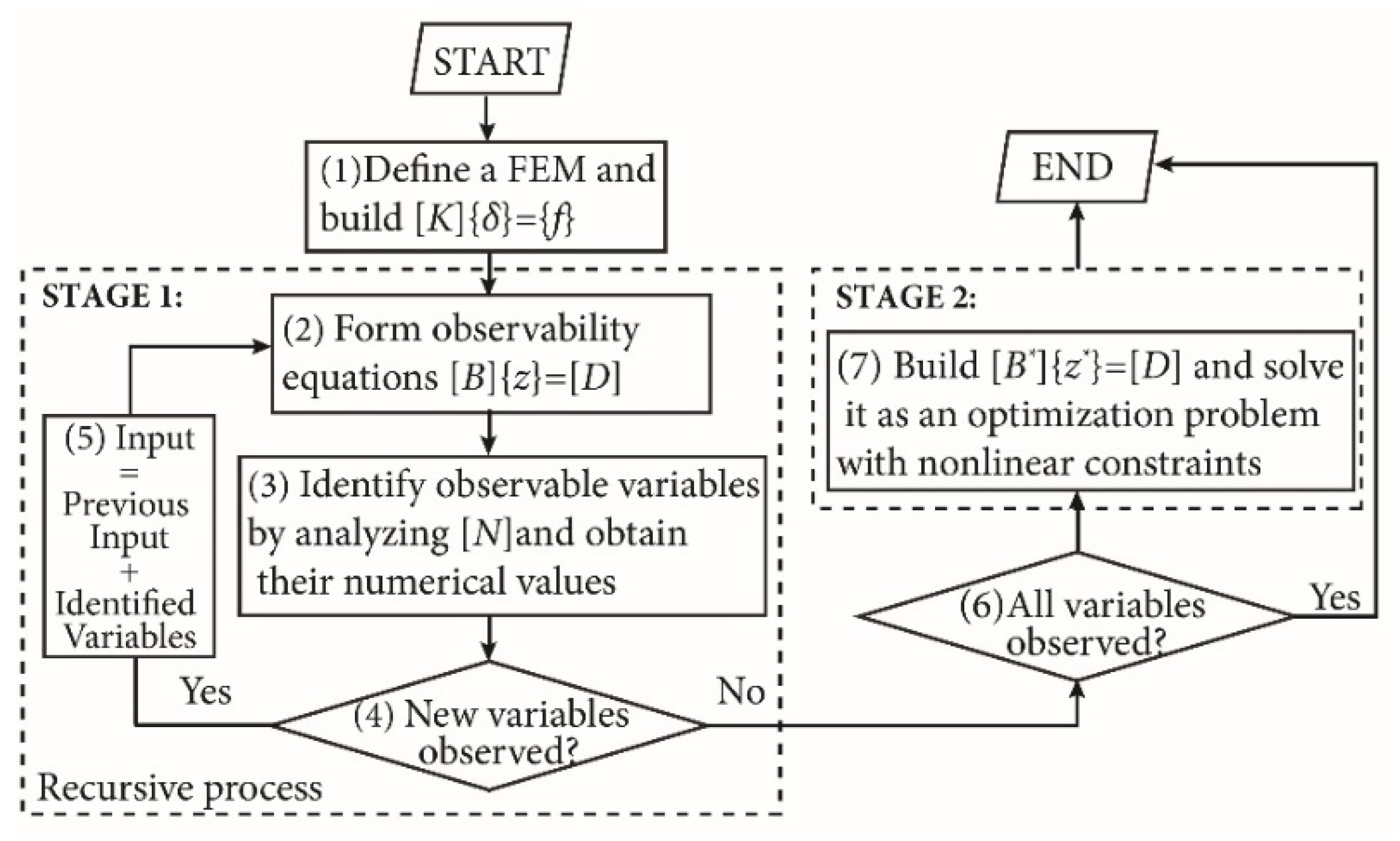
2. Methodology
2.1. Structural System Identification Using the Constrained Observability Method
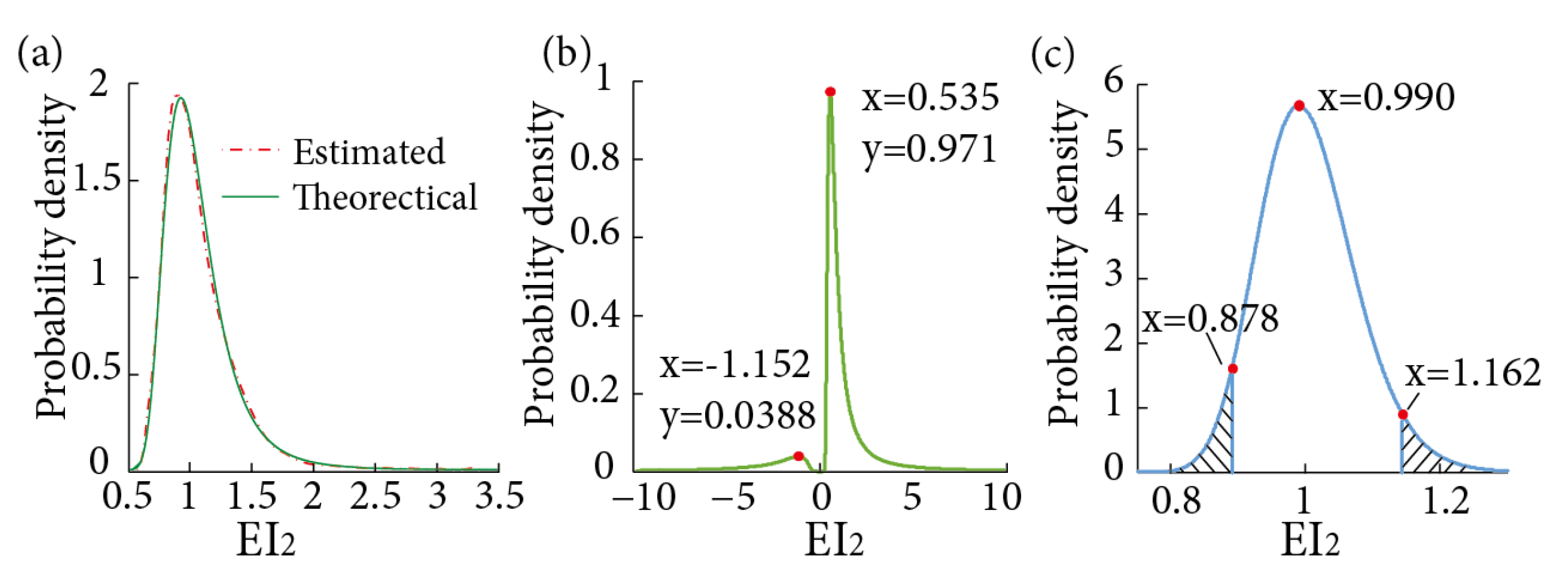
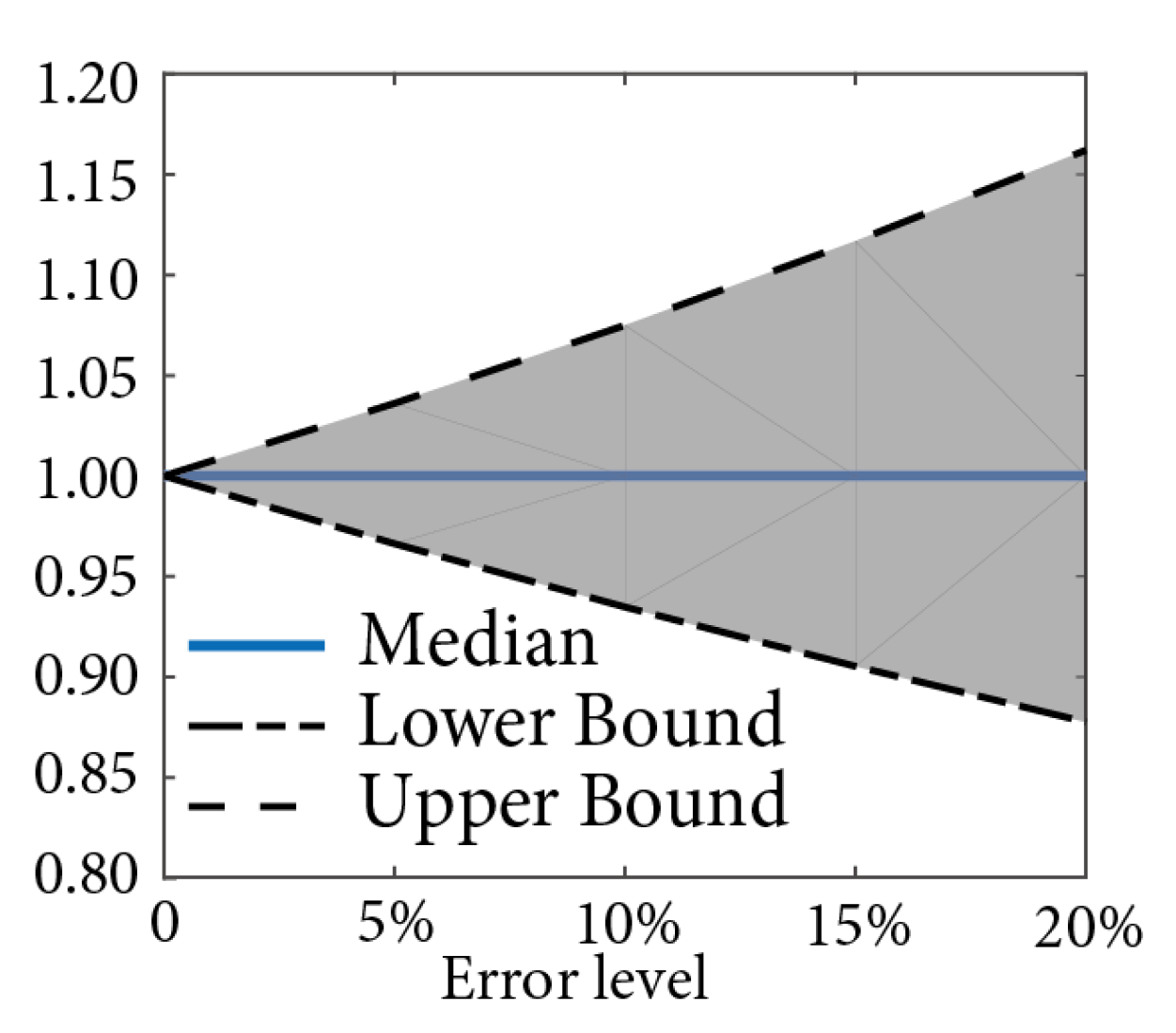
2.2. Procedure for the Statistical Analysis of the Distribution of Estimations
- Step 1: Define a FEM for the structure to be analyzed according to the targeted accuracy of estimations.
- Step 2: Choose a measurement set to obtain the analytical expression for the target parameter θ, employing structural system identification using COM (see Section 2.1). Rewrite this expression for θ as the reciprocal of an expression denoted by Ddenom, i.e., θ = 1/Ddenom.
- Step 3: Calculate the theoretical displacements of the structure using the finite element method.
- Step 4: Analyze the distribution of Ddenom using Equation (10) and the theoretical values obtained in Step 3.
- Step 5: Analyze the distribution of θ = 1/Ddenom using Equations (11) and (12).
3. Theoretical Motivation for Measuring Rotations
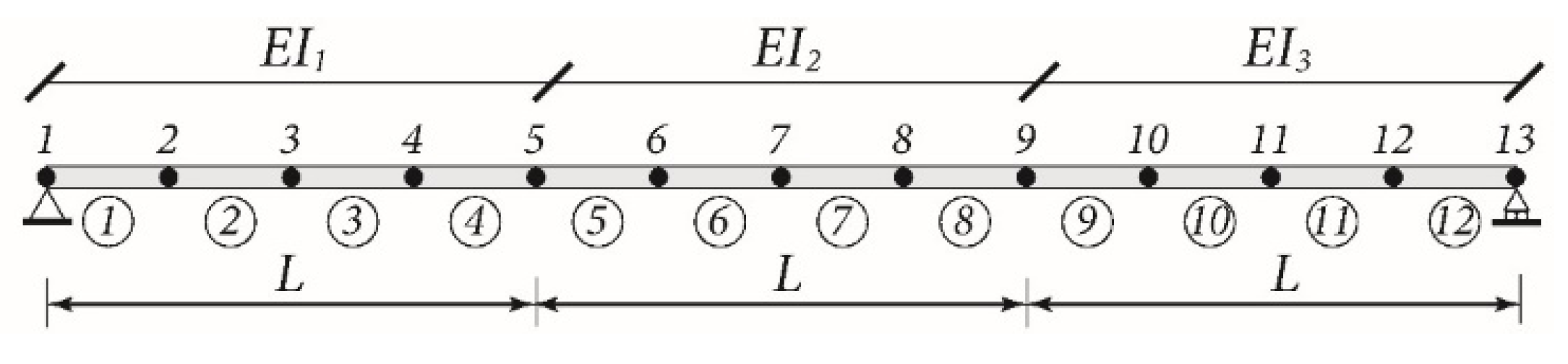
3.1. Statistical Analysis of a Simply Supported Bridge
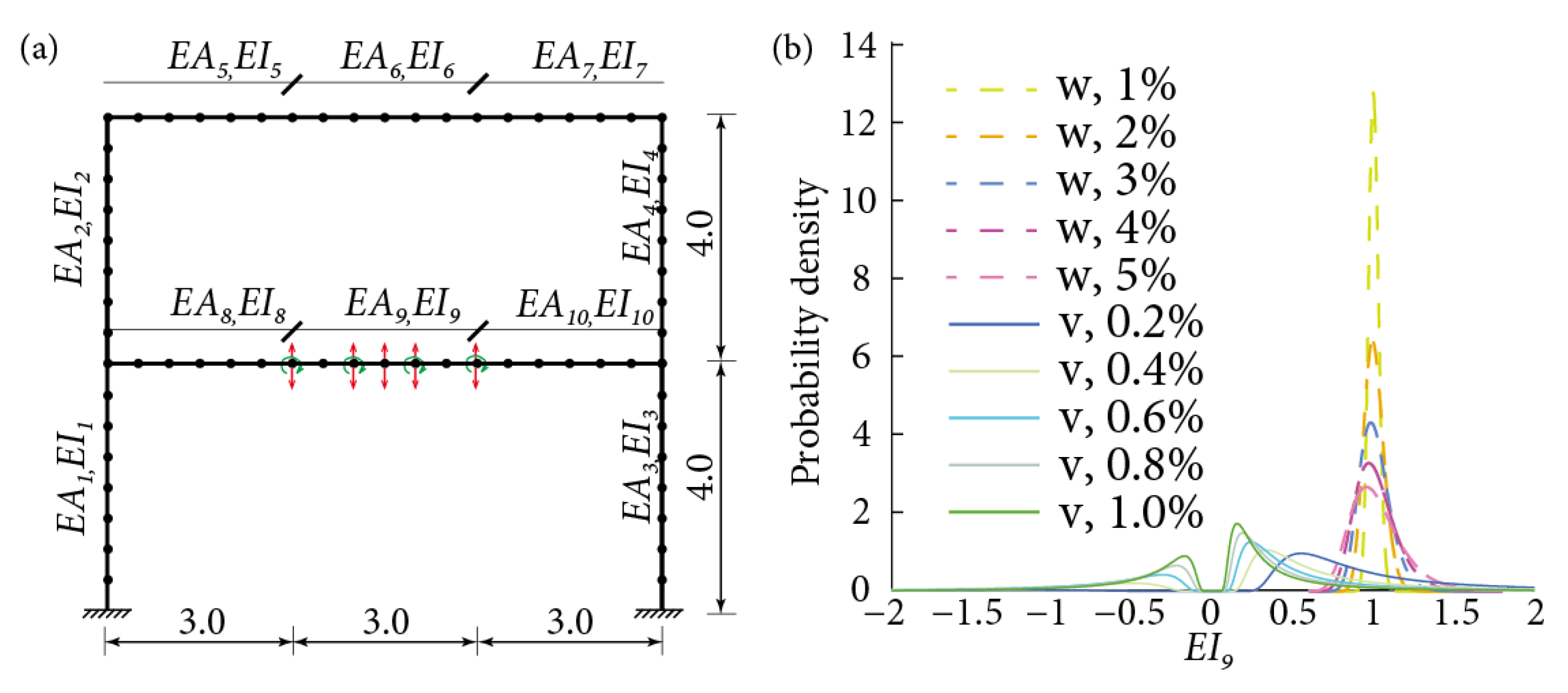
3.2. Statistical Analysis of a Two-Story One-Bay Frame
4. Using Redundant Rotations for Parameter Estimation
4.1. Strategies to Use Redundant Measurements
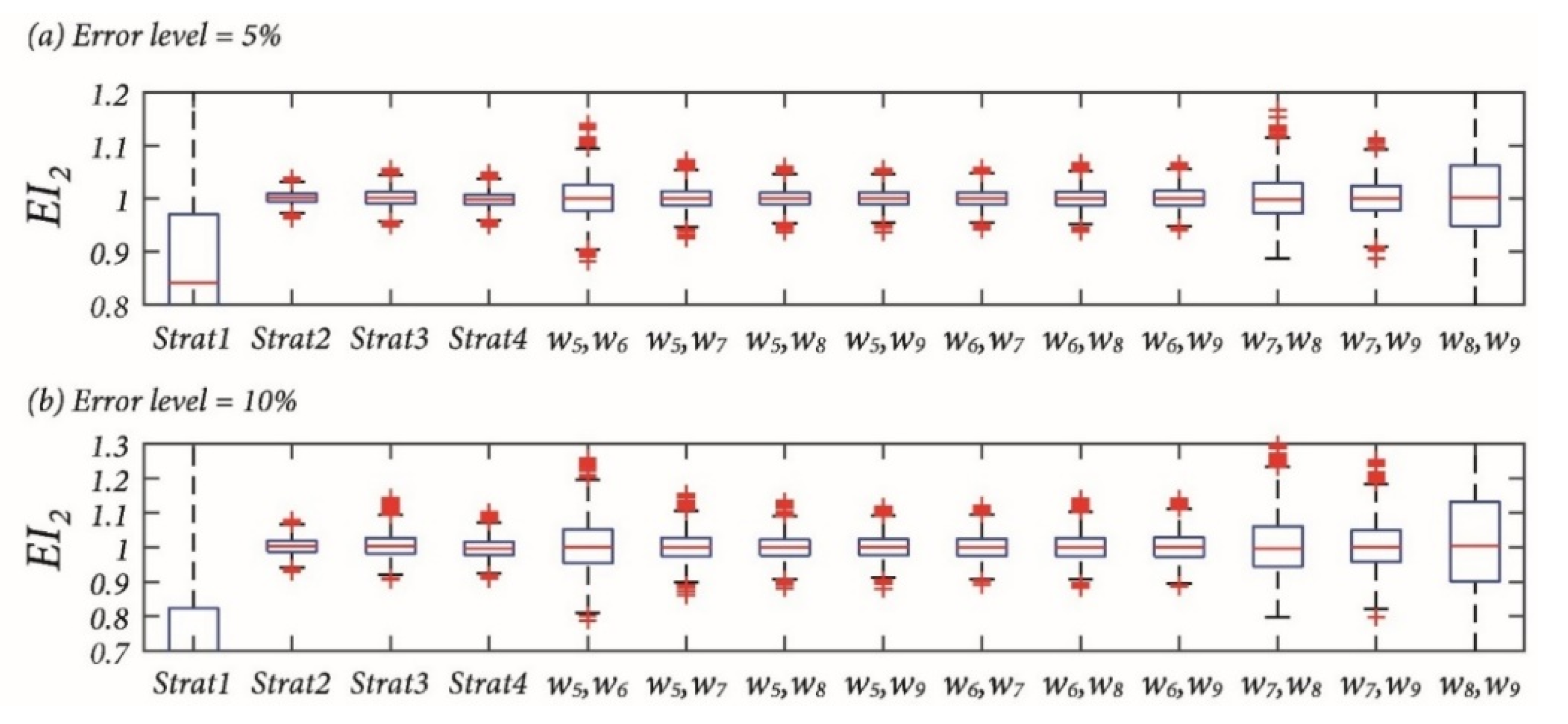
- Strategy 1: Formulate the observability equations (Equation (6)) employing structural system identification using COM with all rotations in one batch. In this case, the equations cannot be satisfied strictly as measurement errors exist and the equations are solved directly using the least squares method.
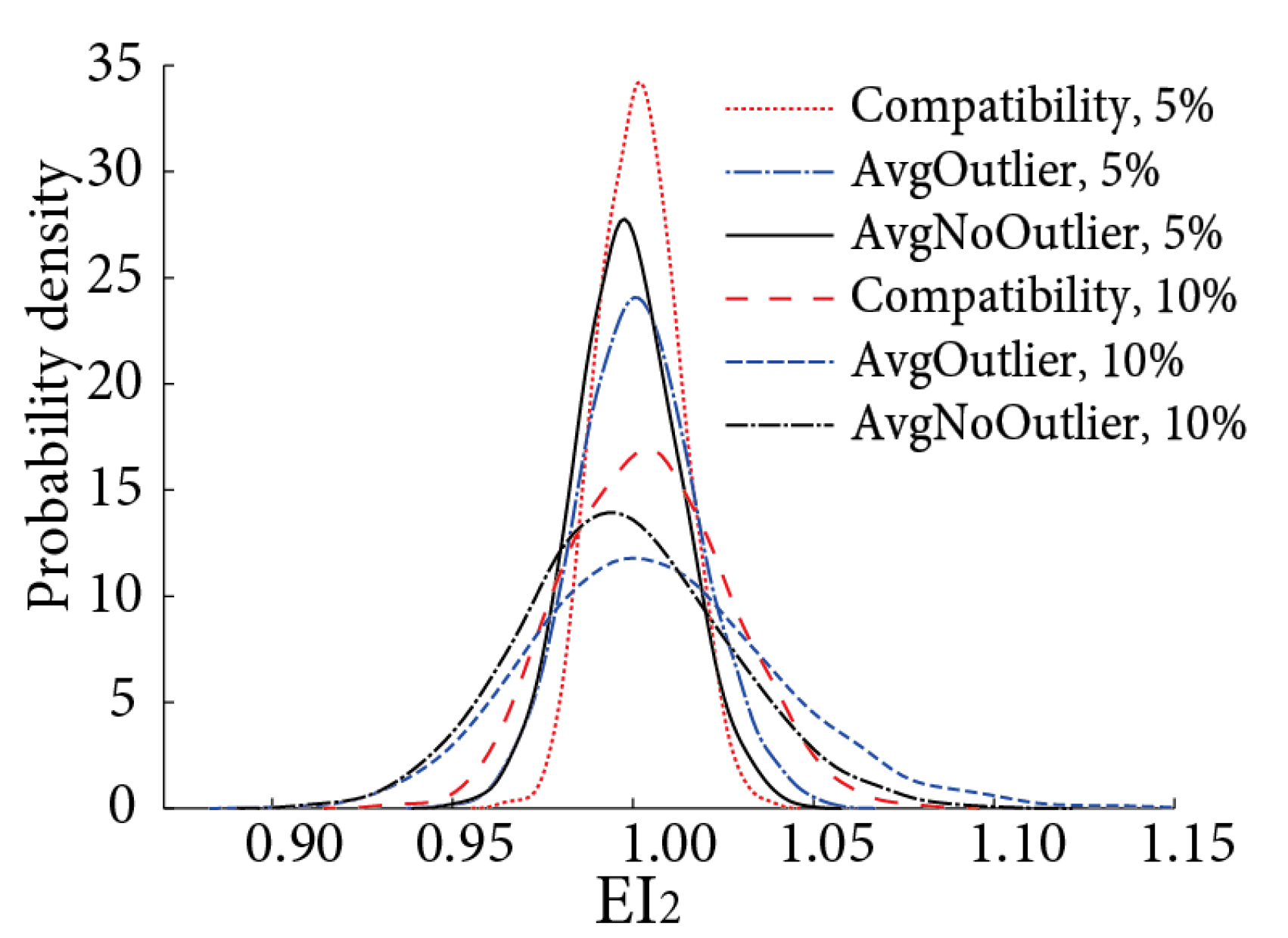
- Strategy 2: Derive the geometrical relations (referred to as compatibility conditions) that the nodal displacements should satisfy first [25]. Impose these compatibility conditions using optimization techniques by minimizing the discrepancy between the measured shape and the compatible one. The estimations of the parameters are obtained by providing the compatible displacements in Equation (6).
- Strategy 3: The estimations using the redundant measurement sets are obtained in several batches. In each batch, the target parameters are obtained using one essential set, which is a subset of the redundant set. The final estimations are the average of the estimations from all batches. This strategy is also noted as an averaging method.
- Strategy 4: The averaging method is carried out first. Then, the outliers in the estimations from different batches are detected and removed. The final estimations are the average of the remaining valid estimations. To determine outliers, the first quantile Q1 and the third quantile Q3 of the estimations from different batches are calculated. By the assumption of normal distribution, valid estimations should fall into the interval [Q1 − 2.7(Q3 − Q1), Q3 + 2.7(Q3 − Q1)] with a coverage of 99.7%. Hence, values outside of this range are invalid and ruled out.
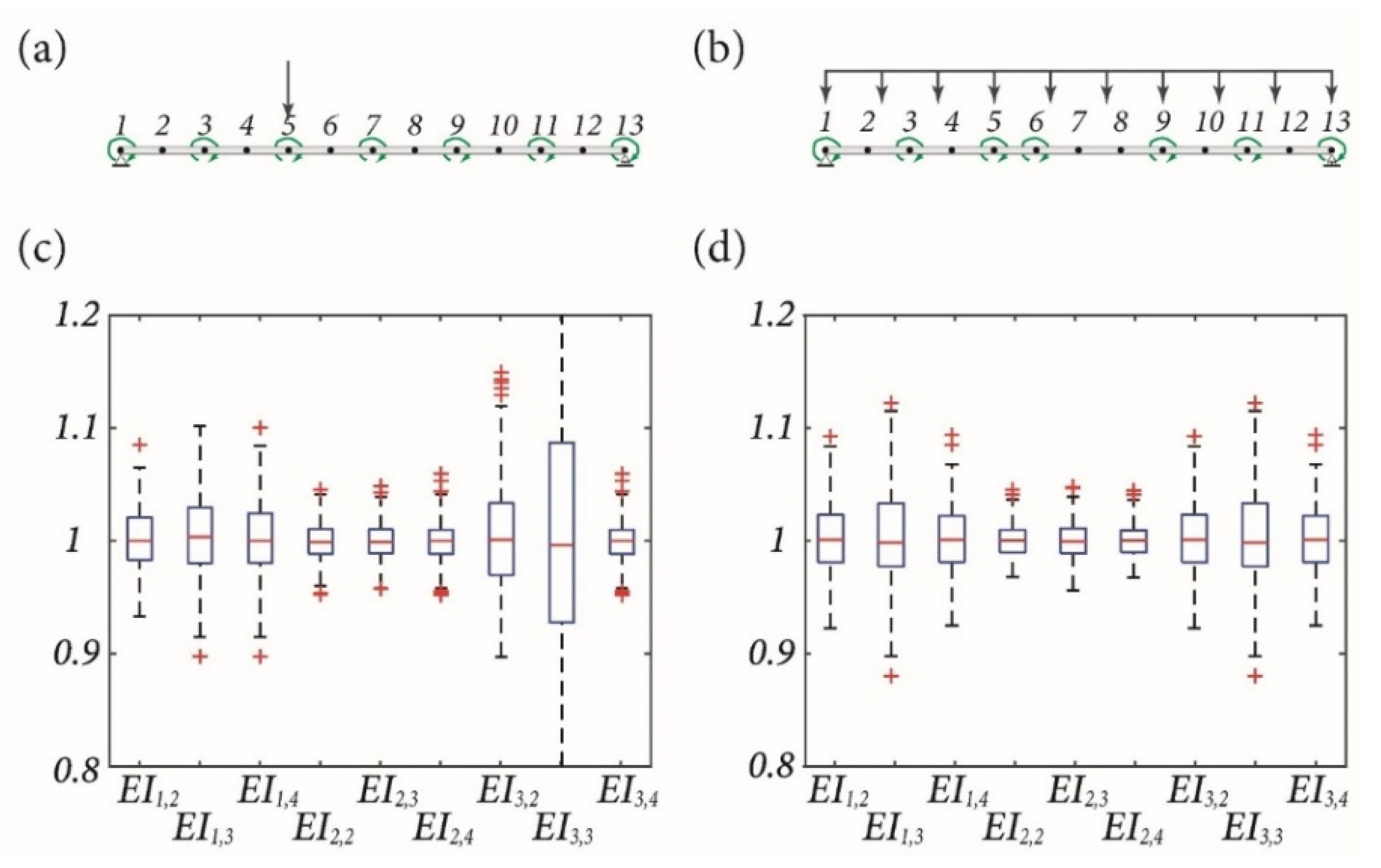
4.2. Verification for a Simply Supported Bridge
4.2.1. Case 1: Parameter Estimation for a Local Region
4.2.2. Case 2: Parameter Estimation for the Whole Structure
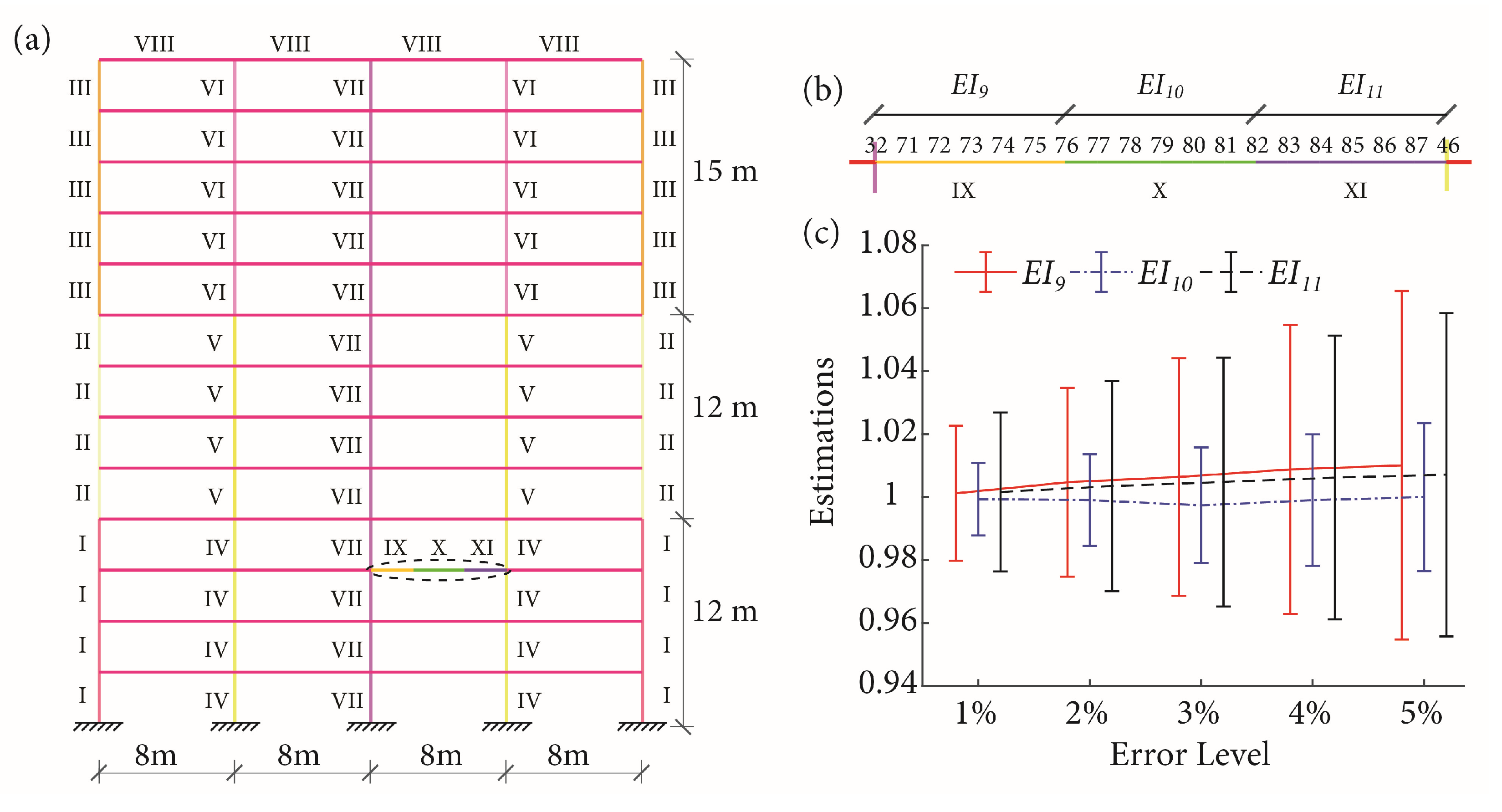
4.3. Verification for a High-Rise Frame Structure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| [A] | A m × n matrix | {z} | Unknown vector |
| [N] | Null space matrix | {zg} | General solution vector |
| [K] | Global stiffness matrix | {zp} | Particular solution vector |
| L | Length | {zh} | One solution vector to the homogeneous equation |
| E | Elastic moduli | {D} | Constant vector |
| A | Area | {ρ} | Coefficient vector |
| I | Inertia | {zs} | Single variables vector |
| {δ} | Displacement vector | {z*} | A new unknown vector by adding {zs} in {z} |
| U | Horizontal deflection | [Ω] | A null matrix |
| V | Vertical deflection | [B*] | A new coefficient matrix by introducing null matrix [Ω] |
| W | Rotation | ε | Residual |
| {ƒ} | Force vector | Random errors | |
| H | Horizontal force | δr | Displacement obtained from FEM |
| V | Vertical force | Elevel | Error level |
| M | Moment | ξ | Random number follows a normal distribution with zero mean and standard deviation 0.5 |
| Ne | Number of elements | μ | Mean value |
| Nn | Number of nodes | σ | Standard deviation |
| [K*] | Modified global stiffness matrix | X | Random variable |
| {δ*} | Modified displacement vector | Y | The inverse distribution of X |
| I | Identity matrices | pY | Probability density function of Y |
| 0 | Null matrices | θ | Target parameter |
| [B] | Coefficient matrix | Ddenom | Reciprocal of target parameter θ |
References
- Al-Hussein, A.; Haldar, A. Structural damage prognosis of three-dimensional large structural systems. Struct. Infrastruct. Eng. 2017, 13, 1596–1608. [Google Scholar] [CrossRef]
- Davoudi, R.; Miller, G.R.; Kutz, J.N. Data-driven vision-based inspection for reinforced concrete beams and slabs: Quantitative damage and load estimation. Autom. Constr. 2018, 96, 292–309. [Google Scholar] [CrossRef]
- Morgenthal, G.; Hallermann, N.; Kersten, J.; Taraben, J.; Debus, P.; Helmrich, M.; Rodehorst, V. Framework for automated UAS-based structural condition assessment of bridges. Autom. Constr. 2019, 97, 77–95. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Ladevèze, P.; Leconte, P. Reduced bases for model updating in structural dynamics based on constitutive relation error. Comput. Methods Appl. Mech. Eng. 2002, 191, 2427–2444. [Google Scholar] [CrossRef] [Green Version]
- Christodoulou, K.; Ntotsios, E.; Papadimitriou, C.; Panetsos, P. Structural model updating and prediction variability using Pareto optimal models. Comput. Methods Appl. Mech. Eng. 2008, 198, 138–149. [Google Scholar] [CrossRef] [Green Version]
- Jensen, H.E.; Millas, E.; Kusanovic, D.; Papadimitriou, C. Model-reduction techniques for Bayesian finite element model updating using dynamic response data. Comput. Methods Appl. Mech. Eng. 2014, 279, 301–332. [Google Scholar] [CrossRef]
- Park, H.S.; Oh, B.K. Real-time structural health monitoring of a supertall building under construction based on visual modal identification strategy. Autom. Constr. 2018, 85, 273–289. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties. I: Bayesian statistical framework. J. Eng. Mech. 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Lombaert, G. The effect of prediction error correlation on optimal sensor placement in structural dynamics. Mech. Syst. Signal Process. 2012, 28, 105–127. [Google Scholar] [CrossRef]
- Goulet, J.-A.; Smith, I.F.C. Structural identification with systematic errors and unknown uncertainty dependencies. Comput. Struct. 2013, 128, 251–258. [Google Scholar] [CrossRef] [Green Version]
- Proverbio, M.; Vernay, D.G.; Smith, I.F.C. Population-based structural identification for reserve-capacity assessment of existing bridges. J. Civ. Struct. Health Monit. 2018, 8, 363–382. [Google Scholar] [CrossRef] [Green Version]
- Alvin, K. Finite element model update via Bayesian estimation and minimization of dynamic residuals. AIAA J. 1997, 35, 879–886. [Google Scholar] [CrossRef] [Green Version]
- Sanayei, M.; Scampoli, S.F. Structural Element Stiffness Identification from Static Test Data. J. Eng. Mech. 1991, 117, 1021–1036. [Google Scholar] [CrossRef] [Green Version]
- Banan, M.; Hjelmstad, K.D. Parameter Estimation of Structures from Static Response. I. Computational Aspects. J. Struct. Eng. 1994, 120, 3243–3258. [Google Scholar] [CrossRef]
- Hjelmstad, K.D.; Shin, S. Damage Detection and Assessment of Structures from Static Response. J. Eng. Mech. 1997, 123, 568–576. [Google Scholar] [CrossRef]
- Yang, Q.; Sun, B. Structural damage localization and quantification using static test data. Struct. Health Monit. 2010, 10, 381–389. [Google Scholar] [CrossRef]
- Sun, Z.; Nagayama, T.; Fujino, Y. Minimizing noise effect in curvature-based damage detection. J. Civ. Struct. Health Monit. 2016, 6, 255–264. [Google Scholar] [CrossRef]
- Castillo, E.; Conejo, A.J.; Pruneda, R.E.; Solares, C. Observability in linear systems of equations and inequalities: Applications. Comput. Oper. Res. 2007, 34, 1708–1720. [Google Scholar] [CrossRef]
- Castillo, E.; Conejo, A.; Pruneda, R.; Solares, C. Observability Analysis in State Estimation: A Unified Numerical Approach. IEEE Trans. Power Syst. 2006, 21, 877–886. [Google Scholar] [CrossRef]
- Castillo, E.; Lozano-Galant, J.A.; Nogal, M.; Turmo, J. New tool to help decision making in civil engineering. J. Civ. Eng. Manag. 2015, 21, 689–697. [Google Scholar] [CrossRef] [Green Version]
- Nogal, M.; Lozano-Galant, J.A.; Turmo, J.; Castillo, E. Numerical damage identification of structures by observability techniques based on static loading tests. Struct. Infrastruct. Eng. 2015, 12, 1216–1227. [Google Scholar] [CrossRef] [Green Version]
- Tomàs, D.; Lozano-Galant, J.A.; Ramos, G.; Turmo, J. Structural system identification of thin web bridges by observability techniques considering shear deformation. Thin-Walled Struct. 2018, 123, 282–293. [Google Scholar] [CrossRef] [Green Version]
- Emadi, S.; Lozano-Galant, J.A.; Xia, Y.; Ramos, G.; Turmo, J. Structural system identification including shear de-formation of composite bridges from vertical deflections. Steel Compos. Struct. 2019, 32, 731–741. [Google Scholar]
- Lei, J.; Lozano-Galant, J.A.; Nogal, M.; Xu, D.; Turmo, J. Analysis of measurement and simulation errors in structural system identification by observability techniques. Struct. Control Health Monit. 2017, 24, e1923. [Google Scholar] [CrossRef]
- Lei, J.; Xu, D.; Turmo, J. Static structural system identification for beam-like structures using compatibility conditions. Struct. Control Health Monit. 2017, 25, e2062. [Google Scholar] [CrossRef] [Green Version]
- Lei, J.; Lozano-Galant, J.A.; Xu, D.; Turmo, J. Structural system identification by measurement error-minimizing observability method. Struct. Control Health Monit. 2019, 26, e2425. [Google Scholar] [CrossRef]
- Chen, Z.W.; Cai, Q.L.; Zhu, S.; Wei, Z.; Qin, C.; Cai, L.; Zhu, S. Damage quantification of beam structures using deflection influence lines. Struct. Control Health Monit. 2018, 25, e2242. [Google Scholar] [CrossRef]
- Ha, D.W.; Park, H.S.; Choi, S.W.; Kim, Y. A Wireless MEMS-Based Inclinometer Sensor Node for Structural Health Monitoring. Sensors 2013, 13, 16090–16104. [Google Scholar] [CrossRef] [Green Version]
- Shang, Z.; Shen, Z. Multi-point vibration measurement and mode magnification of civil structures using video-based motion processing. Autom. Constr. 2018, 93, 231–240. [Google Scholar] [CrossRef]
- Feng, M.Q.; Feng, S.; Beskhyroun, L.D.; Wegner, B.F.; Sparling, D.; Feng, M.Q. Vision-based multipoint displacement measurement for structural health monitoring. Struct. Control Health Monit. 2016, 23, 876–890. [Google Scholar] [CrossRef]
- Lee, J.-J.; Ho, H.-N. A Vision-Based Dynamic Rotational Angle Measurement System for Large Civil Structures. Sensors 2012, 12, 7326–7336. [Google Scholar] [CrossRef] [Green Version]
- Robert-Nicoud, Y.; Raphael, B.; Burdet, O.; Smith, I.F.C. Model Identification of Bridges Using Measurement Data. Comput. Civ. Infrastruct. Eng. 2005, 20, 118–131. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Sun, L.M.; Sun, P.S.W. Bridge-Deflection Estimation through Inclinometer Data Considering Structural Damages. J. Bridg. Eng. 2017, 22, 04016117. [Google Scholar] [CrossRef]
- Park, H.S.; Shin, Y.; Choi, S.W.; Kim, Y. An Integrative Structural Health Monitoring System for the Local/Global Responses of a Large-Scale Irregular Building under Construction. Sensors 2013, 13, 9085–9103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, T.; Yang, B.; Zhang, Q. Health Monitoring System Developed for Tianjin 117 High-Rise Building. J. Aerosp. Eng. 2017, 30, B4016004. [Google Scholar] [CrossRef]
- Kim, T.; Lim, H.; Kim, S.W.; Cho, H.; Kang, K.-I. Inclined construction hoist for efficient resource transportation in irregularly shaped tall buildings. Autom. Constr. 2016, 62, 124–132. [Google Scholar] [CrossRef]
- Liu, D.; Wu, Y.; Li, S.; Sun, Y. A real-time monitoring system for lift-thickness control in highway construction. Autom. Constr. 2016, 63, 27–36. [Google Scholar] [CrossRef]
- Ha, D.W.; Kim, J.M.; Kim, Y.; Park, H.S. Development and application of a wireless MEMS-based borehole inclinometer for automated measurement of ground movement. Autom. Constr. 2018, 87, 49–59. [Google Scholar] [CrossRef]
- Dirksen, J.; Pothof, I.; Langeveld, J.; Clemens, F. Slope profile measurement of sewer inverts. Autom. Constr. 2014, 37, 122–130. [Google Scholar] [CrossRef]
- He, X.; Yang, X.; Zhao, L. New Method for High-Speed Railway Bridge Dynamic Deflection Measurement. J. Bridge Eng. 2014, 19, 05014004. [Google Scholar] [CrossRef]
- Hou, S.; Zeng, C.; Zhang, H.; Ou, J. Monitoring interstory drift in buildings under seismic loading using MEMS inclinometers. Constr. Build. Mater. 2018, 185, 453–467. [Google Scholar] [CrossRef]
- Bertola, N.J.; Papadopoulou, M.; Vernay, D.; Smith, I.F.C. Optimal multi-type sensor placement for structural identification by static-load testing. Sensors 2017, 17, 2904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Papadimitriou, C. Optimal sensor placement methodology for parametric identification of structural systems. J. Sound Vib. 2004, 278, 923–947. [Google Scholar] [CrossRef]
- Argyris, C.; Papadimitriou, C.; Panetsos, P. Bayesian optimal sensor placement for modal identification of civil infra-structures. J. Smart Cities 2017, 2, 69–86. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Lei, J.; Nogal, M.; Lozano-Galant, J.A.; Xu, D.; Turmo, J. Constrained observability method in static structural system identification. Struct. Control Health Monit. 2018, 25, e2040. [Google Scholar] [CrossRef]
- Abur, A.G. Exposito, Power System State Estimation: Theory and Implementation; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Lozano-Galant, J.A.; Nogal, M.; Turmo, J.; Castillo, E. Selection of measurement sets in static structural identification of bridges using observability trees. Comput. Concr. 2015, 15, 771–794. [Google Scholar] [CrossRef]
- Lozano-Galant, J.A.; Nogal, M.; Castillo, E.; Turmo, J. Application of observability techniques to structural system identification. Comput.-Aided Civ. Infrastruct. Eng. 2013, 28, 434–450. [Google Scholar] [CrossRef]
- Zhang, F.-L.; Au, S.-K.; Ni, Y.-C. Two-stage Bayesian system identification using Gaussian discrepancy model. Struct. Health Monit. Int. J. 2021, 20, 580–595. [Google Scholar] [CrossRef]
- Zhang, F.L.; Kim, C.W.; Goi, Y. Efficient Bayesian FFT method for damage detection using ambient vibration data with consideration of uncertainty. Struct. Control Health Monit. 2021, 28, e2659. [Google Scholar] [CrossRef]
- Ni, Y.C.; Zhang, F.L. Uncertainty quantification in fast Bayesian modal identification using forced vibration data considering the ambient effect. Mech. Syst. Signal Process. 2021, 148, 107078. [Google Scholar] [CrossRef]


| Displacements | Values | Unit |
|---|---|---|
| v5 | −0.010971 | m |
| v7 | −0.011829 | m |
| v9 | −0.009600 | m |
| w5 | −0.001829 | rad |
| w9 | 0.002286 | rad |
| Parameter | Load Case 1 | Load Case 2 | ||
|---|---|---|---|---|
| Mean | c.o.v. | Mean | c.o.v. | |
| EI1,2 | 1.001 | 0.027 | 1.001 | 0.030 |
| EI1,3 | 1.003 | 0.038 | 1.003 | 0.043 |
| EI1,4 | 1.002 | 0.035 | 1.002 | 0.031 |
| EI2,2 | 1.000 | 0.017 | 1.000 | 0.014 |
| EI2,3 | 1.000 | 0.018 | 1.001 | 0.017 |
| EI3,4 | 1.000 | 0.017 | 1.000 | 0.014 |
| EI3,2 | 1.003 | 0.050 | 1.001 | 0.030 |
| EI3,3 | 1.014 | 0.123 | 1.003 | 0.043 |
| EI3,4 | 1.002 | 0.055 | 1.002 | 0.031 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, J.; Lozano-Galant, J.A.; Xu, D.; Zhang, F.-L.; Turmo, J. Robust Static Structural System Identification Using Rotations. Appl. Sci. 2021, 11, 9695. https://doi.org/10.3390/app11209695
Lei J, Lozano-Galant JA, Xu D, Zhang F-L, Turmo J. Robust Static Structural System Identification Using Rotations. Applied Sciences. 2021; 11(20):9695. https://doi.org/10.3390/app11209695
Chicago/Turabian StyleLei, Jun, José Antonio Lozano-Galant, Dong Xu, Feng-Liang Zhang, and Jose Turmo. 2021. "Robust Static Structural System Identification Using Rotations" Applied Sciences 11, no. 20: 9695. https://doi.org/10.3390/app11209695
APA StyleLei, J., Lozano-Galant, J. A., Xu, D., Zhang, F.-L., & Turmo, J. (2021). Robust Static Structural System Identification Using Rotations. Applied Sciences, 11(20), 9695. https://doi.org/10.3390/app11209695







