Towards Single 2D Image-Level Self-Supervision for 3D Human Pose and Shape Estimation
Abstract
:1. Introduction
- We construct a 3D human pose and shape estimation framework that could be trained by 2D single image-level self-supervision without the use of other forms of supervision signals, such as explicit 2D/3D skeletons, video-level, or multi-view priors;
- We propose four types of self-supervised losses based on the 2D single images themselves and introduce a method to effectively train the entire networks. In particular, we investigate which are the most promising combinations of losses to effectively achieve the 2D single image-level self-supervision for 3D human mesh reconstruction;
- The proposed method outperforms the competitive 3D human pose estimation algorithms, proving that leveraging single 2D images could be used for strong supervision to train networks for the 3D mesh reconstruction task.
2. Related Works
2.1. Three-Dimensional Human Pose Estimation
2.2. Three-Dimensional Human Pose and Shape Estimation
2.3. Weakly/Semi-Supervised Learning in 3D Human Mesh Estimation
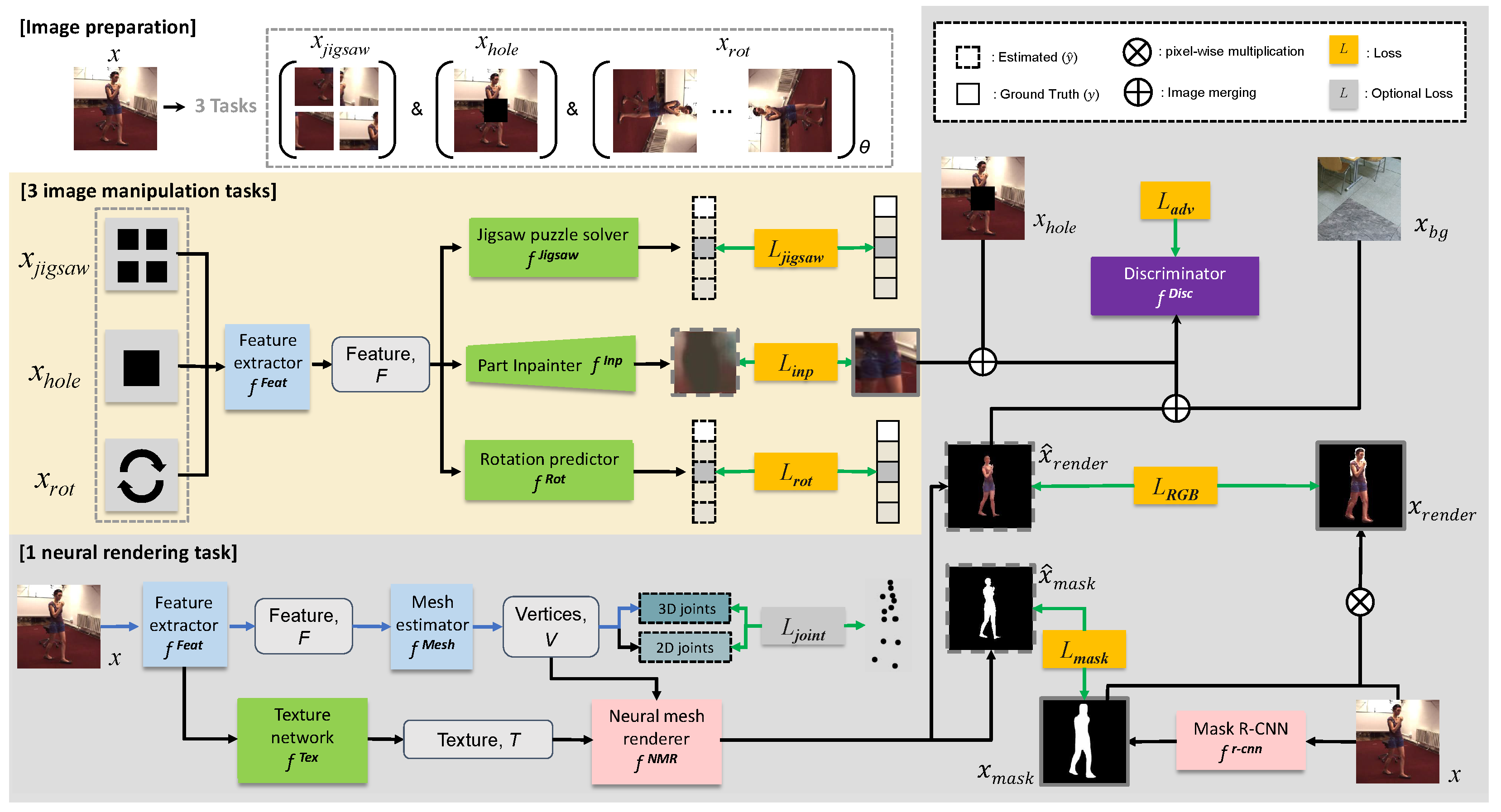
3. Method
3.1. Network Architectures
3.2. Training Method
3.2.1. Summary of the Entire Training Process
3.2.2. Pre-Training Stage
| Algorithm 1: The summary of our entire training process |
 |
3.2.3. Mesh Training Stage
4. Experiments
4.1. Dataset
4.2. Evaluation Method
4.3. Results
4.4. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Newell, A.; Yang, K.; Deng, J. Stacked hourglass networks for human pose estimation. In Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Wei, S.E.; Ramakrishna, V.; Kanade, T.; Sheikh, Y. Convolutional pose machines. In Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Zhou, X.; Zhu, M.; Leonardos, S.; Derpanis, K.G.; Daniilidis, K. Sparseness meets deepness: 3d human pose estimation from monocular video. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Martinez, J.; Hossain, R.; Romero, J.; Little, J.J. A simple yet effective baseline for 3d human pose estimation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Kanazawa, A.; Black, M.J.; Jacobs, D.W.; Malik, J. End-to-end Recovery of Human Shape and Pose. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Kocabas, M.; Athanasiou, N.; Black, M.J. VIBE: Video inference for human body pose and shape estimation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Sun, Y.; Bao, Q.; Liu, W.; Fu, Y.; Black, M.J.; Mei, T. CenterHMR: Multi-person center-based human mesh recovery. arXiv 2020, arXiv:2008.12272. [Google Scholar]
- Guan, S.; Xu, J.; Wang, Y.; Ni, B.; Yang, X. Bilevel online adaptation for out-of-domain human mesh reconstruction. arXiv 2021, arXiv:2103.16449. [Google Scholar]
- Bogo, F.; Kanazawa, A.; Lassner, C.; Gehler, P.; Romero, J.; Black, M.J. Keep it SMPL: Automatic estimation of 3D human pose and shape from a single image. In Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Pavlakos, G.; Choutas, V.; Ghorbani, N.; Bolkart, T.; Osman, A.A.; Tzionas, D.; Black, M.J. Expressive body capture: 3d hands, face, and body from a single image. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5693–5703. [Google Scholar]
- Yang, W.; Ouyang, W.; Wang, X.; Ren, J.; Li, H.; Wang, X. 3d human pose estimation in the wild by adversarial learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5255–5264. [Google Scholar]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A skinned multi-person linear model. ACM Trans. Graph. 2015, 34, 248. [Google Scholar] [CrossRef]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3.6m: Large scale datasets and predictive methods for 3d human sensing in natural environments. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
- Varol, G.; Laptev, I.; Schmid, C.; Zisserman, A. Synthetic humans for action recognition from unseen viewpoints. arXiv 2019, arXiv:1912.04070. [Google Scholar]
- Varol, G.; Romero, J.; Martin, X.; Mahmood, N.; Black, M.J.; Laptev, I.; Schmid, C. Learning from synthetic humans. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Shrivastava, A.; Pfister, T.; Tuzel, O.; Susskind, J.; Wang, W.; Webb, R. Learning from simulated and unsupervised images through adversarial training. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Rad, M.; Oberweger, M.; Lepetit, V. Feature mapping for learning fast and accurate 3D pose inference from synthetic images. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Noroozi, M.; Favaro, P. Unsupervised learning of visual representations by solving jigsaw puzzles. In Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Gidaris, S.; Singh, P.; Komodakis, N. Unsupervised representation learning by predicting image rotations. arXiv 2018, arXiv:1803.07728. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Kato, H.; Ushiku, Y.; Harada, T. Neural 3D mesh renderer. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.K.; Wang, Z.; Smolley, S.P. Least squares generative adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Xu, T.; Takano, W. Graph Stacked Hourglass Networks for 3D Human Pose Estimation. arXiv 2021, arXiv:2103.16385. [Google Scholar]
- Moreno-Noguer, F. 3d human pose estimation from a single image via distance matrix regression. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Chen, C.H.; Ramanan, D. 3d human pose estimation= 2d pose estimation+ matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7035–7043. [Google Scholar]
- Rayat, M.; Hossain, I.; Little, J.J. Exploiting temporal information for 3D pose estimation. arXiv 2017, arXiv:1711.08585. [Google Scholar]
- Akhter, I.; Black, M.J. Pose-conditioned joint angle limits for 3D human pose reconstruction. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Ramakrishna, V.; Kanade, T.; Sheikh, Y. Reconstructing 3d human pose from 2d image landmarks. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Fish Tung, H.Y.; Harley, A.W.; Seto, W.; Fragkiadaki, K. Adversarial inverse graphics networks: Learning 2D-to-3D lifting and image-to-image translation from unpaired supervision. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Sanzari, M.; Ntouskos, V.; Pirri, F. Bayesian image based 3d pose estimation. In Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Zhou, X.; Zhu, M.; Leonardos, S.; Daniilidis, K. Sparse representation for 3D shape estimation: A convex relaxation approach. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1648–1661. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, A.; Triggs, B. Recovering 3D human pose from monocular images. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 44–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balan, A.O.; Black, M.J. The naked truth: Estimating body shape under clothing. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008. [Google Scholar]
- Guler, R.A.; Kokkinos, I. Holopose: Holistic 3d human reconstruction in-the-wild. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Omran, M.; Lassner, C.; Pons-Moll, G.; Gehler, P.; Schiele, B. Neural body fitting: Unifying deep learning and model based human pose and shape estimation. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018. [Google Scholar]
- Pavlakos, G.; Zhu, L.; Zhou, X.; Daniilidis, K. Learning to estimate 3D human pose and shape from a single color image. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Tan, J.K.V.; Budvytis, I.; Cipolla, R. Indirect Deep Structured Learning for 3D Human Body Shape and Pose Prediction. In Proceedings of the British Machine Vision Conference (BMVC), London, UK, 4–7 September 2017; BMVA Press: Durham, UK, 2017; pp. 15.1–15.11. [Google Scholar]
- Tung, H.Y.F.; Tung, H.W.; Yumer, E.; Fragkiadaki, K. Self-supervised learning of motion capture. arXiv 2017, arXiv:1712.01337. [Google Scholar]
- Saito, S.; Huang, Z.; Natsume, R.; Morishima, S.; Kanazawa, A.; Li, H. Pifu: Pixel-aligned implicit function for high-resolution clothed human digitization. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Saito, S.; Simon, T.; Saragih, J.; Joo, H. Pifuhd: Multi-level pixel-aligned implicit function for high-resolution 3d human digitization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Huang, Y.; Bogo, F.; Lassner, C.; Kanazawa, A.; Gehler, P.V.; Romero, J.; Akhter, I.; Black, M.J. Towards accurate marker-less human shape and pose estimation over time. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Lassner, C.; Romero, J.; Kiefel, M.; Bogo, F.; Black, M.J.; Gehler, P.V. Unite the people: Closing the loop between 3d and 2d human representations. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Kolotouros, N.; Pavlakos, G.; Black, M.J.; Daniilidis, K. Learning to reconstruct 3D human pose and shape via model-fitting in the loop. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Lin, K.; Wang, L.; Liu, Z. End-to-end human pose and mesh reconstruction with transformers. arXiv 2021, arXiv:2012.09760. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Long Beach, CA, USA, 2017; pp. 6000–6010. [Google Scholar]
- Kanazawa, A.; Zhang, J.Y.; Felsen, P.; Malik, J. Learning 3d human dynamics from video. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Arnab, A.; Doersch, C.; Zisserman, A. Exploiting temporal context for 3D human pose estimation in the wild. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Kolotouros, N.; Pavlakos, G.; Daniilidis, K. Convolutional mesh regression for single-image human shape reconstruction. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Pavlakos, G.; Kolotouros, N.; Daniilidis, K. Texturepose: Supervising human mesh estimation with texture consistency. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Dabral, R.; Mundhada, A.; Kusupati, U.; Afaque, S.; Sharma, A.; Jain, A. Learning 3d human pose from structure and motion. In Proceedings of the 15th European Conference, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Iqbal, U.; Molchanov, P.; Kautz, J. Weakly-Supervised 3D Human Pose Learning via Multi-view Images in the Wild. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Chen, C.H.; Tyagi, A.; Agrawal, A.; Drover, D.; Stojanov, S.; Rehg, J.M. Unsupervised 3d pose estimation with geometric self-supervision. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Li, Y.; Li, K.; Jiang, S.; Zhang, Z.; Huang, C.; Da Xu, R.Y. Geometry-driven self-supervised method for 3d human pose estimation. AAAI Conf. Artif. Intell. 2020, 34, 11442–11449. [Google Scholar] [CrossRef]
- Kocabas, M.; Karagoz, S.; Akbas, E. Self-supervised learning of 3d human pose using multi-view geometry. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Rhodin, H.; Salzmann, M.; Fua, P. Unsupervised geometry-aware representation for 3d human pose estimation. In Proceedings of the 15th European Conference, Munich, Germany, 8–14 September 2018. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Mehta, D.; Rhodin, H.; Casas, D.; Fua, P.; Sotnychenko, O.; Xu, W.; Theobalt, C. Monocular 3d human pose estimation in the wild using improved cnn supervision. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Andriluka, M.; Pishchulin, L.; Gehler, P.; Schiele, B. 2d human pose estimation: New benchmark and state of the art analysis. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the 13th European Conference, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Johnson, S.; Everingham, M. Clustered Pose and Nonlinear Appearance Models for Human Pose Estimation. In Proceedings of the British Machine Vision Conference, BMVC 2010, Aberystwyth, UK, 31 August–3 September 2010. [Google Scholar]
- von Marcard, T.; Henschel, R.; Black, M.J.; Rosenhahn, B.; Pons-Moll, G. Recovering accurate 3d human pose in the wild using imus and a moving camera. In Proceedings of the 15th European Conference, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Kundu, J.N.; Rakesh, M.; Jampani, V.; Venkatesh, R.M.; Babu, R.V. Appearance Consensus Driven Self-supervised Human Mesh Recovery. In Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Varol, G.; Ceylan, D.; Russell, B.; Yang, J.; Yumer, E.; Laptev, I.; Schmid, C. Bodynet: Volumetric inference of 3d human body shapes. In Proceedings of the 15th European Conference, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Chang, I.; Park, M.G.; Kim, J.; Yoon, J.H. Multi-View 3D Human Pose Estimation with Self-Supervised Learning. In Proceedings of the 2021 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Jeju Island, Korea, 13–16 April 2021. [Google Scholar]



| Layer | Operation | Kernel | Dimensionality |
|---|---|---|---|
| Input: Feature map | - | 10,240 × 1 | |
| 1 | Linear + ReLU + Dropout (0.5) | - | |
| 2 | Linear | - |
| Layer | Operation | Kernel | Dimensionality |
|---|---|---|---|
| Input: Feature map | - | 10,240 × 1 | |
| 1 | Linear + ReLU + Dropout(0.5) | - | |
| 2 | Linear | - |
| Layer | Operation | Kernel | Dimensionality |
|---|---|---|---|
| Input: Feature map | - | ||
| 1 | ConvT. + B.N. + ReLU | ||
| 2 | ConvT. + B.N. + ReLU | ||
| 3 | ConvT. + B.N. + ReLU | ||
| 4 | ConvT. + B.N. + ReLU | ||
| 5 | ConvT. + Tanh |
| Layer | Operation | Kernel | Dimensionality |
|---|---|---|---|
| Input: Feature map + Pose, Shape, Camera param. | - | 2205 | |
| 1 | Linear + Dropout (0.5) | - | 1024 |
| 2 | Linear + Dropout (0.5) | - | 1024 |
| 3-1 | Linear | - | 72 |
| 3-2 | Linear | - | 10 |
| 3-3 | Linear | - | 3 |
| 4 | SMPL layer [5] | - |
| Methods | Dataset | MPJPE(↓) | PA-MPJPE(↓) |
|---|---|---|---|
| Ours (self-sup)—— | Full | 96.8 | 62.1 |
| Ours (self-sup)— | Full | 95.7 | 60.3 |
| Ours (self-sup) | H36M | 90.4 | 55.4 |
| Ours (self-sup) | Full w/o Y | 86.5 | 54.9 |
| Ours (self-sup) | Full | 84.2 | 54.4 |
| Ours (weakly-sup) | Full | 80.7 | 52.7 |
| Ours (semi-sup) | Full | 65.8 | 44.9 |
| Methods | PA-MPJPE(↓) |
|---|---|
| Fully-supervised & Semi-supervised | |
| Lassner et al. [43] | 93.9 |
| Pavlakos et al. [37] | 75.9 |
| Omran et al. [36] | 59.9 |
| HMR [5] | 56.8 |
| Temporal-HMR [47] | 56.9 |
| Arnab et al. [48] | 54.3 |
| Kolotouros et al. [49] | 50.1 |
| TexturePose [50] | 49.7 |
| Kundu et al. [64] | 48.1 |
| Ours (semi-sup) | 44.9 |
| Weakly-supervised | |
| HMR unpaired [5] | 66.5 |
| Kundu et al. [64] | 58.2 |
| Iqbal et al. [52] | 54.5 |
| Ours (weakly-sup) | 52.7 |
| Self-supervised | |
| Kundu et al. [64] | 90.5 |
| Chang et al. [66] (multi-view-sup) | 77.0 |
| Kundu et al. [64] (multi-view-sup) | 74.1 |
| Ours (self-sup) | 54.4 |
| * Li et al. [54] (multi-view-sup) | 45.7 |
| Methods | MPJPE(↓) | PA-MPJPE(↓) |
|---|---|---|
| Martinez et al. [4] | - | 157.0 |
| SMPLify [9] | 199.2 | 106.1 |
| TP-NET [51] | 163.7 | 92.3 |
| HMR [5] | 130.0 | 76.7 |
| Temporal-HMR [47] | 127.1 | 80.1 |
| Kundu et al. [64] (semi-sup) | 125.8 | 78.2 |
| Ours (semi-sup) | 106.0 | 66.0 |
| Kundu et al. [64] (weakly-sup) | 153.4 | 89.8 |
| Ours (weakly-sup) | 107.4 | 69.1 |
| Kundu et al. [64] (self-sup) | 187.1 | 102.7 |
| Ours (self-sup) | 124.7 | 88.5 |
| Methods | FG-BG Seg. | Part Seg. | ||
|---|---|---|---|---|
| Acc. (↑) | F1 (↑) | Acc. (↑) | F1 (↑) | |
| Optimization-based | ||||
| SMPLify oracle [9] | 92.17 | 0.88 | 88.82 | 0.67 |
| SMPLify [9] | 91.89 | 0.88 | 87.71 | 0.64 |
| SMPLify on [37] | 92.17 | 0.88 | 88.24 | 0.64 |
| Bodynet [65] | 92.75 | 0.84 | - | - |
| Fully-supervised & Semi-supervised | ||||
| HMR [5] | 91.67 | 0.87 | 87.12 | 0.60 |
| Kolotouros et al. [49] | 91.46 | 0.87 | 88.69 | 0.66 |
| TexturePose [50] | 91.82 | 0.87 | 89.00 | 0.67 |
| Kundu et al. [64] | 91.84 | 0.87 | 89.08 | 0.67 |
| Ours (semi-sup) | 93.28 | 0.90 | 89.90 | 0.70 |
| Weakly-supervised | ||||
| HMR unpaired [5] | 91.30 | 0.86 | 87.00 | 0.59 |
| Kundu et al. [64] | 91.70 | 0.87 | 87.12 | 0.60 |
| Ours (weakly-sup) | 93.31 | 0.90 | 89.86 | 0.70 |
| Self-supervised | ||||
| Kundu et al. [64] | 91.46 | 0.86 | 87.26 | 0.64 |
| Ours (self-sup) | 92.62 | 0.89 | 87.72 | 0.63 |
| Methods | Human3.6M | 3DPW | LSP | |||
|---|---|---|---|---|---|---|
| BG-FG Seg. | Part Seg. | |||||
| MPJPE (↓) | PA-MPJPE (↓) | MPJPE (↓) | PA-MPJPE (↓) | Acc. (↑) | Acc. (↑) | |
| Ours (self-sup) - - | 90.1 | 55.5 | 126.7 | 89.5 | 92.80 | 88.15 |
| Ours (self-sup) - - | 93.1 | 60.0 | 137.5 | 98.4 | 92.86 | 88.06 |
| Ours (self-sup) - - | 91.2 | 58.2 | 135.9 | 98.7 | 92.76 | 87.70 |
| Ours (self-sup) | 84.2 | 54.4 | 124.7 | 88. | 92.62 | 87.72 |
| Ours (weakly-sup) - - | 83.7 | 53.0 | 112.1 | 69.3 | 93.39 | 89.78 |
| Ours (weakly-sup) - - | 86.3 | 54.7 | 110.5 | 68.2 | 93.37 | 89.76 |
| Ours (weakly-sup) - - | 84.1 | 53.9 | 109.6 | 68.2 | 93.45 | 89.88 |
| Ours (weakly-sup) | 80.7 | 52.7 | 107.4 | 69.1 | 93.31 | 89.86 |
| Ours (semi-sup) - - | 67.7 | 46.0 | 105.8 | 64.9 | 93.18 | 89.84 |
| Ours (semi-sup) - - | 68.4 | 45.9 | 108.0 | 65.7 | 93.23 | 89.79 |
| Ours (semi-sup) - - | 67.6 | 46.5 | 106.9 | 65.0 | 93.22 | 89.88 |
| Ours (semi-sup) | 65.8 | 44.9 | 106.0 | 66.0 | 93.28 | 89.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cha, J.; Saqlain, M.; Lee, C.; Lee, S.; Lee, S.; Kim, D.; Park, W.-H.; Baek, S. Towards Single 2D Image-Level Self-Supervision for 3D Human Pose and Shape Estimation. Appl. Sci. 2021, 11, 9724. https://doi.org/10.3390/app11209724
Cha J, Saqlain M, Lee C, Lee S, Lee S, Kim D, Park W-H, Baek S. Towards Single 2D Image-Level Self-Supervision for 3D Human Pose and Shape Estimation. Applied Sciences. 2021; 11(20):9724. https://doi.org/10.3390/app11209724
Chicago/Turabian StyleCha, Junuk, Muhammad Saqlain, Changhwa Lee, Seongyeong Lee, Seungeun Lee, Donguk Kim, Won-Hee Park, and Seungryul Baek. 2021. "Towards Single 2D Image-Level Self-Supervision for 3D Human Pose and Shape Estimation" Applied Sciences 11, no. 20: 9724. https://doi.org/10.3390/app11209724
APA StyleCha, J., Saqlain, M., Lee, C., Lee, S., Lee, S., Kim, D., Park, W. -H., & Baek, S. (2021). Towards Single 2D Image-Level Self-Supervision for 3D Human Pose and Shape Estimation. Applied Sciences, 11(20), 9724. https://doi.org/10.3390/app11209724







