Figure 1.
Card fraud worldwide from 2010 to 2027 [
1].
Figure 1.
Card fraud worldwide from 2010 to 2027 [
1].
Figure 2.
Fraud class histogram with the imbalanced dataset.
Figure 2.
Fraud class histogram with the imbalanced dataset.
Figure 3.
Plot Amount value.
Figure 3.
Plot Amount value.
Figure 4.
SMOTE linear interpolation of a random choose minority sample (k = 4 neighbors).
Figure 4.
SMOTE linear interpolation of a random choose minority sample (k = 4 neighbors).
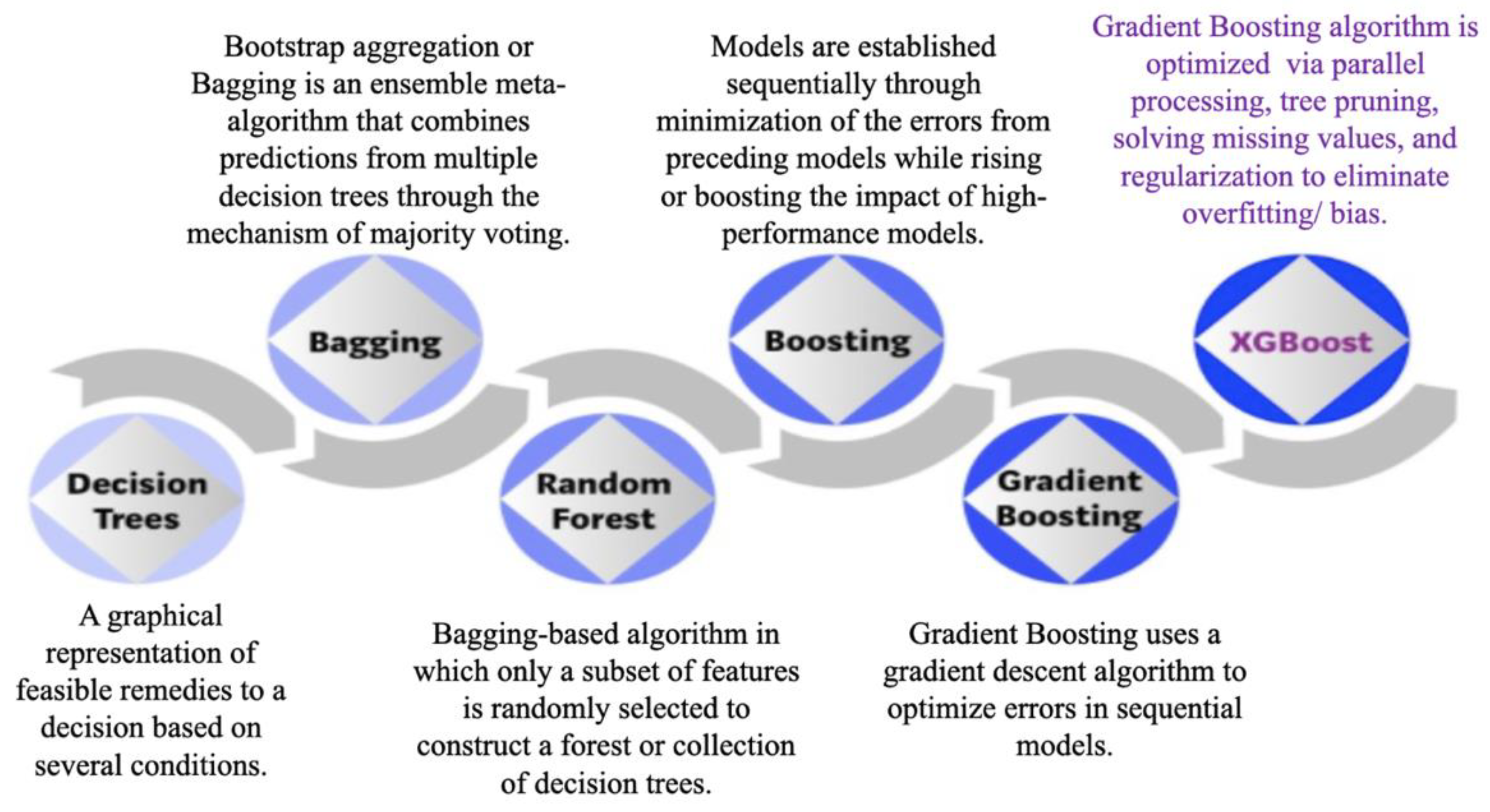
Figure 5.
Machine learning algorithms.
Figure 5.
Machine learning algorithms.
Figure 6.
Sigmoid function.
Figure 6.
Sigmoid function.
Figure 7.
Random forest with two trees [
34].
Figure 7.
Random forest with two trees [
34].
Figure 8.
Evolution of XGBoost Algorithm from Decision Trees [
40].
Figure 8.
Evolution of XGBoost Algorithm from Decision Trees [
40].
Figure 9.
Structure of DNN.
Figure 9.
Structure of DNN.
Figure 10.
Classification evaluation indexes.
Figure 10.
Classification evaluation indexes.
Figure 11.
ICMDP process.
Figure 11.
ICMDP process.
Figure 12.
Fundamental classification performance measurements of ML algorithms with SMOTE based on resampling approach 1.
Figure 12.
Fundamental classification performance measurements of ML algorithms with SMOTE based on resampling approach 1.
Figure 13.
Fundamental classification performance measurements of ML algorithms with ADASYN based on resampling approach 1.
Figure 13.
Fundamental classification performance measurements of ML algorithms with ADASYN based on resampling approach 1.
Figure 14.
Combined classification performance measurements with SMOTE based on resampling approach 1.
Figure 14.
Combined classification performance measurements with SMOTE based on resampling approach 1.
Figure 15.
Combined classification performance measurements with ADASYN based on resampling approach 1.
Figure 15.
Combined classification performance measurements with ADASYN based on resampling approach 1.
Figure 16.
AUC measurement performance of machine learning algorithms with SMOTE based on resampling approach 1.
Figure 16.
AUC measurement performance of machine learning algorithms with SMOTE based on resampling approach 1.
Figure 17.
AUC measurement performance of machine learning algorithms with ADASYN based on resampling approach 1.
Figure 17.
AUC measurement performance of machine learning algorithms with ADASYN based on resampling approach 1.
Figure 18.
Fundamental classification performance measurements of ML algorithms with SMOTE based on resampling approach 2.
Figure 18.
Fundamental classification performance measurements of ML algorithms with SMOTE based on resampling approach 2.
Figure 19.
Fundamental classification performance measurements of ML algorithms with ADASYN based on resampling approach 2.
Figure 19.
Fundamental classification performance measurements of ML algorithms with ADASYN based on resampling approach 2.
Figure 20.
Combined classification performance measurements with SMOTE based on resampling approach 2.
Figure 20.
Combined classification performance measurements with SMOTE based on resampling approach 2.
Figure 21.
Combined classification performance measurements with ADASYN based on resampling approach 2.
Figure 21.
Combined classification performance measurements with ADASYN based on resampling approach 2.
Figure 22.
AUC measurement performance of machine learning algorithms with SMOTE based on resampling approach 2.
Figure 22.
AUC measurement performance of machine learning algorithms with SMOTE based on resampling approach 2.
Figure 23.
AUC measurement performance of machine learning algorithms with ADASYN based on resampling approach 2.
Figure 23.
AUC measurement performance of machine learning algorithms with ADASYN based on resampling approach 2.
Table 1.
Data description.
Table 1.
Data description.
| Descriptions | Details |
|---|
| Number of columns | 31 |
| Number of features | 30 |
| Labels | Class 0 and class 1 |
| Number of rows | 284,807 |
| Feature type | Object |
| Missing values | None |
| No frauds vs Frauds | 99.828% vs. 0.172% |
Table 2.
Confusion matrix.
Table 2.
Confusion matrix.
| Actual Values | Predicted Values |
| Class | Negative (0) | Positive (1) |
| Negative (0) | True Negative
(TN) | False Positive
(FP) |
| Positive (1) | False Negative
(FN) | True Positive
(TP) |
Table 3.
Interpretation of Thresholds of Positive Likelihood.
Table 3.
Interpretation of Thresholds of Positive Likelihood.
| L Value | Contribution of Model |
|---|
| >10 | Good |
| 5–10 | Fair |
| 1–5 | Poor |
| 1 | Negligible |
Table 4.
AUC Performance.
Table 4.
AUC Performance.
| AUC Value | Performance of Model |
|---|
| 0.9–1.0 | Excellent |
| 0.8–0.9 | Very good |
| 0.7–0.8 | Good |
| 0.6–0.7 | Fair |
| 0.5–0.6 | Poor |
Table 5.
TP, FP, TN, FN rates of machine learning algorithms on imbalanced dataset.
Table 5.
TP, FP, TN, FN rates of machine learning algorithms on imbalanced dataset.
| Rate | RF | KNN | DT | LR | AdaBoost | XGBoost | DNN |
|---|
| TP | 113 | 106 | 111 | 91 | 101 | 115 | 119 |
| FP | 6 | 7 | 25 | 12 | 17 | 8 | 24 |
| TN | 85,290 | 85,289 | 85,271 | 85,284 | 85,279 | 85,288 | 85,272 |
| FN | 1 | 41 | 36 | 1 | 46 | 32 | 32 |
Table 6.
Accuracies of the ML models on imbalanced dataset.
Table 6.
Accuracies of the ML models on imbalanced dataset.
| Algorithms | RF | KNN | DT | LR | AdaBoost | XGBoost | DNN |
|---|
| Accuracy | 99.95% | 99.94% | 99.91% | 99.92% | 99.92% | 99.95% | 99.94% |
Table 7.
TP, FP, TN, FN rates of machine learning algorithms with SMOTE based on resampling approach 1.
Table 7.
TP, FP, TN, FN rates of machine learning algorithms with SMOTE based on resampling approach 1.
| Rate | RF with SMOTE | KNN with SMOTE | DT with SMOTE | LR with SMOTE | AdaBoost with SMOTE | XGBoost with SMOTE | DNN with SMOTE |
|---|
| TP | 85,427 | 85,427 | 85,314 | 78,171 | 82,219 | 85,496 | 85,238 |
| FP | 19 | 209 | 270 | 2117 | 1466 | 53 | 262 |
| TN | 85,143 | 84,953 | 84,892 | 83,045 | 83,663 | 85,040 | 85,020 |
| FN | 0 | 0 | 113 | 7256 | 3241 | 0 | 69 |
Table 8.
TP, FP, TN, FN rates of machine learning algorithms with ADASYN based on resampling approach 1.
Table 8.
TP, FP, TN, FN rates of machine learning algorithms with ADASYN based on resampling approach 1.
| Rate | RF with ADASYN | KNN with ADASYN | DT with ADASYN | LR with ADASYN | AdaBoost with ADASYN | XGBoost with ADASYN | DNN with ADASYN |
|---|
| TP | 85,428 | 85,429 | 85,366 | 73,864 | 71,308 | 85,205 | 85,276 |
| FP | 30 | 179 | 218 | 7194 | 1475 | 111 | 503 |
| TN | 85,128 | 84,979 | 84,940 | 77,244 | 84,028 | 85,271 | 84,778 |
| FN | 1 | 0 | 63 | 11,565 | 13,776 | 0 | 30 |
Table 9.
Positive Likelihood Ratio based on resampling approach 1.
Table 9.
Positive Likelihood Ratio based on resampling approach 1.
| ML Algorithms | Positive Likelihood Ratio | Model Contribution |
|---|
| RF | SMOTE | 4482.21 | Good |
| ADASYN | 2838.57 | Good |
| KNN | SMOTE | 407.47 | Good |
| ADASYN | 475.74 | Good |
| DT | SMOTE | 315.00 | Good |
| ADASYN | 390.34 | Good |
| LR | SMOTE | 36.81 | Good |
| ADASYN | 10.15 | Good |
| AdaBoost | SMOTE | 55.87 | Good |
| ADASYN | 48.58 | Good |
| XGBoost | SMOTE | 1605.52 | Good |
| ADASYN | 769.21 | Good |
| DNN | SMOTE | 325.24 | Good |
| ADASYN | 169.49 | Good |
Table 10.
TP, FP, TN, FN rates of machine learning algorithms with SMOTE based on resampling approach 2.
Table 10.
TP, FP, TN, FN rates of machine learning algorithms with SMOTE based on resampling approach 2.
| Rate | RF with SMOTE | KNN with SMOTE | DT with SMOTE | LR with SMOTE | AdaBoost with SMOTE | XGBoost with SMOTE | DNN with SMOTE |
|---|
| TP | 120 | 127 | 113 | 135 | 128 | 123 | 126 |
| FP | 14 | 127 | 168 | 2100 | 1086 | 37 | 180 |
| TN | 85,282 | 85,169 | 85,128 | 83,196 | 84,210 | 85,259 | 85,156 |
| FN | 27 | 20 | 34 | 12 | 19 | 24 | 21 |
Table 11.
TP, FP, TN, FN rates of machine learning algorithms with ADASYN based on resampling approach 2.
Table 11.
TP, FP, TN, FN rates of machine learning algorithms with ADASYN based on resampling approach 2.
| Rate | RF with ADASYN | KNN with ADASYN | DT with ADASYN | LR with ADASYN | AdaBoost with ADASYN | XGBoost with ADASYN | DNN with ADASYN |
|---|
| TP | 117 | 127 | 108 | 139 | 128 | 120 | 122 |
| FP | 13 | 128 | 150 | 7543 | 2670 | 44 | 134 |
| TN | 85,283 | 85,168 | 85,146 | 77,753 | 82,626 | 85,252 | 85,162 |
| FN | 30 | 20 | 39 | 8 | 19 | 27 | 25 |
Table 12.
Positive Likelihood Ratio based on resampling approach 2.
Table 12.
Positive Likelihood Ratio based on resampling approach 2.
| ML Algorithms | Positive Likelihood Ratio | Model Contribution |
|---|
| RF | SMOTE | 4973.53 | Good |
| ADASYN | 5222.20 | Good |
| KNN | SMOTE | 580.24 | Good |
| ADASYN | 575.71 | Good |
| DT | SMOTE | 390.28 | Good |
| ADASYN | 417.78 | Good |
| LR | SMOTE | 37.30 | Good |
| ADASYN | 10.69 | Good |
| AdaBoost | SMOTE | 68.39 | Good |
| ADASYN | 27.82 | Good |
| XGBoost | SMOTE | 1928.92 | Good |
| ADASYN | 1582.49 | Good |
| DNN | SMOTE | 406.36 | Good |
| ADASYN | 528.28 | Good |
Table 13.
Classification measurements indexes of ML algorithms based on SMOTE for two resampling approaches.
Table 13.
Classification measurements indexes of ML algorithms based on SMOTE for two resampling approaches.
| ML Algorithms Based on SMOTE | Accuracy | Precision | Sensitivity | Specificity | F1 Score | G-Mean | Balanced Accuracy | MCC | AUC |
|---|
| RF approach 1 | 99.99% | 99.98% | 100.00% | 99.98% | 99.99% | 99.99% | 99.99% | 99.98% | 100.00% |
| RF approach 2 | 99.95% | 89.55% | 81.63% | 99.98% | 85.41% | 90.34% | 90.81% | 85.48% | 90.81% |
| KNN approach 1 | 99.88% | 99.76% | 100.00% | 99.75% | 99.88% | 99.88% | 99.88% | 99.76% | 100.00% |
| KNN approach 2 | 99.83% | 50.00% | 86.39% | 99.85% | 63.34% | 92.88% | 93.12% | 65.65% | 93.12% |
| DT approach 1 | 99.78% | 99.68% | 99.87% | 99.68% | 99.78% | 99.78% | 99.78% | 99.55% | 99.80% |
| DT approach 2 | 99.76% | 40.21% | 76.87% | 99.80% | 52.80% | 87.59% | 88.34% | 55.50% | 88.34% |
| LR approach 1 | 94.51% | 97.36% | 91.51% | 97.51% | 94.34% | 94.46% | 94.51% | 89.17% | 98.90% |
| LR approach 2 | 97.53% | 6.04% | 91.84% | 97.54% | 11.34% | 94.64% | 94.69% | 23.21% | 94.68% |
| AdaBoost approach 1 | 97.24% | 98.25% | 96.20% | 98.28% | 97.21% | 97.24% | 97.24% | 94.50% | 97.24% |
| AdaBoost approach 2 | 98.71% | 10.54% | 87.07% | 98.73% | 18.81% | 92.72% | 92.90% | 30.05% | 92.90% |
| XGBoost approach 1 | 99.97% | 99.94% | 99.94% | 100% | 99.97% | 99.97% | 99.97% | 99.94% | 99.67% |
| XGBoost approach 2 | 99.93% | 76.88% | 83.67% | 100% | 80.13% | 91.45% | 91.82% | 80.17% | 91.82% |
| DNN approach 1 | 99.81% | 99.69% | 99.92% | 99.69% | 99.81% | 99.81% | 99.81% | 99.61% | 99.97% |
| DNN approach 2 | 99.76% | 41.18% | 85.71% | 99.79% | 55.63% | 92.48% | 92.75% | 59.32% | 95.28% |
Table 14.
Classification measurements indexes of ML algorithms based on ADASYN for two resampling approaches.
Table 14.
Classification measurements indexes of ML algorithms based on ADASYN for two resampling approaches.
| ML Algorithms Based on ADASYN | Accuracy | Precision | Sensitivity | Specificity | F1 Score | G-Mean | Balanced Accuracy | MCC | AUC |
|---|
| RF approach 1 | 99.98% | 99.96% | 100.00% | 99.96% | 99.98% | 99.98% | 99.98% | 99.96% | 100.00% |
| RF approach 2 | 99.95% | 90.00% | 79.59% | 99.98% | 84.48% | 89.21% | 89.79% | 84.61% | 89.79% |
| KNNapproach 1 | 99.90% | 99.79% | 100.00% | 99.79% | 99.90% | 99.89% | 99.89% | 99.79% | 100.00% |
| KNN approach 2 | 99.83% | 49.80% | 86.39% | 99.85% | 63.18% | 92.88% | 93.12% | 65.52% | 93.12% |
| DT approach 1 | 99.84% | 99.75% | 99.93% | 99.74% | 99.84% | 99.84% | 99.84% | 99.67% | 99.80% |
| DT approach 2 | 99.78% | 41.86% | 73.47% | 99.82% | 53.33% | 85.64% | 86.65% | 55.36% | 86.65% |
| LR approach 1 | 88.96% | 91.12% | 86.46% | 91.48% | 88.73% | 88.94% | 88.97% | 77.23% | 95.90% |
| LR approach 2 | 91.16% | 1.81% | 94.56% | 91.16% | 3.55% | 92.84% | 92.86% | 12.42% | 92.85% |
| AdaBoost approach 1 | 91.06% | 97.97% | 83.81% | 98.27% | 90.34% | 90.75% | 91.04% | 82.98% | 91.04% |
| AdaBoost approach 2 | 96.85% | 4.57% | 87.07% | 96.87% | 8.69% | 91.84% | 91.97% | 30.05% | 91.97% |
| XGBoost approach 1 | 99.93% | 99.87% | 100% | 99.87% | 99.93% | 99.93% | 99.93% | 99.87% | 99.93% |
| XGBoost approach 2 | 99.92% | 73.17% | 82% | 99.95% | 77.17% | 90.33% | 90.79% | 77.24% | 90.79% |
| DNN approach 1 | 99.69% | 99.41% | 99.96% | 99.41% | 99.69% | 99.69% | 99.69% | 99.90% | 99.38% |
| DNN approach 2 | 99.81% | 47.66% | 82.99% | 99.84% | 60.55% | 91.03% | 91.42% | 62.81% | 97.05% |
Table 15.
Confusion matrix of DRL on imbalanced dataset.
Table 15.
Confusion matrix of DRL on imbalanced dataset.
| True Values | Predicted Values |
| Class | 0 | 1 |
| 0 | 29,701 | 55,595 |
| 110 | 34 | 37 |
Table 16.
Classification metrics for DRL on imbalanced CCF dataset.
Table 16.
Classification metrics for DRL on imbalanced CCF dataset.
| Classification Measurements | Accuracy | Precision | Sensitivity | Specificity | F1 Score | G-Mean | Balanced Accuracy |
| 34.8% | 0.067% | 25.17% | 34.82% | 13.27% | 29.60% | 29.99% |