Prediction of Total Imperviousness from Population Density and Land Use Data for Urban Areas (Case Study: South East Queensland, Australia)
Abstract
:1. Introduction
- Whether or not a sub-pixel classification approach can extract imperviousness with acceptable accuracy in our case study, which is a complex urban–rural frontier.
- What is the nature of the relationship, linear or nonlinear, between population density and total imperviousness, and between population density and the residential impervious at the suburb scale?
- Whether or not population density is a better predictor of residential imperviousness than total imperviousness at suburb scale?
- Whether or not our recommended method could be used to estimate total imperviousness more accurately than previous regression models between population density and total imperviousness in dense residential suburbs?
2. Material and Methods
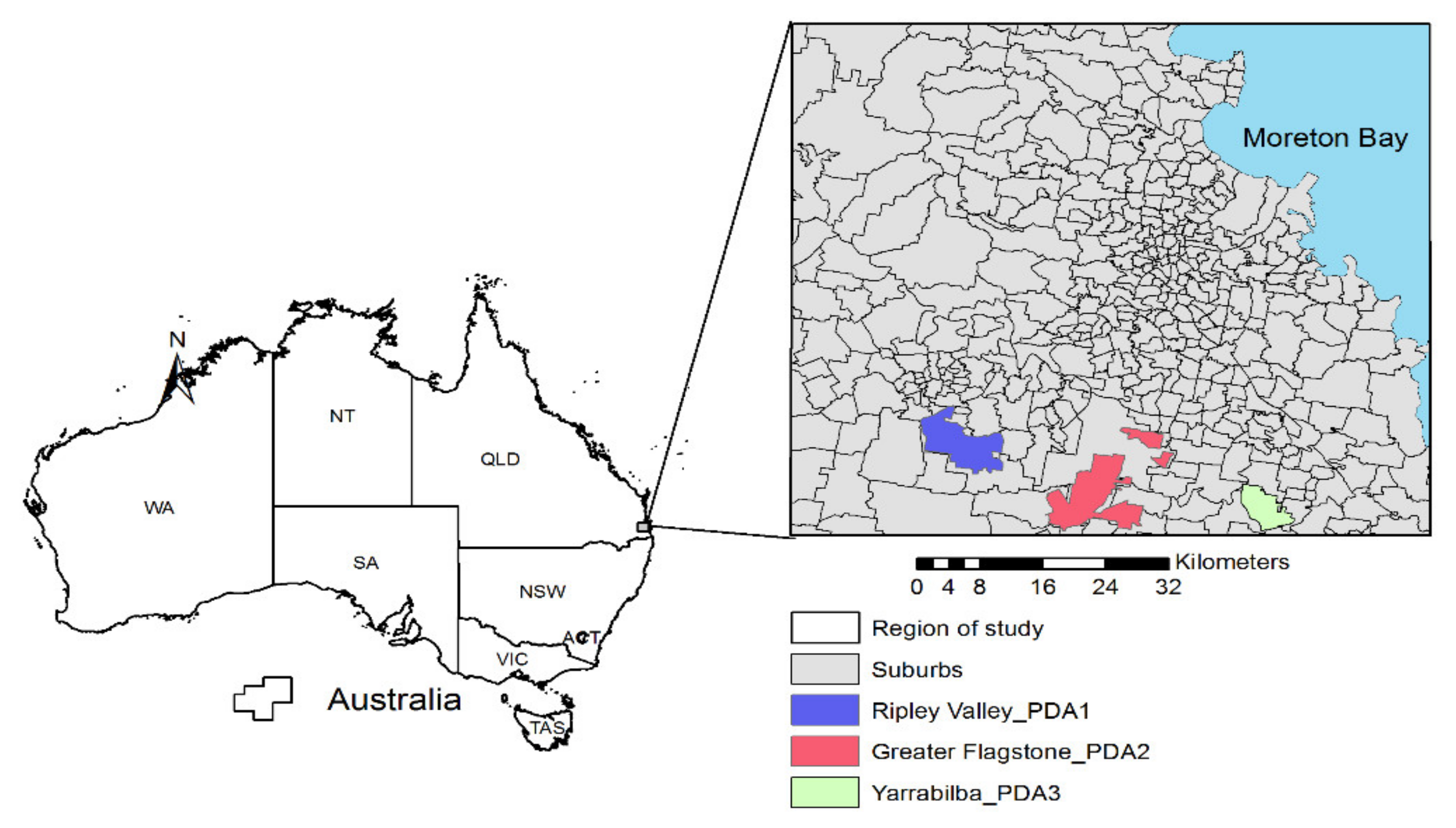
2.1. Study Area
2.2. Dataset
2.3. Extraction of Total Imperviousness
- Step 1: Removal of water bodies
- Step 2: Sub-pixel classification approach
2.4. Relatioship between Population Density and Total Imperviousness
2.5. Model Development between Population Density and Residential Imperviousness
2.6. Estimation of the Total Imperviousness Dense Residential Suburbs
3. Results
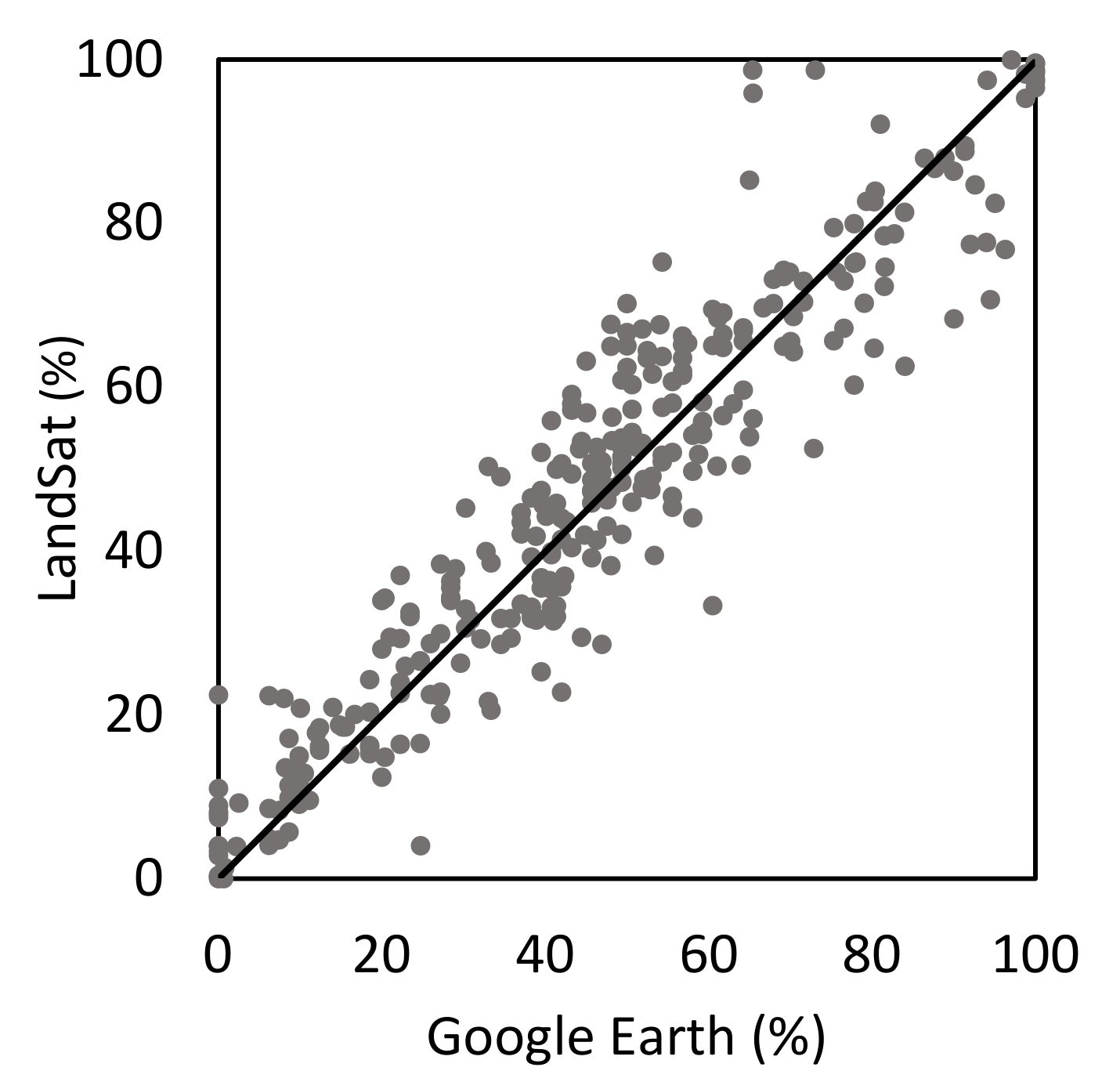
3.1. Evaluation of Extracted Total Imperviousness
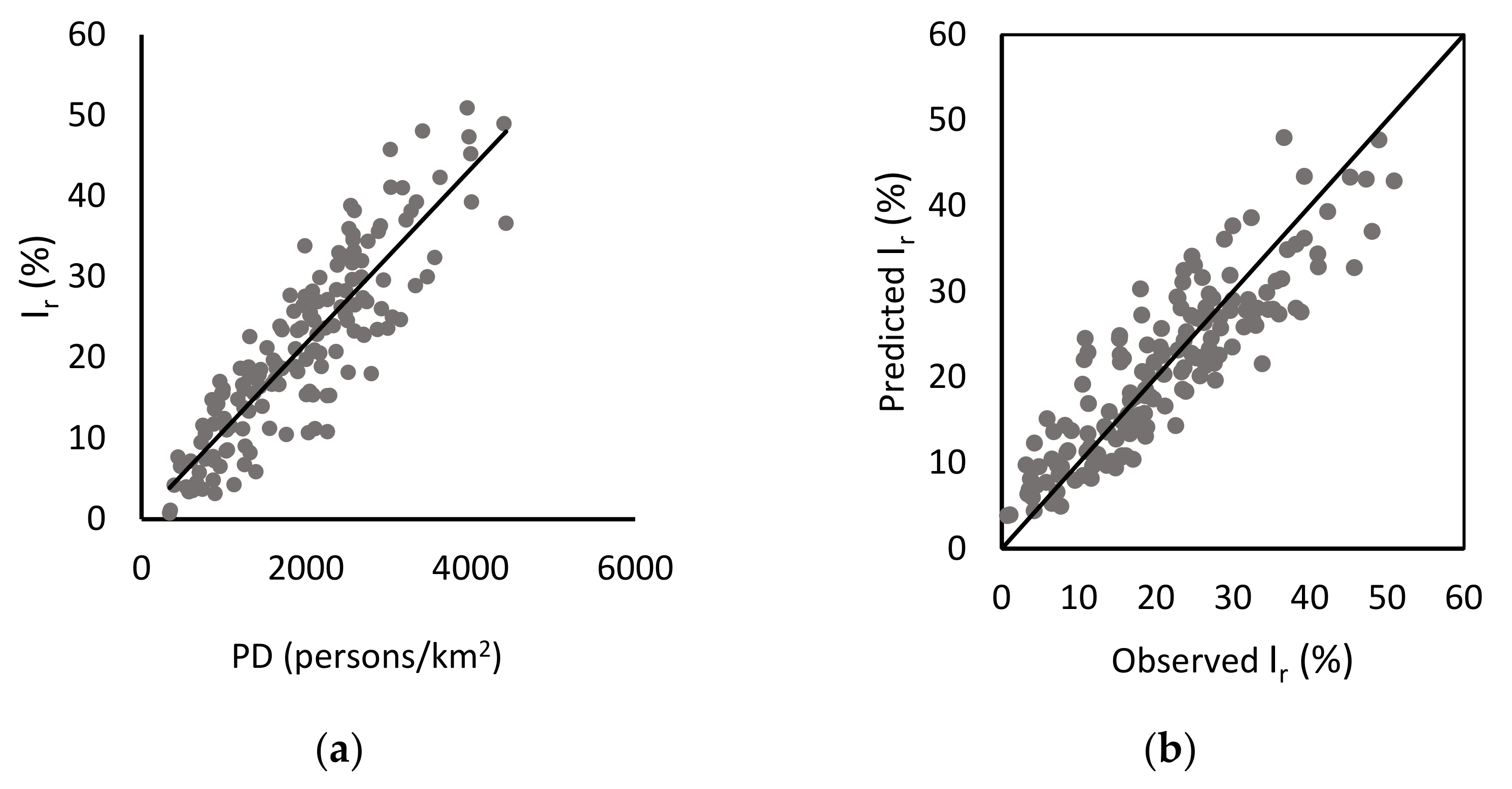
3.2. Relationship between the Total Imperviousness and Population Density
3.3. Relationship between the Population Density and Residential Imperviousness
3.4. Accuracy Assessment of the Two Methods for Dense Residential Suburbs
3.5. Prediction of Total Imperviousness for New Urban Regions in 2057
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arnold, C.L., Jr.; Gibbons, C.J. Impervious surface coverage: The emergence of a key environmental indicator. J. Am. Plan. Assoc. 1996, 62, 243–258. [Google Scholar] [CrossRef]
- Li, C.; Liu, M.; Hu, Y.; Shi, T.; Qu, X.; Walter, M.T. Effects of urbanization on direct runoff characteristics in urban functional zones. Sci. Total Environ. 2018, 643, 301–311. [Google Scholar] [CrossRef] [PubMed]
- Morabito, M.; Crisci, A.; Georgiadis, T.; Orlandini, S.; Munafò, M.; Congedo, L.; Rota, P.; Zazzi, M. Urban Imperviousness Effects on Summer Surface Temperatures Nearby Residential Buildings in Different Urban Zones of Parma. Remote Sens. 2017, 10, 26. [Google Scholar] [CrossRef] [Green Version]
- Zhi, X.; Chen, L.; Shen, Z. Impacts of urbanization on regional nonpoint source pollution: Case study for Beijing, China. Environ. Sci. Pollut. Res. 2018, 25, 9849–9860. [Google Scholar] [CrossRef] [PubMed]
- Fox, D.M.; Youssaf, Z.; Adnès, C.; Delestre, O. Relating imperviousness to building growth and developed area in order to model the impact of peri-urbanization on runoff in a Mediterranean catchment (1964–2014). J. Land Use Sci. 2019, 14, 210–224. [Google Scholar] [CrossRef]
- Sang, L.; Zhang, C.; Yang, J.; Zhu, D.; Yun, W. Simulation of land use spatial pattern of towns and villages based on CA–Markov model. Math. Comput. Model. 2010, 54, 938–943. [Google Scholar] [CrossRef]
- Palacios-Lopez, D.; Bachofer, F.; Esch, T.; Marconcini, M.; MacManus, K.; Sorichetta, A.; Zeidler, J.; Dech, S.; Tatem, A.; Reinartz, P. High-Resolution Gridded Population Datasets: Exploring the Capabilities of the World Settlement Footprint 2019 Imperviousness Layer for the African Continent. Remote Sens. 2021, 13, 1142. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Zhao, M.; Hou, J.; Zhang, Y.; Gu, J. Mapping the Population Density in Mainland China using NPP/VIIRS and Points-Of-Interest Data Based on a Random Forests Model. Remote Sens. 2020, 12, 3645. [Google Scholar] [CrossRef]
- Adhikari, S.; Southworth, J. Simulating Forest Cover Changes of Bannerghatta National Park Based on a CA-Markov Model: A Remote Sensing Approach. Remote Sens. 2012, 4, 3215–3243. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Lu, D. Mapping population density distribution at multiple scales in Zhejiang Province using Landsat Thematic Mapper and census data. Int. J. Remote Sens. 2016, 37, 4243–4260. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Y.; Liu, Z.; Fu, B. Estimating The Population Distribution in a County Area in China Based on Impervious Surfaces. Photogramm. Eng. Remote Sens. 2015, 81, 155–163. [Google Scholar] [CrossRef]
- Harvey, J.T. Population estimation models based on individual TM pixels. Photogramm. Eng. Remote. Sens. 2002, 68, 1181–1192. [Google Scholar]
- Stevens, F.F.R.; Gaughan, A.A.E.; Linard, C.; Tatem, A.A.J. Disaggregating Census Data for Population Mapping Using Random Forests with Remotely-Sensed and Ancillary Data. PLoS ONE 2015, 10, e0107042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amaral, S.; Gavlak, A.A.; Escada, M.I.S.; Monteiro, A.M.V. Using remote sensing and census tract data to improve representation of population spatial distribution: Case studies in the Brazilian Amazon. Popul. Environ. 2012, 34, 142–170. [Google Scholar] [CrossRef]
- Azar, D.; Engstrom, R.; Graesser, J.; Comenetz, J. Generation of fine-scale population layers using multi-resolution satellite imagery and geospatial data. Remote Sens. Environ. 2013, 130, 219–232. [Google Scholar] [CrossRef]
- Azar, D.; Graesser, J.; Engstrom, R.; Comenetz, J.; Leddy, R.M., Jr.; Schechtman, N.G.; Andrews, T. Spatial refinement of census population distribution using remotely sensed estimates of impervious surfaces in Haiti. Int. J. Remote. Sens. 2010, 31, 5635–5655. [Google Scholar] [CrossRef]
- Xu, F.; Cao, X.; Chen, X.; Somers, B. Mapping impervious surface fractions using automated Fisher transformed unmixing. Remote Sens. Environ. 2019, 232, 111311. [Google Scholar] [CrossRef]
- Song, S.; Xu, Y.; Wu, Z.; Deng, X.; Wang, Q. The relative impact of urbanization and precipitation on long-term water level variations in the Yangtze River Delta. Sci. Total Environ. 2019, 648, 460–471. [Google Scholar] [CrossRef]
- Li, C.; Yang, M.; Li, Z.; Wang, B. How Will Rwandan Land Use/Land Cover Change under High Population Pressure and Changing Climate? Appl. Sci. 2021, 11, 5376. [Google Scholar] [CrossRef]
- Cracknell, C.; Downton, A.C. TABS: Script-based software framework for research in image processing, analysis and understanding. IEE Proc.—Vision, Image, Signal Process. 1998, 145, 194–202. [Google Scholar] [CrossRef]
- Weng, Q. Remote sensing of impervious surfaces in the urban areas: Requirements, methods, and trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar] [CrossRef]
- Lu, D.; Li, G.; Kuang, W.; Moran, E. Methods to extract impervious surface areas from satellite images. Int. J. Digit. Earth 2014, 7, 93–112. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Y.; Wallace, J.; Campbell, E. Estimating annual runoff in response to forest change: A statistical method based on random forest. J. Hydrol. 2020, 589, 125168. [Google Scholar] [CrossRef]
- Lu, Z.; Im, J.; Quackenbush, L.; Halligan, K. Population estimation based on multi-sensor data fusion. Int. J. Remote Sens. 2010, 31, 5587–5604. [Google Scholar] [CrossRef]
- Sunde, M.; He, H.S.; Zhou, B.; Hubbart, J.A.; Spicci, A. Imperviousness Change Analysis Tool (I-CAT) for simulating pixel-level urban growth. Landsc. Urban Plan. 2014, 124, 104–108. [Google Scholar] [CrossRef]
- Stankowski, S.J.; Trenton, N.J. Population Density as an Indirect Indicator of Urban and Suburban Land-Surface Modifications. In U.S. Geological Survey Professional Paper; U.S. Government Printing Office: Washington, DC, USA, 1972; pp. 219–224. [Google Scholar]
- Bagan, H.; Yamagata, Y. Analysis of urban growth and estimating population density using satellite images of nighttime lights and land-use and population data. GISci. Remote Sens. 2015, 52, 765–780. [Google Scholar] [CrossRef]
- Liu, X.H.; Kyriakidis, P.C.; Goodchild, M.F. Population-density estimation using regression and area-to-point residual kriging. Int. J. Geogr. Inf. Sci. 2008, 22, 431–447. [Google Scholar] [CrossRef]
- Sutton, P.C. A scale-adjusted measure of “urban sprawl” using nighttime satellite imagery. Remote. Sens. Environ. 2003, 86, 353–369. [Google Scholar] [CrossRef]
- Carlson, T.N. Analysis and prediction of surface runoff in an urbanizing watershed using satellite imagery. JAWRA J. Am. Water Resour. Assoc. 2004, 40, 1087–1098. [Google Scholar] [CrossRef]
- Zhou, Q.; Leng, G.; Su, J.; Ren, Y. Comparison of urbanization and climate change impacts on urban flood volumes: Importance of urban planning and drainage adaptation. Sci. Total Environ. 2018, 658, 24–33. [Google Scholar] [CrossRef]
- Zhao, J.; Tsutsumida, N. Mapping Fragmented Impervious Surface Areas Overlooked by Global Land-Cover Products in the Liping County, Guizhou Province, China. Remote Sens. 2020, 12, 1527. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.; Yu, W.; Zhao, Y.; Xu, Y. Comparison of baseline period choices for separating climate and land use/land cover change impacts on watershed hydrology using distributed hydrological models. Sci. Total Environ. 2018, 622–623, 1016–1028. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sens. Environ. 2003, 84, 493–505. [Google Scholar] [CrossRef]
- Iovanna, R.; Vance, C. Modeling of continuous-time land cover change using satellite imagery: An application from North Carolina. J. Land Use Sci. 2007, 2, 147–166. [Google Scholar] [CrossRef] [Green Version]
- Xian, G.; Homer, C. Updating the 2001 National Land Cover Database Impervious Surface Products to 2006 using Landsat Imagery Change Detection Methods. Remote Sens. Environ. 2010, 114, 1676–1686. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Xie, C.; Cui, B.; Xie, T.; Yu, S.; Liu, Z.; Chen, C.; Ning, Z.; Wang, Q.; Zou, Y.; Shao, X. Hydrological connectivity dynamics of tidal flat systems impacted by severe reclamation in the Yellow River Delta. Sci. Total Environ. 2020, 739, 139860. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Ferreira, V.G.; Onojeghuo, A.O.; Agutu, N.O.; Emengini, E.; Getirana, A. Influence of global climate on freshwater changes in Africa’s largest endorheic basin using multi-scaled indicators. Sci. Total Environ. 2020, 737, 139643. [Google Scholar] [CrossRef]
- Bie, W.; Fei, T.; Liu, X.; Liu, H.; Wu, G. Small water bodies mapped from Sentinel-2 MSI (MultiSpectral Imager) imagery with higher accuracy. Int. J. Remote Sens. 2020, 41, 7912–7930. [Google Scholar] [CrossRef]
- Șerban, R.-D.; Jin, H.; Șerban, M.; Luo, D.; Wang, Q.; Jin, X.; Ma, Q. Mapping thermokarst lakes and ponds across permafrost landscapes in the Headwater Area of Yellow River on northeastern Qinghai-Tibet Plateau. Int. J. Remote Sens. 2020, 41, 7042–7067. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 Site. J. Geophys. Res. 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. Use of impervious surface in urban land-use classification. Remote Sens. Environ. 2006, 102, 146–160. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Liu, L.; Wang, Z.; Zhang, H.; Li, S.; Ding, M. Mapping Changing Population Distribution on the Qinghai–Tibet Plateau since 2000 with Multi-Temporal Remote Sensing and Point-of-Interest Data. Remote Sens. 2020, 12, 4059. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. Spectral Mixture Analysis of the Urban Landscape in Indianapolis with Landsat ETM+ Imagery. Photogramm. Eng. Remote Sens. 2004, 70, 1053–1062. [Google Scholar] [CrossRef] [Green Version]
- Joseph, M.; Wang, L.; Wang, F. Using Landsat Imagery and Census Data for Urban Population Density Modeling in Port-au-Prince, Haiti. GISci. Remote Sens. 2012, 49, 228–250. [Google Scholar] [CrossRef]
- Jia, Y.; Tang, L.; Wang, L. Influence of Ecological Factors on Estimation of Impervious Surface Area Using Landsat 8 Imagery. Remote Sens. 2017, 9, 751. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Moran, E.; Hetrick, S. Detection of impervious surface change with multitemporal Landsat images in an urban–rural frontier. ISPRS J. Photogramm. Remote Sens. 2011, 66, 298–306. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Weng, Q.; Li, G. Residential population estimation using a remote sensing derived impervious surface approach. Int. J. Remote Sens. 2006, 27, 3553–3570. [Google Scholar] [CrossRef]
- Van De Voorde, T.; De Roeck, T.; Canters, F. A comparison of two spectral mixture modelling approaches for impervious surface mapping in urban areas. Int. J. Remote Sens. 2009, 30, 4785–4806. [Google Scholar] [CrossRef]
- Bewick, V.; Cheek, L.; Ball, J. Statistics review 7: Correlation and regression. Crit. Care 2003, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Murray, A.T. A cokriging method for estimating population density in urban areas. Comput. Environ. Urban Syst. 2005, 29, 558–579. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. Population Estimation Using Landsat Enhanced Thematic Mapper Imagery. Geogr. Anal. 2007, 39, 26–43. [Google Scholar] [CrossRef]


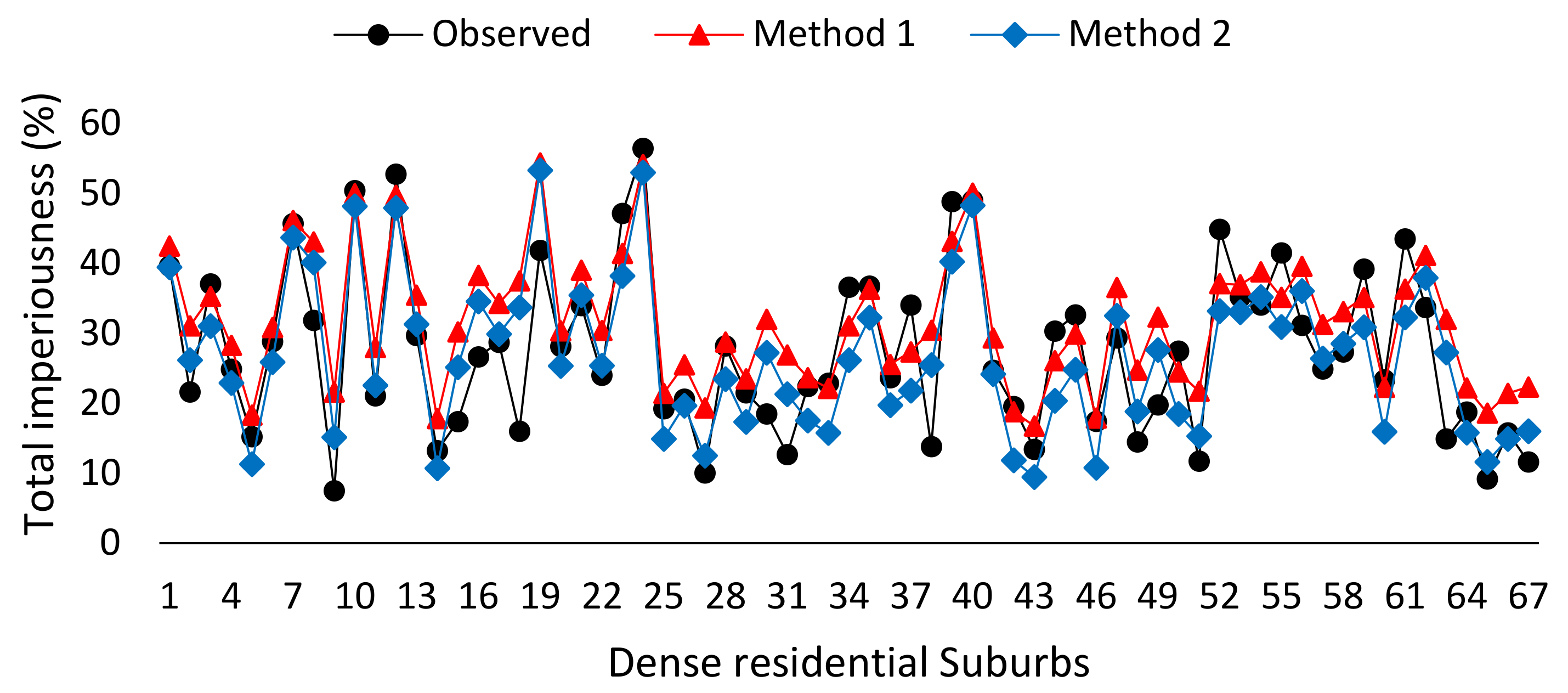
| References | R2 | MAE (%) | RMSE (%) |
|---|---|---|---|
| This study | 0.87 | 7 | 9 |
| Lu et al. [44] | 0.7 | NA | 10 |
| Lu et al. [49] | NA | NA | 9 |
| Li and Lu [10] | NA | 10 | NA |
| Van de Voorde et al. [50] | NA | 12.90 | NA |
| Type of Regression | Equation | R2 | MAE | RMSE |
|---|---|---|---|---|
| Linear | 0.52 | 6.77 | 9.06 | |
| Nonlinear (power) | 0.51 | 6.99 | 9.22 | |
| Nonlinear (exponential) | 0.49 | 7.31 | 9.77 | |
| Nonlinear (logarithmic) | 0.48 | 7.24 | 9.43 |
| Type of Regression | Equation | R2 | MAE | RMSE |
|---|---|---|---|---|
| Linear | 0.77 | 4.4 | 5.4 | |
| Nonlinear (power) | 0.76 | 4.5 | 5.55 | |
| Nonlinear (exponential) | 0.67 | 5.84 | 7.43 | |
| Nonlinear (logarithmic) | 0.71 | 4.84 | 6.01 |
| PDA | Population Density (Persons/km2) | Non-Residential Imperviousness (%) | Residential Imperviousness (%) and 95% Prediction Intervals | Total Imperviousness (%) (Method 2) |
|---|---|---|---|---|
| Ripley Valley | 2609 | 3.1 | 28.3 (±3.7) | 31.4 (27.7–35.1) |
| Greater Flagstone | 1667 | 2 | 18.2 (±3.6) | 20.2 (16.6–23.8) |
| Yarrabilba | 2273 | 2.7 | 24.7 (±3.6) | 27.4 (23.8–31) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramezani, M.R.; Yu, B.; Che, Y. Prediction of Total Imperviousness from Population Density and Land Use Data for Urban Areas (Case Study: South East Queensland, Australia). Appl. Sci. 2021, 11, 10044. https://doi.org/10.3390/app112110044
Ramezani MR, Yu B, Che Y. Prediction of Total Imperviousness from Population Density and Land Use Data for Urban Areas (Case Study: South East Queensland, Australia). Applied Sciences. 2021; 11(21):10044. https://doi.org/10.3390/app112110044
Chicago/Turabian StyleRamezani, Mohammad Reza, Bofu Yu, and Yahui Che. 2021. "Prediction of Total Imperviousness from Population Density and Land Use Data for Urban Areas (Case Study: South East Queensland, Australia)" Applied Sciences 11, no. 21: 10044. https://doi.org/10.3390/app112110044
APA StyleRamezani, M. R., Yu, B., & Che, Y. (2021). Prediction of Total Imperviousness from Population Density and Land Use Data for Urban Areas (Case Study: South East Queensland, Australia). Applied Sciences, 11(21), 10044. https://doi.org/10.3390/app112110044







