Discrete and Continuum Approaches for Modeling Solids Motion Inside a Rotating Drum at Different Regimes
Abstract
:1. Introduction
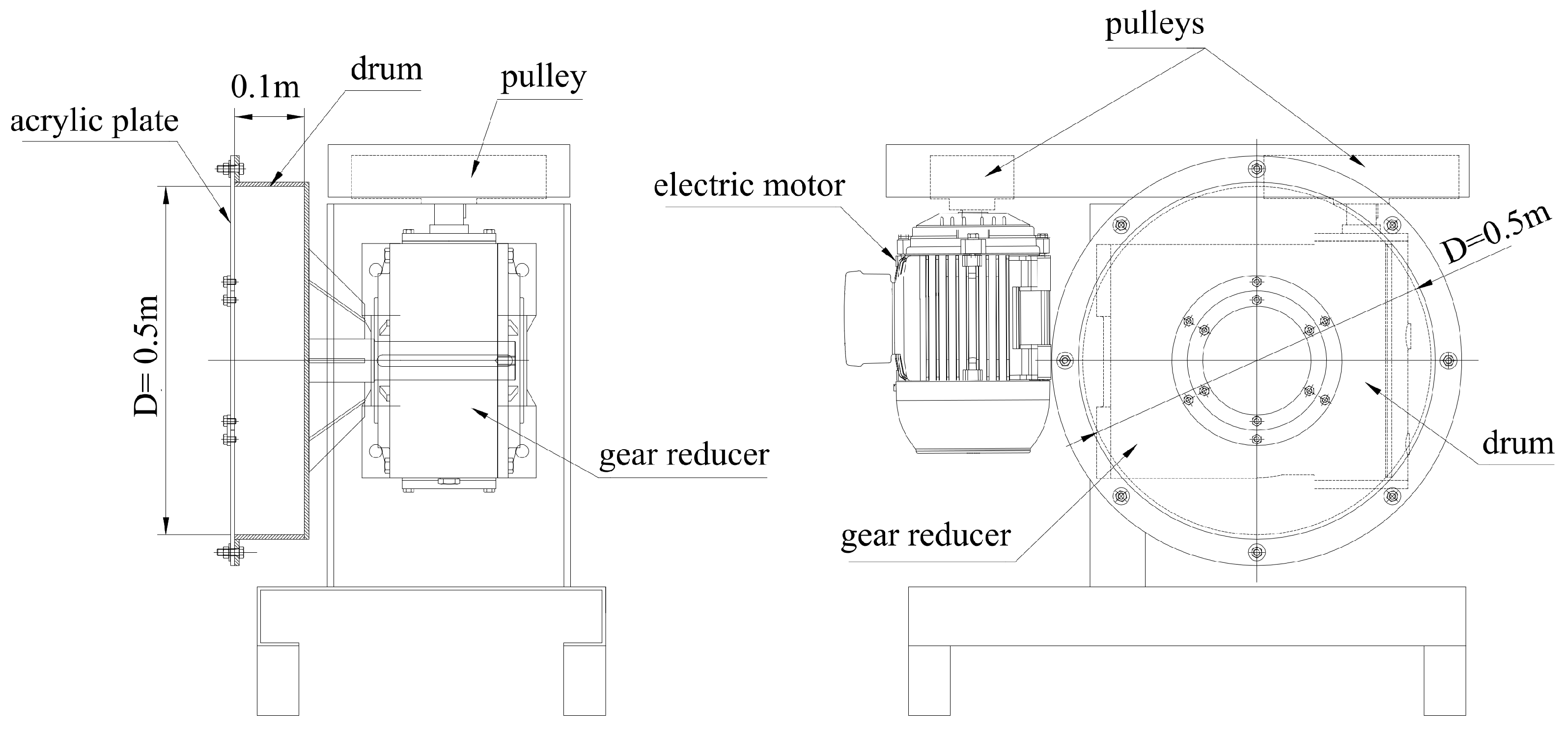
2. Experimental Setup
3. Computational Approach
3.1. Continuum Model (CM)
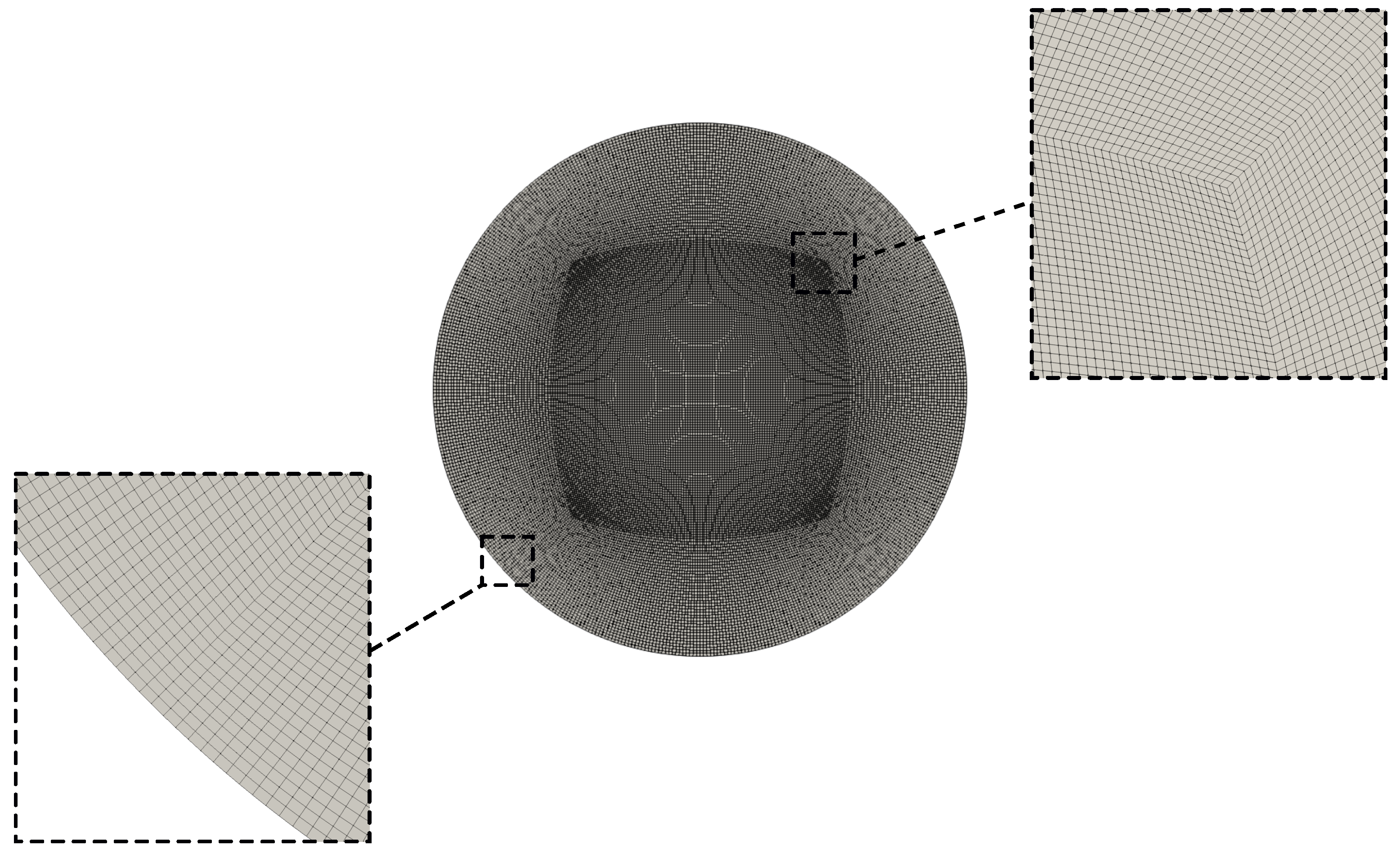
3.2. Discrete Elements Method (DEM)
3.3. Test Cases
4. Results
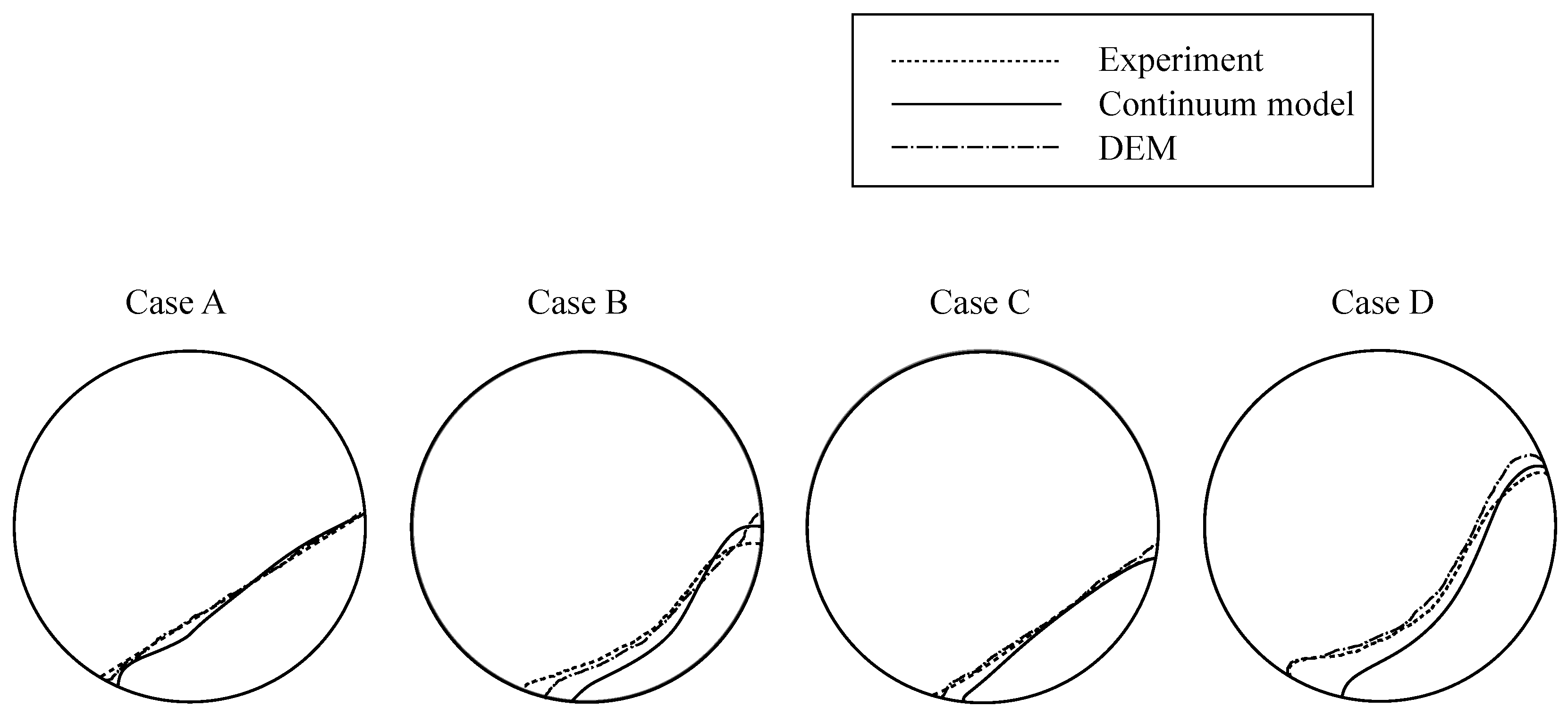
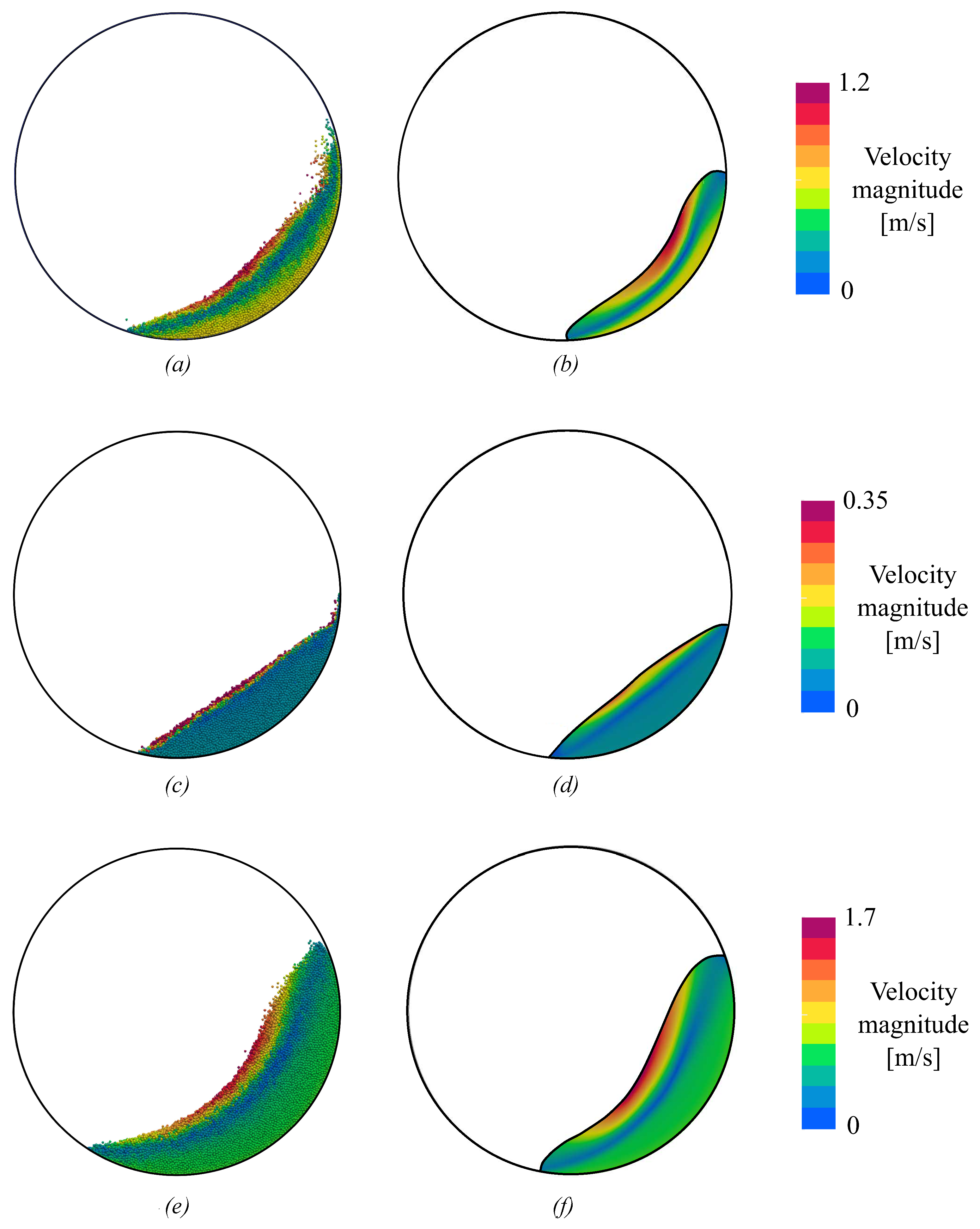
4.1. Particles Distribution
4.2. Velocity Distribution
4.3. Mixing Patterns
5. Conclusions
- The solids distribution for each regime was correctly predicted with both techniques, except for the slumping regime, which could not be captured by the CM approach. This was attributed to the use of a high-viscosity threshold instead of a yield criterion in the implementation of the rheology model. In the fastest regimes, DEM predicted more splashing of particles than the experimental observations;
- The velocity of the particles predicted by the models was mostly in agreement with the experimental results. Neither of the computational models stood out over the other in this regard as both tend to detach more from the experimental observations where the material flow backwards relative to the rotation of the drum;
- The rate of mixing of two different materials in a cascading regime was well predicted by both models, reaching a fairly similar level of mixing at different instants in time. While the DEM results were in very good agreement with the experiments, the CM predicted a slower dragging of the material as the system was accelerated but reaching similar steady-state profiles of the interface between the bed of particles and the air. This drawback might be attributed to the lack of non-local effects and a yield criterion that reign over the inertial regime at slow speeds;
- In the rolling regime, CM saved around 20% of computational time compared to DEM, both with an optimized set of numerical parameters. This suggests that, when the dimensions of the problem shifted from pilot-plant to industrial-scale, CM might still be suitable while the computational costs of DEM might become prohibitive.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Henein, H.; Brimacombe, J.; Watkinson, A. Experimental study of transverse bed motion in rotary kilns. Metall. Trans. B 1983, 14, 191–205. [Google Scholar] [CrossRef]
- Henein, H.; Brimacombe, J.; Watkinson, A. The modeling of transverse solids motion in rotary kilns. Metall. Trans. B 1983, 14, 207–220. [Google Scholar] [CrossRef]
- Mellmann, J. The transverse motion of solids in rotating cylinders—Forms of motion and transition behavior. Powder Technol. 2001, 118, 251–270. [Google Scholar] [CrossRef]
- Ding, Y.; Forster, R.; Seville, J.; Parker, D. Segregation of granular flow in the transverse plane of a rolling mode rotating drum. Int. J. Multiph. Flow 2002, 28, 635–663. [Google Scholar] [CrossRef]
- Aissa, A.A.; Duchesne, C.; Rodrigue, D. Effect of friction coefficient and density on mixing particles in the rolling regime. Powder Technol. 2011, 212, 340–347. [Google Scholar] [CrossRef]
- Liu, X.Y.; Specht, E.; Mellmann, J. Experimental study of the lower and upper angles of repose of granular materials in rotating drums. Powder Technol. 2005, 154, 125–131. [Google Scholar] [CrossRef]
- Chou, S.; Hsiau, S. Dynamic properties of immersed granular matter in different flow regimes in a rotating drum. Powder Technol. 2012, 226, 99–106. [Google Scholar] [CrossRef]
- Huang, A.; Kuo, H. A study on the transition between neighbouring drum segregated bands and its application to functionally graded material production. Powder Technol. 2011, 212, 348–353. [Google Scholar] [CrossRef]
- Orpe, A.V.; Khakhar, D. Scaling relations for granular flow in quasi-two-dimensional rotating cylinders. Phys. Rev. E 2001, 64, 031302. [Google Scholar] [CrossRef]
- Santos, D.A.; Barrozo, M.A.; Duarte, C.R.; Weigler, F.; Mellmann, J. Investigation of particle dynamics in a rotary drum by means of experiments and numerical simulations using DEM. Adv. Powder Technol. 2016, 27, 692–703. [Google Scholar] [CrossRef]
- Santos, D.A.; Dadalto, F.O.; Scatena, R.; Duarte, C.R.; Barrozo, M.A. A hydrodynamic analysis of a rotating drum operating in the rolling regime. Chem. Eng. Res. Des. 2015, 94, 204–212. [Google Scholar] [CrossRef]
- Marigo, M.; Cairns, D.; Davies, M.; Ingram, A.; Stitt, E. A numerical comparison of mixing efficiencies of solids in a cylindrical vessel subject to a range of motions. Powder Technol. 2012, 217, 540–547. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, C.; Zhou, Z.; Du, J.; Hu, D. 2D DEM simulation of particle mixing in rotating drum: A parametric study. Particuology 2010, 8, 141–149. [Google Scholar] [CrossRef]
- Liu, P.; Yang, R.; Yu, A. DEM study of the transverse mixing of wet particles in rotating drums. Chem. Eng. Sci. 2013, 86, 99–107. [Google Scholar] [CrossRef]
- Watanabe, H. Critical rotation speed for ball-milling. Powder Technol. 1999, 104, 95–99. [Google Scholar] [CrossRef]
- Chand, R.; Khaskheli, M.A.; Qadir, A.; Ge, B.; Shi, Q. Discrete particle simulation of radial segregation in horizontally rotating drum: Effects of drum-length and non-rotating end-plates. Phys. A Stat. Mech. Its Appl. 2012, 391, 4590–4596. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, Z.; Mellmann, J.; Weigler, F.; Herz, F.; Bück, A.; Tsotsas, E. Influence of the number of flights on the dilute phase ratio in flighted rotating drums by PTV measurements and DEM simulations. Particuology 2021, 56, 171–182. [Google Scholar] [CrossRef]
- Huang, A.; Cheng, T.; Hsu, W.; Huang, C.; Kuo, H. DEM study of particle segregation in a rotating drum with internal diameter variations. Powder Technol. 2021, 378, 430–440. [Google Scholar] [CrossRef]
- Harish, V.; Cho, M.; Shim, J. Effect of rotating cylinder on mixing performance in a cylindrical double-ribbon mixer. Appl. Sci. 2019, 9, 5179. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; Yu, A.; McElroy, L.; Bao, J. Numerical simulation of particle dynamics in different flow regimes in a rotating drum. Powder Technol. 2008, 188, 170–177. [Google Scholar] [CrossRef]
- Gan, J.; Zhou, Z.; Yu, A. A GPU-based DEM approach for modeling of particulate systems. Powder Technol. 2016, 301, 1172–1182. [Google Scholar] [CrossRef]
- Lun, C.; Savage, S.B.; Jeffrey, D.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Venier, C.M.; Damian, S.M.; Nigro, N.M. Numerical aspects of Eulerian gas–particles flow formulations. Comput. Fluids 2016, 133, 151–169. [Google Scholar] [CrossRef]
- Venier, C.M.; Marquez Damian, S.; Nigro, N.M. Assessment of gas-particle flow models for pseudo-2D fluidized bed applications. Chem. Eng. Commun. 2018, 205, 456–478. [Google Scholar] [CrossRef]
- Venier, C.M. Resolución Computacional de Flujos Multifásicos Granulares Por Métodos Eulerianos. Ph.D. Thesis, Universidad Nacional del Litoral, Santa Fe, Argentina, 2018. [Google Scholar]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Enwald, H.; Peirano, E.; Almstedt, A.E. Eulerian two-phase flow theory applied to fluidization. Int. J. Multiph. Flow 1996, 22, 21–66. [Google Scholar] [CrossRef]
- Taghipour, F.; Ellis, N.; Wong, C. Experimental and computational study of gas–solid fluidized bed hydrodynamics. Chem. Eng. Sci. 2005, 60, 6857–6867. [Google Scholar] [CrossRef]
- Loha, C.; Chattopadhyay, H.; Chatterjee, P.K. Assessment of drag models in simulating bubbling fluidized bed hydrodynamics. Chem. Eng. Sci. 2012, 75, 400–407. [Google Scholar] [CrossRef]
- Makkawi, Y.T.; Wright, P.C.; Ocone, R. The effect of friction and inter-particle cohesive forces on the hydrodynamics of gas–solid flow: A comparative analysis of theoretical predictions and experiments. Powder Technol. 2006, 163, 69–79. [Google Scholar] [CrossRef]
- Passalacqua, A.; Fox, R.O. Implementation of an iterative solution procedure for multi-fluid gas–particle flow models on unstructured grids. Powder Technol. 2011, 213, 174–187. [Google Scholar] [CrossRef]
- Patil, D.; van Sint Annaland, M.; Kuipers, J. Critical comparison of hydrodynamic models for gas–solid fluidized beds—Part I: Bubbling gas–solid fluidized beds operated with a jet. Chem. Eng. Sci. 2005, 60, 57–72. [Google Scholar] [CrossRef]
- Patil, D.; van Sint Annaland, M.; Kuipers, J. Critical comparison of hydrodynamic models for gas–solid fluidized beds—Part II: Freely bubbling gas–solid fluidized beds. Chem. Eng. Sci. 2005, 60, 73–84. [Google Scholar] [CrossRef]
- Santos, D.; Duarte, C.; Barrozo, M. Segregation phenomenon in a rotary drum: Experimental study and CFD simulation. Powder Technol. 2016, 294, 1–10. [Google Scholar] [CrossRef]
- Rong, W.; Feng, Y.; Schwarz, P.; Witt, P.; Li, B.; Song, T.; Zhou, J. Numerical study of the solid flow behavior in a rotating drum based on a multiphase CFD model accounting for solid frictional viscosity and wall friction. Powder Technol. 2020, 361, 87–98. [Google Scholar] [CrossRef]
- Rong, W.; Li, B.; Feng, Y.; Schwarz, P.; Witt, P.; Qi, F. Numerical analysis of size-induced particle segregation in rotating drums based on Eulerian continuum approach. Powder Technol. 2020, 376, 80–92. [Google Scholar] [CrossRef]
- Machado, M.; Nascimento, S.; Duarte, C.; Barrozo, M. Boundary conditions effects on the particle dynamic flow in a rotary drum with a single flight. Powder Technol. 2017, 311, 341–349. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, M.; Liu, H. Numerical simulation of three-dimensional unsteady granular flows in rotary kiln. Powder Technol. 2014, 253, 138–145. [Google Scholar] [CrossRef]
- Schaeffer, D.G. Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 1987, 66, 19–50. [Google Scholar] [CrossRef] [Green Version]
- Johnson, P.C.; Jackson, R. Frictional–collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech 1987, 176, 67–93. [Google Scholar] [CrossRef]
- Jop, P.; Forterre, Y.; Pouliquen, O. A constitutive law for dense granular flows. Nature 2006, 441, 727–730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Da Cruz, F.; Emam, S.; Prochnow, M.; Roux, J.N.; Chevoir, F. Rheophysics of dense granular materials: Discrete simulation of plane shear flows. Phys. Rev. E 2005, 72, 021309. [Google Scholar] [CrossRef] [Green Version]
- GDR MiDi. On dense granular flows. Eur. Phys. J. 2004, 14, 341–365. [Google Scholar]
- De Monaco, G.; Greco, F.; Maffettone, P. Flow of Dry Grains Inside Rotating Drums. In Challenges in Mechanics of Time-Dependent Materials, Volume 2; Springer: Berlin, Germany, 2015; pp. 121–129. [Google Scholar]
- Arseni, A.M.; De Monaco, G.; Greco, F.; Maffettone, P.L. Granular flow in rotating drums through simulations adopting a continuum constitutive equation. Phys. Fluids 2020, 32, 093305. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Márquez Damián, S.; Nigro, N.M. An extended mixture model for the simultaneous treatment of small-scale and large-scale interfaces. Int. J. Numer. Methods Fluids 2014, 75, 547–574. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD-DEM. Prog. Comput. Fluid Dyn. An Int. J. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Forterre, Y.; Pouliquen, O. Flows of dense granular media. Annu. Rev. Fluid Mech. 2008, 40, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Kamrin, K. Nonlinear elasto-plastic model for dense granular flow. Int. J. Plast. 2010, 26, 167–188. [Google Scholar] [CrossRef] [Green Version]
- Dunatunga, S.; Kamrin, K. Continuum modeling and simulation of granular flows through their many phases. J. Fluid Mech. 2015, 779, 483–513. [Google Scholar] [CrossRef] [Green Version]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particle in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F. An improved integral non-linear model for the contact of particles in distinct element simulations. Chem. Eng. Sci. 2005, 60, 1303–1312. [Google Scholar] [CrossRef]
- Iwashita, K.; Oda, M. Rolling resistance at contacts in simulation of shear band development by DEM. J. Eng. Mech. 1998, 124, 285–292. [Google Scholar] [CrossRef]
- Iwashita, K.; Oda, M. Micro-Deformation Mechanism of Shear Banding Process Based on Modified Distinct Element Method. Powder Technol. 2000, 2, 192–205. [Google Scholar] [CrossRef]
- Ai, J.; Chen, J.F.; Rotter, J.; Ooi, J. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Jensen, A.; Fraser, K.; Laird, G. Improving the Precision of Discrete Element Simulations through Calibration Models. In Proceedings of the 13 th International LS-DYNA Users Conference, Dearborn, MI, USA, 8–10 June 2014; pp. 1–12. [Google Scholar]
- Zhou, Y.; Wright, B.; Yang, R.; Xu, B.; Yu, A. Rolling friction in the dynamic simulation of sandpile formation. Phys. A Stat. Mech. Its Appl. 1999, 269, 536–553. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, B.; Yu, A.; Zulli, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technol. 2002, 125, 45–54. [Google Scholar] [CrossRef]
- Frankowski, P.; Morgeneyer, M. Calibration and validation of DEM rolling and sliding friction coefficients in angle of repose and shear measurements. AIP Conf. Proc. 2013, 1542, 851. [Google Scholar]
- Henann, D.L.; Kamrin, K. Continuum modeling of secondary rheology in dense granular materials. Phys. Rev. Lett. 2014, 113, 178001. [Google Scholar] [CrossRef] [PubMed] [Green Version]


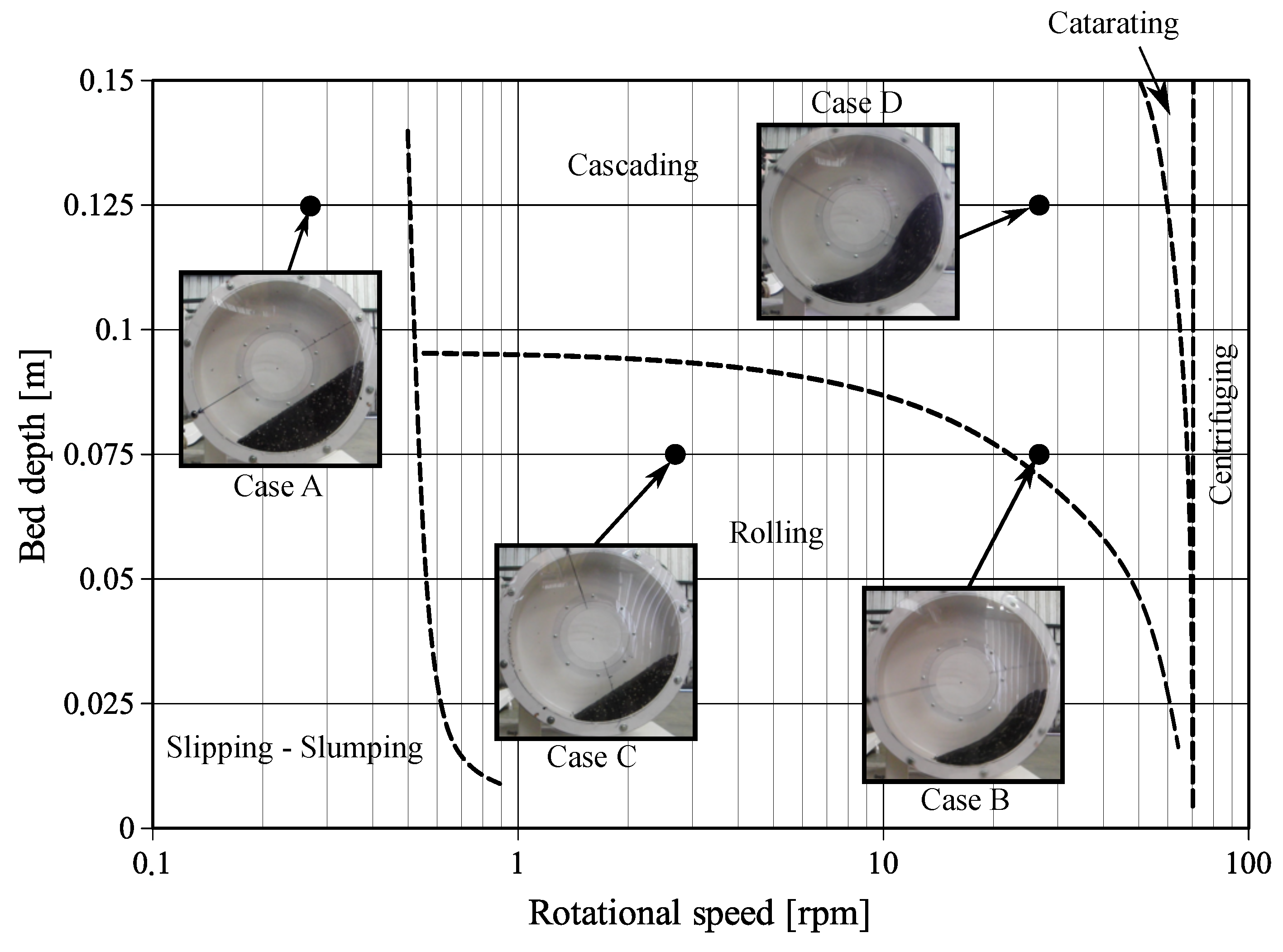




| Case | Bed Depth [m] | Rotational Speed [rpm] | Observed Regime |
|---|---|---|---|
| A | Slumping | ||
| B | 25 | Transitional (Rolling/Cascading) | |
| C | Rolling | ||
| D | 25 | Cascading |
| Property | Value |
|---|---|
| Effective density () | 920 Kg/m |
| Solids density () | 1600 Kg/m |
| Maximum viscosity coefficient () | 0.9 |
| Reference inertial number () | 0.4 |
| Maximum time step () | 2 s |
| SIMPLE iterations | 3 |
| Time discretization | second order implicit |
| Advection schemes | second order linear upwind |
| Volume fraction iterations | 5 |
| Interphase compression factor (cAlpha) | 0.25 |
| Relaxation factor for velocity | 0.7 |
| Relaxation factor for pressure | 0.3 |
| Maximum residuals allowed for each field |
| Property | Value |
|---|---|
| Time step | s |
| Total number of particles | |
| Young modulus | Pa |
| Poisson ratio (p-p, p-w) | |
| Coefficient of restitution (p-p, p-w) | |
| Sliding friction coefficient (p-p) | |
| Sliding friction coefficient (p-w) | |
| Rolling friction coefficient (p-p) | |
| Rolling friction coefficient (p-w) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venier, C.M.; Márquez Damián, S.; Bertone, S.E.; Puccini, G.D.; Risso, J.M.; Nigro, N.M. Discrete and Continuum Approaches for Modeling Solids Motion Inside a Rotating Drum at Different Regimes. Appl. Sci. 2021, 11, 10090. https://doi.org/10.3390/app112110090
Venier CM, Márquez Damián S, Bertone SE, Puccini GD, Risso JM, Nigro NM. Discrete and Continuum Approaches for Modeling Solids Motion Inside a Rotating Drum at Different Regimes. Applied Sciences. 2021; 11(21):10090. https://doi.org/10.3390/app112110090
Chicago/Turabian StyleVenier, César Martín, Santiago Márquez Damián, Sergio Eduardo Bertone, Gabriel Darío Puccini, José María Risso, and Norberto Marcelo Nigro. 2021. "Discrete and Continuum Approaches for Modeling Solids Motion Inside a Rotating Drum at Different Regimes" Applied Sciences 11, no. 21: 10090. https://doi.org/10.3390/app112110090
APA StyleVenier, C. M., Márquez Damián, S., Bertone, S. E., Puccini, G. D., Risso, J. M., & Nigro, N. M. (2021). Discrete and Continuum Approaches for Modeling Solids Motion Inside a Rotating Drum at Different Regimes. Applied Sciences, 11(21), 10090. https://doi.org/10.3390/app112110090







